The origin of uniaxial negative thermal expansion in layered perovskites

Abstract

Why is it that ABO₃ perovskites generally do not exhibit negative thermal expansion (NTE) over a wide temperature range, whereas layered perovskites of the same chemical family often do? It is generally accepted that there are two key ingredients that determine the extent of NTE: the presence of soft phonon modes that drive contraction (have negative Grüneisen parameters); and anisotropic elastic compliance that predisposes the material to the deformations required for NTE along a specific axis. This difference in thermal expansion properties is surprising since both ABO₃ and layered perovskites often possess these ingredients in equal measure in their high-symmetry phases. Using first principles calculations and symmetry analysis, we show that in layered perovskites there is a significant enhancement of elastic anisotropy due to symmetry breaking that results from the combined effect of layering and condensed rotations of oxygen octahedra. This feature, unique to layered perovskites of certain symmetry, is what allows uniaxial NTE to persist over a large temperature range. This fundamental insight means that symmetry and the elastic tensor can be used as descriptors in high-throughput screening and to direct materials design.

Introduction

Due to their unusual lattice couplings and dynamics, there has been renewed recent interest in tuning the properties of layered materials based on the perovskite structure, including proper,^1,2 and improper,^3,4,5 ferroelectricity, the electrocaloric effect,⁶ and colossal magnetoresistance.⁷ Unprecedented control of ferroelectricity in layered perovskites has been achieved, for example, by engineering non-polar lattice instabilities that can combine in the ground state to produce a net polarisation. This approach to designing improper ferroelectrics has been particularly successful when the property in question arises solely from the ground state structure, rather than any lattice or spin dynamics, and the relevant lattice couplings can be elucidated from symmetry analysis and static first principles calculations,^3,4 However, many of the physical properties listed above rely on excitations of the ground state structure and are mediated by phonon interactions and electron–phonon couplings. We seek here to understand one of the most obvious consequences of phonon couplings, namely thermal expansion, and how it may be tuned in layered perovskites to achieve zero or even negative thermal expansion (NTE).

While elastically soft organometallic framework materials exhibiting NTE are becoming increasingly common, the number of elastically hard ionic solids exhibiting this property remains few. The prototypical NTE ceramic is zirconium tungstate (ZrW₂O₈) which displays a large, isotropic NTE of −9 p.p.m./K over a wide temperature range of 0.3–1050 K.⁸ Since the discovery of NTE in ZrW₂O₈, a small number of NTE materials have been identified, such as LiAlSiO₄,⁹ (Zn,Cd)(CN)₂,^10,11,12 and Mn₃(Co(CN)₆)₂,¹³ which all possess flexible network structures.¹⁴ In many of these materials, NTE has been explained using the theory of rigid unit modes (RUMs)¹⁵ whereby the contraction of the material is driven by soft vibrations of approximately rigid polyhedral units. With increasing temperature, the amplitudes of these vibrations increase and all units are drawn closer together through an effect known as the tension mechanism.¹⁶ Active modes that drive NTE have negative Grüneisen parameters γ, which quantify how mode frequencies change with cell volume and, thereby, the contribution of each mode to the overall thermal expansion or contraction.

Surprisingly, although bulk ABO₃ perovskites are often proposed as a textbook example of a material containing a large number of RUMs, NTE over a significant temperature range in these systems where octahedral rotations are the dominant mechanism is extremely rare. Conversely, we have recently highlighted the occurrence of uniaxial NTE in layered perovskite Ruddlesden–Popper (RP) oxides, A _n+1B _n X_3n+1. NTE in the n = 2 (RP2) system, for example, appears to be linked to not just a particular space group symmetry (Acaa), but also proximity to a thermodynamically competing phase of specific symmetry.¹⁷ This understanding allowed us to tune the chemistry of the RP2 solid solution Ca_3−3x Sr_3x Mn₂O₇ in the phase diagram space to precisely control its NTE.¹⁸ Very recently NTE has also been reported in the n = 1 (RP1) compound Sr₂RhO₄.¹⁹ Examination of the literature reveals that Ca₂MnO₄,²⁰ Sr₂RhO₄ ²¹ and Sr₂IrO₄,²² which all crystallise in an equivalent I4₁/acd phase and exhibit evidence of uniaxial NTE (although the significance of this is not commented on). While NTE in Sr₂RhO₄ and Ca₂MnO₄ has been ascribed to static changes in octahedral rotation angle¹⁹ our explanation for NTE in the RP2 phase directly implicates specific soft phonon modes of RUM- like character with negative Grüneisen parameters. This understanding from prior publications leaves us with the question: (i) If NTE originates from octahedral rotations of RUM character, why is similar NTE not observed in equivalent bulk ABO ₃ perovskite phases? Further to this, if phonons are soft and active in child NTE RP phases and given that the symmetry-breaking structural distortions are so small, it is not obvious why these same phonons should not be soft and drive NTE in the parent phase, and yet NTE has only been previously reported in RP phases with condensed rotations. This leads to a second question: (ii) Why can small changes in symmetry have a large effect upon the sign and magnitude of thermal expansion?

To answer these questions, we begin by studying the RP oxide A _n+1B _n O_3n+1 with n = 1 (Fig. 1a), which is the most structurally distinct phase from the perovskite (i.e., n = ∞). We find that while phonon modes with negative Grüneisen parameters associated with a phase competition between an NTE and PTE phase are important, crucially, it is the large off-diagonal elastic constant elements particular to the NTE phase that enhances NTE. These off-diagonal elements have the effect of cross-coupling PTE in the biaxial direction to NTE in the uniaxial direction, and only by considering these off-diagonal elements can the NTE observed experimentally be reproduced by first principles calculations over the whole temperature range. We show that the switching on and off of large off-diagonal elements in the elastic constant tensor at a symmetry changing phase transition not only explains the pronounced NTE in phases of these RP materials with frozen octahedral rotations, but is a general feature of a large number of other related layered perovskites. We show through symmetry arguments that the combined symmetry-breaking from the layering and condensed octahedral distortions gives rise to the strong strain coupling responsible for the large elastic anisotropy. As elastic tensors are more readily calculated than phonons and Grüneisen parameters, we suggest that this is a productive route for computational screening and data mining of NTE materials.

Fig. 1

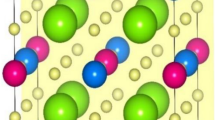
a The octahedral rotation and tilting of the n = 1 Ruddlesden–Popper (RP1) Ca₂GeO₄ structure (Ca = green, Ge = grey, O = red). b Δc/c ₀ against temperature for: calculated equilibrium Ca₂GeO₄ structures (under 4.3 GPa biaxial stress) within the quasi-harmonic approximation (QHA) and neutron diffraction data for Ca₂MnO₄. QHA and experimental Δθ and Δa/a ₀ against temperature (inset). c Elements of the elastic compliance matrix, s _pq , bulk compressibility, β, and lowest-frequency Γ-point phonons compared between the fully relaxed Ca₂MnO₄ I4₁/acd phase and I4₁/acd Ca₂GeO₄ under 4.3 GPa biaxial stress. Ca₂MnO₄ phonons are paired with the Ca₂GeO₄ mode to which their eigenvectors have the greatest overlap. Γ-point I4₁/acd modes are labelled if they are non-orthogonal to an irrep in the I4/mmm basis corresponding to an unstable I4/mmm mode, or else coloured grey

Results

Our calculations (Fig. 1b) performed within the quasi-harmonic approximation (QHA) on Ca₂GeO₄ show uniaxial NTE over the full simulated temperature range with close agreement of the c lattice strain to neutron diffraction measurements of Ca₂MnO₄, especially at low temperatures. We simulated Ge in place of Mn for computational ease because Ge⁴⁺ and Mn⁴⁺ are known to have equal ionic radii²³ and spin-polarised calculations on Mn-based systems were extremely expensive, making lattice dynamics calculations over the full Brillouin zone for multiple structures unfeasible. Fig. 1c shows that the elastic compliances and lowest-frequency Γ-point phonons have very close agreement between equivalent phases of Ca₂MnO₄ and Ca₂GeO₄. We also point out that the softest phonon modes retain the same eigenvector character between the different structures since this was used as a criterion to match them. The Ca₂GeO₄ phase was simulated with a 4.3 GPa biaxial pressure to fix the in-plane lattice parameter to that of relaxed Ca₂MnO₄—see Methods section for details.

Simulations predict a maximum negative coefficient of linear thermal expansion (CLTE) along the c axis, α ₃, of −4.7 p.p.m./K compared to −6 p.p.m./K in experiment. There is close agreement between predicted and observed changes in a and the frozen octahedral rotation angle θ, which was extracted from Rietveld refinements performed against neutron powder diffraction data. The small disparity between simulation and experiment, which becomes greater at higher temperatures, is likely the result of higher-order anharmonic interactions that are not included in the QHA.

In a tetragonal material, a useful measure for thermal expansion is the anisotropic mode Grüneisen parameter, $\gamma _q^i$, describing the change in frequency, ω ⁱ, of phonon i with changing cell axis q with all other axes fixed:

$$\gamma _q^i = - \frac{q}{{{\omega ^i}}}\left( {\frac{{\partial {\omega ^i}}}{{\partial q}}} \right) = - \frac{{\partial \,{\rm{ln}}\left( {{\omega ^i}} \right)}}{{\partial \,{\rm{ln}}\left( q \right)}},$$

(1)

the subscript, q = (1, 2, 3), corresponds to the directions of the (a, b, c) unit cell vectors, respectively.

Analysis of the phonon density of states (PDOS) (Fig. 2) of an example structure on the QHA grid (close to the minimum of the enthalpy landscape), shows a number of low frequency Γ-point phonons with negative Grüneisen parameters, γ ₃, corresponding to irreducible representations (irreps) with octahedral tilt character. When projected onto an I4/mmm basis (Wyckoff Positions: Ge:(0, 0, 0), Ca:(0, 0, 0.64554), O:(0, 0.5, 0), O:(0, 0, 0.16268)), these modes overlap strongly with $X_3^ +$ and P ₅ irreps, which lie on the same phonon branches. In the unstressed Ca₂GeO₄, the softest mode $\left( {X_3^ + } \right)$ is unstable and allowing the structure to fully relax with this mode condensed leads to a lower symmetry Pbca child structure with Δc = −0.47 Å, thereby indicating in static calculations that the $X_3^ +$ tilt reduces c. This phase competition is reminiscent of that which we identify as driving the NTE in the RP2 phase where the magnitude of NTE measured experimentally in Ca_3−x Sr _x Mn₂O₇ correlated with the computed imaginary frequency of an unstable octahedral tilt mode.¹⁸

Fig. 2

Grüneisen parameters along a, γ ₁(ω); and c, γ ₃(ω), computed for Γ-point phonons; and full PDOS, g(ω). Γ-point I4₁/acd modes are labelled if they are non-orthogonal to an irrep in the I4/mmm basis corresponding to an unstable I4/mmm phonon. Calculated about an I4₁/acd Ca₂GeO₄ structure with a = 5.129 Å and c = 24.321 Å

Unlike in isotropic materials, in tetragonal structures the CLTE is dependent upon the effects of phonon modes upon both independent cell axes. Considering the tetragonal cell to retain shape (assuming no shearing) the CLTEs along the a and c axes are:²⁴

$${\alpha _1}\left( T \right) = \mathop {\sum}\limits_i C_v^{{\kern 1pt} i}\left( T \right)\left[ {\left( {{s_{11}} + {s_{12}}} \right)\gamma _1^{{\kern 1pt} i} + {s_{13}}{\kern 1pt} \gamma _3^{{\kern 1pt} i}} \right]$$

(2a)

$${\alpha _3}\left( T \right) = \mathop {\sum}\limits_i C_v^{{\kern 1pt} i}\left( T \right)\left[ {2{s_{13}}{\kern 1pt} \gamma _1^{{\kern 1pt} i} + {s_{33}}{\kern 1pt} \gamma _3^{{\kern 1pt} i}} \right]$$

(2b)

In Eqs. (2a) and (2b), $C_v^{{\kern 1pt} i}\left( T \right)$ is the contribution of mode i to the specific heat capacity at temperature T. s _pq is a component of a 3 × 3 matrix s and represents the normal elastic compliance of axis p in response to the normal strain of axis q. s is, in principle, temperature dependent (although ignored in this work). We must stress that the compliance matrix s is not the same as the elastic compliance tensor, which is rank-4 since it relates stress and strain, both rank-2 quantities. Use of the 3 × 3 matrix s relies on all shear stresses and strains being equal to 0 (enforcing at least orthorhombic symmetry) and therefore using 3-dimensional vectors within Voigt notation.

For clarity of discussion we generalise Eqs. (2a) and (2b) to the orthorhombic case (still ignoring shear strains):

$${\alpha _p}\left( T \right) = \mathop {\sum}\limits_q {s_{pq}}\left\{ {\mathop {\sum}\limits_i C_v^{{\kern 1pt} i}\left( T \right)\gamma _q^{{\kern 1pt} i}} \right\} = \mathop {\sum}\limits_q {s_{pq}}{\Phi _q}\left( T \right),$$

(3)

where α _p (T) and Φ _q (T) are respectively components of α(T), the thermal expansion vector and Φ(T), a vector representing the dynamic driving force for thermal expansion from all modes. Equation (3) shows that α(T) is given by the action of the matrix of elastic compliances s on the vector Φ(T). The direction of α(T) is thus dependent upon both the anisotropic thermodynamic driving force for thermal expansion and the elastic coupling between axes. In a material with largely decoupled axes (small off-diagonal s _pq components) the direction of α(T) would track Φ(T). However, in an anisotropic material where off-diagonal components s _pq are large, α(T) may be rotated by the compliance tensor in the plane of a and c normal lattice strains towards a region corresponding to enhanced NTE (as illustrated in Fig. 3a).

Fig. 3

a Illustration of how a vector (in the space of a and c strains) representing the dynamic driving force, Φ, is transformed by a matrix of compliances, s, for a tetragonal material to give the thermal expansion α. b α ₁(T) and c α ₃(T) for Ca₂MnO₄ fitted neutron data (blue) and Ca₂GeO₄ QHA simulations (solid red). As a computational thought experiment, α _struc (T) for other structures predicted in coloured dashed lines (see legend) by transforming the ${{\bf{\Phi }}_{{\rm{I}}{{\rm{4}}_{{\rm{1/acd}}}}}}\left( T \right)$, from the Ca₂GeO₄ QHA calculation by s for each structure

Figure 3b, c display the α ₁(T) and α ₃(T) CLTEs, computed by numerical derivative with respect to T, for the Ca₂GeO₄ QHA data and fitted Ca₂MnO₄ neutron data shown Fig. 1b. The dynamic contribution to thermal expansion, ${{\bf{\Phi }}_{{\rm{I}}{{\rm{4}}_{{\rm{1/acd}}}}}}\left( T \right)$ is extracted from α(T) for the Ca₂GeO₄ QHA calculation by transforming α(T) by ${\boldsymbol{s}}_{{\rm{I}}{{\rm{4}}_{{\rm{1/acd}}}}}^{ - 1}$ (that is to say by inverting Eq. (3)).

To highlight the importance of the elastic compliance matrix to thermal expansion, we may perform a computational thought experiment whereby we predict the α(T) that would arise if the same phonons were present in different related structures. α(T) for other structures is predicted by transforming ${{\bf{\Phi }}_{{\rm{I}}{{\rm{4}}_{{\rm{1/acd}}}}}}\left( T \right)$ by s of that phase; thereby assuming that these structures have the same dynamic phonons as I4₁/acd Ca₂GeO₄ and that only the elastic constants have changed. Although qualitatively we may expect related structures to have similar lattice dynamics, it would be nïave to assume that Φ(T) could be transferred directly between materials to quantitatively predict thermal expansion. Instead this experiment allows us to isolate the effects of different s matrices on α(T).

We first imagine a fictitious isotropic structure with no coupling between different lattice directions (i.e., s ₁₃ = s ₁₂ = 0). We then fix s ₁₁ = s ₃₃ = β, the bulk compressibility (the reciprocal of the Reuss bulk modulus) of I4₁/acd Ca₂GeO₄, and transform Φ(T) as in Eq. (3). NTE is predicted along c only up to 20 K, above which there is PTE. Figure 2 showed that at frequencies, ω ⁱ > 150 cm⁻¹, modes which form a large weight of the overall PDOS have small $\gamma _3^i >0$. As these modes populate with increasing T, they outweigh the contribution from the few soft $\gamma _3^i < 0$ tilts. Whereas along c slight NTE and later moderate PTE are predicted, large PTE along a is predicted at all but the lowest temperatures. This gives an indication of the thermal expansion which would be predicted if there was no effect from I4₁/acd Ca₂GeO₄’s elastic constants.

Applying now to Φ(T) the compliance matrices, s, computed from density functional theory (DFT) for various Ca _n+1Ge _n O_3n+1 structures, Fig. 3c predicts NTE over a larger temperature range using every s. This shows that the large Φ component along the a axis is transformed to give NTE along c via the s ₁₃ off-diagonal terms. As expected, the s of I4₁/acd Ca₂GeO₄ predicts the most negative α ₃. On the other hand, taking the s of bulk perovskite CaGeO₃ results in NTE of almost an order of magnitude less and only at much lower T. Perhaps more surprisingly, the I4/mmm Ca₂GeO₄ compliance matrix too predicts NTE over a much narrower temperature range and with a reduced magnitude, despite having a similar structure to I4₁/acd with only a slight difference in the phase symmetry.

To understand how small changes in symmetry can lead to a large change in thermal expansion behaviour, the compliance matrices s are plotted in Fig. 4a–d as quadratic forms projected on the 2-dimensional plane of tetragonal deformations. The principal directions (eigenvectors) associated with the highest, s _H, and lowest, s _L, principal components of s are also plotted and labelled by the corresponding principal values. I4₁/acd Ca₂GeO₄ (Fig. 4d) has a strongly anisotropic s with the eigenvector corresponding to s _H lying in a strain direction that corresponds to cooperative expansion of a and contraction of c. Although other structures have their most compliant eigenvector in a similar direction, it is clear from the eigenvalue s _H that this direction is particularly compliant in I4₁/acd Ca₂GeO₄, despite s _L and the bulk compressibility, β, being similar to I4/mmm Ca₂GeO₄. Values of s _H and β are presented alongside experimental CLTE measurements for NTE phases for all structures discussed in Table 1.

Fig. 4

Matrix, s, displayed in quadratic form in the $\left( {1\bar 10} \right)$ plane of tetragonal deformations for CaGeO₃ and Ca₂GeO₄ structures, with eigenvectors labelled with corresponding eigenvalues (TPa⁻¹) for a $Pm\bar{3}m$ CaGeO₃ b I4/mcm CaGeO₃ c I4/mmm Ca₂GeO₄ d I4 ₁/acd Ca₂GeO₄

Table 1 Bulk compressibility, β, and most compliant eigenvalue, s _H, tabulated for all phases alongside κ, the anisotropy ratio (κ = s _H /s _L ) and experimental α of NTE phase, with measurement temperature ranges in K given in brackets

The link between compliant cooperative deformations and uniaxial NTE may be extended to other layered perovskite systems. Within the RP family, the Acaa phase in the n = 2 series also shows NTE experimentally,^17,18 and interestingly consists of an analogous frozen octahedral rotation as in the n = 1 I4₁/acd. We find that Ca₃Ge₂O₇ possesses a similarly compliant eigenvector to Ca₂GeO₄ when compared to its parent I4/mmm structure. It should be noted that the unrelated ferroelectric Cmc2₁ phase of Ca₃Ti₂O₇ has also been predicted to show NTE when under sufficient pressure,²⁵ but is beyond the scope of the current study. Considering two more layered perovskite families with related uniaxial NTE: the tetragonal I4/m phase of the double perovskite Sr₂MgWO₆ (NTE along the c axis between 15–300 K²⁶) and the orthorhombic Cmc2₁ phase of LaTaO₄, belonging to the n = 2 member of the A _n B _n O_{3n +2} family, (NTE along the b axis normal to the layering 373–573 K²⁷), we again find more compliant s _H eigenvalues as compared to higher symmetry parent phases of the same structure, $Fm\bar 3m$ Sr₂MgWO₆ and Cmcm LaTaO₄, respectively. Structural data of all relaxed structures may be found in Table S1 and the full elastic compliance matrices and eigenvectors in Table S2.

Discussion

Uniaxial NTE predicted in I4₁/acd Ca₂GeO₄ arises due to soft phonon modes with octahedral tilt character that have γ ₁ > 0 and γ ₃ < 0 which drive the contraction of the c axis with increasing T, as a result of the large s ₁₃ components in the elastic compliance matrix. Equations (2a) and (2b) imply that a thermodynamic driving force is essential for NTE, and the Grüneisen parameters computed for Γ-point phonons in Fig. 2 suggest that the softest modes provide this. The importance of anisotropic elasticity becomes evident in Fig. 3c where we see that if the same lattice dynamics coexisted with an elastic compliance matrix other than that for I4₁/acd Ca₂GeO₄, then uniaxial NTE would not be predicted over such a wide temperature range. The range and magnitude of NTE is highly-dependent upon the level of coupling between the a and c axes. That our results show good quantitative agreement with experimental measurements of analogous Ca₂MnO₄ suggests that at low temperatures, the QHA captures most of the physics required to understand NTE in these materials.

The result that an anisotropic elastic compliance matrix is important for uniaxial NTE echoes theories first suggested many decades ago but with little atomic-level analysis. Equations (2a) and (2b), as originally formulated by Grüneisen and Goens²⁸ utilise off-diagonal components to s and Munn²⁹ used these equations to compare the thermodynamic and elastic driving force for anisotropic thermal expansion in elemental materials based upon experimental observation. More recently, anisotropic NTE has been reported in metal-organic framework structures (MOFs),^30,31 In these materials with large open pores, which are typified by Ag₃[Co(CN)₆] cyanide “wine-rack structures”, large off-diagonal elements in the elastic compliance matrix seem to be responsible both for the observed NTE and the observed negative linear compressibility under hydrostatic pressure.³² DFT calculations³³ of Ag₃[Co(CN)₆] uncover atomic vibrations with highly anisotropic Grüneisen parameters and a large value of s ₁₃ leading to a massive compliance eigenvalue, s _H, of 79 TPa⁻¹ in a uniaxial NTE direction. Although anisotropy has been linked to NTE in these MOF materials and an atomistic explanation for the elastic anisotropy has been found, these MOFs are structurally very different to the ionic compounds of the present investigation.

As well as discovering the origin of uniaxial NTE in Ca₂MnO₄, this study set out to answer two more fundamental questions: (i) If NTE originates from octahedral rotations of RUM character, why is similar NTE not observed in equivalent bulk ABO ₃ perovskite phases? and also (ii) Why can small changes in symmetry have a large effect upon the sign and magnitude of thermal expansion?

It appears that the answer to both of these questions is: because the layered NTE phase is more elastically anisotropic. Considering the Ca _n+1Ge _n O_3n+1 and Sr₂MgWO₆ systems in Table 1, we see that the bulk compressibility, β, between all high- and low-symmetry structures are very similar. Furthermore the anisotropy ratio, κ, of the compliance matrix remains approximately constant across these high-symmetry phases. The effect of the phase transition in all systems therefore is to enhance the value of κ and in fact the measure of anisotropy in the NTE phase correlates with the magnitude of NTE measured experimentally. The low-symmetry RP phases (that experimentally exhibit NTE) similarly have increased values of κ compared to the equivalent CaGeO₃ phase. Although structurally a very different system, an enhancement in κ is also simulated in LaTaO₄ across the transition between high- and low-symmetry structures and this system has both the largest calculated elastic anisotropy and the largest reported uniaxial NTE. That such a drastic change in elastic anisotropy accompanies phase transitions between a high-symmetry parent and a uniaxial NTE child phase has not been discussed previously to the best of our knowledge.

This correlation between uniaxial NTE in certain low-symmetry layered perovskite phases and anisotropic compliance is supported by the computational experiment performed in Fig. 3b, c on the Ca₂GeO₄ system. Even if the same octahedral tilts were active in the parent I4/mmm phase as in I4₁/acd Ca₂GeO₄, or in the analogous I4/mcm CaGeO₃ phase (characterised like I4₁/acd Ca₂GeO₄ by a frozen anti-phase rotation about c), in both phases NTE is predicted over a more narrow temperature range than if the I4₁/acd Ca₂GeO₄ compliance matrix were used.

For an explanation of why certain layered perovskite systems have greater elastic anisotropy, we need to consider the atomic structure at the layer interface. All of the NTE structures investigated have at least two internal degrees of atomic structural freedom: one from the atoms involved in the layering along the axis perpendicular to the layers (the NTE axis) and another from symmetry breaking due to a frozen octahedral rotation—which allows movement along at least one other axis (a PTE axis). Therefore if these degrees of freedom, which are necessarily of the $\Gamma _1^ +$ irrep, can couple to each other and to the strain of the axis along which they exist, then they facilitate a strain–$\Gamma _1^ +$–strain coupling.

This effect is illustrated for an I4₁/acd A₂BO₄ phase in Fig. 5a. As a result of the inherent symmetry-breaking caused by the inclusion of the AO layer, A and apical O ions have a degree of freedom along the c axis. This leads to the rumpling observed in the AO layer of RP phases. Furthermore, due to the frozen octahedral rotation, there is a degree of freedom in the a–b plane, represented by the rotation angle θ. Based upon the calculations of bond stiffness in I4₁/acd Ca₂GeO₄, chemical bonds are labelled as rods or springs depending on their relative stiffness. Assuming rods remain perfectly stiff and only bonds represented as springs may change length, one can picture how a compressive strain Δa could induce a tensile strain Δc: The compression Δa necessarily leads to an increase in rotation angle Δθ which in turn pushes the A cation upwards along c and extends the c-axis by Δc. Since none of these changes are required by symmetry to deform stiff metal–oxygen bonds, these cooperative a and c deformations are low in energy.

Fig. 5

The structure of a the ABO₃/AO interface in the I4₁/acd phase of an A₂BO₄ RP oxide and b the I4/mcm phase of an ABO₃ perovskite. Ions shown as spheres and bonds as rods or springs depending on bond strength. Bond strengths based on data calculated on Ca _n+1Ge _n O_3n+1 systems as shown. Bond extension data for both relaxed systems in response to a Δθ = +1° change in fixed frozen rotation angle is also given and agrees with the computed stiffnesses. Arrows in figures illustrate which bonds would have to deform by symmetry to accommodate a decrease in a and subsequent increase in θ and c. In the high-symmetry I4/mmm Ca₂GeO₄ phase bonds 4 and 5 are of equal stiffness since there is no frozen rotation (for the full table for stiffnesses see Table S3)

This coupling leads to a correlation between a, θ and c reported in prior studies on I4₁/acd A₂BO₄ rotation phases,^19,20,21 which we also observe in both simulation and experiment (inset Fig. 1b). That the system is compliant to coupled changes in a, θ and c explains why θ and c temperature behaviour is correlated but does not imply, as has been previously asserted, that it is a change in θ which causes uniaxial NTE.

In contrast to I4₁/acd A₂BO₄, I4/mcm ABO₃ (Fig. 5b) does not allow the same strong a–$\Gamma _1^ +$–c coupling. Although the frozen anti-phase octahedral rotation does create an in-plane degree of freedom in the rotation angle, there is no internal atomic freedom along c for this to couple to. This is because without the symmetry breaking caused by the rock salt layer, A cations are fixed to c coordinates half way between neighbouring octahedra. There is also no way to strain c without stretching stiff B–O bonds. One might therefore speculate whether an ABO₃ phase with frozen in-plane rotations and tilts along c could exhibit strong a–c coupling and hence anisotropic thermal expansion. The problem would then be that with frozen tilts along the c axis, active tilts become unfavourable and there would be little thermodynamic driving force for NTE. The layering in RP structures thus breaks structural symmetry and creates internal degrees of freedom along the perpendicular axis before any octahedral distortions have condensed.

We do not conclude that uniaxial NTE along c could not occur in an I4/mcm ABO₃ phase; soft octahedral tilts may provide a thermodynamic driving force and an increase in anisotropic elasticity is seen in the transition between $Pm\bar 3m$ and I4/mcm CaGeO₃ (Fig. 4a, b). It merely seems that without the strong a–$\Gamma _1^ +$–c coupling of many layered structures, anisotropic compliance is not as great in I4/mcm ABO₃ as in equivalent layered phases.

Considering now the NTE structures studied from other systems we can find similar symmetry arguments for compliance. Since the RP1 mechanism is specific to the AO/BO₃ interface of an A₂BO₄ structure with a frozen octahedral rotation, it may be easily generalised to A _n+1B _n O_3n+1 phases with a frozen rotation of higher n. I4/m A₂BB’O₆ has a degree of structural freedom in the a–b plane from the frozen octahedral rotation, but, unlike I4/mcm ABO₃, also has a degree of freedom in the apical O positions along the c axis between dissimilar BO₆ and B’O₆ octahedra. Finally, the NTE Cmc2₁ LaTaO₄ phase has a frozen octahedral rotation about a. Further $\Gamma _1^ +$ structural freedom in the b–c plane is achieved as the BO₆ octahedra themselves are distorted to give four different O–B–O angles and A cations are also not constrained to high-symmetry positions along any direction in the b–c plane. This means that combined changes in external and internal octahedral rotation angles allow b to respond to changes in c, or visa versa, without extending any stiff B–O or A–O bonds. Annotated structures illustrating these symmetry arguments may be found in Figs. S1–S3.

Our ceramic systems differ significantly from the MOFs discussed previously,^30,31,32,33 since they are not elastically soft, having bulk moduli that are orders of magnitude harder. Consequently the kind of connectivity required for a wine-rack type mechanism cannot be achieved in these systems. However, we demonstrate here that similar enhancements of off-diagonal elements in the elastic constants may be achieved through the systematic lowering of the symmetry of various layered perovskite structures by the condensation of octahedral rotations. Moreover, despite the reduced connectivity, internal coupling between different degrees of structural freedom creates intricate atomic mechanisms, reminiscent of MOF wine-rack structures, to facilitate high compliance to specific cooperative deformations.

We have explained how the combination of structural distortions, such as layering, and more subtle symmetry breaking distortions, such as the condensation of octahedral rotation modes, can control the elastic compliance matrix in perovskite-like structures. Although major structural distortions are necessarily a feature of material systems, control of subtle symmetry-breaking can have large influences on elasticity and hence on the thermal expansion properties. Figure 3a illustrates schematically how altering s could transform phonon-driven PTE, Φ, into uniaxial NTE, which corresponds to the case studied here at intermediate T. One can imagine alternative interesting scenarios, such as the transformation of phonon-driven bulk PTE into anisotropic volume NTE.

Anisotropic thermal expansion is controlled in a large part by the elastic compliance matrix which we have shown can be engineered to make NTE more favourable. This thus poses the possibility to screen for potential uniaxial NTE materials using the elastic compliance matrix and space group symmetry as descriptors. Elastic constant tensors are straightforward to calculate using many first principles methods and avoids the need for more taxing lattice dynamics computations.

We conclude that robust uniaxial NTE in layered perovskites is due to the combination of soft RUMs and highly anisotropic compliance. Through symmetry analysis we have found that this anisotropic compliance arises from coupling between internal degrees of structural freedom and lattice axes. This coupling requires the combination of symmetry breaking distortions both perpendicular and parallel to the axis of NTE and thus phases of layered perovskites with condensed octahedral rotations are predisposed to uniaxial NTE. Our results hence explain that while bulk ABO₃ perovskites often show soft phonon modes with negative Grüneisen parameters, they tend not to exhibit pronounced NTE due to their symmetry restricting a more isotropic compliance. Moreover, this observation may prove useful to screen for potential NTE materials since one may initially compute only elastic constant tensors.

Methods

The thermal expansion of tetragonal I4₁/acd Ca₂MnO₄ was determined from neutron diffraction at ambient pressure and compared with DFT calculations within the QHA. To reduce computational cost, most of the DFT calculations were in practice performed on Ca₂GeO₄, justified by the fact that Ge⁴⁺ and Mn⁴⁺ have equal ionic radii,²³ and the observation that structural changes across the magnetic transition are negligible, indicating that magnetism has little effect on the thermal expansion. We note that magnetoelastic super-exchange interactions do, however, alter slightly the tetragonality of the cell, which we capture by applying a compressive biaxial pressure of 4.3 GPa to Ca₂GeO₄, chosen to match the a lattice parameter of relaxed Ca₂MnO₄ with experimental spin ordering.³⁴ DFT calculations show the elastic compliance and the lowest frequency phonon modes to have close quantitative agreement between I4₁/acd phases of relaxed Ca₂MnO₄ and Ca₂GeO₄ with this corrective biaxial pressure applied (these results may be seen in Fig. 1c and are tabulated in Tables S2 and S4, respectively).

Experimental details

Ca₂MnO₄ was prepared by grinding the starting materials (MnO₂, 99.99% and CaCO₃, 99.95%) together in the desired stoichiometry and calcining at 900 °C for 8 h. The sample was then fired at 1200 °C for 4 × 24 h with intermediate regrindings. The resulting phase pure polycrystalline sample was studied at the high resolution powder diffractometer (HRPD) at the ISIS neutron spallation source in the temperature range 4.75–400 K. The diffraction data from the high resolution back-scattering bank was fit in TOPAS using the Rietveld method to extract both the lattice parameters and the amplitude of the MnO₆ octahedral rotation as a function of temperature. The structure was found to crystalise in the space group I4₁/acd (basis {(−1 −1 0),(1 1 0),(0 0 2)} + (1/4 3/4 3/4) with respect to the I4/mmm parent setting described in the paper) and retain this symmetry down to the lowest temperature studied.

Fitting procedure for neutron diffraction data

Lattice parameters, a(T) and c(T), and the frozen octahedral rotation angle, θ(T), as measured from neutron diffraction data were fitted to the forms as a function of temperature, T:

$$a\left( T \right) = {a_0} + \frac{{{k_1}}}{{{\rm{exp}}\left( {\frac{{{k_2}}}{T}} \right) - 1}},$$

(4)

$$c\left( T \right) = {c_0} - \frac{{k_1^n}}{{{\rm{exp}}\left( {\frac{{k_2^n}}{T}} \right) - 1}} + \frac{{k_1^p}}{{{\rm{exp}}\left( {\frac{{k_2^p}}{T}} \right) - 1}},$$

(5)

$$\theta \left( T \right) = {\left[ {\theta _0^2 - \frac{{k_1^2}}{{{\rm{exp}}\left( {\frac{{{k_2}}}{T}} \right) - 1}}} \right]^{12}}.$$

(6)

In the above, a ₀, c ₀, θ ₀ and all ks are fitting parameters optimised to the dataset. Equations (4) and (5) are derived from Eq. (3) and use Bose–Einstein distributions to represent, within the Einstein approximation, the population of a single γ ₁ > 0 phonon or one γ ₃ < 0 and another γ ₃ > 0 phonon, respectively. Equation (6) is adapted from the derivation by Dove³⁵ using the Einstein approximation to assume population of phonons with a single frequency.

Calculation parameters

CASTEP version 7.03,³⁶ a plane-wave³⁷ DFT code, is used for all DFT and DFPT calculations. The PBEsol³⁸ exchange-correlation functional has been used since this functional has been developed specifically for ionic solids and has been shown in similar studies to accurately reproduce structural parameters.³⁹ In all Ca _n+1Ge _n O_3n+1 systems, a 1400 eV energy cutoff for the plane-wave basis is used with a 3× denser ‘fine grid’ to represent norm-conserving pseudopotentials⁴⁰ (generated on-the-fly within CASTEP version 16.0). A 7 × 7 × 2 Monkhorst–Pack⁴¹ grid of k-points shifted away from the Γ-point is employed for calculations of Ca₂GeO₄ I4/mmm symmetry structures and an appropriately scaled grid is used for other cells. All energies are converged within 1 meV/atom. In all structural relaxation calculations, forces have been relaxed to within 10⁻⁴ eV/Å and stresses within 10 MPa. DFPT phonons were computed on a 4 × 4 × 1 q-point grid for a ($\sqrt 2$ × $\sqrt 2$ × 2) equivalent I4/mmm supercell and this dynamical matrix was interpolated onto a 32 × 32 × 4 grid to generate each PDOS. Calculation parameters for other chemistries may vary and have been tabulated, alongside all pseudopotential strings used, in Tables S5 and S6.

The quasi-harmonic approximation

In the QHA, relaxed structures are found for a range of volumes and the harmonic phonon frequencies computed for each structure. Since I4₁/acd Ca₂GeO₄ is tetragonal, the a and c lattice parameters were varied independently to create 40 relaxed structures (see Fig. S4). For each structure, the PDOS was computed for harmonic phonons and using this PDOS, g(ω), the vibrational free energy, F _vib, was calculated by:

$${F_{{\rm{vib}}}}\left( T \right) = {\int} g\left( \omega \right)\left[ {1{\rm{/}}2\hbar + {{\rm{k}}_{\rm{B}}}T\,{\rm{ln}}\left( {1 - {e^{\frac{{ - \hbar \omega }}{{{{\rm{k}}_{\rm{B}}}T}}}}} \right)} \right]d\omega .$$

(7)

Hence the full Gibbs free energy, G, of a structure could be calculated at a given temperature, T:

$$G = {E_{{\rm{DFT}}}} + P{V_0} + {V_0}Tr\left( {{{\boldsymbol{\sigma }}_{{\rm{ext}}}}{{\epsilon }}} \right) + {F_{{\rm{vib}}}}\left( T \right),$$

(8)

where E _DFT is the cell energy calculated using DFT, σ _ext is the external stress tensor (corresponding to the applied biaxial stress of 4.3 GPa), P is the effective hydrostatic pressure (P = 1/3Tr(σ _ext)), and ${\bf{\epsilon }}$ the strain tensor with respect to the fully relaxed structure with no external stress.⁴² The equilibrium lattice parameters were found at each T as those which minimised G: For each a, a Murnaghan equation⁴³ was fitted to the isothermal energy surface to find the equilibrium volume, V _e|a , and hence lattice parameter c _e|a . These minimum c _e|a ’s thus formed a valley in a−c space (described by a fourth order polynomial, p(a)) and a second Murnaghan equation could be fitted to the volumes along this valley to give the global minimum volume, V _e . Thus the equilibrium lattice parameters, a _e and c _e , were found by solving p(a) with the constraint ${V_e} = a_e^2{c_e}$.

Equilibrium lattice parameters were found every 0.25 K over the range 0–250 K. Above this temperature, the equilibrium structure predicted had a softest phonon mode with a frequency so close to zero that its contribution to the free energy began to diverge causing it to dominate the overall lattice dynamics. Hence the temperature range was truncated to avoid unphysical behaviour due to the QHA. α(T) was computed numerically at each temperature by linear interpolation of all equilibrium lattice parameters vs T in a ±5 K range. θ _e (T) data was found by inputting (a _e (T), c _e (T)) into a cubic spline of θ(a, c) fitted to the grid of relaxed structures.

DFT force constants

Force constants were computed by applying small displacements to O ions along each bond axis and recording the change in force on the adjoined ion. Simulations were performed in a relaxed 2$\sqrt 2$ × 2$\sqrt 2$ × 1 supercell (to separate periodic displacements) of a Ca₂GeO₄ phase with (and without in Table S3) a single frozen in-phase rotation or a 2$\sqrt 2$ × 2$\sqrt 2$ × 2 supercell of I4/mcm CaGeO₃.

Subsequent bond extension calculations were performed on single unit cells of rotation phases in which the rotation angle, θ, was altered and all epitaxial O ions constrained but all other ions and cell lengths free to relax in response.

Data availability

Data underlying this article can be accessed on figshare at DOI:10.6084/m9.figshare.4491521, and used under the Creative Commons Attribution licence.