Introduction

Ferroic crystals (or ferroics)1 are a generic name for ferromagnets, ferroelectrics, and ferroelastics, as well as very recently reported ferrotoroidics.2 They originate from a disorder–order ferroic phase transition at a critical temperature (T c) and have a long-range ordering of magnetic moment in ferromagnets, electric dipole in ferroelectrics, or lattice strain in ferroelastics below T c (ref. 1). The ordering or symmetry-breaking leads to degenerate states of equivalent domains with the same free energy but different orientations, and in order to minimize the internal energy ferroics naturally possess a multi-domain configuration. Under the external stimuli (such as magnetic/electric/mechanical field, temperature), they exhibit many technologically important phenomena such as a hysteresis loop (a switching behavior between different domains) and magnetic/electric/mechanical strain coupling, and have a wide range of applications as memory devices, actuators, sensors, transduces, etc.1,3,4,5,6,7 However, because of the first-order nature,1,3,4,5,6,7,8,9 the hysteresis is usually quite large especially in ferroelastics and ferroelectrics,3,4,5,6,7 leading to energy loss and fatigue issues. Moreover, a normal ferroic transition renders many of the interesting properties of ferroic crystals (e.g., superelasticity) that are achievable only in a narrow temperature window around the transition temperature. In this review, we show other two classes of ferroic materials: ferroic glass and glass-ferroic. The former has unique properties that overcome these drawbacks in the ferroic crystal, whereas the latter can exhibit some superior property combination of its two components. Furthermore, experimental and simulated results have revealed a generic phase diagram that exhibits a simple and accessible approach to find the ferroic glass and glass-ferroic.

Ferroic glass and its unusual properties

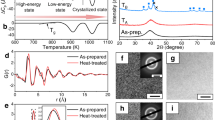
The concept of ferroic glass10 was proposed recently to unify glass phenomena in three kinds of ferroic systems: spin glass in ferromagnetic systems, relaxor in ferroelectric systems and strain glass in ferroelastic systems (see Fig. 1). Looking back to the history, we can see these three types of glasses were independently developed in three different communities at different time.

Fig. 1
figure 1

Historical development of relaxor, spin glass, strain glass, and ferroic glass. The three insets show a universal feature of ferroic glass transition, the frequency-dependence of susceptibility peak temperature (reproduced with permission from ref. 10, copyright John Wiley and Sons 2014)

Full size image

Relaxor was reported in 1960 in ferroelectric community.11 It was found that through heavy doping the sharp, frequency-independent susceptibility peak at ferroelectric transition is gradually changed into a broad, frequency-dependent peak. This phenomenon is similar with a relaxation phenomenon and thereby was named “relaxor”. Later, it was realized that relaxor cannot be explained by the conventional relaxation (Debye relaxation) and actually originates from a glass transition12; but the name is still being used to date.

“Dirty magnetism” that in some magnetic systems a normal Curie–Weiss susceptibility peak disappears at the magnetic transition, has long been known in magnetic community. Rather, it shows a frequency-dependent susceptibility cusp and the absence of ferromagnetism. This phenomenon was named “spin glass” in 1972 (ref. 13,14).

In ferroelastic/martensitic community, strain glass was first discovered in a Ni-rich Ti–Ni shape memory alloy in 2005 (ref. 15), although the possibility of glass behavior in martensitic systems was theoretically suggested as early as 1990s (ref. 16,17,18,19). Strain glass is characterized by a frequency-dependency dip in the elastic modulus (the inverse of elastic susceptibility), which very much resembles that of a spin glass and a relaxor. Since then, strain glass was reported in various systems ranging from Ti–Ni-based and Ti-Pd-based shape-memory alloys, magnetic shape memory alloys, Ti-based alloys to even ceramics.20,21,22,23,24,25,26,27,28,29 It should be noted that the same terminology “strain glass” was coincidentally used in the same year of 2005 for a manganite, a strongly-correlated system,30 which has electronic and magnetic degrees of freedom and strain plays a minor role. No direct evidence for strain glass (e.g., susceptibility anomaly or non-ergodicity measurements, see below) has been provided for such a system so far.

Ferroic glass originates from a gradual freezing process of the disordered ferroic state—the so-called ferroic glass transition. As a consequence, the ferroic glass transition has several unique features that a ferroic transition does not possess.10,31,32 (I) There exists a frequency-dependent susceptibility anomaly at the ferroic glass transition temperature Tg [Insets of Fig. 1], following a Vogel–Fulcher relation; (II) the ferroic glass system shows a history-dependence or so-called non-ergodicity, as manifested by the deviation in zero-field-cool/field-cool (ZFC/FC) curves; (III) there is no average structure change during a ferroic glass transition (this means ferroic glass cannot be detected by normal diffraction techniques like the X-ray diffraction); (IV) local order or short-range order persists in the frozen glass state, manifested by existing nano-sized domains (this means the ferroic glass can be reviewed as a nanoscale ferroics, which is characterized by the glassy behavior). Here, as an example we only show the microstructure evolution of strain glass with temperature. Other information on the ferroic glass transition can be found in our previous review papers.10,31,32 Figure 2a–d shows in situ high-resolution transmission electron microscopy observations of Ti50Pd41Cr9 strain glass alloy.33 Well above the glass freezing temperature T 0, the lattice is basically undistorted, showing nearly ideal B2 symmetry of austenite. With decreasing temperature, some nano-sized martensite-like strain domains appear and these domains exhibit a “tweed” pattern (characterized by a cross-hatched nano-sized strain domain structure16,17,18,32,33). Upon further cooling, the nano-domains further grow and are eventually frozen, without transforming into a martensite. This is a microstructure basis for understanding and designing the ferroic glass property (see below).

Fig. 2
figure 2

Demonstration of microstructure-property relationship in the strain glass. a–d In situ HRTEM observations of an Ti50Pd41Cr9 strain glass alloy, showing the gradual formation and growth of nano-domains. Insets show the corresponding diffraction patterns. e Solution-treated and cold-rolled TNTZ-1.2O strain glass states show normal (positive) thermal expansion (TE), negative thermal expansion and zero expansion (Invar), depending on the different treatment. f Elinvar effect (the invariance of elastic modulus with temperature) of cold-rolled TNTZ-1.2O strain glass as compared with the solution-treated strain glass and martensite (inset). g, h Schematic picture for the nano-domain distribution in solution-treated and cold-rolled strain glass states, respectively. The gradual property change of thermal expansion and elastic modulus originates from the gradual microstructure evolution of nano-domains, and the quantitative difference depends on the configuration of nano-domains as illustrated in g and h. (a–d reproduced with permission from ref. 33, copyright American Physical Society 2014; e–h reproduced with permission from ref. 25, copyright Nature Publishing Group 2014)

Full size image

As a new class of ferroic materials, ferroic glasses are not only intriguing phenomena of condensed matter physics, but also may lead to novel applications. Most spin glass systems have very low freezing temperature, and this imposes a limitation for their practical applications. But some theoretical applications exist, such as, in neural networks (theoretical brain research) and combinatorial optimization.34,35 In the following we shall focus on the unique properties of strain glass and relaxor, which are unachievable in the corresponding ferroic crystals.

As indicated by the gradual microstructure change in Fig. 2a–d, a unique feature of ferroic glass is its weak temperature-dependence of physical properties. For example, in ferroelectric community, the broad and high dielectric susceptibility peak of relaxor has been the foundation of ceramic capacitor applications.7,36,37 On the other hand, in ferroelastic/martensitic field, unusual properties of Invar effect and Elinvar effect were reported in non-transforming cold-rolled Ti-23Nb-0.7Ta-2Zr-1.2O alloys (GUM metals).38 Invar effect refers to the dimensional invariance with temperature and Elinvar effect refers to the elasticity invariance with temperature. These two properties are important for many precision device applications. Recent work shows that GUM metals are the strain glass25 and two unusual properties can also be understood based on the strain glass microstructure evolution with temperature. As shown in Fig. 2e, the solution-treated Ti-23Nb-0.7Ta-2Zr-1.2O (TNTZ-1.2O) alloy exhibits a normal thermal expansion behavior; whereas a thermal contraction behavior occurs in the sever cold-rolled state. An Invar behavior (zero thermal expansion) appears only when the cold-rolled sample is heated to 573 K. These phenomena can be understood to be a balance between a normal thermal expansion behavior and an opposite effect from aligned strain glass nano-domains.10,25 In the solution-treated state, the randomly distributed nano-domains (Fig. 2g) make the opposite effect zero, and thus a normal thermal expansion appears. In the heavily cold-rolled state, the longer axis of nano-domains is preferred to align along the rolling direction (Fig. 2h). Therefore, upon cooling the growth of nano-domains will give rise to a cooling-expansion in the rolling direction. However, the domain alignment will become less aligned due to the heat treatment, i.e., the cooling-expansion becomes smaller. Consequently, an Invar behavior can be expected when the cooling-expansion compensates for the normal thermal expansion.

As shown in Fig. 2f, the Elinvar effect is observed in the cold-rolled state and a broad modulus dip appears in the solution-treated one. Notably, both states show a sluggish change of elasticity, different from that of the Ti–20 Nb martensitic alloy (inset of Fig. 2f). The Elinvar effect is also related with the strain glass microstructure that can be viewed as a composite of austenitic matrix and martensitic nano-domains. Upon cooling, the modulus of austenitic matrix decreases while the modulus of martensitic nano-domains increases. Such two opposite contributions lead to a weak temperature-dependent elasticity. Compared with the solution-treated state, the cold-rolled one has more additional dislocation defects and thus the elasticity change of both the austenitic matrix and martensitic nano-domains becomes even weaker, resulting in an Elinvar effect. Therefore, the dimensional invariance (Invar effect) and elasticity invariance (Elinvar effect) can be understood to be the length compensation and modulus compensation from strain glass nano-domains, an excellent demonstration of microstructure-property relationship. Nevertheless, there is also a possibility that nano-domains can indirectly change lattice anharmonicity and hence contribute to the Invar and Elinvar effect39; this possibility needs further exploration. Note that very recently in ferroelectric materials, it has been reported that the polar nano-domain alignment makes a major contribution to the ultrahigh piezoelectricity of Pb(Mg1/3Nb2/3)O3-PbTiO3 (PMN–PT).40,41

Another well-known application of ferroic crystals is actuators which output strain in response to electric field or mechanical stress. However, a severe problem of ferroelectric electrostrictive materials or shape memory materials is the large hysteresis due to the switching of large ferroic domains or first-order ferroic transition, thereby limiting applications needing high precision and a high fatigue life. The hysteresis originates from the energy barrier of ferroic transition, thereby seeming hard to avoid. However, ferroic glass provides a solution to this problem. For example, the Ti50Ni44Fe6 strain glass alloy exhibits a superelasticity with narrow hysteresis over a much wider temperature range while the Ti50Ni48Fe2 martensitic alloy shows a superelasiticity with large hysteresis owing to the stress-induced first-order transition (see Fig. 3a–b).42 Similarly, the relaxor of Pb(Mg1/3Nb2/3)O3 (PMN) shows the same behavior of slim hysteresis over a broad temperature window36,37 whereas the ferroelectric Pb(Zr0.57Ti0.43)O3 shows the typical butterfly shape of electrostriction (see Fig. 3c, d).7 The small hysteresis of ferroic glass originates from the gradual growth or shrink of certain already existing nano-domains without nucleation events; hence the energy loss due to the nucleation is avoided.42 This mechanism is different from the domain rotation mechanism of normal ferroelectrics at morphotropic phase boundary,43 which yield the well-observed hysteresis loop under bipolar loading.7

Fig. 3
figure 3

Superelasticity of Ti50Ni44Fe6 strain glass and electrostriction of Pb(Mg1/3Nb2/3)O3 relaxor with narrow hysteresis, in comparison with large hysteresis of Ti50Ni44Fe2 ferroelastic/martensite and Pb(Zr0.57Ti0.43)O3 ferroelectric. The inset in c shows a typical butterfly-type electrostriction of ferroelectric phase, and the inset in d shows a typical electrostriction of relaxor. (a–b reproduced with permission from ref. 42, copyright Elsevier 2014; c reproduced with permission from ref. 7, copyright CRC Press 2009; d reproduced with permission from ref. 36, copyright Springer 2012)

Full size image

Models of ferroic glasses and a generic ferroic glass phase diagram

Experiments above have shown that ferroic glasses appear when sufficient amount of point defects is doped into ferroic crystals, i.e., the formation of ferroic glass can be understood to stem from the destruction of long-range ferroic ordering by point defects. Recently, Wang et al. have provided rigorous modeling and phase field simulation on both strain glass44,45,46 and relaxor,47 and their results reproduce all known features of strain glass and relaxor including the experimental phase diagram.44,45,46,47 According to their model two effects caused by point defects were important (Fig. 4): (I) global transition temperature effect (GTTE) which changes the global thermodynamic stability of ferroic phase; (II) local field effect (LFE) which changes the local stability and breaks the local symmetry. The increase of the defect concentration can enhance LFE, thereby promoting the formation of ferroic glass (see Figs. 5–6). Details on the modeling can refer to previous papers.44,45,46,47

Fig. 4
figure 4

Global transition temperature effect (GTTE) and local field effect (LFE) caused by point defects. a Experimental results for the relationship between martensitic transition temperature and defect concentration in Ni50+xTi50-x.b Schematic picture of the Landau free energy without defects (black curve) and with defects (blown curve). GTTE describes the free energy curves with different defects (i.e., compositions) that reflect the thermodynamic stability of ferroic phase. c Local lattice distortions caused by a doped point defect (black dot). d–f Landau free energy curves with different temperature at three different locations. (a reproduced with permission from ref. 5, copyright Elsevier 2005; c–f reproduced with permission from ref. 44, copyright American Physical Society 2010)

Full size image
Fig. 5
figure 5

Comparison of simulated and experimental strain glass phase diagrams, where M s, T g, and T nd denote the martensitic starting temperature, strain glass transition temperature, nano-domain formation temperature, respectively. (a reproduced with permission from ref. 44, copyright American Physical Society 2010; b reproduced with permission from ref. 48, copyright American Physical Society 2010)

Full size image
Fig. 6
figure 6

Simulated microstructure evolution. The defect concentration c increases from left to right and the temperature decreases from top to bottom. a Simulated martensitic microstructure at different defect concentrations. Gray color describes the austenitic phase, white and black color describes the two martensitic variants, respectively. b Polar domain structures at different defect concentrations. Different colors describe different polarization domains, and arrows indicate the polarization directions. The insets in the bottom row are the diffuse scattering of the corresponding domain structures. (a reproduced with permission from ref. 44, copyright American Physical Society 2010; b reproduced with permission from ref. 47, copyright American Physical Society 2010)

Full size image

Figure 5a, b shows a striking similarity between the simulated and experimental phase diagrams of strain glass.44,48 The simulated phase diagram based the model well reproduce the most important features of a ferroic glass system: (I) a crossover from a normal ferroic transformation to a glass transition at a critical defect concentration; (II) the existence of a precursor state or tweed state below a critical temperature T nd.

Figure 6a, b shows the corresponding simulated microstructure evolution as a function of temperature at various defect concentrations.44,47 It is found that above a critical doping level (c > 0.125 in the martensitic system; c > 0.2 in the ferroelectric system), upon cooling no ferroic transformation can be identified and instead the system is frozen into a nano-domain microstructure, the glass state.

In short, a generic ferroic glass phase diagram (Fig. 7) is established based on previous studies31 and above modeling, which can be used as a guide to design ferroic glasses. Figure 7 shows that increasing dopant concentration lowers ferroic transition temperature and beyond a critical dopant concentration x c, the system becomes a ferroic glass.

Fig. 7
figure 7

A generic temperature vs. defect-concentration phase diagram for a defect-containing ferroic system. Relationship among four different ferroic states (para-phase, ferroic crystal, unfrozen ferroic glass, and ferroic glass) is shown. A crossover from a ferroic transition to a ferroic glass transition occurs when defect concentration x exceeds a critical value x c

Full size image

It should be noted that alternative theories to explain the strain glass have been developed, in terms of elastic anisotropy49,50,51 and analogy with spin glass.52,53,54 The presence of polar nano-domains of relaxors has also been reported to originate from Anderson localization.55,56,57,58 Interested readers may refer to refs. 49,50,51,52,53,54,55,56,57,58 for details.

Glass-ferroic

The liquid to crystal transition is known to be a disorder–order transition, which shows a long-range order of atomic configuration and produces a crystal.10,31,59 Besides, another large class of transitions, the glass transitions, have also been widely found, where the disordered state is gradually frozen with a short range order and forms a structural glass.10,31,59 Sometimes, certain structural glass can further spontaneously transform into a crystal, namely the crystallization transition of glass. It subsequently leads to the formation of glass-crystal (e.g., glass-ceramic, devitrified metallic glass and semicrystalline polymer).59,60

In ferroic systems, the existence of ferroic crystal and ferroic glass are already known, as shown before. Next, we shall introduce the third ferroic state, glass-ferroic, an analog of glass-crystal (Table 1). It can be produced by the crystallization transition of ferroic glass through isothermal aging or continuous cooling.

Table 1 Three classes of transitions and three classes of resulting structural and ferroic materials (reproduced with permission from ref. 68, copyright American Physical Society 2015)
Full size table

The spontaneous transition from a ferroic glass to a ferroic crystal, which we call “crystallization transition”, has been reported in many ferroelastic systems [such as Ti48.7Ni51.3 (ref. 61), Ti50Ni44.5Fe5.5 (ref. 62), Ti50Pd40Cr10 (ref. 63) and Ni45Co10Mn20Ga25 (ref. 64)] and ferroelectric systems [such as Pb0.87La0.13(Zr0.4Ti0.6)0.9675O3 (ref. 65), Pb(Sc1/2Ta1/2)O3 (ref. 66) and Pb(Sc1/2Nb1/2)O3 (ref. 67)]. Above the spontaneous/crystallization transition temperature (T s), the system keeps frozen and forms a glass state, because its temperature is below the freezing temperature T g, but not low enough to provide the driving force of forming a ferroic crystal. Interestingly, such a glass state (i.e., T s < T < T g) can gradually transform into the ferroic phase by an isothermal aging. For example, a relaxor of Pb0.87La0.13(Zr0.4Ti0.6)0.9675O3 (PZT-13La) shows the formation and growth of ferroelectric phase (characterized by the typical ferroelectric domain structure) during the isothermal aging at a temperature between T s and glass transition temperature T m, as shown in Fig. 8a–f (ref. 65). In Fig. 8a, no ferroelectric domain appears at 0 h. At 4 h, the fuzzy ferroelectric domain starts to appear, as shown by the dotted circle in Fig. 8b. With further increasing isothermal time to 8 h (Fig. 8c) and 12 h (Fig. 8d), the domain contrast becomes clearer and the ferroelectric domains become larger. At 16 h (Fig. 8e), the ferroelectric domain fraction increases only. By comparison, Fig. 8f shows the ferroelectric domains image at room temperature. During the isothermal process, other physical properties also show a time-dependent behavior, e.g., a gradual decrease of dielectric permittivity.65

Fig. 8
figure 8

a–f Evidence for the time-dependent crystallization of relaxor in Pb0.87La0.13(Zr0.4Ti0.6)0.9675O3 (PZT-13La). a–e In-situ TEM observation at 90 °C for 0, 4, 8, 12, and 16 h, respectively. The inset in a shows the dielectric permittivity curve, where the relaxor transition temperature (T m ~ 109 °C) and spontaneous transition temperature (T s ~ 79.5 °C) are determined. f TEM image at 25 °C cooled from isothermal aging temperature 90 °C after 16 h. “Ferro.” is short for ferroelectric. Dotted lines show the interface between ferroelectric and paraelectric. g–j Evidence for the time-dependent crystallization of strain glass in Ti48.7Ni51.3. g Temperature monitor of the isothermal aging experiment. h Resistivity increase during isothermal aging, which reveals the formation of R-martensite. i Time dependence of in situ X-ray diffraction patterns. Additional peaks gradually appear close to (220)B2 peak and are determined to be the (224)R and (600)R. j, Simulated microstructure evolution with time through phase field modeling. (a–f reproduced with permission from ref. 65, copyright American Institute of Physics 2013; g–h reproduced with permission from ref. 61, copyright American Physical Society 2015)

Full size image

Similarly, in a ferroelastic/martensitic Ti48.7Ni51.3 alloy, an isothermal formation of martensite was also found in the strain glass state.61 The time-dependent increase of resistivity at 193.1 K (~M s + 14.5 K) indicated the formation of R martensite (Fig. 8h), because R-martensite has higher resistivity than the paraelastic/austenitic phase (B2 phase).5 Moreover, the average structure (revealed by the X-ray diffraction) changes with time (Fig. 8i), showing that additional diffraction peaks gradually appeared adjacent to the (220)B2 peak and were determined to be the (224)R and (600)R, respectively. The corresponding microstructure evolution simulated by the phase field modeling (Fig. 8j) further shows that the nano-domains of strain glass gradually grow and form large domains (coarse domain structure). The formation of ferroic crystal during the isothermal process can be understood in a framework of free-energy landscape, where point defects produce local barriers and a slowing-down of the kinetics (because the formed ferroic glass has very slow dynamics). At the isothermal temperature (T s < T < T g), the ferroic phase cannot appear immediately because the system is trapped among local barriers (i.e., a ferroic glass state). After the isothermal aging, the system has sufficient time to overcome the local barrier and forms ferroic phase. This time-dependent crystallization transition from ferroic glass determines that the glass-ferroic can be produced by controlling the isothermal time at different temperatures, very much resembling the heat treatment of structural materials for the desirable property.

It should be noted that the isothermal crystallization of ferroic glass may give rise to the formation of new ferroic phase, being non-existent in the standard phase diagram determined by the cooling. For example, in a solution-treated binary Ti48.7Ni51.3 alloy, the known equilibrium martensite is B19' phase, and R martensite is expected to be non-existent under such conditions.5,48 However, R martensite appears during the isothermal aging of strain glass as shown in Fig. 8g–i. The discovery of an isothermal R martensite will add a new equilibrium phase into the Ti–Ni phase diagram, as shown in Fig. 9a. The previous phase diagram (see Fig. 5b) can be viewed to be the cross section of aging time t iso = 0 h. With the increasing isothermal aging time, R martensite appears and the new phase diagram corresponds to the cross-section at t iso = 5 h. Furthermore, based on this 3D phase diagram, a well-known puzzle in Ti–Ni alloys, i.e., R-phase-like signatures of both the precursor strain state and strain glass state,48 can be explained to be a reminiscence of the B2-R phase transition. The R phase as an intermediate state in the equilibrium phase diagram also solves a long-standing puzzle about why the R-like precursor signatures appear prior to the B19' martensitic transition. Therefore, it seems that the martensitic phase diagram of a strain glass system strongly depends on time, in additional to temperature. This is similar to the case of a diffusional transformation phase diagram.

Fig. 9
figure 9

a Time evolution of the Ti–Ni (solution-treated) phase diagram. The two cross sections (t iso = 0 h and t iso = 5 h) correspond to the Ti–Ni phase diagram without and with isothermal aging, respectively. (Reprinted with permission from ref. 61) b Generic temperature vs. defect-concentration ferroic phase diagram. Three classes of ferroic states, i.e., ferroic phase, glass-ferroic and ferroic glass, are produced by three corresponding classes of transitions, i.e., ferroic transition, crystallization transition and glass transition, respectively. The insets show the simulated microstructure of different states, where the colored region represents different domains/variants. (a reproduced with permission from ref. 61, copyright American Physical Society 2015; b reproduced with permission from ref. 68, copyright American Physical Society 2015)

Full size image

On the other hand, the glass-ferroic can also be produced by an alternative method, a continuous cooling.68 This can be understood that lowering the temperature leads to increasing the driving force and thus accelerating the crystallization transition of ferroic glass, which is equivalent to increasing the isothermal time for producing ferroic phase at constant temperature. Figure 9b shows the typical phase diagram where there exists three ferroic state at the low temperature, i.e., ferroic phase, glass-ferroic and ferroic glass. These three class of ferroic materials are correspondingly produced by three classes of transitions, i.e., ferroic transition, crystallization transition and glass transition.

Outlook

Recent progress in the ferroic glass and glass-ferroic completes the transition cycle among disorder state, order state and glass state. In ferroic systems there are also three class of transitions as in structural systems: the ferroic transition from a parent phase to a ferroic phase, the glass transition from a parent phase to a ferroic glass, and the crystallization from a ferroic glass to a ferroic phase. These three class of transitions correspond to three classes of materials in both structural and ferroic systems (see Table 1): structural/ferroic crystal, structural/ferroic glass, and glass-crystal/glass-ferroic. We believe two new classes of ferroic materials (ferroic glass and glass-ferroic) may open new avenues for achieving novel properties. Especially for the glass-ferroic, it can have the superior property combination of two components,69 as the glass-crystal has already proved.59,60

Moreover, the established phase diagram in Fig. 9b demonstrates where and how to find glass-ferroic and ferroic glass. The experimental and simulation results indicate that both states can be produced through controlling the defect concentration.

Data availability

All of the data generated and analyzed during this study are included in this paper. The data that support the findings of this study are available from the corresponding author upon reasonable request.