Atomic structures of twin boundaries in hexagonal close-packed metallic crystals with particular focus on Mg

Abstract

We have investigated twin boundaries in double-lattice hexagonal close-packed metallic materials, focusing on their atomic geometry. Combining accurate ab-initio methods and large-scale atomistic simulations we address the following two fundamental questions: (i) What are the possible intrinsic twin boundary structures in hcp crystals? (ii) Are these structures stable against small distortions? In order to help end a decade-long controversy over the experimental observations of the atomic structures of twin boundaries, we have determined the energetics, spectra, and transition mechanisms of the twin boundaries. Our results confirm that the mechanical stability controls structures which are observed.

Introduction

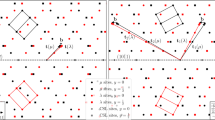
The hexagonal close-packed (hcp) structure is one of the three principal crystal structures for metallic materials (the other two are face-centered cubic, fcc, and body-centered cubic).¹ Compared with the cubic phases, hcp crystals have a lower number of symmetry operations and have an extra structural variable in describing its crystal structure. In contrast to the other two that embrace only one atom in the primitive unit cells in case of pure elements, there are two atoms in the unit cell of hcp elements, i.e., hcp is a double-lattice structure. These two atoms are symmetrically equivalent in a perfect hcp structure while in defected structures, e.g., twin boundaries (TBs),² the two atoms constitute two inequivalent sub-planes (except in the case of basal plane stacking). This results in non-unique structures for many extended defects (e.g., twins, see Fig. 1, the crystallographic components are illustrated in Fig. 1 in the supplementary material).

Fig. 1

Supercells of $\{10\bar{1}1\}$ (1 × 1 × 80, 80 atoms) and $\{10\bar{1}2\}$ twins (1 × 1 × 60, 60 atoms) which are indicated by rectangles. Vector $\overrightarrow{a}$ is the plane normal of the displacement plane (i.e. $\mathrm{1/3}\langle 1\bar{2}10\rangle$ in both cases), $\overrightarrow{b}$ is parallel to the displacement direction (see “TD” in Table 1), $\overrightarrow{c}$ is perpendicular to the twin boundary. a glide twin of $\{10\bar{1}1\}$, b reflection twin of $\{10\bar{1}1\}$, c Glide twin of $\{10\bar{1}2\}$, d reflection twin of $\{10\bar{1}2\}$. The black lines indicate the atoms in the centers of the TBs. The basal planes are denoted by red lines. When compressive stress is exerted perpendicular to the basal plane, the compression twins nucleate and grow; when tensile stress is exerted, the tensile twins form. For metals with c/a < 1.633, e.g. Mg, $\{10\bar{1}1\}$ is a compression twinning plane, while $\{10\bar{1}2\}$ a tensile twinning plane. For more details see ref. 3

Many hcp metals (except Tl, Zr, Ti, and Hf³) possess only limited room temperature deformability (e.g., magnesium alloys^3,4,5,6), which hinders their broader industrial applications. The low room-temperature deformability is believed to be caused by an insufficient number of active deformation modes (von Mises criterion) and is associated with their highly anisotropic crystal structures. In these materials twins are critically important, since they are among the deformation modes that supply out-of-basal-plane deformations.^{3, 7, 8} However, the roles that twins play in hcp materials are not fully understood yet. Recently Lentz et al. experimentally confirmed that twinning has no correlation with the nucleation of cracking embryos in Mg-4 wt.%-Li,⁹ which stimulates scientists to rethink what role twinning plays in improving the ductility of hcp alloys. A crucial component of our thorough understanding to the role that twins play in plasticity is to investigate the geometric structures of these important defects in hcp metals.

Unlike the simple geometric structures of twins in fcc materials, the more complex TB structures in hcp materials involve both shear and shuffle of atoms^{2, 10} and thus are less well understood. The structural complexity is also a common feature in multi-component structures (e.g. γ-TiAl¹¹). More than two decades ago, Hagège et al. ¹² for the first time proposed that there exist two variants (so-called glide and reflection TBs) for each twinning system in hcp materials based on simulations with a Lennard–Jones potential. Since then researchers have been consistently interested in studying the structures of the two variants both experimentally and theoretically.^13,14,15 In 1995 Braisaz et al. reported their experimental observation of the two twin variants in pure zinc.¹³ After that no further observation of the glide twins have been reported, while the reflection twins have been frequently identified.^{16, 17} Hitherto it is still not well understood why the theoretically predicted TBs (see Fig. 1) are rarely observed experimentally. A related and more general question is whether other types of TBs exist theoretically. Applying modern accurate simulation techniques we can address these questions.

Results and discussion

Search for possible twin structures

The concept of so-called generalized stacking fault energy surfaces for dislocations (i.e. gamma surfaces) was proposed by Vítek¹⁸ in 1968. Gamma surfaces were previously employed to search for possible stable stacking faults on a slip plane.^18,19,20 We generalize this concept to search for possible twin structures in one twinning plane based on one of the twin variants (i.e. the glide twin). To fully consider the internal freedom of twin nucleation in hcp crystals we define the Gibbs energy G(ε,s) at 0 K for the twinned system as a function of both the shear parameter ε and the shuffle parameter s. Apart from these parameters, other possible degrees of freedom are not controlled/fixed in our simulations but atoms are allowed to relax to their respective equilibrium configuration. More specifically, the shear parameter is the shear displacement along the twinning direction normalized by half of the twinning vector $\overrightarrow{b}$. The shuffle parameter is the shuffle displacement of atoms next to the twinning plane normalized by the atomic plane distance d. These parameters are illustrated in Fig. 2(a) and tabulated in Table 1. By these definitions $G(\epsilon ,s)=G(\epsilon |\frac{1}{2}\overrightarrow{b}|),sd,\,0\le \epsilon \le \mathrm{1,}\,0\le s\le 1$. According to the geometric symmetry, G(ε,s) = G(ε,−s) = G(−ε,s) and G(1−ε,s) = G(1+ε,s). The relative Gibbs energies ΔG = G(ε,s)−G(0,0) for compression and tensile twins in pure Mg are computed and shown in Figs. 2 (c) and (d).

Fig. 2

The Gibbs energies for the $\{10\bar{1}1\}$ compression c and $\{10\bar{1}2\}$ tensile d twins in pure Mg computed by one Mg–Y EAM potential developed by Pei et al.¹⁹ Definitions of the two parameters, $\varepsilon \cdot |\frac{1}{2}\overrightarrow{b}|$ (0 ≤ ε ≤ 1) and s·d (0 ≤ s ≤ 1) are illustrated in a. In both energy surfaces there are only two local minima that correspond to the glide twin boundary (TB1) and reflection twin boundary (TB2), respectively. The zigzag functions for these two twins are shown in b. The c/a range for all hcp metals and maxima of zigzag functions are denoted by black arrows

Table 1 Crystallographic elements and parameters of twin systems in hcp metals

The resulting potential energy surfaces show only two local minima. Their existence is independent on the employed potentials albeit with different energetics, as is tested by the potentials of Pei et al. ¹⁹ and Sun et al.²¹ The two local minima correspond to the glide (TB1) and reflection (TB2) TBs, respectively (see Fig. 1). The Gibbs energy surface reflects the crystallographic symmetry. The reflection twin boundary has a mirror operation around the twinning plane. In this case the atoms directly adjacent to the twinning plane have to stay in the same plane in order to maintain the overall mirror symmetry. For the glide twin boundary, the mirror operation is broken. The matrix and twinned part have an extra relative displacement of half a twinning vector, i.e., $\mathrm{1/2}\overrightarrow{b}$. So the atoms next to the twinning plane are not forced to be in the same plane but arranged in a zigzag way to minimize Gibbs energies.

We define a function f(x) to quantitatively describe the zigzag degree of the glide TB in hcp metals with a c/a ratio of x and sub-plane distance d (see Fig. 2 (a)). Since the zigzag degree is characterized by both the coordinates of TB atoms parallel to the twinning vector and perpendicular to the twinning plane, we define a unit-less function $f(x)=d/|\frac{1}{2}\overrightarrow{b}|$ (see Table 1), which is shown in Fig. 2 (b) for the two twins. For all hcp metals (1.56 < x < 1.89), the zigzag degrees of $\{10\bar{1}1\}$ vary from 0.126 to 0.142. Interestingly, the $\{10\bar{1}2\}$ twins in all hcp metals have almost the same zigzag degree, i.e., ~0.166. Therefore the structures of the tensile TBs are geometrically equivalent albeit exhibiting different scaling factors.

Twin boundary energies of hcp metals

Figure 3 provides the TB energies (TBEs) of compression and tensile twins in pure Mg and TBEs of tensile twins in five other hcp metals. In pure Mg, both our present and previous studies^{12, 14, 15} using different total energy methods (empirical potentials as well as DFT with different exchange-correlation functionals) predict that glide TBEs are close to reflection TBEs with differences of smaller than 4% with respect to TBEs (see Table 2). Hagège et al.¹² predicted the glide TB of pure Mg being more stable than the reflection TB employing the Lennard–Jones pair potential. Later, Morris et al. ¹⁴ employed the DFT method with local density approximation (LDA) to the exchange-correlation functional and predicted identical TBEs. This is not consistent with our TBEs with LDA and generalized gradient approximation (GGA) functionals but also with the GGA-based data of Wang et al.,¹⁵ which shows that reflection TBEs are lower than glide TBEs. Our calculations for other hcp metals also show the same trend.

Fig. 3

Twin boundary energies of $\{10\bar{1}1\}$ and $\{10\bar{1}2\}$ twins computed by DFT and the Lennard–Jones potential. PI represents the $\{10\bar{1}1\}$ compression twin, PII $\{10\bar{1}2\}$ tensile twin. Unless explicitly pointed out, the other computed twin boundary energies are for $\{10\bar{1}2\}$ twins

Table 2 The TBEs of $\{10\bar{1}2\}$ twins in Mg and five other hcp metals

Why are glide TBs not observed?

TB structures that were observed by high resolution transmission electron microscopy in hcp metals have been reported in the literature.^{13, 17, 22, 23} Exclusively reflection TBs were reported (particularly in the last 3 years), whereas glide TBs of tensile twins were only reported by Braisaz et al. ¹³ in 1995. Interestingly, we already find the tensile glide TBs in all hcp metals to be structurally equivalent albeit with different scaling factors (i.e., lattice constants). Next, we apply DFT simulations to obtain a deeper understanding of these experimental results.

Introduction of additional force fields is able to destroy the symmetries of a system, and thus can help unstable systems to leave the saddle point configurations of the energy surface. Solutes can induce such force fields, therefore in the following the impact of a single solute on the stability of TBs in pure Mg is examined in the presence of symmetry breaking fields as induced by a single solute such as Y. In this study yttrium is chosen as the solute, since it is significantly different in size from Mg and since we have developed and tested a reliable embedded atom method (EAM) potential for this material system.¹⁹ The energetics of a series of solute sites in glide TBs are computed and shown in Fig. 4. The relaxed atomic structures indicate transformations from glide TBs to reflection TBs are spontaneously triggered in both glide twins on $\{10\bar{1}1\}$ and $\{10\bar{1}2\}$. Differently, when one yttrium atom is introduced into the reflection TBs no transformation from reflection TBs to glide TBs is observed (see Fig. 5). This information indicates that the reflection TBs are more stable than glide TBs when solutes are present. Since solutes may change the potential energy surface and thus be responsible for the instability instead of triggering a motion away from the saddle point only, we need further information to identify the intrinsic stability of glide and reflection TBs.

Fig. 4

Segregation energies of yttrium atom in the vicinity of TBs of $\{10\bar{1}1\}$ and $\{10\bar{1}2\}$. The initial solute sites in $\{10\bar{1}1\}\langle 10\bar{1}2\rangle$ twin are in red, while in the other twin are in blue in the inset. To differentiate twins of glide from reflection variants, subscript “g” is used to represent the glide twin. When one yttrium atom is introduced into the glide variants of TBs (sites 1-10), transformations from glide to reflection TBs are observed in the simulations. In the case of $\{10\bar{1}1\}\langle 10\bar{1}2\rangle$ twins, regardless of the segregation sites of yttrium, the glide TB always transforms to the reflection variant. The transformed reflection TB is always located at the previous glide TB. Differently, when one yttrium segregates in the vicinity of the glide TB of $\{10\bar{1}2\}\langle 10\bar{1}1\rangle$ twinning, the impurity cannot only transform the glide to reflection TB, but also drag the boundary to its current location

Fig. 5

Segregation energies of one yttrium atom in the vicinity of reflection TBs of $\{10\bar{1}1\}\langle 10\bar{1}2\rangle$ and $\{10\bar{1}2\}\langle 10\bar{1}1\rangle$ twinning in Mg. The initial solute sites in $\{10\bar{1}1\}\langle 10\bar{1}2\rangle$ twin are in red, while in the other twin they are in blue in the inset. To differentiate twins of glide and reflection variants, subscript “r” is introduced to represent the reflection twin. Twelve sites are selected (i.e., two sites in the TBs and ten other sites away from the boundaries) to inspect the stability of reflection TBs. For all twelve configurations, there is no transformation from reflection TBs to glide TBs being observed

To further check the stability of both variants of TBs, the phonon spectra of glide and reflection variants of $\{10\bar{1}2\}$ TBs are calculated and shown in Fig. 6. The two imaginary modes of the glide variant indicate that the structure is gaining energy when displacing the atoms. In contrast, there are no imaginary modes in the reflection variant. These results clearly show that the glide variant is even in the absence of solutes unstable and that the reflection variant is structurally stable.

Fig. 6

Phonon spectra of $\{10\bar{1}2\}$ a glide and b reflection TBs in pure Mg, and c minimum energy paths for the transition from glide to reflection TBs on $\{10\bar{1}2\}$ plane. In Figure c normalized TBEs are given to show the trends of Mg, Ti, and Y, respective reflection TBEs as normalization constant. The atomic displacements corresponding to the two imaginary modes in a are visualized in d and e

The displacements belonging to the two imaginary modes of the glide TB are shown in Figs. 6 (d) and (e). The two vibrational modes involve almost identical atomic displacements in the middle parts in terms of displacement directions and magnitudes. These displacements result in reflection TBs that are one atomic layer above the original glide TBs. The atomic plane distances above and below the glide TB (0.27 Å) are only half of the distance in the glide TB (0.66 Å). As a consequence, these atomic layers are energetically easier to transform into a reflection TB (i.e. flat TB). More importantly, only these atomic layers can transform into a reflection TB without an energy barrier, while for the layer in the glide TB there exists an energy barrier. For the other TB located at the end of the supercell, the transformations take place either below the glide TB, i.e. in phase with the first TB (Fig. 6 (d)), or above, i.e. opposite to the first TB. This corresponds to the two imaginary modes. Therefore the two imaginary modes describe the same transformation from glide to reflection TBs since the slightly different distances between the TBs in the finite-size supercells are physically not relevant.

To describe and analyze the transformation from one variant into the other, the minimum energy path from glide to reflection variants of $\{10\bar{1}2\}$ TBs is computed by the nudged elastic band (NEB) method. The minimum energy path yields the pathway of the transformation from glide to reflection variants. Fig. 6 (c) shows the minimum energy paths of pure Mg, Ti, and Y at zero pressure (i.e. the shape of the supercell is fully relaxed). In Fig. 6 (c) normalized TBEs are employed to show the trends of three elements (Mg, Ti, Y) having different absolute TBEs in one graph. In these three examples, there are no energy barriers along the reaction coordinate, which confirms again that glide twins are mechanically and thermodynamically unstable and spontaneously transform into reflection twins. It is important to mention that in NEB simulation the glide TBs move up (or down) by one atomic layer (or two sub-layers) through shearing and shuffling and then transform into reflection TBs. Thus, the minimum energy paths cannot be visualized in the Gibbs energy surfaces since when searching for possible twin structures the TBs are fixed at the same location, i.e., the reaction path for the transformation is orthogonal to the shuffle and glide degrees of freedom used to map the potential energy surface.

Previous studies (e.g.,¹⁴) proposed that the nucleation and/or growth mechanisms of the twins control the formation of one or the other variant (i.e. reflection twins being predominantly observed in experiment while glide twins not), i.e., the glide twins are more difficult to either nucleate or migrate. According to twin nucleation models (e.g., Yoo et al.,^{3, 24} for more discussion, see the last part of this section), however, the nucleation process is primarily controlled by TBEs. The small TBE difference of several to tens of mJm⁻² (see Table 2) does not indicate that the nucleation rates are very different.

The structural differences between the two twins consist of two parts (see Fig. 1): (i) the twinned parts of glide twins have extra displacement of half twinning vectors relative to the matrix while that of reflection twins do not, and (ii) glide twins have micro-faceted twinning planes while the reflection twins possess straight geometric planes. Interestingly, even with these structural differences the two structures are able to transform from one into the other through a small atomic shuffle and a twin boundary migration by one atomic layer. Through the atomic shuffles the two structures are actually closely connected.

Once the twins are nucleated, the displacement of part (i) is already created and therefore is not an essential factor in controlling twin growth. The distances between the two sub-planes of Mg are 0.13a for Pyramidal I twin and 0.20a for Pyramidal II twin, respectively. In the case of Pyramidal II twin, the distance is even smaller than the atomic shuffle 0.29a during the migration of its reflection TB.²⁵ So part (ii) is also not essential in controlling the subsequent twin growth. Therefore the only possible reason is that glide twins are not stable. We note that our considerations are limited to T = 0 K. Since the mechanisms revealed by these studies explain the experimental observations, we expect that they also apply at elevated temperatures. A full calculation of the temperature dependent stability of the TB structures, however, remains a task for future investigations.

Our finding is particularly relevant for simulations of the mechanical behavior of Mg at larger length scales as e.g. crystal plasticity simulations. The reduction to reflection TBs allows one to use the characteristic shear strains of reflection TBs in the crystal plasticity models. Further MD computations should focus on the potential role of mechanically unstable glide TBs for the formation of stable reflection TBs, which is essential for mechanical induced twin growth and mechanical de-twinning.

Conclusions

We propose a new method to search for all possible twin structures which results in only two variants of TBs in each twinning plane, i.e. glide TBs and reflection TBs. A new perspective of twin boundary stability is developed to explain why glide TBs have not been observed in experiments although they are theoretically predicted in hcp metals. Our simulations clearly show that it is due to the mechanical instability, i.e., the absence of a metastable configuration of the glide TBs rather than the nucleation or growth mechanisms.

Following this work, we are performing more simulations based on the stable reflection TBs in Mg. Our predictions paves the way towards twinning-based formability descriptors for high throughput design of ductile Mg alloys and similarly other hcp metallic materials as well. Combining them with the developed dislocation-based ductility descriptors (e.g.,^{26, 27}) will allow for a more comprehensive description of the deformation mechanisms active in Mg and Mg alloys.

Methods

Computational details

The computations have been performed using the Vienna Ab-initio Simulation Package (VASP)^{28, 29} in the framework of DFT^{30, 31} and the EAM^{32, 33} implemented in the Large-scale Atomic/Molecular Massively Parallel Simulator (LAMMPS)³⁴ package. GGA with the Perdew–Burke–Ernzerhof parameterization³⁵ is employed to describe the exchange-correlation interaction. The applied plane-wave cutoff energy of 350 eV and Gamma-based-scheme k-points × atoms of ≥9600 (≈18000 for $\{10\bar{1}1\}$ twins) guarantee that the computed total energies of TBs and surfaces are converged within 10⁻⁴ eV. The minimum energy path of the transition from the glide to reflection TBs is calculated using the climbing image-NEB method as implemented in the Transition State Tools for VASP (VTST) code³⁶ as an extension to VASP. Phonon dispersions are calculated with the finite displacement method in a 2 × 2 × 1 supercell (240 atoms). The pre-processing to generate unique displacements based on symmetry and the post-processing to construct the dynamical matrix and thus the phonon frequencies in reciprocal space are performed employing the S/PHI/nX code.³⁷ In terms of computing TBEs and surface energies, a series of supercells with different numbers of layers (perpendicular to the twinning or surface planes) are employed in order to evaluate the spurious interaction between the defect and its images (due to employment of periodic boundary conditions). The computed lattice constants for pure Mg (a = 3.189 Å and c/a = 1.626) and pure yttrium (a = 3.647 Å and c/a = 1.551) are in very good agreement with experimental data (pure Mg, a = 3.209 Å, c/a = 1.624 and pure yttrium, a = 3.648 Å, c/a = 1.571).¹

Definitions of physical quantities in this work

The total energy of a twinned supercell is computed by allowing the atoms to fully relax. If the total energy of a twinned supercell is E _twin and the total energy with a perfect hcp supercell of the same atom number and atom species is E _bulk, the TBE is computed by

$${\gamma }_{t}=\frac{{E}_{{\rm{twin}}}-{E}_{{\rm{bulk}}}}{2{A}_{t}}$$

(1)

where A _t is the TB area. Since each twinned supercell contains two TBs a factor of 2 is included.

When one yttrium atom is introduced into the twinned supercell, its segregation energy is computed by

$${E}_{{\rm{seg}}}={[E({{\rm{Mg}}}_{N-1}{\rm{Y}})-E({{\rm{Mg}}}_{N})]}_{{\rm{twin}}}-{[E({{\rm{Mg}}}_{M-1}{\rm{Y}})-E({{\rm{Mg}}}_{M})]}_{{\rm{bulk}}}$$

(2)

where M, N are the respective sizes of the bulk and twinned supercells. In this study the same number of atoms for twinned and bulk supercells is used. The employed supercells for $\{10\bar{1}1\}$ twins and $\{10\bar{1}2\}$ twins are shown in Fig. 1.

When we compare the definitions of TBE (Eq. (1)) and SE (Eq. (2)) and note that the difference in planar areas of pure Mg and Mg–Y is ignorable (<0.1% in present simulations), the following linear relationship between SE E _seg(Mg _N−1Y) and TBE γ _t (Mg _N−1Y) is found,

$${E}_{{\rm{seg}}}({{\rm{Mg}}}_{N-1}{\rm{Y}})=2{A}_{t}({\gamma }_{t}({{\rm{Mg}}}_{N-1}{\rm{Y}})-{\gamma }_{t}({{\rm{Mg}}}_{N}))$$

(3)

The slope of the linear relationship is twice of the TB area, i.e., 2A _t .