Abstract
Renewable electricity-powered CO evolution from CO2 emissions is a promising first step in the sustainable production of commodity chemicals, but performing electrochemical CO2 reduction economically at scale is challenging since only noble metals, for example, gold and silver, have shown high performance for CO2-to-CO. Cu is a potential catalyst to achieve CO2 reduction to CO at the industrial scale, but the C-C coupling process on Cu significantly depletes CO* intermediates, thus limiting the CO evolution rate and producing many hydrocarbon and oxygenate mixtures. Herein, we tune the CO selectivity of Cu by alloying a second metal Sb into Cu, and report an antimony-copper single-atom alloy catalyst (Sb1Cu) of isolated Sb-Cu interfaces that catalyzes the efficient conversion of CO2-to-CO with a Faradaic efficiency over 95%. The partial current density reaches 452 mA cm−2 with approximately 91% CO Faradaic efficiency, and negligible C2+ products are observed. In situ spectroscopic measurements and theoretical simulations reason that the atomic Sb-Cu interface in Cu promotes CO2 adsorption/activation and weakens the binding strength of CO*, which ends up with enhanced CO selectivity and production rates.
Similar content being viewed by others
Introduction
The massive emission of CO2 caused by fossil fuel combustion has led to a dramatic increase in CO2 concentrations in the atmosphere, which has triggered global concerns about climate change1,2,3,4. The electrochemical CO2 reduction reaction (CO2RR) offers a sustainable approach to directly convert CO2 into value-added chemicals and fuels under ambient conditions, which reduces CO2 emissions and alleviates the dependence on fossil fuels5,6,7,8,9. Among the products obtained from CO2RR, CO is one of the most important feedstocks that can be used in the sustainable production of commodity chemicals10,11,12. To perform this reaction economically at scale, a catalyst capable of mediating the efficient formation of CO with high selectivity at high current densities is a prerequisite. Currently, gold and silver are the most active catalysts for this process, with near-unity CO selectivity under low to modest production rates. To maintain high CO selectivity, the partial current densities of CO (jCO) of these noble metals are typically lower than 200 mA cm−2 13,14,15. Further increasing the bias will simultaneously promote the competitive hydrogen evolution reaction (HER) and thus suppress the CO Faradaic efficiency (FE). Other more abundant, less expensive metals generally have poor selectivity for CO2-to-CO16,17. Very recently, earth-abundant molecular electrocatalysts18,19 and single-atom catalysts20,21,22 have been demonstrated to exhibit an FE of CO formation comparable with those of noble metal catalysts. However, most of these catalysts, in which the catalytic metal sites are isolated and well-defined, have also failed to drive CO2-to-CO at a commercially relevant scale (at least jCO > 200 mA cm−2) due to the partial reduction of the ligands around the atomically dispersed metal sites under a high applied potential23,24,25,26.
Cu possesses excellent activity towards CO2 activation, but the control over the selectivity of CO2RR on Cu is a major challenge given that it can produce at least sixteen different hydrocarbons/oxygenates27,28,29,30. Generally, during the CO2RR, CO2 molecules first undergo adsorption and activation on surface atoms. Further proton-coupled electron transfer converts CO2* into COOH* (further evolves to CO*) or HCOO*, the key intermediates forming CO and HCOOH, respectively31,32. On Cu catalysts, proper binding energy to CO* endows Cu with the ability to couple CO* to generate other C2+ products (e.g., C2H433, C2H5OH34, and C3H7OH35). This situation prompted us to consider whether substantially and acutely tuning the local electronic/geometric configuration of Cu could inhibit C-C coupling without reducing intrinsic activity, thus achieving commercially relevant CO2 electrolysis to CO. We reasoned that weakening the binding strength of H* and CO* intermediates, and thus decreasing the CO* coverage, could potentially suppress HER and CO* dimerization while promoting CO generation during the CO2RR, so as to be the solution of the CO activity-selectivity dilemma on Cu. Herein, we report an antimony-copper single-atom alloy (Sb1Cu) catalyst (Fig. 1a) with isolated Sb-Cu interfaces that catalyzed the efficient conversion of CO2-to-CO with an FE of ca. 91% at 500 mA cm−2.
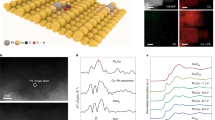
a Schematic illustration of CO2 conversion into CO over the Sb1Cu-5 catalyst. b HAADF-STEM image of the as-prepared Sb1Cu-5 catalyst. The black circles highlight single Sb atoms. c STEM-EDS mapping of Cu and Sb in the as-prepared Sb1Cu-5 catalyst, confirming the even distribution of Sb in the Cu host. d Ex situ EXAFS at the Sb K-edge of the as-prepared and post-catalysis Sb1Cu-5 without phase correction. Sb foil and Sb2O3 are shown as references. e EXAFS wavelet transforms (WT) for the Sb K-edge of the Sb1Cu-5 catalyst. f In situ Cu K-edge XANES spectra of the Sb1Cu-5 catalyst under applied potentials during the CO2RR. Cu, Cu2O, and CuO are shown as references. All potentials were calibrated to the RHE scale.
Results
The Sb1Cu catalyst was synthesized via the co-reduction of Cu2+ and Sb3+ using a NaBH4 solution in an ice bath (see Methods). The morphology of the as-synthesized Cu-Sb catalyst was characterized by transmission electron microscopy (TEM) with sizes ranging from 10 to 20 nm (Supplementary Fig. 1). The powder X-ray diffraction (PXRD) pattern of the as-prepared Cu-Sb catalyst displayed obvious CuOx diffraction peaks without Sb or Sb oxides signals, excluding the formation of Sb nanoparticles (Supplementary Fig. 2). The formation of copper oxides was attributed to the oxygen susceptibility of the Cu nanocrystal surface when exposed to air. The chemical states of CuI and SbIII in the Cu-Sb sample were identified by X-ray photoelectron spectroscopy (XPS) (Supplementary Figs. 3–5) and X-ray absorption near-edge structure (XANES) (Supplementary Figs. 6, 7), reconfirming the spontaneous oxidation of the samples. High-angle annular dark-field scanning transmission electron microscopy (HAADF-STEM) clearly identified isolated bright spots representative of atomically dispersed Sb atoms in the Cu matrix for Sb1Cu (Fig. 1b), suggesting the successful formation of isolated Sb-Cu interfaces. Scanning transmission electron microscopy energy-dispersive X-ray spectroscopy (STEM-EDS) mapping (Fig. 1c) affirmed the even distribution of Sb in Cu without observable Sb aggregation. The concentration of Sb in Sb1Cu was ca. 5.0 at% (denoted as Sb1Cu-5), as determined by inductively coupled plasma atomic emission spectroscopy (ICP-AES). The above analyses implied the formation of a Sb1Cu-5 single-atom alloy with well-defined isolated Sb-Cu atomic sites.
To obtain atomic coordination information of Sb in Sb1Cu-5 samples, extended X-ray absorption fine structure (EXAFS) measurements of the Sb K-edge were carried out. As displayed in Fig. 1d, the peak at ~1.50 Å was attributed to the Sb-O bond in the as-synthesized Sb1Cu-5 catalyst. No Sb-Sb bond was observed, indicating the isolated form of Sb atoms. The peak at approximately 2.10 Å was attributed to the Sb-Cu bond, which proved the successful formation of Sb-Cu atomic interfaces. Wavelet transform analysis further corroborated the EXAFS fitting results (Fig. 1e and Supplementary Table 1). The Cu K-edge EXAFS results illustrated the coexistence of Cu-Cu bonds (~2.50 Å) and Cu-O bonds (~1.75 Å), indicating the formation of oxides on the surface of the Sb1Cu-5 catalyst (Supplementary Fig. 8), in agreement with the XRD and XPS measurements32. We also prepared Cu, Sb1Cu-1.5, and Sb1Cu-10 as controls using a similar strategy (see Methods). Notably, the Sb1Cu-1.5 catalyst presented the same Sb-Cu atomic interface but a lower site concentration than Sb1Cu-5 (Supplementary Figs. 2–12), while the Sb1Cu-10 catalyst showed Sb aggregation (Supplementary Fig. 13). In an effort to elucidate the electronic structure of the Sb1Cu-5 catalyst under reaction conditions, we conducted an in situ X-ray absorption spectroscopy (XAS) study. Cu K-edge in situ X-ray absorption fine structure (XAFS) demonstrated that CuI in the as-prepared Sb1Cu-5 was reduced to metallic Cu during the CO2RR (Fig. 1f and Supplementary Fig. 14). Unfortunately, we failed to detect Sb signals in situ, probably due to the strong background interference caused by the fluorescence of Cu and the aqueous environment. Thus, we further explored the atomic geometry of Sb1Cu-5 after CO2 electrolysis. As expected, we still observed highly monodispersed Sb atoms in the Cu host (Supplementary Figs. 15, 16) by HAADF-STEM, in agreement with XRD analysis for post-catalysis Sb1Cu-5 (Supplementary Fig. 17). Moreover, ex situ Sb K-edge EXAFS exhibited unchanged isolated Sb-Cu atomic interfaces, suggesting that these atomic sites should be robust during electrolysis (Fig. 1d, Supplementary Fig. 18, and Table 1). The above results, taken together, suggest that the active phase of Sb1Cu-5 during the CO2RR is metallic Cu alloyed with isolated Sb atoms.
The CO2RR performance of Sb1Cu-5 was evaluated in a three-electrode flow cell using 0.5 M KHCO3 as the electrolyte (see details in Methods). Gas products were analyzed by gas chromatography (GC), and the liquid products were analyzed using nuclear magnetic resonance (NMR) spectroscopy and anion chromatography (AC). As manifested by the linear sweep voltammetry (LSV) curve of Sb1Cu-5, the current density was much higher under CO2 flow than that in Ar atmosphere, indicating the participation of CO2 in electrolysis (Supplementary Fig. 19). NMR results showed that the solution-phase product only contained formate (Supplementary Fig. 20), and the GC analysis revealed CO and H2 as major gas-phase products (Supplementary Fig. 21). We further found that the Sb1Cu-5 catalyst exhibited high selectivity towards CO even at very high current densities. The maximal FECO reached 95% at −150 mA cm−2, while FECO remained over 90% even at −500 mA cm−2 (Fig. 2a). The selectivity towards HER was suppressed to below 3%, while over 90% FECO was achieved at all applied current densities. The CO partial current density (jCO) reached a maximum of −452 mA cm−2 at −1.16 V vs. RHE with 90.4% FECO. In addition, we observed that the Sb1Cu-5 catalyst showed a lower onset potential for CO2-to-CO and much suppressed C-C coupling (>150 mV onset potential for C2H4) compared to pure Cu using in situ differential electrochemical mass spectrometry (DEMS) (Fig. 2b)36. This leads us to believe that the intrinsic activity and selectivity of Cu was significantly modulated by the introduction of isolated Sb-Cu atomic interfaces. The stability test showed that FECO remained at approximately 95% after 11 h of continuous electrolysis at −100 mA cm−2 using a membrane electrode assembly (MEA), and the cell voltage was quite stable without obvious fluctuation (Fig. 2c). In order to exclude the influence of structural decay of gas diffusion electrode during long-term electrolysis, we further evaluated the intrinsic stability of Sb1Cu-5 catalyst in an H-cell, exhibiting a stable cathode potential with ca. 90% FECO for 100 h (Supplementary Fig. 22). The impressive performance for CO2-to-CO on Sb1Cu-5 outperforms the previously reported state-of-the-art CO-selective electrocatalysts37,38,39 (Fig. 2d, e, Supplementary Fig. 23, and Tables 2–4).
a FEs of all CO2RR products at different current densities and the corresponding j-V curve of Sb1Cu-5. b In situ DEMS measurement of (up) CO and (down) C2H4 production during CO2RR on Cu and Sb1Cu-5 catalysts. c Stability test at −100 mA cm−2 current density in MEA for over 10 h, indicating an average CO FE of approximately 95%, as estimated by GC analysis. Performance metrics of different reported CO2RR-to-CO d Cu-based and e non-Cu-based catalysts. Comparison of product FEs on f Cu, g Sb, and h Sb1Cu-1.5. The error bars correspond to the standard deviation of three independent measurements.
We next analyzed the possible mechanism for exclusive CO production on the Sb1Cu catalyst. We first compared the CO2RR performance of pure Cu, Sb, Sb1Cu-1.5, and Sb1Cu-10 catalysts. Various products were obtained in the Cu catalyst, as expected, which showed an increasing C2+/C1 ratio with increasing current density (Fig. 2f). It is worth noting that, compared with Sb1Cu-5 catalyst, Cu exhibited higher selectivity towards C2+ products due to the preferable C-C coupling at higher current densities (e.g., 42% at −400 mA cm−2). The performance of pure Sb is given in Fig. 2g, showing a maximum FECO of 34.8%. For the Sb1Cu-1.5 catalyst (Fig. 2h), owing to the formation of isolated Sb-Cu atomic interfaces, FECO reached 89% at −100 mA cm−2. However, larger amounts of C2+ products also appeared at high current densities (up to 27% at −400 mA cm−2) because only a smaller portion of the pristine Cu surface was modulated by Sb atoms and the coordination environments of most Cu sites remained the same. Owing to the formation of Sb aggregates, a relatively higher selectivity of formate was found on the Sb1Cu-10 catalyst (Supplementary Fig. 24). These comparisons directly link the exclusive CO selectivity to the impact from alloyed Sb single atoms in the Sb1Cu catalyst.
We then sought to carry out kinetic analysis to further understand how the isolated Sb-Cu atomic interface steers the CO2-to-CO pathway on Sb1Cu-5. Tafel plots (Supplementary Fig. 25) revealed a faster kinetic process of CO generation on the Sb1Cu-5 catalyst (177 mV dec−1) compared with pure Cu (253 mV dec−1). The Tafel slope of 177 mV dec−1 on Sb1Cu-5 indicated that the first electron transfer step of *CO2 was the rate-determining step (RDS)31. The slopes were larger than the frequently mentioned Tafel slope of 118 mV dec−1 for CO2 activation RDS (Supplementary Table 5), which could be attributed to the differences in the numerical selection for the symmetry factor (α = 0.5 for 118 mV dec−1) regarding more complicated electron transfer and chemical processes under realistic conditions40. Thus, we employed Fourier-transform alternating current voltammetry (FTacV) to gain further mechanistic insights into electron transfer processes during the CO2RR on Sb1Cu-541. In FTacV, a large amplitude periodic alternating current (ac) waveform was superimposed onto the direct current (dc) ramp to generate higher harmonic components. The high harmonic ac components were highly sensitive to electron transfer kinetics and devoid of nonfaradaic background current contributions42, thereby leading to direct access to underlying electron transfer processes. The fourth harmonic components of FTacV obtained on Sb1Cu-5 in CO2-saturated 0.5 M KHCO3 showed a well-defined reduction peak at approximately −0.60 V vs. RHE, which was absent in the Ar-saturated electrolyte, confirming the involvement of CO2 in the process (Fig. 3a). Simulations of FTacV (see details in Methods) showed that the standard rate constant (ks) of the one-electron CO2-to-*CO2− the process was smaller than that for the one-electron *COOH-to-*COOH− (Supplementary Table 6), indicating the first electron-transfer step as the RDS. In addition, based on the fitting transfer coefficient (α = 0.34) for CO2-to-*CO2−, we estimated the Tafel slope to be 174 mV dec−1 on Sb1Cu-5, which is close to the experimental value of 177 mV dec−1 and thus, in turn, verifies our simulations. Taken together, the Tafel and FTacV analyses indicated an improved electron transfer process of CO production on Sb1Cu-5, highlighting the critical role of isolated Sb atoms in boosting CO2-to-CO conversion.
a Fourth harmonic components of FTacV derived on Sb1Cu-5 in 0.5 M KHCO3 solution saturated with CO2 (solid line) and Ar (dashed line). The FTacV parameters are f = 9.02 Hz, ΔE = 80 mV, and scan rate = 10.57 mV s−1. The fitting of the fourth harmonic component is also displayed at the bottom. In situ ATR-SEIRAS spectra of b Sb1Cu-5 and c Cu at different potentials. Abs absorbance. d Potential-dependent CO* peak position on Sb1Cu-5 and Cu in in situ ATR-SEIRAS spectra. e CO* and f CO32− peaks of Sb1Cu-5 and Cu in in situ Raman spectra at different potentials. All potentials were calibrated to the RHE scale.
In pursuit of a molecular-level understanding of the CO2-to-CO conversion pathway, we first conducted in situ attenuated total reflection surface-enhanced infrared absorption spectroscopy (ATR-SEIRAS) to dynamically monitor the evolution of reactive intermediates. Figures 3b and 3c show the in situ ATR-SEIRAS spectra acquired for the Cu and Sb1Cu-5 electrodes during a negative-going potential sweep from −0.2 to −0.8 V vs. RHE. Upon applying the cathodic potential, a fingerprint infrared band appeared at 2000–2100 cm−1 for both Sb1Cu-5 and Cu catalysts, which was assigned to surface-bond CO (CO*). For either electrode, the CO* band frequencies redshifted with a negatively going potential due to the Stark effect. Notably, the CO* bands are redshifted and broadened on Sb1Cu-5, in comparison to the counterparts on Cu at given potentials. As the surface coverage could impact the frequency of vibrational bands via dynamical dipole coupling43, the lower frequency of the CO* peak on Sb1Cu-5 implied weakened CO* adsorption and much lower CO coverage relative to Cu (Fig. 3d). After increasing the bias to −0.8 V vs. RHE, the CO* peak vanished on Sb1Cu-5 but was still present on Cu, indicating more facile desorption of the CO intermediate from the Sb1Cu-5 surface to form gaseous CO. In addition, after suspension of the applied potential and sweeping adsorbates with Ar flow, Sb1Cu-5 showed a faster attenuation rate and shorter retention time of CO* compared with pure Cu, further confirming its better CO desorption ability (Supplementary Fig. 26). The same conclusions were also drawn from the in situ Raman spectra, where the peaks at 2000–2100 cm−1 were ascribed to CO* intermediates44 (Fig. 3e). As shown in Fig. 3f, the peak at 1060 cm−1, which is associated with ν(CO32−) vibration45, was much weaker on Sb1Cu-5 than that on Cu at a given potential, inferring a surface environment of a lower pH value46. It has been demonstrated that a higher surface pH is conducive to promoting C-C coupling47. Thus, endowed with the capabilities of weak adsorption for CO* and facile desorption for CO, Sb1Cu-5 predominantly prefers CO evolution to CO* dimerization in the case of lower surface pH.
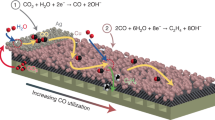
Density function theoretical (DFT) calculations were performed to further understand the enhanced FECO on Sb1Cu-5. As discussed previously48, a step surface is more active for the CO2RR. Thus, the Cu (211) surface model was first constructed (Supplementary Fig. 27). A single Sb dopant was substitutionally created to simulate a Sb1Cu-5 (211) surface. It was found that the electrochemical interface is close to a capacitor (Supplementary Fig. 28) regarding the correlations between the amount of electron transfer from the electrode to the water layer (Δq) and the relative work function change of the systems (ΔΦ) at initial, transition, and final states49. Therefore, the activation barriers at varying potentials were explicitly calculated within a capacitor model with the “charge-extrapolation” scheme50,51,52. Figure 4a shows that CO2 can be electroreduced to CO and HCOOH via COOH* or HCOO* pathway, respectively, at −1.0 V vs. RHE. The kinetic barrier of HCOOH formation is higher than that for CO production on both Cu (211) and Sb1Cu-5 (211), which is consistent with the experiments that FEHCOOH is lower than FECO on both Cu and Sb1Cu-5. Figure 4b shows that all the adsorption energies of CO*, COOH*, and HCOO* on Sb1Cu-5 (211) are lower than those on Cu (211). The CO* desorption is easier on Sb1Cu-5 (211) compared to Cu (211), which can enhance CO production and selectivity. To further understand the effect of isolated Sb in Cu, the projected density of states (PDOS) was calculated for Cu (211) and Sb1Cu-5 (211) (Fig. 4c). The d-band center of the Cu atom is lower after Sb doping (from −2.07 to −2.17 eV), which explains well the weaker adsorption energy on Sb1Cu-5 (211) than that for Cu (211).
a CO2RR to CO and HCOOH on Cu (211) and Sb1Cu-5 (211). b The adsorption energies of HCOO*, CO* and COOH* on Cu (211) and Sb1Cu-5 (211). c The projected d-band states of Cu atoms on Cu (211) and Sb1Cu-5 (211). d Barriers for CO*-CO* coupling on Cu (211) and Sb1Cu-5 (211). The initial (IS), transition (TS), and final (FS) structures are shown as insets, where Cu, Sb, C, O, and H are represented in orange, purple, gray, red, and white, respectively. e Comparison between the calculated FECO from microkinetic simulations on Cu (211) and Sb1Cu-5 (211) and the experimental FECO on Cu and Sb1Cu-5. f Free energy diagrams of the CO2RR into CO under different potentials; insets are structures of the initial (IS), transition (TS), and final (FS) states of CO2 protonation (1) and CO* formation (2). The symbols with the same color represent the same atoms in figure d and f. g Experimental activity versus a theoretical rate of CO production.
As C2+ products also have a lower FE for the CO2RR on the Sb1Cu-5 electrode, the barriers of CO*-CO* coupling were calculated. As shown in Fig. 4d, the kinetic barrier of CO* dimerization on Sb1Cu-5 (211) is higher than that on Cu (211), thus resulting in slower production of C2+ products, and this is another reason for the high FECO on Sb1Cu-5. Microkinetic modeling further validated the enhanced FECO on Sb1Cu-5 (211), and the results are shown in Fig. 4e. The calculated FECO was comparable to the experimental results for both pristine Cu and Sb1Cu-5. It was found that CO* takes up 70% coverage of the total sites for the CO2RR on pristine Cu, whereas that on Sb1Cu-5 (211) is only 7% (Supplementary Fig. 29). Finally, we further calculated the activity of CO production on Sb1Cu-5 (211) at varying potentials (Fig. 4f). As the potential decreases, all the barriers of electrochemical protonation gradually decrease, which will increase the reaction rate. A good linear correlation (slope = 1.05) was obtained between the experimental jCO and the theoretical rate of CO production, as shown in Fig. 4g. This indicates that the reaction mechanism and energetic trend above should be reliable.
To sum up, in this work, Sb1Cu catalysts were successfully synthesized using a co-reduction method, with isolated Sb-Cu atomic interfaces verified by HAADF-STEM and EXAFS. Sb1Cu-5 achieved an FECO of 95% at a current density of −150 mA cm−2 and maintained >90% FECO at −500 mA cm−2. Distinct from Cu with major C2+ products at high current density, high activity and selectivity towards CO production on Sb1Cu-5 was elaborated by tuning the Cu electronic structure via forming an isolated Sb-Cu atomic interface, and the improved performance can be explained by the enhanced ability of CO2 activation and CO desorption for Cu. This report provides a facile strategy to manipulate the reaction pathway through isolated heteroatom interfaces, which could be widely used in general element combinations and other electrocatalytic reactions.
Methods
Material synthesis
Chemicals
Copper (II) chloride dihydrate (CuCl2·2H2O, ACS), antimony trichloride (SbCl3, 99.9%), citric acid (H3Cit, 99.5%), sodium borohydride (NaBH4, 97%), hydrochloric acid (HCl, GR), antimony powder (Sb, 99%) and isopropanol (IPA, 99.5%) were purchased from Macklin. All chemicals were used without further purification.
Synthesis
Sb1Cu catalysts were synthesized by co-reduction of CuCl2 and SbCl3 with NaBH4. SbCl3 mixture solution was first prepared, including 1 mmol SbCl3, 3 mmol H3Cit, and 20 ml deionized (DI) water. In the typical synthesis of the Sb1Cu-5 catalyst, 3.2 ml SbCl3 mixture solution, 2 ml 1 M CuCl2·2H2O solution, and 1 ml 3 M HCl were added into 13.8 ml DI water to obtain the precursor solution. The above solution was then rapidly added into 10 ml 1 M NaBH4 solution in an ice bath and aged for 1 h. After a violent reaction, the obtained black precipitate was then washed with DI water and IPA several times, and dried under a vacuum overnight. The obtained black powder was kept in a glove box under an Ar atmosphere for storage. For the synthesis of the Sb1Cu-1.5 catalyst, 1.2 ml SbCl3 mixture solution, 2 ml 1 M CuCl2·2H2O solution, and 1 ml 3 M HCl were added into 15.8 ml DI water to obtain the precursor solution. The following steps were the same as Sb1Cu-5.
For the synthesis of the Cu catalyst, the precursor solution was obtained by adding 2 ml 1 M CuCl2·2H2O solution and 1 ml 3 M HCl into 17 ml DI water. For the synthesis of the Sb1Cu-10 catalyst, the precursor solution was obtained by adding 8 ml SbCl3 mixture solution, 2 ml 1 M CuCl2·2H2O solution, and 1 ml 3 M HCl into 9 ml DI water. The following steps were the same as the synthesis of Sb1Cu.
Electrochemical measurements
CO2RR performance test
All electrochemical measurements were conducted at room temperature using BioLogic VMP3. Typical three-electrode cell measurements were performed using a conventional flow cell and a glass H-cell. For the CO2RR measurements in the flow cell, precursor ink (18 mg of catalyst, mixed with 36 μL of 5% Nafion 117 solution solved in 5 ml of IPA) was sprayed onto a gas diffusion layer (YLS-30T) as the cathode electrode with a mass loading of ~1 mg cm−2. The Ag/AgCl wire in saturated KCl solution was used as the reference electrode, and Ni foam was used as the counter electrode. The working and counter electrodes were then placed on opposite sides of two 1-cm-thick polytetrafluoroethylene (PTFE) sheets with 0.4 cm × 1.5 cm channels such that the catalyst layer interfaced with the flowing electrolyte. The geometric surface area of the catalyst was 0.6 cm2. A Nafion 115 membrane was sandwiched between the two PTFE sheets to separate the chambers. CO2 flowed through the gas room behind the cathode, and the flow rate was kept at 30 sccm (monitored by an Alicat Scientific mass flow controller). In addition, 0.5 M KHCO3 was circulated as the cathode electrolyte at a flow rate of 0.7 ml min−1, while 1 M KOH was purged as the anode electrolyte. For measurements in the H-cell, catalysts were loaded on carbon paper (1 cm × 2 cm) as the working electrode. 0.5 M KHCO3 as the cathode electrolyte and 1 M KOH as the anode electrolyte were separated by a Nafion 115 film. All potentials were converted to the RHE reference scale using the relation ERHE = EAg/AgCl + 0.197 + pH × 0.059 and compensated for the solution resistance by 85%.
CO2RR product analysis
The gaseous products were tested by an online GC (PerkinElmer Clarus 690), which was equipped with a flame ionization detector, a thermal conductivity detector, and Molsieve 5 Å Column. The liquid products of Cu and Sb1Cu-1.5 were quantified by a 400 MHz NMR spectrometer (BUKER). About 100 μl of D2O (Sigma Aldrich, 99.9 at.%) and 0.05 μl of dimethyl sulfoxide (Sigma Aldrich, 99.9%) as an internal standard was added into 600 μl of the electrolyte after the electrolysis. The liquid products of Sb, Sb1Cu-5, and Sb1Cu-10 were determined by NMR and ion chromatography (Thermo Fisher Scientific ICS-600).
Long-term stability test
A membrane electrode assembly (MEA) was used for the long-term stability test with a zero-gap configuration where the anode, membrane, and cathode were compressed together to form one reactor. IrO2/Ti mesh was used as the anode, and an anion exchange membrane (Sustainion X37-FA, Dioxide Materials) was placed between the anode and cathode. CO2 was humidified upstream to the MEA and fed to the GDL cathode at 50 sccm. About 0.1 M KHCO3 was fed to the anode at 3 ml min−1 to supply anode oxygen evolution. A 100-h intrinsic stability test was conducted in the H-cell. Catalysts were loaded on carbon paper (1.5 cm × 2 cm) as the working electrode, with a graphite rod as the counter electrode. 0.5 M KHCO3 as the cathode electrolyte and 1 M KOH as the anode electrolyte were separated by a bipolar film. A 20 sccm CO2 flow was bubbled into the cathode electrolyte.
Tafel plot
The Tafel plots were employed to evaluate the CO2RR catalytic kinetics and fitted with the following equation: η = k×log(jCO) + b, where jCO is the CO partial current density, η is the overpotential for CO2+H2O+2e-→CO+2OH- (E0 = −0.11 V vs. RHE). The smaller slope k indicates faster kinetics towards CO production. If the rate-determining step (RDS) is the first electron transfer CO2-to-*CO2−, the Tafel slope is calculated by the following formula:
In this equation, α is the transfer coefficient and F is the Faraday constant. The standard values of the Tafel slopes based on different RDSs are further given in Supplementary Table 5.
FTacV measurements and analysis
FTacV experiments were carried out by a CHI 660e electrochemical workstation using an applied sine wave perturbation with an amplitude (ΔE) of 80 mV and a frequency (f) of 9.02 Hz superimposed onto the direct current (dc) ramp from 0 V to −1.20 V vs. RHE with a scan rate (v) of 10.57 mV s−1. A standard three-electrode H-cell setup was used. Ni foam was used as the counter electrode, and Ag/AgCl was used as the reference electrode. Sb1Cu-5 catalyst was coated on glassy carbon as the working electrode. After the use of an FT-inverse FT sequence, the ac data can be resolved into a dc component as well as fundamental, second, and higher-order ac harmonic components. The fourth harmonic components are very sensitive to fast heterogeneous electron transfer processes but essentially devoid of contributions from catalytic and background charging currents. The MECSim package was used for the simulation of the fourth harmonic component in FTacV, utilizing the ECEC model for four elementary steps, as illustrated in Supplementary Table 6. The parameters of kinetics were fitted through trial and error until a good fit was achieved.
In situ DEMS measurement
In situ differential electrochemical mass spectrometry (DEMS) was performed using a custom-made electrochemical capillary DEMS flow cell. The catalysts were loaded on the gas diffusion layer as the cathode, where CO2 flowed behind. A capillary was put into the gas outlet of the flow cell to draw the gas products into the DEMS sensor (PrismaPro). The signals of the mass-to-charge ratio (m/z) of 26 and 28 represented the products of C2H4 and CO, respectively. Linear sweep voltammetry (LSV) with a scan rate of 5 mV s−1 was conducted on the cathode. The onset potentials were determined according to the positions where the signal-to-noise ratio was greater than 5.
Characterization techniques
Transmission electron microscope (TEM) images were conducted on Hitachi H-7650 TEM equipment, and the acceleration voltage was 100 kV. Powder X-ray diffraction (PXRD) patterns were taken on a Philips X’Pert Pro Super diffractometer, and the standard λ value was 1.54178 Å for Cu-Kα radiation. X-ray photoelectron spectroscopy (XPS) measurements were conducted on VG ESCALAB MK II equipment, and the exciting source was Al Kα = 1486.6 eV. C 1 s of 284.6 eV was used to reference the binding energies. HAADF-STEM images and energy-dispersive spectra (EDS) elemental mapping were carried out on a Themis Z field-emission transmission electron microscope using Mo-based TEM grids, and the accelerating voltage was 200 kV. The in situ X-ray absorption fine structure (XAFS) spectra of the Cu K-edge were obtained at the BL11B beamline of the Shanghai Synchrotron Radiation Facility with a constant current of 200 mA, recorded under fluorescence mode with a Lytle detector in an H-cell, operated at 3.5 GeV under “top-up” mode. The XAFS spectra of the Sb K-edge were obtained at beamline 44 A of the Taiwan Photon Source (TPS). The Demeter software package was used to process the XAFS data. In situ Raman analysis was conducted using a LabRAM HR laser Raman analyzer (Horiba/Jobin Yvon, Longjumeau) equipped with a frequency-doubled Nd:YAG 785 nm laser. In situ electrochemical attenuated total reflection surface-enhanced infrared absorption spectroscopy (ATR-SEIRAS) experiments were conducted on a Thermo Scientific Nicolet iS50 FTIR spectrometer with silicon as the prismatic window at room temperature.
Computational details
We employed the Vienna Ab initio Simulation Package (VASP) to perform all density functional theory (DFT)53,54 calculations with the generalized gradient approximation (GGA) using the revised Perdew–Burke–Ernzerhof (rPBE) functional55. We chose the projected augmented wave (PAW)56,57 and a plane wave basis set with a kinetic energy cutoff of 400 eV. Geometry optimizations were performed with a force convergence smaller than 0.05 eV Å−1. Cu (211) and Sb1Cu-5 (211) surface models were built with four layers comprising 48 atoms. The two layers at the bottom were fixed, while the other atoms relaxed. Monkhorst-Pack k-points of (4 × 2 × 1) were applied for all the calculations on Cu (211) and Sb1Cu-5 (211). The Cu site nearest to the Sb atom has been discussed in the main text. The Cu sites far from the Sb atom should be very similar to pure Cu. We further studied the reaction activity of the Cu site, which is the next-nearest to the Sb atom on Sb1Cu-5 (211), as shown in Supplementary Fig. 30. CO is also the main product due to the lower barrier compared to HCOOH and C2+ formation. However, the adsorption energy of CO* at the top site on Cu (next-nearest to Sb atom, −0.21 eV) was close to pure Cu (−0.20 eV), more stable than CO* at the top site of Cu (nearest to Sb atom, −0.11 eV). CO* accounts for 77% of the total sites for CO2RR. This is inconsistent with the results of spectroscopic measurements, where the lower frequency of the CO* peak on Sb1Cu-5 implied weakened CO* adsorption and much lower *CO coverage relative to Cu (Fig. 3d). Hence, the Cu sites (next-nearest to Sb atom) on Sb1Cu-5 should not be the main active sites, as listed in the supplementary information. The Cu sites (nearest to the Sb atom) on Sb1Cu-5 should have major activity contributions, as shown in the main text.
All the adsorption energies were referenced to the gas phase energies of CO, H2O, and H2. The reaction-free energies (ΔG) were calculated as follows. ΔG = ΔE + ΔZPE –TΔS (T = 300 K), where ΔE is the electronic energy based on DFT calculations directly, and ΔZPE and ΔS are the corrections of zero point energy and entropy, respectively. Only vibrational motion was considered for adsorbates on the surface, while translational, rotational, and vibrational motions were all calculated for gas-phase species. The climbing image nudged elastic band (CI-NEB) method was used to locate the transition states58. The solvation effect was also calculated using implicit models through VASPsol59 calculations for both Cu (211) and Sb1Cu-5 (211). It has been validated that the CO adsorption energy on Cu (211) is comparable with previous work48 with an explicit solvation model and van der Waals corrections. In addition, the chemical potential of (H+ + e−) was calculated by G (H+ + e−) = ½ G (H2) at 0 V vs. RHE. A computational hydrogen electrode model was used to calculate the free energy change at varying potential60. Note that the desorption of CO* was considered to be potentially independent in the calculation of free energy change32.
Microkinetic modeling was used to simulate the reaction rate in the CO2RR, solved by CATKINAS code:61,62
The reaction rate on surfaces was described by63
Equations (2–4) were referred to in a previous work64. A temperature of 300 K was applied with all the gas-phase pressures (including PH+) set to 1.065. The reaction rate of CO2RR to C2+ products was estimated based on the Arrhenius equation and the CO* coverage at a steady state.
The FE was described by
where n(i) represents the electron transfer number and TOF(i) is the turnover frequency obtained by microkinetic simulation for product i.
We have also strictly investigated the potential effects on the adsorption energy of CO*. An electric field was applied in DFT calculations. Based on a parallel-plate capacitor model, a linear correlation between the electric field and absolute potential was approximated as following:66
where σ is the surface charge density and ε and ε0 are the dielectric constants of vacuum and water near the interface, which were set to 8.85 × 10−12 F m−1 and 2 (unitless), respectively. CH refers to the Helmholtz capacitance (μF cm−2), which was set to 25 μF cm−2. USHE is the electrode potential referenced to a standard hydrogen electrode (SHE). UPZC refers to the potential of zero charge (PZC) versus SHE, which was set to be −0.9 V67.
The SHE could be converted to the RHE by the following formula:
The calculated adsorption energies of CO* changed very little (<0.05 eV) with potentials between 0 and −1.2 V vs. RHE, which showed consistent trends for Cu (211) and Sb1Cu-5 (211). All insights and conclusions shown in the main text are still reliable. In addition, by varying potentials from −0.2 to −0.7 V vs. RHE, the calculated adsorption energies of CO* weaken from −0.13 to −0.11 eV on Sb1Cu-5 (211) and from −0.23 to −0.20 eV on Cu (211), which showed consistent trends with the results of the in situ ATR-SEIRAS spectra (Fig. 3b–d).
Additional microkinetic modeling was performed to double-check the reliability of the present kinetic analysis. All conclusions are not affected. Overall, the potential effects on the adsorption energy of CO* were ignored in the calculation of free energy change.
Data availability
All data were available in the main text or the supplementary materials. Source data of the figures in the main text are provided. Source data are provided with this paper.
References
Hepburn, C. et al. The technological and economic prospects for CO2 utilization and removal. Nature 575, 87–97 (2019).
Zhu, P. & Wang, H. High-purity and high-concentration liquid fuels through CO2 electroreduction. Nat. Catal. 4, 943–951 (2021).
Gattuso, J. P. et al. Contrasting futures for ocean and society from different anthropogenic CO(2) emissions scenarios. Science 349, aac4722 (2015).
Shafaat, H. S. & Yang, J. Y. Uniting biological and chemical strategies for selective CO2 reduction. Nat. Catal. 4, 928–933 (2021).
Kim, C. et al. Tailored catalyst microenvironments for CO2 electroreduction to multicarbon products on copper using bilayer ionomer coatings. Nat. Energy 6, 1026–1034 (2021).
Kim, J. Y. T. et al. Recovering carbon losses in CO2 electrolysis using a solid electrolyte reactor. Nat. Catal. 5, 288–299 (2022).
Gu, J. et al. Modulating electric field distribution by alkali cations for CO2 electroreduction in strongly acidic medium. Nat. Catal. 5, 268–276 (2022).
Xia, C. et al. Continuous production of pure liquid fuel solutions via electrocatalytic CO2 reduction using solid-electrolyte devices. Nat. Energy 4, 776–785 (2019).
Fan, L., Xia, C., Zhu, P., Lu, Y. & Wang, H. Electrochemical CO2 reduction to high-concentration pure formic acid solutions in an all-solid-state reactor. Nat. Commun. 11, 3633 (2020).
Monteiro, M. C. O., Philips, M. F., Schouten, K. J. P. & Koper, M. T. M. Efficiency and selectivity of CO2 reduction to CO on gold gas diffusion electrodes in acidic media. Nat. Commun. 12, 4943 (2021).
Chen, Y. et al. Carbon-based catalysts for Fischer-Tropsch synthesis. Chem. Soc. Rev. 50, 2337–2366 (2021).
Zhang, X. et al. Molecular engineering of dispersed nickel phthalocyanines on carbon nanotubes for selective CO2 reduction. Nat. Energy 5, 684–692 (2020).
Monteiro, M. C. O. et al. Absence of CO2 electroreduction on copper, gold and silver electrodes without metal cations in solution. Nat. Catal. 4, 654–662 (2021).
Zheng, T., Jiang, K. & Wang, H. Recent advances in electrochemical CO2 -to-CO conversion on heterogeneous catalysts. Adv. Mater. 30, e1802066 (2018).
Mariano, R. G., McKelvey, K., White, H. S. & Kanan, M. W. Selective increase in CO2 electroreduction activity at grain-boundary surface terminations. Science 358, 1187–1191 (2017).
Vijay, S. et al. Unified mechanistic understanding of CO2 reduction to CO on transition metal and single atom catalysts. Nat. Catal. 4, 1024–1031 (2021).
Zhong, M. et al. Accelerated discovery of CO2 electrocatalysts using active machine learning. Nature 581, 178–183 (2020).
Ren, S. et al. Molecular electrocatalysts can mediate fast, selective CO2 reduction in a flow cell. Science 365, 367–369 (2019).
Su, J. et al. Building a stable cationic molecule/electrode interface for highly efficient and durable CO2 reduction at an industrially relevant current. Energ. Environ. Sci. 14, 483–492 (2021).
Hai, X. et al. Scalable two-step annealing method for preparing ultra-high-density single-atom catalyst libraries. Nat. Nanotechnol. 17, 174–181 (2022).
Ren, W. et al. Isolated copper-tin atomic interfaces tuning electrocatalytic CO2 conversion. Nat. Commun. 12, 1449 (2021).
Zhang, G. et al. A general route via formamide condensation to prepare atomically dispersed metal–nitrogen–carbon electrocatalysts for energy technologies. Energ. Environ. Sci. 12, 1317–1325 (2019).
Zhao, L. et al. Cascade anchoring strategy for general mass production of high-loading single-atomic metal-nitrogen catalysts. Nat. Commun. 10, 1–11 (2019).
Zhao, Y. et al. Anchoring sites engineering in single-atom catalysts for highly efficient electrochemical energy conversion reactions. Adv. Mater. 33, e2102801 (2021).
Zhang, W. et al. Emerging dual-atomic-site catalysts for efficient energy catalysis. Adv. Mater. 33, e2102576 (2021).
Yu, S. et al. Nanoparticle assembly induced ligand interactions for enhanced electrocatalytic CO2 conversion. J. Am. Chem. Soc. 143, 19919–19927 (2021).
Kuhl, K. P., Cave, E. R., Abram, D. N. & Jaramillo, T. F. New insights into the electrochemical reduction of carbon dioxide on metallic copper surfaces. Energ. Environ. Sci. 5, 7050–7059 (2012).
Ma, W. et al. Electrocatalytic reduction of CO2 and CO to multi-carbon compounds over Cu-based catalysts. Chem. Soc. Rev. 50, 12897–12914 (2021).
Zhang, T. et al. Highly selective and productive reduction of carbon dioxide to multicarbon products via in situ CO management using segmented tandem electrodes. Nat. Catal. 5, 202–211 (2022).
Nitopi, S. et al. Progress and perspectives of electrochemical CO2 reduction on copper in aqueous electrolyte. Chem. Rev. 119, 7610–7672 (2019).
Deng, W., Zhang, P., Seger, B. & Gong, J. Unraveling the rate-limiting step of two-electron transfer electrochemical reduction of carbon dioxide. Nat. Commun. 13, 803 (2022).
Zheng, T. et al. Copper-catalysed exclusive CO2 to pure formic acid conversion via single-atom alloying. Nat. Nanotechnol. 16, 1386–1393 (2021).
Liu, C. et al. Nanoconfinement engineering over hollow multi-shell structured copper towards efficient electrocatalytical C-C coupling. Angew. Chem. Int. Ed. 61, e202113498 (2022).
Timoshenko, J. et al. Steering the structure and selectivity of CO2 electroreduction catalysts by potential pulses. Nat. Catal. 5, 259–267 (2022).
Peng, C. et al. Double sulfur vacancies by lithium tuning enhance CO2 electroreduction to n-propanol. Nat. Commun. 12, 1580 (2021).
Wang, X. et al. Morphology and mechanism of highly selective Cu(II) oxide nanosheet catalysts for carbon dioxide electroreduction. Nat. Commun. 12, 794 (2021).
Li, H. et al. Selective reduction of CO2 to CO on an Sb-modified Cu electrode: spontaneous fabrication and physical insight. ACS Catal. 11, 6846–6856 (2021).
Mou, S. et al. Cu2Sb decorated Cu nanowire arrays for selective electrocatalytic CO2 to CO conversion. Nano Res. 14, 2831–2836 (2021).
Zeng, J. et al. Novel insights into Sb-Cu catalysts for electrochemical reduction of CO2. Appl. Catal. B Environ. 306, 121089 (2022).
Limaye, A. M., Zeng, J. S., Willard, A. P. & Manthiram, K. Bayesian data analysis reveals no preference for cardinal Tafel slopes in CO2 reduction electrocatalysis. Nat. Commun. 12, 703 (2021).
Snitkoff-Sol, R. Z. et al. Quantifying the electrochemical active site density of precious metal-free catalysts in situ in fuel cells. Nat. Catal. 5, 163–170 (2022).
Zhang, Y. et al. Direct detection of electron transfer reactions underpinning the tin-catalyzed electrochemical reduction of CO2 using fourier-transformed ac voltammetry. ACS Catal. 7, 4846–4853 (2017).
Chang, X. et al. Determining intrinsic stark tuning rates of adsorbed CO on copper surfaces. Catal. Sci. Technol. 11, 6825–6831 (2021).
An, H. et al. Sub-second time-resolved surface-enhanced Raman spectroscopy reveals dynamic CO intermediates during electrochemical CO2 reduction on copper. Angew. Chem. Int. Ed. 60, 16576–16584 (2021).
Chernyshova, I. V., Somasundaran, P. & Ponnurangam, S. On the origin of the elusive first intermediate of CO2 electroreduction. P. Nalt. Acad. Sci. USA 115, E9261–E9270 (2018).
Yin, J. et al. Customizable CO2 electroreduction to C1 or C2+ products through Cuy/CeO2 interface engineering. ACS Catal. 12, 1004–1011 (2022).
Schouten, K. J. P., Qin, Z., Gallent, E. P. & Koper, M. T. M. Two pathways for the formation of ethylene in CO reduction on single-crystal copper electrodes. J. Am. Chem. Soc. 134, 9864–9867 (2012).
Liu, X. et al. Understanding trends in electrochemical carbon dioxide reduction rates. Nat. Commun. 8, 15438 (2017).
Guo, C., Fu, X. & Xiao, J. Theoretical insights on the synergy and competition between thermochemical and electrochemical steps in oxygen electroreduction. J. Phys. Chem. C 124, 25796–25804 (2020).
Chan, K. & Norskov, J. K. Potential dependence of electrochemical barriers from ab initio calculations. J. Phys. Chem. Lett. 7, 1686–1690 (2016).
Chan, K. & Norskov, J. K. Electrochemical barriers made simple. J. Phys. Chem. Lett. 6, 2663–2668 (2015).
Fang, Y.-H., Wei, G.-F. & Liu, Z.-P. Constant-charge reaction theory for potential-dependent reaction kinetics at the solid–liquid interface. J. Phys. Chem. C 118, 3629–3635 (2014).
Kresse, G. & Hafner, J. Ab initio molecular-dynamics simulation of the liquid-metal–amorphous-semiconductor transition in germanium. Phys. Rev. B 49, 14251–14269 (1994).
Kresse, G. & Furthmuller, J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comp. Mater. Sci. 6, 15–50 (1996).
Perdew, J. P., Burke, K. & Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865–3868 (1996).
Blochl, P. E., Jepsen, O. & Andersen, O. K. Improved tetrahedron method for Brillouin-zone integrations. Phys. Rev. B 49, 16223–16233 (1994).
Kresse, G. & Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 59, 1758–1775 (1999).
Henkelman, G., Uberuaga, B. P. & Jonsson, H. A climbing image nudged elastic band method for finding saddle points and minimum energy paths. J. Chem. Phys. 113, 9901–9904 (2000).
Mathew, K., Sundararaman, R., Letchworth-Weaver, K., Arias, T. A. & Hennig, R. G. Implicit solvation model for density-functional study of nanocrystal surfaces and reaction pathways. J. Chem. Phys. 140, 084106 (2014).
Nørskov, J. K., Rossmeisl, J., Logadottir, A. & Lindqvist, L. Origin of the overpotential for oxygen reduction at a fuel-cell cathode. J. Phys. Chem. B 108, 17886–17892 (2004).
Chen, J., Jia, M., Hu, P. & Wang, H. CATKINAS: a large-scale catalytic microkinetic analysis software for mechanism auto-analysis and catalyst screening. J. Comput. Chem. 42, 379–391 (2021).
Guo, C., Mao, Y., Yao, Z., Chen, J. & Hu, P. Examination of the key issues in microkinetics: CO oxidation on Rh(111). J. Catal. 379, 52–59 (2019).
Chorkendorff, I. & Niemantsverdriet, J. W. Concepts of Modern Catalysis and Kinetics: Reaction Rate Theory (John Wiley & Sons, 2003).
Fu, X., Li, J., Long, J., Guo, C. & Xiao, J. Understanding the product selectivity of syngas conversion on ZnO surfaces with complex reaction network and structural evolution. ACS Catal. 11, 12264–12273 (2021).
Chen, J., Mao, Y., Wang, H. & Hu, P. Reversibility iteration method to understand reaction networks and to solve micro-kinetics in heterogeneous catalysis. ACS Catal. 6, 7078–7087 (2016).
Kelly, S. R., Kirk, C., Chan, K. & Nørskov, J. K. Electric field effects in oxygen reduction kinetics: rationalizing pH dependence at the Pt(111), Au(111), and Au(100) electrodes. J. Phys. Chem. C 124, 14581–14591 (2020).
Ludwig, T., Singh, A. R. & Nørskov, J. K. Acetonitrile transition metal interfaces from first principles. J. Phys. Chem. Lett. 11, 9802–9811 (2020).
Acknowledgements
C.X. acknowledges the National Key Research and Development Program of China (2022YFB4102000), NSFC (22102018 and 52171201), the Natural Science Foundation of Sichuan Province (2022NSFSC0194), the Central Government Funds of Guiding Local Scientific and Technological Development for Sichuan Province (2021ZYD0043), the Hefei National Research Center for Physical Sciences at the Microscale (KF2021005), and the University of Electronic Science and Technology of China for startup funding (A1098531023601264). J.Z. acknowledges the National Key Research and Development Program of China (2021YFA1500500 and 2019YFA0405600), the National Science Fund for Distinguished Young Scholars (21925204), the National Natural Science Foundation of China (NSFC; U19A2015), the Dalian National Laboratory (DNL) Cooperation Fund, Chinese Academy of Science (CAS; DNL202003), K.C. Wong Education (GJTD-2020-15), Fundamental Research Funds for the Central Universities, Provincial Key Research and Development Program of Anhui (202004a05020074) and University of Science and Technology of China (USTC) Research Funds of the Double First-Class Initiative (YD2340002002). J.X. acknowledges the National Key Research and Development Program of China (No. 2021YFA1500702), the NSFC (22172156), the DNL Cooperation Fund, CAS (DNL202003), the AI S&T Program of Yulin Branch, Dalian National Laboratory For Clean Energy, CAS, Grant No.DNL-YLA202205, and the Strategic Priority Research Program of the Chinese Academy of Sciences (XDB36030200). T.Z. acknowledges the NSFC (22005291 and 22278067). We thank beamline BL11B of the Shanghai Synchrotron Radiation Facility and 44 A of the Taiwan Photon Source (TPS) at the National Synchrotron Radiation Research Center, Taiwan, for providing the beamtime.
Author information
Authors and Affiliations
Contributions
C.X. conceptualized the project. C.X., J.Z., and J.X. supervised the project. J.L. and H.Z. prepared the catalysts and performed the catalytic tests. J.L., H.Z., Z.X., D.Z., and T.Z. performed the catalyst characterizations. S.H. conducted the HAADF-STEM characterizations. Y. Dai and P.C. performed the EXAFS measurements. J.L. and R.Z. performed the in situ measurements. X.D., J.X., Y. Ding, and L.Z. performed the DFT calculations. J.L., C.X., J.Z., and J.X. wrote the paper with input from all authors. All authors discussed the results and commented on the manuscript.
Corresponding authors
Ethics declarations
Competing interests
A China provisional patent application (CN202210385531.1) based on the technology described in this work was filed in April 2022 by C.X., J.L., and H.Z. at the University of Electronic Science and Technology of China. The remaining authors declare no competing interests.
Peer review
Peer review information
Nature Communications thanks the other anonymous reviewer(s) for their contribution to the peer review of this work. Peer review reports are available
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Source data
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Li, J., Zeng, H., Dong, X. et al. Selective CO2 electrolysis to CO using isolated antimony alloyed copper. Nat Commun 14, 340 (2023). https://doi.org/10.1038/s41467-023-35960-z
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-023-35960-z
This article is cited by
-
Promoting Cu-catalysed CO2 electroreduction to multicarbon products by tuning the activity of H2O
Nature Catalysis (2023)
-
Constructing asymmetric double-atomic sites for synergistic catalysis of electrochemical CO2 reduction
Nature Communications (2023)
-
Research progress on electrochemical CO2 reduction for Cu-based single-atom catalysts
Science China Materials (2023)
-
Applications of Metal–Organic Frameworks and Their Derivatives in Electrochemical CO2 Reduction
Nano-Micro Letters (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.