Abstract
Applying in-plane uniaxial pressure to strongly correlated low-dimensional systems has been shown to tune the electronic structure dramatically. For example, the unconventional superconductor Sr2RuO4 can be tuned through a single Van Hove point, resulting in strong enhancement of both Tc and Hc2. Out-of-plane (c axis) uniaxial pressure is expected to tune the quasi-two-dimensional structure even more strongly, by pushing it towards two Van Hove points simultaneously. Here, we achieve a record uniaxial stress of 3.2 GPa along the c axis of Sr2RuO4. Hc2 increases, as expected for increasing density of states, but unexpectedly Tc falls. As a first attempt to explain this result, we present three-dimensional calculations in the weak interaction limit. We find that within the weak-coupling framework there is no single order parameter that can account for the contrasting effects of in-plane versus c-axis uniaxial stress, which makes this new result a strong constraint on theories of the superconductivity of Sr2RuO4.
Similar content being viewed by others
Introduction
Sr2RuO4 is a famous exemplar of unconventional superconductivity, due to the quality of the available samples and the precision of knowledge about its normal state, and because the origin of its superconductivity remains unexplained in spite of strenuous effort1,2,3,4. No proposed order parameter is able straightforwardly to account for all the existing experimental observations. The greatest conundrum is posed by evidence that the order parameter combines even parity5,6,7,8 with time reversal symmetry breaking9,10,11. This combination of properties implies, if there is no fine tuning, that the superconducting order parameter is dxz ± idyz12. Under conventional understanding, this is not expected because the horizontal line node at kz = 0 implies interlayer pairing, while the electronic structure of Sr2RuO4 is highly two-dimensional13,14.
This puzzle has led to substantial theoretical activity. Two recent proposals are s ± id15,16 and d ± ig17,18 order parameters, which require tuning to obtain TTRSB ≈ Tc (where TTRSB is the time reversal symmetry breaking temperature), but avoid horizontal line nodes. A mixed-parity state19 and superconductivity that breaks time reversal symmetry only in the vicinity of extended defects20 have been proposed to account for the absence of a resolvable heat capacity anomaly at TTRSB21. Interorbital pairing through Hund’s coupling is also under discussion22,23,24,25; with some tuning of parameters this mechanism could yield dxz ± idyz order. Quasiparticle interference data, on the other hand, give evidence for a \({d}_{{x}^{2}-{y}^{2}}\)-like gap, and a recent junction experiment shows time-reversal invariance26,27.
Uniaxial stress has become an important probe of the superconductivity of Sr2RuO4. When stress is applied along the [100] direction, the largest Fermi surface sheet (the γ sheet— see Fig. 1) distorts anisotropically, and undergoes a Lifshitz transition from an electron-like to an open geometry at −0.75 GPa (where negative values denote compression)28. The effect on the superconductivity is profound: Tc increases from 1.5 K in unstressed Sr2RuO4 to 3.5 K, while the c-axis upper critical field Hc2 increases by a factor of twenty29. This very strong enhancement is qualitatively consistent with, for example, a \({d}_{{x}^{2}-{y}^{2}}\) order parameter. Under compression along the [100] direction, the Lifshitz transition occurs at approximately (kx, ky) = (0, ± π/a), which we label the Y point. As the transition occurs, the Fermi velocity at the Y point falls to nearly zero, which in general is expected to increase Tc and Hc2 of order parameters such as \({d}_{{x}^{2}-{y}^{2}}\) in which the gap is large at the Y point. The data under [100] uniaxial stress argue against, for example, a dxy order parameter.
a–c Cross-sections at kz = 0 of calculated Fermi surfaces of Sr2RuO4 at the indicated strains. The heavy dashed lines indicate the zone of the RuO2 sheet, and the thin gray lines the 3D zone of Sr2RuO4. X and Y label high-symmetry points of the RuO2 zone. (To simplify discussion, we refer throughout this paper to the X and Y points defined in the 2D zone, rather than the points of the full 3D zone). a The electron-to-open Lifshitz transition induced by in-plane strain, from Ref. 29. It occurs at εxx = −0.0075 in the calculation, and εxx = −0.0044 experimentally28. b Unstressed Sr2RuO4. c The electron-to-hole Lifshitz transition under c-axis compression. d Calculated Fermi-level DOS against energy for a series of strains εzz. e Calculated Fermi-level DOS against εzz.
Naively, then, Tc and Hc2 might be expected to rise even further under compression along the c axis. c-axis compression raises the energy of the dxz and dyz bands relative to the dxy band, and the resulting transfer of carriers expands the γ sheet, pushing it towards a Lifshitz transition from an electron-like to a hole-like geometry30. This transition occurs at both the X and Y points — see Fig. 1c — so the increase in the Fermi-level density of states (DOS) as it is approached is expected to be larger than for the electron-to-open Lifshitz transition induced by in-plane stress. Under a-axis compression Tc increases strongly well before the Lifshitz transition is reached, and so generically we expect this to occur for c-axis stress, too. The weak-coupling renormalization group study of Ref. 31 and functional renormalization group study of Ref. 32 both predict a rapid increase in Tc with approach to the electron-to-hole Lifshitz transition.
The electron-to-hole transition has been approached, and crossed, in thin films through epitaxial strain, and in bulk crystals by substitution of La for Sr33,34,35, but in both cases the superconductivity was suppressed by disorder. Here, we apply up to 3.2 GPa along the c axis of Sr2RuO4. This is a record uniaxial stress for bulk Sr2RuO4, and was achieved by sculpting samples with a focused ion beam to concentrate stress. Hc2 increases, as expected from the increasing density of states. However, unexpectedly, Tc decreases. In other words, approaching the Lifshitz transition at either the X or Y point dramatically enhances Tc, while approaching both suppresses Tc. This is a major surprise. In a first attempt to address this issue we present calculations in the limit of weak coupling, that take into account the three-dimensional structure of the Fermi surfaces. Although these show that c-axis compression reduces the transition temperatures of certain order parameters, no order parameter could be identified for which the effects of both out-of-plane and in-plane pressure were captured. Our experimental finding therefore consitutes a major new constraint on theories of the superconductivity of Sr2RuO4.
Results
Electronic structure calculations
We start with density functional theory (DFT) calculations of Sr2RuO4 under c-axis compression, as a guide to the likely effects of c-axis strain on the electronic structure. Figure 1 shows our results. Panel a shows the Fermi surfaces under 0.75% compression along the a axis, panel b those of the unstrained lattice, and panel c those under 2.5% compression along the c axis. The calculations are done under conditions of uniaxial stress, meaning that the transverse strains are the longitudinal strain times the relevant Poisson’s ratios for Sr2RuO4. DFT calculations reproduce well the changes under [100] uniaxial stress observed in ARPES measurements36. Technical details of the calculation are provided in the Methods section.
The calculations predict that the electron-to-hole transition will occur at εzz = −0.025. Under a-axis compression, these calculations predict that the electron-to-open transition occurs at εxx = −0.0075, whereas it was observed experimentally to occur at εxx = −0.004428, so this c-axis prediction might similarly overestimate the level of compression required. The uncertainty arises from the fact that the distance to the Lifshitz transition is sensitive to meV-level energy shifts, likely driven by many-body renormalisation28. Low-temperature ultrasound data give a c-axis Young’s modulus of 219 GPa37, so εzz = −0.025 corresponds to σzz ≈ −5.5 GPa. Separately, we note also that while kz warping increases on all the Fermi sheets, as expected for c-axis compression, the β sheet has the strongest kz warping both at εzz = 0 and at the Lifshitz transition; see the Methods section for an illustration.
Experimental results
Four samples were measured. For good stress homogeneity, samples should be elongated along the stress axis, which is a challenge for the c axis because the cleave plane of Sr2RuO4 is the ab plane. A plasma focused ion beam, in which material is milled using a beam of Xe ions, was therefore used to shape the samples. Sample 1 was prepared with a uniform cross section, and a large enough stress, σzz = −0.84 GPa, was achieved to observe a clear change in Tc. To go further, the other samples were all sculpted into dumbell shapes, with the wide ends providing large surfaces for coupling force into the sample. FIB microstructuring has been used to achieve large c-axis stress in CaFe2As238, but here we needed to retain sufficient sample volume for high-precision magnetic susceptibility measurements. For measurement of Tc in the neck portion, two concentric coils of a few turns each were wound around the neck. Samples 1 and 4 also had electrical contacts, for measurement of the c-axis resistivity ρzz. Photographs of samples 2 and 4 are shown in the Methods section.
Sample 4 was measured in apparatus that incorporated a sensor of the force applied to the sample39, from which the stress in the sample could be accurately determined. Samples 1–3 were mounted into apparatus that had a sensor only of the displacement applied to the sample, which is an imperfect measure of the sample strain because the measured displacement includes deformation in the epoxy that holds the sample. Therefore, a displacement-to-stress conversion was applied to samples 1–3 to bring the rate of change of Tc over the stress range 0.92 < σzz < − 0.20 GPa into agreement with that of sample 4. In other words, we impose on our data an assumption that the initial rate of decrease in Tc is the same in all the samples, which is reasonable because their zero-stress Tc’s are very similar: all are between 1.45 and 1.50 K.
We begin by showing resistivity data, in Fig. 2. The plotted resistivities are corrected for the expected stress-induced change in sample geometry (reduced length and increased width), using the low-temperature elastic moduli reported in Ref. 37, and making the assumption that stress and strain are linear over this entire range. At zero stress the resistivity of sample 4 shows a sharp transition into the superconducting state at 1.55 K. This sharpness, and the fact that it only slightly exceeds the transition temperature seen in susceptibility, indicate high sample quality. With compression, Tc decreases. The normal-state resistivity also decreases, following the general expectations that c-axis compression should increase kz dispersion.
Main panel: c-axis resistivity ρzz versus stress σzz at 1.9 K, normalized by its σzz = 0 value. Note that the stress scale of sample 1 is adjusted so that dTc/dσzz as measured through the Meissner effect matches that from sample 4 over the range − 0.92 < σzz < − 0.2 GPa. At σzz = 0, ρzz(1.9K) of samples 1 and 4 is 0.278 and 0.228 mΩ-cm, respectively. Inset: ρzz versus temperature for sample 4 at 0, − 0.37, − 0.85, − 1.25, and − 1.64 GPa.
We find elastoresistivities (1/ρzz)dρzz/dεzz, obtained from linear fits over the range − 0.5 < σzz < 0 GPa, of 37 and 32 for samples 1 and 4, respectively. Sample 4 was compressed to −1.7 GPa, and its resistivity does not show any major deviation from linearity over this range. The scatter in the data at strong compression may be a consequence of cracking in the electrical contacts— we show below that the sample deformation was almost certainly elastic.
We now show the effects of c-axis compression on magnetic susceptibility. Figure 3a–c shows the transitions of samples 2–4 in susceptibility; the data shown are the mutual inductance M of the sense coils versus temperature. To check that sample deformation remained elastic, we repeatedly cycled the stress to confirm that the form of the M(T) curves remained unchanged; see the Methods section for examples. For samples 3 and 4, the transition remained narrow as stress was applied, indicating high stress homogeneity. For sample 2, there was a tail on the high-temperature side of the transition, that was stronger at higher compressions. We attribute it to in-plane strain, possibly originating in the fact that sample 2 was not as well aligned as samples 3 and 4. A similar, though weaker, tail is also visible for sample 3.
a–c Mutual inductance M of the sense coils versus temperature for samples 2–4, at various applied stresses σzz. The lines indicate the selected thresholds for determination of Tc. For sample 2, under large ∣σzz∣ a tail appears on the transitions, which we attribute to in-plane stress, and a low threshold is chosen to avoid this tail. d Tc versus stress for all the samples. The stress scales for samples 1–3 are scaled to bring dTc/dσzz into agreement with that of sample 4 over the stress range labeled “fitted range”, − 0.92 to − 0.20 GPa.
We note that the width of the transitions in Fig. 3a–c — ≈ 50 mK — will be a consequence of defects and/or an internal distribution in the in-plane strain. Although there will also be inhomogeneity in εzz, this is not the driver of the transition width: the distribution would have to have a width of ~1 GPa, which is not plausible.
Figure 3 (d) shows Tc versus stress for all the samples. Tc is taken as the temperature where M crosses a threshold. For samples 1, 3, and 4, we select a threshold at ≈ 50% of the height of the transition, and for sample 2, 20%, in order to minimize the influence from the high-temperature tail. Tc is seen to decrease almost linearly out to σzz ≈ − 1.8 GPa. For sample 4 (to which, as described above, the other samples are referenced), dTc/dσzz in the limit σzz → 0 is 76 ± 5 mK/GPa. The error is 6%: we estimate a 5% error on the calibration of the force sensor of the cell, and a 3% error on the cross-sectional area of the sample (155 × 106 μm2).
At σzz ≲ − 1.8 GPa, the stress dependence of Tc flattens markedly. In sample 3, Tc resumes its decrease for σzz < − 3 GPa. We show in the Methods section that both the flattening and this further decrease reproduce when the stress is cycled, which, in combination with the narrowness of the transitions, shows that this behavior is intrinsic, not an artefact of any drift or non-elastic deformation in the system.
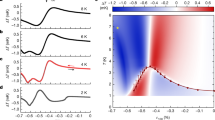
Figure 4 shows measurements of the c-axis upper critical field. M(H) for samples 2 and 3 at constant temperature T ≈ 0.3 K is shown in panels a and b. In Fig. 4c, we plot Hc2 versus stress, taking Hc2 as the fields at which M crosses the thresholds indicated in panels a–b. Hc2 increases as stress is applied, as generally expected when the density of states increases. The increase is faster for sample 2 than sample 3, which may be an artefact of the tail on the transition for sample 2.
a, b Susceptibility versus applied field ∥c for samples 2 and 3, at fixed temperatures of 300 mK and 310 mK. For sample 3, the raw data are plotted. For sample 2, the signal magnitude shifted from run to run, probably due to slipping of the coils against the sample, so data are normalized by the readings at 0 and 100 mT. The horizontal lines indicate the thresholds for determination of Hc2. c Hc2(T ≈ 0.3K) versus stress for samples 2 and 3. d \({H}_{{{{{{{{\rm{c2}}}}}}}}}/{T}_{{{{{{{{\rm{c}}}}}}}}}^{2}\), normalized by its zero-stress value, versus stress for sample 3.
The quantity \({H}_{{{{{{{{\rm{c2}}}}}}}}}/{T}_{{{{{{{{\rm{c}}}}}}}}}^{2}\) is particularly informative: if pairing strength were modified without changing the gap structure, Hc2 would be proportional to \({T}_{{{{{{{{\rm{c}}}}}}}}}^{2}\). As shown in Fig. 4d, we observe \({H}_{{{{{{{{\rm{c2}}}}}}}}}/{T}_{{{{{{{{\rm{c}}}}}}}}}^{2}\) to increase by 40% by σzz = − 3.0 GPa. Slower quasiparticles are less strongly affected by magnetic field, so what this result means is that the Fermi velocity decreases on portions of the Fermi surface where the gap is large.
We conclude this section with a note on the peak effect — the small maximum in the susceptibility just below Hc2, visible in Fig. 4 (a, b). The peak effect occurs when there is a range of temperature below Tc where vortex motion is uncorrelated, allowing individual vortices to find deeper pinning sites40. The peak is suppressed by c-axis compression, and it is suppressed downward rather than by being smeared horizontally along the H axis, which means that this suppression is not an artefact of a spread in Hc2 due to strain inhomogeneity. It could indicate stronger pinning, due to the reduction in the coherence length.
Weak-coupling calculations
As explained in the introduction, there is an apparent contradiction between the increase of Tc under a-axis strain reported in previous work (which suggests anti-nodes at the X and Y points) and the decrease of Tc under c-axis pressure (which suggests nodes at the X and Y points). To see if this puzzle has a straightforward solution, we perform weak-coupling calculations for repulsive Hubbard models, as developed in Refs. 41,42,43,44,45,46,47,48,49,50. To capture possible changes in the 3D gap structure, we employ three-dimensional Fermi surfaces51. These are described by a three-band (4d xy, xz, and yz) tight-binding model. The hopping integrals are derived from the Ru-centred Wannier functions obtained in the DFT calculation presented above. Our tight-binding model takes the form
\({{{{{{{{\boldsymbol{\psi }}}}}}}}}_{s}({{{{{{{\bf{k}}}}}}}})={[{c}_{xz,s}({{{{{{{\bf{k}}}}}}}}),{c}_{yz,s}({{{{{{{\bf{k}}}}}}}}),{c}_{xy,\bar{s}}({{{{{{{\bf{k}}}}}}}})]}^{T}\), and \({{{{{{{{\mathcal{H}}}}}}}}}_{s}({{{{{{{\bf{k}}}}}}}})\) incorporates spin-orbit coupling, inter-orbital and intra-orbital terms. The complete set of tight-binding parameters retained here is given in the Methods section.
In Fig. 5a, we show the tight-binding Fermi surfaces at εzz = 0 and − 0.02. In Fig. 5b, we show the orbital weight on the γ sheet at kz = 0. As the γ sheet expands, the orbital mixing around its avoided crossings with the β sheet is reduced, and it becomes more dominated by xy orbital weight.
a Cuts through the tight-binding Fermi surfaces employed in our weak-coupling calculations, at εzz = 0 and − 0.02. The surfaces at εzz = − 0.02 are colored by orbital content. The solid lines show the Brillouin zone boundaries of the body-centred tetragonal unit cell of Sr2RuO4, and the dotted line of the 2D zone of the RuO2 sheets. b Orbital weights on the γ sheet at kz = 0 in this model. c Leading eigenvalues as a function of εzz for J/U = 0.15, and d \({H}_{{{{{{{{\rm{c2}}}}}}}}}(T\to 0)/{T}_{{{{{{{{\rm{c}}}}}}}}}^{2}\), normalised by its value at zero strain, of the leading eigenstate versus εzz in each channel. In the legend, fi is any function that transforms as \(\sin {k}_{i}\), d0(k) is the gap function for the even-parity irreducible representations, and d(k) the d-vector for Eu. In the A2g channel, there is a level crossing between εzz = 0 and − 0.0075, that results an anomalously strong increase in \({H}_{{{{{{{{\rm{c2}}}}}}}}}/{T}_{{{{{{{{\rm{c}}}}}}}}}^{2}\). e Gap structure in the B2g channel versus εzz, on the α, β, and γ Fermi sheets.
To H0 we add on-site Coulomb terms projected onto the t2g orbitals52 (Methods Eq. (8)) and study the solutions to the linearized gap equation in the weak-coupling limit U/t ≪ 1, where U is the intraorbital Coulomb repulsion and t is the leading tight-binding term. We take the interorbital on-site Coulomb repulsion to be \({U}^{\prime}=U-2J\), where J is the Hund’s coupling, and the pair-hopping Hund’s interaction \({J}^{\prime}\) to be equal to the spin-exchange Hund’s interaction J. Under these assumptions, the remaining free parameter is J/U. We take J/U = 0.15, which is close to the value J/U = 0.17 found in Refs. 53,54. The linearized gap equation reads
where μ and ν are band indices, ∣Sν∣ is the area of Fermi surface sheet ν, and \(\bar{{{\Gamma }}}\) is the two-particle interaction vertex calculated consistently to order \({{{{{{{\mathcal{O}}}}}}}}({U}^{2}/{t}^{2})\). Solutions to Eq. (2) with λ < 0 signal the onset of superconductivity, at the critical temperature \({T}_{c} \sim W\exp (-1/|\lambda|)\), where W is the bandwidth.
In a pseudo-spin basis each eigenvector φ belongs to one of the ten irreducible representations of the crystal point group D4h48,55. We calculate the leading eigenvalues in four even-parity channels, B1g, B2g, A1g, and A2g — see the legend of Fig. 5c–d. The Eg channel — dxz ± idyz — has been found to be strongly disfavored in weak-coupling calculations51, and so is not considered here.
A subset of the present authors have found, in a previous weak-coupling calculation, that the odd-parity order parameters track each other closely as J/U is varied, with a splitting that is small compared with that between the even-parity orders, and between the odd- and even-parity orders51. Ref. 56, likewise, finds the splitting between the odd-parity orders to be small. For this reason, we calculate only one odd-parity channel, Eu (px ± ipy), and its behaviour can safely be taken to represent the qualitative behaviour of odd-parity order.
The leading eigenvalues in each channel as a function of εzz are shown in Fig. 5c. Although, as in Ref. 51, odd-parity order is found to be favored, calculations in the random phase approximation at similar J/U tend to favor even-parity order15,56. A tendency towards odd-parity order appears to be a feature of calculations in the weak-coupling limit. We note also that the ordering of the channels differs from what was found in Ref. 51, due to a different tight-binding parametrisation. The ordering is sensitive to the parametrisation, and so we focus discussion here on trends with applied strain.
The weak-coupling results show a dichotomy in the strain dependence of Tc: Tc in the channels that have symmetry-imposed nodes at the X and Y points (Eu, A2g, and B2g) decreases with initial c-axis compression. These nodes coincide with the regions of highest local density of states, and this result is an indication that order parameters in these channels are less able to take advantage of the increase in Fermi-level density of states induced by c-axis compression. However, under stronger compression Tc increases modestly in all channels.
In the weak-coupling calculations of Ref. 29, the contrast in the response to a-axis uniaxial stress between order parameters with and without nodes at the X and Y points was found to be stronger in \({H}_{{{{{{{{\rm{c2}}}}}}}}}/{T}_{{{{{{{{\rm{c}}}}}}}}}^{2}\) than Tc, and so we also calculate \({H}_{{{{{{{{\rm{c2}}}}}}}}}/{T}_{{{{{{{{\rm{c}}}}}}}}}^{2}\), following the procedure in Ref. 29. Results are shown in Fig. 5d. We find that changes in \({H}_{{{{{{{{\rm{c2}}}}}}}}}/{T}_{{{{{{{{\rm{c}}}}}}}}}^{2}\) correlate closely with shifts in the gap weight onto the γ sheet, which has the lowest Fermi velocity. For example, gap weight in the B2g channel, shown in Fig. 5e, shifts from the β to the γ sheet as stress is initially applied, and \({H}_{{{{{{{{\rm{c2}}}}}}}}}/{T}_{{{{{{{{\rm{c}}}}}}}}}^{2}\) correspondingly increases. At strong compression, gap weight shifts back to the β sheet, and \({H}_{{{{{{{{\rm{c2}}}}}}}}}/{T}_{{{{{{{{\rm{c}}}}}}}}}^{2}\) decreases. This occurs because as the γ sheet expands it comes closer to its copies in adjacent zones, which disfavours a large gap on this sheet because in the B2g channel the gap changes sign across the zone boundary. Among the even-parity channels, for εzz < − 0.015\({H}_{{{{{{{{\rm{c2}}}}}}}}}/{T}_{{{{{{{{\rm{c}}}}}}}}}^{2}\) increases for those without nodes along the Γ-X and Γ-Y lines, and decreases for those with. The complete set of calculated gap structures is shown in the Methods section.
We conclude this section by noting that although a kz dependence of the gap structure is seen in all channels, we do not find dramatic stress-induced changes in the kz dependence in any channel. Separately, in the A2g channel there is a level crossing between εzz = 0 and −0.0075. We plot only the leading eigenvalues in Fig. 5; this level crossing causes a large change in the leading gap structure and an anomalously large increase in \({H}_{{{{{{{{\rm{c2}}}}}}}}}/{T}_{{{{{{{{\rm{c}}}}}}}}}^{2}\).
Discussion
The unexpected decrease of Tc as two Van Hove points in k-space are approached under c-axis compression is the key experimental result that we report. It might provide a vital clue about the nature of the superconducting state in Sr2RuO4, because it is so different to the response to in-plane, a-axis pressure. The DFT calculations indicate that our largest achieved stress, −3.2 GPa, is around 60% of the way to the Lifshitz transition, and if the calculations overestimate the compression required to reach the Lifshitz transition, as they did for in-plane stress, we might have come even closer. The contrast between the effects of a- and c-axis stress is unmistakable: 60% of the way to the electron-to-open Lifshitz transition under a-axis stress, Tc is 0.7 K higher than in the unstressed sample28.
The response of Tc under c-axis compression allows resolution of the stress dependence of Tc into components through comparison with the the effect of hydrostatic compression, which also suppresses Tc. We obtain the coefficients α and β in the expression
where ΔV/V = εxx + εyy + εzz is the fractional volume change of the unit cell, and εzz − (εxx + εyy)/2 is a volume-preserving tetragonal distortion. Refs. 12,57,58 report dTc/dσhydro = 0.22 ± 0.02, 0.24 ± 0.02, and 0.21 ± 0.03 K/GPa; we take dTc/dσhydro = 0.23 ± 0.01 K/GPa. Employing the low-temperature elastic moduli from Ref. 37 to convert stress to strain, we find α = 34.8 ± 1.6 K and β = − 2.2 ± 1.2 K. (Under hydrostatic stress, σzz/εzz = 396 GPa and εxx = 0.814εzz.) The small value of β means that a volume-preserving reduction in the lattice parameter ratio c/a would have little effect on Tc: the increase in density of states by approaching the electron-to-hole Lifshitz transition is balanced, somehow, by weakening of the pairing interaction. The challenge for theory is to understand why that weakening takes place.
In the three-dimensional weak-coupling calculations presented here, it is the A2g and B2g channels, both of which have nodes along the Γ-X and Γ-Y lines, that best match observations. Due to differences between the actual and tight-binding electronic structure the εzz = 0 point in the calculations should not be considered too literally as equivalent to εzz = 0 in reality, and the key point is that it is only in the A2g and B2g channels that Tc is found to decrease and \({H}_{{{{{{{{\rm{c2}}}}}}}}}/{T}_{{{{{{{{\rm{c}}}}}}}}}^{2}\) to increase over some range of strain. However, as we have noted, A2g and B2g order parameters do not appear to be consistent with data under a-axis stress.
In other words, weak-coupling calculations do not explain the contrasting responses to a- versus c-axis stress, and this provides an opportunity: models of pairing in Sr2RuO4 should be tested against this feature, for it might provide substantial resolving power between different models. There may, for example, be stress-driven changes in the interactions that drive superconductivity, though to attempt to calculate this is beyond the scope of this paper.
We highlight two other possible explanations. One is interorbital pairing22,23,24,25. The superconducting energy scale is too weak to induce substantial band mixing, and so these models depend on the proximity of the γ and β sheets, and the resulting mixing of xy and xz/yz orbital weight over substantial sections of Fermi surface23. We have noted that c-axis compression reduces this mixing, by pushing the γ and β sheets apart, which could then suppress Tc59. In contrast, under in-plane uniaxial compression these sheets are pushed closer together along one direction and further apart along the other36.
The other is three-dimensional effects. Another feature of the electronic structure that varies oppositely under a- versus c-axis compression is the interlayer coupling. Under a-axis compression, the RuO2 sheets are pushed further apart, and under c-axis compression, closer together. For example, an increase in warping of the Fermi surfaces along kz under c-axis compression could reduce the quality of nesting and so weaken spin fluctuations in Sr2RuO4, and the weak-coupling calculations here might not have fully captured the effect on the superconductivity.
In summary, we have demonstrated methods to apply uniaxial stress of multiple GPa along the interlayer axis of layered materials in samples large enough to permit high-precision magnetic susceptibility measurements. Under such a compression, we find that Tc decreases even though the Fermi-level DOS increases, in striking contrast to the effect of in-plane uniaxial stress. Weak-coupling calculations do not provide a clear answer to this puzzle, which makes it important for models of superconductivity in Sr2RuO4 to be tested against application of both types of stress. At a more general level, our findings motivate the use of out-of-plane stress as a powerful tool for investigation of other low dimensional strongly correlated system in which the strength of the interlayer coupling is suspected of playing an important role in their electronic properties.
Methods
Density functional theory calculation
DFT structure calculations were performed using the full-potential local orbital FLPO60,61 version fplo 18.00-52 (http://www.fplo.de). For the exchange-correlation potential, the local density approximation applying the parametrizations of Perdew-Wang62 was chosen. Spin-orbit coupling was treated non-perturbatively by solving the four-component Kohn-Sham-Dirac equation63. To obtain precise band structure and Fermi surface information in the presence of a Van Hove singularity close to the Fermi level, the final calculations were carried out on a well-converged mesh of 343,000 k points. (70 × 70 × 70; 23,022 points in the in the irreducible wedge of the Brillouin zone). As a starting point, for the unstrained lattice structure the structural parameters at 15 K from Ref. 64 were used. Longitudinal strain εzz is taken as the independent variable, and εxx and εyy are set following the low-temperature Poisson’s ratio from Ref. 37, which is 0.223 for stress along the c axis. The apical oxygen position was relaxed independently at each strain, by minimising the force to below 1 meV/Å. However, the effect of relaxing this internal parameter is small in comparison with the effect of the stress-driven change in lattice parameters.
The calculated Fermi surfaces of unstressed Sr2RuO4 and under interlayer compression, including the warping along kz and the Fermi velocities, are shown in Fig. 6. The β sheet is the most strongly warped both at zero stress and at εzz = −0.025.
Experimental details
Sr2RuO4 samples were grown using a floating-zone method65,66. The four samples here were taken from the same original rod, and from a portion that we verified to have high Tc and a low-density of Ru inclusions; our aim in taking multiple samples was to test reproducibility in sample preparation and mounting.
Uniaxial stress was applied using piezoelectric-driven apparatus39,67, and precision in sample mounting is important because Sr2RuO4 is much more sensitive to in-plane than c-axis uniaxial stress: Tc decreases by 0.13 K under a c-axis stress of σzz = − 3.0 GPa, but increases by 0.13 K under an in-plane uniaxial stress of only 0.2 GPa29. Applying c-axis pressure could generate in-plane stress through bending and/or sample inhomogeneity. In a previous experiment68, c-axis compression raised Tc and broadened the transition. However, the stress was applied at room temperature, where the elastic limit of Sr2RuO4 is low39, so these effects may have been a consequence of in-plane strain due to defects introduced by the applied stress.
Samples 2–4 were mounted into two-part sample carriers; that for samples 2 and 3 is diagrammed in Fig. 7a. The purpose was to protect samples from inadvertent application of tensile stress. Samples are mounted across a gap between a fixed and a moving portion of part B of the carrier, and can be compressed, but not tensioned, by bringing part A into contact with part B. In Fig. 7b, we show Tc of samples 2 and 3 versus applied displacement, and the point where parts A and B come into contact and Tc starts changing is clearly visible. For sample 2 the point of contact is rounded on the scale of a few microns, due to roughness and/or misalignment of the contact faces, and in all figures below we exclude data points that we estimate to be affected by this rounding.
a Schematic of the sample configuration for samples 2 and 3. These samples were sculpted into a dumbell shape with a plasma focused ion beam. They were mounted with their ends embedded in epoxy. The cap blocks incorporate slots into which the sample fits, and the sample is compressed by bringing parts A and B into contact. b Tc versus applied displacement for samples 2 and 3. When parts A and B are brought into contact, force is applied to the sample, and Tc changes. c, d Photographs of samples 2 and 4. The graphics at the lower right of each panel are schematic cross sections: the end tabs of samples 2 were epoxied into slots, while sample 4 was sandwiched between two surfaces. e A photograph of the sample carrier for sample 4. f Tc of sample 3 versus applied displacement, with the data points coloured by the order in which they were taken. The sequence of data points with thick borders, during which ∣σzz∣ was monotonically decreased, are those shown in Fig. 3d. g Sense coil mutual inductance M(T) at points A and B in panel (f). h Force versus displacement for sample 4. i M(T) at points A, B, and C in panel (h).
The samples were mounted with Stycast 2850. This epoxy layer constitutes a conformal layer that ensures even application of stress67. Photographs of samples 2 and 4 are shown in Fig. 7c and d. The carrier for sample 4, which has a different design to those used for samples 2 and 3, is shown in Fig. 7e. Where electrical contacts were made, Du-Pont 6838 silver paste annealed at 450∘ for typically 30 min was used. This is longer than usual, in order to penetrate a thin insulating layer deposited during the ion beam milling.
As noted above, samples 1–3 were mounted in apparatus that had a sensor only of the displacement applied to the sample, while for sample 4 there was also a force sensor. Displacement sensors are less reliable as sensors of the state of the sample, because they also pick up deformation of the epoxy that holds the sample. In Fig. 7f the complete set of measurements of Tc of sample 3, plotted against applied displacement, are shown. Data points are colored by the order in which they were collected. The data drifted leftward over time: stronger compression was needed to reach the same Tc. However, the qualitative form of the curve — initial decrease in Tc, then a flattening, and then further decrease — reproduced over multiple stress cycles, and in Fig. 7g it is shown that the form of the transition was the same before and after application of the strongest compression. (We attribute the small apparent shift in Tc to an artefact of inadvertent mechanical contact between the stress cell and inner vacuum can of the cryostat).
We therefore conclude that the sample deformed elastically and that it was the epoxy holding the sample that was compressed non-elastically; plastic deformation has previously been observed to broaden the superconducting transition69 of Sr2RuO4. In Fig. 3, in the main text, we show only the data taken after the epoxy was maximally compressed. Force versus displacement data for sample 4 are shown in Fig. 7h–i, and here it can be seen that there was very substantial non-elastic compression of the epoxy. As with sample 3, the shape of the superconducting transition in the Sr2RuO4 was the same before and after application of large stress. Over regions where the sample and epoxy deformed elastically, the combined spring constant was 1.45 N/μm. The spring constant of the flexures in the carrier, on the other hand, is calculated to be ~0.03 N/μm, meaning that almost all of the applied force was transferred to the sample.
Calculated gap structure in other channels
In Fig. 8 the calculated gap structures in the A1g, A2g, and B1g channels are shown. [The B2g gap structures are shown in Fig. 5e.] c-axis compression favors large gaps on the γ sheet in all channels. In the A2g channel, this shift occurs as a first-order change in gap structure between εzz = 0 and εzz = − 0.0075. At the largest compression reached, gap weight in the A2g channel shifts back away from the γ sheet, as it does in the B2g channel. This does not occur in the A1g and B1g channels.
Details of the weak-coupling calculation
The tight-binding Hamiltonian from Eq. (1) takes the form
where we used the Ru orbital shorthand notation A = xz, B = yz, C = xy, and where \(\bar{s}=-s\) (s being spin). In Eq. (4) the energies εAB(k) account for intra-orbital (A = B) and inter-orbital (A ≠ B) hopping, and η1, η2 parametrize the spin-orbit coupling. We define εAA(k) = ε1D(kx, ky, kz), εBB(k) = ε1D(ky, kx, kz), and εCC(k) = ε2D(kx, ky, kz), and we retain the following terms in the matrix elements:
Here the first Brillouin zone is defined as BZ = [−π, π]2 × [ − 2π, 2π]. For the four values of c-axis compression εzz = 0, − 0.0075, − 0.015, − 0.020 we extract the entire set of parameters from DFT calculations consistent with Fig. 1; see Table 1.
For the interactions we use the (on-site) Hubbard–Kanamori Hamiltonian
where i is site, a is orbital, and \({n}_{ias}={c}_{ias}^{{{{\dagger}}} }{c}_{ias}\) is the density operator. We further assume that \({U}^{\prime}=U-2J\) and \({J}^{\prime}=J\)52. In the weak-coupling limit this leaves J/U as a single parameter fully characterizing the interactions.
In the linearized gap equation (2) the (dimensionless) two-particle interaction vertex \(\bar{{{\Gamma }}}\) is defined as48
where \({\rho }_{\mu }=\vert {S}_{\mu }|/[{\bar{v}}_{\mu }{(2\pi )}^{3}]\) is the density of states, and \(1/{\bar{v}}_{\mu }={\int}_{{S}_{\mu }}{{{{{{{\rm{d}}}}}}}}{{{{{{{\bf{k}}}}}}}}/\left(|{S}_{\mu }|{v}_{\mu }({{{{{{{\bf{k}}}}}}}})\right)\). Here, Γ is the irreducible two-particle interaction vertex which to leading order retains the diagrams shown in Fig. 9.
Second-order diagrams taken into account in Γ in a the even-parity channel, and b the odd-parity channel. The vertical arrows denote pseudo-spin, and the dashed lines contain all the terms of Eq. (8). The approach is asymptomatically exact in the weak-coupling limit, U/t → 0.
An eigenfunction φ of Eq. (2) corresponding to a negative eigenvalue λ yields the superconducting order parameter
In the chosen pseudo-spin basis each eigenvector φ belongs to one of the ten irreducible representations of the crystal point group D4h48,55.
Data availability
The data that support the findings of this study are openly available from the Max Planck Digital Library70.
References
Maeno, Y. et al. Superconductivity in a layered perovskite without copper. Nature 372, 532 (1994).
Mackenzie, A. P. & Maeno, Y. The superconductivity of Sr2RuO4 and the physics of spin-triplet pairing. Rev. Mod. Phys. 75, 657 (2003).
Maeno, Y., Kittaka, S., Nomura, T., Yonezawa, S. & Ishida, K. Evaluation of Spin-Triplet Superconductivity in Sr2RuO4. J. Phys. Soc. Jpn. 81, 011009 (2012).
Mackenzie, A. P., Scaffidi, T., Hicks, C. W. & Maeno, Y. Even odder after twenty-three years: the superconducting order parameter puzzle of Sr2RuO4. npj Quant. Mat. 2, 40 (2017).
Pustogow, A. et al. Constraints on the superconducting order parameter in Sr2RuO4 from oxygen-17 nuclear magnetic resonance. Nature 574, 72 (2019).
Ishida, K., Manago, M., Kinjo, K. & Maeno, Y. Reduction of the 17-O Knight Shift in the Superconducting State and the Heat-up Effect by NMR Pulses on Sr2RuO4. J. Phys. Soc. Jpn. 89, 034712 (2020).
Chronister, A. et al. Evidence for even parity unconventional superconductivity in Sr2RuO4. PNAS 118, e2025313118 (2021).
Petsch, A. N. et al. Reduction of the Spin Susceptibility in the Superconducting State of Sr2RuO4 Observed by Polarized Neutron Scattering. Phys. Rev. Lett. 125, 217004 (2020).
Luke, G. M. et al. Time-reversal symmetrybreaking superconductivity in Sr2RuO4. Nature 394, 558 (1998).
Grinenko, V. et al. Split superconducting and time-reversal symmetry-breaking transitions in Sr2RuO4 under stress. Nat. Phys. 17, 748 (2021).
Xia, J., Maeno, Y., Beyersdorf, P. T., Fejer, M. M. & Kapitulnik, A. High Resolution Polar Kerr Effect Measurements of Sr2RuO4: Evidence for Broken Time-Reversal Symmetry in the Superconducting State. Phys. Rev. Lett. 97, 167002 (2006).
Grinenko, V. et al. Unsplit superconducting and time reversal symmetry breaking transitions in Sr2RuO4 under hydrostatic pressure and disorder. Nat. Comm. 12, 3920 (2021).
Bergemann, C., Mackenzie, A. P., Julian, S. R., Forsythe, D. & Ohmichi, E. Quasi-two-dimensional Fermi liquid properties of the unconventional superconductor Sr2RuO4. Adv. Phys. 52, 639–725 (2003).
Ohmichi, E. et al. Magnetoresistance of Sr2RuO4 under high magnetic fields parallel to the conducting plane. Phys. Rev. B 61, 7101 (2000).
Rømer, A. T., Scherer, D. D., Eremin, I. M., Hirschfeld, P. J. & Andersen, B. M. Knight Shift and Leading Superconducting Instability from Spin Fluctuations in Sr2RuO4. Phys. Rev. Lett. 123, 247001 (2019).
Rømer, A. T., Hirschfeld, P. J. & Andersen, B. M. Superconducting state of Sr2RuO4 in the presence of longer-range Coulomb interactions. Phys. Rev. B 104, 064507 (2021).
Kivelson, S. A., Yuan, A. C., Ramshaw, B. & Thomale, R. A proposal for reconciling diverse experiments on the superconducting state in Sr2RuO4. npj Quantum Mater. 5, 43 (2020).
Wagner, G., Røising, H. S., Flicker, F. & Simon, S. H. A microscopic Ginzburg-Landau theory and singlet ordering in Sr2RuO4. Phys. Rev. B 104, 134506 (2021).
Scaffidi, T. Degeneracy between even- and odd-parity superconductivity in the quasi-1D Hubbard model and implications for Sr2RuO4. Preprint at https://arxiv.org/abs/2007.13769 (2020).
Willa, R., Hecker, M., Fernandes, R. M. & Schmalian, J. Inhomogeneous time-reversal symmetry breaking in Sr2RuO4. Phys. Rev. B 104, 024511 (2021).
Li, Y.-S. et al. High-sensitivity heat-capacity measurements on Sr2RuO4 under uniaxial pressure. PNAS 118, e2020492118 (2021).
Suh, H.-G. et al. Stabilizing even-parity chiral superconductivity in Sr2RuO4. Phys. Rev. Res. 2, 032023(R) (2020).
Clepkens, J., Lindquist, A. W. & Kee, H.-Y. Shadowed triplet pairings in Hund’s metals with spin-orbit coupling. Phys. Rev. Res. 3, 013001 (2021).
Gingras, O., Nourafkan, R., Tremblay, A.-M. S. & Côté, M. Superconducting symmetries of Sr2RuO4 from first-principles electronic structure. Phys. Rev. Lett. 123, 217005 (2019).
Ramires, A. & Sigrist, M. Superconducting order parameter of Sr2RuO4: a microscopic perspective. Phys. Rev. B 100, 104501 (2019).
Sharma, R. et al. Momentum-resolved superconducting energy gaps of Sr2RuO4 from quasiparticle interference imaging. PNAS 117, 5222 (2020).
Kashiwaya, S. et al. Time-reversal invariant superconductivity of Sr2RuO4 revealed by Josephson effects. Phys. Rev. B 100, 094530 (2019).
Barber, M. E. et al. Role of correlations in determining the Van Hove strain in Sr2RuO4. Phys. Rev. B 100, 245139 (2019).
Steppke, A. et al. Strong peak in Tc of Sr2RuO4 under uniaxial pressure. Science 355, eaaf9398 (2017).
Burganov, B. et al. Strain control of fermiology and many-body interactions in two-dimensional ruthenates. Phys. Rev. Lett. 116, 197003 (2016).
Hsu, Y.-T. et al. Manipulating superconductivity in ruthenates through Fermi surface engineering. Phys. Rev. B 94, 045118 (2016).
Liu, Y.-C., Wang, W.-S., Zhang, F.-C. & Wang, Q.-H. Superconductivity in Sr2RuO4 thin films under biaxial strain. Phys. Rev. B 97, 224522 (2018).
Kikugawa, N. et al. Rigid-band shift of the Fermi level in the strongly correlated metal: Sr2−yLayRuO4. Phys. Rev. B 70, 060508(R) (2004).
Kikugawa, N., Bergemann, C., Mackenzie, A. P. & Maeno, Y. Band-selective modification of the magnetic fluctuations in Sr2RuO4: A study of substitution effects. Phys. Rev. B 70, 134520 (2004).
Shen, K. M. et al. Evolution of the Fermi surface and quasiparticle renormalization through a van Hove singularity in Sr2−yLay RuO4. Phys. Rev. Lett. 99, 187001 (2007).
Sunko, V. et al. Direct Observation of a Uniaxial Stress-driven Lifshitz Transition in Sr2RuO4. npj Quantum Mater. 4, 46 (2019).
Ghosh, S. et al. Thermodynamic Evidence for a Two-Component Superconducting Order Parameter in Sr2RuO4. Nat. Phys. 17, 199 (2021).
Sypek, J. T. et al. Superelasticity and cryogenic linear shape memory effects of CaFe2As2. Nat. Comm. 8, 1083 (2017).
Barber, M. E., Steppke, A., Mackenzie, A. P. & Hicks, C. W. Piezoelectric-based uniaxial pressure cell with integrated force and displacement sensors. Rev. Sci. Inst. 90, 023904 (2019).
Yamazaki, K. et al. Angular dependence of vortex states in Sr2RuO4. Phys. C. 378-381, 537 (2002).
Kohn, W. & Luttinger, J. M. New Mechanism for Superconductivity. Phys. Rev. Lett. 15, 524–526 (1965).
Baranov, M. A. & Kagan, M. Y. D-wave pairing in the two-dimensional Hubbard model with low filling. Z. Phys. B 86, 237–239 (1992).
Kagan, M. Y. & Chubukov, A. Increase in superfluid transition in polarized Fermi gas with repulsion. JETP Lett. 50, 517 (1989).
Chubukov, A. V. & Lu, J. P. Pairing instabilities in the two-dimensional Hubbard model. Phys. Rev. B 46, 11163–11166 (1992).
Baranov, M. A., Chubukov, A. V. & Kagan, M. Y. Superconductivity and superfluidity in Fermi systems with repulsive interactions. Int. J. Mod. Phys. A 06, 2471–2497 (1992).
Fukazawa, H. & Yamada, K. Third Order Perturbation Analysis of Pairing Symmetry in Two-Dimensional Hubbard Model. J. Phys. Soc. Jpn. 71, 1541–1547 (2002).
Hlubina, R. Phase diagram of the weak-coupling two-dimensional \(t-{t}^{\prime}\) Hubbard model at low and intermediate electron density. Phys. Rev. B 59, 9600–9605 (1999).
Raghu, S., Kivelson, S. A. & Scalapino, D. J. Superconductivity in the repulsive Hubbard model: An asymptotically exact weak-coupling solution. Phys. Rev. B 81, 224505 (2010).
Raghu, S., Kapitulnik, A. & Kivelson, S. A. Hidden Quasi-One-Dimensional Superconductivity in Sr2RuO4. Phys. Rev. Lett. 105, 136401 (2010).
Scaffidi, T., Romers, J. C. & Simon, S. H. Pairing symmetry and dominant band in Sr2RuO4. Phys. Rev. B 89, 220510 (2014).
Røising, H. S., Scaffidi, T., Flicker, F., Lange, G. F. & Simon, S. H. Superconducting order of Sr2RuO4 from a three-dimensional microscopic model. Phys. Rev. Res. 1, 033108 (2019).
Dagotto, E., Hotta, T. & Moreo, A. Colossal magnetoresistant materials: the key role of phase separation. Phys. Rep. 344, 1–153 (2001).
Mravlje, J. et al. Coherence-incoherence crossover and the mass-renormalization puzzles in Sr2RuO4. Phys. Rev. Lett. 106, 096401 (2011).
Tamai, A. et al. High-Resolution Photoemission on Sr2RuO4 Reveals Correlation-Enhanced Effective Spin-Orbit Coupling and Dominantly Local Self-Energies. Phys. Rev. X 9, 021408 (2019).
Sigrist, M. & Ueda, K. Phenomenological theory of unconventional superconductivity. Rev. Mod. Phys. 63, 239–311 (1991).
Wang, Z., Wang, X. & Kallin, C. Spin-orbit coupling and spin-triplet pairing symmetry in Sr2RuO4. Phys. Rev. B 101, 064507 (2020).
Forsythe, D. et al. Evolution of Fermi-Liquid Interactions in Sr2RuO4 under Pressure. Phys. Rev. Lett. 89, 166402 (2002).
Svitelskiy, O. et al. Influence of hydrostatic pressure on the magnetic phase diagram of superconducting Sr2RuO4 by ultrasonic attenuation. Phys. Rev. B 77, 052502 (2008).
Beck, S., Hampel, A., Zingl, M., Timm, C. & Ramires, A. Effects of strain in multiorbital superconductors: The case of Sr2RuO4. Phys. Rev. Res. 4, 023060 (2022).
Koepernik, K. & Eschrig, H. Full-potential nonorthogonal local-orbital minimum-basis band-structure scheme. Phys. Rev. B 59, 1743 (1999).
Opahle, I., Koepernik, K. & Eschrig, H. Full-potential band-structure calculation of iron pyrite. Phys. Rev. B 60, 14035 (1999).
Perdew, J. P., Burke, K. & Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865 (1996).
Eschrig, H., Richter, M. and Opahle, I. Relativistic solid state calculations. Relativistic Electronic Structure Theory, Part 2. Applications 13 (2014).
Chmaissem, O., Jorgensen, J. D., Shaked, H., Ikeda, S. & Maeno, Y. Thermal expansion and compressibility of Sr2RuO4. Phys. Rev. B 57, 5067 (1998).
Mao, Z. Q., Maeno, Y. & Fukazawa, H. Crystal growth of Sr2RuO4. Mater. Res. Bull. 35, 1813 (2000).
Bobowski, J. S. et al. Improved single-crystal growth of Sr2RuO4. Condens. Matter 4, 6 (2019).
Hicks, C. W., Barber, M. E., Edkins, S. D., Brodsky, D. O. & Mackenzie, A. P. Piezoelectric-based apparatus for strain tuning. Rev. Sci. Inst. 85, 065003 (2014).
Kittaka, S., Taniguchi, H., Yonezawa, S., Yaguchi, H. & Maeno, Y. Higher-Tc superconducting phase in Sr2RuO4 induced by uniaxial pressure. Phys. Rev. B 81, 180510 (2010).
Taniguchi, H., Nishimura, K., Goh, S. K., Yonezawa, S. & Maeno, Y. Higher-Tc superconducting phase in Sr2RuO4 induced by in-plane uniaxial pressure. J. Phys. Soc. Jpn. 84, 014707 (2015).
Data available at the Max Planck Digital Library: https://doi.org/10.17617/3.3O1ZM2.
Acknowledgements
We thank Aline Ramires and Carsten Timm for helpful discussions, Markus König for training on the focused ion beam, and Felix Flicker for help with development and running of the code. H.R. thanks U. Nitzsche for technical support. F.J., A.P.M., and C.W.H. acknowledge the financial support of the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) - TRR 288 - 422213477 (project A10). H.S.R. and S.H.S. acknowledge the financial support of the Engineering and Physical Sciences Research Council (UK). H.S.R. acknowledges support from the Aker Scholarship. T.S. acknowledges the support of the Natural Sciences and Engineering Research Council of Canada (NSERC), in particular the Discovery Grant [RGPIN-2020-05842], the Accelerator Supplement [RGPAS-2020-00060], and the Discovery Launch Supplement [DGECR-2020-00222]. This research was enabled in part by support provided by Compute Ontario (http://www.computeontario.ca) and Compute Canada (http://www.computecanada.ca). N.K. is supported by a KAKENHI Grants-in-Aids for Scientific Research (Grant Nos. 17H06136, 18K04715, and 21H01033), and Core-to-Core Program (No. JPJSCCA20170002) from the Japan Society for the Promotion of Science (JSPS) and by a JST-Mirai Program (Grant No. JPMJMI18A3).
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Contributions
F.J., C.W.H., and A.P.M. designed the research project; F.J. and A.S. performed the measurements; N.K. and D.A.S. grew the samples; H.R. performed the density functional theory and H.S.R., T.S. and S.H.S. the weak-coupling calculations; F.J. and C.W.H. analyzed data; and F.J. and C.W.H. wrote the paper with contributions from the other authors.
Corresponding authors
Ethics declarations
Competing interests
C.W.H. has 31% ownership of Razorbill Instruments, a company that markets uniaxial pressure cells. All other authors declare no competing interests.
Peer review
Peer review information
Nature Communications thanks the anonymous reviewer(s) for their contribution to the peer review of this work.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Jerzembeck, F., Røising, H.S., Steppke, A. et al. The superconductivity of Sr2RuO4 under c-axis uniaxial stress. Nat Commun 13, 4596 (2022). https://doi.org/10.1038/s41467-022-32177-4
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-022-32177-4
This article is cited by
-
Controlling crystal-electric field levels through symmetry-breaking uniaxial pressure in a cubic super heavy fermion
npj Quantum Materials (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.