Abstract
Molecular organic fluorophores are currently used in organic light-emitting diodes, though non-emissive triplet excitons generated in devices incorporating conventional fluorophores limit the efficiency. This limit can be overcome in materials that have intramolecular charge-transfer excitonic states and associated small singlet-triplet energy separations; triplets can then be converted to emissive singlet excitons resulting in efficient delayed fluorescence. However, the mechanistic details of the spin interconversion have not yet been fully resolved. We report transient electron spin resonance studies that allow direct probing of the spin conversion in a series of delayed fluorescence fluorophores with varying energy gaps between local excitation and charge-transfer triplet states. The observation of distinct triplet signals, unusual in transient electron spin resonance, suggests that multiple triplet states mediate the photophysics for efficient light emission in delayed fluorescence emitters. We reveal that as the energy separation between local excitation and charge-transfer triplet states decreases, spin interconversion changes from a direct, singlet-triplet mechanism to an indirect mechanism involving intermediate states.
Similar content being viewed by others
Introduction
Thermally activated delayed fluorescence (TADF) organic molecules convert electricity to light more efficiently than traditional organic fluorophores, making them attractive materials for organic light-emitting diodes (OLEDs)1,2,3,4,5,6. Spin statistics for OLEDs dictate that 75% of electrically-generated excitons populate triplet (spin = 1) states (T1), which, in the case of traditional fluorophores, limits electroluminescence (EL) efficiency since radiative de-excitation of these states to the singlet (spin = 0) ground state (S0) is spin-forbidden7,8. Current commercial OLED devices employ organometallic chromophores based on iridium and platinum as red and green emitters. In such materials, enhanced spin–orbit coupling from the heavy element promotes direct emission from triplet excitons (phosphorescence), allowing up to 100% internal quantum efficiency (IQE) for EL9,10,11. Blue emitters based on the same approach have remained elusive, particularly because the long lifetimes of high-energy triplet excitons lead to OLED degradation12,13. Consequently, blue OLEDs typically employ organic fluorophores, with an enhancement of EL IQE achieved using triplet-triplet annihilation (TTA, T1 + T1 → S1 + S0), which can harvest up to half of the triplet excitons for light emission via singlets14,15,16. TTA-based OLEDs can in principle achieve up to 62.5% EL IQE. Within this context, TADF emitters present an alternative approach to achieving 100% EL IQE in devices, thereby offering a step-change in performance for blue OLED technologies17,18.
In TADF devices, indirect emission from dark triplet states via bright singlet excitons (T1 → S1 → S0) is activated by ambient thermal energy. There is general agreement that TADF emitters should be designed to have small singlet-triplet exchange energies that promote rapid forward and reverse intersystem crossing (ISC) between singlet and triplet excitons; such small exchange energies can be engineered by spatial separation of the highest occupied and lowest unoccupied molecular orbitals (HOMO and LUMO)1,2,3,4,5,6. However, there is no agreement on the spin interactions and spin-flip mechanisms responsible for the singlet-triplet interconversion in fluorophores exhibiting TADF with intramolecular charge-transfer (CT) states19,20,21,22. Typical TADF emitters have low-lying singlet and triplet excitonic states with mixed local excitation (LE) and intramolecular CT character21,23. Emission from the predominantly CT singlet excitonic state (1CT) via prompt or delayed fluorescence is desirable. Therefore, the triplet excitons populating either CT or local excitation states (3CT and 3LE) must be efficiently converted to 1CT. ISC between the singlet and triplet manifolds of fluorophores can be driven by a spin-orbit coupling (SOC) mediated spin conversion, whereby an orbital transition between two states generates a torque capable of flipping an electron’s spin. Direct SOC (dependent only on the electronic character of the coupled states) will in general be suppressed between a singlet and triplet state if they possess similar orbital character (El Sayed’s Rule)24,25. Therefore, in order to achieve singlet-triplet ISC between two electronic states of the same orbital character (e.g. 1CT to 3CT) additional processes must occur, which are dependent on both the electronic character and nuclear coordinates of the coupled states. However, the presence of a significant change in orbital character upon spin-flip (e.g. 1CT to 3LE) is not in itself sufficient to guarantee rapid ISC and, furthermore, it has been shown that direct SOC alone cannot explain high rates of ISC observed26,27,28. Vibration-mediated SOC has been suggested to explain this discrepancy, and also to facilitate singlet-triplet conversion between states of similar orbital character18,29. Vibrational contributions from an additional, or ‘intermediate’, triplet state give rise to the ‘spin-vibronic mechanism’ for the efficient conversion of dark triplet excitons to emissive singlet excitons (reverse ISC) in TADF emitters30,31,32. Revealing the character and formation dynamics of intermediate triplet states is challenging, although critical to understanding the TADF mechanism33,34.
Here we use transient electron spin resonance (trESR) spectroscopy to study the role of spin-orbit coupling and vibrational perturbations in ISC for TADF. While optical spectroscopy has proved a powerful tool to examine the photophysics and spin-conversion rates in TADF30,31,35,36, trESR provides a complementary window into the underlying spin physics. TrESR is sensitive to paramagnetic states and can therefore probe the formation dynamics and coupling mechanisms of triplet excitons37, as highlighted by broad applications in studying triplet excitons in organic photovoltaics38,39,40, singlet fission41,42,43,44, photosensitizers37,45,46,47, and molecular electronics48,49. Because trESR is not sensitive to singlet excitons (due to their diamagnetism) it can only explicitly probe forward ISC. However, assuming microscopic reversibility, the triplet exciton formation dynamics revealed are applicable to TADF-relevant reverse ISC. We have previously shown using trESR that spin-orbit coupling interactions mediate ISC for two benchmark TADF molecules: 1,2,3,5-tetrakis(carbazol-9-yl)-4,6-dicyanobenzene (4CzIPN) and 1,2-bis(carbazol-9-yl)-4,5-dicyanobenzene (2CzPN)20. The trESR data suggested a dynamic picture of SOC-mediated ISC involving vibrational modes, although the excited-state ordering and coupling requirements for efficient ISC were not established. To reveal these requirements, here we have conducted trESR studies on a series of ten molecular organic fluorophores exhibiting delayed fluorescence with varying 3LE–3CT energy gaps; this allows us to probe the spin-vibronic mechanism directly and resolve the nature of intermediate triplet states. TrESR gives conclusive evidence that 3LE can be populated from the singlet manifold by the vibrational SOC ISC mechanism. However, when the 3LE–3CT gap is sufficiently small, trESR reveals that additional spin conversion pathways emerge, and 3CT is populated via the spin-vibronic ISC mechanism because of enhanced 3LE–3CT coupling. TrESR can crucially resolve these different ISC mechanisms, which are influenced by difficult to predict molecular properties beyond the excited-state character and energetics measured with optical spectroscopy. Our spin-sensitive measurements reveal direct evidence that distinct triplet excitonic states (T1 + T2) mediate the spin conversion responsible for delayed fluorescence. These findings uncover the fundamental mechanism of the spin-vibronic ISC pathway relevant in TADF emitters, providing detail on the nature of the process by probing distinct yet vibronically-accessible 3LE and 3CT states.
Results
Design and detection of multiple triplet excitonic states
Three donor-acceptor emitters sharing a common 4-(3,6-di-tert-butyl-9H-carbazol-9-yl)diphenyl sulfone (DTCz-DPS) core structure were synthesised. We employed inductively electron-withdrawing fluorine substituents on a phenyl group linking carbazolyl and sulfone moieties to lower the LUMO energy of the DTCz-DPS core, resulting in lowered CT state energies as in our previous study50. The three emitters, DTCz-DPS-1, -2, and -3 (Fig. 1b–d) share a fixed 3LE energy level, associated with the carbazole donor, but possess increasingly red-shifted 1CT and 3CT, from DTCz-DPS-1 to -3, consistent with time-dependent density-functional theory (TD-DFT) calculations (Supplementary Table 1), described in ‘Methods’. The calculated Gibbs free energy difference between the 3LE and 3CT minima (the 3LE–3CT gap), in their optimised geometries, is reduced from DTCz-DPS-1 to -3 (Table 1). Importantly, our calculations also found that the direct SOC matrix elements between 1CT and 3LE are relatively constant for the three emitters (Table 1). Therefore, our structural modifications of excited-state energies allow higher-order SOC effects to be studied due to changing of the 3LE–3CT energy gap and energetic landscape, while direct SOC matrix elements between 1CT and 3LE are fixed.
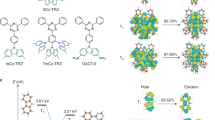
a Schematic diagram depicting the zero-field splitting (ZFS) of the lowest-lying triplet state (T1) into its three sublevels (Tx,y,z). The magnitude of the ZFS parameters, D and E, describes the splitting of the triplet sublevels where x, y, and z are the ZFS axes along which spin density is distributed. The energetic spacing is not to scale. Molecular structures of (b) DTCz-DPS-1, (c) DTCz-DPS-2, and (d) DTCz-DPS-3. The in-plane molecular axes a and c and the 3LE ZFS axes z and x are shown. e Schematic diagram depicting the Zeeman energy separation of the triplet sublevels (low-field: Tx,y,z; high-field: T−1,0,+1) when a magnetic field (B) is applied parallel to the z axis and the absorptive (A) and emissive (E) transitions that occur between sublevels when microwave radiation is resonant with energetic separation. Spin-polarised trESR signals collected at 30 K in toluene for (f) DTCz-DPS-1, (g) DTCz-DPS-2, and (h) DTCz-DPS-3. Solid lines show the trESR signal recorded 2 μs after 355 nm laser excitation and integrated over 1 μs. Dashed and dotted lines are the simulated local excitation triplet state (3LE) and charge-transfer triplet state (3CT) polarisation patterns, respectively. Dash-dot grey lines are the weighted sums of the 3LE and 3CT simulations. The spin-polarised patterns are characterised by absorptive (A) and emissive (E) features. i Spin-vibronic coupling of 1CT, 3LE and 3CT potential energy surfaces.
For the trESR measurements, pulsed laser excitation (355 nm) and cryogenic temperatures (30 K) were used to generate long-lived, molecular triplet excitons in dilute (500 μM), deoxygenated and flash-frozen toluene solutions. A variable applied magnetic field (200–500 mT) induced Zeeman energy separation of the triplet sublevels from the zero-field splitting (ZFS) eigenstates (Tx,y,z, Fig. 1a, e). A continuous wave microwave source (~9.7 GHz) induced triplet sublevel transitions (absorptive, A, and emissive, E) when resonant with the sublevel energetic spacing; the intensity of these transitions is dependent on the triplet sublevel population (Px,y,z), which is determined by the nature of the triplet formation (ISC) process. The magnetic field positions of the positive (absorptive) and negative (emissive) peaks in the trESR signal (also known as ‘polarisation pattern turning points’) are determined by the ZFS parameters, D and E (Fig. 1a). The spin–spin dipolar interaction contribution to ZFS can yield a D-dependence on spin-density delocalisation across the molecule that allows for more LE- and CT-type triplets to be distinguished; a smaller D-value typically correlates with greater delocalisation, indicative of a CT state in the molecules investigated here19,51. D, E, and Px,y,z are obtained from inspection, simulation and least-squares fitting (using EasySpin52) of the spin-polarised trESR signal. Following photoexcitation, the all-organic emitters have typically low triplet yield and hence data acquisition times of 4–12 h were required for each trESR spectrum.
Each emitter exhibited spin-polarised trESR signals with lifetimes of several microseconds, throughout which the spectral shapes were conserved. The trESR signal of DTCz-DPS-1 (Fig. 1f) has a 6-turning point EEEAAA polarisation pattern with a preferential population of Tx and Tz (Px,y,z = 0.38, 0.00, 0.62). The ZFS parameters (|D | , | E | = 108, 9 mT), the position of the half-field transition (161 mT, Supplementary Fig. 4), and EEEAAA polarisation pattern of DTCz-DPS-1 are all typical of triplet states in organic chromophores51. These parameters are consistent with the 3LE associated with the carbazole monomer53, leading us to attribute the trESR signal to a triplet exciton localised on the carbazole donor. The trESR signals of DTCz-DPS-2 and -3 (Fig. 1g, h) show spin signatures of two overlapping triplet signals. It is evident from the line shape of the DTCz-DPS-2 trESR spectrum that the wider triplet signal resembles that seen for DTCz-DPS-1. Furthermore, the prominent half-field transition peak in the DTCz-DPS-2 trESR spectrum (162 mT, Supplementary Fig. 4) matches well with that in DTCz-DPS-1. After subtracting the 3LE contribution from the trESR signal of DTCz-DPS-2, the resulting triplet is narrower (|D | , | E | = 23, 3 mT) and has a spin-polarisation pattern that indicates relative overpopulation of Tx and Ty (Px,y,z = 0.4, 0.6, 0.0). A reduced magnitude of D of this scale typically indicates an increased spatial separation of interacting spins; therefore, we attribute the narrow signal to the delocalised 3CT19,51.
The trESR signal of DTCz-DPS-3 (Fig. 1h) comprises a more intense central feature compared to DTCz-DPS-2. The total width of the DTCz-DPS-3 signal is unchanged and the same 161 mT half-field transition peak is recorded as in DTCz-DPS-1 (Supplementary Fig. 4); therefore, the same 3LE is assigned to the broad triplet signal. By subtracting the 3LE contribution from the total DTCz-DPS-3 trESR spectrum a narrower triplet signal ascribed to 3CT is obtained with Px,y,z = 0.6, 0.4, 0.0, |D | , | E | = 56, 19 mT and a half-field transition peak at 169 mT; the breadth of the DTCz-DPS-3 3CT signal compared to the DTCz-DPS-2 3CT signal is a point to which we will later return. These results show that with decreasing 3LE–3CT gap (from DTCz-DPS-1 to -3), the recorded trESR spectra progress from a relatively pure 3LE signal to one resulting from contributions of both 3LE and 3CT polarisation patterns. The triplet ZFS simulation parameters of all three emitters are shown in Table 2.
Similarly, we observe the emergence of unstructured 3CT emission, in addition to structured 3LE emission, with decreasing 3LE–3CT gap in the frozen (77 K) toluene phosphorescence spectra (solid lines in Fig. 2d–f)50,54. We note that the phosphorescence was recorded at 77 K, which is a higher temperature than used in the trESR experiment (30 K). Crucially, both these temperatures are well below the freezing point of toluene (178 K). Therefore, the energetic relaxation of the 1CT states (a common phenomenon undergone by intramolecular CT states in solution) observed when comparing the photoluminescence (PL) in frozen (77 K) and solution (295 K) toluene (Fig. 2a–f) is minimised at both 30 K and 77 K. The progression in trESR and phosphorescence shows that 3LE and 3CT are both populated when the 3LE–3CT gap is sufficiently small55. Time-resolved PL measurements confirmed that all three of the emitters exhibit intramolecular CT character in prompt and delayed fluorescence at room temperature (295 K) in deoxygenated toluene (Fig. 2, Table 1, and Supplementary Fig. 10). The contribution of delayed fluorescence to the total emission was determined from the integrated time-resolved PL and is listed in Table 1. The electroluminescence performance of DTCz-DPS-1 and DTCz-DPS-3 were also evaluated in preliminary solution-processed OLEDs and are presented in the Supplementary Information (Supplementary Fig. 11 and Supplementary Table 7).
Normalised absorbance (dotted line) and photoluminescence (filled line) spectra in deoxygenated toluene at 295 K (a DTCz-DPS-1, b DTCz-DPS-2, c DTCz-DPS-3). Normalised steady-state photoluminescence (dashed line) and gated (0.5 ms) phosphorescence (solid line) spectra in deoxygenated toluene at 77 K (d DTCz-DPS-1, e DTCz-DPS-2, f DTCz-DPS-3). Normalised integrated photoluminescence kinetics in deoxygenated toluene at 295 K (g DTCz-DPS-1, h DTCz-DPS-2, i DTCz-DPS-3).
Density-functional theory calculations
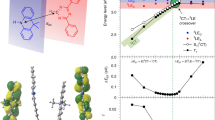
Optimised geometries and molecular orbitals were established for the low-lying excitonic states of DTCz-DPS-1, -2, and -3 (Fig. 3a–c) using the range-separated LC-BLYP functional56. The calculations predicted both 3LE and 3CT in close proximity to the 1CT, supporting our experimental observation of both triplets being populated in trESR and PL measurements in frozen toluene. The relative energy and donor-acceptor dihedral angle was calculated in the 3LE, 3CT configurations, and also at the minimal-energy conical intersection where two electronic triplet states are equal in energy and electronically coupled (Fig. 3). The geometrical change between the 3LE and 3CT configuration is predominantly characterised by rotation around the donor-acceptor linker: see dihedral angle between shaded planes in Fig. 3d–f.
The local excitation triplet state (3LE) and charge-transfer triplet state (3CT) configurations and highest occupied and lowest unoccupied molecular orbitals (HOMO and LUMO) of (a) DTCz-DPS-1, (b) DTCz-DPS-2, and (c) DTCz-DPS-3. The molecular geometry, relative Gibbs free energy, and donor–acceptor dihedral angle of (d) DTCz-DPS-1, (e) DTCz-DPS-2, and (f) DTCz-DPS-3 in the 3LE, 3CT configurations and at the minimum-energy conical intersection where two electronic triplet states are equal in energy and electronically coupled.
The ZFS tensors (D and E parameters) were calculated for each 3LE and 3CT (Table 2) using the DFT-based method reported by Neese et al.57,58 that considers contributions to ZFS from both spin–spin interactions and spin–orbit interactions (Supplementary Table 2). DFT predicted D < 0 in all cases, therefore, D was assumed to be negative in all trESR spectral simulations. The sign of E was chosen such that axes labelling conformed with molecular axes labelling convention, as opposed to ESR convention. The total D and E values calculated for the 3LE configurations are in good quantitative agreement with the values obtained from trESR measurements. The calculated contribution to total D from spin–spin interactions decreases from 3LE to 3CT, whereas the contribution from spin–orbit interactions does not decrease. The resulting 3CT total D and E values are overestimated in comparison to those obtained from trESR measurements, although the experimental observation that the ZFS D-value of DTCz-DPS-3 3CT is larger than DTCz-DPS-2 3CT is correctly predicted. The larger calculated D-value of DTCz-DPS-3 compared to DTCz-DPS-2 arises from a greater spin–spin interaction contribution to ZFS (Supplementary Table 2). Variation in spin–spin interaction can be rationalised by examining the 3CT molecular orbitals in Fig. 3: the electron-withdrawing effect of the additional fluorine atoms in DTCz-DPS-3 localises the LUMO more strongly on the fluorinated phenyl ring than in DTCz-DPS-2 where the LUMO is more delocalised over both phenyl rings. Closer average HOMO-LUMO proximity leads to reduced spin-spin distance and enhanced interaction, which typically manifests as larger D-value.
Further transient electron spin resonance studies: molecular modifications and concentration series
We designed a number of additional experiments to test our interpretation that the trESR signals comprise polarisation patterns arising from 3LE and 3CT excitonic molecular states. First, we explored the effect of molecular substitutions on excited-state energies and subsequently the photophysics and ISC mechanism. We modified the donor groups of DTCz-DPS-2 and DTCz-DPS-3 by removing the tertiary butyl groups (to give Cz-DPS-1 and -2, respectively), or by replacing the tertiary butyl groups with additional carbazole units (to give 3Cz-DPS-1 and -2, respectively). The 3LE–3CT gap was decreased by fluorination on going from Cz-DPS-1 to −2 and from 3Cz-DPS-1 to -2; we observed with decreasing gap: (a) emergence of the 3CT trESR signals (Fig. 4) and 3CT phosphorescence (Supplementary Fig. 7, 8) and (b) increase in contribution to total PL from delayed fluorescence. These observations are consistent with our findings for DTCz-DPS-1, -2, and -3. Photophysics and trESR simulation parameters can be found in the Supplementary Information (Supplementary Fig. 7, 8, and Supplementary Table 4, 5). Trends in the calculated excited-state energies and direct SOC matrix elements between 1CT and 3LE for Cz-DPS-1 and -2 and 3Cz-DPS-1 and -2 (Supplementary Table 6) are also consistent with the trends identified for DTCz-DPS-1, -2, and -3. In non- or partially-fluorinated versions of the emitters (Cz-DPS-0, DTCz-DPS-0, 3Cz-DPS-0) the CT states were blue-shifted, widening both the 3LE–1CT and 3LE–3CT gaps such that no substantial delayed component of the time-resolved PL was detected at room temperature (Supplementary Fig. 9). The trESR spectra of the fluorescent emitters (Cz-DPS-0, DTCz-DPS-0, and 3Cz-DPS-0) exhibit only EEEAAA polarisation patterns, with signal widths and half-field peaks consistent with the 3LE associated with monomer carbazole, as before (Supplementary Fig. 9). The effects of changing the molecular environment by switching the solvent from toluene to 2-methyltetrahydrofuran were compared for DTCz-DPS-1 and 3Cz-DPS-2 and are discussed in the Supplementary Information (Supplementary Fig. 6). Finally, to rule out intermolecular interactions we reduced the concentration of DTCz-DPS-1, DTCz-DPS-3, and 3Cz-DPS-2 in toluene from 500 μM to 20 μM. No significant differences in trESR signal were observed, supporting our interpretation of the mechanisms responsible for triplet state formation as all being intramolecular processes, rather than concentration-dependent aggregate states or intermolecular energy transfer (Supplementary Fig. 5).
Molecular structures and spin-polarised trESR signal collected at 30 K in deoxygenated toluene of (a) Cz-DPS-1, (b) Cz-DPS-2, (c) 3Cz-DPS-1, and (d) 3Cz-DPS-2. Solid lines show the trESR signal, recorded 2 μs after 355 nm laser excitation and integrated over 1 μs. Dashed and dotted lines are the simulated local excitation triplet state (3LE) and charge-transfer triplet state (3CT) polarisation patterns, respectively. Dash-dot grey lines are the weighted sums of the 3LE and 3CT simulations.
Discussion
TADF facilitated by spin-orbit coupling, as described in the ‘Introduction’, can be interpreted within the following framework of ISC mechanisms26,59:
-
(I)
Direct spin–orbit coupling between 1CT and 3LE;
-
(II)
Vibrational spin–orbit coupling between 1CT and 3LE;
-
(III)
Spin-vibronic coupling between 1CT and 3CT via intermediate 3LE.
Vibrational modes can enhance ISC in (II) because spin–orbit coupling matrix elements for 1CT–3LE transitions depend on the nuclear degree of freedom, \({Q}_{\alpha }\). The vibronic coupling in (III) drives rapid internal conversion between 3CT and 3LE, equilibrating their population; 3LE is then coupled to 1CT via either (I) or (II)26,30. 3LE is considered an intermediate in the sequence of state formation: 1CT–3LE–3CT (Fig. 1i). Any initial population of 1LE is assumed to rapidly convert to 1CT, as will be discussed later. Here, the 3CT–3LE vibronic coupling in (III) is assigned to modes associated with the donor–acceptor linker20,60,61. These three ISC processes are expressed together by the sum of their first non-zero terms:
where \(\varPsi\) is the molecular wavefunction of states coupled either by the spin–orbit (\({\hat{H}}_{{SO}}\)) or vibronic (\({\hat{H}}_{{vib}}\)) Hamiltonian26. The vibronic coupling between two states generally increases as the energy gap between the states decreases and hence mechanism (III) only significantly contributes to the full spin–orbit interaction if the 3LE–3CT gap (ΔG) is sufficiently small (<0.5 eV). Furthermore, orbital and vibrational mode-dependent mechanisms are determined by the geometry of a molecule and differently affect ISC mechanisms (I), (II), and (III)22,25,26. TrESR polarisation patterns are fingerprints for the relative spin population of the triplet ZFS sublevels (x, y, z), which are also related to the molecular geometry62—Fig. 1 shows how the 3LE ZFS axes are related to the molecular axes (a, b, c) in DTCz-DPS-1, -2, and -3. These relationships mean that triplet formation by each ISC mechanism will yield a particular trESR polarisation pattern that can be distinguished by the ISC mechanism’s orbital and/or vibrational mode dependence on molecular geometry.
TADF emitters generally comprise all-organic electron donor and acceptor units. Individually the donor and acceptor units, on which LE states are localised, typically possess at least a C2 symmetry axis; symmetry does not persist in the delocalised CT states. Under these symmetry conditions the triplet sublevel populations describing the trESR polarisation pattern for each ISC mechanism in a TADF emitter is as follows:
-
(I)
Overpopulation along the C2 symmetry axis (x here);
-
(II)
Overpopulation of the in-plane axes (x and z here);
-
(III)
Redistribution of the population from the in-plane (x and z here) to the out-of-plane (y here) axes.
The difference between ISC mechanisms (II) and (III) is the CT-like transition from 3LE to 3CT upon internal conversion. In a donor–acceptor emitter, the electron density in the 3LE configuration is localised on either the acceptor or, in this case, the donor unit and hence the triplet ZFS (x, y, z) and molecular (a, b, c) axes will be well-aligned. In contrast, the electron density in a 3CT configuration will be delocalised across both the donor and acceptor units (Fig. 3). The donor-acceptor twist, integral to TADF design, results in the rotation of the 3CT ZFS axes relative to the 3LE ZFS axes63. Therefore, the spin-density redistribution upon charge-transfer internal conversion from 3LE to 3CT rotates the triplet ZFS axes such that overpopulation of the out-of-plane axes (relative to the 3LE ZFS axes) can arise. This additional out-of-plane population causes the difference between the population of Tx,y,z in ISC mechanism (II) and (III)64,65. The donor–acceptor twist is a fundamental TADF molecular design rule because the spatial separation of HOMO and LUMO is required to reduce singlet-triplet offset and enable reverse ISC. Therefore, we can expect the relationship between molecular structure, ISC mechanism, and trESR pattern to be applicable to many classes of TADF emitters, as well as to donor–acceptor CT-type molecules in general.
Applying the framework outlined above to the triplet sublevel populations from experimental spectra (Table 2), we can infer the ISC mechanisms responsible for the population of 3LE and 3CT in each emitter. The 3LE states of DTCz-DPS-1, -2, and -3 (and Cz-DPS-1 and -2, 3Cz-DPS-1 and -2) are populated via vibrational SOC with the photoexcited 1CT – mechanism (II) – apparent from the overpopulation of Tx and Tz45,51,62,66,67. On the other hand, the triplet sublevel corresponding to the out-of-plane molecular axis (Ty) is relatively overpopulated in the 3CT polarisation patterns of DTCz-DPS-2 and -3 (and Cz-DPS-2 and 3Cz-DPS-2). The distinct triplet trESR spectra, therefore, reveal that spin-vibronic coupling between 1CT and 3CT via intermediate 3LE – mechanism (III) – is responsible for 3CT population20,59,60. The ability to resolve these ISC mechanisms from one another is a crucial advantage of using trESR; it is not possible to predict how excited states interact based purely on optical measurements of their separation energies or excitation character because additional factors arising from molecular structure affect ISC.
Our computational results qualitatively support the experimental triplet sublevel population assignments of the trESR spectra, and the involvement of vibrational and vibronic enhancement to SOC. First, the calculated \(\left\langle {\varPsi }_{^1{CT}}|{\hat{H}}_{{SO}}|{\varPsi }_{^3{LE}}\right\rangle\) at the optimised 3LE geometries (described in the ‘Methods’) confirms that if direct SOC between 3LE and 1CT – mechanism (I) – were the dominant mechanism we would indeed observe overpopulation predominantly in the 3LE x plane (Supplementary Table 3, 6). The DFT calculations also predict the relationship between the 3LE ZFS and in-plane molecular axes (overpopulation in Tx and Tz). A rotation of the in-plane x–z frame upon charge-transfer internal conversion would redistribute population from Tz to Ty, consistent with the experimental observations (Table 2). The most significant mode identified in the calculations that are associated with the 3LE–3CT conversion is the rotation around the single bond between the DTCz donor and DPS acceptor in DTCz-DPS-1, -2, and -3 (Fig. 3d–f); this torsional mode likely drives vibronic coupling20.
The D and E values predicted by DFT for 3LE in each emitter agree well quantitively with those obtained from the measured trESR (Table 2). However, only the qualitative trend in relative magnitude is well-predicted in DFT calculations of 3CT; the calculated D and E values are overestimated compared to those obtained from the measured trESR (Table 2). As discussed, we would expect spin–orbit interactions related to 3CT configurations to be weaker compared to their 3LE counterparts; no such reduction in the contribution to D from spin–orbit interactions is predicted in the DFT calculations (Supplementary Table 2). We suggest that the mismatch between predicted and measured 3CT D and E values is a result of this overestimation of spin–orbit interactions between 3CT and other nearby electronic states. This discrepancy highlights the current limitations of common computational calculations and the necessity for experimental trESR to reveal the complex nature of multiple triplet states, which underpin the spin physics of TADF-type organic emitters.
To reiterate: our findings show that it is indirect, not direct, coupling of 3CT to the singlet manifold that facilitates ISC. This assertion is supported by the following pieces of evidence, which rule out direct ISC between 3CT and either 1CT or 1LE. Direct ISC from 1CT to 3CT would need to be mediated by hyperfine coupling because the lack of orbital change suppresses SOC. Hyperfine-mediated ISC facilitates the transfer from the singlet state to only the energetically closest high-field triplet sublevel and consequently has a trESR polarisation pattern that is distinct from the SOC-mediated ISC patterns described above, and it is not observed in our measurements19,39. If 1LE to 3CT ISC were prevalent, we would not observe a dependence of the 3CT trESR signal on the 3LE–3CT gap, and would instead observe the 3CT spectra in all measurements, which we do not. Further, we would not expect a substantial population of 1LE for two reasons. First, 1LE to 1CT internal conversion is rapid (ps) compared with ISC (ns)22,45,68,69,70,71. Second, in the experiment, the 1CT absorption band was selectively excited (and is spectrally distinct from the 1LE absorption) in order to mimic operational OLED conditions where the lowest energy excitonic states are electrically generated (Fig. 2a–c solid lines and Supplementary Table 1). To summarise, the progression from a purely 3LE polarisation pattern to a combination of both 3LE and 3CT polarisation patterns with decreasing 3LE–3CT gap is evidence that a small 3LE–3CT gap regime exists in which strong vibronic coupling persists, even at low temperatures (kT < 3 meV), such that 3LE and 3CT are simultaneously populated. It is worth noting that, as TADF development is predominantly focused on the critical task of achieving efficient blue emission, the above outlined spin-vibronic mechanism is described in the context of the energetic regime attainable in blue emitters and shown in Fig. 1i: 1CT > 3CT > 3LE6,22. However, the same principles can be applied to a donor–acceptor emitter exhibiting a different excited-state ordering. We note that the unusual observation of multiple, distinct triplet signals in trESR spectra has also been reported for twisted donor–acceptor triplet photosensitizers, although the mechanism through which both triplets were populated was not rationalised;45,46,47 we postulate that the spin-vibronic mechanism may be active in such triplet photosensitizers.
Finally, we return to discuss the photophysical results in light of the spin-vibronic mechanism determined from trESR. The increase of 3CT spectral contribution with decreasing 3LE–3CT gap observed here (and in other systems55,69,72,73) reinforces the direct evidence for the spin-vibronic mechanism from trESR. Furthermore, the emergence of the additional 3CT trESR spectra, reflecting the strength of vibronic coupling, correlates with increased contribution to total emission from delayed fluorescence. However, as the 3LE–3CT gap decreases so does the 3LE–1CT gap and therefore their combined effect on delayed fluorescence cannot be decoupled. We note that the dynamics of excited state couplings are also affected by time- and temperature-dependent molecular reorganisation, as is evident when comparing the 295 K fluorescence with the 77 K fluorescence (dashed lines in Fig. 2a–c versus dashed lines in Fig. 2d–f). The spectral redshift undergone by charge-transfer states from 77 K to 295 K (due to post-photoexcitation molecular reorganisation) increases from DTCz-DPS-1 to -3. The differing reorganisation complicates the temporal evolution of energetic spacing between 1CT, 3LE, and 3CT, and hence coupling dynamics at room temperature are not directly comparable to frozen solution measurements.
TrESR has been used previously to probe triplet excitons in twisted donor-acceptor emitters that, due to their large T1–T2 energy gap (>0.6 eV), are non-interacting and exhibit delayed fluorescence through either the hot-exciton74 or hyperfine pathways75. Our experimental results for the present series of donor–acceptor molecules, supported by computational calculations, show that coupling between the singlet and triplet manifold is facilitated by the spin-vibronic mechanism when 3LE is in energetic proximity (<100 meV) to 3CT. This coupling drives ISC, and therefore TADF-relevant reverse ISC (assuming microscopic reversibility). We have demonstrated that trESR can reveal mechanistic details of ISC, providing a critical, complementary approach to optical spectroscopy methods33,76,77 and have established a trESR framework to study the spin-vibronic mechanism in TADF emitters. We have demonstrated that the mechanism for ISC within an emitter can be tuned through chemical modifications; engineering and measuring the spin properties are critical for the informed development of efficient TADF emitters. We have characterised the nature of triplet excitations in the chemically modified set of delayed fluorescence emitters, resolving two distinct triplet excitonic states (T1 and T2) involved in spin-vibronic coupling. This distinction supports the basis for achieving spin-vibronic TADF by engineering distinct yet vibronically-accessible 3LE and 3CT states. As discussed, the mechanism of 3CT population by vibronic coupling with 3LE may find further application in the development of heavy-atom free triplet photosensitizer design45,46,47. Tuning spin–orbit coupling in molecular systems and their subsequent trESR signatures, as demonstrated here, is not only of paramount importance to blue OLED development but may also find resonance more broadly in the development of organic materials for light-controlled quantum information and spintronics78,79,80,81,82.
Methods
Synthesis of emitters
The emitters were generally synthesised by nuclophilic substitution reactions between the appropriate carbazole derivatives and partially fluorinated derivatives of diphenylsulfone in dimethylsulfoxide in the presence of potassium carbonate, as described in the detail in the Supplementary Information. The fluorinated diphenylsulfones were obtained by reaction of lithio(fluoroarenes), obtained through bromine-lithium exchange or deprotonation, with 1,2-diphenyldisulfane, followed by oxidation with 3-chlorobenzoperoxoic acid.
Transient electron spin resonance spectroscopy
Dilute solutions were prepared at 500 μM in toluene in a nitrogen environment. The solutions were contained within 3.8 mm O.D. clear-fused quartz tubes and degassed by 4 freeze-pump-thaw cycles before being flame-sealed. Measurement of transient continuous wave ESR (trESR) was done in the Centre for Advanced ESR (CAESR) in the Department of Chemistry of the University of Oxford, using a Bruker BioSpin EleXSys I E680 at X-band (9.7 GHz, 0.2 mW) with an ER 4118X-MD5W resonator. The temperature was controlled with an Oxford Instruments CF935O cryostat under liquid helium flow and an ITC-503S controller. An Opotek Opolete HE355 LASER was used for optical excitation of the samples and it was synchronised to the spectrometer by a Stanford Research DG645 delay generator. Use of a Stanford Research SR560 low-noise preamplifier of the Schottky diode-detected CW Mode signal at 3–300 kHz was in substitute of the video amplifier, following verification against the quadrature mix-down DC-AFC Transient Mode signal of 20 MHz bandwidth setting. Spectra were recorded for between 4 and 12 h. Data was processed with MatLab (The Mathworks, Natick, N.J.) and ESR simulations made use of the EasySpin routines53.
Density-functional theory calculations
The linear-response TD-DFT calculations were performed using the LC-BLYP/6-31 G(d) within the Tamm–Dancoff approximation83 implemented in the Gaussian 16 programme. The geometry optimisation of the minimum-energy conical intersection between the 3LE and the 3CT was performed with the GRRM17 programme84, which refers to the energy and gradient calculated by the Gaussian 16 programme. \(\left\langle {\varPsi }_{^1{CT}}|{\hat{H}}_{{SO}}|{\varPsi }_{^3{LE}}\right\rangle\) was calculated using the TD-DFT LC-BLYP/6-31 G(d) with the scalar relativistic zeroth-order regular approximation (ZORA) Hamiltonian85,86 implemented in the ORCA 4.2.1 programme. The ZFS parameters of the 3LE and the 3CT were simulated using the DFT PBE0/6–31 G(d) with the spin-spin term calculated from the spin-densities derived from the unrestricted natural orbitals57 and the spin-orbit term calculated by the coupled-perturbed SOC approach58 implemented in the ORCA 4.2.1 programme.
Steady-state absorption and emission spectra
Dilute solutions were prepared at 100 μM in toluene. UV−vis absorption spectra were measured using a Cary 5000UV−vis−NIR spectrophotometer. PL spectra were recorded on a Horiba FL3-2i Fluorometer equipped with a liquid nitrogen attachment in solution at ambient temperature or either as steady-state or gated spectra at 77 K.
Time-resolved photoluminescence
Dilute solutions were prepared at 100 μM in deoxygenated toluene in a nitrogen environment and subsequently measured in a nitrogen environment. Time-resolved PL spectra were recorded using an electrically-gated intensified charge-coupled device (ICCD) camera (Andor iStar DH740 CCI-010) connected to a calibrated grating spectrograph (Andor SR303i). Pulsed 325 nm photoexcitation was provided at a repetition rate of 1 kHz. Temporal evolution of the PL was obtained by stepping the ICCD gate delay with respect to the excitation pulse. The minimum gate width of the ICCD was 5 ns. Recorded data was subsequently corrected to account for camera sensitivity.
Data availability
The data underlying this article are available at: https://doi.org/10.6084/m9.figshare.14428766.
Code availability
Codes used to analyse data in this manuscript are available from the corresponding author upon reasonable request.
References
Uoyama, H., Goushi, K., Shizu, K., Nomura, H. & Adachi, C. Highly efficient organic light-emitting diodes from delayed fluorescence. Nature 492, 234–238 (2012).
Goushi, K., Yoshida, K., Sato, K. & Adachi, C. Organic light-emitting diodes employing efficient reverse intersystem crossing for triplet-to-singlet state conversion. Nat. Photonics 6, 253–258 (2012).
Congrave, D. G. et al. A simple molecular design strategy for delayed fluorescence toward 1000 nm. J. Am. Chem. Soc. 141, 18390–18394 (2019).
Freeman, D. M. E. et al. Synthesis and exciton dynamics of donor-orthogonal acceptor conjugated polymers: reducing the singlet-triplet energy gap. J. Am. Chem. Soc. 139, 11073–11080 (2017).
Park, I. S., Matsuo, K., Aizawa, N. & Yasuda, T. High-performance dibenzoheteraborin-based thermally activated delayed fluorescence emitters: molecular architectonics for concurrently achieving narrowband emission and efficient triplet-singlet spin conversion. Adv. Funct. Mater. 28, 1802031 (2018).
Kim, J. U. et al. Nanosecond-time-scale delayed fluorescence molecule for deep-blue OLEDs with small efficiency rolloff. Nat. Commun. 11, 1765 (2020).
Huang, R. et al. Balancing charge-transfer strength and triplet states for deep-blue thermally activated delayed fluorescence with an unconventional electron rich dibenzothiophene acceptor. J. Mater. Chem. C. 7, 13224–13234 (2019).
Masui, K., Nakanotani, H. & Adachi, C. Analysis of exciton annihilation in high-efficiency sky-blue organic light-emitting diodes with thermally activated delayed fluorescence. Org. Electron. 14, 2721–2726 (2013).
Li, T.-Y. et al. Rational design of phosphorescent iridium(III) complexes for emission color tunability and their applications in OLEDs. Coord. Chem. Rev. 374, 55–92 (2018).
Song, W. & Lee, J. Y. Degradation mechanism and lifetime improvement strategy for blue phosphorescent organic light-emitting diodes. Adv. Opt. Mater. 5, 1600901 (2017).
Giebink, N. C. et al. Intrinsic luminance loss in phosphorescent small-molecule organic light emitting devices due to bimolecular annihilation reactions. J. Appl. Phys. 103, 044509 (2008).
Seifert, R. et al. Chemical degradation mechanisms of highly efficient blue phosphorescent emitters used for organic light emitting diodes. Org. Electron. 14, 115–123 (2013).
Moraes, I. R. De, Scholz, S., Lüssem, B. & Leo, K. Analysis of chemical degradation mechanism within sky blue phosphorescent organic light emitting diodes by laser-desorption/ionization time-of-flight mass spectrometry. Org. Electron. 12, 341–347 (2011).
Chou, P. Y. et al. Efficient delayed fluorescence via triplet–triplet annihilation for deep-blue electroluminescence. Chem. Commun. 50, 6869–6871 (2014).
Peng, L. et al. Efficient soluble deep blue electroluminescent dianthracenylphenylene emitters with CIE y (y≤0.08) based on triplet-triplet annihilation. Sci. Bull. 64, 774–781 (2019).
Ieuji, R., Goushi, K. & Adachi, C. Triplet–triplet upconversion enhanced by spin–orbit coupling in organic light-emitting diodes. Nat. Commun. 10, 5283 (2019).
Kondakov, D. Y., Pawlik, T. D., Hatwar, T. K. & Spindler, J. P. Triplet annihilation exceeding spin statistical limit in highly efficient fluorescent organic light-emitting diodes. J. Appl. Phys. 106, 124510 (2009).
Samanta, P. K., Kim, D., Coropceanu, V. & Brédas, J.-L. Up-conversion intersystem crossing rates in organic emitters for thermally activated delayed fluorescence: impact of the nature of singlet vs triplet excited states. J. Am. Chem. Soc. 139, 4042–4051 (2017).
Ogiwara, T., Wakikawa, Y. & Ikoma, T. Mechanism of intersystem crossing of thermally activated delayed fluorescence molecules. J. Phys. Chem. A 119, 3415–3418 (2015).
Evans, E. W. et al. Vibrationally assisted intersystem crossing in benchmark thermally activated delayed fluorescence molecules. J. Phys. Chem. Lett. 9, 4053–4058 (2018).
Olivier, Y., Moral, M., Muccioli, L. & Sancho-García, J.-C. Dynamic nature of excited states of donor–acceptor TADF materials for OLEDs: how theory can reveal structure–property relationships. J. Mater. Chem. C. 5, 5718–5729 (2017).
Eng, J. & Penfold, T. J. Understanding and designing thermally activated delayed fluorescence emitters: beyond the energy gap approximation. Chem. Rec. 1–27 (2020) https://doi.org/10.1002/tcr.202000013.
Olivier, Y. et al. Nature of the singlet and triplet excitations mediating thermally activated delayed fluorescence. Phys. Rev. Mater. 1, 1–6 (2017).
El‐Sayed, M. A. Spin—orbit coupling and the radiationless processes in nitrogen heterocyclics. J. Chem. Phys. 38, 2834–2838 (1963).
Salem, L. & Rowland, C. The electronic properties of diradicals. Angew. Chem. Int. Ed. Engl. 11, 92–111 (1972).
Penfold, T. J., Gindensperger, E., Daniel, C., & Marian, C. M. Spin-vibronic mechanism for intersystem crossing. Chem. Rev. 118, 6975–7025 (2018).
Marian, C. M. Spin-orbit coupling and intersystem crossing in molecules. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2, 187–203 (2012).
Kleinschmidt, M., Tatchen, J., & Marian, C. M. Spin-orbit coupling of DFT/MRCI wavefunctions: method, test calculations, and application to thiophene. J. Comput. Chem. 23, 824–833 (2002).
Chen, X. K., Zhang, S. F., Fan, J. X. & Ren, A. M. Nature of highly efficient thermally activated delayed fluorescence in organic light-emitting diode emitters: nonadiabatic effect between excited states. J. Phys. Chem. C. 119, 9728–9733 (2015).
Gibson, J., Monkman, A. P. & Penfold, T. J. The importance of vibronic coupling for efficient reverse intersystem crossing in thermally activated delayed fluorescence molecules. ChemPhysChem 17, 2956–2961 (2016).
Etherington, M. K., Gibson, J., Higginbotham, H. F., Penfold, T. J. & Monkman, A. P. Revealing the spin–vibronic coupling mechanism of thermally activated delayed fluorescence. Nat. Commun. 7, 13680 (2016).
Gibson, J. & Penfold, T. J. Nonadiabatic coupling reduces the activation energy in thermally activated delayed fluorescence. Phys. Chem. Chem. Phys. 19, 8428–8434 (2017).
Tsuchiya, Y. et al. Molecular design based on donor-weak donor scaffold for blue thermally-activated delayed fluorescence designed by combinatorial DFT calculations. Front. Chem. 8, 2–11 (2020).
Aizawa, N., Harabuchi, Y., Maeda, S. & Pu, Y.-J. Kinetic prediction of reverse intersystem crossing in organic donor–acceptor molecules. Nat. Commun. 1–6 (2020) https://doi.org/10.26434/chemrxiv.12203240.
Santos, P. L. et al. Engineering the singlet–triplet energy splitting in a TADF molecule. J. Mater. Chem. C. 4, 3815–3824 (2016).
Dias, F. B. et al. The role of local triplet excited states and D-A relative orientation in thermally activated delayed fluorescence: photophysics and devices. Adv. Sci. 3, 1600080 (2016).
Hou, Y. et al. Charge separation, charge recombination, long-lived charge transfer state formation and intersystem crossing in organic electron donor/acceptor dyads. J. Mater. Chem. C. 7, 12048–12074 (2019).
Biskup, T. Structure–function relationship of organic semiconductors: detailed insights from time-resolved EPR spectroscopy. Front. Chem. 7, 10 (2019).
Kraffert, F. et al. Charge separation in PCPDTBT:PCBM blends from an EPR perspective. J. Phys. Chem. C. 118, 28482–28493 (2014).
Thomson, S. A. J. et al. Charge separation and triplet exciton formation pathways in small-molecule solar cells as studied by time-resolved EPR spectroscopy. J. Phys. Chem. C. 121, 22707–22719 (2017).
Weiss, L. R. et al. Strongly exchange-coupled triplet pairs in an organic semiconductor. Nat. Phys. 13, 176–181 (2017).
Tait, C. E., Bedi, A., Gidron, O. & Behrends, J. Photoexcited triplet states of twisted acenes investigated by Electron Paramagnetic Resonance. Phys. Chem. Chem. Phys. 21, 21588–21595 (2019).
Bayliss, S. L. et al. Spin signatures of exchange-coupled triplet pairs formed by singlet fission. Phys. Rev. B 94, 045204 (2016).
Bae, Y. J. et al. Competition between singlet fission and spin‐orbit‐induced intersystem crossing in anthanthrene and anthanthrone derivatives. Chempluschem 84, 1432–1438 (2019).
Dong, Y. et al. Spin–orbit charge-transfer intersystem crossing (SOCT-ISC) in bodipy-phenoxazine dyads: effect of chromophore orientation and conformation restriction on the photophysical properties. J. Phys. Chem. C. 123, 22793–22811 (2019).
Zhao, Y. et al. Efficient intersystem crossing in the Tröger’s base derived from 4‐Amino‐1,8‐naphthalimide and application as a potent photodynamic therapy reagent. Chem. – A Eur. J. 26, 3591–3599 (2020).
Wang, Z. et al. Insights into the efficient intersystem crossing of bodipy-anthracene compact dyads with steady-state and time-resolved optical/magnetic spectroscopies and observation of the delayed fluorescence. J. Phys. Chem. C. 123, 265–274 (2019).
Richert, S., Limburg, B., Anderson, H. L. & Timmel, C. R. On the influence of the bridge on triplet state delocalization in linear porphyrin oligomers. J. Am. Chem. Soc. 139, 12003–12008 (2017).
Olshansky, J. H., Zhang, J., Krzyaniak, M. D., Lorenzo, E. R. & Wasielewski, M. R. Selectively addressable photogenerated spin qubit pairs in DNA hairpins. J. Am. Chem. Soc. 142, 3346–3350 (2020).
Li, Y. et al. The role of fluorine-substitution on the π-bridge in constructing effective thermally activated delayed fluorescence molecules. J. Mater. Chem. C. 6, 5536–5541 (2018).
Richert, S., Tait, C. E. & Timmel, C. R. Delocalisation of photoexcited triplet states probed by transient EPR and hyperfine spectroscopy. J. Magn. Reson. 280, 103–116 (2017).
Stoll, S. & Schweiger, A. EasySpin, a comprehensive software package for spectral simulation and analysis in EPR. J. Magn. Reson. 178, 42–55 (2006).
Saiful, I. S. M. et al. Interplanar interactions in the excited triplet states of carbazole dimers by means of time-resolved EPR spectroscopy. Mol. Phys. 104, 1535–1542 (2006).
Aloïse, S. et al. The benzophenone S1(n,π*) →T1(n,π *) states intersystem crossing reinvestigated by ultrafast absorption spectroscopy and multivariate curve resolution. J. Phys. Chem. A 112, 224–231 (2008).
Dos Santos, P. L., Etherington, M. K. & Monkman, A. P. Chemical and conformational control of the energy gaps involved in the thermally activated delayed fluorescence mechanism. J. Mater. Chem. C. 6, 4842–4853 (2018).
Iikura, H., Tsuneda, T., Yanai, T. & Hirao, K. A long-range correction scheme for generalized-gradient-approximation exchange functionals. J. Chem. Phys. 115, 3540–3544 (2001).
Sinnecker, S. & Neese, F. Spin−spin contributions to the zero-field splitting tensor in organic triplets, carbenes and biradicals—a density functional and ab initio study. J. Phys. Chem. A 110, 12267–12275 (2006).
Neese, F. Calculation of the zero-field splitting tensor on the basis of hybrid density functional and Hartree-Fock theory. J. Chem. Phys. 127, 164112 (2007).
Budil, D. E. & Thurnauer, M. C. The chlorophyll triplet state as a probe of structure and function in photosynthesis. BBA - Bioenerg. 1057, 1–41 (1991).
Marian, C. M. Mechanism of the triplet-to-singlet upconversion in the assistant dopant ACRXTN. J. Phys. Chem. C. 120, 3715–3721 (2016).
Kim, D. H. et al. High-efficiency electroluminescence and amplified spontaneous emission from a thermally activated delayed fluorescent near-infrared emitter. Nat. Photonics 12, 98–104 (2018).
Antheunis, D. A., Schmidt, J. & van der Waals, J. H. Spin-forbidden radiationless processes in isoelectronic molecules: anthracene, acridine and phenazine. Mol. Phys. 27, 1521–1541 (1974).
Baryshnikov, G., Minaev, B. & Ågren, H. Theory and calculation of the phosphorescence phenomenon. Chem. Rev. 117, 6500–6537 (2017).
Keijzers, C. P. & Haarer, D. EPR spectroscopy of delocalized and localized charge-transfer excitons in phenanthrene-PMDA single crystals. J. Chem. Phys. 67, 925–932 (1977).
Di Valentin, M., Salvadori, E., Barone, V. & Carbonera, D. Unravelling electronic and structural requisites of triplet-triplet energy transfer by advanced electron paramagnetic resonance and density functional theory. Mol. Phys. 111, 2914–2932 (2013).
Tait, C. E., Neuhaus, P., Peeks, M. D., Anderson, H. L. & Timmel, C. R. Transient EPR reveals triplet state delocalization in a series of cyclic and linear π-conjugated porphyrin oligomers. J. Am. Chem. Soc. 137, 8284–8293 (2015).
Tatchen, J., Gilka, N., & Marian, C. M. Intersystem crossing driven by vibronic spin-orbit coupling: a case study on psoralen. Phys. Chem. Chem. Phys. 9, 5209–5221 (2007).
Hou, Y. et al. Spin–orbit charge recombination intersystem crossing in phenothiazine–anthracene compact dyads: effect of molecular conformation on electronic coupling, electronic transitions, and electron spin polarizations of the triplet states. J. Phys. Chem. C. 122, 27850–27865 (2018).
Nobuyasu, R. S. et al. The influence of molecular geometry on the efficiency of thermally activated delayed fluorescence. J. Mater. Chem. C. 7, 6672–6684 (2019).
Zhang, Q. et al. Efficient blue organic light-emitting diodes employing thermally activated delayed fluorescence. Nat. Photonics 8, 326–332 (2014).
Dance, Z. E. X. et al. Intersystem crossing mediated by photoinduced intramolecular charge transfer: julolidine−anthracene molecules with perpendicular π systems. J. Phys. Chem. A 112, 4194–4201 (2008).
Etherington, M. K. et al. Regio- and conformational isomerization critical to design of efficient thermally-activated delayed fluorescence emitters. Nat. Commun. 8, 14987 (2017).
dos Santos, P. L., Ward, J. S., Bryce, M. R. & Monkman, A. P. Using guest–host interactions to optimize the efficiency of TADF OLEDs. J. Phys. Chem. Lett. 7, 3341–3346 (2016).
Sharma, N. et al. Exciton efficiency beyond the spin statistical limit in organic light emitting diodes based on anthracene derivatives. J. Mater. Chem. C. 8, 3773–3783 (2020).
Tang, G. et al. Red thermally activated delayed fluorescence and the intersystem crossing mechanisms in compact naphthalimide-phenothiazine electron donor/acceptor dyads. J. Phys. Chem. C. 123, 30171–30186 (2019).
Noda, H. et al. Critical role of intermediate electronic states for spin-flip processes in charge-transfer-type organic molecules with multiple donors and acceptors. Nat. Mater. 18, 1084–1090 (2019).
Hosokai, T. et al. Evidence and mechanism of efficient thermally activated delayed fluorescence promoted by delocalized excited states. Sci. Adv. 3, e1603282 (2017).
Nelson, J. N. et al. CNOT gate operation on a photogenerated molecular electron spin-qubit pair. J. Chem. Phys. 152, 014503 (2020).
Rugg, B. K. et al. Photodriven quantum teleportation of an electron spin state in a covalent donor–acceptor–radical system. Nat. Chem. 11, 981–986 (2019).
Schott, S. et al. Tuning the effective spin-orbit coupling in molecular semiconductors. Nat. Commun. 8, 15200 (2017).
Wasielewski, M. R. et al. Exploiting chemistry and molecular systems for quantum information science. Nat. Rev. Chem. (2020) https://doi.org/10.1038/s41570-020-0200-5.
Szumska, A. A., Sirringhaus, H. & Nelson, J. Symmetry based molecular design for triplet excitation and optical spin injection. Phys. Chem. Chem. Phys. 21, 19521–19528 (2019).
Hirata, S. & Head-Gordon, M. Time-dependent density functional theory within the Tamm–Dancoff approximation. Chem. Phys. Lett. 314, 291–299 (1999).
Maeda, S., Ohno, K. & Morokuma, K. Updated branching plane for finding conical intersections without coupling derivative vectors. J. Chem. Theory Comput. 6, 1538–1545 (2010).
Van Lenthe, E., Van Leeuwen, R., Baerends, E. J. & Snijders, J. G. Relativistic regular two-component hamiltonians. Int. J. Quantum Chem. 57, 281–293 (1996).
Van Wüllen, C. Molecular density functional calculations in the regular relativistic approximation: method, application to coinage metal diatomics, hydrides, fluorides and chlorides, and comparison with first-order relativistic calculations. J. Chem. Phys. 109, 392–399 (1998).
Acknowledgements
B.H.D. thanks Dr Saul Jones and Daniel Sowood for useful discussions regarding interpretation of photophysical and trESR data, and thanks Dr Yi-Ting Lee and Antti Reponen for preliminary TD-DFT calculations and interpretation. B.H.D. and E.W.E. thank Dr Claudia Tait and Prof. Sir. Richard H. Friend for informative discussions of the ESR and optoelectronics context. This work was supported by the Engineering and Physical Sciences Research Council (grant no. EP/M005143/1) and the European Research Council (ERC). B.H.D. acknowledges support from the EPSRC Cambridge NanoDTC (grant no. EP/L015978/1). E.W.E is grateful to the Leverhulme Trust (ECF-2019-054) and Isaac Newton Trust for Fellowship funding. E.W.E is thankful to the Royal Society for a University Research Fellowship (URF/R1/201300). N.A. acknowledges support from the JST PRESTO (grant no. JPMJPR17N1). Y. X. thanks the China Scholarship Council for a Fellowship. The Centre for Advanced Electron Spin Resonance is supported by the EPSRC (EP/L011972/1).
Author information
Authors and Affiliations
Contributions
B.H.D., N.A., Y.Z., D.C., S.R.M., E.W.E. designed research; B.H.D. and W.K.M. performed and analysed trESR; B.H.D. and M.C. performed and analysed emission and absorption spectra; N.A. performed the computational calculations, the results of which were analysed by N.A. and B.H.D.; Y.Z., Y.X., M.C., S.B. and S.R.M. designed the materials and Y.Z., Y.X. and M.C. synthesised the materials and characterised their optical properties; Q.G. fabricated and measured OLEDs; L.R.W. and A.J.G. contributed to discussion of the work; all authors wrote the paper; S.B., D.C., Y.J.P., S.R.M., E.W.E. supervised the research.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Peer review information Nature Communications thanks Marc Etherington and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Drummond, B.H., Aizawa, N., Zhang, Y. et al. Electron spin resonance resolves intermediate triplet states in delayed fluorescence. Nat Commun 12, 4532 (2021). https://doi.org/10.1038/s41467-021-24612-9
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-021-24612-9
This article is cited by
-
Understanding of complex spin up-conversion processes in charge-transfer-type organic molecules
Nature Communications (2024)
-
Enhancing operational stability of OLEDs based on subatomic modified thermally activated delayed fluorescence compounds
Nature Communications (2023)
-
Dielectric control of reverse intersystem crossing in thermally activated delayed fluorescence emitters
Nature Materials (2022)
-
Constructing high-efficiency orange-red thermally activated delayed fluorescence emitters by three-dimension molecular engineering
Nature Communications (2022)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.