Abstract
A quantitative understanding of the electromagnetic response of materials is essential for the precise engineering of maximal, versatile, and controllable light–matter interactions. Material surfaces, in particular, are prominent platforms for enhancing electromagnetic interactions and for tailoring chemical processes. However, at the deep nanoscale, the electromagnetic response of electron systems is significantly impacted by quantum surface-response at material interfaces, which is challenging to probe using standard optical techniques. Here, we show how ultraconfined acoustic graphene plasmons in graphene–dielectric–metal structures can be used to probe the quantum surface-response functions of nearby metals, here encoded through the so-called Feibelman d-parameters. Based on our theoretical formalism, we introduce a concrete proposal for experimentally inferring the low-frequency quantum response of metals from quantum shifts of the acoustic graphene plasmons dispersion, and demonstrate that the high field confinement of acoustic graphene plasmons can resolve intrinsically quantum mechanical electronic length-scales with subnanometer resolution. Our findings reveal a promising scheme to probe the quantum response of metals, and further suggest the utilization of acoustic graphene plasmons as plasmon rulers with ångström-scale accuracy.
Similar content being viewed by others
Introduction
Light is a prominent tool to probe the properties of materials and their electronic structure, as evidenced by the widespread use of light-based spectroscopies across the physical sciences1,2. Among these tools, far-field optical techniques are particularly prevalent, but are constrained by the diffraction limit and the mismatch between optical and electronic length scales to probe the response of materials only at large length scales (or, equivalently, at small momenta). Plasmon polaritons—hybrid excitations of light and free carriers—provide a mean to overcome these constraints through their ability to confine electromagnetic radiation to the nanoscale3.
Graphene, in particular, supports gate-tunable plasmons characterized by an unprecedentedly strong confinement of light4,5,6. When placed near a metal, graphene plasmons (GPs) are strongly screened and acquire a nearly linear (acoustic-like) dispersion7,8,9,10 (contrasting with the square-root-type dispersion of conventional GPs). Crucially, such acoustic graphene plasmons (AGPs) in graphene–dielectric–metal (GDM) structures have been shown to exhibit even higher field confinement than conventional GPs with the same frequency, effectively squeezing light into the few-nanometer regime8,9,10,11. Recently, using scanning near-field optical microscopy, these features were exploited to experimentally measure the conductivity of graphene, σ(q,ω), across its frequency (ω) and momentum (q) dependence simultaneously8. The observation of momentum dependence implies a nonlocal response (i.e., response contributions at position r from perturbations at \({\bf{r}}^{\prime}\)), whose origin is inherently quantum mechanical. Incidentally, traditional optical spectroscopic tools cannot resolve nonlocal response in extended systems due to the intrinsically small momenta k0 ≡ ω/c carried by far-field photons. Acoustic graphene plasmons, on the other hand, can carry large momenta—up to a significant fraction of the electronic Fermi momentum kF and with group velocities asymptotically approaching the electron’s Fermi velocity vF—and so can facilitate explorations of nonlocal (i.e., q-dependent) response not only in graphene itself but also, as we detail in this Article, in nearby materials. So far, however, only aspects related to the quantum response of graphene have been addressed8, leaving any quantum nonlocal aspects of the adjacent metal’s response unattended, despite their potentially substantial impact at nanometric graphene–metal separations12,13,14,15,16.
Here, we present a theoretical framework that simultaneously incorporates quantum nonlocal effects in the response of both the graphene and of the metal substrate for AGPs in GDM heterostructures. Further, our approach establishes a concrete proposal for experimentally measuring the low-frequency nonlocal electrodynamic response of metals. Our model treats graphene at the level of the nonlocal random-phase approximation (RPA)4,9,17,18,19 and describes the quantum aspects of the metal’s response—including nonlocality, electronic spill-out/spill-in, and surface-enabled Landau damping—using a set of microscopic surface-response functions known as the Feibelman d-parameters12,13,15,16,20,21. These parameters, d⊥ and d∥, measure the frequency-dependent centroids of the induced charge density and of the normal derivative of the tangential current density, respectively (Supplementary Note 1). Using a combination of numerics and perturbation theory, we show that the AGPs are spectrally shifted by the quantum surface-response of the metal: toward the red for \({\rm{Re}} {\,}{d}_{\perp } > \,0\) (associated with electronic spill-out of the induced charge density) and toward the blue for \({\rm{Re}} {\,}{d}_{\perp } < \,0\) (signaling an inward shift, or “spill-in”). Interestingly, these shifts are not accompanied by a commensurately large quantum broadening nor by a reduction of the AGP’s quality factor, thereby providing the theoretical support explaining recent experimental observations11. Finally, we discuss how state-of-the-art measurements of AGPs could be leveraged to map out the low-frequency quantum nonlocal surface response of metals experimentally. Our findings have significant implications for our ability to optimize photonic designs that interface far- and mid-infrared optical excitations—such as AGPs—with metals all the way down to the nanoscale, with pursuant applications in, e.g., ultracompact nanophotonic devices, nanometrology, and in the surface sciences more broadly.
Results
Theory
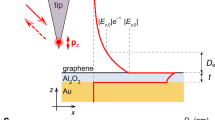
We consider a GDM heterostructure (see Fig. 1) composed of a graphene sheet with a surface conductivity σ ≡ σ(q,ω) separated from a metal substrate by a thin dielectric slab of thickness t and relative permittivity ϵ2 ≡ ϵ2(ω); finally, the device is covered by a superstrate of relative permittivity ϵ1 ≡ ϵ1(ω). While the metal substrate may, in principle, be represented by a nonlocal and spatially non-uniform (near the interface) dielectric function, here we abstract its contributions into two parts: a bulk, local contribution via \({\epsilon }_{\text{m}}\equiv {\epsilon }_{\text{m}}(\omega )={\epsilon }_{\infty }(\omega )-{\omega }_{\text{p}}^{2}/({\omega }^{2}+\text{i}\omega {\gamma }_{\text{m}})\), and a surface, quantum contribution included through the d-parameters. These parameters are quantum-mechanical surface-response functions, defined by the first moments of the microscopic induced charge (d⊥) and of the normal derivative of the tangential current (d∥); see Fig. 1 (Supplementary Note 1 gives a concise introduction). They allow the leading-order corrections to classicality to be conveniently incorporated via a surface dipole density (∝ d⊥) and a surface current density (∝ d∥)9,15,16, and can be obtained either by first-principles computation20,21, semiclassical models, or experiments15.
The graphene–metal separation, t, is controlled by the thickness of the dielectric (ϵ2) spacer. The close-up (near the metal–spacer interface) shows a pictorial representation of the surface–response functions d⊥ and d∥ along with the related the microscopic quantities characterizing the metal surface, namely the equilibrium electronic density, n0(z), and the induced charge density, ρind(z).
The electromagnetic excitations of any system can be obtained by analyzing the poles of the (composite) system’s scattering coefficients. For the AGPs of a GDM structure, the relevant coefficient is the p-polarized reflection (or transmission) coefficient, whose poles are given by \(1\ -\ {r}_{p}^{2|{\mathrm{g}}| 1}\ {r}_{p}^{2|{\mathrm{m}}}\ {\text{e}}^{{\text{i}}2{k}_{z,2}t}=0\) (ref. 22). Here, \({r}_{p}^{2| \text{g}| 1}\) and \({r}_{p}^{2| \text{m}}\) denote the p-polarized reflection coefficients for the dielectric–graphene–dielectric and the dielectric–metal interface (detailed in Supplementary Note 2), respectively. Each coefficient yields a material-specific contribution to the overall quantum response: \({r}_{p}^{2|\text{g}| 1}\) incorporates graphene’s via σ(q,ω) and \({r}_{p}^{2| \text{m}}\) incorporates the metal’s via the d-parameters (see Supplementary Note 2). The complex exponential [with \({k}_{z,2}\equiv {({\epsilon }_{2}{k}_{0}^{2}-{q}^{2})}^{1/2}\), where q denotes the in-plane wavevector] incorporates the effects of multiple reflections within the slab. Thus, using the above-noted reflection coefficients (defined explicitly in Supplementary Note 2), we obtain a quantum-corrected AGP dispersion equation:
for in-plane AGP wavevector q and out-of-plane confinement factors \({\kappa }_{j}\equiv ( {q}^{2}-{\epsilon }_{j}{k}_{0}^{2} )^{1/2}\) for j ∈ {1, 2, m}.
Since AGPs are exceptionally subwavelength (with confinement factors up to almost 300)8,10,11, the nonretarded limit (wherein κj → q) constitutes an excellent approximation. In this regime, and for encapsulated graphene, i.e., where ϵd ≡ ϵ1 = ϵ2, Eq. (1) simplifies to
For simplicity and concreteness, we will consider a simple jellium treatment of the metal such that d∥ vanishes due to charge neutrality21,23, leaving only d⊥ nonzero. Next, we exploit the fact that AGPs typically span frequencies across the terahertz (THz) and mid-infrared (mid-IR) spectral ranges, i.e., well below the plasma frequency ωp of the metal. In this low-frequency regime, ω ≪ ωp, the frequency dependence of d⊥ (and d∥) has the universal, asymptotic dependence
as shown by Persson et al.24,25 by exploiting Kramers–Kronig relations. Here, ζ is the so-called static image-plane position, i.e., the centroid of induced charge under a static, external field26, and ξ defines a phase-space coefficient for low-frequency electron–hole pair creation, whose rate is ∝ qωξ21: both are ground-state quantities. In the jellium approximation of the interacting electron liquid, the constants ζ ≡ ζ(rs) and ξ ≡ ξ(rs) depend solely on the carrier density ne, here parameterized by the Wigner–Seitz radius \({r}_{s}{a}_{\text{B}}\equiv {(3{n}_{\text{e}}/4\pi )}^{1/3}\) (Bohr radius, aB). In the following, we exploit the simple asymptotic relation in Eq. (3) to calculate the dispersion of AGPs with metallic (in addition to graphene’s) quantum response included.
Quantum corrections in AGPs due to metallic quantum surface-response
The spectrum of AGPs calculated classically and with quantum corrections is shown in Fig. 2. Three models are considered: one, a completely classical, local-response approximation treatment of both the graphene and the metal; and two others, in which graphene’s response is treated by the nonlocal RPA4,9,17,18,19 while the metal’s response is treated either classically or with quantum surface-response included (via the d⊥-parameter). As noted previously, we adopt a jellium approximation for the d⊥-parameter. Figure 2a shows that—for a fixed wavevector—the AGP’s resonance blueshifts upon inclusion of graphene’s quantum response, followed by a redshift due to the quantum surface-response of the metal (since \({\rm{Re}} {\,}{d}_{\perp } > \,0\) for jellium metals; electronic spill-out)13,15,16,21,27,28. This redshifting due to the metal’s quantum surface-response is opposite to that predicted by the semiclassical hydrodynamic model (HDM) where the result is always a blueshift14 (corresponding to \({\rm{Re}}{\,}{d}_{\perp }^{\text{HDM}} < \,0\); electronic “spill-in”) due to the neglect of spill-out effects29. The imaginary part of the AGP’s wavevector (that characterizes the mode’s propagation length) is shown in Fig. 2b: the net effect of the inclusion of d⊥ is a small, albeit consistent, increase of this imaginary component. Notwithstanding this, the modification of \({\rm{Im}}\, q\) is not independent of the shift in \({\rm{Re}}{\,}q\); as a result, an increase in \({\rm{Im}}{\,}q\) does not necessarily imply the presence of a significant quantum decay channel [e.g., an increase of \({\rm{Im}}{\,}q\) can simply result from increased classical loss (i.e., arising from local response alone) at the newly shifted \({\rm{Re}}\, q\) position]. Because of this, we inspect the quality factor \(Q\equiv {\rm{Re}}{\,}q/{\rm{Im}}{\,}q\) (or “inverse damping ratio”30,31) instead32 (Fig. 2c), which provides a complementary perspective that emphasizes the effective (or normalized) propagation length rather than the absolute length. The incorporation of quantum mechanical effects, first in graphene alone, and then in both graphene and metal, reduces the AGP’s quality factor. Still, the impact of metal-related quantum losses in the latter is negligible, as evidenced by the nearly overlapping black and red curves in Fig. 2c.
Three increasingly sophisticated tiers of response models are considered: (i) classical, local response for both the graphene and the metal [gray dot-dashed line]; (ii) nonlocal RPA and local Drude response for the graphene and the metal, respectively [black dashed line]; and (iii) nonlocal RPA and d-parameter-augmented response for the graphene and the metal, respectively [red solid line]. a AGP dispersion diagram, ω/(2π) versus \({\rm{Re}}{\,}q\). The hatched region indicates the graphene’s electron–hole continuum. b Associated imaginary part of the AGP wavevector, \({\rm{Im}}\, q\). c Corresponding quality factor \(Q\equiv {\rm{Re}}\, q/{\rm{Im}}\, q\). The inset shows a zoom of the indicated region. System parameters: we take a graphene–metal separation of t = 1 nm; for concreteness and simplicity, we consider an unscreened jellium metal with plasma frequency \(\hbar\)ωp ≈ 9.07 eV (corresponding to rs = 3) where ζ ≈ 0.8 Å and ξ ≈ 0.3 Å24, with Drude-type damping \(\hbar\)γm = 0.1 eV; for graphene, we take EF = 0.3 eV and \(\hbar\)γ = 8 meV; finally, we have assumed ϵd ≡ ϵ1 = ϵ2 = 1 (for consistency with the d-parameter data which assumes a metal–vacuum interface24).
To better understand these observations, we treat the AGP’s q-shift due to the metal’s quantum surface-response as a perturbation: writing q = q0 + q1, we find that the quantum correction from the metal is q1 ≃ q0d⊥/(2t), for a jellium adjacent to vacuum in the \({\omega }^{2}/{\omega }_{\text{p}}^{2}\ll {q}_{0}t\ll 1\) limit (Supplementary Note 3). This simple result, together with Eq. (3), provides a near-quantitative account of the AGP dispersion shifts due to metallic quantum surface-response: for ω ≪ ωp, (i) \({\rm{Re}}\, {d}_{\perp }\) tends to a finite value, ζ, which increases (decreases) \({\rm{Re}}\, q\) for ζ > 0 (ζ < 0); and (ii) \({\rm{Im}}{\,}{d}_{\perp }\) is \(\mathop{\propto}\omega\) and therefore asymptotically vanishing as ω/ωp → 0 and so only negligibly increases \({\rm{Im}}\, q\). Moreover, the preceding perturbative analysis warrants \({\rm{Re}}{\,}{q}_{1}/{\rm{Re}}{\,}{q}_{0} \approx {\rm{Im}}{\,}{q}_{1}/{\rm{Im}}{\,}{q}_{0}\) (Supplementary Note 3), which elucidates the reason why the AGP’s quality factor remains essentially unaffected by the inclusion of metallic quantum surface-response. Notably, these results explain recent experimental observations that found appreciable spectral shifts but negligible additional broadening due to metallic quantum response10,11.
Next, by considering the separation between graphene and the metallic interface as a renormalizable parameter, we find a complementary and instructive perspective on the impact of metallic quantum surface-response. Specifically, within the spectral range of interest for AGPs (i.e., ω ≪ ωp), we find that the “bare” graphene–metal separation t is effectively renormalized due to the metal’s quantum surface-response from t to \(\tilde{t}\equiv t-s\), where s ≃ d⊥ ≃ ζ (see Supplementary Note 4), corresponding to a physical picture where the metal’s interface lies at the centroid of its induced density (i.e., \({\rm{Re}}{\,}{d}_{\perp }\)) rather than at its “classical” jellium edge. With this approach, the form of the dispersion equation is unchanged but references the renormalized separation \(\tilde{t}\) instead of its bare counterpart t, i.e.:
This perspective, for instance, has substantial implications for the analysis and understanding of plasmon rulers33,34,35 at nanometric scales.
Furthermore, our findings additionally suggest an interesting experimental opportunity: as all other experimental parameters can be well-characterized by independent means (including the nonlocal conductivity of graphene), high-precision measurements of the AGP’s dispersion can enable the characterization of the low-frequency metallic quantum response—a regime that has otherwise been inaccessible in conventional metal-only plasmonics. The underlying idea is illustrated in Fig. 3; depending on the sign of the static asymptote ζ ≡ d⊥(0), the AGP’s dispersion shifts toward larger q (smaller ω; redshift) for ζ > 0 and toward smaller q (larger ω; blueshift) for ζ < 0. As noted above, the q-shift is ~q0ζ/(2t). Crucially, despite the ångström-scale of ζ, this shift can be sizable: the inverse scaling with the spacer thickness t effectively amplifies the attainable shifts in q, reaching up to several μm−1 for few-nanometer t. We stress that these regimes are well within current state-of-the-art experimental capabilities8,10,11, suggesting a new path toward the systematic exploration of the static quantum response of metals.
Probing the quantum surface-response of metals with AGPs
The key parameter that regulates the impact of quantum surface corrections stemming from the metal is the graphene–metal separation, t (analogously to the observations of nonclassical effects in conventional plasmons at narrow metal gaps13,36,37); see Fig. 4. For the experimentally representative parameters indicated in Fig. 4, these come into effect for t ≲ 5 nm, growing rapidly upon decreasing the graphene–metal separation further. Chiefly, ignoring the nonlocal response of the metal leads to a consistent overestimation (underestimation) of AGP’s wavevector (group velocity) for d⊥ < 0, and vice versa for d⊥ > 0 (Fig. 4a); this behavior is consistent with the effective renormalization of the graphene–metal separation mentioned earlier (Fig. 4b). Finally, we analyze the interplay of both t and EF and their joint influence on the magnitude of the quantum corrections from the metal (we take d⊥ = −4 Å, which is reasonable for the Au substrate used in recent AGP experiments7,8,11); in Fig. 4c we show the relative wavevector quantum shift (excited at λ0 = 11.28 μm32). In the few-nanometer regime, the quantum corrections to the AGP wavevector approach 5%, increasing further as t decreases—for instance, in the extreme, one-atom-thick limit (t ≈ 0.7 nm11, which also approximately coincides with edge of the validity of the d-parameter framework, i.e., t ≳ 1 nm15) the AGP’s wavevector can change by as much as 10% for moderate graphene doping. The pronounced Fermi level dependence exhibited in Fig. 4c also suggests a complementary approach for measuring the metal’s quantum surface-response even if an experimental parameter is unknown (although, as previously noted, all relevant experimental parameters can in fact be characterized using currently available techniques8,10,11,15): such an unknown variable can be fitted at low EF using the “classical” theory (i.e., with d⊥ = d∥ = 0), since the impact of metallic quantum response is negligible in that regime. A parameter-free assessment of the metal’s quantum surface-response can then be carried out subsequently by increasing EF (and with it, the metal-induced quantum shift). We emphasize that this can be accomplished in the same device by doping graphene using standard electrostatic gating8,10,11.
a AGP’s wavevector as a function of the graphene–metal separation t, contrasting the metal’s response based on classical (d⊥ = 0) and quantum (d⊥ = ±4 Å) treatments. Inset: corresponding group velocity \({v}_{\text{p}}=\partial \omega /\partial q{| }_{q = q({\omega }_{0})}\). b Dependence of the renormalized graphene–metal separation \(\tilde{t}\equiv t-s\) versus t. Setup parameters: rs = 3, \(\hbar\)γm = 0.1 eV, ϵd = 4, EF = 0.3 eV, and \(\hbar\)γ = 8 meV; we assume an excitation at λ0 = 11.28 μm (\(\hbar\)ω0 ≈ 110 meV or f0 ≈ 26.6 THz)32. c Relative quantum shift of the AGP wavevector, \({\rm{Re}}\, {{\Delta }}q/{\rm{Re}}\, {q}_{0}\), with Δq ≡ q0 − q where q0 and q denote the AGP wavevector associated with d⊥ = 0 and d⊥ = −4 Å, respectively. The results presented in both a and c are based on the exact, numerical solution of Eq. (1).
Discussion
In this Article, we have presented a theoretical account that establishes and quantifies the influence of the metal’s quantum response for AGPs in hybrid GDM structures. We have demonstrated that the nanoscale confinement of electromagnetic fields inherent to AGPs can be harnessed to determine the quantum surface-response of metals in the THz and mid-IR spectral ranges (which is typically inaccessible with traditional metal-based plasmonics). Additionally, our findings elucidate and contextualize recent experiments10,11 that have reported the observation of nonclassical spectral shifting of AGPs due to metallic quantum response but without a clear concomitant increase of damping, even for atomically thin graphene–metal separations. Our results also demonstrate that the metal’s quantum surface-response needs to be rigorously accounted for—e.g., using the framework developed here—when searching for signatures of many-body effects in the graphene electron liquid imprinted in the spectrum of AGPs in GDM systems8, since the metal’s quantum-surface response can lead to qualitatively similar dispersion shifts, as shown here. In passing, we emphasize that our framework can be readily generalized to more complex graphene–metal hybrid structures either by semi-analytical approaches (e.g., the Fourier modal method38 for periodically nanopatterned systems) or by direct implementation in commercially available numerical solvers (see refs. 15,39), simply by adopting d-parameter-corrected boundary conditions15,16.
Further, our formalism provides a transparent theoretical foundation for guiding experimental measurements of the quantum surface-response of metals using AGPs. The quantitative knowledge of the metal’s low-frequency, static quantum response is of practical utility in a plethora of scenarios, enabling, for instance, the incorporation of leading-order quantum corrections to the classical electrostatic image theory of particle–surface interaction20 as well as to the van der Waals interaction21,25,40 affecting atoms or molecules near metal surfaces. Another prospect suggested by our findings is the experimental determination of ζ ≡ d⊥(0) through measurements of the AGP’s spectrum. This highlights a new metric for comparing the fidelity of first-principle calculations of different metals (inasmuch as ab initio methods can yield disparate results depending on the chosen scheme or functional)41,42 with explicit measurements.
Our results also highlight that AGPs can be extremely sensitive probes for nanometrology as plasmon rulers, while simultaneously underscoring the importance of incorporating quantum response in the characterization of such rulers at (sub)nanometric scales. Finally, the theory introduced here further suggests additional directions for exploiting AGP’s high-sensitivity, e.g., to explore the physics governing the complex electron dynamics at the surfaces of superconductors43 and other strongly correlated systems.
Data availability
The data that underlie the findings of this study are available from the corresponding authors upon reasonable request.
Code availability
The codes developed in this study are available from the corresponding authors upon reasonable request.
References
Tkachenko, N. Optical Spectroscopy: Methods and Instrumentations 1st edn (Elsevier, 2006).
Hollas, J. M. Modern Spectroscopy 4th edn (Wiley, 2004).
Gramotnev, D. K. & Bozhevolnyi, S. I. Plasmonics beyond the diffraction limit. Nat. Photonics 4, 83 (2010).
Gonçalves, P. A. D. & Peres, N. M. R. An Introduction to Graphene Plasmonics 1st edn (World Scientific, 2016).
Koppens, F. H. L., Chang, D. E. & García de Abajo, F. J. Graphene plasmonics: a platform for strong light-matter interactions. Nano Lett. 11, 3370 (2011).
García de Abajo, F. J. Graphene plasmonics: challenges and opportunities. ACS Photonics 1, 135 (2014).
Alonso-González, P. et al. Acoustic terahertz graphene plasmons revealed by photocurrent nanoscopy. Nat. Nanotechnol. 12, 31 (2017).
Lundeberg, M. B. et al. Tuning quantum nonlocal effects in graphene plasmonics. Science 357, 187 (2017).
Gonçalves, P. A. D. Plasmonics and Light–Matter Interactions in Two-Dimensional Materials and in Metal Nanostructures: Classical and Quantum Considerations (Springer Nature, 2020).
Epstein, I. et al. Far-field excitation of single graphene plasmon cavities with ultracompressed mode volumes. Science 368, 1219 (2020).
Iranzo, D. A. et al. Probing the ultimate plasmon confinement limits with a van der Waals heterostructure. Science 360, 291 (2018).
Yan, W., Wubs, M. & Mortensen, N. A. Projected dipole model for quantum plasmonics. Phys. Rev. Lett. 115, 137403 (2015).
Christensen, T., Yan, W., Jauho, A.-P., Soljačić, M. & Mortensen, N. A. Quantum corrections in nanoplasmonics: shape, scale, and material. Phys. Rev. Lett. 118, 157402 (2017).
Dias, E. J. C. et al. Probing nonlocal effects in metals with graphene plasmons. Phys. Rev. B 97, 245405 (2018).
Yang, Y. et al. A general theoretical and experimental framework for nanoscale electromagnetism. Nature 576, 248 (2019).
Gonçalves, P. A. D. et al. Plasmon–emitter interactions at the nanoscale. Nat. Commun. 11, 366 (2020).
Wunsch, B., Stauber, T., Sols, F. & Guinea, F. Dynamical polarization of graphene at finite doping. N. J. Phys. 8, 318 (2006).
Hwang, E. H. & Das Sarma, S. Dielectric function, screening, and plasmons in two-dimensional graphene. Phys. Rev. B 75, 205418 (2007).
Jablan, M., Buljan, H. & Soljačić, M. Plasmonics in graphene at infrared frequencies. Phys. Rev. B 80, 245435 (2009).
Feibelman, P. J. Surface electromagnetic-fields. Prog. Surf. Sci. 12, 287 (1982).
Liebsch, A. Electronic Excitations at Metal Surfaces (Springer, 1997).
Chew, W. C. Waves and Fields in Inhomogenous Media (Wiley-IEEE Press, 1995).
Apell, P. A simple derivation of the surface contribution to the reflectivity of a metal, and its use in the van der Waals interaction. Phys. Scr. 24, 795 (1981).
Persson, B. N. J. & Apell, P. Sum rules for surface response functions with application to the van der Waals interaction between an atom and a metal. Phys. Rev. B 27, 6058 (1983).
Persson, B. N. J. & Zaremba, E. Reference-plane position for the atom-surface van der Waals interaction. Phys. Rev. B 40, 5669 (1984).
Lang, N. D. & Kohn, W. Theory of metal surfaces: induced surface charge and image potential. Phys. Rev. B 7, 3541 (1973).
Liebsch, A. Dynamical screening at simple-metal surfaces. Phys. Rev. B 36, 7378 (1987).
Liebsch, A. Surface-plasmon dispersion and size dependence of Mie resonance: silver versus simple metals. Phys. Rev. B 48, 11317 (1993).
Raza, S., Bozhevolnyi, S. I., Wubs, M. & Mortensen, N. A. Nonlocal optical response in metallic nanostructures. J. Phys. Condens. Matter 27, 183204 (2015).
Woessner, A. et al. Highly confined low-loss plasmons in graphene-boron nitride heterostructures. Nat. Mater. 14, 421 (2015).
Low, T. et al. Polaritons in layered two-dimensional materials. Nat. Mater. 16, 182 (2017).
Ni, G. X. et al. Fundamental limits to graphene plasmonics. Nature 557, 530 (2018).
Sönnichsen, C., Reinhard, B. M., Liphardt, J. & Alivisatos, A. P. A molecular ruler based on plasmon coupling of single gold and silver nanoparticles. Nat. Biotechnol. 23, 741 (2005).
Hill, R. T. et al. Plasmon ruler with angstrom length resolution. ACS Nano 6, 9237 (2012).
Teperik, T. V., Nordlander, P., Aizpurua, J. & Borisov, A. G. Robust subnanometric plasmon ruler by rescaling of the nonlocal optical response. Phys. Rev. Lett. 110, 263901 (2013).
Zhu, W. et al. Quantum mechanical effects in plasmonic structures with subnanometre gaps. Nat. Commun. 7, 11495 (2016).
Raza, S., Christensen, T., Wubs, M., Bozhevolnyi, S. I. & Mortensen, N. A. Nonlocal response in thin-film waveguides: loss versus nonlocality and breaking of complementarity. Phys. Rev. B 88, 115401 (2013).
Lavrinenko, A. V., Lægsgaard, J., Gregersen, N., Schmidt, F. & Søndergaard, T. Numerical Methods in Photonics 1st edn (CRC Press, 2014).
Rodríguez Echarri, A. et al. Optical response of noble metal nanostructures: Quantum surface effects in crystallographic facets. Optica 8, 710–721 (2021).
Zaremba, E. & Kohn, W. Van der waals interaction between an atom and a solid surface. Phys. Rev. B 13, 2270 (1976).
Mata, R. A. & Suhm, M. A. Benchmarking quantum chemical methods: are we heading in the right direction? Angew. Chem. Int. Ed. 56, 11011 (2017).
Lejaeghere, K. et al. Reproducibility in density functional theory calculations of solids. Science 351, aad3000 (2016).
Costa, A. T. et al. Harnessing ultraconfined graphene plasmons to probe the electrodynamics of superconductors. Proc. Natl Acad. Sci. USA 118, e2012847118 (2021).
Acknowledgements
N.A.M. is a VILLUM Investigator supported by VILLUM FONDEN (Grant No. 16498) and Independent Research Fund Denmark (Grant No. 7026-00117B). The Center for Nano Optics is financially supported by the University of Southern Denmark (SDU 2020 funding). The Center for Nanostructured Graphene (CNG) is sponsored by the Danish National Research Foundation (Project No. DNRF103). This work was partly supported by the Army Research Office through the Institute for Soldier Nanotechnologies under Contract No. W911NF-18-2-0048. N.M.R.P. acknowledges support from the European Commission through the project “Graphene-Driven Revolutions in ICT and Beyond” (No. 881603, Core 3), COMPETE 2020, PORTUGAL 2020, FEDER and the Portuguese Foundation for Science and Technology (FCT) through project POCI-01-0145-FEDER-028114 and through the framework of the Strategic Financing UID/FIS/04650/2019. F.H.L.K. acknowledges financial support from the Government of Catalonia through the SGR grant and from the Spanish Ministry of Economy and Competitiveness (MINECO) through the Severo Ochoa Programme for Centres of Excellence in R&D (SEV-2015-0522), support by Fundació Cellex Barcelona, Generalitat de Catalunya through the CERCA program, and the MINECO grants Plan Nacional (FIS2016-81044-P) and the Agency for Management of University and Research Grants (AGAUR) 2017 SGR 1656. Furthermore, the research leading to these results has received funding from the European Union’s Horizon 2020 program under the Graphene Flagship Grant Agreements No. 785219 (Core 2) and no. 881603 (Core 3), and the Quantum Flagship Grant No. 820378. This work was also supported by the ERC TOPONANOP (Grant No. 726001).
Author information
Authors and Affiliations
Contributions
P.A.D.G., T.C., N.M.R.P., I.E., F.H.L.K., M.S. and N.A.M. conceived the research. P.A.D.G. and T.C. spearheaded the research and drafted the manuscript. N.M.R.P., A.-P.J., M.S., and N.A.M. supervised the work. All authors provided significant contributions to all aspects of this work and to the writing of the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Peer review information Nature Communications thanks Luca Bursi, Marco Ornigotti and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Gonçalves, P.A.D., Christensen, T., Peres, N.M.R. et al. Quantum surface-response of metals revealed by acoustic graphene plasmons. Nat Commun 12, 3271 (2021). https://doi.org/10.1038/s41467-021-23061-8
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-021-23061-8
This article is cited by
-
Relaxing Graphene Plasmon Excitation Constraints Through the Use of an Epsilon-Near-Zero Substrate
Plasmonics (2023)
-
Cyclotron resonance overtones and near-field magnetoabsorption via terahertz Bernstein modes in graphene
Nature Physics (2022)
-
Two-dimensional Dirac plasmon-polaritons in graphene, 3D topological insulator and hybrid systems
Light: Science & Applications (2022)
-
Extremely confined gap plasmon modes: when nonlocality matters
Nature Communications (2022)
-
Strong in-plane scattering of acoustic graphene plasmons by surface atomic steps
Nature Communications (2022)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.