Abstract
Chiral superconductors have been proposed as one pathway to realize Majorana normal fluid at its boundary. However, the long-sought 2D and 3D chiral superconductors with edge and surface Majorana normal fluid are yet to be conclusively found. Here, we report evidence for a chiral spin-triplet pairing state of UTe2 with surface normal fluid response. The microwave surface impedance of the UTe2 crystal was measured and converted to complex conductivity, which is sensitive to both normal and superfluid responses. The anomalous residual normal fluid conductivity supports the presence of a significant normal fluid response. The superfluid conductivity follows the temperature behavior predicted for an axial spin-triplet state, which is further narrowed down to a chiral spin-triplet state with evidence of broken time-reversal symmetry. Further analysis excludes trivial origins for the observed normal fluid response. Our findings suggest that UTe2 can be a new platform to study exotic topological excitations in higher dimension.
Similar content being viewed by others
Introduction
Topological insulators, with nonzero topological invariants, possess metallic states at their boundary1. Chiral superconductors, a type of topological superconductors with nonzero topological invariants, possess Majorana fermions at their boundary2,3,4,5. Majorana fermions are an essential ingredient to establish topological quantum computation6. Hence, great effort has been given to search for chiral superconducting systems. So far, evidence for the 1D example has been found from a semiconductor nanowire with end-point Majorana states7. However, 2D and 3D chiral superconductors with a surface Majorana normal fluid has not been unequivocally found3. Recently, a newly discovered heavy-fermion superconductor UTe2 (ref. 8) is proposed to be a long-sought 3D chiral superconductor with evidence of the chiral in-gap state from a scanning tunneling microscopy (STM) study9. This raises a great deal of interest in the physics community to independently establish the existence of the normal fluid response, determining whether or not the response is intrinsic, and identifying the nature of the pairing state of UTe2.
To address these three questions, the microwave surface impedance of a UTe2 crystal was measured by the dielectric resonator technique (see Supplementary Notes 1–3). The obtained impedance was converted to the complex conductivity, where the real part is sensitive to the normal fluid response and the imaginary part is sensitive to the superfluid response. By examining these results, here we confirm the existence of the significant normal fluid response of UTe2, verify that the response is intrinsic, and identify that the gap structure is consistent with the chiral spin-triplet pairing state.
Results
Anomalous residual normal fluid response
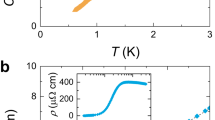
Figure 1 shows the surface impedance Zs = Rs + iXs of the sample as a function of temperature, measured from the disk dielectric resonator setup (Supplementary Note 2 and ref. 10). The surface resistance Rs decreases monotonically below ≈1.55 K and reaches a surprisingly high residual value Rs(0) ≈ 14 mΩ at 11.26 GHz. This value is larger by an order of magnitude than that of another heavy-fermion superconductor CeCoIn5 (Rs(0) ≈ 0.9 mΩ at 12.28 GHz)11. Subsequently its electrical resistance was determined by transport measurement and a midpoint Tc of 1.57 K was found.
The measured temperature dependence of the surface impedance of a UTe2 sample at 11.26 GHz. The blue curve represents the surface resistance Rs and the red curve represents the surface reactance Xs. The determination of the error bars of Rs and Xs is described in the Supplementary Note 1.
With the surface impedance, the complex conductivity \(\tilde{\sigma }={\sigma }_{1}-i{\sigma }_{2}\) of the sample can be calculated. In the local electrodynamics regime (Supplementary Note 4), one has \({Z}_{\mathrm{s}}=\sqrt{i{\mu }_{0}\omega /\tilde{\sigma }}\). Figure 2a shows σ1 and σ2 of the sample as a function of temperature. Here, an anomalous feature is the monotonic increase of σ1(T) as T decreases below Tc. Note that σ1 is a property solely of the normal fluid. For superconductors with a topologically trivial pairing state, most of the normal fluid turns into superfluid and is depleted as T → 0. As a result, in the low-temperature regime, σ1 shows a strong decrease as temperature decreases, and is expected to reach a theoretically predicted residual value σ1(0)/σ1(Tc) = 0 (for fully gapped s-wave12), <0.1 (for the bulk state of a point nodal p-wave13), and 0.1–0.3 (for line nodal \({d}_{{x}^{2}-{y}^{2}}\)-wave14,15). As shown in Fig. 2b, this behavior is observed for the case of Ti16 (s-wave), as well as CeCoIn5 (ref. 11, \({d}_{{x}^{2}-{y}^{2}}\)-wave). In contrast, the UTe2 crystal shows a monotonic increase in σ1 as the temperature decreases and reaches a much larger σ1(0)/σ1(Tc) = 2.3, implying the normal fluid conduction channel is still active and provides a significant contribution even at the lowest temperature.
a Real (red) and imaginary (blue) part of the complex conductivity \(\tilde{\sigma }={\sigma }_{1}-i{\sigma }_{2}\) of the UTe2 sample at 11.26 GHz. b Normalized (by σn = σ1(Tc)) real part of conductivity of UTe2 (red), a line nodal \({d}_{{x}^{2}-{y}^{2}}\)-wave superconductor CeCoIn5 (blue)11, and a fully gapped s-wave superconductor Ti (green)16 versus reduced temperature T/Tc. All measurements are done with the same, low frequency-to-gap ratio of ℏω/2Δ0 ≈ 0.08. Note that the error bar of the \(\tilde{\sigma }\) is propagated from that of the Zs in Fig. 1.
Axial triplet pairing state from superfluid response
Another property one can extract from the complex conductivity is the effective penetration depth. The imaginary part of the complex conductivity σ2(T) determines the absolute value of the effective penetration depth at each temperature as \({\sigma }_{2}(T)=1/{\mu }_{0}\omega {\lambda }_{{\rm{eff}}}^{2}(T)\). Once the absolute value of the penetration depth is known, the normalized superfluid density can be calculated as \({\rho }_{\mathrm{s}}(T)={\lambda }_{{\rm{eff}}}^{2}(0)/{\lambda }_{{\rm{eff}}}^{2}(T)\) (see “Methods” for how λeff(0) is determined), and its low-temperature behavior is determined by the low-energy excitations of the superconductor, which is sensitive to the pairing state17. The s and d-wave pairing states, representative spin-singlet pairing states, are inconsistent with our penetration depth data (see Supplementary Note 5). More crucially, singlet states cannot explain either the reported upper critical field Hc2, which is larger than the paramagnetic limiting field8, or the absence of a change in the Knight shift across the Tc (refs. 8,18). Thus, only the spin-triplet pairing states are discussed below.
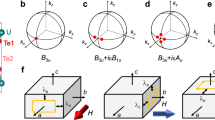
For a spin-triplet pairing state, ρs(T) follows different theoretical low-temperature behaviors depending on two factors17,19. One is whether the magnitude of the energy gap \(| {{\Delta }}(\widehat{{\bf{k}}},T)|\) follows that of an axial state \({{{\Delta }}}_{0}(T)| \widehat{{\bf{k}}}\times \widehat{{\bf{I}}}|\) (Fig. 3a) or a polar state \({{{\Delta }}}_{0}(T)| \widehat{{\bf{k}}}\cdot \widehat{{\bf{I}}}|\) (Fig. 3b), where Δ0(T) is the gap maximum. The other is whether the vector potential direction \(\widehat{{\bf{A}}}\) is parallel or perpendicular to the symmetry axis of the gap \(\widehat{{\bf{I}}}\). Figure 3c shows fits of ρs(T) to the theoretical behavior (refs. 17,19 and Supplementary Note 8) of the various triplet pairing states. Apparently, the data follows the behavior of the axial pairing state with the direction of the current aligned to \(\widehat{{\bf{I}}}\). The axial state can be either chiral or helical depending on the presence or absence of time-reversal symmetry breaking (TRSB) of the system3. Recently, direct evidence for TRSB in this system was found by a finite polar Kerr rotation angle developing below Tc (ref. 20). Also, a specific heat study, a sensitive probe to resolve multiple superconducting transitions, showed two jumps near 1.6 K (ref. 20). This implies that two nearly degenerate order parameters coexist, allowing the chiral pairing state from the group theory perspective20. Therefore, one can argue that UTe2 shows ρs(T) consistent with the chiral triplet pairing state. In addition, since the symmetry axis connects the two point nodes of the chiral pairing order parameter, and the measurement surveys the ab-plane electrodynamics, one can further conclude that the point nodes are located near the ab-plane. The low-temperature asymptote of ρs(T) in this case is given as \({\rho }_{\mathrm{s}}(T)=1-{\pi }^{2}{({k}_{\mathrm{B}}T/{{{\Delta }}}_{0}(0))}^{2}\). The fitting in Fig. 3c yields an estimate for the gap size Δ0(0) = 1.923 ± 0.002kBTc ≈ 0.265 meV. Note that a recent STM study9 measures a similar gap size (0.25 meV).
a A schematic plot of the gap magnitude ∣Δ(k)∣ (orange) and the Fermi surface (blue) in momentum space for the axial triplet pairing state. I represents the symmetry axis of the gap function. Note that two point nodes (red) exist along the symmetry axis. b For the case of the polar state. A line node (red) exists along the equatorial plane. c Low-temperature behavior of the normalized superfluid density ρs(T) in UTe2 with best fits for various triplet pairing states, and relative direction between the symmetry axis I and the vector potential A. Since I connects the two point nodes of the gap of the axial pairing state and the measurement surveys the ab-plane electrodynamics, one can conclude that the point nodes are located near the ab-plane. Evidence of broken time-reversal symmetry20 further narrows down the pairing state from axial to chiral.
Examination of extrinsic origins
Our study shows evidence for the chiral triplet pairing state and a substantial amount of normal fluid response in the ground state of UTe2. Before attributing this residual normal fluid response to an intrinsic origin, one must first examine the possibilities of an extrinsic origin. One of the possible extrinsic origins would be a large bulk impurity scattering rate Γimp. However, if one fits the temperature dependence of the normalized superfluid density to ρs(T) = 1 − aT2 and compares the estimated coefficient a with the modified theoretical asymptote for the chiral triplet state, which includes Γimp (ref. 19),
one obtains a quadratic equation for (Γimp, Δ0(0)), and two solutions: Γimp ≤ 0.06Δ0(0) and Γimp ≥ 4.36Δ0(0) for the range of Δ0(0) ≤ 0.280 meV. For a nodal superconductor, the large Γimp ≥ 4.36Δ0(0) suppresses Tc more than 80% (refs. 21,22). Such suppression was not observed for the samples grown by the chemical vapor transport method8,20. They show a consistent Tc ~ 1.6 K, including the sample in this study. In contrast, the samples prepared by the flux-growth method23 show suppression in Tc all the way down to <0.1 K, as their normal state dc resistivity is much higher. This observation leaves the small Γimp < 0.06Δ0 solution as the only physically reasonable choice in our sample. Note that this small bulk Γimp is consistent with the absence of the residual linear term in the thermal conductivity24, both implying the clean limit Γimp ≪ 2Δ0(0). These results are inconsistent with the impurity-induced bulk normal fluid scenario. Note that the temperature independent Γimp here is much different from the scattering rate above Tc (see Supplementary Note 4), possibly suggesting the presence and dominance of highly temperature-dependent inelastic scattering due to spin fluctuations in the normal state.
Another possibility is a quasiparticle response excited by the microwave photons of the measurement signal. However, this scenario is also improbable because the maximum energy gap Δ0(0) = 265 μeV is much larger than that of the microwave photon Eph = 45 μeV used here. At this low Eph/Δ0(0) ratio, even when the upper limit of Γimp = 0.06Δ0(0) ~ 0.1kBTc is assumped, a theoretical estimate13 predicts only a small residual normal response from the bulk states σ1(0)/σn < 0.1, which cannot explain the measured value of σ1(0)/σn = 2.3.
Possible intrinsic origin
With several candidates for extrinsic origin excluded, now one can consider the possibility of an intrinsic origin. One important constraint to consider is the recent bulk thermal conductivity measurement in UTe2 (ref. 24). It revealed the absence of a residual linear term as a function of temperature in the thermal conductivity, implying the absence of residual normal carriers, at least in the bulk (see Supplementary Note 7). This result suggests the microwave conductivity data can be explained by a combination of a surface normal fluid and bulk superfluid. Topologically trivial origins for the surface normal fluid (e.g., pair breaking rough surface) are first examined, and shown to be inconsistent with the monotonic increase of σ1 as T → 0 in Fig. 2b (see Supplementary Note 11). Instead, considering the evidence of the chiral triplet pairing state from the superfluid density analysis and polar Kerr rotation measurement20, a more pluasible source of the surface normal fluid is the gapless chiral-dispersing surface states of a 3D chiral superconductor4. Point nodes of a chiral superconductor can possess nonzero Chern number with opposite sign. These point nodes in the superconducting gap are analogous to the Weyl points in the bulk energy bands of a Weyl semimetal. The nodes are predicted to introduce gapless surface Majorana arc states that connect them5. Evidence for these surface states in UTe2 is seen in a chiral in-gap density of states from an STM study9.
If this scenario is true, the anomalous monotonic increase in σ1 down to zero temperature from this surface impedance study (Fig. 2b) may be understood as the enhancement of the scattering lifetime of the surface normal fluid. With its chiral energy dispersion, direct backscattering can be suppressed. As the temperature decreases, the superconducting gap Δ0(T) that provides this topological protection increases, while thermal fluctuations kBT which poison the protection decrease. As a result, the suppression of the backscattering becomes stronger as T → 0, which can end up enhancing the surface scattering lifetime (and σ1). Although this argument is speculative at the moment, we hope the anomalous behavior of the σ1(T) reported in this work motivates quantitative theoretical investigation for the microwave response of the topological surface state of chiral superconductors.
In conclusion, our findings imply that UTe2 may be the first example of a 3D chiral spin-triplet superconductor with a surface Majorana normal fluid. With topological excitations in a higher dimension, this material can be a new platform to pursue unconventional superconducting physics, and act as a setting for topological quantum computation.
Methods
Growth and preparation of UTe2 single crystals
The single-crystal sample of UTe2 was grown by the chemical vapor transport method, using iodine as the transport agent8. For the microwave surface impedance measurement, the top and bottom ab-plane facets were polished on a 0.5 μm alumina polishing paper inside a nitrogen-filled glove bag (O2 content < 0.04%). After polishing was done, the sample was encapsulated by Apeizon N-grease (see Supplementary Note 10) before being taken out from the bag, and then mounted to the resonator so that the sample is protected from oxidization. Long-term storage of the sample is done in a glove box with O2 content < 0.5 p.p.m. Note that the electrical properties of oxidized uranium are summarized in Supplementary Note 9. The sample size after polishing is about ~1.5 × 0.7 × 0.3 mm3 with the shortest dimension being along the crystallographic c-axis of the orthorhombic structure. The midpoint Tc of the sample from DC transport measurements was 1.57 K.
Microwave surface impedance measurement
Due to its large volume, the measurement setup, data processing procedure, and interpretation are decribed in detail in the Supplementary Notes 1 and 2.
Determining of the value of the zero temperature absolute penetration depth and comparison to other uranium-based superconductors
The effective penetration depth at each temperature (T ≥ 50 mK) can be obtained from \({\sigma }_{2}(T)=1/{\mu }_{0}\omega {\lambda }_{{\rm{eff}}}^{2}(T)\), where σ2(T) is obtained by the surface impedance Zs(T) data. The effective penetration depth at zero temperature can be obtained by extrapolating the data with a power law fit λeff(T) − λeff(0) = aTc over the low-temperature regime T < 0.3Tc, resulting in λeff(0) = 791 nm and c = 2.11. This value is similar to those found in the uranium-based ferromagnetic superconductor series, such as UCoGe (λeff(0) ~ 1200 nm)25 and URhGe (λeff(0) ~ 900 nm)26, where UTe2 represents the paramagnetic end member of the series8. This result is also consistent with recent muon-spin rotation measurements on UTe2, which concluded λeff(0) ~ 1000 nm (ref. 27).
Error bar of the fitting parameters of the normalized superfluid density
In the fitting of the normalized superfluid density, the error bar of the fitting parameter (e.g., Δ0) was determined by the deviation from the estimated value, which increases the root-mean-square error of the fit by 1%.
Data availability
The datasets generated and analysed in this work are provided with the paper in the Source data tab. Source data are provided with this paper.
References
Hasan, M. Z. & Kane, C. L. Colloquium: topological insulators. Rev. Mod. Phys. 82, 3045–3067 (2010).
Schnyder, A. P., Ryu, S., Furusaki, A. & Ludwig, A. W. W. Classification of topological insulators and superconductors in three spatial dimensions. Phys. Rev. B 78, 195125 (2008).
Kallin, C. & Berlinsky, J. Chiral superconductors. Rep. Prog. Phys. 79, 054502 (2016).
Kozii, V., Venderbos, J. W. F. & Fu, L. Three-dimensional Majorana fermions in chiral superconductors. Sci. Adv. 2, e1601835 (2016).
Sato, M. & Ando, Y. Topological superconductors: a review. Rep. Prog. Phys. 80, 076501 (2017).
Kitaev, A. Fault-tolerant quantum computation by anyons. Ann. Phys. 303, 2–30 (2003).
Deng, M. T. et al. Majorana bound state in a coupled quantum-dot hybrid-nanowire system. Science 354, 1557–1562 (2016).
Ran, S. et al. Nearly ferromagnetic spin-triplet superconductivity. Science 365, 684–687 (2019).
Jiao, L. et al. Chiral superconductivity in heavy-fermion metal UTe2. Nature 579, 523–527 (2020).
Bae, S., Lee, S., Zhang, X., Takeuchi, I. & Anlage, S. M. Microwave Meissner screening properties of proximity-coupled topological-insulator/ superconductor bilayers. Phys. Rev. Mater. 3, 124803 (2019).
Truncik, C. J. S. et al. Nodal quasiparticle dynamics in the heavy fermion superconductor CeCoIn5 revealed by precision microwave spectroscopy. Nat. Commun. 4, 2477 (2013).
Klein, O., Nicol, E. J., Holczer, K. & Grüner, G. Conductivity coherence factors in the conventional superconductors Nb and Pb. Phys. Rev. B 50, 6307–6316 (1994).
Hirschfeld, P. J., Wölfle, P., Sauls, J. A., Einzel, D. & Putikka, W. O. Electromagnetic absorption in anisotropic superconductors. Phys. Rev. B 40, 6695–6710 (1989).
Hirschfeld, P. J., Putikka, W. O. & Scalapino, D. J. Microwave conductivity of d-wave superconductors. Phys. Rev. Lett. 71, 3705–3708 (1993).
Zhang, K. et al. Measurement of the ab plane anisotropy of microwave surface impedance of untwinned YBa2Cu3O6.95 single crystals. Phys. Rev. Lett. 73, 2484–2487 (1994).
Thiemann, M., Dressel, M. & Scheffler, M. Complete electrodynamics of a BCS superconductor with μeV energy scales: Microwave spectroscopy on titanium at mK temperatures. Phys. Rev. B 97, 214516 (2018).
Prozorov, R. & Giannetta, R. W. Magnetic penetration depth in unconventional superconductors. Supercond. Sci. Technol. 19, R41 (2006).
Nakamine, G. et al. Superconducting properties of heavy fermion UTe2 revealed by 125Te-nuclear magnetic resonance. J. Phys. Soc. Jpn 88, 113703 (2019).
Gross, F. et al. Anomalous temperature dependence of the magnetic field penetration depth in superconducting UBe13. Z. Phy. B 64, 175–188 (1986).
Hayes, I. M. et al. Weyl superconductivity in UTe2. Preprint at https://arxiv.org/abs/2002.02539 (2020).
Radtke, R. J., Levin, K., Schüttler, H.-B. & Norman, M. R. Predictions for impurity-induced Tc suppression in the high-temperature superconductors. Phys. Rev. B 48, 653–656 (1993).
Mackenzie, A. P. et al. Extremely strong dependence of superconductivity on disorder in Sr2RuO4. Phys. Rev. Lett. 80, 161–164 (1998).
Aoki, D. et al. Unconventional Superconductivity in Heavy Fermion UTe2. J. Phys. Soc. Jpn. 88, 043702 (2019).
Metz, T. et al. Point-node gap structure of the spin-triplet superconductor UTe2. Phys. Rev. B 100, 220504 (2019).
Huy, N. T. Ferromagnetism, Superconductivity and Quantum Criticality in Uranium Intermetallics, Ph.D. thesis, Universiteit van Amsterdam (2008).
Aoki, D. et al. Coexistence of superconductivity and ferromagnetism in URhGe. Nature 413, 613–616 (2001).
Sundar, S. et al. Coexistence of ferromagnetic fluctuations and superconductivity in the actinide superconductor UTe2. Phys. Rev. B 100, 140502 (2019).
Acknowledgements
This work is supported by NSF grant No. DMR-1410712 (Support of S.B.), DMR-2004386 (data analysis), DOE grants No. DE-SC 0017931 (support of S.A.), DE-SC 0018788 (support of S.B. for low-temperature surface impedance measurements), DE-SC-0019154 (low-temperature transport measurements), Gordon and Betty Moore Foundation’s EPiQS Initiative through Grant GBMF9071 (single-crystal synthesis), NIST (crystal synthesis and sample characterization), and the Maryland Quantum Materials Center (facilities support). Identification of commercial materials does not imply endorsement by NIST.
Author information
Authors and Affiliations
Contributions
S.B., N.P.B., and S.M.A. conceived the project. S.B. polished the sample, conducted the microwave surface impedance measurements, and carried out analysis on the complex conductivity. H.K. and Y.S.E. performed the transport measurements. S.R., I.L., and W.T.F. grew the UTe2 single crystal used in this study. S.B., H.K., J.P., N.P.B., and S.M.A. interpreted the results. S.B. and S.M.A. wrote the manuscript with input from other authors.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Peer review information Nature Communications thanks Satoshi Fujimoto and the other, anonymous, reviewer(s) for their contribution to the peer review of this work. Peer reviewer reports are available.
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Source data
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Bae, S., Kim, H., Eo, Y.S. et al. Anomalous normal fluid response in a chiral superconductor UTe2. Nat Commun 12, 2644 (2021). https://doi.org/10.1038/s41467-021-22906-6
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-021-22906-6
This article is cited by
-
Unconventional superconductivity in Cr-based compound Pr3Cr10−xN11
npj Quantum Materials (2024)
-
Quasi-2D Fermi surface in the anomalous superconductor UTe2
Nature Communications (2024)
-
Chiral superconductivity in UTe2 probed by anisotropic low-energy excitations
Nature Communications (2023)
-
Magnetic-field-sensitive charge density waves in the superconductor UTe2
Nature (2023)
-
Anapole superconductivity from \({{{{{{{\mathcal{PT}}}}}}}}\)-symmetric mixed-parity interband pairing
Communications Physics (2022)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.