Abstract
Most known porphyry Cu deposits formed in the Phanerozoic and are exclusively associated with moderately oxidized, sulfur-rich, hydrous arc-related magmas derived from partial melting of the asthenospheric mantle metasomatized by slab-derived fluids. Yet, whether similar metallogenic processes also operated in the Precambrian remains obscure. Here we address the issue by investigating the origin, fO2, and S contents of calc-alkaline plutonic rocks associated with the Haib porphyry Cu deposit in the Paleoproterozoic Richtersveld Magmatic Arc (southern Namibia), an interpreted mature island-arc setting. We show that the ca. 1886–1881 Ma ore-forming magmas, originated from a mantle-dominated source with minor crustal contributions, were relatively oxidized (1‒2 log units above the fayalite-magnetite-quartz redox buffer) and sulfur-rich. These results indicate that moderately oxidized, sulfur-rich arc magma associated with porphyry Cu mineralization already existed in the late Paleoproterozoic, probably as a result of recycling of sulfate-rich seawater or sediments from the subducted oceanic lithosphere at that time.
Similar content being viewed by others
Introduction
Porphyry Cu systems presently contribute ~75% of the world’s Cu production and of the known deposits most formed in Phanerozoic arc-related settings1,2. The arc-related calc-alkaline, intermediate magmas responsible for most known porphyry Cu deposit formation are hydrous, moderately oxidized (ΔFMQ + 1 to +2; where ΔFMQ is fO2 in log units relative to the fayalite-magnetite-quartz mineral redox buffer), and sulfur-rich, reflecting partial melting of the asthenospheric mantle metasomatized by slab-derived oxidized fluids3,4,5. Chalcophile metals (e.g., Cu) behave as incompatible elements in moderately oxidized magma and are transported to upper crustal levels where they partition efficiently into exsolving S- and Cl-bearing magmatic-hydrothermal ore fluids to form economic deposits under optimal ore-formation conditions1,5.
The apparent rarity of porphyry Cu deposits in the Precambrian is attributed to poor preservation of upper crustal rocks in tectonically active environments, and/or unfavorable tectonomagmatic conditions which precluded their formation6,7. The predominance of ferrous iron and sulfide in terrigenous sediments, anoxic ocean water, and hydrothermally altered reduced submarine basalts during the Precambrian8,9,10 suggest that a significant proportion of H2S would have been released to the sub-arc mantle in subduction zones, thus maintaining stability of mantle sulfides during partial melting in the source region of arc magmas6,11,12, depleting juvenile silicate melts of chalcophile metals, and limiting the ore-forming potential of ascending magma13,14.
The hypothesis that tectonomagmatic conditions in the Precambrian are unfavorable for porphyry Cu deposit formation remains poorly constrained because pervasive metamorphism, deformation, and alteration in Precambrian terrains have variably modified the primary mineralogy and textures of old rocks, rendering estimation of magmatic conditions and original composition difficult. Haib represents one of the largest and best-preserved Paleoproterozoic porphyry Cu deposits (indicated resource of 456.9 million tonnes at a Cu grade of 0.31%, using a cut-off grade of 0.25%, and minor Mo; https://www.deepsouthresources.com/) and only records minimal deformation and relatively low-grade metamorphism. Here we investigate the absolute timing of emplacement of the ore-related magmas at Haib using high-precision geochronology, and constrain the origin, and, in particular, the oxidation states and S contents of the magmas. Mineral inclusions in robust zircon and titanite were sought out to minimize potential effects of alteration and metamorphism. Contrary to previous knowledge6,11, our findings demonstrate that similar metallogenic processes for Phanerozoic porphyry Cu deposits operated at ~1.88 Ga, a period of rapid crustal growth, oxygenation of Earth’s atmosphere and oceans, and sulfur cycling in subduction zones.
Results
Geological setting
The Haib deposit is hosted mainly by the high-K calc-alkaline intrusions of the Vioolsdrif Suite and subaerial volcanic rocks of the Orange River Group along the western part of the Paleoproterozoic Richtersveld Magmatic Arc (RMA) of southern Namibia15,16,17,18 (Fig. 1, Supplementary Note 1 and Supplementary Figs. 1, 2), which formed in a mature island-arc setting at 1.85‒1.91 Ga15,18. The pre-mineralization Orange River Group mainly contains plagioclase-phyric andesite porphyry and interleaved rhyolitic tuff (Fig. 1, Supplementary Fig. 2). The Vioolsdrif Suite mainly comprises equigranular granodiorite, with quartz-monzonite enclaves, and diorite succeeded by shallower syn-ore granodiorite porphyry and leucocratic granodiorite porphyry crosscut by poorly mineralized and carbonate-altered aplite dikes (Fig. 1, Supplementary Figs. 2 and 3). Rocks in the RMA, including the Haib deposit, evolved along a fractionation trend controlled by amphibole and minor plagioclase as indicated by listric-shaped rare-earth element (REE) patterns, moderate negative Eu anomalies15, and a negative relationship between Dy/Yb ratios and SiO2 contents (Fig. 2).
The map is modified from ref. 83. The red dashed line represents the defined mineralization zone for Haib (report from Deep South Resources, Inc.).
Disseminated and veinlet chalcopyrite mineralization with minor magnetite is associated with biotite ± K-feldspar ± epidote ± anhydrite ± titanite ± rutile alteration locally overprinted by chlorite and sericite alteration (Supplementary Figs. 1 and 4). Early dark micaceous veins are more common than A-, B-, and D-type veins (Supplementary Fig. 4; see terminology for the various vein types in ref. 19), which reflects relatively deep levels of exposure of the system. Emplacement pressure for the plutonic host rocks and mineralization is estimated at ~200‒300 MPa16, which is comparable to deeper parts of typical Phanerozoic porphyry Cu systems. The area underwent metamorphism up to greenschist facies and localized intense shearing in the volcanic rocks during the ~1.1 Ga Namaqua orogeny20.
High-precision U–Pb geochronology
Zircon U–Pb geochronology by laser ablation multi-collector inductively coupled plasma-mass spectrometry (LA-MC-ICP-MS) and chemical abrasion isotope dilution thermal ionization mass spectrometry (CA-ID-TIMS) constrains the absolute timing of the crystallization of the igneous rocks and related mineralization. Zircons from two samples of andesite porphyry and one sample of rhyolitic tuff yielded LA-MC-ICP-MS upper concordia intercept ages of 1912 ± 10 Ma, 1892 ± 9 Ma, and 1892 ± 6 Ma, respectively (Fig. 3a, Supplementary Fig. 5). Zircon from equigranular granodiorite, quartz-monzonite enclave, and diorite of the Vioolsdrif Suite yielded LA-MC-ICP-MS upper concordia intercept ages of 1887 ± 7 Ma, 1886 ± 5 Ma, and 1875 ± 10 Ma, respectively (Fig. 3a, Supplementary Fig. 5). These ages are consistent with ages for other rocks in the RMA15,17.
a Crystallization ages of magmatic zircons from ten pre-, syn-, and post-ore igneous rocks (identified from cross-cutting relationship, details in Supplementary Note 1) and a hydrothermal rutile (sample HB-21, syn-ore granodiorite porphyry) associated with chalcopyrite mineralization in Haib, dated using LA-ICP-MS (samples HB-61, HB-28, HB-24, HB-32, HB-33, and HB-30) and CA-ID-TIMS (samples HB-18, HB-51, HB-29, and HB-20) methods. b Zircon Hf isotopic composition (as εHf calculated at 1880 Ma). c Zircon δ18O ratios for representative igneous samples. Filled symbols in (b) and (c) are average values for each sample; smaller pale symbols represent individual analyses. Mantle zircon field in (c) is from ref. 85. Error bars indicate 2σ uncertainties. See Supplementary Data 1 for sample locations and descriptions.
Mitigation of Pb loss in zircons from samples of mineralized granodiorite porphyry and leucocratic granodiorite porphyry, and poorly mineralized aplite was accomplished using chemical abrasion, and the CA-ID-TIMS U–Pb isotopic system provides the most precise dates (Fig. 3a, Supplementary Fig. 6). These three samples yielded weighted mean 207Pb/206Pb ages (Th-corrected) of 1885.47 ± 0.93, 1886.0 ± 1.6, and 1881.02 ± 0.71 Ma, respectively (Fig. 3a, Supplementary Fig. 6). Mild chemical abrasion of six small zircon grains (<30 µm) from one carbonate-altered aplite dike from the ore zone partially mitigated Pb loss, with five of the six grains yielding a weighted mean 207Pb/206Pb age (Th-corrected) of 1881.8 ± 1.2 Ma (Fig. 3a, Supplementary Fig. 6). These results are interpreted to best constrain the emplacement age of the Vioolsdrif Suite and are consistent with the LA-ICP-MS zircon U–Pb age data (Fig. 3a). The age range between the granodiorite porphyry and the carbonate-altered aplite brackets the porphyry Cu mineralization to 1883.6 ± 1.8 Ma, which broadly agrees, within uncertainty, with the LA-ICP-MS upper concordia intercept U–Pb age of 1891 ± 34 Ma for hydrothermal rutile associated with chalcopyrite mineralization (Fig. 3a, Supplementary Fig. 7).
Zircon Hf-O isotopes
Xenocrysts are rare in zircons from the igneous rocks sampled. Some petrographically distinct cores identified as antecrysts yielded LA-ICP-MS 207Pb/206Pb dates that are indistinguishable from ages of the host rocks (Supplementary Fig. 5). Zircons from these rocks yielded initial εHf values of −2.6 ± 0.6 to −1.0 ± 0.9 (2σ, n = 99, −2.0 ± 1.6 on average) and δ18O values of 5.56 ± 0.64 ‰ to 7.10 ± 0.39 ‰ (2σ, n = 102, 6.14 ± 1.19 ‰ on average; Fig. 3b, c). Considering the rarity of zircon inheritance, the narrow ranges of the isotope ratios for the igneous rocks are consistent with homogenized primary arc magma variably contaminated with recycled upper crustal materials (e.g., from an earlier arc nearby RMA15) in its source region. The elevated zircon δ18O values for the volcanic and porphyritic rocks compared to the equigranular rocks (Fig. 3c) indicate more contamination from the recycled upper crustal materials that had undergone low-temperature alteration21. The near-constant Hf isotope ratios among the samples (Fig. 3b) suggest a limited effect of the crustal contaminants on the Hf isotopic systematics of the source and also support insignificant crustal assimilation during magma ascent.
Relatively oxidized magmas
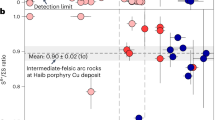
The fO2 of the causative Haib magmas, from which the mineralizing ore fluid evolved, is estimated using three independent oxybarometers (see Methods in refs. 22,23,24, Fig. 4a‒c). Magmatic fO2 is estimated using synchrotron-based micro X-ray absorption near-edge structure spectroscopy (µ-XANES) at the S K-edge to measure the S6+/ΣS ratios of zircon-hosted F-rich apatite inclusions remote from fractures (Fig. 4a, Supplementary Fig. 8). Because most zircons yielded concordant U–Pb dates indicating closed system behavior (Supplementary Figs. 5 and 6), analysis of apatite inclusions in the zircons eliminates the effects of post-crystallization metamorphism and/or alteration. The equant to sub-equant morphology of these monophase apatite inclusions and the absence of other coeval silicate mineral inclusions are consistent with crystallization as early mineral phases under near-equilibrium, near-liquidus conditions (Fig. 4a, b). Based on thermodynamic models in ref. 25 that predict apatite halogen compositions evolve along different trajectories during volatile-undersaturated and water-saturated crystallization, these fluorapatite inclusions are interpreted to have crystallized prior to the melt reaching volatile saturation (Supplementary Note 2, Supplementary Fig. 9). The µ-XANES data reveal that sulfur in apatite is dominantly S6+ (Fig. 4d, Supplementary Fig. 10), and integrated S6+/ΣS peak area ratios (Fig. 4e) yield fO2 values that range from ΔFMQ + 0.85 ± 0.08 to ΔFMQ + 1.07 ± 0.11 (1σ, ΔFMQ + 0.89 ± 0.04 on average) based on the apatite oxybarometer experimentally calibrated at 1000 °C and 300 MPa22. Changes in temperature and pressure are reported to shift the sulfide–sulfate transition in fO2 space for silicate glasses26,27. Thus if we consider that the effect of temperature and pressure on silicate glasses is proportional to the effect of sulfur incorporation into apatite22, the P-T-corrected fO2 values for the Haib plutonic and volcanic rocks are ΔFMQ + 1.24 ± 0.01 and ΔFMQ + 1.37 ± 0.02 (1σ), respectively (Fig. 4f; Supplementary Note 3). The results for the plutonic rocks are interpreted to provide the best estimate of the pre-degassed redox state of the ore-forming magmas.
a Representative apatite inclusion in zircon from sample HB-30; BSE. b Zircon overgrowth on apatite with both hosted in magmatic titanite from sample HB-30; BSE. c Biotite, plagioclase (An number = 24, calculated from energy-dispersive X-ray analysis), and magnetite in titanite from diorite sample HB-30; BSE. d Normalized μ-XANES spectra at the S K-edge of apatite in zircons for representative igneous rocks from Haib. Spectra for only one apatite inclusion (n = 1) were obtained for samples HB-28 and HB-51, respectively, while the others represent averaged spectra of a number of apatite inclusions (HB-18, n = 4; HB-24, n = 2; HB-30, n = 3; HB-32, n = 3). Peak positions for S2−, S4+, and S6+ are at 2470 eV, 2477 eV, and 2482 eV, respectively, and are shown as dotted gray lines. The average S6+/ΣS ratios (1σ) are calculated from the merged spectra following ref. 22. e Plot of apatite S6+/ΣS ratios and S contents versus MgO for the representative samples. f ΔFMQ values versus MgO for the representative samples. Error bars in (e) and (f) represent 1σ uncertainties. An anorthite, Ap apatite, Bt biotite, Mt magnetite, Pl plagioclase, Ttn titanite, Zrn zircon. Symbols and colors are the same as in Fig. 3.
The Ce, Ti, and age-corrected initial U concentrations in zircon from the syn-ore plutonic rocks (the diorite, granodiorite and quartz monzonite, granodiorite porphyries) yield magmatic fO2 values ranging from ΔFMQ + 1.3 ± 0.3 to ΔFMQ + 2.1 ± 0.6 (1σ, ΔFMQ + 1.9 ± 0.6 on average) using a new empirical oxybarometer23 (see screening criteria of zircon geochemistry data in notes in Supplementary Data 5). These results are consistent with the titanite + magnetite + quartz assemblage in the diorite which constrains the redox state of the melt to be >ΔFMQ + 0.7 ± 0.1 at 768 ± 23 °C (1σ, temperature calculated using titanium-in-zircon thermometer)24,28 (Fig. 2c, f), although the result is interpreted to be less reliable because of the difficulty in finding credible equilibrated mineral assemblages.
Sulfur-rich apatite and melt
Magmatic apatite inclusions in zircon and titanite from the Haib system contain relatively high S contents ranging from 0.11 ± 0.04 to 0.19 ± 0.08 wt.% (Fig. 4e, Supplementary Data 9), which are comparable to those reported for basaltic-andesitic to rhyolitic arc magmas and igneous rocks associated with Phanerozoic porphyry Cu systems (Fig. 5a). Recent studies suggest that the partition coefficient for S between apatite and silicate melt (DSap/m) varies with magmatic fO2 and temperature and is not significantly affected by melt composition22,29,30. Because a DSap/m model involving all these parameters is not currently available, we developed a method based on published experimental results (Method 1) and used a published thermodynamic method (Method 2) to determine partition coefficients for S between apatite and silicate melt (see details in ‘Methods’ section), which in turn were used to estimate melt S contents for the Haib samples that range from 0.07 ± 0.03 to 0.17 ± 0.08 wt.% S (1σ, 0.11 ± 0.06 wt.% on average), and 0.02 ± 0.001 to 0.08 ± 0.04 wt.% S (1σ, 0.04 ± 0.03 wt.% on average), respectively. The two independent estimates of melt S content agree within one order of magnitude and are broadly similar to S concentrations in many Phanerozoic arc melts (SiO2 ≥ 52 wt.%, with limited degassing; Fig. 5b) and those associated with Phanerozoic porphyry Cu systems.
a Igneous apatites from intermediate to felsic arc magmas (0.15 ± 0.07 wt.% S on average; 1σ, n = 349, basaltic-andesitic to rhyolitic composition with SiO2 presumably ≥52 wt.%; most of them are from the Circum-Pacific volcanic arcs) and a subset from those associated with Phanerozoic porphyry Cu systems (0.12 ± 0.065 wt.% S on average; 1σ, n = 64) and Haib (n = 6). b Measured S concentrations of melt inclusions in olivine and minor pyroxene in arc rocks (0.09 ± 0.07 wt.% on average; 1σ, n = 69; SiO2 ≥ 52 wt.%; data from GEOROC database) and in rocks associated with Phanerozoic porphyry Cu systems, as well as those estimated using apatite-melt partition coefficients for S from the Haib igneous apatites. The melt inclusion data for arc rocks were filtered using CO2 ≥ 50 ppm to identify those with limited degassing (see ref. 86). N represents numbers of samples or groups of apatites and melt inclusions. See data sources in Supplementary Note 4.
Discussion
The calc-alkaline arc-type magmas, from which the mineralizing fluid evolved, formed at ~1886–1881 Ma, coinciding with a period of rapid crustal growth31 and supercontinent assembly in Earth history. Pervasive hydrothermal anhydrite, part of the potassic alteration stage, is associated with chalcopyrite mineralization in the Haib deposit and indicates the hydrothermal system was relatively oxidized and consistent with exsolution of hydrothermal fluids from a relatively oxidized ore-related magma. The pre-degassed magmas were moderately oxidized (ΔFMQ + 1‒2) and sulfur-rich, which are salient characteristics for Phanerozoic arc magmatism.
The elevated magmatic fO2 values of the Haib magmas relative to mid-oceanic ridge basalts (MORB; ΔFMQ − 2‒0)32 are strongly reminiscent of Phanerozoic oxidized island-arc magmas that are generally thought to originate from the oxidized sub-arc mantle3,4,11,12,33,34,35,36,37,38. Deep crustal garnet fractionation has recently been hypothesized to auto-oxidize magma for porphyry Cu deposit formation39,40. However, the Haib rocks have listric REE patterns and moderately negative Eu anomalies which indicate low-pressure differentiation with amphibole ± plagioclase fractionation (Fig. 2). Amphibole preferentially incorporates middle REEs over heavy REEs and garnet incorporates heavy REEs relative to light REEs, thus amphibole fractionation will decrease, but garnet fractionation will increase, residue melts of Dy/Yb ratios41,42. The decreasing Dy/Yb ratios with increasing SiO2 content (Fig. 2) support amphibole-dominated fractionation without or with minimal garnet influence, leading us to discount the possibility that the elevated magmatic fO2 of the Haib magmas is a result of garnet fractionation. In addition, the narrow ranges of zircon Hf and O isotopic compositions combined with the rarity of zircon inheritance (i.e., xenocrysts) in the Haib plutonic rocks suggest that modification of the magmatic fO2 by crustal contamination during magma ascent is insignificant.
Considering that modern plate tectonics or its equivalent may have, at least on a local scale, operated since 1.8‒1.9 Ga or earlier43,44,45,46, we argue that the Haib magmas are more likely derived from partial melting of the mantle lithosphere that was modified by oxidized slab-derived fluids in the Paleoproterozoic. This is consistent with the recent findings that thick layers of evaporites and an abrupt elevation of marine sulfate content (up to at least 10 mmol/kg, compared to modern seawater sulfate content of 28 mmol/kg) occurred at ~2.0 Ga47,48,49,50, which supports the hypothesis that surface sulfate would have been available to be recycled into the mantle since the middle Paleoproterozoic. Although the hydrothermally altered oceanic basalt at that time is considered to be relatively reduced9, the sulfate-rich fluid released from the oxidized sediments in the subducted oceanic lithosphere may have been able to oxidize the sub-arc mantle without direct addition of Fe3+,3,51, culminating in the formation of relatively oxidized and sulfur-rich magmas.
The oxidized and sulfur-rich features of the derivative basaltic to dacitic magma can delay high-volume sulfide saturation and deep-crustal loss of chalcophile metals, which is the first-order control required for the magma to form the preserved Paleoproterozoic porphyry Cu deposit upon its emplacement in the upper crust52. Our findings suggest that similar metallogenic processes for Phanerozoic porphyry Cu deposits have operated much earlier than generally considered, as recently suggested by others6,11.
Methods
Sample preparation
Sixty-two samples of volcanic and intrusive igneous rocks, including a minority of altered and vein-type samples, were collected from drill core and outcrops in October 2018. To investigate the nature of the magmatism, least-altered samples were targeted for collection, but most of the drill core samples are variably altered owing to proximity to the ore deposit. Nineteen of the petrographically least-altered samples were chosen for analytical work (Supplementary Data 1).
Zircons were separated from representative samples of the major igneous phases by traditional magnetic and density methods after electric-pulse disaggregation at Overburden Drilling Management Inc., Ottawa, Canada. Zircon grains devoid of cracks and mineral and/or fluid inclusions as well as inclusion-rich grains were hand-picked and mounted in separate sets of epoxy pucks and polished to expose their middle-sections. Magmatic zircon and titanite crystals, and contained mineral inclusions, as well as hydrothermal rutile, were characterized using a Tescan Vega 3 scanning electron microscope with backscattered electron (BSE) imaging, cathodoluminescence, and Bruker energy-dispersive spectroscopy (EDS) at Laurentian University.
Whole-rock geochemistry
Eighteen of the least-altered samples collected from drill cores and outcrops from Haib were crushed and ground at Australian Laboratory Services (ALS), Sudbury, Canada for whole-rock geochemical analyses. The powdered samples were analyzed using X-ray fluorescence (XRF) and inductively coupled plasma-mass spectrometry (ICP-MS) with pre-fusion (lithium metaborate; CCP-PKG01 analytical package) at ALS, Vancouver, Canada. One secondary reference sample LK-NIP-1 (Nipissing diabase, https://www.mndm.gov.on.ca/sites/default/files/2018_geo_labs_brochure.pdf) was analyzed as an unknown to verify the analytical quality during the analytical session, and the results are consistent with standard values (see Supplementary Data 2). Some elements of samples HB-23, HB-51, and HB-61 were duplicated. The results are reported in Supplementary Data 2.
Zircon U–Pb isotope and trace element analyses
Zircon uranium–lead (U–Pb) isotope and trace element analyses were conducted in the Mineral Exploration Research Centre—Isotope Geochemistry Laboratory (MERC‒IGL) at Laurentian University. A 193 nm Photon Machines Analyte G2 ArF excimer laser equipped with a two-volume Helex II laser cell was used to ablate the zircons. To minimize the common lead contamination from surface material prior to ablation, the samples were polished using alumina powder, put in an ultrasonic bath with milli-Q water, and cleaned with ethanol by Kim wipe. The detailed instrumental parameters of laser ablation and ICP-MS, as well as data processing, for these analyses are listed in Supplementary Data 3.
The parameters for the laser were a fluence of 2 J/cm2, a repetition rate of 7 Hz, and a spot size of 35 µm. Ablation duration was 10 s, leaving an estimated ablation pit depth of <5 µm. The ablated aerosol downstream of the sample cell was split into two mass spectrometers for measuring the U–Pb isotope ratios and trace element abundances simultaneously53. U–Pb isotopic ratios, and U, Th, and Pb concentrations were measured on a Thermo Scientific Neptune Plus multi-collector ICP-MS equipped with a Jet interface and nine Faraday cups, whereas trace elements were analyzed on a Thermo Scientific iCap triple-quadrupole (TQ) ICP-MS in single quad mode to ensure maximum sensitivity on low to intermediate mass range. Sixty seconds of background were measured at the beginning and end of each analytical session, with 30 s of background measured between each analysis.
Correction of laser-induced element fractionation, instrumental drift, and downhole fractionation was performed with the U–Pb Geochronology data reduction scheme implemented within Iolite v. 3.6 software54,55, with U–Pb isotope ratios normalized to the zircon primary reference material OGC-01 that was periodically dispersed into the analytical sessions. The secondary reference materials TanBrA and Grn were analyzed to monitor the accuracy and reproducibility of the unknown analyses, with results consistent with standard values (Supplementary Data 4). Within-run variance in the measured ratios for OGC-01 was propagated into the 2SE uncertainty for all unknowns. No additional uncertainty propagation was applied to the 207Pb/206Pb ratios of the unknown analyses because long-term variance of 207Pb/206Pb ratios of the verification reference materials across all sessions is limited with statically acceptable MSWD (mean square of weighted deviates; that is, ~1). Concordia age calculation and data plotting were completed using Isoplot v. 4.1556, in which uranium decay constant uncertainties were not considered. The MSWD of the dates are statistically acceptable for population sizes at the 95% confidence interval. Trace element data were processed using the internal standard data reduction scheme within Iolite v. 3.6 and normalized to the synthetic glass NIST610. The stoichiometric concentration of Si in zircon was assumed to be 15.284 wt.%. The synthetic glass NIST612 and zircon 91500 were used to verify the accuracy of the analyses. The results are reported in Supplementary Data 4.
CA-ID-TIMS zircon U–Pb dating
Chemical abrasion isotope dilution thermal ionization mass spectrometry (CA-ID-TIMS) U–Pb geochronology of single zircon crystals and fragments was undertaken at the Geochronology and Tracers Facility, British Geological Survey, Keyworth, the UK. Chemical abrasion was undertaken at 190 °C for 12 h for samples HB-18, HB-29, and HB-51, within the exception of sample HB-20 that was leached at 180 °C following the method in ref. 57. The methodology for all other analytical procedures, instrumental conditions, corrections, and data reduction follows that outlined in detail in ref. 58 using the ET2535 tracer59,60. Isotope ratio measurements were made using a Thermo Triton thermal ionization mass-spectrometer (TIMS), with the U decay constants of ref. 61, the 238U/235U ratio of ref. 62, and the 230Th decay constants of ref. 63. The 206Pb/238U and 207Pb/206Pb dates were corrected for initial 230Th disequilibrium64 using a value of Th/U [magma] = 3.5. The results are reported in Supplementary Data 5.
The best estimate of emplacement age was selected from the population of concordant data where the 207Pb/206Pb weighted mean date had a statistically acceptable MSWD for the given population size at 95% confidence interval. For zircons from sample HB-20, the Pb loss has not been completely mitigated, we report the weighted mean 207Pb/206Pb age with acceptable MSWD of 0.15. All uncertainties are reported at 2σ level considering analytical and tracer calibration uncertainty but excluding the contribution from uncertainties of decay constants.
Rutile U–Pb isotopes
In-situ U–Pb isotopes of rutile in thin section were measured using the Thermo Neptune Plus MC-ICP-MS coupled to a 193 nm Photon Machines Analyte G2 laser equipped with a two-volume Helex II laser cell in MERC‒IGL at Laurentian University. The laser ablation was carried out with a fluence of 2‒3 J·cm−2, a repetition rate of 7 Hz, and a spot size of 35 µm. Each analysis lasted for 35 s. Primary reference material was R10 (1095 ± 4.7 Ma)65 and secondary materials were R19 (489.5 ± 0.9 Ma)66 and Sugluk (1723 ± 6.8 Ma)67, which were periodically analyzed throughout the analytical run. The detailed instrumental parameters of laser ablation and ICP-MS, as well as data processing, are listed in Supplementary Data 3. The results for secondary reference materials of rutile are reported in Supplementary Data 6 and are in agreement with the published standard values. Results for unknown analyses are also reported in Supplementary Data 6.
Zircon Lu–Hf isotopes
Lu–Hf isotopes were measured on the same spots as O isotopes and some of the zircon U–Pb isotope and trace element analyses. The same analytical equipment as for the U–Pb analyses were used. Laser ablation was carried out with a fluence of 6 J cm−2, a repetition rate of 7 Hz, and a spot size of 40 µm. Ablation duration was 60 s, leaving an estimated ablation pit depth of ~30 µm. One primary and five secondary reference standards (Pleosovice; 91500, R33, FC1, OGC, MUN1, and MUN3) were periodically analyzed during the analytical runs. The details for the instrumental parameters of laser ablation and ICP-MS, as well as data processing, for these analyses are listed in Supplementary Data 3.
The raw Hf isotope data were processed in Iolite v.3.6, with baseline subtraction, instrumental drift, and mass bias corrections performed with a modified version of the Hf isotope data reduction scheme. Within-run variance in the measured ratios for Plesovice was propagated into the 2SE uncertainty for all unknowns. Similar to the U–Pb isotopic analyses, no additional uncertainty propagation was applied to the Hf isotope ratios for the unknown analyses. Instrumental mass bias and interference correction factors were determined within the session through the iterative calculation of the effective 176Yb/173Yb ratio required to yield identical 176Hf/177Hf ratios of MUN1 and MUN3. The effective (mass bias-corrected) within-session 176Yb/173Yb was then applied in the interference correction for all analyses as part of the data reduction scheme. The corrected 176Hf/177Hf ratios are 0.282309 ± 0.000030 (2σ, n = 13) for 91500, 0.282750 ± 0.000022 (2σ, n = 13) for R33, 0.282184 ± 0.000031 (2σ, n = 13) for FC1, 0.280558 ± 0.000054 (2σ, n = 13) for OGC, and 0.282127 ± 0.000019 (2σ, n = 10) for MUN. These results are identical to the published values within uncertainties68,69,70. The initial 176Hf/177Hf ratios and εHf(t) values are calculated using a 176Lu decay constant of 1.867 × 10−11/a71 and the chondritic parameters from ref. 72. The results are reported in Supplementary Data 7.
Zircon O isotopes
Oxygen isotopes (18O and 16O) in zircon were analyzed using a Cameca IMS 1280 multi-collector ion microprobe in the Canadian Centre for Isotopic Microanalysis at the University of Alberta. Most of the samples were analyzed in session IP19029 prior to U–Pb–Lu–Hf isotope analyses, except for samples HB-30 and HB-33 which were analyzed in session IP20013 and the analyses were conducted on different sets of grains for U–Pb-Lu–Hf isotopes. Counts of 16O1H/16O for zircons in the session IP19029, in which some of the samples were collected from the ore deposit, were simultaneously analyzed with the O isotopes to monitor the effect of hydrothermal alteration. Most of the analyses yielded low 16O1H/16O, and only a few analyses having significantly higher values than the standards (Delta OH > 40%) were excluded.
The zircons were analyzed using a 20 keV 133Cs+ primary beam with a spot size of ~10 μm. Detailed instrumental parameters have been described by ref. 73. Instrumental mass fractionation was monitored by repeated analysis of the zircon primary reference material (S0081, δ18OVSMOW = + 4.87; R. Stern, unpublished laser fluorination data, University of Oregon) after every four unknown analyses. The 18O−/16O− dataset for S0081 was processed collectively for two analytical sessions (n = 64 and 12), yielding standard deviations of 0.12‰ and 0.09‰, respectively, following correction for a systematic within-session drift of ≤0.4‰. Zircon secondary reference material TEM2 was analyzed following every eight unknown analyses. Multiple spots on different TEM2 grains yielded weighted mean δ18OVSMOW values of +8.23 ± 0.12 ‰ (SD, n = 42, MSWD = 1.07) for session IP19029 and +8.27 ± 0.09‰ (SD, n = 23, MSWD = 0.74) for session IP20013, which is consistent with the published standard δ18OVSMOW value of +8.2‰74. The individual spot uncertainties of δ18OVSMOW for unknowns in the two sessions have medians of ±0.25‰ and ±0.20‰ at 95% confidence, which includes errors relating to within-spot counting statistics, geometric effects, and correction for instrumental mass fractionation. The results are reported in Supplementary Data 8.
Electron microprobe analysis
Major and minor element compositions of apatite were acquired using a Cameca SX100 electron microprobe analyzer with wavelength-dispersive spectroscopy at Ontario Geosciences Laboratory, with results reported in Supplementary Data 9. An accelerating voltage of 15 keV, a beam current of 10 nA, and rastered beam sizes of 2 or 5 µm (depending on the apatite grain size) were used for all element analyses. X-ray lines, analyzing crystals, and counting times (for both peak and background measurements) were as follows: P Kα, LPET5, 15 s; Si Kα, LTAP2, 20 s; Al Kα, LTAP2, 20 s; Mg Kα, LTAP2, 20 s; Ca Kα, LPET5, 15 s; Mn Kα, LiF4, 40 s; Fe Kα, LiF4, 40 s; Sr Lα, LPET5, 30 s; Na Kα, LTAP2, 20 s; K Kα, PET3, 20 s; S Kα, LPET3, 60 s; F Kα, PCO, 20 s; Cl Kα, LPET5, 20 s; Zr Lα, LPET5, 5 s. The detection limits for these elements were calculated to be as follows: P2O5, 680 ppm; SiO2, 130 ppm; Al2O3, 140 ppm; MgO, 140 ppm; CaO, 340 ppm; MnO, 520 ppm; FeO, 520 ppm; SrO, 850 ppm; Na2O, 170 ppm; K2O, 140 ppm; SO3, 270 ppm; F, 880 ppm; and Cl, 190 ppm.
Due to the small size of the apatites analyzed, zirconium concentrations were measured to monitor the contamination from the host zircon crystal. Analyses with ZrO2 > 1% were excluded. The decomposition of apatite caused by electron beam damage75,76 under the conditions used for this study was also tested (see Supplementary Data 9). The compositions of the test samples (beam size of 2 µm) typically show, with analytical time: (1) an increase or decrease in F count rate; (2) slightly decrease in Cl count rate; and (3) a nearly constant S count rate. The test demonstrates that the S and Cl abundances are reliable and the F concentrations might not be well constrained. Beam damage of apatite obtained at a larger beam size of 5 µm can be minimized, particularly for apatite grains with c-axis perpendicular to the electron beam.
Micro X-ray absorption near-edge structure spectroscopy (µ-XANES)
To measure the sulfur oxidation states of the pristine apatite inclusions (i.e., previously not analyzed by electron microprobe), micro X-ray absorption near-edge structure spectroscopy at the sulfur K-edge (S µ-XANES) was conducted at the Advanced Photon Source (APS) of the Argonne National Laboratory in Chicago, IL, USA, and at the Swiss Light Source (SLS) of the Paul Scherrer Institute in Villigen, Switzerland. The analyses at the APS were performed at the GSECARS X-ray microprobe beamline on sector 13-ID-E and those at the SLS were performed at the PHOENIX X07MA/B tender X-ray microspectroscopy beamline. The APS beamline has an energy range of 2.3‒28 keV, whereas the SLS beamline has an energy range of 0.35‒8 keV. Both beamlines use undulator X-ray sources to provide photons for µ-XANES measurements and employ double crystal (silicon 111) monochromators to generate monochromatic radiation focused with a Kirkpatrick–Baez mirror system. The monochromatic beam was focused down to a size of 2 × 2 µm at APS and 3 µm diameter at SLS. The energy at both beamlines was calibrated to the ~2482 eV white line of sulfate, using clear double-sided sticky tape at APS (2481.8 eV) and powdered CaSO4 at SLS (2482 eV). Differences in the calibration are attributed to slight differences in monochromator calibration and setup.
To minimize the Compton and Rayleigh scattering contribution, the polished surface of the samples was positioned at 45° from the incoming beam. We followed the collection and processing procedures described in refs. 22,77. XRF maps were acquired at the beamlines immediately proceeding spectra collection to locate the apatite inclusions in zircon. The incoming energy for maps was fixed at 2482 eV and measured fluorescence lines of S, Si, P, and Al to discriminate different phases in the maps (e.g., zircon, apatite, and epoxy). The dwell time of the detector was set at 1 s for each 3 × 3 µm pixel at SLS and 0.02 s for each 2 × 2 µm pixel at APS. At both beamlines sulfur fluorescence spectra were collected using four-element silicon drift diode detector arrays positioned at an angle of 90° to the incident beam and corrected for detector dead time.
The S µ-XANES spectra were collected by scanning the incident beam energy from 2440 to 2550 eV using a slightly different setup at each beamline, but all scans were divided into the same three energy regions: (i) a pre-edge region from 2440‒2460 eV, (ii) the edge region from 2460‒2500 eV, and (iii) a post-edge region from 2500‒2550 eV. At APS, step sizes of 1, 0.3, and 2 eV were used in the pre-edge, edge, and post-edge regions, respectively, while at SLS step sizes of 2, 0.3, and 2 eV were used. The counting duration for all regions at APS was 3 s and at SLS was 1 s per step in the pre- and post-edge regions and 2 s per edge step. The total scan duration was ~9 min at APS and ~12 min at SLS, with differences in beamline mechanics and scan setup resulting in different scan durations. The European Synchrotron Radiation Facility S K-edge XANES spectra database was used to identify the S6+ (~2482 eV; anhydrite), S4+ (~2478 eV; sodium sulfite), and S2− (~2470 eV; pyrrhotite) peak energy position for the unknowns. Spectra of pyrrhotite (Fe1−xS) and anhydrite powder (CaSO4) are shown in Supplementary Fig. 10a to illustrate the differences in S2− from S6+ spectra.
Two scans were collected at each point to improve counting statistics and monitor for beam damage caused by irradiation of the focused X-ray beam and contribution from other phases (e.g., host zircon, epoxy). Beam damage manifests as the growth or shrinkage of absorption peaks from the first to second scan and can easily be identified. Beam damage was not observed in any apatite spectra collected here, which is consistent with previous observations that apatite is robust and does not easily incur beam damage at the energies used for S µ-XANES, even after more than 1 h of beam exposure22,77. However, contribution from the host zircon was observed, most severely on relatively small apatite grains (~4 µm or less in diameter). Zircon contribution to the spectra was characterized by an intense peak that begins ~2540 eV in the post-edge region, corresponding to the Zr Lγ2 transition (Supplementary Fig. 10b). The intensity of the Zr peak was less than half the intensity of the S6+ peak in apatite in spectra collected on large apatite grains (>10 µm diameter) and the spectra was discarded if the Zr peak intensity surpassed and drowned out the S6+ signal, illustrated in Supplementary Fig. 10b. Scans collected on host zircon showed very low sulfur counts and no characteristic edge step, therefore any contribution from zircon to the sulfur spectra is considered insignificant. Following the criteria described in ref. 22, S µ-XANES spectra were monitored for contribution of sulfur-bearing epoxy. Any spectra exhibiting contribution from other phases were discarded.
S µ-XANES spectra collected from the same apatite grain were normalized against the incident flux (I0), the pre- and post-edge set to 0 and 1, respectively, and were merged using the XAS software analysis package Athena or Ifeffit78. Peak positions and areas were then fitted and calculated using the Fityk software version 1.3.179, from which the integrated S6+/ΣS peak area ratios were calculated and input to the calibration equation in ref. 22 to calculate the values of logfO2 relative to FMQ.
Methods in estimating melt sulfur content
Method 1 uses experimental DSap/m calculated for a mafic melt varying with logfO2 at a temperature of ~1000 °C and pressure of ~300 MPa22. The effect of temperature (from ~1000 °C to the calculated model apatite saturation temperature80) was evaluated using the DSap/m (T) from ref. 81 that was derived for an oxidized rhyolitic melt. Although ref. 30 also reported an equation relating the DSap/m with temperature (ln (DSap/m) = 21,330/T (K) −16.2), the equation does not consider the effects of depleting phosphate concentration in the melt following apatite saturation with decreasing temperature82 and the experiment in ref. 30 conducted at ~800 °C may not represent the equilibrium S content because of early apatite crystallization from melt during annealing81. We therefore chose not to use it. The combined equation can be expressed as:
The values of DSap/m (fO2) are 0.85 and 1 for plutonic and volcanic rocks at FMQ + 1.24 and +1.37, whereas DSap/m (AST) are estimated to be 10.2, 13.3 ± 0.2, and 10.7 at temperatures of 867 °C (HB-24, andesite porphyry), 914 ± 4 °C (HB-18 and HB-51, granodiorite porphyries; HB-32, granodiorite; and HB-30, diorite), and 951 °C (HB-33; quartz-monzonite enclave), respectively.
Method 2 to calculate the partition coefficient of S between apatite and melt is derived from ref. 82 and involves activities of phosphate, sulfate, and silica, as well as percentages of crystals, and is sensitive to the apatite saturation temperature (see details in ref. 82). We followed the method of the linear negative relationship between DSap/m and temperature and assumed DSap/m (AST) = 3.91 at 930 °C30. The DSap/m are estimated to be 7.7, 4.9 ± 0.2, and 2.7 at temperatures of 867 °C (HB-24, andesite porphyry), 914 ± 4 °C (HB-18 and HB-51, granodiorite porphyries; HB-32, granodiorite; and HB-30, diorite), and 951 °C (HB-33, quartz-monzonite enclave), respectively.
Data availability
The datasets generated and discussed in this study are available in Supplementary Information (Supplementary Notes 1–4, Supplementary Figs. 1–10, Supplementary Data 1–9).
References
Sillitoe, R. H. Porphyry copper systems. Economic Geol. 105, 3–41 (2010).
Sinclair, W. D. Porphyry deposits. in: Mineral Deposits of Canada: a Synthesis of Major Deposit-types, District Metallogeny, the Evolution of Geological Provinces, Andexploration Methods, Vol. 5. 223–243 (Geological Association of Canada, Mineral Deposits Division, Special Publication, 2007).
Kelley, K. A. & Cottrell, E. Water and the oxidation state of subduction zone magmas. Science 325, 605–607 (2009).
Zellmer, G. F., Edmonds, M. & Straub, S. M. Volatiles in subduction zone magmatism. Geol. Soc. Lond. Spec. Publ. 410, 1–17 (2015).
Richards, J. P. The oxidation state, and sulfur and Cu contents of arc magmas: implications for metallogeny. Lithos 233, 27–45 (2015).
Richards, J. P. & Mumin, A. H. Magmatic-hydrothermal processes within an evolving Earth: Iron oxide-copper-gold and porphyry Cu ± Mo ± Au deposits. Geology 41, 767–770 (2013).
Wilkinson, B. H. & Kesler, S. E. Tectonism and exhumation in convergent margin orogens: insights from ore deposits. J. Geol. 115, 611–627 (2007).
Fakhraee, M., Hancisse, O., Canfield, D. E., Crowe, S. A. & Katsev, S. Proterozoic seawater sulfate scarcity and the evolution of ocean–atmosphere chemistry. Nat. Geosci. 12, 375–380 (2019).
Stolper, D. A. & Keller, C. B. A record of deep-ocean dissolved O2 from the oxidation state of iron in submarine basalts. Nature 553, 323–327 (2018).
Shields-Zhou, G. & Och, L. The case for a Neoproterozoic oxygenation event: geochemical evidence and biological consequences. GSA Today 21, 4–11 (2011).
Evans, K. A. & Tomkins, A. G. The relationship between subduction zone redox budget and arc magma fertility. Earth Planet. Sci. Lett. 308, 401–409 (2011).
Stolper, D. A. & Bucholz, C. E. Neoproterozoic to early Phanerozoic rise in island arc redox state due to deep ocean oxygenation and increased marine sulfate levels. Proc. Natl Acad. Sci. USA 116, 8746–8755 (2019).
Candela, P. A. A review of shallow, ore-related granites: textures, volatiles, and ore metals. J. Petrol. 38, 1619–1633 (1997).
Candela, P. A. Controls on ore metal ratios in granite-related ore systems: an experimental and computational approach. Earth Environ. Sci. Trans. R. Soc. Edinb. 83, 317–326 (1992).
Macey, P. H. et al. Origin and evolution of the <1.9 Ga Richtersveld Magmatic Arc, SW Africa. Precambrian Res. 292, 417–451 (2017).
Minnitt, R. C. A. Porphyry copper-molybdenum mineralization at Haib River, South West Africa/Namibia. In: Mineral Deposits of Southern Africa Vol II. 1567–1585 (Geological Society of South Africa, 1986).
Grumbley, N. L. The Geological Evolution of the Haib Cu-Mo Porphyry, Namibia. Master thesis (Trinity College Dublin, 2015).
Reid, D. L., Erlank, A. J., Welke, H. J. & Moyes, A. The Orange River Group: a major Proterozoic calcalkaline volcanic belt in the western Namaqua Province, Southern Africa. Geol. Soc. Lond. Spec. Publ. 33, 327–346 (1987).
Seedorff, E. Porphyry deposits: characteristics and origin of hypogene Features. in Economic Geology 100th Anniversary Volume. (Society of economist Geologists, Inc., Canada, 2005).
Jacobs, J., Pisarevsky, S., Thomas, R. J. & Becker, T. The Kalahari Craton during the assembly and dispersal of Rodinia. Precambrian Res. 160, 142–158 (2008).
Valley, J. W. et al. 4.4 billion years of crustal maturation: oxygen isotope ratios of magmatic zircon. Contrib Mineral. Petrol. 150, 561–580 (2005).
Konecke, B. A., Fiege, A., Simon, A. C., Linsler, S. & Holtz, F. An experimental calibration of a sulfur-in-apatite oxybarometer for mafic systems. Geochim. Cosmochim. Acta 265, 242–258 (2019).
Loucks, R. R., Fiorentini, M. L. & Henríquez, G. J. New magmatic oxybarometer using trace elements in zircon. J. Petrol. 61, 1–30 (2020).
Wones, D. R. Significance of the assemblage titanite + magnetite + quartz in granitic rocks. Am. Mineral 74, 744–749 (1989).
Stock, M. J. et al. Tracking volatile behaviour in sub-volcanic plumbing systems using apatite and glass: insights into pre-eruptive processes at Campi Flegrei, Italy. J. Petrol. 59, 2463–2492 (2018).
Nash, W. M., Smythe, D. J. & Wood, B. J. Compositional and temperature effects on sulfur speciation and solubility in silicate melts. Earth Planet. Sci. Lett. 507, 187–198 (2019).
Matjuschkin, V., Blundy, J. D. & Brooker, R. A. The effect of pressure on sulphur speciation in mid- to deep-crustal arc magmas and implications for the formation of porphyry copper deposits. Contrib. Mineral. Petrol. 171, 66 (2016).
Ferry, J. M. & Watson, E. B. New thermodynamic models and revised calibrations for the Ti-in-zircon and Zr-in-rutile thermometers. Contrib. Mineral. Petrol. 154, 429–437 (2007).
Parat, F., Holtz, F. & Streck, M. J. Sulfur-bearing magmatic accessory minerals. Rev. Mineral. Geochem. 73, 285–314 (2011).
Peng, G. Y., Luhr, J. F. & McGee, J. J. Factors controlling sulfur concentrations in volcanic apatite. Am. Mineral. 82, 1210–1224 (1997).
Condie, K. C. Episodic continental growth and supercontinents: a mantle avalanche connection? Earth Planet. Sci. Lett. 163, 97–108 (1998).
Carmichael, I. S. E. The redox states of basic and silicic magmas: a reflection of their source regions? Contrib. Mineral. Petrol. 106, 129–141 (1991).
Ballhaus, C., Berry, R. F. & Green, D. H. Oxygen fugacity controls in the Earth’s upper mantle. Nature 348, 437–439 (1990).
Wood, B. J., Bryndzia, L. T. & Johnson, K. E. Mantle oxidation state and its relationship to tectonic environment and fluid speciation. Science 248, 337–345 (1990).
Parkinson, I. J. & Arculus, R. J. The redox state of subduction zones: insights from arc-peridotites. Chem. Geol. 160, 409–423 (1999).
Brounce, M., Kelley, K. A., Cottrell, E. & Reagan, M. K. Temporal evolution of mantle wedge oxygen fugacity during subduction initiation. Geology 43, 775–778 (2015).
Benard, A. et al. Oxidising agents in sub-arc mantle melts link slab devolatilisation and arc magmas. Nat. Commun. 9, 3500 (2018).
Bucholz, C. E. & Kelemen, P. B. Oxygen fugacity at the base of the Talkeetna arc, Alaska. Contrib. Mineral. Petrol. 174, 79 (2019).
Tang, M., Erdman, M., Eldridge, G. & Lee, C. T. A. The redox “filter” beneath magmatic orogens and the formation of continental crust. Sci. Adv. 4, eaar4444 (2018).
Lee, C. T. A. & Tang, M. How to make porphyry copper deposits. Earth Planet. Sci. Lett. 529, 115868 (2020).
Macpherson, C. G., Dreher, S. T. & Thirlwall, M. F. Adakites without slab melting: High pressure differentiation of island arc magma, Mindanao, the Philippines. Earth Planet. Sci. Lett. 243, 581–593 (2006).
Davidson, J., Turner, S., Handley, H., Macpherson, C. & Dosseto, A. Amphibole “sponge” in arc crust? Geology 35, 787–790 (2007).
Weller, O. M. & St-Onge, M. R. Record of modern-style plate tectonics in the Palaeoproterozoic Trans-Hudson orogen. Nat. Geosci. 10, 305–311 (2017).
Francois, C., Debaille, V., Paquette, J. L., Baudet, D. & Javaux, E. J. The earliest evidence for modern-style plate tectonics recorded by HP-LT metamorphism in the Paleoproterozoic of the Democratic Republic of the Congo. Sci. Rep. 8, 15452 (2018).
Möller, A., Appel, P., Mezger, K. & Schenk, V. Evidence for a 2 Ga subduction zone: Eclogites in the Usagaran belt of Tanzania. Geology 23, 1067–1070 (1995).
Yin, A., Brandl, G. & Kröner, A. Plate-tectonic processes at ca. 2.0 Ga: Evidence from >600 km of plate convergence. Geology 48, 103–107 (2019).
Blättler, C. L. et al. Two-billion-year-old evaporites capture Earth’s great oxidation. Science 360, 320–323 (2018).
Planavsky, N. J., Bekker, A., Hofmann, A., Owens, J. D. & Lyons, T. W. Sulfur record of rising and falling marine oxygen and sulfate levels during the Lomagundi event. Proc. Natl Acad. Sci. USA 109, 18300–18305 (2012).
Lyons, T. W. & Gill, B. C. Ancient sulfur cycling and oxygenation of the early biosphere. Elements 6, 93–99 (2010).
Steadman, J. A. et al. Evidence for elevated and variable atmospheric oxygen in the Precambrian. Precambrian Res. 343, 105722 (2020).
de Hoog, J. C. M., Mason, P. R. D. & van Bergen, M. J. Sulfur and chalcophile elements in subduction zones: constraints from a laser ablation ICP-MS study of melt inclusions from Galunggung Volcano, Indonesia. Geochim. Cosmochim. Acta 65, 3147–3164 (2001).
Richards, J. P. Tectono-magmatic precursors for porphyry Cu-(Mo-Au) deposit formation. Econ. Geol. 98, 1515–1533 (2003).
Kylander-Clark, A. R. C., Hacker, B. R. & Cottle, J. M. Laser-ablation split-stream ICP petrochronology. Chem. Geol. 345, 99–112 (2013).
Paton, C., Hellstrom, J., Paul, B., Woodhead, J. & Hergt, J. Iolite: Freeware for the visualisation and processing of mass spectrometric data. J. Anal. At. Spectrom. 26, 2508–2518 (2011).
Paton, C. et al. Improved laser ablation U–Pb zircon geochronology through robust downhole fractionation correction. Geochem. Geophys. Geosyst. 11, Q0AA06 (2010).
Ludwig, K. R. User’s Manual for Isoplot Version 3.75–4.15: A Geochronological Toolkit for Microsoft Excel (Berkley Geochronological Center Special Publication, 2012).
Mattinson, J. M. Zircon U–Pb chemical abrasion (“CA-TIMS”) method: Combined annealing and multi-step partial dissolution analysis for improved precision and accuracy of zircon ages. Chem. Geol. 220, 47–66 (2005).
Tapster, S. et al. Rapid thermal rejuvenation of high-crystallinity magma linked to porphyry copper deposit formation; evidence from the Koloula Porphyry Prospect, Solomon Islands. Earth Planet. Sci. Lett. 442, 206–217 (2016).
McLean, N. M., Condon, D. J., Schoene, B. & Bowring, S. A. Evaluating uncertainties in the calibration of isotopic reference materials and multi-element isotopic tracers (EARTHTIME Tracer Calibration Part II). Geochim Cosmochim Acta 164, 481–501 (2015).
Condon, D. J., Schoene, B., McLean, N. M., Bowring, S. A. & Parrish, R. R. Metrology and traceability of U–Pb isotope dilution geochronology (EARTHTIME Tracer Calibration Part I). Geochim. Cosmochim. Acta 164, 464–480 (2015).
Jaffey, A. H., Flynn, K. F., Glendenin, L. E., Bentley, W. C. & Essling, A. M. Precision measurement of half-lives and specific activities of 235U and 238U. Phys. Rev. C. 4, 1889 (1971).
Hiess, J., Condon, D. J., McLean, N. & Noble, S. R. 238U/235U systematics in terrestrial uranium-bearing minerals. Science 335, 1610–1614 (2012).
Cheng, H. et al. The half-lives of uranium-234 and thorium-230. Chem. Geol. 169, 17–33 (2000).
Schärer, U. The effect of initial 230Th disequilibrium on young U–Pb ages: the Makalu case, Himalaya. Earth Planet. Sci. Lett. 67, 191–204 (1984).
Luvizotto, G. L. et al. Rutile crystals as potential trace element and isotope mineral standards for microanalysis. Chem. Geol. 261, 346–369 (2009).
Zack, T. et al. In situ U–Pb rutile dating by LA-ICP-MS: 208Pb correction and prospects for geological applications. Contrib. Mineral. Petrol. 162, 515–530 (2011).
Bracciali, L., Parrish, R. R., Horstwood, M. S. A., Condon, D. J. & Najman, Y. UPb LA-(MC)-ICP-MS dating of rutile: New reference materials and applications to sedimentary provenance. Chem. Geol. 347, 82–101 (2013).
Wiedenbeck, M. et al. Three natural zircon standards for U-Th-Pb, Lu–Hf, trace element and REE analyses. Geostand. Newsl. 19, 1–23 (1995).
Kemp, A. I. S., Vervoort, J. D., Bjorkman, K. E. & Iaccheri, L. M. Hafnium isotope characteristics of Palaeoarchaean zircon OG1/OGC from the Owens Gully Diorite, Pilbara Craton, Western Australia. Geostand. Geoanalytical Res. 41, 659–673 (2017).
Fisher, C. M., Vervoort, J. D. & DuFrane, S. A. Accurate Hf isotope determinations of complex zircons using the “laser ablation split stream” method. Geochem. Geophys. Geosyst. 15, 121–139 (2014).
Söderlund, U., Patchett, P. J., Vervoort, J. D. & Isachsen, C. E. The 176Lu decay constant determined by Lu–Hf and U–Pb isotope systematics of Precambrian mafic intrusions. Earth Planet. Sci. Lett. 219, 311–324 (2004).
Bouvier, A., Vervoort, J. D. & Patchett, P. J. The Lu–Hf and Sm-Nd isotopic composition of CHUR: Constraints from unequilibrated chondrites and implications for the bulk composition of terrestrial planets. Earth Planet. Sci. Lett. 273, 48–57 (2008).
Rezeau, H. et al. Temporal and genetic link between incremental pluton assembly and pulsed porphyry Cu-Mo formation in accretionary orogens. Geology 44, 627–630 (2016).
Black, L. P. et al. Improved 206Pb/238U microprobe geochronology by the monitoring of a trace-element-related matrix effect; SHRIMP, ID-TIMS, ELA-ICP-MS and oxygen isotope documentation for a series of zircon standards. Chem. Geol. 205, 115–140 (2004).
Stormer, J. C., Pierson, M. L. & Tacker, R. C. Variation of F-X-Ray and Cl-X-Ray intensity due to anisotropic diffusion in apatite during electron-microprobe analysis. Am. Mineralogist 78, 641–648 (1993).
Goldoff, B., Webster, J. D. & Harlov, D. E. Characterization of fluor-chlorapatites by electron probe microanalysis with a focus on time-dependent intensity variation of halogens. Am. Mineral. 97, 1103–1115 (2012).
Konecke, B. A., Fiege, A., Simon, A. C., Parat, F. & Stechern, A. Co-variability of S6+, S4+, and S2− in apatite as a function of oxidation state: Implications for a new oxybarometer. Am. Mineral. 102, 548–557 (2017).
Ravel, B. & Newville, M. ATHENA, ARTEMIS, HEPHAESTUS: data analysis for X-ray absorption spectroscopy using IFEFFIT. J. Synchrotron Radiat. 12, 537–541 (2005).
Wojdyr, M. Fityk: a general‐purpose peak fitting program. J. Appl. Crystallogr. 43, 1126–1128 (2010).
Piccoli, P. & Candela, P. Apatite in felsic rocks: a model for the estimation of initial halogen concentrations in the Bishop Tuff (Long Valley) and Tuolumne Intrusive Suite (Sierra Nevada Batholith) magmas. Am. J. Sci. 294, 92–135 (1994).
Parat, F. & Holtz, F. Sulfur partitioning between apatite and melt and effect of sulfur on apatite solubility at oxidizing conditions. Contributions Mineral. Petrol. 147, 201–212 (2004).
Streck, M. J. & Dilles, J. H. Sulfur evolution of oxidized arc magmas as recorded in apatite from a porphyry copper batholith. Geology 26, 523–526 (1998).
Minnitt, R. C. A. The Geological Setting of Porphyry-type Copper Mineralization in the Haib River Area, South West Africa. Ph.D. thesis (University of the Witwatersrand, 1979).
Sun, S. S. & McDonough, W. F. Chemical and isotopic systematics of oceanic basalts: implications for mantle composition and processes. Geol. Soc. Lond. Spec. Publ. 42, 313–345 (1989).
Valley, J. W., Kinny, P. D., Schulze, D. J. & Spicuzza, M. J. Zircon megacrysts from kimberlite: oxygen isotope variability among mantle melts. Contrib. Mineral. Petrol. 133, 1–11 (1998).
Kelley, K. A. et al. Mantle melting as a function of water content beneath the Mariana Arc. J. Petrol. 51, 1711–1738 (2010).
Acknowledgements
The research was supported by Natural Sciences and Engineering Research Council of Canada Discovery Grant (RGPIN/5082-2017) and Canada First Research Excellence Fund through a Metal Earth thematic project to J.P.R, as well as a student research grant from the Geological Society of America and a China Scholarship Council award to X.M. We acknowledge the access permission to the drill cores and exploration database, and the logistic assistance from P. Leveille and V. Stuart-Williams at the Deep-South Resources Inc. We appreciate the assistance from D. Crabtree at Ontario GeoLabs on electron microprobe analyses. Thanks to T. Huthwelker and C. Nicoleta at SLS in Switzerland and A. Lanzirotti and M. Newville at APS in the USA for beamline assistance. We acknowledge the Paul Scherrer Institut, Villigen, Switzerland at beamline X07MB for provision of synchrotron radiation beamtime. This research also used synchrotron resources (Sector 13-ID-E) of the Advanced Photon Source, a U.S. Department of Energy (DOE) Office of Science User Facility operated for the DOE Office of Science by Argonne National Laboratory under Contract No. DE-AC02-06CH11357. S.R.T. and L.R. acknowledge financial support from NERC FAMOS NE/P01724X/1 grant and DSI-NRF Centre of Excellence, University of Johannesburg, respectively. Harquail School of Earth Sciences, Mineral Exploration Research Centre contribution MERC-ME-2021-028.
Author information
Authors and Affiliations
Contributions
X.M. and J.P.R. conceived the study and collected the samples with assistance from L.R. and G.M.B. X.M. performed petrography and sample preparation, electron microprobe analyses, LA-ICP-MS isotope and trace element analyses (with assistance from J.H.M.), as well as data compilation from literature. J.M.K. and X.M. conducted the XANES analyses. S.R.T. and R.A.S. completed zircon CA-ID-TIMS dating and O isotopes, respectively. X.M. wrote the earliest version of the manuscript as part of his Ph. D. studies with contributions from J.M.K., A.C.S., D.J.K., P.J.J. and all other co-authors.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Peer review information Nature Communications thanks Ross Large, Robert Nicklas and the other, anonymous, reviewer(s) for their contribution to the peer review of this work. Peer reviewer reports are available.
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Meng, X., Kleinsasser, J.M., Richards, J.P. et al. Oxidized sulfur-rich arc magmas formed porphyry Cu deposits by 1.88 Ga. Nat Commun 12, 2189 (2021). https://doi.org/10.1038/s41467-021-22349-z
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-021-22349-z
This article is cited by
-
Sub-arc mantle fugacity shifted by sediment recycling across the Great Oxidation Event
Nature Geoscience (2023)
-
Apatite evidence for a fluid-saturated, crystal-rich magma reservoir forming the Quellaveco porphyry copper deposit (Southern Peru)
Contributions to Mineralogy and Petrology (2023)
-
Formation of oxidized sulfur-rich magmas in Neoarchaean subduction zones
Nature Geoscience (2022)
-
The long-lived fertility signature of Cu–Au porphyry systems: insights from apatite and zircon at Tampakan, Philippines
Contributions to Mineralogy and Petrology (2022)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.