Abstract
Burstiness, the tendency of interaction events to be heterogeneously distributed in time, is critical to information diffusion in physical and social systems. However, an analytical framework capturing the effect of burstiness on generic dynamics is lacking. Here we develop a master equation formalism to study cascades on temporal networks with burstiness modelled by renewal processes. Supported by numerical and data-driven simulations, we describe the interplay between heterogeneous temporal interactions and models of threshold-driven and epidemic spreading. We find that increasing interevent time variance can both accelerate and decelerate spreading for threshold models, but can only decelerate epidemic spreading. When accounting for the skewness of different interevent time distributions, spreading times collapse onto a universal curve. Our framework uncovers a deep yet subtle connection between generic diffusion mechanisms and underlying temporal network structures that impacts a broad class of networked phenomena, from spin interactions to epidemic contagion and language dynamics.
Similar content being viewed by others
Introduction
Temporal networks provide a representation of real-world complex systems where interactions between components vary in time1,2,3. Although initially modelled as Poisson processes, where independent events are homogeneously distributed in time, real-world networked interactions have been found to be heterogeneously distributed and to exhibit temporal correlations4,5,6. In particular, interaction events in real systems concentrate within short periods of intense activity followed by long intervals of inactivity, an effect known as burstiness. Bursty dynamics appear in diverse physical phenomena including earthquakes7 and solar flares8, biological processes like neuron firing9, as well as the dynamics of human social interaction5,10.
Burstiness in temporal interactions has profound implications for the diffusion of information over temporal networks, as demonstrated in a growing number of works11,12,13,14,15,16,17. This is true in the case of epidemic processes, often referred to as simple contagion, where the probability of infection of an uninfected node depends linearly on the number of exposures, i.e., temporal interactions with infected neighbours in the network18. Epidemic models successfully describe the spread of biological disease19, and have been shown to critically depend on burstiness and other patterns of temporal interactions12,20,21,22,23. Epidemic spreading over temporal networks appears to be slowed owing to burstiness in some cases11,24,25,26, whereas accelerated in others14,27,28. However, these conclusions are known to depend on the stage at which we observe the spreading process. It has been argued that at early stages of epidemics, short interevent times may accelerate spreading13, whereas at later stages, long interevent times may decelerate dynamics16,26. Threshold mechanisms provide another class of phenomena where bursty temporal networks have a crucial role. Threshold dynamics, also known as complex contagion, are used to model the spread of information where infection requires the reinforced influence of at least a certain fraction of neighbours in the egocentric network29. Threshold-driven dynamics over static networks have been extensively studied both empirically30 and theoretically30,31,32,33,34, but analysis of their behaviour on temporal networks is so far limited to a small number of empirical studies35,36,37,38. Using random reference models of temporal networks, it has been shown that when infection is driven by the fraction of infected neighbours, rather than their absolute number, bursty interactions may lead to deceleration35,36,38. In contrast, if the threshold measure of influence is absolute, burstiness may have an accelerative effect35. Acceleration has also been observed in the case of history-dependent contagion37.
Information diffusion in social and economic settings must overcome limits inherent to our social and cognitive capacities, namely that we have finite attention. This has motivated the concept of the attention economy39,40, where relative to an abundance of content and information, attention is a scarce resource. A mechanism that has emerged to deal with these limitations is ephemeral content41,42. Variously referred to as stories, snaps or fleets, depending on the platform, ephemeral content disappears after a specified amount of time, in principle concentrating the attention of viewers. In contrast, persistent content is not explicitly erased, but owing to cognitive limits and competing content, gradually decreases in visibility. Here, we propose an analytical framework to systematically describe the relationship between the diffusion of information, bursty temporal interactions, and inherent limits to our attention and memory, thus providing the theoretical foundation necessary to shed light on the role of burstiness in generic diffusion processes, including simple and complex contagion models of physical, biological and social phenomena.
We incorporate the most widely documented features of temporal interactions into a framework of binary-state dynamics and benchmark its behaviour with standard models of threshold driven and epidemic spreading. Although stochastic bursty interactions are likely emergent phenomena4,43, their dynamics are well approximated by renewal processes44. Temporal heterogeneity in network interactions can then be characterised by the variability in interevent times τ, the time between consecutive events on a given edge, parameterised by the interevent time distribution ψ(τ), whereas other features of the temporal network are considered maximally random. Renewal processes represent the simplest model of bursty, non-Markovian dynamics, and a departure from the memoryless assumption implicit in Poisson processes. Nevertheless, we are able to show that such a system can be accurately captured by a master equation formalism, which is essentially memoryless, implying the existence of a purely Markovian system with almost identical behaviour. We show both analytically and numerically that bursty temporal interactions give rise to a percolation transition in the connectivity of the temporal network, separating phases of slow and rapid dynamics for both epidemic and threshold models of information diffusion. We find that diffusion dynamics are sensitive to the choice of interevent time distribution, particularly in regard to its skewness, and we demonstrate a data collapse across distributions when controlling for this effect.
Results
Temporal network model
To model a temporal network, we consider an undirected, unweighted static network of N nodes as the underlying structure, acting as a skeleton on top of which temporal interactions take place. The degree of a node, or how many neighbours it has, takes discrete values k = 0, …, N − 1 from a degree distribution p(k). Pairwise temporal interactions, or events, occur independently at random on each static edge via a renewal process with interevent time distribution ψ(τ). Time is continuous and events are instantaneous, whereas consecutive interevent times are uncorrelated. We also assume that the renewal process is stationary (for further details, see Methods and Supplementary Note 4). By using a static underlying network, we assume that the time scales of edge formation and node addition or removal are far longer and thus negligible relative to the time scale of event dynamics over existing edges.
In its simplest form, information diffusion is a binary-state process where each node occupies one of two mutually exclusive states, which we term uninfected and infected. The probability of a node changing state is a function of the state of its neighbours, as well as the strength of their interactions. Interaction strength, also referred to as mutual influence, is a non-negative scalar that we consider to be a function of the elapsed renewal process time series. We desire that the mean of the emergent distribution of interaction strengths be stationary, and invariant to the underlying burstiness of the system. This is achieved when the contribution of a single event to interaction strength (i) goes to zero as the event ages, and (ii) is additive, meaning a spike in edge activity leads to a spike in the interaction strength between neighbours.
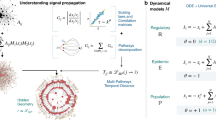
To satisfy these conditions, we are free to choose a memory kernel, or distribution of event memory times. One such coupling is a step function, i.e., the contribution of an event to the actual interaction strength is constant for a duration η, after which it goes to zero. This is best used to model information diffusion via ephemeral content, where the lifetime of an interaction is expressly finite. An alternative is an exponential memory kernel, where an event is forgotten at a constant rate 1/η, modelling persistent content with attention decaying due to other factors. For all choices of memory kernel, we define the interaction strength wj of an edge at time t (or state j for short), as the number j of events in active memory. In the case of a step-function memory kernel, the focus of our work, it is simply the number of events in the preceding time window of width η (Fig. 1). Nevertheless, all studied memory kernels qualitatively lead to the same results.
a Interaction events appear on edges according to independent renewal processes. Under a step-function memory kernel, interaction strength is determined by the number of events j having occurred within a time window of length η. Memory windows are highlighted in violet, with a darker shade indicating infection. b The edge-state configuration of node u is determined by the renewal process in a. Node u has three neighbours, with v3 being infected, so k = 3 and m = 1. The degree vector k of u contains zeros except when j = 0, 3 and 9, where entries equal 1. The infected degree vector m contains zeros, except when j = 3, where the entry is 1. For v1, v2 and v3, k contains zeros, except when j = 9, 0 and 3, respectively, where entries equal 1. In each case, m contains only zeros. The dynamical response of node u to its local configuration is given by the infection rate Fk,m, which here assumes a relative threshold (RT case) of ϕ = 0.3, an absolute threshold (AT case) of Mϕ = 3, and a transmission rate (SI case) of λ.
It follows that the local configuration of a node is determined by the number kj of its neighbours connected via edges in state j, with the degree k of the node related to its kj values by k = ∑jkj at any time t. We introduce mj as the number of infected neighbours of a node connected via edges in state j. Consequently, 0 ≤ mj ≤ kj with m = ∑jmj the total number of infected neighbours. For each node, we store kj and mj for all j in vectors k and m, providing a description of edge and node states in the local neighbourhood of a node. Nodes in class (k, m) become infected at a rate Fk,m, and are statistically identical in this sense. We also store the interaction strength wj = j in the vector w for all j. The dynamics of a given node, through Fk,m, are thus fully determined by (k, m) and w.
Information diffusion over temporal networks
To examine the effect of temporal interactions on information diffusion, we explore three widely known models of transmission. We consider both relative (RT) and absolute (AT) variants of a threshold mechanism29,31,45, as well as the susceptible-infected (SI) model of epidemic spreading46 (see Table 1 for details). All models are non-recovery, meaning the uninfected state cannot be re-entered, and we consider infection owing to external noise at a low, but non-zero rate p.
The study of threshold dynamics focuses on the conditions leading to cascades, or large avalanches of infections that sweep through the network. In the simplest implementation of threshold dynamics, infection occurs when the number m of infected neighbours of an uninfected node exceeds a fraction ϕ of its degree k29,31. Generalising this rule to the case of arbitrary interaction strength33,47, in the RT model infection occurs when the influence of infected neighbours, m ⋅ w, exceeds a fraction ϕ of all potential influence, k ⋅ w. The RT model captures instances of real-world diffusion where interaction between elements affect the probability of infection only in aggregate, similar to the response of individuals to new behavioural patterns or transmission in biological neural networks48,49. When considering the RT model over temporal networks, the probability of infection may increase during bursts of interaction events with infected neighbours or, conversely, bursts of activity with uninfected neighbours may temporarily maintain a node in the uninfected state. This is the case in Fig. 1b, where influence from a single infected neighbour is insufficient to overcome that from uninfected neighbours. In the AT model, influence from infected neighbours is not normalised, but compared with some absolute value Mϕ45. In contrast to the RT model, infection is not hindered by interaction activity with uninfected neighbours, and bursts can only increase the probability of infection. In the SI model, finally, each interaction event with an infected neighbour triggers infection at a rate λ. In our framework of temporal networks, infected neighbours trigger infection via edges in state j at a rate λj. Writing λ = λw, the infection rate for a node with a neighbourhood of infected nodes described by m is m ⋅ λ. Similar to the AT model, bursts can only increase the probability of infection in the SI model (Fig. 1).
Master equation solution
We extend a master equation formalism33,50 to account for network temporality. We introduce the state space of all configurations (k, m) allowed by the underlying degree distribution p(k), under the condition that each edge is in one of a finite number of possible edge states (see Methods, and Supplementary Note 1 for lattice diagrams of this space). We introduce the state vector s(t) containing the probability that a randomly selected node with underlying degree k is uninfected and in class (k, m) at time t. The time evolution of s is governed by the matrix W(s, t), containing the transition rate Wij from the ith to the jth configuration (k, m) at time t. Transitions arise from three mechanisms. First, ego transitions, contained in the matrix Wego, describe the loss to configuration (k, m) owing to its nodes becoming infected. This occurs at a rate Fk,m, as per Table 1, so the diagonal terms of Wego are given by −Fk,m and off-diagonals are zero. Second, neighbour transitions, contained in matrix Wneigh, describe the gain or loss to configuration (k, m) owing to the infection of neighbours of nodes related to this class. This transition is determined by βjdt, the probability of an uninfected neighbour in configuration j becoming infected over an interval dt (see Methods for an explicit calculation). Taken together, Wego and Wneigh accurately describe diffusion dynamics over static networks with heterogeneous edge types, such as weighted and multiplex networks33,34.
Temporal networks require a third component, edge transitions, contained in the matrix Wedge, describing the gain or loss to configuration (k, m) due to changes in an edge’s state j. This applies to any temporal network model that can be formulated in terms of discrete, dynamic edge states. We denote by μjdt and νjdt the probabilities that a randomly selected edge in state j undergoes a positive or negative transition and enters state j + 1 or j − 1, respectively, over an interval dt. Combining these terms gives the master equation
Modelling temporal network dynamics amounts to solving Eq. (1), which along with the initial condition s(0), determines the evolution of the system.
To apply this formalism we derive the edge transition rates μj and νj in the case of renewal processes. We first note that microscopically, on the scale of a single edge, transitions from state j to j ± 1 cannot be described by a constant rate. In a renewal process, the probability of an event occurring is conditional on the time elapsed since the previous event. Therefore, this probability is history dependent, meaning edges have an effective memory and are non-Markovian by definition. Further, since it is only the previous event that is determinant, there is clearly no j dependence at this scale. A renewal process may then seem at odds with a Markovian master equation [where s(t + dt) depends only on s(t), as per Eq. (1)]. Macroscopically, however, on the scale of large ensembles of edges, the renewal process exhibits effective j-dependent rates that are constant in time. We can calculate the probability Ej that a randomly selected edge is in state j, and the probability that it transitions to state j ± 1 over an interval dt, giving μj and νj [see Methods for explicit expressions for j > 0, with the j = 0 case of Ej and μj comprising a special case that we define in Eqs. (2) and (3) below].
As the rates μj and νj are heterogeneous in terms of j, they can be viewed as a signature of the model parameters ψ(τ) and η, and of the non-Markovianity inherent at the scale of a single edge. On a macroscopic scale, μj, νj, and Ej are constant in time, meaning our system is indistinguishable from a continuous-time Markov chain model of edge state. That is, a random walk on the non-negative integers, with transition rates given by μj and νj, and a stationary distribution of walkers given by Ej (see Supplementary Note 2 for an illustration of μj and νj in the case of gamma-distributed interevent times). Applying the system-wide rates μj and νj at the finer-grained level of configurations (k, m) amounts to a mean field approximation. Monte Carlo simulations (see Supplementary Fig. 10) demonstrate that the actual edge transition rates deviate slightly from μj and νj for each class (k, m), even if they are exact for the network as a whole, in the limit of large N. The accuracy of the master equation solution provides a measure of the remarkable similarity between a renewal process, where Eq. (1) is an approximation, and the biased random walk interpretation of edge state, where Eq. (1) is exact.
Information diffusion and burstiness
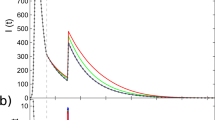
We validate our analytical framework with Monte Carlo simulations of diffusion dynamics over temporal networks. Simulations use an underlying static, configuration-model network with lognormal degree distribution of mean 〈k〉 and standard deviation σk. We measure the time tc required to reach an arbitrary density ρc of infected nodes, in the presence of background noise at rate p. We also measure ρf, the relative frequency of infections due to external noise, such that 0 < ρf ≤ 1, with 1/ρf the ratio of total to noise-induced infections, measuring the catalytic effect of external noise (for a detailed description of ρf see Methods). We normalise tc by the time taken to reach the desired density by noise alone, providing tf, such that 0 < tf ≤ 1 . Remarkably, ρf and tf are close to linearly proportional (Fig. 2a, inset). A value of ρf = tf = 1 indicates slow diffusion with complete reliance on external noise, whereas small ρf and tf represent rapid diffusion with external noise producing a substantial catalytic effect. Together, they measure the extent to which the temporal network, rather than external noise, drives the diffusion of information.
Normalised diffusion time tf produces an almost identical effect (see a, inset). The small στ limit, leading to regular patterns in τ, comprises the quenched limit in a where η = 1 and the network is effectively static. The large στ limit produces large bursts in activity, comprising the annealed regime where the network is effectively sparsified and plays no role in information diffusion (ρf = 1). Mirroring results are achieved by varying memory η for fixed στ in generated, b, and empirical, c–d, temporal networks. Analytic solution is denoted by dashed lines, and Monte Carlo results by solid lines. Generated networks have lognormal degree distribution with mean 〈k〉 = 7 and standard deviation σk = 2. We use Weibull-distributed interevent times with mean 〈τ〉 = 1. Plot b uses στ = 1. For empirical data description see Methods. Node dynamics correspond to the RT model with threshold ϕ = 0.15 and external noise p = 2 × 10−4. Cutoff density is ρc = 0.4. Monte Carlo simulations are averaged over 104 realisations. Network size is 106 in a, and 5 × 103 in b.
We first examine the effect of varying interevent time standard deviation στ for fixed memory η = 〈τ〉 = 1 (Fig. 2a). We choose a Weibull interevent time distribution ψ(τ), used widely to model behavioural bursts in both human51 and animal52 dynamics. A Weibull distribution reduces to the exponential distribution when στ = 〈τ〉 = 1. Node dynamics follow the RT model with threshold ϕ = 0.15 and background noise p = 2 × 10−4. Approaching the small στ limit from above, events arrive in an increasingly regular pattern, and an increasing fraction of edges are frozen in the mean state η/〈τ〉 = 1. We refer to this as the quenched regime, whereby edges converge to a single state and the network is effectively static. In the opposing limit of large στ, burstiness means that at any given time, edge activity is concentrated among an arbitrarily small fraction of edges that undergo large spikes in activity, with the remainder in state j = 0. We refer to this as the annealed regime, where the network is maximally sparse and has a vanishingly small role in information diffusion (ρf and tf approach one).
Both quenched and annealed regimes lead to slow, noise-reliant diffusion, with the expected edge state η/〈τ〉 preserved in each case (Fig. 2a). For intermediate values of στ, there is a well-mixed regime where relatively rapid diffusion occurs, owing to edge-state fluctuations that are ultimately favourable to transmission. In the RT model this implies a spike of activity on an infected neighbour overcoming a node’s threshold, or decreased activity on uninfected edges lowering the relative influence to be overcome. The decelerative effect of quenching is increased for narrower underlying degree distributions, as an increasing fraction of nodes are frozen in a state unfavourable to transmission, a static network effect already reported in ref. 31.
As seen in Fig. 2a, if the system is more bursty than a Poisson process, i.e., if στ ≥ 1, values of ρf coincide regardless of the underlying degree distribution. The degree distribution is degenerate in this sense, as temporal fluctuations, rather than the underlying degree, determine local connectivity over short time scales. In Supplementary Note 6, we show that clustering is another such property, where even densely clustered configuration-model networks53 are functionally treelike in the annealed phase, with long interevent times τ inducing edges to the non-interacting state, thereby deconstructing cycles. We conjecture that local properties, like node degree and clustering, are degenerate in the presence of uncorrelated temporal fluctuations, whereas collective properties like modularity and eigenvector centrality are not. In Supplementary Fig. 9 we demonstrate using the Watts-Strogatz model54 that average path length, a manifestly collective property, is clearly non-degenerate. Interestingly, these results suggest that temporal correlations between edges on a local scale may break the degeneracy observed in Fig. 2a. The study of such correlations is an active line of research55.
A mirroring effect can be obtained by varying memory η for constant στ = 〈τ〉 = 1 (Fig. 2b). The quenched limit is recovered for large η, as large samples of events on each edge result in edges converging to a mean state, η/〈τ〉, with an increasingly narrow distribution, owing to the central limit theorem. As for the case of fixed η, quenching may be decelerative if cascades on the corresponding static network are noise dependent. For example, increasing ϕ can cause slower diffusion in the quenched limit (Fig. 2b). The annealed, or noise-reliant regime is effectively recovered when η is vanishingly small, meaning almost all edges are in state j = 0 and the role of the network in information diffusion vanishes (ρf = tf = 1). The correspondence between στ and η suggests data-driven experiments that allow an indirect inference of the effects of varying στ in real systems, an open problem in the study of information diffusion. We simulate the RT model on two empirical temporal networks and vary only the memory η, recovering qualitatively the effects observed on synthetic networks (Fig. 2c, d, see Methods for data description). This suggests the accelerative and decelerative effects of burstiness may well be a feature of real-world information diffusion.
Comparing interevent time distributions
Next, we compare the dynamical outcomes of diffusion under lognormal, Weibull and gamma interevent time distributions. Each of these are two-parameter distributions, whose values we determine by specifying their mean 〈τ〉 and standard deviation στ. Consider first the AT model with Mϕ = 2 and η = 〈τ〉 = 1 (Fig. 3b). Here, we observe a striking dependence of diffusion dynamics on ψ(τ), with the lognormal distribution leading to the most rapid diffusion, outpacing the gamma distribution in diffusion speed and relative noise dependence by up to a factor of 83, and the Weibull distribution by up to a factor of 14. Consider too that in order to achieve an identical dynamical outcome as the gamma distribution, say ρf = 0.1, the standard deviation of the lognormal distribution must be increased by over three orders of magnitude. These dramatic differences can be accounted for by comparing the rate of onset of annealing in terms of the fraction of edges in state j = 0, as we increase στ. To quantify this effect, we introduce
and
where ξE equals E0, the fraction of edges in state zero, and ξμ equals μ0, the probability that a randomly selected edge in state zero enters state one over an interval dt. We may refer to ξE as the effective sparsification, or alternatively, the effective annealing. Here Ψ(τ) is the complementary cumulative distribution relating to ψ(τ). The gamma distribution rapidly anneals the network, yielding the largest ξE values of all choices of distribution, meaning the most edges in state j = 0. As a result, it exhibits the slowest, most noise-reliant diffusion. In terms of the value of ξE induced, the gamma is followed by the Weibull distribution, then the lognormal distribution. In fact, the lognormal requires orders-of-magnitude larger στ to produce equal values of ξE as the Weibull and gamma distributions. By plotting ρf against ξE we observe the data to collapse approximately onto a single curve, revealing ξE to be a far better predictor of dynamics than στ (see Fig. 3c in contrast to Fig. 3b). Some disagreement persists, however (Fig. 3c, left inset), which can be explained by noting that increased rates of mixing ξμ (Fig. 3c, right inset) ensure that the small number of active edges redistribute about the network at a greater rate, thus mediating cascades more effectively. An identical effect is observed for the SI model (Fig. 3e, f).
Information diffuses following the AT, or absolute threshold model, a–c, and the SI, or susceptible-infected model, d–f. Analytic solution is denoted by dashed lines, and Monte Carlo results by solid lines. a Effect of absolute threshold Mϕ. b Dependence of ρf on choice of ψ(τ). c Data collapse of b after controlling for effective sparsity ξE. Left inset is a closeup of the main plot in linear scale, revealing that differences in ρf remain after controlling for ξE. This is explained by the differing mixing rates ξμ (inset right). e, f Corresponding results for the SI model. Cutoff node density is ρc = 0.4, with η = 〈τ〉 = 1. Analytic solution is shown by dashed lines, Monte Carlo simulations by solid lines. Degree distribution is lognormal with 〈k〉 = 7 and σk = 1. We use a threshold Mϕ = 2 for the AT model, \(\lambda = 0.02\) in the SI model, and external noise p = 2 × 10−4 in each. Monte Carlo simulations involve 104 realisations on networks of size N = 106.
The data collapse in Fig. 3c, f confirm that above all it is ξE, the density of edges in state j = 0, that ultimately determines the diffusion dynamics in our framework. The sensitivity of ξE to the choice of interevent time distribution ψ can be seen in Eq. (2), where the dependence is functional. We wish to go further, however, and identify the properties of a given distribution ψ that contribute to the value of ξE, beyond its mean and standard deviation. We explore these properties using the generalised gamma distribution in the following section.
Temporal network phase transition
We systematically explore (στ, η) space using Monte Carlo simulations of the SI model (Fig. 4). We aim first to understand how the temporal connectivity evolves as a function of στ and η. As previously observed, the quenched regime appears either in the small στ limit for constant (but sufficiently large) η, or in the large η limit for constant στ. The temporal network enters the annealed regime in two ways, either by taking the small η limit for constant στ, or the large στ limit for constant η. The two regimes are separated by an edge percolation transition, i.e., the emergence of a giant connected component in the sub-graph formed by edges in state j > 0, that can be expected with high probability at any given time (see regimes and boundary in Fig. 4a). The giant component is dynamic, meaning its composition in terms of both nodes and edges is constantly evolving, but can always be expected to percolate through the network. Above percolation, a giant components facilitates the diffusion of information, that would otherwise rely on small, temporally disconnected components in order to propagate. We denote by q(k) the degree distribution obtained by randomly removing a fraction ξE of edges in a static configuration-model network with degree distribution p(k), which is identical to that of the expected sub-graph formed by removing state zero edges in the stochastic temporal network. The percolation transition for q(k) can be computed analytically (see Supplementary Note 3), and despite the static assumption, provides an excellent estimate of the boundary between quenched and annealed regimes of the temporal network (Fig. 4a), indicating the onset of slow, noise-dependent diffusion for all diffusion dynamics considered.
a Heat map is diffusion time tf for an SI process with λ = 0.02 under a Weibull interevent time distribution, and a step-function memory kernel. The underlying degree distribution is lognormal with 〈k〉 = 7 and σk = 0.5, and network size N = 105. The slope of the temporal network phase transition, dashed lines, depends on the choice of the interevent time distribution, and can be parameterised by its skewness, γτ. b For a given η, the critical σc varies for the gamma, Weibull and lognormal distributions, which are special and limiting cases of the generalised gamma distribution, parameterised here by γτ. Solid lines in b result from simulating the temporal network with smoothly varying γτ under the generalised gamma distribution. Symbols are data taken from a, the results of direct simulation of the gamma, Weibull and lognormal distributions. Dashed lines are extrapolation from solid lines to lognormal data.
The percolation transition in Fig. 4a is heavily dependent on ψ, as seen in the angle formed in the (στ, η) plane by the gamma, Weibull and lognormal interevent time distributions (left to right). For a given value of memory η, we denote by σc the critical value of interevent time standard deviation, indicating the collapse of the giant temporally connected component. To appreciate the importance of the choice of ψ, consider that when memory is set to η = 10, the collapse of the giant component occurs at σc = 15 under the gamma distribution, then orders-of-magnitude later at 80 and 1300 under the Weibull and lognormal distributions, respectively. Above all, these results emphasise that for an arbitrary interevent time distribution, mean and standard deviation alone are insufficient to estimate dynamical quantities, such as temporal connectivity.
To better understand the behaviour of the temporal network phase transition, critical values of interevent time standard deviation, σc, are drawn from Fig. 4a and plot as symbols in Fig. 4b. We do this for select values of memory, η. Then, we exploit the fact that the distributions in Fig. 4a are either special (gamma and Weibull) or limiting (lognormal) cases of the generalised gamma distribution, a three-parameter distribution that may be used to model interevent times directly, or be used to discriminate between two-parameter models in empirical settings56. We specify two of the three parameters in the generalised gamma distribution using 〈τ〉 and στ, leaving a third parameter that may be used to control a number of higher order properties, such as the interevent time skewness, γτ. Other parameterisations are possible, such as differential entropy, defined in Supplementary Note 8. The solid curves in Fig. 4b give the critical point σc observed when smoothly varying γτ in the generalised gamma distribution. As expected, σc in the simulated network interpolates between that of the gamma and Weibull distributions. The lognormal distribution is numerically challenging to recover in this manner, being a limiting case, but in principle belongs to the same family. The dashed line is the extrapolation to this case.
The variation between phase transitions in Fig. 4a appears to be characterised by a single parameter, namely the angle formed in the (στ, η) plane. This intuition is validated by the generalised gamma distribution, whose third parameter, specified here by interevent time skewness γτ, accounts for this effect. Skewness should be viewed here as a proxy of higher order structure, as a number of other quantities, such as differential entropy, vary alongside γτ. A consequence of this may be the following. Given a set of empirical interevent time data, measurements of its mean and standard deviation alone are insufficient to infer its dynamics, such as spreading time (as in Fig. 3b, d), or whether the temporal network is above percolation, below percolation, or at criticality (as in Fig. 4a). Figure 4 demonstrates that performing just one additional measurement, such as the skewness of the τ data, is sufficient to characterise the temporal connectivity, and consequently, the diffusion dynamics.
These results are unchanged qualitatively when the step-function memory kernel is replaced with an exponential kernel with mean η. The difference lies in the slope of the transition in the (στ, η) plane, with the giant component proving more robust everywhere in the exponential case (see Supplementary Fig. 12). For instance, when η = 10, the giant component collapses at στ = 80 under a step-function memory kernel, but not until 300 under an exponential kernel. Although a substantial effect, it is small relative to that of varying interevent time skewness. Further, since the basic connectivity of the temporal network is determined by ψ and η, the outcome of information diffusion (as measured by tf in Supplementary Fig. 7) is qualitatively similar across diffusion models. In particular, below percolation, all transmission events take place in small temporally disconnected components, that appear and disappear dynamically. Above percolation, the diffusion process is accelerated thanks to the giant connected component. The percolation transition is clear regardless of one’s choice of diffusion model.
Discussion
Our study shows that generic dynamics of information diffusion are closely tied to the level of burstiness in the underlying temporal network. By considering three binary-state models of transmission, we have demonstrated that they differ in their response to burstiness only in their details. For instance, while having a purely decelerative effect on SI models, increasing burstiness at intermediate values can be accelerative for threshold models. Nevertheless, the prevailing trend suggests that increasing burstiness is strongly decelerative overall, with the onset of the decelerative phase heavily dependent on the choice of the interevent time distribution. The key assumptions here are that the underlying network is fixed, and that owing to a memory mechanism, a fraction of edges enter a non-interacting state owing to long waiting times. These assumptions result in a temporal network topology that has profound implications for many dynamical processes. It is likely that structural features of the temporal network, such as the percolation transition separating slow and fast diffusion, will also be critical for the more general class of binary-state dynamics.
Indeed, one of the strengths of our master equation formalism is that it is straightforward to extend to general binary-state models of node dynamics. This includes not only threshold and epidemic models, but language, voter, and Ising models, among others (see Supplementary Note 1). Our framework can also accommodate a broad class of temporal network models. In particular, any model that can be formulated in terms of discrete, dynamic edge states is a candidate for our approach. This includes growing, decaying and adaptive networks, as well as models of rewiring. In line with our use of renewal processes, a large family of point processes have natural descriptions in terms of discrete edge state, such as cascading Poisson, Cox and Hawkes processes. Extensions to the Poisson process in general represent promising applications of our methodology. The main limitation of our approach, however, is the sheer size of the master equation solution, in that it can be just as fast to simulate the dynamics as to solve its equations numerically. In particular, note that we did not solve the system at large values of memory η, as this entails a large average edge state, and a prohibitively large configuration space.
Although a master equation is unlikely to be one’s first choice of tool when analysing empirical temporal network data, the by-products of a master equation study are immediately applicable. In particular, our study highlights the importance of moments beyond mean and standard deviation when fitting interevent time distributions. We have used the generalised gamma distribution to interpolate between the lognormal, Weibull and gamma distributions, and in so doing, demonstrated a remarkable sensitivity of dynamic quantities such as the temporal network percolation transmission. Estimating the connectivity of empirical systems, for example, by accounting for interevent time skewness, is one intriguing application of this technique. Further, our treatment of non-Markovianity may be applied to other systems. That is, while a single component in a large system may be strongly non-Markovian, as was the case in our renewal process, stationary statistics may emerge at an ensemble level that act as a signature of the non-Markovianity in play microscopically. Our biased random walk interpretation of the renewal process model shows that strikingly similar Markovian counterparts may be available for analysis. Incidentally, biased random walk models of edge state suggest a broad class of Markovian models to which our master equation applies exactly. Markovian systems may then be used in this way as a probe of various complex systems where memory is critical.
Methods
Master equation configuration space
We provide here an outline of the master equation formalism. In this work, our approach has been to assign one of a finite number of types to each edge, and to allow this quantity to evolve over time. To formulate a master equation solution, one defines a state space of allowed node configurations, which we term configuration space. The second step is to define the allowed transitions between node configurations. The time evolution of a probability density over this state space amounts to a set of first-order differential equations, or rate equations, that among other things, provides the total density of infected nodes at a given time.
First, we define Ck,m, the set of all nodes in the network with local configuration (k, m), such that 0 ≤ mj ≤ kj, for all j. Whereas Ck,m is a set of nodes, we define Ck as the set of all sets Ck,m with total degree k. In a similar way we define the configuration space C as the set of all possible sets Ck,m, given a degree distribution p(k). These sets can be written
and
where the union is over all k in the support of p(k). Importantly, C leads to a partition of the network at any given time. Written this way, C is potentially infinite. Imposing the constraint that it be finite, we assume an upper cutoff in the degree distribution p(k), and the set of edge states to be of a finite size n. Note that C includes any set for which Ck,m is empty at a given time. The cardinality ∣C∣ of configuration space is thus determined entirely by the support of p(k), along with n. Since (k, m) does not convey ego state, just edge and neighbour configuration, we partition Ck,m into sets of uninfected and infected nodes, such that Ck,m = Sk,m ∪ Ik,m. Similar definitions allow us to introduce Sk and Ik, Sk and Ik, as well as S and I. Although in general ∣Sk,m∣ ≠ ∣Ik,m∣, the structure of the uninfected and infected configuration spaces is identical, such that ∣C∣ = ∣S∣ = ∣I∣, ∣Ck∣ = ∣Sk∣ = ∣Ik∣ and ∣Ck∣ = ∣Sk∣ = ∣Ik∣.
Density of states
The evolution of a dynamical process over a network amounts to a flow of nodes through the sets Sk,m and Ik,m over time. As the number of nodes N in the network is conserved, it is their distribution over the sets Sk,m and Ik,m that evolves in time. These distributions provide the state of the process at time t. As our formalism is independent of network size, we deal with the densities of nodes rather than the absolute sizes of these sets. To this end, we introduce
as shorthand for the number of nodes with underlying degree k. This is in contrast to ∣Ck∣ and ∣Ck∣, which give the number of configurations with degrees k and k, respectively. To convert from absolute node count to node density, we need to normalise Sk,m and Ik,m by some non-zero quantity that is conserved over the course of a dynamical process. As our temporal network models assume a static underlying network, a node’s underlying degree k is preserved, and as a result, so is ∥Ck∥, defined in Eq. (6). The density of uninfected nodes in class (k, m) in this case is given by
with ik,m defined analogously. The node conservation principle leads to the condition \({\sum }_{{C}_{k}}({s}_{{\bf{k}},{\bf{m}}}+{i}_{{\bf{k}},{\bf{m}}})=1\), which is to say that the sum of all densities sk,m and ik,m with underlying degree k, is one. We then have
and
with ρk giving the probability that a randomly selected node with underlying degree k will be infected, and ρ the probability that any randomly selected node will be infected.
As discussed in the main text, s is the ∣C∣-dimensional vector storing the densities sk,m. In practice, we use lexicographic ordering of the tuples in C to define a one-to-one mapping (k, m) ↦ i, for some i in the range 1 ≤ i ≤ ∣C∣, to define the ith element of s. In Supplementary Note 1, we argue that for fixed n and limiting k the size of configuration space behaves like Θ(k2n). We demonstrate this analytically, and validate it numerically by constructing C over a wide range of parameters.
Master equation transition rates
We indicate in Table 2 the relationship between (k, m) and its neighbouring classes in configuration space. Classes that can be reached from (k, m) via ego, neighbour, and edge transitions are shown in the left column, with the corresponding transition type given in the right column. The rates at which nodes flow between classes are given in the middle column. The following notation is used to describe relative changes to the class (k, m). First, ej is the jth unit vector, and determines the change to a degree vector as a result of a neighbour transition. Second, we define \({\Delta }_{j}^{\pm }=-{{\bf{e}}}_{j}+{{\bf{e}}}_{j\pm 1}\), which determines the change to a degree vector as a result of an edge transition. When an edge increments or decrements state, adjacent nodes lose a j-type edge, and gain a j ± 1-type edge, all while preserving the underlying degree k. Transitions appear as directed edges in the lattice diagram illustrations of configuration space (see Supplementary Note 1).
Ego transitions occur at rates Fk,m, and involve the flow of nodes from set Sk,m to Ik,m. As such, no change to the ego’s local neighbourhood (k, m) takes place, and the transition represents a type of self-edge, or loop, in the lattice representation of configuration space. The rates Fk,m are encoded in transmission functions such as those shown in Table 1. Flux measurements of these transitions, such as those in Supplementary Note 7, are expected to be exact. This is because node infection is directly determined by Fk,m. As nodes are infected at constant rates, we draw the waiting time to infection from an exponential distribution with mean 1/Fk,m. As such, flux measurements of ego transitions must agree with Fk,m, by construction. This makes them a useful benchmark for verifying one’s implementation. The rates Fk,m are contained in the matrix Wego.
Neighbour transitions are based on the probability βjdt that an uninfected neighbour of an uninfected node becomes infected over an interval dt. To calculate βj we use a straightforward ensemble average over S. To obtain the expected fraction of neighbours undergoing transitions, we observe the number of nodes undergoing ego transitions at time t, and count the number of neighbour transitions produced as a result. That is, when an uninfected node in class (k, m) becomes infected, which occurs with probability Fk,mdt, it has kj − mj uninfected neighbours that observe this transition, or kj − mj nodes undergoing neighbour transitions. The number of such edges across the entire network is given by ∑Spk(kj − mj)Fk,msk,m, where the sum is over all uninfected classes. We compare this with the total number of uninfected-uninfected edges, ∑Spk(kj − mj)sk,m, giving the neighbour transition rate
which has previously been used in master equation solutions of binary-state dynamics on static networks. The rates βj are contained in the matrix Wneigh, weighted by the values kj and mj of the relevant classes (k, m), as detailed in Supplementary Note 1.
Edge transitions occur at rates μj and νj, and give the probability of edges in state j transitioning to state j + 1 or j − 1, respectively, over an interval dt. Their value depends upon the temporal network model in question. In this work, edge transition rates are determined by renewal processes following interevent time distributions ψ(τ), with complementary cumulative distributions Ψ. If the state of an edge is determined by the number of events j having occurred in the preceding time window of duration η owing to a renewal process, edge transition rates are
and
with
giving the probability that a randomly selected edge is in state j. It is this quantity that provides the normalising constant for the rates μj and νj. Here, ψ*j is the jth convolution power of ψ. A complete derivation of these quantities is given in Supplementary Note 1. The Gaver–Stehfest algorithm is used to compute the inverse Laplace transforms, and an efficient numerical procedure reducing μj and νj to a matrix-vector product is developed in Supplementary Note 5. These expressions hold for j > 0, with Eqs. (2) and (3) in the main text giving the special case of j = 0 for Ej and μj, respectively. Regardless of the form of ψ, the mean edge state η/〈τ〉 is always conserved on a network-wide level. Applying Eqs. (11) and (12) at the level of class transitions amounts to a mean field approximation, since flux measurements of Monte Carlo simulation show edge transition rates to deviate slightly from μj and νj at the class level (k, m), even if exact for the network as a whole, as shown in Supplementary Note 7.
Monte Carlo simulation
We simulate networks \({\mathcal{G}}=({\mathcal{V}},{\mathcal{E}})\) composed of a node set \({\mathcal{V}}\) of size N, and an underlying edge set \({\mathcal{E}}\). The edge set is produced by a desired degree distribution, wired according to the configuration model. Overlying temporal network activity is initialised to the steady state, such that at time t = 0, the time to the first event follows exactly the residual distribution Ψ, in the limit of large networks. Specifically, we set the time to t = −η, and draw \(| {\mathcal{E}}|\) residual times from Ψ, or one for each edge. Subsequent interevent times are drawn from ψ. Advancing in time from −η ensures that a stationary distribution of edge states Ej is achieved exactly at t = 0, when we begin to allow node dynamics to evolve. Owing to the large values of interevent time standard deviation studied in this work, out-of-the-box sampling routines were either inefficient or broke down for large στ. As such, we develop a simple, yet efficient routine in Supplementary Note 4 based on approximate inverse transform sampling of ψ and Ψ, using a bisection method. This is performed on a numerical grid of Ψ values, with relevant details of the probability distributions outlined in detail in Supplementary Note 9. A third-order spline interpolation on a logarithmic scale provides intermediate values of the grid, such that the resultant underlying distribution is close to exact.
Node dynamics are implemented via a Gillespie algorithm, which uses the fact that the waiting time to infection for an uninfected node in class (k, m) follows an exponential distribution with mean 1/Fk,m. Initially all nodes are in the uninfected state, and the diffusion process is triggered by low-level background noise at rate p. To simulate the temporal network itself, a time-ordered sequence of edge events is implemented in parallel with the node update sequence. This amounts to two separate time-ordered sequences of events executed simultaneously. Algorithms are described in detail in Supplementary Note 4 with pseudocode.
We use the normalised density of noise-induced infections, ρf, and normalised diffusion time, tf, as measures of the diffusion process. We define these quantities as follows. The probability that a randomly selected node has been infected as a result of external noise is
meaning \(0\,<\, \tilde{\rho }\, \le\, \rho\). We define ρf as the fraction of infections that are due to noise, \({\rho }_{f}=\tilde{\rho }/\rho\), such that 0 < ρf ≤ 1. This value cannot equal zero since there must be at least one noise induced infection, namely, the first infection in the diffusion process. A value approaching ρf = 1 means almost all infection is due to external noise. This occurs in the annealed limit, when almost all edges are in state j = 0, and network interactions play a vanishingly small role in the diffusion process. As a consequence, the time evolution of the diffusion process is governed by
whose solution ρ = 1 − e−pt can be inverted to give the time required to the achieve a given density ρ of infections relying solely on noise, that is,
If tc is the time required in the general case to reach a cutoff density of infections ρc, normalising tc by Eq. (16) evaluated at ρc defines tf, such that 0 < tf ≤ 1. A value of tf = 1 means the system is driven entirely by noise, and a value approaching 0 a rapid diffusion process. An important feature of this work is that tf and ρf seem to be interchangeable, as per the inset of Fig. 2a, and any result shown in terms of ρf produces an identical picture in tf.
Data description
In this work, we use two empirical temporal networks used by ref. 57 and references therein, which we describe below. The first is a temporal network of email exchange57,58, extracted from the log files of a university email server. The sender, recipient and the timestamp are used to form the network. The data set consists of N = 3,188 nodes, and \(| {\mathcal{E}}| ={\,}\)31,857 underlying edges, such that the average degree is 19.9. A total of 308,730 events were recorded, with a resolution of one second over a period of 81.3 days. An average of 9.69 events occur per edge. We determine the interevent time distribution by taking the subset of edges observing more than one event, of which there are 21,199. The mean interevent time is then calculated to be 〈τ〉 = 3.13 days, with standard deviation στ = 6.62 days. This yields a coefficient of variation στ/〈τ〉 = 2.12.
The second data set is a temporal network of online forum interactions57,59. Similar to the email data set, the sender, recipient and the timestamp are extracted from the messages. The data set consists of N = 7,083 nodes, and \(| {\mathcal{E}}| ={\,}\)138,144 underlying edges, such that the average degree is 39.0. A total of 1,428,493 events were recorded, with a resolution of one second over a period of 3,133 days. An average of 10.3 events occur per edge. We determine the interevent time distribution by taking the subset of edges observing more than one event, of which there are 70,902. The mean interevent time is then calculated to be 〈τ〉 = 16.6 days, with standard deviation στ = 76.5 days. This yields a coefficient of variation στ/〈τ〉 = 4.61.
Data availability
The data that support the findings of this study are openly available through direct request to the authors of original publications.
Code availability
The code that supports the findings of this study is available upon request from the corresponding authors.
References
Holme, P. & Saramäki, J. Temporal networks. Phys. Rep. 519, 97–125 (2012).
Masuda, N. & Lambiotte, R. A Guide to Temporal Networks (World Scientific, 2016).
Holme, P. Modern temporal network theory: a colloquium. Eur. Phys. J. B 88, 234 (2015).
Barabási, A.-L. The origin of bursts and heavy tails in human dynamics. Nature 435, 207 (2005).
Goh, K.-I. & Barabási, A.-L. Burstiness and memory in complex systems. EPL 81, 48002 (2008).
Karsai, M., Kaski, K., Barabási, A.-L. & Kertész, J. Universal features of correlated bursty behaviour. Sci. Rep. 2, 1–7 (2012).
Davidsen, J. & Kwiatek, G. Earthquake interevent time distribution for induced micro-, nano-, and picoseismicity. Phys. Rev. Lett. 110, 068501 (2013).
de Arcangelis, L., Godano, C., Lippiello, E. & Nicodemi, M. Universality in solar flare and earthquake occurrence. Phys. Rev. Lett. 96, 051102 (2006).
Turnbull, L., Dian, E. & Gross, G. The string method of burst identification in neuronal spike trains. J. Neurosci. Methods 145, 23–35 (2005).
Karsai, M., Jo, H.-H. & Kaski, K. Bursty Human Dynamics (Springer, 2018).
Karsai, M. et al. Small but slow world: how network topology and burstiness slow down spreading. Phys. Rev. E 83, 025102 (2011).
Lambiotte, R., Tabourier, L. & Delvenne, J.-C. Burstiness and spreading on temporal networks. Eur. Phys. J. B 86, 320 (2013).
Jo, H.-H., Perotti, J. I., Kaski, K. & Kertész, J. Analytically solvable model of spreading dynamics with non-Poissonian processes. Phys. Rev. X 4, 011041 (2014).
Horváth, D. X. & Kertész, J. Spreading dynamics on networks: the role of burstiness, topology and non-stationarity. N. J. Phys. 16, 073037 (2014).
Williams, O. E., Lillo, F. & Latora, V. Effects of memory on spreading processes in non-Markovian temporal networks. N. J. Phys. 21, 043028 (2019).
Vazquez, A., Rácz, B., Lukács, A. & Barabási, A.-L. Impact of non-Poissonian activity patterns on spreading processes. Phys. Rev. Lett. 98, 158702 (2007).
Mancastroppa, M., Vezzani, A., Muñoz, M. A. & Burioni, R. Burstiness in activity-driven networks and the epidemic threshold. J. Stat. Mech. 2019, 053502 (2019).
Pastor-Satorras, R., Castellano, C., Van Mieghem, P. & Vespignani, A. Epidemic processes in complex networks. Rev. Mod. Phys. 87, 925–979 (2015).
Vespignani, A. et al. Modelling COVID-19. Nat. Rev. Phys. 2, 279–281 (2020).
Starnini, M., Gleeson, J. P. & Boguñá, M. Equivalence between non-Markovian and Markovian dynamics in epidemic spreading processes. Phys. Rev. Lett. 118, 128301 (2017).
Liu, S., Perra, N., Karsai, M. & Vespignani, A. Controlling contagion processes in activity driven networks. Phys. Rev. Lett. 112, 118702 (2014).
Masuda, N. & Holme, P. Temporal Network Epidemiology (Springer, 2017).
Masuda, N. & Holme, P. Small inter-event times govern epidemic spreading on networks. Phys. Rev. Res. 2, 023163 (2020).
Miritello, G., Moro, E. & Lara, R. Dynamical strength of social ties in information spreading. Phys. Rev. E 83, 045102 (2011).
Hiraoka, T. & Jo, H.-H. Correlated bursts in temporal networks slow down spreading. Sci. Rep. 8, 1–12 (2018).
Min, B., Goh, K.-I. & Vazquez, A. Spreading dynamics following bursty human activity patterns. Phys. Rev. E 83, 036102 (2011).
Rocha, L. E., Liljeros, F. & Holme, P. Simulated epidemics in an empirical spatiotemporal network of 50,185 sexual contacts. PLoS Comput. Biol. 7, e1001109 (2011).
Iribarren, J. L. & Moro, E. Branching dynamics of viral information spreading. Phys. Rev. E 84, 046116 (2011).
Granovetter, M. Threshold models of collective behavior. Am. J. Sociol. 83, 1420–1443 (1978).
Karsai, M., Iñiguez, G., Kikas, R., Kaski, K. & Kertész, J. Local cascades induced global contagion: how heterogeneous thresholds, exogenous effects, and unconcerned behaviour govern online adoption spreading. Sci. Rep. 6, 27178 (2016).
Watts, D. J. A simple model of global cascades on random networks. Proc. Natl Acad. Sci. USA 99, 5766–5771 (2002).
Gleeson, J. P. Cascades on correlated and modular random networks. Phys. Rev. E 77, 046117 (2008).
Unicomb, S., Iñiguez, G. & Karsai, M. Threshold driven contagion on weighted networks. Sci. Rep. 8, 3094 (2018).
Unicomb, S., Iñiguez, G., Kertész, J. & Karsai, M. Reentrant phase transitions in threshold driven contagion on multiplex networks. Phys. Rev. E 100, 040301 (2019).
Karimi, F. & Holme, P. Threshold model of cascades in empirical temporal networks. Phys. A 392, 3476–3483 (2013).
Karimi, F. & Holme, P. A temporal network version of Watts’s cascade model. In Holme, P. & Saramäki, J. (eds.) Temporal Networks, 315–329 (Springer Berlin Heidelberg, 2013).
Takaguchi, T., Masuda, N. & Holme, P. Bursty communication patterns facilitate spreading in a threshold-based epidemic dynamics. PLoS ONE 8, e68629 (2013).
Backlund, V.-P., Saramäki, J. & Pan, R. K. Effects of temporal correlations on cascades: threshold models on temporal networks. Phys. Rev. E 89, 062815 (2014).
Terranova, T. Attention, economy and the brain. Culture Machine 13 (2012).
Lerman, K. Information is not a virus, and other consequences of human cognitive limits. Future Internet 8, 21 (2016).
Bayer, J. B., Ellison, N. B., Schoenebeck, S. Y. & Falk, E. B. Sharing the small moments: ephemeral social interaction on snapchat. Inf., Commun. Soc. 19, 956–977 (2016).
Shein, E. Ephemeral data. Commun. ACM 56, 20–22 (2013).
Vázquez, A. et al. Modeling bursts and heavy tails in human dynamics. Phys. Rev. E 73, 036127 (2006).
Whitt, W. Approximating a point process by a renewal process, I: two basic methods. Oper. Res. 30, 125–147 (1982).
Centola, D. & Macy, M. Complex contagions and the weakness of long ties. Am. J. Soc. 113, 702–734 (2007).
Valdano, E., Ferreri, L., Poletto, C. & Colizza, V. Analytical computation of the epidemic threshold on temporal networks. Phys. Rev. X 5, 021005 (2015).
Yağan, O. & Gligor, V. Analysis of complex contagions in random multiplex networks. Phys. Rev. E 86, 036103 (2012).
Gerstner, W., Kistler, W. M., Naud, R. & Paninski, L. Neuronal Dynamics: from Single Neurons to Networks and Models of Cognition (Cambridge University Press, 2014).
Iyer, R., Menon, V., Buice, M., Koch, C. & Mihalas, S. The influence of synaptic weight distribution on neuronal population dynamics. PLoS Comput. Biol. 9, e1003248 (2013).
Gleeson, J. P. High-accuracy approximation of binary-state dynamics on networks. Phys. Rev. Lett. 107, 068701 (2011).
Jiang, Z.-Q. et al. Calling patterns in human communication dynamics. Proc. Natl. Acad. Sci. USA 110, 1600–1605 (2013).
Sorribes, A., Armendariz, B. G., Lopez-Pigozzi, D., Murga, C. & de Polavieja, G. G. The origin of behavioral bursts in decision-making circuitry. PLoS Comput. Biol. 7, e1002075 (2011).
Newman, M. E. Random graphs with clustering. Phys. Rev. Lett. 103, 058701 (2009).
Watts, D. J. & Strogatz, S. H. Collective dynamics of ‘small-world’ networks. Nature 393, 440 (1998).
Hiraoka, T., Masuda, N., Li, A. & Jo, H.-H. Modeling temporal networks with bursty activity patterns of nodes and links. Phys. Rev. Res. 2, 023073 (2020).
Lawless, J. F. Inference in the generalized gamma and log gamma distributions. Technometrics 22, 409–419 (1980).
Saramäki, J. & Holme, P. Exploring temporal networks with greedy walks. Eur. Phys. J. B 88, 334 (2015).
Eckmann, J.-P., Moses, E. & Sergi, D. Entropy of dialogues creates coherent structures in e-mail traffic. Proc. Natl Acad. Sci. USA 101, 14333–14337 (2004).
Karimi, F., Ramenzoni, V. C. & Holme, P. Structural differences between open and direct communication in an online community. Phys. A 414, 263–273 (2014).
Acknowledgements
S.U. acknowledges the Pôle Scientifique de Modélisation Numérique from ENS Lyon for their computing support, and Loïs Taulelle for valuable technical advice. G.I. acknowledges support by the European Commission through H2020 projects HumanE AI (G.A. no. 761758) and HumanE AI Net (G.A. no. 952026), and from the Air Force Office of Scientific Research under award number FA8655-20-1-7020. J.P.G. is supported by Science Foundation Ireland (grant numbers 16/IA/4470, 16/RC/3918, 12/RC/2289 P2, and 18/CRT/6049) with co-funding from the European Regional Development Fund. M.K. is supported by the DataRedux (ANR-19-CE46-0008) and SoSweet (ANR-15-CE38-0011) projects funded by ANR and the SoBigData++ (H2020-871042) project. We are grateful to Petter Holme and Jean-Pierre Eckmann for providing access to the forum and email data sets. We acknowledge the Department of Computer Science at Aalto University for access to their data repository.
Author information
Authors and Affiliations
Contributions
S.U. derived the master equation solution, performed related calculations, and designed the numerical experiments. S.U., G.I., J.P.G. and M.K. discussed the results and wrote the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Peer review information Nature Communications thanks the anonymous reviewers for their contribution to the peer review of this work. Peer reviewer reports are available.
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Unicomb, S., Iñiguez, G., Gleeson, J.P. et al. Dynamics of cascades on burstiness-controlled temporal networks. Nat Commun 12, 133 (2021). https://doi.org/10.1038/s41467-020-20398-4
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-020-20398-4
This article is cited by
-
Dynamics of collective cooperation under personalised strategy updates
Nature Communications (2024)
-
Constructing temporal networks with bursty activity patterns
Nature Communications (2023)
-
Temporal-topological properties of higher-order evolving networks
Scientific Reports (2023)
-
Dynamics of diffusion on monoplex and multiplex networks: a message-passing approach
Economic Theory (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.