Abstract
The fate of subducted CO2 remains the subject of widespread disagreement, with different models predicting either wholesale (up to 99%) decarbonation of the subducting slab or extremely limited carbon loss and, consequently, massive deep subduction of CO2. The fluid history of subducted rocks lies at the heart of this debate: rocks that experience significant infiltration by a water-bearing fluid may release orders of magnitude more CO2 than rocks that are metamorphosed in a closed chemical system. Numerical models make a wide range of predictions regarding water mobility, and further progress has been limited by a lack of direct observations. Here we present a comprehensive field-based study of decarbonation efficiency in a subducting slab (Cyclades, Greece), and show that ~40% to ~65% of the CO2 in subducting crust is released via metamorphic decarbonation reactions at forearc depths. This result precludes extensive deep subduction of most CO2 and suggests that the mantle has become more depleted in carbon over geologic time.
Similar content being viewed by others
Introduction
Subduction of oceanic lithosphere is arguably the most important process in global geochemical cycling. Subduction delivers material from Earth’s surface into the deep mantle, but chemical reactions in the subducting slab can also release volatiles which ultimately return to the atmosphere1,2,3. There is, however, a long-standing debate surrounding the fate of subducted CO2. Recent papers have argued that the vast majority of oceanic carbon is deeply subducted4 or that the vast majority is released by subarc depths2.
Carbon dioxide is released during metamorphism when a carbonate mineral such as aragonite or dolomite breaks down via prograde decarbonation reactions5. A model reaction is 2 Quartz + 3 Dolomite + 2 Albite + H2O = 3 Aragonite + Glaucophane + 3 CO2. For decades, thermodynamic models of subducted rocks have been used to estimate the degree of carbon loss6,7,8,9,10. However, the modeling results vary widely, due mostly to uncertainties on the nature of aqueous fluid infiltration into subducting rocks. Closed-system models predict evolution under relatively water-poor conditions6,7, whereas models that consider open-system fluid infiltration allow for more water-rich environments8,9,10. The presence of a water-bearing fluid has a profound effect on carbonate stability, decreasing reaction temperatures by as much as hundreds of Kelvin11. Thus, it is essential to constrain the nature and extent of fluid infiltration to estimate the resultant CO2 release.
Given a lack of observational constraints, models predict that anywhere from ~0.0001 to 52 Megatons of oceanic carbon will be deeply subducted annually2. These large uncertainties in our current understanding of CO2 subduction leave basic questions about global geochemical cycling unanswered. For example, has the deep Earth become depleted or enriched in carbon over geologic time? To what extent might enhanced carbonate subduction add CO2 to Earth’s atmosphere? Providing answers to such questions requires a new constraint on the fate of subducted CO2.
Here, we provide an extensive field-based record of decarbonation efficiency in a subducted slab. We combine detailed observations, stable isotope measurements, and bulk chemical analysis with thermodynamic modeling to show that subducted rocks from the Cycladic Blueschist Unit in Greece underwent major fluid infiltration and decarbonation. Our results show that at least ~40%, and more likely ~65%, of the CO2 in the typical subducting oceanic crust is released at forearc depths by decarbonation reactions. Other processes, such as stoichiometric carbonate dissolution4, would add to the total. Whether the released carbon is ultimately stored in the overriding lithosphere or delivered to Earth’s atmosphere, much of it is not returned to the deep mantle, which, as a consequence, has likely become more depleted in carbon over geologic time.
Results
Geologic background
The Cycladic Blueschist Unit (CBU) in Greece is an ideal field area to test existing models of subduction zone decarbonation. It was metamorphosed in the Eocene when the African plate subducted northward beneath Eurasia12,13,14. Rocks reached peak temperatures (T) of ~500 to ~550 °C and peak pressures (P) of ~1.5 to 2.0 GPa15,16,17,18. Preservation of subduction-related features in the CBU is superlative—Syros Island in particular is home to one of the best-preserved and most thoroughly studied subduction complexes on Earth. Apart from its exceptional preservation, the CBU represents a normal subduction complex, with multiple studies using observations of the CBU for inferences about subduction in general19,20,21,22,23.
We collected more than 600 hand samples of carbonate-bearing rocks from the islands of Syros and Tinos (see “Methods”; Supplementary Fig. 1). These can be broadly categorized in four groups according to their protolith: carbonate-bearing siliciclastic rocks, limestones, heavily altered basaltic volcanics, and more lightly altered basaltic oceanic crust. Of these, 211 were selected for carbon and oxygen isotope analysis. A subset of 56 representative rocks underwent detailed geochemical analysis including major, minor, and trace element chemistry (Supplementary Data 1) and thermodynamic modeling (see “Methods”; Supplementary Table 1). These rocks were selected as the best-preserved representatives of the breadth of lithologies in the CBU, with no evidence of appreciable metamorphic retrogression during exhumation.
Estimating CO2 loss
Samples preserve their mineralogy, and therefore mineral-bound CO2 content, from peak P–T conditions. In order to estimate the fraction of carbon released by each sample (∆CO2), we compare its modern CO2 content to its composition before major metamorphic devolatilization began. The modern CO2 content is easily measured (see “Methods”), but the initial volatile content is not directly preserved. Thus we need a technique to determine how much CO2 was in each rock prior to metamorphic decarbonation.
A new modeling approach is used to backproject this initial volatile content for each sample. We calculate the phase equilibria for each rock with a CO2-bearing fluid present in excess at lower grade P–T conditions (310 °C and 0.8–1.0 GPa) consistent with estimates of the prograde P–T path on Syros16 and warm subduction in general24,25. The initial back-projected composition is then taken as the composition of the solid minerals at these lower P–T conditions. In most samples, the modeled CO2 content is insensitive to changes in P, T, or fluid mole fraction of CO2 (\(X_{{\mathrm{CO}}_{2}}\)) in this lower P–T range. For ten samples that do show significant variation, we select the minimum plausible initial CO2 content, ensuring that our estimated results for ∆CO2 are also minima and, thus, are conservative (see “Methods”; Supplementary Fig. 3).
The back-projection method requires only three assumptions. (1) Rocks were in equilibrium with a CO2-bearing fluid (regardless of its \(X_{{\mathrm{CO}}_{2}}\)) at lower P–T conditions. (2) Rocks that contained carbonate at peak P–T contained an equal or greater mass of carbonate prior to metamorphism. (3) Rocks did not undergo major element metasomatism other than volatile loss. The most likely metasomatic process is stoichiometric carbonate dissolution26 which would add to the total CO2 released. Thus, once again, our estimates for ∆CO2 are conservative.
Forward modeling metamorphism
With this initial composition, forward modeling is performed for two end-member scenarios: (1) a fully closed system6,7 and (2) a system open to fluid infiltration, approximated with a fixed-\(X_{{\mathrm{CO}}_{2}}\) fluid in excess27 (see “Methods”). Fully closed-system models are run at peak P–T conditions (525 °C and 1.5 GPa) to estimate the resulting rock and fluid compositions. Fluid-infiltrated models use observations of the mineral assemblage in each sample (see “Methods”; Supplementary Table 1) in combination with calculated pressure–activity of CO2 diagrams to constrain the equilibrium fluid composition (\(X_{{\mathrm{CO}}_{2}}\)) recorded by each sample at peak P–T.
Furthermore, we estimate the maximum plausible CO2 loss for each sample. The mineral assemblage is calculated at peak conditions with a very water-rich (\(X_{{\mathrm{CO}}_{2}}\) = 0.0001) fluid in excess. The CO2 content of this assemblage is then compared to the back-projected wt% CO2 to calculate the potential (or maximum) ∆CO2 of each sample.
Using higher P–T values of 550 °C and 2.0 GPa does not impact our conclusions (see below).
Evidence for fluid infiltration
The equilibrium fluid compositions required by rock mineralogy are consistently water-rich. Figure 1 shows the maximum activity of CO2 (\(a_{{\mathrm{CO}}_{2}}\)) recorded by each sample. In nearly all cases, the mineralogy requires low-CO2 (i.e., water-rich) conditions (\(a_{{\mathrm{CO}}_{2}}\) = 0.06 ± 0.07 2σ standard deviation). Because CO2–H2O mixing is highly nonideal at subduction zone conditions, this corresponds to an even lower \(X_{{\mathrm{CO}}_{2}}\), averaging ~0.006. Two outliers are excluded from the above statistics because they contain very simple mineral assemblages that offer almost no constraints on the equilibrium fluid compositions (0 < \(a_{{\mathrm{CO}}_{2}}\) < 0.95).
Blue squares show maximum possible fluid CO2 activity of each sample. The equivalent \(X_{{\mathrm{CO}}_{2}}\) is shown on the right axis. Note the nonlinear relationship between activity of CO2 and \(X_{{\mathrm{CO}}_{2}}\). Red circles are CO2 activities achieved in a closed system. The vast majority of samples record water-rich fluids, inconsistent with evolution in a closed system. Two samples are unconstrained, with any CO2 activity < ~0.95 being plausible (blue arrows). The shaded area shows the 2σ standard deviation range of equilibrium activity values (0.06 ± 0.07), excluding the two unconstrained outliers.
In contrast, closed-system modeling of these samples systematically predicts fluid compositions that are clearly richer in CO2 (Fig. 1). This demonstrates that the water-rich conditions recorded by most of the rocks could not be achieved through evolution in a closed system, and therefore required open-system infiltration of a water-bearing fluid.
Carbon and oxygen isotope data show a wide range of values from δ13CVPDB = −4.9 to +3.7 ‰ and δ18OVSMOW = +10.1 to +30.8 ‰ (Fig. 2). While many of these samples lie within the range expected for seafloor carbonates (δ13CVPDB = ~+1 to +4 ‰ and δ18OVSMOW = ~+26 to +31 ‰)28, most (>70%) record significantly lighter C and O isotope signatures.
Some of the variations in δ18O may result from the prograde exchange with local silicates29, but very low δ18O must be attributed to external fluid infiltration26, perhaps up-temperature fluid flow in particular30. Low δ13C values may indicate the presence of reduced carbon, isotope fractionation as a result of high degrees of decarbonation31, or infiltration by a low δ13C fluid.
Dewatering of subducted serpentinite or other hydrated lithologies (e.g., metasediments) is expected to release substantial water9,32,33; we conclude that this is the most likely source of the water-bearing fluid which eventually traveled into the carbonate rocks, perhaps as part of a channelized flow system34, altering isotopic compositions and phase equilibria.
Decarbonation efficiency
Rocks record a wide array of observed decarbonation (∆CO2) values, ranging from 0 to 91% CO2 loss by mass (Fig. 3a). Importantly, these values do not depend on the \(X_{{\mathrm{CO}}_{2}}\) estimates. The data define a consistent trend: very pure marbles starting with ~40 wt% CO2 released little to no CO2 while more carbonate-poor rocks, particularly mixed carbonate-siliciclastic metasediments, underwent extensive decarbonation. The potential decarbonation values for the same samples range from 0 to 100% CO2 loss. In terms of the mass of CO2 produced, both the observed and potential datasets show a peaked distribution (Fig. 3b), with intermediate-composition rocks (whether metasedimentary or metavolcanic) releasing the greatest mass of CO2. Conversely, nearly pure limestone and relatively carbonate-poor altered oceanic crust release an appreciably smaller mass of CO2.
Blue symbols show the observed CO2 loss of each sample whereas green symbols show the maximum potential CO2 loss as a function of initial wt% CO2. a Percent of CO2 released. Nearly pure carbonate rocks degas the smallest proportion of CO2. b The kg CO2 released per kg rock. This shows a peaked distribution, with intermediate-CO2-content rocks degassing the greatest mass of CO2 in both observed and potential datasets.
The results shown in Fig. 3 comprise a comprehensive field-based record of decarbonation efficiency in subducted lithologies. One implication for global carbon cycling is that the degree of decarbonation varies markedly from one rock type to the next. Thus, two subduction zones that subduct an identical mass of CO2 per year could have dramatically different CO2 fluxes off the slab, depending on whether CO2 is hosted in, for instance, pure limestones or heavily altered volcanics. For this reason, phase equilibria modeling of decarbonation of a composite or average rock composition6,7,8 is unlikely to illuminate the full spectrum of devolatilization behavior during subduction. It is essential to know the local chemical environment of subducted carbon to predict whether it is devolatilized or retained within the slab.
Global carbon mobility
Using this record of major, but variable, metamorphic decarbonation, we can consider the efficiency of carbonate subduction in individual modern or ancient subduction zones or the Earth system as a whole. For example, we calculate the proportion of CO2 released from a fictive slab that is roughly equivalent to the global average subducting crust, with 25 m of carbonate-bearing siliciclastics, 25 m of limestone, 50 m of heavily altered volcanics, and 200 m of lightly altered oceanic crust. This gives a global input of CO2 into subduction zones of 5.08 Tmol CO2 yr−1, well within the range of lower and upper bounds from refs. 2,3.
The global average flux from subducting slabs, F, can then be expressed according to Eq. (1):
where z is depth, \(C_{{\mathrm{CO}}_{2}}\) is the initial concentration of CO2, L is the global trench length, R is the global average convergence rate, and ρ is rock density. For this global average crust, we find F = 2.06 Tmol CO2 yr−1, corresponding to ~40% CO2 loss. As the rocks of the CBU record maximum depths of ~50 to ~70 km, this flux of CO2 is generated in the forearc region.
Pulsed decarbonation
We also consider where along the subduction path this CO2 was devolatilized. We forward model CO2 loss in three representative samples for each of the four general lithologies for a total of 12 detailed forward models. Models are calculated along two linear P–T paths spanning the range of possible metamorphic conditions on Syros and Tinos. The modeling differs considerably from previous approaches in that it is constrained by the fluid compositions and decarbonation extent recorded by natural subducted samples (see “Methods”). This allows us to calculate (1) the P–T conditions at which decarbonation occurred, (2) the rate of CO2 release, and (3) how decarbonation may have proceeded if the rocks had continued to subduct. Using the same global average crustal stack, we generate curves showing the percentage of the initial CO2 released at each P–T step with a 20 °C moving mean (Fig. 4).
a The percentage of CO2 degassed along two linear P–T paths. Both paths begin at 310 °C and 1.0 GPa; path A continues through peak field conditions of 525 °C and 1.5 GPa, while path B passes through 550 °C and 2.0 GPa. Paths A and B end at 650 °C and 1.8 or 2.4 GPa, respectively. A sharp pulse of decarbonation is seen around peak-T conditions. b The constructed moles of CO2 subducting globally and the amount of CO2 released at both peak conditions (observed) and up to 650 °C (observed + modeled). The arc volcanic CO2 flux1 is shown for reference.
A sharp pulse of decarbonation is seen near the observed maximum P–T conditions (Fig. 4a), with relatively little carbon loss before or after this pulse. This is true for both the hotter and colder P–T paths, with the colder model predicting CO2 release of approximately the same magnitude, just at greater depth. Thus our results suggest that, for rocks to undergo the ~40% decarbonation which we observe, most of the CO2 would need to be devolatilized in a pulse around ~500–550 °C.
This is new field-based evidence for pulsed decarbonation, which had previously been predicted with a purely modeling-driven approach8. Furthermore, by extending these models beyond the observed P–T conditions, we predict that the rocks would have lost an additional ~25 to 30% of their initial CO2 had they continued to subduct to 650 °C and 1.8 to 2.4 GPa, conditions still representing forearc depths.
There is an intriguing coincidence between the location of this pulse and peak P–T conditions. This is not an artifact of our model but rather suggests that there may be some link between devolatilization, exhumation processes, and/or kinetic preservation of the observed mineralogy. Further work is needed to determine whether a similar coincidence can be observed in other exhumed slabs.
Heterogeneous subduction of carbon
Because the proportion of CO2 devolatilized is heavily dependent on the subducting lithologies, we expect the degree of decarbonation to vary markedly from one subduction zone to another. As an example, we calculate the CO2 loss for two end-member modern subduction zones: Central America and Tonga. The subducting material beneath Central America is dominated by relatively pure CaCO3 limestones atop young (~23 Ma) altered oceanic crust. Assuming a crustal stack with 250 m of limestone (a rough approximation of the sediments recorded at DSDP site 495)35, and 100 m of lightly altered oceanic crust, we predict only ~6% CO2 loss by 550 °C, much less than the global average of ~40%. Tonga represents the other extreme, with essentially no carbonate-bearing sediments, and nearly all subducted CO2 hosted in lightly altered oceanic crust36. We would, therefore, predict that metamorphic reactions would release ~45% of the rock’s CO2 at comparable conditions. The differences become even more pronounced in the projection to 650 °C, where Central American and Tongan subducted lithologies are predicted to have undergone ~10% and ~95% decarbonation, respectively. These results are fully consistent with those predicted on a conceptual basis by ref. 3.
Discussion
Rocks of the CBU record a robust and consistent record of substantial aqueous fluid infiltration which drove metamorphic decarbonation. The CO2 loss ranges considerably, but systematically, across rocks of different compositions. Assuming lithologic proportions representing average oceanic crust and sediments, these rocks record that ~40% of subducted CO2 was released. Forward modeling predicts an additional ~25% CO2 loss into the forearc, with most decarbonation concentrated in a sharp peak.
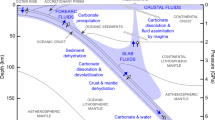
This leaves ~35% of the initial CO2 in the slab to travel to subarc depths and, perhaps, beyond (Fig. 5). As noted above, this global average is not necessarily representative of any specific subduction zone, with subduction beneath Central America or Tonga expected to deliver 90% or 5% of crustal CO2 to the subarc, respectively.
This schematic representation shows the ~40% CO2 loss recorded in the field and the total predicted 65% CO2 loss by 650 °C in the forearc; most decarbonation is concentrated in a sharp peak at ~500–550 °C. The remaining ~35% of subducted CO2 in the slab continues to greater depths where it could be released by processes such as dissolution or melting, or retained in the slab past the subarc. Global estimates are based on observations from the Cycladic Blueschist Unit.
Other processes such as melting37 or diapirsm38 could add to the amount of CO2 released. In particular, our approach does not quantify carbonate dissolution26,39, which was likely only beginning at the depths reached by the CBU, and could have been much more extensive at greater depths26. Slab dehydration continues well into the subarc40, providing the fluids needed to drive dissolution and melting processes.
It is important to consider how well the CBU represents subduction in general. Indeed, it has been suggested that the entire global suite of exhumed subduction complexes may be anomalously warm relative to average subduction25,41. The CBU is, in this sense, certainly not representative of thermal conditions in all subduction zones. Nevertheless, we find that a similar degree of decarbonation is achieved along differing P–T paths (Fig. 4); CO2 release is simply delayed to greater depths along a colder geotherm. Thus we expect that colder or hotter subduction zone paths will result in similar total degrees of decarbonation, provided only that a water-bearing fluid is present.
Once released, the fate of devolatilized CO2 is uncertain. A substantial proportion may be stored in the lithospheric mantle of the overriding plate; the mass of CO2 release we calculate is greater than most estimates of the CO2 flux from arc systems into Earth’s atmosphere. This is consistent with recent evidence for major carbonate precipitation in forearc lithosphere through both surface measurements42 and observation of carbonated ultramafic lithologies from the slab or mantle wedge43,44. In fact, a deep lithospheric CO2 reservoir may be required to reconcile our results with global mass-balance arguments4. On the other hand, some CO2 will escape to Earth’s atmosphere as part of a diffuse CO2 flux and/or by contributing to arc volcanic CO2 emissions2.
The strong compositional dependence of decarbonation suggests the proportion of CO2 release will vary across space and time depending upon what rocks are being subducted. While the thermal structure of a given subduction zone will control the depth at which these decarbonation reactions occur, we predict that the same total degree of CO2 loss may be expected over a wide range of P–T paths—the caveat being that fluid infiltration is essential to drive decarbonation, thus variability in fluid mobility across different subduction regimes may result in very different degrees of decarbonation.
We predict a relatively small proportion of CO2—a maximum of ~35% globally—will be retained in the slab past forearc depths. Thus, subduction is inefficient at returning CO2 to the mantle: our model predicts less than ~2 Tmol CO2 yr−1 is subducted past the forearc. This is comparable to the amount released by arc volcanism annually1, but whether it is the source of arc CO2 is an outstanding open question. Decarbonation reactions would be unable to release this CO2 in the subarc (Fig. 4), which means that other processes, such as sediment melting, congruent dissolution, or diapirism, would have to operate there. In addition, mantle corner flow could, perhaps, transport carbonated forearc mantle into the subarc melting region8. Consequently, we do not consider evidence of slab-derived CO2 in volcanic arcs45, to be at odds with our observations.
Regardless of whether the ~2 Tmol CO2 yr−1 is released by arcs or subducted deeper into the mantle, it is far less than recent estimates of mantle-derived CO2 outgassing, totaling ~5 to ~7 Tmol CO2 yr−1 3. Therefore, CO2 fluxes into and out of Earth’s convecting mantle appear out of balance on the modern Earth. If this imbalance has persisted on long timescales, we posit that the deep mantle has been progressively depleted in carbon through Earth history, and it may lose more CO2 as the evolution of our planet continues46. In the very distant future, a CO2-starved mantle would supply minimal CO2 to the atmosphere via mid-ocean-ridge or intraplate volcanism, possibly resulting in the eventual cooling of the surface environment.
Methods
Sample collection and preparation
The locations of 217 samples selected for isotopic and/or chemical analysis are shown in Supplementary Fig. 147,48,49,50,51.
We avoid samples from the center of Syros island as they are subject to higher degrees of weathering and retrogression. Thin sections were prepared in the Yale University Department of Earth and Planetary Sciences and viewed on a Leitz Sm-Lux-Pol petrographic microscope. Samples for bulk chemical analysis were cut with a diamond rock saw to remove weathering rinds and joint surfaces, abraded using SiC paper and ultrasonicated in distilled deionized water prior to crushing. Powders for isotope analysis were extracted with a dental drill equipped with a 5-mm diamond-tipped drill bit.
Chemical measurement and data reduction
Samples were analyzed for major elements via X-ray fluorescence on borate fused discs at SGS laboratories in Lakefield, Ontario, Canada. Minor elements were measured via X-ray fluorescence of pressed pellets. The full set of chemical measurements is available in Supplementary Data 1.
Major element oxide weight percentages were converted to moles element for input into thermodynamic modeling software. Loss-on-ignition (LOI) was corrected for ferric iron with Fe3+/Fetotal ranging from 0 to 0.15 based on modal mineralogy.
This corrected LOI was then converted to weight percent CO2 and H2O with results from point-counting of representative thin sections. Samples were point-counted in detail to constrain wt% H2O, and the remaining LOI was assumed to be CO2 (i.e., wt% CO2 = wt% LOIcorrected ‒ wt% H2O). For heavily altered volcanics and lightly altered oceanic crust (samples with relatively low LOI where wt% H2O might have a large effect), every sample was point-counted. For carbonate-bearing siliciclastics and limestones, three representative samples of each type were point-counted. These results were extrapolated to the remaining samples of that type assuming a linear relationship between wt% H2O and wt% LOI within each sample group such that:
where slimestone = −0.0319 ± 0.0044, blimestone = 1.41 ± 0.17, sclastic = −0.1159 ± 0.1171, and bclastic = 3.39 ± 1.85 (all errors 2σ standard deviation).
Note that the entire range of water contents is fairly small (0.01–3.8 wt% H2O) compared to wt% CO2 (1.5–43.8) (Supplementary Data 1). Taking each sample’s water content as the highest or lowest possible value from its lithologic group would not have a significant effect on any of our results or conclusions.
Rocks were sorted into four categories based on their protolith: heavily altered volcanics, lightly altered oceanic crust, carbonate-bearing siliciclastics, and limestones. Samples with SiO2 < 20 wt% were categorized as limestones. Carbonate-bearing siliciclastic rocks were differentiated from the meta-igneous suites based on observations of mineralogy (high abundance of micas being a particular feature of metasediments) and field context, with visible continuous compositional layering in a cohesive section indicating metasedimentary origin. Heavily altered volcanics were differentiated from lightly altered basaltic crust based on the degree of observed and back-projected carbonation, with lightly altered samples having initial CO2 < 10 wt%.
Stable isotopes
Carbon and oxygen stable isotopes were analyzed in the Yale Analytical and Stable Isotope Center on either a Thermo MAT 253 KIEL IV with carbonate device or Thermo DeltaPlus XP Stable Isotope Ratio mass spectrometer with a Thermo Gasbench II interface. Consistency between the two methods was ensured via analysis of in-house standards and repeat analysis of a subset of samples. Precision is better than ± 0.1 per mille (1σ).
Carbon and oxygen isotope values are reported in δ notation relative to Vienna Pee Dee Belemnite (V-PDB) and Vienna Standard Mean Ocean Water (V-SMOW), respectively. (Fig. 2 and Supplementary Data 2). Isotope measurements represent a composite of the composition of all carbonate minerals in the sample. In most cases, this is only calcite (pseudomorphous after aragonite), but may include dolomite.
Thermodynamic modeling
Thermodynamic calculations (including \({\mathrm{P}}{\hbox{-}}a_{{\mathrm{CO}}_{2}}\) diagrams and P–T pseudosections) were performed in the system Na2O–CaO–K2O–FeO–Fe2O3–MgO–MnO–Al2O3–SiO2–CO2–H2O–TiO2 using the Theriak-Domino software package52 with code as in ref. 53 and the database of ref. 54. Mineral and fluid activity models55,56,57,58,59 are given in Supplementary Table 1. The equations of state for H2O and CO2 are from ref. 60, while remaining fluid endmembers are from ref. 61. Additions to the default database file for full COH fluid mixing are also given in Supplementary Data 3.
Back projection
The initial volatile content of each sample is calculated as described in the main text at low-grade P–T conditions of 310 °C and 0.8–1.0 GPa. These conditions are consistent with estimates of the prograde P–T path for the CBU16; critically, they are cold enough that the rock would have undergone little to no metamorphic carbon loss at this point62, but warm enough that the thermodynamic mixing models selected for peak P–T are still valid. Temperature-versus-CO2 loss curves calculated over a wide range of fluid compositions converge at this low P–T (Supplementary Fig. 2a, c), indicating that the back-projection procedure is insensitive to the fluid history of the rock.
We calculate the stable minerals in each sample at this lower P–T in a system with fluid in excess; we vary the composition of this fluid from extremely water-rich conditions (X\(_{{\mathrm{CO}}_{2}}\) = 0.0001), to a pure CO2 fluid (\(X_{{\mathrm{CO}}_{2}}\) = 1.0). The back-projected precursor composition is then taken as the composition of the solid minerals at a given set of low-grade P, T, and \(X_{{\mathrm{CO}}_{2}}\) conditions. For example, a modeled precursor that contains 10 moles of aragonite, CaCO3, and 10 moles of dolomite, CaMg(CO3)2, would have 30 moles CO2. Note that the proportions of nonvolatile species (e.g., SiO2, CaO) are fixed to match the modern bulk composition, and only volatile components (CO2 and H2O) are variable.
In all cases, the CO2 content forms a flat or stepped function with broad plateaus as a function of \(X_{{\mathrm{CO}}_{2}}\). In most samples, the modeled CO2 content is nearly constant across the entire range of conditions, insensitive to changes in P, T, or \(X_{{\mathrm{CO}}_{2}}\) (Supplementary Fig. 2d). For the ten samples which do show significant variation, we conservatively select the minimum plausible initial CO2 content, and therefore, minimum ∆CO2 (Supplementary Fig. 2b). We make the reasonable assumption that samples have undergone prograde devolatilization, and therefore determine that back-projected precursor compositions with volatile contents less than the modern rock are not plausible (Supplementary Fig. 2b, d).
We note that the selected low-grade P–T conditions do lie near the H2O−CO2 miscibility gap57,63. However, because the back-projected rock composition is insensitive to the fluid composition (\(X_{{\mathrm{CO}}_{2}}\)), it is also insensitive to the location, presence, or absence of the H2O–CO2 solvus (Supplementary Fig. 2a, c).
Calculating carbon loss
Carbon dioxide loss is calculated through a comparison of the initial and final wt% CO2 for each sample. We normalize to a nonvolatile chemical species (selecting SiO2, though any other major element would yield identical results) such that
where mi is the mass of a species, Ci is the concentration of a species, and ′ and o denote the final and initial rock compositions, respectively26. The ΔCO2observed is calculated with C′i from modern measured samples, whereas ΔCO2potential is calculated with C′i from rock compositions resulting from forward modeling as described in the main text.
Flux calculation
We construct a model crustal stack approximately representative of the global average subducted sediments + crust. The CO2 loss of each lithology type is taken as the average CO2 loss of the corresponding type in our dataset (i.e., ΔCO2 = 0.032 for limestones, 0.51 for carbonate-bearing siliciclastics, 0.69 for heavily altered volcanics, and 0.46 for lightly altered basaltic crust), as is the initial weight fraction of CO2 for each rock type (\(C_{{\mathrm{CO}}_{2}}\) = 0.39 for limestone, 0.19 for carbonate-bearing siliciclastics, 0.16 for heavily altered volcanics, and 0.06 for the altered basaltic crust.) As a weighted average using the unit thickness and densities of 2700 kg m−3 and 3000 kg m−3 for sedimentary and mafic rock types, respectively, the total CO2 loss fraction is 0.41 (or 41%). The total input flux into subduction zones is calculated using these thicknesses and densities in combination with global subduction length (L = 4.45 × 107 m)36 and average convergence rate (R = 0.05 m yr−1)36 to find Eq. (4):
Multiplied by the total CO2 loss fraction, this gives a flux off the slab of 2.06 Tmol CO2 yr−1.
The decarbonation proportions of Central American and Tongan crustal stacks are calculated via an analogous procedure, changing only the thickness of each lithologic unit as specified in the main text. Note that we do not take into account the specific thermal structure of these end-member subduction zones, but this does not have a substantial effect on the total decarbonation predicted by our model (see main text).
Decarbonation along a P–T path
The CO2 loss of average subducting crust is calculated along two linear prograde P–T paths. Both paths begin at 310 °C and 1.0 GPa; the hotter path, path A, passes through ‘peak field conditions’ of 525 °C and 1.5 GPa and proceeds up to 650 °C and 1.8 GPa. Path B passes through peak field conditions at 550 °C and 2.0 GPa, proceeding up to 650 °C and 2.4 GPa. Note that the pressures reached at 650 °C are prescribed by the assumption of a path that is linear in P–T space.
Beginning with the back-projected composition, each sample is forward modeled in a system with a fluid of a prescribed \(X_{{\mathrm{CO}}_{2}}\). The peak equilibrium fluid compositions (ranging from \(X_{{\mathrm{CO}}_{2}}\) = 0.0046–0.0081) are selected such that the rock volatile content and mineralogy predicted at peak pressure and temperature are consistent with observations of each modern sample. The CO2 content of each rock is determined at steps of 1 °C along the prograde P–T paths, passing through the peak field conditions, and continuing up to 650 °C.
Recall that we model 12 representative samples (three from each lithologic group). In nine samples, the fluid composition is fixed at a given \(X_{{\mathrm{CO}}_{2}}\) with fluid in excess. The three samples of lightly altered oceanic crust are treated slightly differently. In the case of these rocks, back projection at \(X_{{\mathrm{CO}}_{2}}\) = ~0.0001 gives plausible initial compositions and, as described above, we select these lowest CO2 compositions to be conservative. However, the observed mineralogy and final volatile content of these rocks require \(X_{{\mathrm{CO}}_{2}}\) closer to ~0.01, thus the fluid composition is allowed to evolve from \(X_{{\mathrm{CO}}_{2}}\) = ~0.0001 to \(X_{{\mathrm{CO}}_{2}}\) = ~0.01 as P and T increase from starting to peak conditions. The other nine samples can achieve the most conservative back-projected CO2 content and the observed modern mineralogy and CO2 content at the same \(X_{{\mathrm{CO}}_{2}}\), so they are modeled with a fixed fluid composition.
Note that each of the 12 samples requires a slightly different fluid composition for the differing P–T paths (A and B) in order to match our observations. That is, the system is underdetermined: given our observations of mineralogy and volatile content and two of the set {P, T, \(X_{{\mathrm{CO}}_{2}}\)}, we can constrain the third parameter. For example, for sample JAGSY-147Y, the fluid composition which matches the observed assemblage would be \(X_{{\mathrm{CO}}_{2}}\) = 0.0073 at 525 °C and 1.5 GPa, whereas at conditions of 550 °C and 2.0 GPa the equilibrium fluid would need to be \(X_{{\mathrm{CO}}_{2}}\) = 0.0056 to produce the same assemblage.
The CO2 content of each selected rock is calculated at steps of 1 °C along both P–T paths. The incremental CO2 released at each P–T step is calculated by difference with the preceding steps. The average mass change of CO2 of each lithologic type is combined with the same unit thicknesses and densities from the global flux calculation to arrive at a weighted average degree of decarbonation for the stack.
The three samples representing each lithology were forced to match the average decarbonation of their whole lithologic group by multiplying by some constant value. These are small corrections, the largest being an adjustment of the CO2 loss fraction of the three representative metamorphosed limestones, multiplying by ~0.7 to correct from 4.5% CO2 loss to the total group average of 3.2%. In this way, the total decarbonation of the crustal section is forced to equal 41% at peak P–T conditions. The same factor is used in the forward modeling to higher P–T conditions: for example, the three metamorphosed limestones average 6.5% decarbonation at 650 °C, which is multiplied by 0.7 to arrive at 4.5% decarbonation for the whole suite of metamorphosed limestones. The correction factors for the three remaining lithologic types are all between 0.95 and 1.05 for both P–T paths. Similarly, the initial average wt% CO2 of each lithologic group is set to match the entire dataset. Supplementary Fig. 4 shows the mass change of the twelve representative samples along each P–T path and the adjusted average mass change for each lithologic group.
Data availability
The authors declare that the data supporting the findings of this study are available within the paper and its supplementary information files.
References
Dasgupta, R. & Hirschmann, M. M. The deep carbon cycle and melting in Earth’s interior. Earth Planet. Sci. Lett. 298, 1–13 (2010).
Kelemen, P. B. & Manning, C. E. Reevaluating carbon fluxes in subduction zones, what goes down, mostly comes up. Proc. Natl Acad. Sci. USA 112, E3997–E4006 (2015).
Plank, T. & Manning, C. E. Subducting carbon. Nature 574, 343–352 (2019).
Hirschmann, M. M. Comparative deep Earth volatile cycles: the case for C recycling from exosphere/mantle fractionation of major (H2O, C, N) volatiles and from H2O/Ce, CO2/Ba, and CO2/Nb exosphere ratios. Earth Planet. Sci. Lett. 502, 262–273 (2018).
Goldschmidt, V. M. Die Gesetze der Gesteinsmetamorphose mit Beispielen aus der Geologie des Südlichen Norwegens (the laws of rock metamorphism with examples from the geology of southern Norway). Norsk Videnskapsselskaps Skrifter I. Matematisk-Naturvidenskapelig Klasse, 22, 1–16 (1912).
Kerrick, D. M. & Connolly, J. A. D. Metamorphic devolatilization of subducted marine sediments and the transport of volatiles into the Earth’s mantle. Nature 411, 293 (2001).
Kerrick, D. M. & Connolly, J. A. D. Metamorphic devolatilization of subducted oceanic metabasalts: implications for seismicity, arc magmatism and volatile recycling. Earth Planet. Sci. Lett. 189, 19–29 (2001).
Gorman, P. J., Kerrick, D. M. & Connolly, J. A. D. Modeling open system metamorphic decarbonation of subducting slabs. Geochem. Geophys. Geosyst. 7, Q04007 (2006).
Gorce, J. S., Caddick, M. J. & Bodnar, R. J. Thermodynamic constraints on carbonate stability and carbon volatility during subduction. Earth Planet. Sci. Lett. 519, 213–222 (2019).
Tian, M., Katz, R. F., Rees Jones, D. W. & May, D. A. Devolatilization of subducting slabs, Part II: volatile fluxes and storage. Geochem. Geophys. Geosyst. 20, 6199–6222 (2019).
Stewart, E. M. et al. Carbonation and decarbonation reactions: implications for planetary habitability. Am. Miner. 104, 1369–1380 (2019).
Jolivet, L. & Brun, J. P. Cenozoic geodynamic evolution of the Aegean. Int. J. Earth Sci. 99, 109–138 (2010).
Ring, U., Glodny, J., Will, T. & Thomson, S. The Hellenic subduction system: high-pressure metamorphism, exhumation, normal faulting, and large-scale extension. Annu. Rev. Earth Planet Sci. 38, 45–76 (2010).
Philippon, M., Brun, J. P. & Gueydan, F. Tectonics of the Syros blueschists (Cyclades, Greece): from subduction to Aegean extension. Tectonics, 30, TC4001 (2011).
Trotet, F., Jolivet, L. & Vidal, O. Tectono-metamorphic evolution of Syros and Sifnos islands (Cyclades, Greece). Tectonophysics 338, 179–206 (2001).
Schumacher, J. C., Brady, J. B., Cheney, J. T. & Tonnsen, R. R. Glaucophane-bearing marbles on Syros, Greece. J. Petrol. 49, 1667–1686 (2008).
Philippon, M., Gueydan, F., Pitra, P. & Brun, J. P. Preservation of subduction‐related prograde deformation in lawsonite pseudomorph‐bearing rocks. J. Metamorph. Geol. 31, 571–583 (2013).
Skelton, A. et al. Preservation of high‐P rocks coupled to rock composition and the absence of metamorphic fluids. J. Metamorph. Geol. 37, 359–381 (2019).
Marschall, H. R. & Schumacher, J. C. Arc magmas sourced from mélange diapirs in subduction zones. Nat. Geosci. 5, 862–867 (2012).
Dragovic, B., Samanta, L. M., Baxter, E. F. & Selverstone, J. Using garnet to constrain the duration and rate of water-releasing metamorphic reactions during subduction: an example from Sifnos, Greece. Chem. Geol. 314, 9–22 (2012).
Dragovic, B., Baxter, E. F. & Caddick, M. J. Pulsed dehydration and garnet growth during subduction revealed by zoned garnet geochronology and thermodynamic modeling, Sifnos, Greece. Earth Planet. Sci. Lett. 413, 111–122 (2015).
Ashley, K. T., Caddick, M. J., Steele‐MacInnis, M. J., Bodnar, R. J. & Dragovic, B. Geothermobarometric history of subduction recorded by quartz inclusions in garnet. Geochem. Geophys. Geosyst. 15, 350–360 (2014).
Miller, D. P., Marschall, H. R. & Schumacher, J. C. Metasomatic formation and petrology of blueschist-facies hybrid rocks from Syros (Greece): implications for reactions at the slab–mantle interface. Lithos 107, 53–67 (2009).
Syracuse, E. M., van Keken, P. E. & Abers, G. A. The global range of subduction zone thermal models. Phys. Earth Planet. Inter. 183, 73–90 (2010).
Penniston-Dorland, S. C., Kohn, M. J. & Manning, C. E. The global range of subduction zone thermal structures from exhumed blueschists and eclogites: rocks are hotter than models. Earth Planet. Sci. Lett. 428, 243–254 (2015).
Ague, J. J. & Nicolescu, S. Carbon dioxide released from subduction zones by fuid-mediated reactions. Nat. Geosci. 7, 355–360 (2014).
Stewart, E. M. & Ague, J. J. Infiltration-driven metamorphism, New England, USA: regional CO2 fluxes and implications for Devonian climate and extinctions. Earth Planet. Sci. Lett. 489, 123–134 (2018).
Veizer, J. et al. 87Sr/86Sr, δ13C and δ18O evolution of Phanerozoic seawater. Chem. Geol. 161, 59–88 (1999).
Epstein, G. S., Bebout, G. E., Angiboust, S. & Agard, P. Scales of fluid-rock interaction and carbon mobility in the deeply underplated and HP-Metamorphosed Schistes Lustrés, Western Alps. Lithos 354, 105229 (2020).
Brovarone, A. V. et al. Intra-slab COH fluid fluxes evidenced by fluid-mediated decarbonation of lawsonite eclogite-facies altered oceanic metabasalts. Lithos 304, 211–229 (2018).
Tracy, R. J., Rye, D. M., Hewitt, D. A. & Schiffries, C. M. Petrologic and stable-isotopic studies of fluid-rock interactions, south-central Connecticut: I. The role of infiltration in producing reaction assemblages in impure marbles. Am. J. Sci. 283, 589–616 (1983).
van Keken, P. E., Hacker, B. R., Syracuse, E. M. & Abers, G. A. Subduction factory: 4. Depth‐dependent flux of H2O from subducting slabs worldwide. J. Geophys. Res. 116, B01401 (2011).
Hacker, B. R. H2O subduction beyond arcs. Geochem. Geophys. Geosyst. 9, GC001707 (2008).
Plümper, O., John, T., Podladchikov, Y. Y., Vrijmoed, J. C. & Scambelluri, M. Fluid escape from subduction zones controlled by channel-forming reactive porosity. Nat. Geosci. 10, 150–156 (2017).
Aubouin, J. et al. Site 495; Cocos Plate, Middle America Trench outer slope. Init. Rep. DSDP 67, 79–141 (1982).
Jarrard, R. D. Subduction fuxes of water, carbon dioxide, chlorine, and potassium. Geochem. Geophys. Geosyst. 4, 8905 (2003).
Poli, S. Carbon mobilized at shallow depths in subduction zones by carbonatitic liquids. Nat. Geosci. 8, 633–636 (2015).
Hacker, B. R., Kelemen, P. B. & Behn, M. D. Differentiation of the continental crust by relamination. Earth Planet. Sci. Lett. 307, 501–516 (2011).
Frezzotti, M. L., Selverstone, J., Sharp, Z. D. & Compagnoni, R. Carbonate dissolution during subduction revealed by diamond-bearing rocks from the Alps. Nat. Geosci. 4, 703–706 (2011).
Schmidt, M. W. & Poli, S. Devolatilization during subduction. In The Crust (ed. Rudnick, R. L.), Vol 4. of Treatise on Geochemistry, Vol. 2 (eds Holland, H. D. & Turekian, K. K.) 669–701 (Elsevier, Amsterdam, 2014).
van Keken, P. E., Wada, I., Abers, G. A., Hacker, B. R. & Wang, K. Mafic high‐pressure rocks are preferentially exhumed from warm subduction settings. Geochem., Geophysics, Geosyst. 19, 2934–2961 (2018).
Barry, P. H. et al. Forearc carbon sink reduces long-term volatile recycling into the mantle. Nature 568, 487–492 (2019).
Scambelluri, M. et al. Carbonation of subduction-zone serpentinite (high-pressure ophicarbonate; Ligurian Western Alps) and implications for the deep carbon cycling. Earth Planet. Sci. Lett. 441, 155–166 (2016).
Piccoli, F. et al. Carbonation by fluid–rock interactions at high-pressure conditions: implications for carbon cycling in subduction zones. Earth Planet. Sci. Lett. 445, 146–159 (2016).
Li, K., Li, L., Aubaud, C. & Muehlenbachs, K. Efficient carbon recycling at the Central‐Northern Lesser Antilles Arc: implications to deep carbon recycling in global subduction zones. Geophys. Res. Lett. 47, e2020GL086950 (2020).
Lee, C. T. A., Jiang, H., Dasgupta, R. & Torres, M. A framework for understanding whole-earth carbon cycling. In Deep Carbon: Past to Present (eds Orcutt, B. N., Daniel, I. & Dasgupta, R.) 313–357 (Cambridge University Press, 2019).
Melidonis, N. G. The geological structure and mineral deposits of Tinos island (Cyclades, Greece). The Geology of Greece. 13, 1–80 (1980)
Hecht, J. Map of Greece, Syros Island. scale 1:50,000. (Inst. Geol. Mineral Exploration, Athens, 1984).
Bröcker, M. & Franz, L. Rb-Sr isotope studies on Tinos Island (Cyclades, Greece): additional time constraints for metamorphism, extent of infiltration-controlled overprinting and deformational activity. Geol. Magazine 135, 369–382 (1998).
Bröcker, M. & Franz, L. The base of the Cycladic blueschist unit on Tinos Island (Greece) re-visited: field relationships, phengite chemistry and Rb–Sr geochronology. J. Miner. Abh. 181, 81–93 (2005).
Keiter, M., Piepjohn, K., Ballhaus, C., Bode, M. & Lagos, M. Structural development of high-pressure metamorphic rocks on Syros island (Cyclades, Greece). J. Struct. Geol. 26, 1433–1445 (2004).
de Capitani, C. & Petrakakis, K. The computation of equilibrium assemblage diagrams with Theriak/Domino software. Am. Mineral. 95, 1006–1016 (2010).
Jørgensen, T. R., Tinkham, D. K. & Lesher, C. M. Low‐P and high‐T metamorphism of basalts: Insights from the Sudbury impact melt sheet aureole and thermodynamic modelling. J. Metamorphic Geol. 37, 271–313 (2019).
Holland, T. & Powell, R. An improved and extended internally consistent thermodynamic dataset for phases of petrological interest, involving a new equation of state for solids. J. Metamorph. Geol. 29, 333–383 (2011).
Green, E. C. R. et al. Activity–composition relations for the calculation of partial melting equilibria in metabasic rocks. J. Metamorph. Geol. 34, 845–869 (2016).
Holland, T. & Powell, R. An internally consistent thermodynamic data set for phases of petrological interest. J. Metamorph. Geol. 16, 309–343 (1998).
Holland, T. & Powell, R. Activity–composition relations for phases in petrological calculations: an asymmetric multicomponent formulation. Contrib. Mineral. Pet. 145, 492–501 (2003).
White, R. W., Powell, R., Holland, T. J. B. & Worley, B. A. The effect of TiO2 and Fe2O3 on metapelitic assemblages at greenschist and amphibolite facies conditions: mineral equilibria calculations in the system K2O-FeO-MgO-Al2O3-SiO2-H2O-TiO2-Fe2O3. J. Metamorph. Geol. 18, 497–511 (2000).
White, R. W., Powell, R., Holland, T. J. B., Johnson, T. E. & Green, E. C. R. New mineral activity–composition relations for thermodynamic calculations in metapelitic systems. J. Metamorph. Geol. 32, 261–286 (2014).
Pitzer, K. S. & Sterner, S. M. Equations of state valid continuously from zero to extreme pressures for H2O and CO2. J. Chem. Phys. 101, 3111–3116 (1994).
Holland, T. & Powell, R. A compensated-Redlich-Kwong (CORK) equation for volumes and fugacities of CO2 and H2O in the range 1 bar to 50 kbar and 100–1600 C. Contributions Mineral. Petrol. 109, 265–273 (1991).
Ferry, J. M. Dehydration and decarbonation reactions as a record of fluid infiltration. Rev. Mineral. Geochem. 26, 351–393 (1991).
Abramson, E. H., Bollengier, O. & Brown, J. M. The water-carbon dioxide miscibility surface to 450 °C and 7 GPa. Am. J. Sci. 317, 967–989 (2017).
Acknowledgements
We thank A. Haws, B. Hess, D.S. Keller, D. Levy, S.A. Menemenlis, and M. Wyatt for contributing to fieldwork on Syros and Tinos; F. Piccoli, A. Vitale Brovarone, O. Beyssac, D. Rumble, J-L. Li, M.E. Galvez, E.F. Baxter, M.J. Caddick, B. Dragovic, F. Klein, S.C. Penniston-Dorland, G.E. Bebout, E.A. Codillo, and G.S. Epstein for thoughtful and stimulating discussions; and D.K. Tinkham for assistance with computer code and thermodynamic database files. J.J.A. thanks the Deep Carbon Observatory for their support of a Reservoirs and Fluxes Community workshop on Tectonic Fluxes of Carbon. We gratefully acknowledge funding from the Yale Analytical and Stable Isotope Center to E.M.S. and National Science Foundation grant EAR-1650329 to J.J.A.
Author information
Authors and Affiliations
Contributions
Both authors were responsible for broad study design, sample collection and processing, data analysis, and interpretation. E.M.S. carried out numerical modeling and calculations and was the primary author of the paper and figures. J.J.A. secured funding, contributed to writing and figure design, and prepared thin sections.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Peer review information Nature Communications thanks Craig Manning and Oliver Pluemper for their contribution to the peer review of this work.
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Stewart, E.M., Ague, J.J. Pervasive subduction zone devolatilization recycles CO2 into the forearc. Nat Commun 11, 6220 (2020). https://doi.org/10.1038/s41467-020-19993-2
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-020-19993-2
This article is cited by
-
Carbonate-rich crust subduction drives the deep carbon and chlorine cycles
Nature (2023)
-
Formation of the eclogites of the Atbashi complex, Kyrgyzstan, in a subduction zone mélange diapir
Communications Earth & Environment (2023)
-
Recycled carbonates elevate the electrical conductivity of deeply subducting eclogite in the Earth’s interior
Communications Earth & Environment (2023)
-
Zinc isotopic evidence for recycled carbonate in the deep mantle
Nature Communications (2022)
-
Evolution of Earth’s tectonic carbon conveyor belt
Nature (2022)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.