Abstract
The quantum walk formalism is a widely used and highly successful framework for modeling quantum systems, such as simulations of the Dirac equation, different dynamics in both the low and high energy regime, and for developing a wide range of quantum algorithms. Here we present the circuit-based implementation of a discrete-time quantum walk in position space on a five-qubit trapped-ion quantum processor. We encode the space of walker positions in particular multi-qubit states and program the system to operate with different quantum walk parameters, experimentally realizing a Dirac cellular automaton with tunable mass parameter. The quantum walk circuits and position state mapping scale favorably to a larger model and physical systems, allowing the implementation of any algorithm based on discrete-time quantum walks algorithm and the dynamics associated with the discretized version of the Dirac equation.
Similar content being viewed by others
Introduction
Quantum walks (QWs) are the quantum analog of classical random walks, in which the walker steps forward or backward along a line based on a coin flip. In a QW, the walker proceeds in a quantum superposition of paths, and the resulting interference forms the basis of a wide variety of quantum algorithms, such as quantum search1,2,3,4,5, graph isomorphism problems6,7,8, ranking nodes in a network9,10,11,12, and quantum simulations, which mimic different quantum systems at the low and high energy scale13,14,15,16,17,18,19,20,21,22. In the discrete-time QW (DQW)23,24, a quantum coin operation is introduced to prescribe the direction in which the particle moves in position space at each discrete step. In the continuous-time QW (CQW)25,26, one can directly define the walk evolution on position space itself using continuous-time evolution. We focus on DQWs and their implementation on gate-based quantum circuits in this work.
DQWs can be realized directly on lattice-based quantum systems where position space matches the discrete lattice sites. Such implementations have been reported with cold atoms27,28 and photonic systems29,30,31,32. In trapped ions, a DQW has been implemented by mapping position space to locations in phase space given by the degrees of freedom associated with the harmonic motion of the ion in the trap33,34,35. All these physical implementations have followed an analogue quantum simulation approach. However, implementing QWs on a circuit-based system is crucial to explore the algorithm applications based on QWs. The implementation of a DQW on a three-qubit NMR system36, a CQW on a two-qubit photonic processor37 and a split-step QW on superconducting circuits38,39 are the circuit-based implementations reported to date. To implement DQWs on circuit-based quantum processors, its necessary to map the position space to the available multi-qubit states. The range of the walk is set by the available qubit number and gate depth. The term Quantum Cellular Automaton (QCA) describes a unitary evolution of a particle on a discretized space40,41,42, as occurs with QWs. In this context, the one-dimensional Dirac cellular automaton (DCA) has been derived from the symmetries of the QCA showing how the dynamics of the Dirac equation emerges40,41,42,43,44.
Here we implement efficient quantum circuits for a DQW in one-dimensional position space, which provide the time-evolution up to five steps. We report the experimental realization of a DQW on five qubits within a seven-qubit programmable trapped-ion quantum computer45. With a tunable walk probability at each step we also show the experimental realization of a DCA where the coin bias parameter mimics the mass term in the Dirac equation. This will be central for discrete-time quantum simulation of the dynamics associated with the relativistic motion of a spin-1/2 particle in position space.
Results
Review of quantum walks and the connection to the Dirac equation
The DQW consists of two quantum mechanical systems, an effective coin and the position space of the walker, as well as an evolution operator, which is applied to both systems in discrete time-steps. The evolution is given by a unitary operator defined on a tensor product of two Hilbert spaces \({{\mathcal{H}}}_{{\rm{c}}}\otimes {{\mathcal{H}}}_{{\rm{p}}}\) where, \({{\mathcal{H}}}_{{\rm{c}}}\) is the coin Hilbert space spanned by the internal states \({\left|0\right\rangle }_{{\rm{c}}}\) and \({\left|1\right\rangle }_{{\rm{c}}}\) of a single qubit, while \({{\mathcal{H}}}_{p}\) represents the position Hilbert space given by the position states \(\left|x\right\rangle\) with \(x\in {\mathbb{Z}}\) encoded in several qubits as described below. Here, the unitary quantum coin toss operation, \({\hat{C}}_{\theta }\), is a unitary rotation operator that acts on the coin qubit space,
where θ is a coin bias parameter that can be varied at each step to modify the QW path superposition weights. The conditional position-shift operator, \(\hat{S}\), translates the particle to the left and right conditioned by the state of the coin qubit,
The state of the particle in position space after t steps of the walk, is accomplished by the repeated action of the operator \(\hat{W}=\hat{S}{\hat{C}}_{\theta }\) on the initial state of the particle \({\left|\psi \right\rangle }_{{\rm{c}}}=\alpha {\left|0\right\rangle }_{{\rm{c}}}+\beta {\left|1\right\rangle }_{{\rm{c}}}\) at position x = 0, as shown in Fig. 1,
where \({\psi }_{x,t}^{0(1)}\) denotes the left(right) propagating component of the particle at time-step t. The probability of finding the particle at position x and time t will be \(P(x,t)=| {\psi }_{x,t}^{0}{| }^{2}+| {\psi }_{x,t}^{1}{| }^{2}\).
Recent works have shown a relationship between DQWs and the Dirac equation14,15,16,17,18,43. Starting form a discrete-time evolution operator and then moving from position space to momentum space, Dirac kinematics can be recovered from the diagonal terms of the unitary evolution operator for small momenta in the small mass regime16,17,18. In contrast with these proposals in the Fourier frame, we focus our implementation on the probability distribution of the DQW, which is analogous to the spreading of a relativistic particle. To realize a DCA and recover the Dirac equation, a split-step quantum walk, one form of the DQW, is used40. Each step of a split-step quantum walk is a composition of two half step evolutions with different coin biases and position-shift operators,
where the coin operation \({\hat{C}}_{{\theta }_{j}}\), with j = 1, 2, is given in Eq. (1). The split-step position-shift operators are,
Following Mallick40 and Kumar44, the particle state at time t and position x after the evolution operation \({\hat{W}}_{{\rm{ss}}}\) is described by the differential equation,
The tunability of parameters θ1 and θ2 on the split-step QW permits the study of one-dimensional Dirac equations effectively, within the low momentum subspace, for spin-1/2 particles40,44. It is important to stress out that, the description of the Dirac equation used here corresponds to the 2 × 2 representation, i.e. no spin degree of freedom. For instance, the massless particle Dirac equation can be recovered for \(\cos ({\theta }_{1}+{\theta }_{2})=1\). Thereby, Eq. (7) becomes \(i\hslash [{\partial }_{t}-\cos {\theta }_{2}(\cos {\theta }_{1}{\sigma }_{z}+\sin {\theta }_{1}{\sigma }_{y}){\partial }_{x}]\Psi (x,t)=0\), which is identical to the Dirac equation of a massless particle in the relativistic limit46. In contrast, considering θ1 = 0 and a very small value of θ2 corresponds to the Dirac equation for particles with small mass35,46 in the form \(i\hslash [{\partial }_{t}-(1-{\theta }_{2}^{2}/2){\sigma }_{z}{\partial }_{x}+i{\theta }_{2}{\sigma }_{x}]\Psi (x,t)\approx 0\).
At the same time, by choosing θ1 = 0, the quantum walk operator \({\hat{W}}_{{\rm{ss}}}\) given in Eq. (4) takes the form of the unitary operator for a DCA40,
Within this framework, θ2 determines the mass of the Dirac particle. The split-step DQW described by the operator \({\hat{W}}_{{\rm{ss}}}\) is equivalent to the two period DQW with alternate coin operations, θ1 and θ2, when the alternate points in position space with zero probability are ignored47. Therefore, all the dynamics of a DCA can be recovered from the DQW evolution using \(\hat{W}\) and alternating the two coin operations. See Methods for a comparison between DCA and the explicit solution of the Dirac equation. Typical features of the Dirac equation in relativistic quantum mechanics, such as the Zitterbewegung40 and the Klein paradox48, are also dynamical features of the DCA, as well as the spreading of the probability distribution and the entanglement of localized positive-energy states. We note that these effects have also been shown in direct analog simulations of the Dirac equation with trapped ions35 and BECs49.
Experimental DQW implementation
To realize the DQW on a system of qubits one must pick a mapping of the particle position to the qubit space. As shown in50, there is no unique way to map position states to multi-qubit states, so each circuit decomposition depends on the configuration adopted. A direct mapping of each walker position to one qubit in the chain mimicking the arrangement of the qubit array is inefficient in terms of qubit number and gates required (the former grows linearly and the latter quadratically with the position space size modeled). In order to minimize resource use, we take advantage of a digital representation to map the position space into a multi-qubit state and re-order it in such a way that the state \(\left|0\right\rangle \,(\left|1\right\rangle )\) of the last qubit corresponds to even (odd) position numbers. This allows us to minimize the changes needed in the qubit space configuration during each step of the walk (see Fig. 2). To implement a quantum walk in one-dimensional position Hilbert space of size 2n, (n + 1) qubits are required. One qubit acts as the coin and the other n qubits mimic the position Hilbert space with 2n − 1 positions of a symmetric walk about \(\left|x=0\right\rangle\). We note that the particle can be started from any point in the position space, however setting the initial state reduces the gate counting in the circuit and hence reduces the overall error. The coin operation is achieved by single-qubit rotations on the coin-qubit while the shift operators are realized by using the coin as a control qubit to change the position state during the walk.
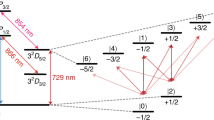
We realize the walk on a chain of seven individual 171Yb+ ions confined in a Paul trap and laser-cooled close to their motional ground state45,51. Five of these are used to encode qubits in their hyperfine-split 2S1/2 ground level. Single-qubit rotations, or R gates, and two-qubit entangling interactions, or XX gates are achieved by applying two counter-propagating optical Raman beams to the chain, one of which features individual addressing (see Methods for experimental details). We can represent up to 15 positions of a symmetric QW, including the initial position \(\left|x=0\right\rangle\).
Based on this position representation a circuit diagram for the DQW on five qubits with the initial state \({\left|0\right\rangle }_{c}\otimes \left|0000\right\rangle\) is composed for up to five steps, see Fig. 3. Each evolution step, \(\hat{W}\), starts with a rotation operation on the coin-qubit, \({\hat{C}}_{{\theta }_{j}}\), followed by a set of controlled gates that change the position state of the particle under \(\hat{S}\). Due to the gratuitous choice of position representation used, it is enough to perform a single-qubit rotation on the last qubit at every step, which could also be done by classical tracking50.
a Circuit diagram for a DQW and DCA. Each dashed block describes one step in the quantum walk. b Discrete-time Quantum Walk. Comparison of the experimental results (left) and the theoretical quantum-walk probability distribution (right) for the first five steps with initial particle state b i and b iv \({\left|\psi \right\rangle }_{{\rm{c}}}={\left|0\right\rangle }_{{\rm{c}}}\), b ii and b iv \({\left|\psi \right\rangle }_{{\rm{c}}}={\left|1\right\rangle }_{{\rm{c}}}\), b iii and b vi \({\left|\psi \right\rangle }_{{\rm{c}}}={\left|0\right\rangle }_{{\rm{c}}}+i{\left|1\right\rangle }_{{\rm{c}}}\), and position state \(\left|x=0\right\rangle\). c Output of a step-5 Dirac Cellular Automaton for θ1 = 0 and, c i and c iv θ2 = π/4, c ii and c v θ2 = π/10 and c iii and c vi θ2 = π/20 with the initial state \(\left|{\Psi }_{{\rm{in}}}\right\rangle =({\left|0\right\rangle }_{{\rm{c}}}+i{\left|1\right\rangle }_{{\rm{c}}})\otimes \left|x=0\right\rangle\).
Computational gates such as CNOT, Toffoli, and Toffoli-4 are generated by a compiler which breaks them down into constituent physical-level single- and two-qubit gates45. A circuit diagram detailing the compiled building blocks is shown in Methods. To prepare an initial particle state different from \({\left|0\right\rangle }_{{\rm{c}}}\) it is enough to perform a rotation on the coin-qubit before the first step. In some cases this rotation can be absorbed into the first gates in step one. Table 1 summarizes the number of native gates needed per step for initial state. To recover the evolution of the Dirac equation in a DQW after five steps, 81 single qubit gates and 32 XX-gates are required.
After evolving a number of steps, we sample the corresponding probability distribution 3000 times and correct the results for readout errors. For the DQW evolution up to five steps shown in Fig. 3, a balanced coin (θ1 = θ2 = π/4) is used where the initial position is \(\left|x=0\right\rangle\) for different initial particle states, \({\left|0\right\rangle }_{{\rm{c}}}\) in Fig. 3b i, \({\left|1\right\rangle }_{{\rm{c}}}\) in Fig. 3b ii, and an equal superposition of both in Fig. 3b iii. In Fig. 3b iv, b v, and b vi we show the ideal output from classical simulation of the circuit for comparison (see Methods for a plot of the difference). With a balanced coin the particle evolves in equal superposition to the left and right position at each time step and upon measurement, there is a 50/50 probability of finding the particle to the left or right of its previous position, just as in classical walk. If we let the DQW evolve for more than three steps before we perform a position measurement, we will find a very different probability distribution compared to the classical random walk52.
The same experimental setup can be used to recover a DCA with a two-period DQW. Here we set θ1 = 0 and varied θ2 to recover the Dirac equation for different mass values. In Fig. 3c, we show experimental results for θ2 = π/4, π/10 and π/20, corresponding to a mass 1.1357, 0.3305, and 0.159 in units of ℏc−2s−1, with the initial particle state in the superposition \({\left|0\right\rangle }_{c}+i{\left|1\right\rangle }_{c}\). The main signature of a DCA for small mass values is the presence of peaks moving outward and a flat distribution in the middle as shown for the cases with small values of θ2, Figs. 3c ii-iii. This bimodal probability distribution in position space is an indication of the one-dimensional analog of an initially localized Dirac particle, with positive energy, evolving in time which spreads in all directions in position space at speeds close to the speed of light53. In contrast, a DCA with θ2 = π/4, Fig. 3c i corresponds to a massive particle and hence there is a slow spread rather than a ballistic trajectory in position space.
Discussion
We have shown how quantum walks form the basic elements for simulation of the dynamics associated with the free Dirac particle with positive energy. Despite the population mismatch of 0.05–0.2 between the simulation and the experimental results after five steps, the final probability density exhibits the characteristic behavior of an initially localized Dirac particle. A key factor on the digitization of DQW/DCA is the mapping of qubit states to position space. An adequate mapping is important to minimize the number of gates on the protocol, and as a consequence, the resource scaling of the evolution. By increasing in the available number of qubits, these quantum circuits can be scaled to implement more steps and simulate a multi-particle DQW. The number of gates has a polynomial growth rate with the number of steps54. The correspondence between DQWs and the dynamics of Dirac particles suggests that the QWs formalism is as a viable approach to reproduce a variety of phenomena underpinned by Dirac particle dynamics in both the high- and low-energy regime22,39,43. Quantum simulations of free quantum field theory43, Yang-Mills gauge-field on fermionic matter55, as well as the effect of mass and space-time curvature on entanglement between accelerated particles20,56,57 have been reported and probing quantum field theory from the algorithmic perspective in an active field of research. However, the circuit complexity for position-dependent coin operations needed for simulating these effects will increase with the complexity of the evolution, which means further improvements in quantum hardware will be necessary for their realization.
Methods
Experimental details
The experiments are performed in a chain of seven individual 171Yb+ ions confined in a Paul trap and laser-cooled close to their motional ground state45,51. In order to guarantee higher uniformity in the ion spacing, matching the equally spaced individual addressing beams, the middle five of these are used to encode qubits in their hyperfine-split 2S1/2 ground level, with an energy difference of 12.642821 GHz. The two edge ions are neither manipulated nor measured, however, their contribution to the collective motion is included when creating the entangling operations. The ions are initialized by an optical pumping scheme and are collectively read out using state-dependent fluorescence detection58, with each ion being mapped to a distinct photo-multiplier tube (PMT) channel. The system has two mechanisms for quantum control, which can be combined to implement any desired operation: single-qubit rotations, or R gates, and two-qubit entangling interactions, or XX gates. These quantum operations are achieved by applying two counter-propagating optical Raman beams from a single 355-nm mode-locked laser59. The first Raman beam is a global beam applied to the entire chain, while the second is split into individual addressing beams, each of which can be controlled independently and targets one qubit. Single-qubit gates are generated by driving resonant Rabi rotations of defined phase, amplitude, and duration. Two-qubit gates are realized by illuminating two ions with beat-note frequencies near to the motional sidebands and creating an effective spin-spin (Ising) interaction via transient entanglement between the state of two ions and all modes of motion60,61,62. The average state detection fidelity for single- and two-qubit gate are 99.5(2)% and 98–99%, respectively. Rotations around the z-axis are achieved by phase advances on the classical control signals. Both the R as well as the XX angle can be varied continuously. State preparation and measurement (SPAM) errors are characterized and corrected by applying the inverse of an independently measured state-to-state error matrix63.
Errors
In order to illustrate how our experiment performs, we plot the absolute value of the difference between measured and simulated position distributions, Fig. 4, they match the theoretical expectation closely. These distributions are obtained after tracing out the coin information of the unitary evolution \(\hat{W}=\hat{S}{\hat{C}}_{\theta }\) for each time-step. In both instances, DQW and DCA, the number of gates and hence the error incurred grows with the number of steps.
Apart from this, the output from the walk both, DQW and DCA, is designed to have zero probabilities for an alternate position, however, due to addressing crosstalk in the system, we see a small amount of population in these states. The same mechanism can populate the state \(\left|1000\right\rangle\) of the logical encoding not included in our mapping. In fact, the average experimental population registered in this state is <2% for the deepest circuits and hence does not affect the results significantly.
Comparison between Dirac kinematics and DCA
We use the explicit time-dependent solution of the one-dimensional Dirac equation provided by Strauch18:
where \(s={[{x}^{2}{(a+it)}^{2}]}^{1/2}\), \({\mathcal{N}}=\sqrt{(\pi /2m)}{[{K}_{1}(2ma)+{K}_{0}(2ma)]}^{-1/2}\) the normalized factor and Kn is the modified Bessel Function of order n, to show the corresponding probability density at time t to the DCA after the time-step t, Fig. 5. The relationship between the mass in the Dirac equation and the coin bias parameter is given by,
Gate block
The compiler breaks down the gate blocks shown in Fig. 3 (Toffoli-CNOT and Toffoli - Toffoli 4 - CNOT) into native R and XX gates as given by the following circuits, which are optimal in the XX-gate count, Fig. 6. Sketch of the XX-gate is meant to symbolize the two-qubit entangling gate between the outer ions inside a square.
Data availability
The data that support the findings of this study are available from the corresponding author upon reasonable request.
References
Childs, A. M. et. al. Exponential algorithmic speedup by a quantum walk. In Proc. Thirty-fifth Annual ACM Symposium on Theory of Computing 59–68 (Association for Computing Machinery, 2003).
Ambainis, A. Quantum walks and their algorithmic applications. Int. J. Quantum Inf. 1, 507–518 (2003).
Shenvi, N., Kempe, J., Whaley, K. B. & Whaley, K. B. Quantum random-walk search algorithm. Phys. Rev. A 67, 052307 (2003).
Ambainis, A. Quantum walk algorithm for element distinctness. SIAM J. Comput. 37, 210–239 (2007).
Magniez, F., Santha, M. & Szegedy, M. Quantum algorithms for the triangle problem. SIAM J. Comput. 37, 413–424 (2007).
Douglas, B. L. & Wang, J. B. A classical approach to the graph isomorphism problem using quantum walks. J. Phys. A: Math. Theor. 41, 075303 (2008).
Gamble, J. K., Friesen, M., Zhou, D., Joynt, R. & Coppersmith, S. N. Two-particle quantum walks applied to the graph isomorphism problem. Phys. Rev. A 81, 052313 (2010).
Berry, S. D. & Wang, J. B. Two-particle quantum walks: entanglement and graph isomorphism testing. Phys. Rev. A 83, 042317 (2011).
Paparo, G. & Martin-Delgado, M. Google in a quantum network. Sci. Rep. 2, 444 (2012).
Paparo, G., Müller, M., Comellas, F. & Martin-Delgado, M. A. Quantum Google in a complex network. Sci. Rep. 3, 2773 (2013).
Loke, T., Tang, J. W., Rodriguez, J., Small, M. & Wang, J. B. Comparing classical and quantum PageRanks. Quantum Inf. Process. 16, 25 (2017).
Chawla, P., Mangal, R. & Chandrashekar, C. M. Discrete-time quantum walk algorithm for ranking nodes on a network. Quantum Inf. Process. 19, 158 (2020).
DiMolfetta, G., Brachet, M. & Debbasch, F. Quantum walks in artificial electric and gravitational fields. Phys. A: Stat. Mech. its Appl. 397, 157–168 (2014).
Chandrashekar, C. M., Banerjee, S. & Srikanth, R. Relationship between quantum walks and relativistic quantum mechanics. Phys. Rev. A 81, 062340 (2010).
DiMolfetta, G., Brachet, M. & Debbasch, F. Quantum walks as massless Dirac fermions in curved space-time. Phys. Rev. A 88, 042301 (2013).
Arrighi, P., Facchini, S. & Forets, M. Quantum walking in curved spacetime. Quantum Inf. Process. 15, 3467–3486 (2016).
Chandrashekar, C. M. Two-component Dirac-like Hamiltonian for generating quantum walk on one-, two-and three-dimensional lattices. Sci. Rep. 3, 2829 (2013).
Strauch, F. W. Relativistic quantum walks. Phys. Rev. A 73, 054302 (2006).
DiMolfetta, G. & Pérez, A. Quantum walks as simulators of neutrino oscillations in a vacuum and matter. N. J. Phys. 18, 103038 (2016).
Mallick, A., Mandal, S., Karan, A. & Chandrashekar, C. M. Simulating Dirac Hamiltonian in curved space-time by split-step quantum walk. J. Phys. Commun. 3, 015012 (2019).
Chandrashekar, C. M. & Busch, T. Localized quantum walks as secured quantum memory. EPL 110, 10005 (2015).
Mallick, A., Mandal, S. & Chandrashekar, C. M. Neutrino oscillations in discrete-time quantum walk framework. Eur. Phys. J. C. 77, 85 (2017).
Aharonov, D., Ambainis, A., Kempe, J. & Vazirani, U., Quantum walks on graphs. In Proc. Thirty-third Annual ACM Symposium on Theoretical Computing 50–59, (Association for Computing Machinery, 2001).
Tregenna, B., Flanagan, W., Maile, R. & Kendon, V. Controlling discrete quantum walks: coins and initial states. N. J. Phys. 5, 83 (2003).
Farhi, E. & Gutmann, S. Quantum computation and decision trees. Phys. Rev. A 58, 915–928 (1998).
Gerhardt, H. & Watrous, J. Continuous-time quantum walks on the symmetric group. In Approximation, Randomization, and Combinatorial Optimization. Algorithms and Techniques, 290–301 (Springer Berlin Heidelberg, 2003).
Perets, H. B. et al. Realization of quantum walks with negligible decoherence in waveguide lattices. Phys. Rev. Lett. 100, 170506 (2008).
Karski, M. et al. Quantum walk in position space with single optically trapped atoms. Science 325, 174–177 (2009).
Peruzzo, A. et al. Quantum walks of correlated photons. Science 329, 1500–1503 (2010).
Schreiber, A. et al. Photons walking the line: a quantum walk with adjustable coin operations. Phys. Rev. Lett. 104, 050502 (2010).
Broome, M. A. et al. Discrete single-photon quantum walks with tunable decoherence. Phys. Rev. Lett. 104, 153602 (2010).
Tamura, M., Mukaiyama, T. & Toyoda, K. Quantum walks of a phonon in trapped ions. Phys. Rev. Lett. 124, 200501 (2020).
Schmitz, H. et al. Quantum walk of a trapped ion in phase space. Phys. Rev. Lett. 103, 090504 (2009).
Zähringer, F. et al. Realization of a quantum walk with one and two trapped ions. Phys. Rev. Lett. 104, 100503 (2010).
Gerritsma, R. et al. Quantum simulation of the Dirac equation. Nature 463, 68–71 (2010).
Ryan, C. A., Laforest, M., Boileau, J. C. & Laflamme, R. Experimental implementation of a discrete-time quantum random walk on an NMR quantum-information processor. Phys. Rev. A 72, 062317 (2005).
Qiang, X. et al. Efficient quantum walk on a quantum processor. Nat. Commun. 7, 11511 (2016).
Ramasesh, V. V., Flurin, E., Rudner, M., Siddiqi, I. & Yao, N. Y. Direct probe of topological invariants using Bloch oscillating quantum walks. Phys. Rev. Lett. 118, 130501 (2017).
Flurin, E., Ramasesh, V. V., Hacohen-Gourgy, S., Martin, L. S., Yao, N. Y. & Siddiqi, I. Observing topological invariants using quantum walks in superconducting circuits. Phys. Rev. X 7, 031023 (2017).
Mallick, A. & Chandrashekar, C. M. Dirac cellular automaton from split-step quantum walk. Sci. Rep. 6, 25779 (2016).
Pérez, A. Asymptotic properties of the Dirac quantum cellular automaton. Phys. Rev. A 93, 012328 (2016).
Meyer, D. A. From quantum cellular automata to quantum lattice gases. J. Stat. Phys. 85, 551–574 (1996).
Bisio, A., D’Ariano, G. M. & Tosini, A. Quantum field as a quantum cellular automaton: the Dirac free evolution in one dimension. Ann. Phys. 354, 244–264 (2015).
Kumar, N. P., Balu, R., Laflamme, R. & Chandrashekar, C. M. Bounds on the dynamics of periodic quantum walks and emergence of the gapless and gapped Dirac equation. Phys. Rev. A 97, 012116 (2018).
Debnath, S. et al. Demonstration of a small programmable quantum computer with atomic qubits. Nature 536, 63–66 (2016).
Thaller, B. The Dirac equation (Springer Science & Business Media, 2013).
Zhang, W.-W., Goyal, S. K., Simon, C. & Sanders, B. C. Decomposition of split-step quantum walks for simulating Majorana modes and edge states. Phys. Rev. A 95, 052351 (2017).
Bisio, A., D’Ariano, G. M. & Tosini, A. Dirac quantum cellular automaton in one dimension: Zitterbewegung and scattering from potential. Phys. Rev. A 88, 032301 (2013).
LeBlanc, L. J. et al. Direct observation of zitterbewegung in a Bose-Einstein condensate. N. J. Phys. 15, 073011 (2013).
Singh, S. et. al. Universal one-dimensional discrete-time quantum walks and their implementation on near term quantum hardware. Preprint at https://arxiv.org/abs/2001.11197 (2020).
Landsman, K. A. et al. Verified quantum information scrambling. Nature 567, 61–65 (2019).
Omar, Y., Paunković, N., Sheridan, L. & Bose, S. Quantum walk on a line with two entangled particles. Phys. Rev. A 74, 042304 (2006).
Bracken, A. J., Ellinas, D. & Smyrnakis, I. Free-Dirac particle evolution as a quantum random walk. Phys. Rev. A 75, 022322 (2007).
Fillion-Gourdeau, F., MacLean, S. & Laflamme, R. Algorithm for the solution of the Dirac equation on digital quantum computers. Phys. Rev. A 95, 042343 (2017).
Arnault, P., DiMolfetta, G., Brachet, M. & Debbasch, F. Quantum walks and non-Abelian discrete gauge theory. Phys. Rev. A. 94, 012335 (2016).
Arrighi, P., DiMolfetta, G. & Facchini, S. Quantum walking in curved spacetime: discrete metric. Quantum 2, 84 (2018).
Singh, S., Balu, R., Laflamme, R. & Chandrashekar, C. M. Accelerated quantum walk, two-particle entanglement generation and localization. J. Phys. Commun. 3, 055008 (2019).
Olmschenk, S. et al. Manipulation and detection of a trapped Yb+ hyperfine qubit. Phys. Rev. A 76, 052314 (2007).
Islam, R. et al. Beat note stabilization of mode-locked lasers for quantum information processing. Opt. Lett. 39, 3238–3241 (2014).
Choi, T. et al. Optimal quantum control of multimode couplings between trapped ion qubits for scalable entanglement. Phys. Rev. Lett. 112, 190502 (2014).
Mølmer, K. & Sørensen, A. Multiparticle entanglement of hot trapped ions. Phys. Rev. Lett. 82, 1835–1838 (1999).
Solano, E., de Matos Filho, R. L. & Zagury, N. Deterministic Bell states and measurement of the motional state of two trapped ions. Phys. Rev. A 59, R2539–R2543 (1999).
Shen, C. & Duan, L. M. Correcting detection errors in quantum state engineering through data processing. N. J. Phys. 14, 053053 (2012).
Acknowledgements
The authors would like to thank to Y. Nam and C. Figgatt for helpful discussions. C.H.A. acknowledges financial support from CONACYT doctoral grant no. 455378. C.M.C. acknowledge the support from DST, Government of India under Ramanujan Fellowship grant no. SB/S2/RJN-192/2014 and US Army ITC-PAC contract no. FA520919PA139. N.M.L. acknowledges financial support from the NSF grant no. PHY-1430094 to the PFC@JQI.
Author information
Authors and Affiliations
Contributions
C.H.A., S.S., N.H.N., D.Z., R.B., C.M., C.M.C. and N.M.L. designed the research, C.H.A., N.H.N., D.Z., and N.M.L. collected and analyzed data. All the authors contributed to this manuscript.
Corresponding author
Ethics declarations
Competing Interests
The authors declare no competing interests.
Additional information
Peer review information Nature Communications thanks the anonymous reviewer(s) for their contribution to the peer review of this work. Peer reviewer reports are available.
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Huerta Alderete, C., Singh, S., Nguyen, N.H. et al. Quantum walks and Dirac cellular automata on a programmable trapped-ion quantum computer. Nat Commun 11, 3720 (2020). https://doi.org/10.1038/s41467-020-17519-4
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-020-17519-4
This article is cited by
-
Quantum-walk search in motion
Scientific Reports (2024)
-
Discrete-time quantum walk-based optimization algorithm
Quantum Information Processing (2024)
-
Open system approach to neutrino oscillations in a quantum walk framework
Quantum Information Processing (2024)
-
Minimal quantum walk simulation of Dirac fermions in curved space-times
Quantum Studies: Mathematics and Foundations (2023)
-
Multi-angle quantum approximate optimization algorithm
Scientific Reports (2022)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.