Abstract
Aerobic lifeforms, including humans, thrive because of abundant atmospheric O2, but for much of Earth history O2 levels were low. Even after evidence for oxygenic photosynthesis appeared, the atmosphere remained anoxic for hundreds of millions of years until the ~2.4 Ga Great Oxidation Event. The delay of atmospheric oxygenation and its timing remain poorly understood. Two recent studies reveal that the mantle gradually oxidized from the Archean onwards, leading to speculation that such oxidation enabled atmospheric oxygenation. But whether this mechanism works has not been quantitatively examined. Here, we show that these data imply that reducing Archean volcanic gases could have prevented atmospheric O2 from accumulating until ~2.5 Ga with ≥95% probability. For two decades, mantle oxidation has been dismissed as a key driver of the evolution of O2 and aerobic life. Our findings warrant a reconsideration for Earth and Earth-like exoplanets.
Similar content being viewed by others
Introduction
The geological record of mass-independent sulfur isotope fractionation shows that O2 first inundated the atmosphere during the Great Oxidation Event (GOE) between 2.4 and 2.1 Ga1. However, redox-sensitive iron and molybdenum isotope data suggest the presence of O2 in the 3.2–3.0-Ga marine photic zone2,3, which implies that O2-producing cyanobacteria existed long before the GOE. Indeed, models show that, under a globally anoxic atmosphere, cyanobacteria-derived O2 produces photic zone oxygen oases4,5. Geological data also indicate the presence of methanotrophy and oxidative nitrogen cycling in Neoarchean oceans and lakes, which suggest that O2 was oxidizing sulfides and ammonium to make sulfate and nitrate, respectively6,7,8. Such inferences are consistent with phylogenetic interpretations that oxygenic photosynthesis evolved by the mid-Archean [e.g., ref. 9]. In addition, paleoredox proxies suggest O2 transients at 2.5 Ga6,7,10,11,12,13,14,15,16, and point to the possibility of pervasive oxygenation of the oceans over continental margins17,18.
The reasons for the delay of oxygenation of the atmosphere for hundreds of millions of years after the advent of oxygenic photosynthesis remain unknown. Numerous hypotheses rely on the notion that the atmospheric O2 level is determined by a kinetic balance between O2 supply and consumption19,20,21,22,23. If the rapid and efficient O2 sinks are larger than the O2 supply, there are excess reductants, and the atmosphere remains anoxic even in the presence of global oxygenic photosynthesis. Rapid sinks include net reactions of O2 with reducing gases emanating from the solid Earth, e.g., H2, CO, H2S, SO2, and CH4.
One possibility is that an increase in O2 fluxes overwhelmed the efficient O2 sinks, causing the GOE. However, the available data are not particularly persuasive. Photosynthetic O2 production is accompanied by organic matter (CH2O) in the net reaction CO2 + H2O = CH2O + O2. Because respiration or oxidative decay reverse this reaction (presently in ~50 years), the long-term net flux of O2 occurs when organic matter is segregated from O2 and buried.
Long-term changes in the burial rate of organic matter—and hence in the net supply of O2—can be inferred from C isotopes in sedimentary rocks. Organic matter concentrates 12C relative to 13C, leaving marine inorganic carbonate 12C depleted; as such, carbon isotopes in marine carbonates and kerogens track forg, the fraction of total carbon buried as organic matter. Isotopic mass balance shows little difference between the average organic burial fraction for 3.6–2.5 Ga of forg = 0.15 ± 0.02 [2 standard deviations (SD)] and that for 1.8–1.0 Ga of forg = 0.18 ± 0.02 [2 SD]24, suggesting no significant increase in O2 flux.
Of course, the inferred organic burial fraction and associated O2 flux depend on assumptions about the carbon cycle. Challenges to a conventional carbon mass balance model include 12C-enriched carbon sequestered into seafloor carbonates25 or into authigenic carbonates26, or isotopic weathering inputs that scaled with the amount of atmospheric O224,27,28. The first two hypotheses lack supporting evidence: Archean seafloor carbonate is not isotopically lighter than typical marine sedimentary carbonates29, and the abundance of authigenic carbonates is low before the GOE compared with afterward30, and is relatively small today31. The third idea is plausible: the lack of oxidative weathering in the Archean could modulate forg27. However, the average organic content of Archean sedimentary rocks (3.59 wt%) is indistinguishable from that of Proterozoic (3.56 wt%)24, and the cumulative distribution of total organic content in organic-rich Archean sedimentary rocks is identical to that of Neogene rocks1.
Here we are interested in examining the potential implications of the trend in mantle redox state on the GOE. A lower Archean O2 flux may be a possible factor, but that is not the foxus of this paper.
Because forg changed little with a conventional carbon cycle model, it has been proposed that a secular decline of efficient O2 sinks, rather than an increase in forg, caused the tipping point that initiated the GOE; this point would have been reached when the efficient O2 sink flux fell below the organic burial flux of O219,22,32,33. Models show that atmospheric O2 would then rapidly accumulate, until oxidative weathering of the continents became a significant sink, causing O2 concentrations to level off34. Proxies suggest that the O2 level, however, was still far below today’s atmospheric O2 concentrations [e.g., ref. 35].
Qualitatively, the pre-GOE O2 sink flux could have declined if the mantle’s oxidation state increased over time32,36,37. The proportion of reducing gases in volcanic emissions depends inversely on the oxygen fugacity (\(f_{{\rm{O}}_{2}}\)) in their magma source region, the upper mantle. Thus, if the Archean mantle’s \(f_{{\rm{O}}_{2}}\!\!\) was low, the H2/H2O and CO/CO2 ratios in Archean volcanic gases would have been high, suppressing atmospheric O2 levels.
Until recently, studies suggested that the mantle’s \(f_{{\rm{O}}_{2}}\!\!\) had been similar to the modern value since at least the early Archean38,39,40,41,42. The mantle \(f_{{\rm{O}}_{2}}\!\!\) estimated by many of these studies has uncertainties that vary between ~1 \({\mathrm{log}}_{10}\) unit38,43 and ~2 \({\mathrm{log}}_{10}\) units41,42. Changes in the oxygen fugacity of the mantle as small as ~0.5 \({\mathrm{log}}_{10}\) units have been suggested to have a significant effect on atmospheric redox evolution32; therefore, prior results do not preclude involvement in the GOE.
A notable study of mantle redox evolution is Li and Lee40, who used the V/Sc ratios of a large database of primitive basalts to report that mantle oxidation state had not changed by more than 0.3 \({\mathrm{log}}_{10}\) units since the Archean. The use of the V/Sc oxybarometer on large amounts of published basalt data relies upon the assumption that all of the studied basalts are the result of similar degrees of partial melting, and that they sample a spinel peridotite source with a primitive mantle V/Sc of ~5. None of these are necessarily safe assumptions. Average degree of partial melting was likely higher in the Archean due to higher mantle potential temperature. In addition, not all of the studied basalts were likely generated from melting of spinel peridotite, and residual garnet can have a potentially strong effect on V/Sc44. Finally, the mantle sources of basalts vary greatly in the degree of previous melt depletion, and remelting of a previously depleted source can generate a low V/Sc melt and an erroneously reduced \(f_{{\rm{O}}_{2}}\). For all these reasons, the conclusions and quoted uncertainties of Li and Lee40 must come into question.
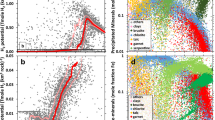
Two new studies reveal an \(f_{{\rm{O}}_{2}}\!\!\) trend. Aulbach and Stagno45 carefully filtered V/Sc data to only include Archean basalts formed in a mid-ocean ridge (MOR)-like environment, while Nicklas et al.46 calculated the \(f_{{\rm{O}}_{2}}\!\!\) of ultramafic lavas directly without making assumptions about their source compositions. These new data, shown in Fig. 1a, indicate that mantle \(f_{{\rm{O}}_{2}}\!\!\) increased by ~1.3 \({\mathrm{log}}_{10}\) units from the early Archean to Proterozoic, and likely represent the current best estimate for mantle redox evolution.
The oxygen fugacity (\(f_{{\rm{O}}_{2}}\!\!\)) is in \({\mathrm{log}}_{10}\) units relative to the Fayalite–Magnetite–Quartz (FMQ) buffer. In a, we show original data of Aulbach and Stagno45 and Nicklas et al.46. Dotted and dashed lines in a represent a linear fit for the data of Aulbach and Stagno45 and Nicklas et al.46, respectively, showing similar trends. Both datasets should converge on an average modern \(f_{{\rm{O}}_{2}}\!\!\) value inferred from mid-ocean ridge basalt (MORB). So, in b, we anchor the datasets to the MORB-inferred \(f_{{\rm{O}}_{2}}\!\!\) of the modern mantle, 0.250. Thus, 0.2 is added to Aulbach and Stagno data45 and −1.00 to Nicklas et al. data46. The black solid line and gray shaded region in b represent the median value and 95% confidence interval of oxygen fugacity, respectively. The error bar represents uncertainty of 1σ. The gray shaded region corresponds to a variation of the slope of the linear fit, which is propagated from the variations of the samples (i.e., the error bars). Note that in b, the variation of the \(f_{{\rm{O}}_{2}}\!\!\) of the modern mantle, which is discussed later, is neglected.
Both datasets in Fig. 1a show a similar \(f_{{\rm{O}}_{2}}\!\!\) trend, but each dataset was determined using a different oxybarometer. The \(f_{{\rm{O}}_{2}}\!\!\) derived from different oxybarometers shows a systematic offset, the reason for which is currently unclear, as oxybarometry performed using different methods on modern rocks gives values that vary outside of analytical uncertainty47. One possible explanation involves the degassing of volatile species, such as SO2, which have the potential to strongly reduce a lava shortly prior to eruption48. Degassing may lead to an offset between these two datasets because the V-partitioning oxybarometer of Nicklas et al.46 measures the \(f_{{\rm{O}}_{2}}\!\!\) of komatiites and picrites, while the V/Sc ratio oxybarometer of Aulbach and Stagno45 infers the \(f_{{\rm{O}}_{2}}\!\!\!\) of basalts and picrites. Komatiites are high-temperature, high-degree partial melts that are undersaturated in sulfur, while basalts are lower-degree, sulfur-saturated melts. Hence, sulfur degasses more from basaltic lavas than komatiitic lavas, i.e., decreases the \(f_{{\rm{O}}_{2}}\!\!\) of basalts more than that of komatiite46.
As each mantle oxidation trend only compares samples analyzed by the same oxybarometry method, and each study also analyzed modern mid-ocean ridge basalt (MORB) with its respective method, we can anchor each trend to the current canonical modern MORB value of +0.2 ± 0.3 \({\mathrm{log}}_{10}\) units above the fayalite–magnetite–quartz (FMQ) buffer as determined by X-ray absorption near-edge spectroscopy49,50. Upon anchoring, the two mantle oxidation trends overlap within their respective uncertainties, lending credence to the idea of mantle oxidation (Fig. 1b).
Although it has been speculated that the secular trends in the mantle \(f_{{\rm{O}}_{2}}\!\!\) in Fig. 1a and the timing of the GOE may be related45,46, this hypothesis has never been quantitatively tested in a redox model for the surface environment using data-derived trends of forg and mantle \(f_{{\rm{O}}_{2}}\).
In this study, we show that the new data imply that reducing Archean volcanic gases would prevent atmospheric O2 from accumulating, and then the GOE would occur by or after ~2.5 Ga with ≥95% probability. Thus, we conclude that secular oxidation of the mantle have indeed triggered oxygenation of the atmosphere.
Results
Oxygenation parameter
We evaluate whether the atmosphere was prone to oxygenation at any given time using an oxygenation parameter, Koxy22,33,34. This parameter is the ratio of O2 source fluxes to kinetically efficient O2 sink fluxes, which we consider here to be dominated by oxidizable volcanic gases
Fluxes are quantified in units of T mol O2 yr−1. When Koxy < 1, gaseous volcanic O2 sinks exceed O2 sources, and excess H2 builds up until balanced by escape to space. When Koxy > 1, O2 sources exceed efficient O2 sinks, and O2 builds up until balanced by oxidative weathering. Box modeling coupled to photochemistry shows that Koxy = 1 defines the point when the atmosphere becomes oxic (see Fig. 7b of Claire et al.34). For detailed information, see the “Methods” section and the Supplementary information.
Evolution of the oxygenation parameter
As an initial, illustrative trial, we took the organic burial fraction (forg) to be constant at 20%, which is a canonical value adopted by previous researchers [e.g., refs. 21,32], to isolate the effect of the secular change in mantle \(f_{{\rm{O}}_{2}}\!\!\) shown in Fig. 1b. As shown in Fig. 2a, the results are that the oxygenation parameter (Koxy) monotonically increases with time.
Solid lines represent median values, and the shaded region bounds 5% to 95% probability quantiles. These are obtained by 10,000 times Monte-Carlo simulations. Gray dotted lines highlight Koxy = 1, above which the atmosphere is oxic; otherwise, it is anoxic. a Organic burial fraction is constant at 20%, and the secular increase in the oxygen fugacity of mantle in Fig. 1b is considered. b Both a change in organic burial fraction from Krissansen-Totton et al.24 and secular increase in the oxygen fugacity in Fig. 1b are considered. c Oxygen fugacity is assumed to be constant at three different levels (blue: FMQ-2, black: FMQ-1, orange: FMQ). The fluctuations come from imposed changes in organic burial fraction. In b, the parameter Koxy exceeds unity by ~2.5 Ga with >= 95% probability.
In Fig. 2a, Koxy larger than unity occurs when the production of O2 via organic burial and deposition of pyrite (i.e., the numerator of Eq. (20)) exceeds the consumption of O2 from oxidizable volcanic gases (i.e., the denominator of Eq. (20)). Then atmospheric O2 accumulates, and oxidative weathering kicks in and balances the excess O2 production22,33,34. In contrast, when Koxy is smaller than unity, the production of O2 via organic burial and deposition of pyrite (i.e., the numerator of Eq. (20)) is smaller than the consumption of O2 by reducing volcanic gases (i.e., the denominator of Eq. (20)). Under such a condition, atmospheric O2 cannot accumulate, and the buildup of excess of reducing gases, such as CH4 and H2, is limited by their decomposition in the upper atmosphere and the escape of hydrogen to space22,33,34.
The 5% probability quantile of Koxy (the lower end of gray shaded region) crosses unity (a dotted gray line) at 2.62 Ga in the purely illustrative case of Fig. 2a. This means that at 2.62 Ga and later, the probability that Koxy is larger than unity, allowing atmospheric oxygenation, is 95% or more. Hereafter, we designate this 95% threshold as the oxic transition time.
In Eq. (20), Koxy also depends on forg, which has fluctuated over time. In Fig. 2b, which we subsequently call our standard case, we included temporal changes in forg from Krissansen-Totton et al.24 derived from the carbon isotope record (Supplementary Fig. 1). Unlike in Fig. 2a, Koxy fluctuates in Fig. 2b because of fluctuations in forg derived from the carbon isotope record. However, Koxy still increases with time. Here, the oxic transition time of this standard case is 2.48 Ga, which is delayed because of relatively low values of forg before 2.5 Ga (Supplementary Fig. 1). Hence, even when we include temporal changes of forg, the atmosphere still becomes oxic at 2.48 Ga (or afterward) with 95% (or more) probability.
On the other hand, the probability of Koxy > 1 is less than 50% before 3.38 Ga, for example, 30% at 3.6 Ga (Fig. 2b, see also Supplementary Fig. 2). This indicates that the atmosphere was likely reducing in the early Archean despite the possible presence of oxygenic photosynthesis. Thus, the increase in \(f_{{\rm{O}}_{2}}\!\!\) of the mantle would cause the atmosphere to shift from reducing to oxic, and the shift seemed to occur before ~2.5 Ga.
For comparison, we also did calculations for three hypothetical scenarios where the mantle \(f_{{\rm{O}}_{2}}\!\!\) was fixed at FMQ-2, FMQ-1, and FMQ (Fig. 2c). We also included temporal fluctuations in forg, as in Fig. 2b, which are reflected in the fluctuations of Koxy. In these scenarios, an oxic transition for Koxy does not occur, although Koxy occasionally becomes greater than 1 in the FMQ-1 case within the gray shaded region of uncertainty in Fig. 2c. Thus, the transitions from Koxy < 1 to Koxy > 1 in Fig. 2a, b are mainly due to the temporal increase in mantle \(f_{{\rm{O}}_{2}}\!\!\) taken from the fit in Fig. 1.
Discussion
As shown above, an empirically-inferred increase in mantle \(f_{{\rm{O}}_{2}}\!\!\) causes an increase in Koxy, resulting in the shift of the atmosphere from reducing to oxic (Fig. 2). However, this result does not exclude a role for other processes in the oxidation of the atmosphere as explained below.
The result of the standard case shows that uncertainties in the \(f_{{\rm{O}}_{2}}\!\!\) time series and the oxygen flux estimates from the carbon isotope record propagate through the calculations, so that the uncertainty envelope allows an oxic regime even before ~2.5 Ga (Fig. 2b). On the other hand, geological evidence, such as mass-independent sulfur isotope fractionation1, indicates an anoxic atmosphere for the Archean Earth before 2.4–2.3 Ga though a recent study suggests that the GOE occured somewhat earlier than 2.4 Ga51. This discrepancy in the timing of the GOE might also be caused by not considering other processes that may delay the oxic transition.
To investigate the effect of processes proposed by previous studies20,21,22,27,52,53, we did some sensitivity studies and obtained the same trends as previous studies. As explained in Supplementary Note 1, Koxy decreases if the degassing pressure is high, if the carbon and/or sulfur degassing fluxes are low, and/or if the rate of magnetite deposition via serpentinization is high, which generates oxidizable hydrogen that is a sink for O2.
If Koxy was lower, the atmosphere in the early Archean would be more reducing, and the oxic transition time would be delayed, because of the following processes: a secular decrease in the degassing pressure due to a transition from submarine to subaerial volcanism [e.g., refs. 20,52], a secular increase in the carbon and/or sulfur degassing due to an increase in their continent and/or ocean floor reservoir21, and/or a secular decrease in the magnetite deposition flux via serpentinization, which might result from a decrease in the degree of partial melting of the mantle caused by secular cooling22. The magnitude of the Archean serpentinization flux of H2 is debated, since it is only significant today from slow-spreading centers where ultramafic rocks are exposed53.
There is another possible process that contributed to the delay in th oxic transition along with slow mantle oxidation. Because of the lack of oxidative weathering in the Archean, the carbon isotope input into the atmosphere-ocean could have been relatively heavy compared with mantle values, and so less organic burial was needed for the mass balance27.
We also investigated the uncertainty of the anchoring value of the mantle \(f_{{\rm{O}}_{2}}\!\!\) evolution (Supplementary Note 1). For the standard case (Fig. 2), we modeled the evolution of the mantle \(f_{{\rm{O}}_{2}}\!\!\) anchoring the trend to the average \(f_{{\rm{O}}_{2}}\!\!\) of modern MORB, i.e., ΔFMQ0 = +0.2 [see also Eq. (4)]50. However, this reference value has an uncertainty of 0.3 \({\mathrm{log}}_{10}\) units50. Anchoring the \(f_{{\rm{O}}_{2}}\!\!\) trend to a lower ΔFMQ0 value causes lower mantle \(f_{{\rm{O}}_{2}}\!\!\) in the past, resulting in a more reducing atmosphere in the Archean and delaying the oxic transition time (Supplementary Fig. 8).
Thus, all of the processes discussed in the preceding three paragraphs might affect the GOEʼs timing and so are potentially complicationg factors.
Observations show that erupted volcanic gas is more oxidized, i.e., has a larger ΔFMQ, than its source melt54,55. The relative oxidative state of the volcanic gas results from reactions within a closed gas mixture due to cooling54,55. Consequently, it has been proposed that secular cooling of the mantle could have facilitated the GOE55. Also, observations seem to indicate that it is not possible to calculate the oxidation effect, i.e., Koxy, of the volcanic gas using the ΔFMQ of its source, although we did this in this study. However, the assumptions of these previous studies54,55 need to be reconsidered, as follows.
Recent work56 discusses how cooling affects the oxidation state and the Koxy of a volcanic gas mixture considering two stages of degassing, i.e., the stage where volcanic gas is buffered by its source melt (melt-buffered stage), and the stage where the volcanic gas is a closed system (closed stage). For the closed stage, the same conclusion was reached as in the previous studies54,55, i.e., cooling increases ΔFMQ of a closed volcanic gas compared with that of its source melt. However, in a closed gas mixture, oxidation of a gas should be accompanied by a reduction of another gas, so any reaction in the closed gas mixture does not change the overall O2 sink in the gas mixture56. Hence, to evaluate the Koxy of volcanic gas, we can neglect the effect of reactions after the volcanic gas separated from its source, i.e., the observed difference in the oxidation state between erupted volcanic gas and its source melt.
For the melt-buffered stage, cooling results in reduction of a gas mixture and a decrease in Koxy if the ΔFMQ of the source melt is buffered and constant56. This is because cooling decreases the absolute value of \(f_{{\rm{O}}_{2}}\!\!\) of the FMQ buffer (Supplementary Fig. 4). A trend of smaller Koxy with lower mantle temperature is shown in Supplementary Fig. 3a. However, the oxic transition time is insensitive to temperature if the temperature is higher than the solidus temperature of dry peridotite (~1390 K)57, as shown in Supplementary Fig. 3b. The mantle temperature in the Archean would be between 1600 and 1900 K [e.g., refs. 57,58,59]. Hence, the secular cooling of the mantle would affect less the GOE.
Note that Holland’s f number [e.g., ref. 32] was used in Moussallam et al.48, while Koxy was used in Kadoya et al.56. However, the temperature dependence of Holland’s f number is essentially the same as that of Koxy. This point is explained in Supplementary Note 2.
A decrease in mantle temperature might delay the oxic transition time if the temperature was lower than the solidus temperature of dry peridotite (Supplementary Fig. 3b). Degassing would occur under such a low temperature in arc volcanism because the hydrous phase of the subducted crust can lower the melting temperature [e.g., ref. 60]. However, the island arc basalts are often more oxidized than the mid-ocean ridge basalts or oceanic island basalts61. Hence, we cannot conclude that arc volcanism, whose degassing temperature would be low, delayed the oxic transition time.
A question might arise about our assumption that the \(f_{{\rm{O}}_{2}}\!\!\) of the volcanic gas was equal to that of the upper mantle. Degassing can reduce the source melt, e.g., SO2 degassing48. However, during the melt-buffer stage, i.e., when the volcanic gas mixture interacts with the ambient melt, the \(f_{{\rm{O}}_{2}}\!\!\) of the gas will be equal to that of the melt. In addition, during the closed stage, i.e., after the gas mixture decouples from the ambient melt, any reaction within the gas mixture does not change the oxygenation effect of the gas56. Thus, the oxygenation effect of the gas should be examined using the \(f_{{\rm{O}}_{2}}\!\!\) of the gas when the gas decouples from the melt. Also, at that time, the \(f_{{\rm{O}}_{2}}\!\!\) of the gas would equal to that of the ambient melt, which has already experienced degassing. Therefore, we can calculate Koxy using the \(f_{{\rm{O}}_{2}}\!\!\) from the Archean that is anchored today to modern MORB \(f_{{\rm{O}}_{2}}\!\!\).
It is also noteworthy that the similar trend of the mantle \(f_{{\rm{O}}_{2}}\!\!\) with time is observed by the measurement of \(f_{{\rm{O}}_{2}}\!\) of different rocks46,59. This similarity indicates that the increase in \(f_{{\rm{O}}_{2}}\!\) of melts follows the same trend of the decreasing mantle \(f_{{\rm{O}}_{2}}\!\!\!\) with time, despite the difference in the degree of partial melting, which also supports our assumption that the \(f_{{\rm{O}}_{2}}\!\!\) of the volcanic gas increased with time.
The assumption of the anchoring value of the \(f_{{\rm{O}}_{2}}\!\!\) bears consideration. In this study, we anchored the \(f_{{\rm{O}}_{2}}\!\!\) of the volcanic gas and the melt at the value of the modern MORB, implicitly assuming that the \(f_{{\rm{O}}_{2}}\!\!\) of the melt does not change after the melt decouples from the gas. However, if the \(f_{{\rm{O}}_{2}}\!\!\) of the melt changes after the decoupling from the gas, it also changes the timing of the GOE as indicated by the parameter study of the anchoring valur of the \(f_{{\rm{O}}_{2}}\!\!\) (Supplementary Fig. 8).
Of course, a major question is what drove the increase in mantle \(f_{{\rm{O}}_{2}}\) and, hence, could have driven the GOE. One possibility is that convection-driven homogenization of an initially redox-stratified primordial mantle was responsible for this change45,46,62. The basic idea is that in the early deep mantle, Fe2+ disproportionated to Fe3+ and Fe metal due to high pressure. The latter was lost to the core, leaving a more oxidized lower mantle below a relatively reduced upper mantle. According to Andrault et al.62, the primitive mantle contained excess of Fe3+ corresponding to ~60% of an ocean’s worth of oxygen.
However, another possible driver of upper mantle oxidation has recently gained evidence in its favor. Ancient air dissolved in inclusions of seawater in Archean quartz shows that the nine isotopes of Xe become increasingly isotopically heavy throughout the Archean and early Proterozoic until the GOE63. The most plausible explanation is a very rapid escape of hydrogen to space that dragged along ionized Xe atoms, which would have fractionated Xe isotopes because of mass-dependent escape64.
Substantial loss of a strong reducing agent, i.e., hydrogen, would have oxidized the Earth, with the oxidation affecting the reservoir from which the hydrogen originated. Thus, the mantle would become gradually more oxidized because the hydrogen comes from the decomposition of water in volcanic melts, schematically represented as 3FeO + H2O → Fe3O4 + H2. The upper mantle (down to ~660-km depth) contains the equivalent of ~20% of an ocean’s worth of oxygen as Fe3+ [ref. 65, p. 207]. The Xe isotope data require Archean hydrogen loss from the equivalent of ~10 s of percent of an ocean64. Thus, if the \(f_{{\rm{O}}_{2}}\) trend in Fig. 1b explains the GOE, as shown in Fig. 2b, the \(f_{{\rm{O}}_{2}}\) trend, in turn, may have been driven by hydrogen escaping to space from the Earth’s pre-GOE anoxic atmosphere [e.g., refs. 19,66].
Hydrogen escape as a mechanism for mantle oxidation36 has been proposed previously, but has been rejected over the last two decades because of reports of seemingly constant mantle \(f_{{\rm{O}}_{2}}\) through time39,67,68. Our results suggest that this mechanism may need to be reconsidered.
In summary, we examined whether new data for increasing mantle oxygen fugacity (\(f_{{\rm{O}}_{2}}\)) since the Archean could explain the GOE, when O2 first accumulated in the Earth’s atmosphere. The onset of the GOE can only be properly quantified by considering sources and sinks of oxygen in a global redox balance of the surface environment. The oxygenation parameter Koxy used for this purpose is defined as the ratio of O2 sources to kinetically rapid sinks. For an anoxic atmosphere, Koxy < 1, while for an oxic atmosphere, Koxy > 1; by evaluating when Koxy = 1, we determined how mantle \(f_{{\rm{O}}_{2}}\) trends affected the onset of the GOE.
A more reducing mantle with low \(f_{{\rm{O}}_{2}}\) produces a greater proportion of reducing volcanic gases. So, we found that the data-derived trend of mantle \(f_{{\rm{O}}_{2}}\) likely prevented O2 building up in the atmosphere with relatively high probability (~70% at 3.6 Ga) and caused an oxic transition from Koxy < 1 to Koxy > 1 with >95% probability after 2.5 Ga.
Our calculated timing of the GOE is relatively insensitive to the mantle potential temperature, but depends on the assumed degassing pressure, and total outgassing fluxes of carbon and sulfur relative to total hydrogen. An additional oxidative sink of ferric iron in magnetite deposition has a minor effect, unless this flux in the Archean exceeded ten times the modern flux.
If a trend in mantle \(f_{{\rm{O}}_{2}}\) controlled the timing of the GOE, then the cause of mantle oxidation is ultimately important for setting the tempo of biological evolution because macroscopic, energy-intensive aerobic life was impossible when O2 levels were negligible. Possible drivers of mantle redox evolution are the mixing of a redox heterogeneous mantle or the time-integrated oxidative effect of the breakdown of mantle water in volcanism, and the escape of hydrogen to space. Such processes could also apply to other Earth-like planets elsewhere, and would thus determine whether such planets could be habitats for complex aerobic life with high O2 demand69.
Methods
The redox tipping point of the atmosphere can only be quantified by considering the global redox flux balance of the early atmosphere and ocean, which is as fundamental as mass or energy conservation22,65, p. 221–223].
To evaluate the redox tipping point of the atmosphere, we use the oxygenation parameter, Koxy, which is the ratio of the O2 source fluxes (Foxi) to non-weathering O2 sink fluxes (Fred)22,34,69:
The fluxes, Foxi and Fred, are calculated using fluxes of volcanic gas, such as CO and SO2, organic burial flux, and pyrite burial flux. In the subsequent sections, we will describe a model of each flux, and then explain models of Foxi and Fred.
Fluxes related to source and sink of oxygen
In this section, we explain the components, which are used to calculate the O2 source (Foxi) and a kinetically rapid sink of O2 (Fred). For the calculation of Foxi and Fred, see the next section.
Hydrogen is degassed to the ocean–atmosphere system as hydrogen molecules (H2), water vapor (H2O), methane (CH4), and hydrogen sulfide (H2S). Accordingly, a total flux of hydrogen (Fhydrogen) can be expressed as follows:
where Fx is a flux of x. Methane contains the equivalent of two H2 molecules, so \({F}_{{{\rm{C}}{\rm{H}}}_{4}}\) is weighted by a factor of 2.
Carbon is degassed to the ocean–atmosphere system as carbon dioxide (CO2), carbon monoxide (CO), and methane (CH4), and deposited as organic matter (org) and carbonate (carb). Since we assume that carbon is in a steady state, the total flux of carbon (Fcarbon) is equal to input and output fluxes, which can be expressed as follows:
where Fx is a flux of x as in Eq. (3).
The ratio of the organic burial to the total carbon flux (i.e., forg = Fcarb/Fcarbon) can be evaluated using the geological record of carbon isotopes in organic and inorganic carbon [e.g., ref. 24]. Supplementary Fig. 1 shows the temporal change in the forg, which is derived by Krissansen-Totton et al.24.
Similarly, sulfur (S) is degassed to the ocean–atmosphere system as sulfur dioxide (SO2) and hydrogen sulfide (H2S), and deposited as pyrite (FeS2) and sulfate (e.g., CaSO4). However, we neglect the deposition of sulfate because we focus on the Archean eon, the surface environment was anoxic, and there was very little sulfate (~2.5 μM, i.e., 0.01% of modern level) in the Archean ocean70,71. Since we assume that sulfur is in steady state, a total flux of sulfur (Fsulfur) is equal to input and output fluxes, which can be expressed as follows:
where Fx is a flux of x as in Eq. (3).
Sources and sinks of oxygen
In this section, we explain models of the O2 source (Foxi) and a kinetically rapid sink of O2 (Fred), which are used for the calculation of Koxy (Eq. (2)).
We take H2O and CO2 to be redox-neutral, so hydrogen (H2), carbon monoxide (CO), and methane (CH4) are sinks of oxygen, as follows:
Hence, one mole of H2 degassing corresponds to 0.5 mole of O2 consumption. Similarly, one mole of CO and CH4 degassing corresponds to 0.5 and 2 moles of O2 consumption, respectively.
On the other hand, the burial of organic matter (CH2O) is a source of oxygen, as follows:
Hence, one mole of the burial of organic matter corresponds to one mole of O2 production.
We also assume that SO2 is redox-neutral, so H2S is a sink of oxygen, as follows:
Also, reduction of SO2 must work as a source of oxygen, as follows:
Hence, one mole of SO2 degassing corresponds to 1.25 mole of O2 production. On the other hand, one mole of H2S degassing corresponds to 0.25 mole of O2 consumption.
As explained above, degassing of H2, CO, CH4, and H2S is a sink of oxygen. Accordingly, Fred is expressed as follows:
On the other hand, burial of organic matter and SO2 degassing are sources of oxygen. Accordingly, Foxi is expressed as follows:
Derivation of oxygenation parameter
Substituting Eqs. (12) and (13) into Eq. (2), Koxy is rewritten as follows:
We now define χc and χs as follows:
In addition, we define \({r}_{{{{\rm{H}}_2}}}\) as the ratio of a flux of hydrogen molecule to a total flux of hydrogen:
Similarly, we defined the following parameters:
If we substitute from the above for the various gas fluxes and flux of organic burial, Eq. (14) can be rewritten as
If we now divide the above equation by Fhydrogen, we arrive at the form
Kasting22 argues that an additional O2 flux, in the form of \({F}_{{{{\rm{Fe}}_3{\rm{O}}_4}}}\), could be included in the denominator of Eq. (2). If we take FeO as the redox reference state of iron for the Archean surface environment, then the formation of ferric iron in magnetite (\({{\rm{Fe}}}_{2}^{3+}{{\rm{Fe}}}^{2+}{{\rm{O}}}_{4}\)) in iron formations or during serpentinization and its burial removes oxidizing power from the surface environment or, equivalently, is an input flux of reducing power. We initially neglect the deposition of magnetite, and then examine its specific influence later. When the magnetite deposition is taken into account, Koxy can be rewritten as
where \({F}_{{{{\rm{Fe}}_3{\rm{O}}_4}}}\) is an O2 consumption via magnetite deposition in the unit of T mol O2 yr−1. For example, the modern \({F}_{{{{\rm{Fe}}_3{\rm{O}}_4}}}\) is 0.05 ∼ 0.2 T mol O2 yr−1 72,73.
Equilibrium state of volcanic gases
In this section, we will explain how to calculate the flux ratios, i.e., rx for each volatile species x in Eq. (20).
To calculate fluxes of volcanic gases, we first assume that equilibrium states are achieved for volcanic volatiles in the silicate melt:
These equations have equilibrium constants that are as follows, in terms of fugacities (fx) for each volatile species x:
We assume that gas fluxes will be in proportion to their fugacities, e.g., \({f}_{{{{\rm{H}}_2}}}={P}_{{\rm{tot}}}\times {F}_{{{\rm{H}}}_{2}}/{F}_{{\rm{tot}}}\). Here, Ptot is a total pressure under which degassing occurs. Ftot is a total degassing flux that can be written as
Then, we obtain the following equations:
where \(f_{{\rm{O}}_{2}}\) is a oxygen fugacity, which we will explain later. We calculate equilibrium constants of the above reactions using data of NIST74. According to Eqs. (3)–(5), we also obtain the following equations:
Hence, given mantle temperature, a total pressure, and oxygen fugacity in the mantle, and solving Eqs. (26) and (27), we obtain fluxes of each molecular species.
Hereafter, we explain how to solve Eqs. (26) and (27). First of all, we defined variables as follows:
Then, Eq. (27) can be rewritten as follows:
Hence,
The unknown variable, \({f}_{{{{\rm{H}}_2{\rm{O}}}}}\), is obtained by solving the following equation:
Oxygen fugacity of mantle
As explained above, we need the oxygen fugacity, \(f_{{\rm{O}}_{2}}\), of volcanic gas to calculate the volcanic gas speciation. To evaluate the Koxy of the gas, we can use the \(f_{{\rm{O}}_{2}}\) of the source of the gas, i.e., the mantle melt56. In addition, both experimental75 and empirical data from natural samples76 show that the mantle melt records the same \(f_{{\rm{O}}_{2}}\) as its mantle residue, and therefore its mantle source. Hence, we evaluate the Koxy using the \(f_{{\rm{O}}_{2}}\) of the mantle.
According to Aulbach and Stagno45 and Nicklas et al.46, the oxygen fugacity of the mantle has increased by +0.9 ± 0.2 [2 SD] in \({\mathrm{log}}_{10}\) units during the past 3 Gyr. Since two independent datasets show the same trend, secular oxidation of the mantle is corroborated. In addition, the oxygen fugacity of the modern mantle is +0.2 ± 0.6 [2 SD] in \({\mathrm{log}}_{10}\) units above the FMQ buffer50. Here, FMQ is the fayalite–magnetite–quartz synthetic buffer, which defines \(f_{{\rm{O}}_{2}}\) at a particular temperature and pressure, e.g., \(f_{{\rm{O}}_{2}}\) = 10−8.5 bar at 1200 °C (1473.15 K and 0.5 MPa). Hence, we modeled the evolution of the mantle \(f_{{\rm{O}}_{2}}\) in \({\mathrm{log}}_{10}\) units above the FMQ buffer as follows:
where t is time in units of Ga, and the slope, a, is −0.29 ± 0.05 [2 SD] in units of per Ga. For the standard case, we set ΔFMQ0 at 0.2 \({\mathrm{log}}_{10}\) units50, and later discuss the effect of the variation of this parameter.
Figure 1b shows the evolutionary range of oxygen fugacity for the standard case with its uncertainties. Further details for the comparison of the datasets of Fig. 1b are given in Supplementary Note 3.
Other input parameters
As indicated in Eqs. (30) and (31), the flux ratios, rx in Eq. (20), depend on the total flux ratios of carbon and sulfur relative to hydrogen, χc and χs. In addition, the flux ratios also depend on the temperature and pressure of the system.
Initially, we assume modern values for the total flux ratios of carbon and sulfur relative to hydrogen. The modern total degassing fluxes of hydrogen, carbon, and sulfur (in all their forms) are 97 ± 20, 9 ± 2, and 2.2 ± 0.7 T mol yr−1, respectively [ref. 65, p. 203 and p. 221]. Hence, present-day χc = 0.1 ± 0.03 and χs = 0.023 ± 0.0086. Later, we examine the effect of these parameters on the results of our modeling.
Similarly, we use a modern mantle potential temperature of 1623.15 K (1350 °C)77 and a pressure of 0.5 MPa78 first. We examine the sensitivity to these parameters later.
Data availability
The datasets generated during the current study are available in the Zenodo repository [https://doi.org/10.5281/zenodo.3668382].
Code availability
The source code used in this study is also available in the Zenodo repository [https://doi.org/10.5281/zenodo.3668382].
References
Lyons, T. W., Reinhard, C. T. & Planavsky, N. J. The rise of oxygen in Earth’s early ocean and atmosphere. Nature 506, 307–315 (2014).
Planavsky, N. J. et al. Evidence for oxygenic photosynthesis half a billion years before the Great Oxidation Event. Nat. Geosci. 7, 283–286 (2014).
Satkoski, A. M., Beukes, N. J., Li, W. Q., Beard, B. L. & Johnson, C. M. A redox-stratified ocean 3.2 billion years ago. Earth Planet. Sci. Lett. 430, 43–53 (2015).
Kasting, J.F., Schopf, J.W. & Klein, C. Models relating to Proterozoic atmospheric and oceanic chemistry. in The Proterozoic Biosphere: A Multidisciplinary Study (eds. Schopf, J. W. & Klein, C.) 1185–1187 (Cambridge University Press, Cambridge, 1992).
Olson, S. L., Kump, L. R. & Kasting, J. F. Quantifying the areal extent and dissolved oxygen concentrations of Archean oxygen oases. Chem. Geol. 362, 35–43 (2013).
Godfrey, L. V. & Falkowski, P. G. The cycling and redox state of nitrogen in the Archaean ocean. Nat. Geosci. 2, 725–729 (2009).
Garvin, J., Buick, R., Anbar, A. D., Arnold, G. L. & Kaufman, A. J. Isotopic evidence for an aerobic nitrogen cycle in the latest Archean. Science 323, 1045–1048 (2009).
Stüeken, E. E. & Buick, R. Environmental control on microbial diversification and methane production in the Mesoarchean. Precambrian Res. 304, 64–72 (2018).
Schirrmeister, B. E., Gugger, M. & Donoghue, P. C. J. Cyanobacteria and the Great Oxidation Event: evidence from genes and fossils. Palaeontology 58, 769–785 (2015).
Kaufman, A. J. et al. Late Archean biospheric oxygenation and atmospheric evolution. Science 317, 1900–1903 (2007).
Anbar, A. D. et al. A whiff of oxygen before the Great Oxidation Event? Science 317, 1903–1906 (2007).
Reinhard, C. T., Raiswell, R., Scott, C., Anbar, A. D. & Lyons, T. W. A late Archean sulfidic sea stimulated by early oxidative weathering of the continents. Science 326, 713–716 (2009).
Duan, Y. et al. Molybdenum isotope evidence for mild environmental oxygenation before the Great Oxidation Event. Geochim. Cosmochim. Acta 74, 6655–6668 (2010).
Kendall, B., Brennecka, G. A., Weyer, S. & Anbar, A. D. Uranium isotope fractionation suggests oxidative uranium mobilization at 2.50 Ga. Chem. Geol. 362, 105–114 (2013).
Kendall, B., Creaser, R. A., Reinhard, C. T., Lyons, T. W. & Anbar, A. D. Transient episodes of mild environmental oxygenation and oxidative continental weathering during the late Archean. Sci. Adv. 1, e1500777 (2015).
Stüeken, E. E., Buick, R. & Anbar, A. D. Selenium isotopes support free O-2 in the latest Archean. Geology 43, 259–262 (2015).
Kendall, B. et al. Pervasive oxygenation along late Archaean ocean margins. Nat. Geosci. 3, 647–652 (2010).
Ostrander, C. M. et al. Fully oxygenated water columns over continental shelves before the Great Oxidation Event. Nat. Geosci. 12, 186–191 (2019).
Catling, D. C., Zahnle, K. J. & McKay, C. P. Biogenic methane, hydrogen escape, and the irreversible oxidation of early Earth. Science 293, 839–843 (2001).
Kump, L. R. & Barley, M. E. Increased subaerial volcanism and the rise of atmospheric oxygen 2.5 billion years ago. Nature 448, 1033–1036 (2007).
Holland, H. D. Why the atmosphere became oxygenated: a proposal. Geochim. Cosmochim. Acta 73, 5241–5255 (2009).
Kasting, J. F. What caused the rise of atmospheric O2? Chem. Geol. 362, 13–25 (2013).
Lee, C. T. A. et al. Two-step rise of atmospheric oxygen linked to the growth of continents. Nat. Geosci. 9, 417–424 (2016).
Krissansen-Totton, J., Buick, R. & Catling, D. C. A statistical analysis of the carbon isotope record from the Archean to Phanerozoic and implications for the rise of oxygen. Am. J. Sci. 315, 275–316 (2015).
Bjerrum, C. J. & Canfield, D. E. New insights into the burial history of organic carbon on the early Earth. Geochem. Geophys. Geosyst. 5, Q08001 (2004).
Schrag, D. P. Authigenic carbonate and the history of the global carbon cycle. Science 339, 1383–1383 (2013).
Derry, L.A. Organic carbon cycling and the lithosphere. in Treatise on Geochemistry (Second Edition) (eds. Holland, H. D. & Turekian, K. K.) 239–249 (Elsevier, Oxford, 2014).
Daines., S. J., Mills, B. J. W. & Lenton, T. M. Atmospheric oxygen regulation at low proterozoic levels by incomplete oxidative weathering of sedimentary organic carbon. Nat. Commun. 8, 14379 (2017).
Nakamura, K. & Kato, Y. Carbonatization of oceanic crust by the seafloor hydrothermal activity and its significance as a CO2 sink in the early archean. Geochim. Cosmochim. Acta 68, 4595–4618 (2004).
Fallick, A.E., Melezhik, V.A. & Simonson, B. M. The ancient anoxic biosphere was not as we know it. in Biosphere Origin and Evolution (eds. Dobretsov, N., Kolchanov, N., Rozanov, A., & Zavarzin, G.) 169–188 (Springer US, Boston, MA, 2008).
Sun, X. L. & Turchyn, A. V. Significant contribution of authigenic carbonate to marine carbon burial. Nat. Geosci. 7, 201–204 (2014).
Holland, H. D. Volcanic gases, black smokers, and the Great Oxidation Event. Geochim. Cosmochim. Acta 66, 3811–3826 (2002).
Catling, D. C. & Claire, M. W. How Earthas atmosphere evolved to an oxic state: a status report. Earth Planet. Sci. Lett. 237, 1–20 (2005).
Claire, M. W., Catling, D. C. & Zahnle, K. J. Biogeochemical modelling of the rise in atmospheric oxygen. Geobiology 4, 239–269 (2006).
Planavsky, N. J. et al. A case for low atmospheric oxygen levels during Earth’s middle history. Emerg. Top. Life Sci. 2, 149–159 (2018).
Kasting, J. F., Eggler, D. H. & Raeburn, S. P. Mantle redox evolution and the oxidation state of the Archean atmosphere. J. Geol. 101, 245–257 (1993).
Kump, L. R., Kasting, J. F. & Barley, M. E. Rise of atmospheric oxygen and the "upside-down” Archean mantle. Geochem. Geophys. Geosyst. 2, 2000GC000114 (2001).
Canil, D. Vanadium partitioning and the oxidation state of archaean komatiite magmas. Nature 389, 842–845 (1997).
Delano, J. W. Redox history of the Earth’s interior: implications for the origin of life. Orig. Life Evol. Biosph. 31, 311–341 (2001).
Li, Z.-X. A. & Lee, C.-T. A. The constancy of upper mantle fO2 through time inferred from V/Sc ratios in basalts. Earth Planet. Sci. Lett. 228, 483–493 (2004).
Trail, D., Watson, E. B. & Tailby, N. D. The oxidation state of Hadean magmas and implications for early Earthas atmosphere. Nature 480, 79–82 (2011).
Rollinson, H., Adetunji, J., Lenaz, D. & Szilas, K. Archaean chromitites show constant Fe3+/Fe in Earth’s asthenospheric mantle since 3.8 Ga. Lithos 282, 316–325 (2017).
Canil, D. & Fedortchouk, Y. Olivine-liquid partitioning of vanadium and other trace elements, with applications to modern and ancient picrites. Can. Mineral. 39, 319–330 (2001).
Wang, J. et al. Oxidation state of arc mantle revealed by partitioning of V, Sc, and Ti between mantle minerals and basaltic melts. J. Geophys. Res. 124, 4617–4638 (2019).
Aulbach, S. & Stagno, V. Evidence for a reducing Archean ambient mantle and its effects on the carbon cycle. Geology 44, 751–754 (2016).
Nicklas, R. W. et al. Secular mantle oxidation across the Archean-Proterozoic boundary: Evidence from V partitioning in komatiites and picrites. Geochim. Cosmochim. Acta 250, 49–75 (2019).
Mallmann, G. & O’Neill, H. S. Calibration of an empirical thermometer and oxybarometer based on the partitioning of Sc, Y and V between olivine and silicate melt. J. Petrol. 54, 933–949 (2013).
Moussallam, Y. et al. The impact of degassing on the oxidation state of basaltic magmas: a case study of Kilauea volcano. Earth Planet Sci. Lett. 450, 317–325 (2016).
Berry, A. J., Stewart, G. A., O’Neill, H. S. C., Mallmann, G. & Mosselmans, J. F. W. A re-assessment of the oxidation state of iron in MORB glasses. Earth Planet. Sci. Lett. 483, 114–123 (2018).
O’Neill, H. S. C., Berry, A. J. & Mallmann, G. The oxidation state of iron in mid-ocean ridge basaltic (MORB) glasses: implications for their petrogenesis and oxygen fugacities. Earth Planet. Sci. Lett. 504, 152–162 (2018).
Philippot, P. et al. Globally asynchronous sulphur isotope signals require re-definition of the Great Oxidation Event. Nat. Commun. 9, 1–10 (2018).
Gaillard, F., Scaillet, B. & Arndt, N. T. Atmospheric oxygenation caused by a change in volcanic degassing pressure. Nature 478, 229–233 (2011).
Keir, R. S. A note on the fluxes of abiogenic methane and hydrogen from mid-ocean ridges. Geophy. Res. Lett. 37, L24609 (2010).
Oppenheimer, C. et al. Influence of eruptive style on volcanic gas emission chemistry and temperature. Nat. Geosci. 11, 678–681 (2018).
Moussallam, Y., Oppenheimer, C. & Scaillet, B. On the relationship between oxidation state and temperature of volcanic gas emissions. Earth Planet. Sci. Lett. 520, 260–267 (2019).
Kadoya, S., Catling, D. C., Nicklas, R. W., Puchtel, I. S. & Anbar, A. D. Mantle cooling causes more reducing volcanic gases and gradual reduction of the atmosphere. Geochem. Perspect. Lett. 13, 25–29 (2020).
Hirschmann, M. M. Mantle solidus: experimental constraints and the effects of peridotite composition. Geochem. Geophys. Geosyst. 1, 2000GC000070 (2000).
Nisbet, E. G., Cheadle, M. J., Arndt, N. T. & Bickle, M. Constraining the potential temperature of the Archean mantle—a review of the evidence from komatiites. Lithos 30, 291–307 (1993).
Aulbach, S. & Arndt, N. T. Eclogites as palaeodynamic archives: evidence for warm (not hot) and depleted (but heterogeneous) Archaean ambient mantle. Earth Planet. Sci. Lett. 505, 162–172 (2019).
Till, C. B., Grove, T. L. & Withers, A. C. The beginnings of hydrous mantle wedge melting. Contrib. Mineral. Petrol. 163, 669–688 (2012).
Carmichael, I. S. E. The redox states of basic and silicic magmas: a reflection of their source regions? Contrib. Mineral. Petrol. 106, 129–141 (1991).
Andrault, D. et al. Large oxygen excess in the primitive mantle could be the source of the great oxygenation event. Geochem. Perspect. Lett. 6, 5–10 (2018).
Avice, G. et al. Evolution of atmospheric xenon and other noble gases inferred from Archean to Paleoproterozoic rocks. Geochim. Cosmochim. Acta 232, 82–100 (2018).
Zahnle, K. J., Gacesa, M. & Catling, D. C. Strange messenger: a new history of hydrogen on Earth, as told by xenon. Geochim. Cosmochim. Acta 244, 56–85 (2019).
Catling, D.C. & Kasting, J.F. Atmospheric Evolution on Inhabited and Lifeless Worlds. (Cambridge University Press, New York, 2017).
Zahnle, K.J. & Catling, D.C. Waiting for oxygen. in Special Paper 504: Early Earth’s Atmosphere and Surface Environment (eds. Shaw, G. H.) 37–48 (Geological Society of America, Boulder, 2014).
Canil, D. Vanadium in peridotites, mantle redox and tectonic environments: Archean to present. Earth Planet. Sci. Lett. 195, 75–90 (2002).
Lee, C. T. A., Leeman, W. P., Canil, D. & Li, Z. X. A. Similar V/Sc systematics in morb and arc basalts: implications for the oxygen fugacities of their mantle source regions. J. Petrol. 46, 2313–2336 (2005).
Catling, D. C., Glein, C. R., Zahnle, K. J. & Mckay, C. P. Why O-2 is required by complex life on habitable planets and the concept of planetary “oxygenation time”. Astrobiology 5, 415–438 (2005).
Canfield, D. E., Habicht, K. S. & Thamdrup, B. The Archean sulfur cycle and the early history of atmospheric oxygen. Science 288, 658–661 (2000).
Crowe, S. A. et al. Sulfate was a trace constituent of Archean seawater. Science 346, 735–739 (2014).
Sleep, N.H. Dioxygen over geologic time. in Metal Ions in Biological Systems, Vol. 43, Biogeochemical Cycles of Elements (eds. Sigel, H. & Sigel, R.) 49–73 (Taylor & Francis, Boca Raton, FL, 2005).
Canfield, D. E., Rosing, M. T. & Bjerrum, C. Early anaerobic metabolisms. Philos. Trans. R. Soc. B 361, 1819–1834 (2006).
Chase, M.W.NIST-JANAF thermochemical tables, Fourth edition (American Institute of Physics, 1998).
Davis, F. A. & Cottrell, E. Experimental investigation of basalt and peridotite oxybarometers: Implications for spinel thermodynamic models and Fe3+ compatibility during generation of upper mantle melts. Am. Mineral. 103, 1056–1067 (2018).
Birner, S. K., Cottrell, E., Warren, J. M., Kelley, K. A. & Davis, F. A. Peridotites and basalts reveal broad congruence between two independent records of mantle fo2 despite local redox heterogeneity. Earth Planet. Sci. Lett. 494, 172–189 (2018).
Herzberg, C., Condie, K. & Korenaga, J. Thermal history of the Earth and its petrological expression. Earth Planet. Sci. Lett. 292, 79–88 (2010).
Holland, H.D. The Chemical Evolution of the Atmosphere and Oceans. (Princeton University Press, Princeton, 1984).
Acknowledgements
Funding support came from NSF Frontiers in Earth System Dynamics award No. 1338810.
Author information
Authors and Affiliations
Contributions
D.C.C. designed the study. S.K. performed the calculation and data analysis. S.K. with D.C.C. wrote the paper with input from R.W.N., I.S.P., and A.D.A. All authors discussed the results and commented on the paper.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Peer review information Nature Communications thanks Bruno Scaillet and the other, anonymous, reviewer(s) for their contribution to the peer review of this work. Peer reviewer reports are available.
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Kadoya, S., Catling, D.C., Nicklas, R.W. et al. Mantle data imply a decline of oxidizable volcanic gases could have triggered the Great Oxidation. Nat Commun 11, 2774 (2020). https://doi.org/10.1038/s41467-020-16493-1
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-020-16493-1
This article is cited by
-
Phosphorus availability on the early Earth and the impacts of life
Nature Geoscience (2023)
-
Sub-arc mantle fugacity shifted by sediment recycling across the Great Oxidation Event
Nature Geoscience (2023)
-
Plate Tectonics: The Stabilizer of Earth’s Habitability
Journal of Earth Science (2023)
-
Reconstructing Earth’s atmospheric oxygenation history using machine learning
Nature Communications (2022)
-
Oxidation of Archean upper mantle caused by crustal recycling
Nature Communications (2022)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.