Abstract
Plasmons depend strongly on dimensionality: while plasmons in three-dimensional systems start with finite energy at wavevector q = 0, plasmons in traditional two-dimensional (2D) electron gas disperse as \(\omega _p \sim \sqrt q\). However, besides graphene, plasmons in real, atomically thin quasi-2D materials were heretofore not well understood. Here we show that the plasmons in real quasi-2D metals are qualitatively different, being virtually dispersionless for wavevectors of typical experimental interest. This stems from a broken continuous translational symmetry which leads to interband screening; so, dispersionless plasmons are a universal intrinsic phenomenon in quasi-2D metals. Moreover, our ab initio calculations reveal that plasmons of monolayer metallic transition metal dichalcogenides are tunable, long lived, able to sustain field intensity enhancement exceeding 107, and localizable in real space (within ~20 nm) with little spreading over practical measurement time. This opens the possibility of tracking plasmon wave packets in real time for novel imaging techniques in atomically thin materials.
Similar content being viewed by others
Introduction
Plasmons are quantum collective motions of electrons in solids arising from the long-range Coulomb interaction. Since these propagating collective modes are strongly affected by boundary/geometric effects, plasmon modes can be tuned by assembling nanostructured materials with repeated patterns, or by selectively exciting modes that only exists on the surface of metals, such as the surface plasmon polaritons (SPPs)1,2,3,4. In addition, there has been great interest in plasmons in atomically thin (one to a few atomic layer) crystalline metals such as graphene5,6,7,8,9. Graphene plasmons are highly tunable and display the typical dispersion relation10 \(\omega _p \sim \sqrt q\) of an ideal 2D electron gas for q → 0, and can be observed with techniques ranging from electron-energy loss spectroscopy (EELS) to nano-imaging of interference patterns generated with atomic-force microscopy (AFM) tips1,2,4,11.
Besides graphene, plasmons in other atomically thin quasi-2D metals have been reported12,13,14, some displaying intriguing dispersion relations. Previous ab initio studies have shown that plasmons on monolayer metallic transition metal dichalcogenides (TMDs) disperse as \(\omega _p \sim \sqrt q\) at small q and can have high energy (~1 eV) that are nearly dispersionless for a large range of wavevectors (q ~ 0.1 Å−1 to 0.3 Å−1)15,16,17,18. Similar findings were found for other quasi-2D metals, such as borophene19. The previous studies however have basically overlooked the origin and significance of this dispersionless behavior. As will become clear in the present paper, dispersionless quasi-2D plasmons could find a variety of exciting applications, as flat dispersion relations can translate into real-space localization of plasmon wave packets using practical excitations. Moreover, it is important to unravel what is the physical origin of these dispersionless plasmons and to assess whether they are (or can be controllably made to be) sufficiently long lived for technological applications20.
Here, we demonstrate rigorously why the plasmon dispersion relation in real, quasi-2D metals is qualitatively different from that in idealized 2D metals (i.e., a homogeneous electron gas), in metallic slabs, and of the SPPs, tending to flatten at relatively large wavevectors for any quasi-2D crystals regardless of their chemical composition or nature of the energy bands crossing the Fermi energy. The local-fields screening arising from interband transitions in real quasi-2D crystalline metals21,22,23,24,25,26,27,28, which is not present in the 2D electron gas model, is the physics behind these dispersionless intrinsic plasmons. This behavior is universal for any atomically thin quasi-2D crystalline metal as long as there is a well-separated band (or set of bands) either completely occupied or unoccupied near the Fermi energy (as shown in Fig. 1a), a condition that is not fulfilled in doped graphene.
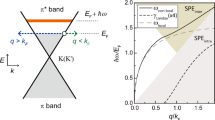
a Calculated GW quasiparticle band structure of a prototypical quasi-2D metal, monolayer TaS2. The arrows highlight the intraband and interband electronic transitions that contribute to a plasmon excitation. The Fermi energy is set at zero. b Calculations of the plasmon dispersion relation of monolayer TaS2. The green curve is the result of the full ab initio calculation, which displays a flattening of the plasmon dispersion relation; the blue curve corresponds to the result of a calculation including only the intraband transitions, which displays a dispersion relation much closer to ~\(\sqrt q\) (red curve). The inset shows the small-q behavior of the plasmon dispersion relation, where both calculations follow a \(\sqrt q\) dependence. c Effective 2D dielectric function εeff(q) for two point charges located at the innermost portion of three different quasi-2D materials. Since εeff(q) does not include intraband (but only interband) transitions, its behavior is similar to quasi-2D semiconductors. For very small wavevectors, there is no screening (εeff(q = 0) = 1)) since very long wavelength perturbations correspond to charges being so far apart that they only experience the screening of vacuum. For increasing wavevector q, the charges get closer, so more of the field lines connecting them are confined to the interior of the quasi-2D material. εeff(q) increases linearly with q until it reaches near a maximum, and subsequently decreases with increasing q after the maximum due to the intrinsic inability of the medium to screen very short-wavelength excitations.
Results
Universal dispersionless plasmons in real quasi-2D metals
To shed light on this universal flat plasmon dispersion relation, we depict in Fig. 1 the computed plasmon dispersion relation from first principles for monolayer TaS2. To perform the calculation, with atomistic local-field effects, we have to develop an algorithm to compute plasmons for arbitrarily small wavevectors, which heretofore was a bottleneck for ab initio calculations (see Methods section). As expected from a homogeneous 2D electron gas picture, we find that plasmons in monolayer TaS2 in Fig. 1b follows a \(\sqrt q\) dispersion relation up to a wavevector of q ~0.05 Å−1; however, the dispersion relation deviates significantly from this \(\sqrt q\) relation afterwards (it becomes flattened), with an onset that is large compared to the wavevector of visible light but still very small compared to the Brillouin zone size of ~1.1 Å−1. This deviation is related to the broken continuous translational symmetry in real crystals (which only have discrete crystal translational symmetry). A homogeneous 2D electron gas with continuous in-plane translation symmetry can only have a single partially occupied electronic band that extends to infinite q, and only the intraband electronic transitions contribute to the system’s dielectric screening. On the other hand, both intraband and interband electronic transitions contribute to screening in a real quasi-2D metal such as monolayer TaS2, and, as we argue here, the interband transitions are the reason behind the appearance of virtually dispersionless plasmons. Indeed, the plasmon dispersion relation of monolayer TaS2 obtained by only considering intraband transitions (blue curve in Fig. 1b) follows a \(\sqrt q\) dispersion relation up to much larger wavevectors16.
To gain some fundamental insights, we derive a general microscopic analytic expression for the plasmon dispersion relation for a quasi-2D metal, going beyond the 2D homogenous electron gas model. Our approach is to recast rigorously the plasmon excitations of a real quasi-2D material into contributions from two components: (1) an effective 2D electron gas (which is defined to consist of only those states of the system in the bands crossing the Fermi level); and (2) a nonlocal polarizable medium that incorporates the effects of the interband transitions in the real material (see Fig. 1a). Under the condition of long plasmon wavelengths, we derive (see SI section), by solving for the zeros of the total dielectric function, the following expression for the plasmon frequency,
where the symbolic notation \(\left[ {\frac{n}{{m^ \ast }}\left( {\mathbf{q}} \right)} \right]_{{\mathrm{eff}}}\) is a function that is a q-dependent generalization of the ratio of the carrier density n by the effective mass \({m^ \ast }\) of an anisotropic 2D system (see Methods section), which only depends on the nature of the band (or set of bands) crossing the Fermi energy. The plasmon frequency is further dependent on an effective 2D dielectric constant, εeff(q), which includes contributions to the screening due to all the intrinsic interband transitions (indicated by the green arrows in Fig. 1a) of the quasi-2D material, excluding the intraband contributions from the set of bands crossing the Fermi energy, as well as due to any external environment (such as a substrate). As demonstrated below, εeff(q) is responsible for the flat dispersion relation discussed above.
The fundamental idea here is that the effective dielectric function εeff(q) from the interband transitions of the material essentially has the same analytical expression and behavior as the dielectric function derived in the context of quasi-2D semiconductor screening (see, e.g., Ref. 28), and it allows us to understand and determine, from Eq. (1), plasmon dispersion relations in quasi-2D metals using established models for quasi-2D semiconductors21 together with information from ab initio calculations23,26,27,28,29,30. In particular, the semiconductor-like interband effective 2D dielectric screening εeff(q) of a monolayer material is not a constant, but increases linearly from unity with wavevector at small q, since very long-wavelength excitations effectively only experience screening from the vacuum or substrate (see Fig. 1c).
We show that, for long wavelength excitations, \(\left[ {\frac{n}{{m^ \ast }}\left( {\mathbf{q}} \right)} \right]_{{\mathrm{eff}}}\) does not depend on q, while \(\varepsilon _{{\mathrm{eff}}}\left( {\mathbf{q}} \right)\) can be approximated as \(\varepsilon _{{\mathrm{eff}}}\left( q \right) \approx \frac{{1 + \varepsilon _s}}{2} + \rho _0q\), where εs is the dielectric constant of the insulating substrate and ρ0 is a screening length intrinsic to the quasi-2D material under consideration arising from the interband transitions (see Methods section). In this limit,
Equation (2) is one of the key results of this work. It shows that plasmons in real quasi-2D metals display a universal tendency to flatten for wavevectors above a critical wavevector qc of the order of \(\sim \frac{{\varepsilon _s + 1}}{{2\rho _0}}\), resulting in a plasmon frequency of \(\omega _p^{{\mathrm{flat}}} = \sqrt {\frac{{2\pi {\mathrm{e}}^2}}{{\rho _0}}\left[ {\frac{{n}}{{{m}^ \ast }}} \right]_{{\mathrm{eff}}}}\) that is independent of the substrate dielectric constant εs, although importantly the substrate dielectric constant can dramatically change the value of qc and the dispersion relation for q < qc. We emphasize here that this phenomenon arises without considering interactions with photons, and hence is not a plasmon-polariton effect. Moreover, Eq. (2) holds in practice even for larger plasmon wavevectors, since the effective ratio \(\left[ {\frac{n}{{m^ \ast }}} \right]_{{\mathrm{eff}}}\left( q \right)\) decreases for larger values of q due to a typical reduction of the quasiparticle band velocity away from the Fermi surface, while the effective interband screening εeff(q) also saturates for larger q28. Since these two effects partially cancel each other, the main features predicted by Eq. (2)−that the plasmon dispersion relation flattens at larger q and has an asymptotic energy that does not depend on the substrate–holds from our ab initio calculations for all quasi-2D materials studied here up to q ~0.3 Å−1.
The plasmon dispersion relation in atomically thin quasi-2D metals is in fact conceptually different from that of metallic slabs with thickness large compared to interatomic distance, which support on each surface (within the classical dielectric response framework) a surface plasmon-polariton dispersion relation that flattens at a wavevector \(q_c \sim \frac{{\omega _p^{{\mathrm{bulk}}}}}{{\sqrt 2 c}}\), where \(\hbar \omega _p^{{\mathrm{bulk}}}\) is the bulk plasmon energy31,32 (Fig. 2a). In contrast, as we demonstrated above, systems with atomically thin thickness support dispersionless quasi-2D plasmons with a very different qc ~ 1/ρ0: the 2D screening length ρ0 in these systems (ρ0~25 Å for monolayer metallic TMDs) is not directly related to the thickness of the material nor the bulk plasmon energy28; it is a new length scale that emerges due to the quantum nature of these systems, which depends primarily on the energy for the interband transitions and the in-plane polarizability of the orbitals involved in these transitions. In addition, as mentioned above, neither retardation effects in the Coulomb interaction nor the hybridization of electronic transitions with the transverse electromagnetic fields are included in our calculations, so conventional hybrid plasmon-polariton modes cannot be responsible for the dispersionless plasmons in atomically thin metals. Further, the dispersionless quasi-2D plasmons here are also qualitatively and quantitatively different from plasmons in conventional thin metallic slabs, which support surface plasmons with an energy relation \(\frac{{\hbar \omega _p^{{\mathrm{bulk}}}}}{{\sqrt 2 }}\sqrt {1 \pm e^{ - qd}}\), where the positive (negative) sign corresponds to a mode of antisymmetric (symmetric) relative oscillations of the electron density on the opposite surfaces, and d is the thickness of the slab31,33,34 (Fig. 2b). For materials such as bulk metallic TMDs, the bulk plasmon energy is of the order of 20 eV; a classical (and inappropriate) dielectric description of a metallic film of atomically thin thickness (d ~ 5Å) would yield a surface plasmon energy and a critical wavevector ~1/d for dispersionless surface plasmons that are both over one order of magnitude larger than the values found in our ab initio calculations for monolayer TaS2 (Fig. 2c). These differences highlight that the dispersionless plasmons in quasi-2D materials given by Eq. (1) are conceptually different from classical surface plasmons or hybrid plasmon-polariton modes, and they have instead their origin in the broken translational symmetry in atomically thin metals.
a Dispersion relation for a surface plasmon and the lower-energy surface plasmon-polariton (SPP) branch on the surface of a three-dimensional metal with a bulk plasmon energy \(\hbar \omega _p^{{\mathrm{bulk}}}\) ~20 eV, similar to that of bulk TaS2. Retardation effects of the Coulomb interaction, which give rise to hybrid SPPs modes, are noticeable around the intersect of the light cone with the surface plasmon dispersion (inset). The colored intensity sketch represents the electric potential associated with the surface plasmon. b Same as a, but for a thin metallic film with thickness d = 100 \(\AA\). The two distinct surface plasmon modes (red and blue solid lines), as well as the two lower-energy SPP modes (red and blue dashed lines), correspond to antisymmetric and symmetric relative oscillations of the electron density on the opposite surfaces, with the symmetric mode being lower in energy. c Dispersion relation for monolayer TaS2. The energy of the intrinsic plasmons in the dispersionless region is one order of magnitude smaller than that of the surface plasmons shown in b, and the critical wavevector 1/ρ0 ≈ 0.04 \({\AA}^{ - 1}\) that defines the flat dispersion in monolayer TaS2 is about an order of magnitude smaller than that of a classical, atomically thin metallic film of the same thickness, which is 1/d1L = 0.2 \({\AA}^{ - 1}\) (ρ0 = 25 \(\AA\) is the screening length and d1L ~ 5 \(\AA\) the thickness of monolayer TaS2). Moreover, when interaction with the light field is considered, the intersection of the light cone with the intrinsic plasmon dispersion in monolayer TaS2 occurs at a wavevector that is orders of magnitude smaller than the critical wavevector shown in Fig. 1b. Thus, the dispersionless plasmons in real quasi-2D materials that is the focus of this work are not the result of hybridizing a plasmon with a photon, i.e., it is not the same as the traditional plasmon polariton (inset).
We illustrate the accuracy of our expression in Eq. (1) by computing, from first principles35,36, the plasmon dispersion relation of monolayer TaS2 on a number of substrates spanning a range of εs ~ 2 to 10 (Fig. 3b). Our novel algorithm for fine sampling of transitions near EF enables the ab initio calculation of the polarizability at arbitrarily small wave vectors q and without requiring mappings to model Hamiltonians, solving an important bottleneck in previous ab initio calculations (see Methods section). We compare our direct ab initio results to those from Eq. (1)–that is, by computing \(\left[ {\frac{n}{{m^ \ast }}({\mathbf{q}})} \right]_{{\mathrm{eff}}}\) and εeff(q) for a suspended monolayer TaS2, while generalizing εeff(q) for the system on different substrates using the Keldysh model but based on ab initio parameters without any additional fitting (see Methods section). The excellent agreement in Fig. 3b confirms the idea that plasmons in quasi-2D metals can be understood as an effective 2D electron gas that experiences an additional screening (due to interband transitions and substrates) of a form of that is characteristic of quasi-2D semiconductors. Figure 3b also highlights that the plasmon group velocity can be changed by roughly an order of magnitude with a suitable choice of substrate, in addition to the tunable plasmon energies.
a A real quasi-2D metal can be formulated as: a 2D electron gas with renormalized properties given by the energy band (or bands) that crosses the Fermi energy (thick band in Fig. 1a) embedded in an environment with an effective screening, which accounts for the interband transitions and environmental effects (Eq. (1) and Fig. 1c). b Calculated plasmon dispersion relation of monolayer TaS2 on a variety of substrates (Polytetrafluoroethylene (PTFE), BN, WSe2)–calculated from first principles (solid colored lines) and computed with the expression given in Eq. (1) (dash colored lines). For the latter, we fit the ab initio computed intrinsic effective dielectric screening εeff(q) of suspended TaS2 to the form of a Keldysh model21. The resulting curves of the model on different substrates are then obtained without any additional fitting. The Landau damping regions are also shown (gray shaded regions), which is associated with the electron-hole continuum of either intraband or interband transitions (Fig. 1a).
Lifetime of quasi-2D plasmons
We now address the fundamental, and technologically important, question of what the lifetime of these collective excitations is. Plasmons are strongly damped when they are inside the Landau damping region, wherein they can decay into free electron-hole pairs37. Previous calculations16 on monolayer metallic TMDs employed density-functional theory (DFT) to compute the Landau damping regions and showed that plasmons in such systems coexist with single-particle excitations for q ≳ 0.15 Å−1 (that is, they are inside Landau damping regions for such large q plasmons), leading to a conclusion of short lifetimes. However, as static DFT is a ground-state theory, it does not yield the needed accurate quasiparticle energies to determine the correct, relevant Landau damping regions35,36 and hence plasmon lifetimes. By means of first-principles GW calculations for the quasiparticle excitations, we can accurately evaluate the Landau damping regimes in quasi-2D materials. Here, we focus on the monolayer metallic TMDs, as these materials are predicted (see Fig. 3) to have large plasmon energies16,24 and are intrinsically metallic and stable above their charge-density-wave38 and/or ferromagnetic39 transition temperature, if any. We find that, in these systems, DFT underestimates the separation between the half-filled d shell bands and the rest of the occupied bands by almost 200 meV and does not yield the correct threshold for single-particle interband excitations. Our quasiparticle GW calculations, on the contrary, show that the plasmon dispersion relation is well outside of the Landau damping regions, and coupling to finite-q interband transitions (electron-hole pair creations) are not a limiting factor for the plasmon lifetime for the materials studied here. The plasmons only reach the continuum of intraband transitions (thus having a decay channel to electron-hole pairs) after q ~ 0.4 Å−1 (Fig. 3b). Hence, monolayer metallic TMDs represent potential systems to implement the concept of lossless metals to support long-lived, dispersionless plasmons40. Other layered metals displaying a favorable electronic structure with interband transitions sufficiently separated in energy may also be good candidates14.
Plasmons not in the Landau damping regions may also decay to free electron-hole pairs, through a higher order process, by additionally emitting or absorbing a phonon. While a first-principles calculation of this higher-order decay channel is quite involved, it can be estimated from a density of final states for decay, D(q), and an effective plasmon-phonon coupling matrix element \(\bar g\) (see Methods section). We compute D(q) and estimate \(\bar g\) for graphene and monolayer TaS2, both quantities from first principles. Even though D(q) is about two orders of magnitude larger for monolayer TaS2 than for graphene due to the larger band velocity in graphene, \(\left| {\bar g} \right|^2\) is about 20 times larger for graphene due to the stronger chemical bonds. The product \(D({\boldsymbol{q}})\overline g\), which determines the plasmon decay rate via phonons, is roughly the same for both systems. We plot in Fig. 4 the calculated q-resolved plasmon spectral function for monolayer TaS2. We obtain a plasmon lifetime τ ~ 2 ps from phonon-mediated decays, comparable to the lifetime of graphene plasmons measured in recent experiments41. More importantly, because plasmons in monolayer metallic TMDs originate mostly from electron orbitals of the innermost transition metal layer, we expect that the plasmon wavefunction does not extend too much outside the structure, and hence plasmons in monolayer metallic TMDs are more robust against substrate phonons than plasmons in graphene. While our estimate of the lifetime is an upper bound for an intrinsic sample, extrinsic effects such as ripples and defects, which needs to be considered in applications, can also be partially reduced with substrate engineering and encapsulation42.
We consider only decay processes solely from phonon-assisted scatterings, since the plasmon is outside of the Landau damping regions for the plotted range of wavevectors. The plasmon linewidth Γ becomes slightly sharper for modes with higher frequencies due to the smaller density of final states that the plasmon can decay to (see Methods section). The intrinsic plasmon linewidth decreases from 1 meV at ~0.15 \(\AA^{{\mathrm{ - 1}}}\) down to 0.3 meV at q ~ 0.3 \(\AA^{{\mathrm{ - 1}}}\).
Slow plasmon wave packets
We now highlight how these finite-q, dispersionless quasi-2D plasmons can be used in experiments to create novel localized plasmon wave packets or use them for novel spectroscopic applications. We first consider a setup where plasmons are excited with an ultrafast laser pulse of duration T which is electromagnetically coupled to the sample through an AFM tip, commonly used to image plasmons1,2,4,11. We model this external excitation from the AFM tip as an oscillating point charge with time dependence \(\rho _{{\mathrm{ext}}}\left( {{\mathrm{\Delta }}t} \right) \sim \sin \omega_0t \; e^{ - \frac{{{\mathrm{\Delta }}t^2}}{{2T^2}}}\) at ~4 Å above the topmost S atoms and compute the induced charge density as a function of space and time on a monolayer TaS2 for \(\hbar \omega _0\sim 1\) eV and T ~ 80 fs. We find the resulting induced charge density moves very slowly through the material: after Δt = 1 ps, the wave packet is still localized around a narrow (25 nm thick) ring with a radius of ~120 nm relative to the AFM tip (see inset of Fig. 5a). In addition, we can deduce that these plasmons are still well-defined excitations by computing the figure of merit L/λ ~ vgτ/λ ~ 60, where L is the plasmon propagation length and λ its wavelength, using the above discussed plasmon lifetime τ of ~2 ps and plasmon group velocity vg ~ 0.6 Å/fs (see Methods section).
a Plasmon modes are excited in monolayer TaS2 with an ultrafast laser pulse (energy \(\hbar \omega _0 = 1.02\) eV, modulated with a Gaussian profile of width of T = 80 fs), which is coupled to the sample through an AFM tip at ~4 Å above the topmost S atoms. The red and blue regions are schematic representations (not to scale) of the positively and negatively induced charge densities, respectively, that make up the plasmon wave packet at a time Δt = 1 ps after the external perturbation and are obtained from first principles. Inset shows a cross-sectional plot of the computed induced charge density which highlights that, 1 ps after the excitation, the plasmon wave packet only traveled ~100 nm and is still localized on a disk ~20 nm thick. b Field enhancement due to slow plasmons in monolayer TaS2. An external field is produced by an oscillating charge density, in the steady-state regime, with frequency ω0 distributed in a thin disk placed 10 Å below the bottom S layer. The field intensity enhancement, computed from first principles, is evaluated as the ratio of the intensity of the total electric field \(\left| {E_{{\mathrm{tot}}}\left( {\mathbf{r}} \right)} \right|^2\) to the maximum intensity of the external field \(\left| {E_{{\mathrm{ext}}}^{{\mathrm{max}}}} \right|^2\). The field intensity enhancement is two orders of magnitude larger and much more confined along the z direction perpendicular to the quasi-2D material when an external field with ħω0 = 0.86 eV excites slower and shorter-wavelength plasmons (right panel), compared to an external field with ħω0 = 0.16 eV which excites faster and longer-wavelength plasmons (left panel).
Slow plasmon wave packets excited such a way should allow one to use pump-probe timing information as a way to probe the electronic structure of complex heterostructures, since nano-imaging techniques employing AFM tips that image plasmon standing waves1,2,4,11 can be adapted to measure plasmon wave packets on quasi-2D metals. For instance, a slow plasmon wave packet created at time t1 can bounce back from the edge of the qusi-2D metal and eventually reach the AFM tip at time t2; the time difference t2 – t1 is a function not only of the distance the plasmon traveled, but also of the plasmon group velocity, which is very sensitive to the local screening environment (see Fig. 3b). Hence, compared to typical plasmon nano-imaging techniques, time-resolved plasmon microscopy should have a very high sensitivity to changes in the local and non-local electronic structure and can therefore detect changes in the substrate supporting a quasi-2D metal and the presence of point defects and interfaces even if these features are not directly on the monolayer material.
Electric field enhancement
Nearly flat plasmon dispersion relations also allow for a high degree of confinement of the electromagnetic radiation: our first-principles calculations show that the resulting field intensity enhancement on both sides of a monolayer TaS2 is extraordinarily large−exceeding 107 for an external field generated by a thin disk placed 10 Å under the bottom S layer (modeling a defect or nanostructured pattern) and oscillating with a time-dependent charge density at a frequency of \(\hbar \omega _0 =\) 0.86 eV (see Fig. 5b and Methods section for details). This giant field intensity enhancement is indeed originating from the strongly localized and slowly moving plasmons. The enhancement obtained at a lower frequency of \(\hbar \omega _0 =\) 0.16 eV, wherein the plasmon group velocity is larger by a factor of ~20×, is only of the order of 104. But more importantly, as illustrated in Fig. 5, the field enhancement can be experienced in a wide spatial region on top of the monolayer material−only possible as the enhancement originates from the intrinsic quasi-2D plasmons of the 2D materials as opposed to from Mie scattering. This would allow for much easier accessing of these plasmon-induced field enhancements in experiments for biosensing, single-molecular spectroscopy, and catalytic applications, among others. Moreover, we envision that excitations of these slowly moving plasmons with light in larger metamaterials would open the possibility of creating arrays of coupled localized bosonic excitations in extended systems, enabling the monitoring of plasmon-plasmon interactions and scattering processes largely evasive to detailed and systematic studies up to now.
Discussion
In summary, our ab initio calculations and effective model analysis show that plasmons in atomically thin quasi-2D metals follow a unique dispersion relation that flattens for larger wavevectors, owing to the characteristics of quasi-2D screening and broken translational symmetry in real atomically thin crystalline materials. We moreover show that monolayer metallic TMDs are especially suited to explore these nearly dispersionless plasmons, as they can support such collective excitations with long lifetime. The high tunability of these plasmons with varying substrates, as well as the flexibility to create plasmon wave packets with different group velocities, opens the possibility of exciting applications such as tracking plasmon wave packets in real time for time-resolved plasmonic imaging and supporting giant field enhancement (exceeding 107) in extended quasi-2D metals over wide spatial regions.
Methods
New computational method for plasmon dispersion calculations
The key quantity required to obtain the plasmon dispersion is the proper, time-ordered polarizability matrix, which is given within the ring approximation by
where Vxtal is the crystal volume, m and n denote band indices, k and q are wavevectors in the Brillouin zone, and f is a Fermi-Dirac occupation factor. The dielectric matrix ε is related, within the RPA, to the proper polarizability by \(\varepsilon _{{\mathbf{GG}}^{\prime} }\left( {{\mathbf{q}},\omega } \right) = \delta _{{\mathbf{GG}}^{\prime} } - v\left( {{\mathbf{q}} + {\mathbf{G}}} \right)\chi _{{\mathbf{GG}}^{\prime} }^0\left( {{\mathbf{q}},\omega } \right)\), where v(q + G) is the Coulomb potential in reciprocal space and G is a reciprocal lattice vector.
In most ab initio codes, one typically needs to employ a uniform Monkhorst-Pack grid to sample all the k points for the virtual transitions involved in building χ0. Within this approach, the plasmon wavevector q is also typically made commensurate with the Monkhorst-Pack grid used to sample the k points. This leads to a serious computational challenge, as the number of k points Nk increases as \(\left( {\frac{1}{q}} \right)^2\) for quasi-2D systems. Note that calculations on semiconductors do not exhibit this difficulty due to the presence of a gap. Here, we use an algorithm based on importance sampling to compute the polarizability matrix at arbitrarily small wavevectors, at a constant computational cost and with negligible and controllable error. First, we separate the proper polarizability matrix into intraband and interband contributions. The interband contribution, while may involve a large number of bands, can be easily sampled on a coarse k-point grid, since there is no Fermi surface to be resolved. The challenge is to efficiently sample the intraband contribution to χ0, which we denote by \(\chi _{{\mathrm{intra}}}^0\).
In our new scheme to efficiently compute \(\chi _{{\mathrm{intra}}}^0\), we sample only the set of k points that are involved with an intraband transition. We first distribute a set of special anchor points {ka} along the different pieces of the Fermi surface, in a way that: (i) v(ka)·q < 0, where v(k) is the band velocity at k (this will later ensure that the product of the occupation factors fmk + q(1−fnk) is nonzero); and (ii) their spacing along the direction perpendicular to q is fixed as 1/Na. Note that Na is not the total number of anchor points, but the maximum number of anchor points that a closed and concave Fermi surface could have. We choose Na to be large enough to finely sample transitions along the Fermi energy, around Na ~ 60; however, note that Na does not depend on the magnitude of q, but on the size of the Fermi surface. We then distribute the actual k points that will go into the calculation of \(\chi _{{\mathrm{intra}}}^0\) in pairs around the anchor points, i.e., as \(\left\{ {{\mathbf{k}}_i = {\mathbf{k}}_i^a \pm \frac{{\mathbf{q}}}{2}} \right\}_i\), so that each pair of k points will sample a transition along the various pieces of the Fermi surface.
We then perform the calculation of \(\chi _{{\mathrm{intra}}}^0\) with these special set of k points and by including only intraband transitions. This is enforced by keeping only transitions between states \(\left. {|m{\mathbf{k}} + {\mathbf{q}}} \right\rangle\) and \(\left. {\left| {n{\mathbf{k}}} \right.} \right\rangle\) with a large overlap, \(\left| {\langle {u_{m{\mathbf{k}} + {\mathbf{q}}}{\mathrm{|}}u_{n{\mathbf{k}}}}\rangle } \right|^2 \ge \frac{1}{2}\). We then compute interband transitions keeping only transitions such that \(\left| {\langle {u_{m{\mathbf{k}} + {\mathbf{q}}}{\mathrm{|}}u_{n{\mathbf{k}}}}\rangle } \right|^2 < \frac{1}{2}\). Since these interband transitions do not sample the Fermi surface, they can be computed with two independent set of 6×6×1 k-point grids shifted by the plasmon wave vector q. Note that, both for the interband and intraband calculations, new set of wavefunctions need to be calculated depending on the wavevector q. The k-point grids can be chosen so that the q-dependent wavefunctions only depend on the valence states, so they can be efficiently recomputed. However, the approximation of only sampling the intraband transitions with set of pairs of k-points around the Fermi surface is only valid for small values of q. For values of q larger than 1/60 of the reciprocal lattice vector, we compute the polarizability with an uniform 60×60×1 k-point grid for transition involving well-separated occupied and unoccupied bands which are both ~2 eV from the Fermi energy, and employing a uniform 6×6×1 k-point for the remaining transitions. Altogether, we can accurately and efficiently compute the polarizability matrix from first principles for all relevant wavevectors.
Finally, we obtain the plasmon excitations by finding the peaks of the loss function \(L\left( {{\mathbf{q}},\omega } \right) = - {\mathrm{Im}}\left[ {\frac{1}{{\varepsilon _m\left( {{\mathbf{q}},\omega } \right)}}} \right] = - {\mathrm{Im}}\, \varepsilon _{00}^{ - 1}\left( {{\mathbf{q}},\omega } \right)\), where \(\varepsilon _m\left( {{\mathbf{q}},\omega } \right) = 1/\left[ {\varepsilon _{00}^{ - 1}({\mathbf{q}},\omega )} \right]\) is the macroscopic dielectric function. Finding the poles of \({\mathrm{Im}}\, \varepsilon _{00}^{ - 1}({\mathbf{q}},\omega )\) typically requires a very dense sampling of different frequencies ω around the plasmon. We avoid this by first decomposing \(u({\mathbf{q}}) + iv({\mathbf{q}}) = 1/\varepsilon _{00}^{ - 1}({\mathbf{q}},\omega )\). Both u(q) and v(q) are smooth, real-valued functions near the peak of the loss function, so they can be accurately interpolated to give the loss function \(L\left( {{\mathbf{q}},\omega } \right) = \frac{{v({\mathbf{q}})}}{{u({\mathbf{q}})^2 + v({\mathbf{q}})^2}}\), the maximum of which we associate with a plasmon energy ωp. The real and imaginary parts of the G=G’=0 components of the inverse dielectric matrix, as well as the real part of the macroscopic dielectric matrix, are shown in Fig. 6. While the absolute values of dielectric matrices reported are not directly observables (i.e., they depend on the stacking spacing used in our supercell calculations, as well as broadening parameters), the poles of the dielectric matrices are not sensitive to these details, and are associated with plasmon excitations.
a Real and (b) imaginary parts of the G = G’ = 0 components of the inverse dielectric matrices of such dilutely stacked monolayers for three different in-plane wavevectors q, where G is a reciprocal lattice vector of the quasi-2D crystal. The imaginary part plotted in panel (b) is proportional to the loss function, the sharp peaks of which are associated with plasmon excitations. c Real part of the macroscopic dielectric matrix, the zeros of which are associated with plasmon collective excitations. While the absolute values of dielectric matrices depend on the stacking spacing and broadening parameter used in our supercell calculations, the poles in panels (a) and (b), as well as the zeros in panel (c), are not sensitive to such details.
GW quasiparticle band structure
Our mean-field DFT calculations are performed with the Quantum ESPRESSO package43. We compute the quasiparticle band structure for monolayer TaS2 in the 2H phase, using the ab initio GW method35 with the BerkeleyGW package36, and using similar convergence parameters as we employed in previous studies on semiconducting monolayer TMDs15. A few notable differences are: (i) we perform the calculations without resorting to any plasmon-pole model by computing the fully frequency-dependent dielectric matrix and self-energy, (ii) we include all unoccupied bands in the calculation of the polarizability matrix and self-energy, and (iii) in order to sample a very dense k-point grid, we use the nonuniform neck subsampling (NNS) method44.
Microscopic analysis and dispersion relation of quasi-2D plasmons
We identify plasmon collective excitations with peaks in the loss function \(L\left( {{\mathbf{q}},\omega } \right) = - {\mathrm{Im}}\frac{1}{{\varepsilon _m\left( {{\mathbf{q}},\omega } \right)}} = - {\mathrm{Im}}\, \varepsilon _{00}^{ - 1}\left( {{\mathbf{q}},\omega } \right)\), where \(\varepsilon _m({\mathbf{q}},\omega ) = \frac{1}{{\varepsilon _{00}^{ - 1}({\mathbf{q}},\omega )}}\) is the macroscopic dielectric function, and \(\varepsilon _{00}^{ - 1}\) is the G = G’ = 0 component of the inverse dielectric matrix. The condition for a plasmon peak is that Re[det ε] = 0. Following the previous discussion, we can separate the proper polarizability into an interband contribution and an intraband contribution and assume for simplicity here that there is a single partially occupied band that is responsible for the intraband transitions.
The real part of the intraband contribution to the proper RPA polarizability, in the long wavelength limit and at zero temperature, is given by
where uk(r) is the periodic part of the Bloch function for the band crossing the Fermi energy with wavevector k, and EF is the Fermi energy.
Since we are interested in plasmon solutions, we know that we evaluate \(\chi _{{\mathrm{intra}}}^0\) at ω = ωp ≫ Ek + q − Ek, the reason being that \(\omega _p \sim \sqrt q\) but Ek + q − Ek scales like q in the long wavelength limit. If we define \(\rho _{\mathbf{k}}\left( {\mathbf{r}} \right) \equiv u_{\mathbf{k}}^ \ast \left( {\mathbf{r}} \right)u_{{\mathbf{k}} \,+\, {\mathbf{q}}}\left( {\mathbf{r}} \right)\) and assume that we are in the long wavelength limit, we can rewrite \(\chi _{{\mathrm{intra}}}^0\) in a basis-set independent way for ω near ωp as
where we define
Lz is the length of the simulation supercell along the normal direction of the plane of the quasi-2D material, FS denotes an integration along the Fermi surface, vk is the band velocity for a wavevector at the Fermi surface, and \(\left[ {\frac{n}{{m^ \ast }}\left( {\mathbf{q}} \right)} \right]_{{\mathrm{eff}}}\) is a q-dependent function that is a generalization of the ratio of the carrier density n to the effective mass \({m^ \ast }\).
The real part of dielectric matrix for frequencies near ωp can now be written as
where \(\varepsilon _{{\mathrm{inter}}}\left( {\mathbf{q}} \right): = I - v\left( {\mathbf{q}} \right)\chi _{{\mathrm{inter}}}^0\left( {\mathbf{q}} \right)\) is the interband contribution to the dielectric matrix, which we may safely assume is purely real in the frequency range of interest. Using Sylvester’s determinant identity, the condition for a plasmon peak is equivalent to
and Winter is the Coulomb potential screened by the interband transitions.
In the long wavelength limit, if the charge density ρ is localized in the monolayer, we can approximate
where Gz is a reciprocal-lattice vector along the confined direction of the material.
As done in the context of quasi-2D semiconductors28, we define an effective quasi-2D dielectric function as
and finally arrive at the expression for the plasmon frequency,
Comparison of first-principles calculations with analytical model
In order to assess the accuracy of the closed-form plasmon dispersion relation used in the model in Eq. (1), we need to compute separately both the interband effective dielectric function, εeff(q), and the effective ratio \(\left[ {\frac{n}{{m^ \ast }}\left( {\mathbf{q}} \right)} \right]_{{\mathrm{eff}}}\) for a suspended monolayer TaS2. We evaluate εeff(q) from first principles using the expression in the previous Methods section, while the ratio \(\left[ {\frac{n}{{m^ \ast }}\left( {\mathbf{q}} \right)} \right]_{{\mathrm{eff}}}\) is obtained by a numerical calculation of the plasmon dispersion relation including only intraband transitions also from first-principles. For q → 0, this is equivalent to the integral written in the previous Methods section, but it is easier to evaluate in practice.
Next, we obtain the substrate-dependent plasmon dispersion for monolayer TaS2. To do so, we first fit εeff(q) obtained for a suspended monolayer TaS2 to the fully q-dependent expression for the Keldysh model21,
where \(\eta _1 = \frac{1}{2}\log (\varepsilon + \varepsilon _s) - \frac{1}{2}\log (\varepsilon - \varepsilon _s)\), \(\eta _s = \frac{1}{2}\log (\varepsilon + 1) - \frac{1}{2}\log (\varepsilon - 1)\), εs is the substrate dielectric constant, and ε and d are effectively fitting parameters intrinsic to the quasi-2D material that were obtained from the suspended calculation (for instance, d does not in general correspond to the thickness of the quasi-2D material). Note that, for small q and large ε, this expression is commonly approximated as \(\varepsilon _{{\mathrm{eff}}}\left( q \right) \approx \frac{{1 \,+\, \varepsilon _s}}{2} + \rho _0q\), where \(\rho _0 \approx \frac{{d\varepsilon }}{2}\) whose value requires explicit first-principles calculation.
For TaS2, we obtain that a fit with ε = 5.52 and d = 10.3 Å reproduces the ab initio curve for εeff(q) up to 0.4 Å−1. We then obtain the values of εeff(q) for different substrates by varying εs, which highlights the versatility of the model in Eq. (1). We take values of εs from experiment (\(\varepsilon _s^{{\mathrm{PTFE}}} \sim 2\), \(\varepsilon _s^{{\mathrm{hBN}}} \sim 4.5\)), with the exception of WSe2, for which we compute \(\varepsilon _s^{{\mathrm{WSe}}_2} \sim 15\) from first principles. The accuracy of the resulting close-form dispersion relations is depicted in Fig. 3b of the main text.
Framework for estimating plasmon lifetime
We consider the decay rate of a plasmon with momentum q to an arbitrary final state f using Fermi’s golden rule,
where M is a coupling matrix element, and here we use atomic Rydberg units \((\hbar = 2m_e = e^2/2 = 1)\).
We consider the case of the decay of a plasmon outside the Landau damping region, such as plasmons in monolayer TMDs (see Fig. 3b), so that a direct decay of a plasmon to an electron-hole pair cannot conserve both energy and momentum. Under these conditions, we need to consider decay processes that involve the emission of a phonon, i.e., in the low-temperature limit. There are three kinds of decay processes to consider that are first-order in the electron-phonon coupling matrix: (1) the direct decay of a plasmon to the electronic ground state by emission of a phonon, (2) the decay of a plasmon to another plasmon by emission of a phonon, and (3) the decay of a plasmon to an electron-hole pair plus a phonon. Process (1) is not relevant for plasmons close to the dispersionless regime, where \(\hbar \omega _p\left( {\mathbf{q}} \right)\sim 1\,{\mathrm{eV}}\), since the phonon energy in monolayer TMDs is smaller by at least one order of magnitude. Process (2), while possible, has a small amplitude, since there is a tight constraint on momentum conservation because of the plasmon dispersion. Therefore, we focus on process (3), which could in principle be quite different between monolayer TMDs and graphene.
We label the final states as follows: the emitted phonon has a wavevector Q, branch index λ and frequency \({\mathrm{\Omega }}_\lambda ^{{\mathrm{ph}}}({\mathbf{Q}})\), while the final electron-hole pair consists of an electron with band index c and wavevector k + q − Q, and a hole with band index v and wavevector k, any combinations which satisfy wavevector conservation. We write the decay rate associated with this process as
where \({\it{\epsilon }}\)nk is the quasiparticle energy for an electron or hole in band n and wavevector k.
The coupling matrix element M between an initial plasmon state \(\left. {|{\mathbf{q}}} \right\rangle\) and a final state \(\left. {|f} \right\rangle\) mediated by the electron-phonon interaction Hamiltonian Hep can be expressed as
with
where Nk is the number of k points in the Brillouin zone, gnmλ(k, Q) is the electron-phonon matrix element, and a† and c† denote the creation operator for a phonon and an electron, respectively. We write the initial plasmon state within the Tamm-Dancoff approximation in the basis of free electron-hole pairs, \(\left. {|{\mathbf{q}}} \right\rangle = \mathop {\sum }\limits_{v^{\prime} c^{\prime} {\mathbf{k}}^{\prime} } A_{v^{\prime} c^{\prime} {\mathbf{k}}^{\prime} }^{\mathbf{q}}|\left. {c^{\prime} {\mathbf{k}}^{\prime} + {\mathbf{q}},v^{\prime} {\mathbf{k}}^{\prime} } \right\rangle\), where \(A_{v^{\prime} c^{\prime} {\mathbf{k}}^{\prime} }^{\mathbf{Q}}\) is an expansion coefficient and \(\left. {\left| {c^{\prime} {\mathbf{k}}^\prime + {\mathbf{q}},v^\prime {\mathbf{k}}^\prime } \right.} \right\rangle\) denotes a free electron-hole pair of Bloch states excited above the ground state, and we write the final state as \(\left. {\left| f \right.} \right\rangle = |\left. {c{\mathbf{k}} + {\mathbf{q}} - {\mathbf{Q}},v{\mathbf{k}},{\mathbf{Q}}\lambda } \right\rangle\) as a free electron-hole pair plus a phonon. The normalization of the initial plasmon state requires that \(A^{\mathbf{q}} \sim N_k^{ - \frac{1}{2}}\), so that \(M\left( {{\mathbf{q}} \to {\mathbf{Q}},\lambda ,v,c,{\mathbf{k}}} \right) \sim N_k^{ - 1}\left[ {g_{cc\lambda }\left( {{\mathbf{k}} + {\mathbf{q}}, - {\mathbf{Q}}} \right) - g_{vv\lambda }\left( {{\mathbf{k}}, - {\mathbf{Q}}} \right)} \right]\).
A fully first-principle evaluation of Γ for a real quasi-2D material with multiple bands is challenging, as it involves the plasmon wavefunction and the fully band-dependent and wavevector-dependent electron-phonon coupling matrix elements. At this point, to make the calculation trackable, we approximate all this dependence into an effective electron-phonon coupling matrix element \(\bar g\), which is estimated from typical values of \(\left| {g_{mn}\left( {{\mathbf{k}},{\mathbf{Q}}} \right)} \right|\) found for each material. This give us an order-of-magnitude estimate of the plasmon-phonon coupling matrix element. Note that this approximation is partially justified by the fact that we are dealing with metallic systems, as the electron-phonon coupling matrix elements are reasonably smooth and do not diverge for vanishing phonon wavevectors.
This also motivates us to define a momentum-integrated joint-density of states (MI-JDOS) as
which is a measure of how many electron-hole pairs can be created with an energy \({\upomega}\), regardless of the momentum.
We then arrive at the following simplified expression to estimate the plasmon decay rate,
where Ωph is a typical phonon frequency associated with \(\bar g^2\). For monolayer metallic TMDs, we simply set Ωph ≈ 0.
We compute from first principles the momentum-integrated JDOS using DFT and GW calculations and compute the electron-phonon matrix elements using density-functional perturbation-theory calculations for graphene and monolayer TaS2. The DFT and GW calculations are performed with the Quantum ESPRESSO43 package and the BerkeleyGW36 package, respectively. We find that the MI-JDOS decreases as a function of energy for monolayer materials for \(\hbar \omega \,\gtrsim\, 0.3\,{\mathrm{eV}}\). At the dispersionless region, we find that the monolayer TMD \({\text{MI}}{\hbox{-}}{\text{JDOS}}\left( {\hbar {\upomega} = 1\,{\mathrm{eV}}} \right) \approx 0.1\,\left( {{\mathrm{eV}}} \right)^{ - 1}\) per unit of TaS2. For graphene doped at EF = 0.5eV, on the other hand, we find that \({\text{MI}}{\hbox{-}}{\text{JDOS}}\left( {\hbar {\upomega} = 1\,{\mathrm{eV}}} \right) \approx 0.001\left( {{\mathrm{eV}}} \right)^{ - 1}\) per two carbon atoms.
We estimate \(\bar g^2\) by computing the average of the electron-phonon coupling matrix elements over all possible momenta for states at the half-filled band. For monolayer TaS2, the values of \(\left| {g_\lambda ({\mathbf{k}},{\mathbf{q}})} \right|^2\) range up to 0.035 eV2 with an average of ~0.0005 eV2, the latter of which we assign to \(\bar g^2\). For doped graphene, the values of \(\left| {g_\lambda ({\mathbf{k}},{\mathbf{q}})} \right|^2\) range up to 0.26 eV2 with an average of ~0.01 eV2. Using these results for \(\bar g^2\) together with the above calculated MI-JDOS, we obtain the plasmon linewidth given in Fig. 4.
The value of the plasmon lifetime \(\tau = (2\Gamma {\mathrm{/}}\hbar )^{ - 1} \sim 2\,{\mathrm{ps}}\) allows us to estimate the figure of merit L/λ = vgτ/λ, where L is the plasmon propagation length, λ is its wavelength, and vg the group velocity. For the wave packets used in the simulations to produce Fig. 5, we have that q ~ 0.3 \(\AA^{ - 1}\) and vg ~ 0.6 Å/fs, so L/λ ~ 60. In fact, the plasmons should be well-defined excitations (i.e., L/λ ≥ 1) provided that their lifetimes are longer than ~35 fs.
Electric field enhancement
We compute the electric field enhancement from first principles by computing the total electric field \(E_{{\mathrm{tot}}}\left( {{\mathbf{q}} + {\mathbf{G}},\omega } \right) = \mathop {\sum }\nolimits_{{\mathbf{G}}^\prime } \varepsilon _{{\mathbf{G}},{\mathbf{G}}^\prime }^{ - 1}\left( {{\mathbf{q}},\omega } \right)E_{{\mathrm{ext}}}({\mathbf{q}} \,+ {\mathbf{G}}^\prime ,\omega )\) given an external longitudinal field Eext . One challenge to compute the total electric field in real space and from first principles is that one needs to perform a Fourier transform of a very sharp function, which depends on the matrix ε−1(q, ω). However, the dielectric matrices are only evaluated for a discrete number of wavevectors. We address this by writing the interacting RPA polarizability matrix close to a plasmon state and for a fixed frequency ω0 in terms of a spectral representation,
where q0 is the plasmon wavevector corresponding to the frequency ω0, i.e., ωp(q0) = ω0, vg is the plasmon group at the wavevector q0, η ≡ τ−1/vg, where τ is the plasmon lifetime (the results do not change for τ ranging from 1 to 10 ps), and CG,G′(q) is an Hermitian matrix that can be fit from the ab initio inverse dielectric matrix. Note that the field enhancement in real space, which depends on the Fourier transform of χG,G′(q, ω0) over its spatial directions, gets enhanced for slower plasmons.
Because of the mismatch in their wavelengths, plasmons in quasi-2D extended materials will not directly couple to light, and thus require a nanostructure with a length scale comparable to that of the wavelength of the plasmon to be excited. This is modeled here as an infinitesimally thin disk with a radius of 10 Å. Because the total field still depends considerably on the geometry of this nanostructure, we define the external field as the longitudinal field created by this nanostructure, which is assumed to be generated by an oscillating charge density uniformly distributed over the disk. We compute the field intensity enhancement as the ratio of the intensity of the total electric field \(\left| {E_{{\mathrm{tot}}}\left( {\mathbf{r}} \right)} \right|^2\) to the maximum intensity of the external field \(\left| {E_{{\mathrm{ext}}}^{{\mathrm{max}}}} \right|^2\) generated by this nanostructure. This definition is likely a lower bound to the field enhancement \(\left| {E_{{\mathrm{tot}}}\left( {\mathbf{r}} \right)} \right|^2/I_{{\mathrm{light}}}\) defined with respect to the intensity Ilight of an external planewave light source, since the nanostructure can also be engineered to enhance the intensity \(\left| {E_{{\mathrm{ext}}}^{{\mathrm{max}}}} \right|^2/I_{{\mathrm{light}}}\).
Data availability
The data that support the findings of this study are available from the corresponding authors upon reasonable request.
Code availability
Ab initio calculations were performed with the BerkeleyGW software package36. The new algorithms proposed here and the post processing scripts that support the findings of this study are available from the corresponding authors upon reasonable request.
References
Fei, Z. et al. Gate-tuning of graphene plasmons revealed by infrared nano-imaging. Nature 487, 82–85 (2012).
Ni, G. X. et al. Ultrafast optical switching of infrared plasmon polaritons in high-mobility graphene. Nat. Photon. 10, 244–247 (2016).
Basov, D. N. & Fogler, M. M. Plasmonic imaging is gaining momentum. Science 357, 132–133 (2017).
Alonso-González, P. et al. Acoustic terahertz graphene plasmons revealed by photocurrent nanoscopy. Nat. Nanotechnol. 12, 31–35 (2016).
Chen, J. et al. Optical nano-imaging of gate-tunable graphene plasmons. Nature 487, 77–81 (2012).
Lundeberg, M. B. et al. Tuning quantum nonlocal effects in graphene plasmonics. Science 357, 187–191 (2017).
Brar, V. W., Jang, M. S., Sherrott, M., Lopez, J. J. & Atwater, H. A. Highly confined tunable mid-infrared plasmonics in graphene nanoresonators. Nano Lett. 13, 2541–2547 (2013).
Woessner, A. et al. Highly confined low-loss plasmons in graphene–boron nitride heterostructures. Nat. Mater. 14, 421–425 (2014).
Ju, L. et al. Graphene plasmonics for tunable terahertz metamaterials. Nat. Nanotechnol. 6, 630–634 (2011).
Hwang, E. H. & Das Sarma, S. Dielectric function, screening, and plasmons in two-dimensional graphene. Phys. Rev. B 75, 205418 (2007).
Hu, F. et al. Imaging the localized plasmon resonance modes in graphene nanoribbons. Nano Lett. 17, 5423–5428 (2017).
Novoselov, K. S., Mishchenko, A., Carvalho, A. & Castro Neto, A. H. 2D materials and van der Waals heterostructures. Science 353, aac9439 (2016).
Zhang, Y., Rubio, A. & Lay, G. Le Emergent elemental two-dimensional materials beyond graphene. J. Phys. D. 50, 053004 (2017).
Gjerding, M. N., Pandey, M. & Thygesen, K. S. Band structure engineered layered metals for low-loss plasmonics. Nat. Commun. 8, 15133 (2017).
Cudazzo, P., Gatti, M. & Rubio, A. Local-field effects on the plasmon dispersion of two-dimensional transition metal dichalcogenides. New J. Phys. 15, 125005 (2013).
Andersen, K. & Thygesen, K. S. Plasmons in metallic monolayer and bilayer transition metal dichalcogenides. Phys. Rev. B 88, 155128 (2013).
Groenewald, R. E., Rösner, M., Schönhoff, G., Haas, S. & Wehling, T. O. Valley plasmonics in transition metal dichalcogenides. Phys. Rev. B 93, 205145 (2016).
Sen, H. S., Xian, L., da Jornada, F. H., Louie, S. G. & Rubio, A. Ab initio modelling of plasmons in metal-semiconductor bilayer transition-metal dichalcogenide heterostructures. Isr. J. Chem. 57, 540–546 (2017).
Huang, Y., Shirodkar, S. N. & Yakobson, B. I. Two-dimensional boron polymorphs for visible range plasmonics: a first-principles exploration. J. Am. Chem. Soc. 139, 17181–17185 (2017).
Basov, D. N., Fogler, M. M. & Garcia de Abajo, F. J. Polaritons in van der Waals materials. Science 354, aag1992 (2016).
Keldysh, L. V. Coulomb interaction in thin semiconductor and semimetal films. JETP Lett. 29, 658–661 (1979).
Hybertsen, M. S. & Louie, S. G. Ab initio static dielectric matrices from the density-functional approach. I. Formulation and application to semiconductors and insulators. Phys. Rev. B 35, 5585–5601 (1987).
Cudazzo, P., Attaccalite, C., Tokatly, I. V. & Rubio, A. Strong charge-transfer excitonic effects and the Bose-Einstein exciton condensate in graphane. Phys. Rev. Lett. 104, 226804 (2010).
Cudazzo, P., Tokatly, I. V. & Rubio, A. Dielectric screening in two-dimensional insulators: Implications for excitonic and impurity states in graphane. Phys. Rev. B 84, 1–7 (2011).
Qiu, D. Y., da Jornada, F. H. & Louie, S. G. Optical spectrum of MoS2: many-body effects and diversity of exciton states. Phys. Rev. Lett. 111, 216805 (2013).
Chernikov, A. et al. Exciton binding energy and nonhydrogenic Rydberg series in monolayer WS2. Phys. Rev. Lett. 113, 076802 (2014).
Latini, S., Olsen, T. & Thygesen, K. S. Excitons in van der Waals heterostructures: the important role of dielectric screening. Phys. Rev. B 92, 245123 (2015).
Qiu, D. Y., da Jornada, F. H. & Louie, S. G. Screening and many-body effects in two-dimensional crystals: monolayer MoS2. Phys. Rev. B 93, 235435 (2016).
Berkelbach, T. C., Hybertsen, M. S. & Reichman, D. R. Theory of neutral and charged excitons in monolayer transition metal dichalcogenides. Phys. Rev. B 88, 045318 (2013).
Rösner, M., Şaşıoğlu, E., Friedrich, C., Blügel, S. & Wehling, T. O. Wannier function approach to realistic Coulomb interactions in layered materials and heterostructures. Phys. Rev. B 92, 085102 (2015).
Economou, E. N. Surface plasmons in thin films. Phys. Rev. 182, 539–554 (1969).
Raether, H. Excitation of Plasmons and Interband Transitions by Electrons. Vol. 88 (Springer-Verlag, 1980).
Ritchie, R. H. Plasma losses by fast electrons in thin films. Phys. Rev. 106, 874–881 (1957).
Stern, E. A. & Ferrell, R. A. Surface plasma oscillations of a degenerate electron gas. Phys. Rev. 120, 130–136 (1960).
Hybertsen, M. S. & Louie, S. G. Electron correlation in semiconductors and insulators: band gaps and quasiparticle energies. Phys. Rev. B 34, 5390–5413 (1986).
Deslippe, J. et al. BerkeleyGW: a massively parallel computer package for the calculation of the quasiparticle and optical properties of materials and nanostructures. Comput. Phys. Commun. 183, 1269–1289 (2012).
Yan, H. et al. Damping pathways of mid-infrared plasmons in graphene nanostructures. Nat. Photon. 7, 394–399 (2013).
Ugeda, M. M. et al. Characterization of collective ground states in single-layer NbSe2. Nat. Phys. 12, 92–97 (2015).
van Loon, E. G. C. P., Rösner, M., Schönhoff, G., Katsnelson, M. I. & Wehling, T. O. Competing Coulomb and electron–phonon interactions in NbS2. npj Quant. Mater. 3, 32 (2018).
Khurgin, J. B. & Sun, G. In search of the elusive lossless metal. Appl. Phys. Lett. 96, 181102 (2010).
Ni, G. X. et al. Fundamental limits to graphene plasmonics. Nature 557, 530–533 (2018).
Raja, A. et al. Dielectric disorder in two-dimensional materials. Nat. Nanotechnol. 14, 832–837 (2019).
Giannozzi, P. et al. QUANTUM ESPRESSO: a modular and open-source software project for quantum simulations of materials. J. Phys. Condens. Matter 21, 395502 (2009).
da Jornada, F. H., Qiu, D. Y. & Louie, S. G. Nonuniform sampling schemes of the Brillouin zone for many-electron perturbation-theory calculations in reduced dimensionality. Phys. Rev. B 95, 035109 (2017).
Acknowledgements
This work was supported by the Center for Computational Study of Excited-State Phenomena in Energy Materials (C2SEPEM) funded by the U.S. Department of Energy, Office of Basic Energy Sciences under Contract No. DE-AC02-05CH11231 at Lawrence Berkeley National Laboratory, as part of the Computational Materials Sciences Program, which provided for theory development, code implementation, and calculations. Computational resources were provided by the National Energy Research Scientific Computing Center (NERSC), which is supported by the Office of Science of the U.S. Department of Energy under Contract No. DE-AC02-05CH11231, and the Extreme Science and Engineering Discovery Environment (XSEDE), which is supported by the National Science Foundation under Grant No. ACI-1053575. We acknowledge financial support from the European Research Council (ERC-2015-AdG-694097). The Flatiron Institute is a division of the Simons Foundation. The authors thank D. Basov, D.Y. Qiu, and H.S. Sen for helpful discussions.
Author information
Authors and Affiliations
Contributions
S.G.L. and A.R. conceived the research. S.G.L. supervised the research and the new formalisms developed. F.H.J. developed the methods/formalisms and performed the DFT and GW studies. L.X. performed DFT calculations. All authors contributed to the analyses of results and writing of the paper.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Peer review information Nature Communications thanks Jacob Khurgin and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
da Jornada, F.H., Xian, L., Rubio, A. et al. Universal slow plasmons and giant field enhancement in atomically thin quasi-two-dimensional metals. Nat Commun 11, 1013 (2020). https://doi.org/10.1038/s41467-020-14826-8
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-020-14826-8
This article is cited by
-
Tunable anisotropic van der Waals films of 2M-WS2 for plasmon canalization
Nature Communications (2024)
-
Efficient GW calculations in two dimensional materials through a stochastic integration of the screened potential
npj Computational Materials (2023)
-
Ultra-flat and long-lived plasmons in a strongly correlated oxide
Nature Communications (2022)
-
Discovering and understanding materials through computation
Nature Materials (2021)
-
Plasmons in the van der Waals charge-density-wave material 2H-TaSe2
Nature Communications (2021)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.