Introduction

Solid-state spins are a leading contender in quantum technology1. Systems such as colour centres in diamond2,3, silicon carbides4,5, rare-earth ions in solids1,6, donors in silicon7,8,9, and quantum dots7,8,9,10 have been investigated thoroughly. Enhancing the inhomogeneous spin-dephasing time (\(T_2^ \ast\)) and the Hahn-echo spin-coherence time (T2) is a central issue. The electron spin plays a significant role for quantum sensing and for coherent connectivity with other qubits, such as photons, nuclear spins, and superconducting qubits11,12. Therefore, these times define the physical behaviour of the quantum device, and their improvement allows new perspectives for quantum applications. For example, their increase directly improves direct current (DC) and alternating current (AC) sensitivities of nitrogen vacancy (NV) sensors3,13, quantum-gate fidelity7,9, and quantum-memory times3,7,8.

From the viewpoint of material science, enhancements of \(T_2^ \ast\) and T2 have been realised by development of growth techniques to suppress paramagnetic defects14, isotope engineering to reduce nuclear spins3,7,15, and annealing techniques to remove defects16. Regarding diamond, there has been remarkable progress in the quality of single crystal diamond grown by chemical vapour deposition (CVD)14. By suppressing impurities and defects, the T2 of NV centres has been enhanced. For example, T2 = 0.7 ms is reported, which is the longest T2 at room temperature among diamond that contains a natural abundance (1.1%) of 13C15,17. Furthermore, by depleting the 13C isotope, the electron spin showed significantly long room-temperature spin-dephasing times (\(T_2^ \ast = 100\) μs18, 470 μs2) and spin-coherence times (T2 = 1.8 ms in single-crystal3 and 2.0 ms in poly-crystal diamond19).

In principle, T2 can be extended closer to T1 (~6 ms20, ~7.5 ms2, more details later on); however, this has not been reached yet. The reason considered is the effect of residual paramagnetic defects and/or impurities in the bulk. During the CVD growth21 and ion-implantation22, it is known that many vacancies are generated. Once they combine, complexes or defect clusters are formed. It is very hard to remove them by annealing techniques, because they are very stable. Therefore, the longest \(T_2^ \ast\) and T2 of single NV centres have been realised by native NV centres created during CVD growth2,3,19, while those of NV centres created by ion-implantation and a high annealing temperature have not exceeded the longest ones16.

Recently, charging of vacancies suppressed the formation of vacancy complexes by confining implantation defects into a space-charge layer of free carriers created by a thin sacrificial boron-doped p-type diamond layer. After removing this layer by an etching process, the T2 of the NV centres was improved  at the shallow surface region only 22. In their research, intrinsic diamond was used, but n-type conductivity is crucially important because of the stabilisation of the negatively charged state of the NV centres (NV−)23 and because of the electrical controls used in diamond quantum devices24,25,26,27.

In the following, by applying a phosphorus-doped n-type CVD diamond growth technique, we demonstrate the longest \(T_2^ \ast\) and T2 ever observed in solid-state systems at room temperature. Utilising the NV centre with the longest T2, we find, as is expected, that it is the most sensitive single NV centre AC magnetic field sensor. Moreover, by performing noise spectroscopy and T1 measurements, we show that the result is amenable to further improvement.

Results

Sample preparation

The n-type diamond samples A–H were epitaxially grown onto Ib-type (111)-oriented diamond substrates by microwave (MW) plasma-assisted CVD with enriched 12C (99.998%) and with phosphorus concentrations ranging from 3 × 1015 to 1 × 1017 atoms cm−328. For all samples, the growth conditions are the same except for the PH3/CH4 gas ratio to change the phosphorus concentration (see “Methods” section). These growth conditions were chosen so as to realise the highest quality of n-type diamond, with electron mobilities similar to the highest ones reported previously (800 cm2 V−1 s−1 at 300 K28, see “Methods” section). The thickness of the resulting layer is in the order of tens of micrometres. We address individual electron spins residing in NV centres with a standard home-built confocal microscope. MW pulses are applied via a thin copper wire, while magnetic fields are induced with a coil near the sample. All experiments were conducted at room temperature.

Doping concentration comparison

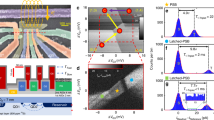
In order to compare the doping concentrations, along with Rabi measurements (Fig. 1a), two parameters were measured for a number of NV centres in every sample: the population of the NV− state, and T2. The NV− population is determined by single-shot charge-state measurements29, and T2 with a Hahn-echo measurement20. The results of samples A–D are plotted in Fig. 1b. In the highly doped diamond samples C and D, a charged state of NV− near 100% is realised23, while, regardless of the paramagnetic dopant (electron spin 1/2), T2 can surpass 2 ms. The different local surroundings of each NV centre are considered to be the reason for the scatter of T2 for each NV− population. NV centres with a higher NV− population show a longer maximum T2. Moreover, sample C with [P] = 6 × 1016 atoms cm−3 seems to produce NV centres with longer T2s than diamond with both smaller and larger phosphorus concentrations, with an average over the first 21 measured NV centres of 〈T2〉 = 1.8 ms and almost 40% has T2 > 2.0 ms. This might indicate a competition between a positive effect of phosphorus doping, discussed later, and the negative effect of magnetic noise stemming from phosphorus, and therefore an optimum concentration could exist.

Fig. 1
figure 1

Measuring nitrogen vacancy (NV) centres in phosphorus-doped diamond. a Result of Rabi measurement (data with blue crosses, sinusoidal fit with red line, 37% contrast). b T2 vs NV− population for four samples A–D with different doping levels: 3 × 1015 (red, crosses), 1 × 1016 (blue, circles), 6 × 1016 (green, up-pointing triangles have verified NV− population, down-pointing triangles were added to show more statistics for T2 only, but do likely have the same population), and 1 × 1017 atoms cm−3 (magenta, diamonds). The error bars indicate standard errors. The top right of the graph is enlarged

Full size image

Additionally, we measured T2 in samples E, F, and G, which have almost the same phosphorus concentration as sample C, and in sample H, which has a larger phosphorus concentration. The population of the NV− state was not measured, but it is considered to be near 100% due to the similarity to samples C and D. In samples E, F, and G, we confirmed that in each sample several NV centres have a T2 > 2.0 ms, while in the high-concentration sample H, T2 was <2.0 ms (see Supplementary Note 1). These results show the reproducibility of obtaining a long T2, and they support the existence of an optimum concentration region. It should be noted that the T2 of NV centres in samples grown under the same conditions but without phosphorus doping is shorter (T2 < 1 ms).

Coherence times

Owing to the pure NV− state and long T2, sample C with [P] = 6 × 1016 atoms cm−3 was investigated more in depth. At first, \(T_2^ \ast\) was studied30, measured via the exponential decay of a free-induction decay measurement (its well-known pulse sequence is illustrated in Fig. 2a). Since it is hard to measure \(T_2^ \ast\) due to the strong effect of the environment, the measurement time is decreased by using both short τ and long τ in one measurement sequence (see Supplementary Note 2), resulting in \(T_2^ \ast = 1.54_{ - 0.50}^{ + 1.91}\) ms (Fig. 2b). Compared with the previously reported long \(T_2^ \ast\) of phosphor in an isotopically engineered 28Si crystal (270 μs7) and of NV centres in diamond (470 ± 100 μs2), this is the longest \(T_2^ \ast\) for an electron spin ever observed in solid-state systems. The DC magnetic field sensitivity of the single NV centre can be derived to be ~6 nT Hz−1/213.

Fig. 2
figure 2

\(T_2^ \ast\) and T2 in sample C. a Pulse sequence for a free-induction decay (FID) measurement, with a complete sequence illustrated at the bottom. b Result of FID measurement (data with blue crosses, sinusoidal exponential-decay fit with red line, \(T_2^ \ast = 1.54_{ - 0.50}^{ + 1.91}\) ms). Please note the breaks on the horizontal axis; all data are fitted with a single function. c Pulse sequence for a Hahn-echo measurement. When applying a final +π/2-pulse, the spin is rotated towards the |0〉 state (S|0〉 measurement); for a final −π/2-pulse, the spin is rotated towards the |1〉 state (S|1〉 measurement). d Results for the S|0〉 measurement (blue crosses) and for the S|1〉 measurement (cyan circles). The top and bottom black dashed lines correspond to a maximum population of the |0〉 and |1〉 states, respectively. The middle black dashed line is when both states are populated equally. e Echo signal derived from subtracting d’s S|1〉 from d’s S|0〉 (data with blue crosses, exponential-decay fit with red line, \(T_2 = 2.43_{ - 0.06}^{ + 0.06}\) ms). The dashed black line at 0 indicates when the states are populated equally

Full size image

To find NV centres with a long T2, Hahn-echo measurements (see Fig. 2c) were conducted for the ones with a long \(T_2^ \ast\). Measurements for the |0〉 state (S|0〉: final π/2-pulse along the x axis, Fig. 2d) and the |1〉 state (S|1〉: final π/2-pulse along the −x axis, Fig. 2d) were subtracted and normalised as (S|0〉 − S|1〉)/(S|0〉 + S|1〉) to reject common-mode noise20, and the result was fitted to the exponential exp(−(τ/T2)n). Figure 2e shows that the longest T2 consistently measured \(2.43_{ - 0.06}^{ + 0.06}\) ms, which is the longest T2 for an electron spin ever observed in solid-state systems at room temperature3,19. In these references, as opposed to our results, the measurements are performed without common-mode noise rejection, the results are rather noisy, and n was fixed at 2 for the fits. Hence, the uncertainty in T2 decreases (since T2 and n appear in the same exponent only), and the fitted T2 increases (since for long T2, generally n < 2; for our measurement, forcing n = 2 gives T2 = 2.93 ms). Moreover (see Fig. 1b), even the average 〈T2〉 = 1.8 ms of our measured NV centres rivals with the longest T2 measured in single-crystal diamond (T2 = 1.8 ms3), and almost 40% are longer than the longest T2 measured in poly-crystal diamond (T2 = 2.0 ms19), while both references only show their best measurement.

Sensitivity

Since the AC magnetic field sensitivity is proportional to \(1/\sqrt {T_2}\)31, the NV centre with the longest T2 was examined. The concept for the measurement is given in Fig. 3a; the population of the spin state oscillates with the magnetic field amplitude (BAC). Therefore, to measure BAC, a working point of maximum gradient is chosen (the green dashed lines in Fig. 3b), and then the Hahn-echo intensity is measured. Via the gradient, this intensity relates directly to BAC. The amplitude of the sinusoidal magnetic field is derived from calibration with a DC magnetic field (see Supplementary Note 3).

Fig. 3
figure 3

Alternating current (AC) magnetic field measurement. a Pulse sequence for a BAC measurement. It is a Hahn-echo sequence (see Fig. 2c) with a synchronised sinusoidal AC magnetic field, which changes its sign during the π-pulse. Hence, the final phase depends on the magnetic field amplitude. A total sequence for a measurement like b is given at the bottom, where the amplitude of the magnetic field is increased at each Hahn-echo sub-sequence. The final microwave π/2-pulse is along the y axis, so that, at BAC = 0 T, the gradient is at a maximum. b Single measurement to find the working points that have the maximum gradient (100,000 iterations, data with blue crosses, sinusoidal fit with red line). The working point indicated with an orange circle is an example, the dashed arrows show how a measured intensity translates to a magnetic field amplitude. c Theoretical sensitivity vs the time period of the magnetic field derived from the T2 data (see Supplementary Note 5), giving an optimum period τoptimum (=1/fB,optimum) of 1.2 ms. The inner-magenta/outer-purple dotted vertical lines mark the range of periods for which the difference with the optimum sensitivity remains within 2%/10%, respectively. d Histogram of the repeatedly measured Hahn-echo intensity at working point BAC = 0 T to determine the uncertainty σ1. For the vertical axis of b and the horizontal axis of d, the same units and scale are used (since the same analysis method is applied), so they cancel when computing δBmin. e Logarithmic plot of δBmin vs Tmeas (data with blue crosses, fit to δBmin = η/Tmeas with red line, \(\eta = 9.1_{ - 0.3}^{ + 0.3}\) nT Hz−1/2)

Full size image

The sensitivity is \(\eta = \delta B_{{\mathrm{min}}}\sqrt {T_{{\mathrm{meas}}}}\) with δBmin the minimum detectable magnetic field amplitude, and Tmeas the measurement time31. δBmin relates directly to the uncertainty of the measurement (see Supplementary Note 4) and is given by δBmin = σ1/grad with σ1 the uncertainty of a single Hahn-echo measurement and grad the gradient in the working point. Since σ1 depends on the noise in the system, which generally scales over measurement time with \(1/\sqrt {T_{{\mathrm{meas}}}}\), the sensitivity is independent of the measurement time, hence its usefulness for comparing systems. Also, please be aware that the sensitivity of a measurement should be determined in the same way the measurement itself is conducted (see Supplementary Note 4), thus a technique such as used here is the only correct way to obtain a sensitivity.

Initially, the T2 data are used to estimate the optimum magnetic field frequency for the measurement. This optimum follows from the solution for τ in

$$\frac{{\tau + t_{{\mathrm{overhead}}}}}{\tau }n\left( {\frac{\tau }{{T_2}}} \right)^n - \frac{{t_{{\mathrm{overhead}}}}}{\tau } = \frac{1}{2},$$
(1)

with τ the time period of the magnetic field, toverhead the overhead time of the pulse sequence, and n the power of the exponent from the fit to the T2 data. Its details and general results are explained in Supplementary Note 5. Figure 3c shows the solution for this NV centre, and although certain realistic circumstances that are not taken into account here (for example, temperature fluctuations) could influence the actual optimum given the flat area, it was opted to measure in the derived optimum point of τoptimum ≈ 1.2 ms (hence fAC ≈ 833 Hz).

To obtain the optimum sensitivity, first, the gradient in the working point was determined. Since this is a constant given the measurement parameters and environment, a relatively long time-averaging measurement can be used. An average result is shown in Fig. 3b, which gives grad = 1.56 × 107 Intensity T−1. Next, the uncertainty of a measurement in the working point is extracted by measuring this point 100 times (Fig. 3d) for a number of measurement times Tmeas ranging from 13 s to 11 min. In Fig. 3e, the resulting δBmin is fitted to \(\eta /\sqrt {T_{{\mathrm{meas}}}}\), from which follows the sensitivity \(\eta = 9.1_{ - 0.3}^{ + 0.3}\) nT Hz−1/2.

Discussion

At first, the AC magnetic field sensitivity might seem worse than the previously reported best of a single NV centre at room temperature3. However, they used a different analysis method, which we investigated in order to compare (see Supplementary Note 6), which shows that we improved it by almost a factor of two. The reasons for this improvement are the longer T2, the larger Rabi contrast (see Fig. 1a)  and the higher photon count due to n-type diamond, and (to lesser account) the optimum sequence length (Supplementary Note 5). Please note that, although we demonstrated a synchronised measurement, other techniques are also limited by this optimal sensitivity, and hence any technique will have an improved sensitivity using our sample.

That the doping of phosphorus extends the spin-coherence times and gives better magnetic field sensitivities is against intuition, because phosphorus is paramagnetic at room temperature in diamond due to a large activation energy of 0.57 eV28 and thus causes magnetic noise. The time extensions in n-type diamond are considered to be due to charging of the vacancies, which suppresses the formation of paramagnetic vacancy complexes during growth. Potentially, this mechanism is similar to the recently reported interpretation of suppression of vacancy creation during ion-implantation through a sacrificial boron-doped p-type layer22. During the CVD growth, it is known that many vacancies are generated21, which causes generation of thermally stable impurity-vacancy and multi-vacancy complexes16,32,33. However, their generation can be suppressed by Coulomb repulsion of charged vacancies in n-type diamond, where an accepter level of the vacancy is located at 2.6 eV below the conduction band34, which is lower than the donor level of phosphorus (0.57 eV28).

For a two-level system, T2 is known to be ultimately limited by the longitudinal spin-relaxation time T1. We applied Carr–Purcell–Meiboom–Gill (CPMG) dynamical-decoupling sequences35,36,37 with common-mode noise rejection, and T2,dd = 3.3 ms was derived (for 512 π-pulses, see Fig. 4a). Although T2,dd is longer than T2, it is still shorter than T1 (~6–7.5 ms2,20). To obtain information about the sources of decoherence, we carried out noise spectroscopy and T1 measurements.

Fig. 4
figure 4

Noise analyses. a T2 vs number of π-pulses from measurements with Carr–Purcell–Meiboom–Gill sequences (datum with black cross for Hahn-echo, data with blue/green crosses for 21–9 π-pulses, exponential fit with red line, exponent n = 0.05 ± 0.01). b Noise spectrum extracted from the same measurements as in a (starting from 21 pulses, data with blue/green dots, Lorentzian fit with red line, correlation time τc fixed to represent the highest probed frequency). The Larmor frequencies of several nuclear spins are indicated (grey dashed lines); B = 1.8 mT. c Single quantum (data with blue crosses, exponential-decay fit with red line, measured \(T_1^{{\mathrm{SQ}}}\) ≈ 7.4 ms) and double quantum (data with cyan circles, exponential-decay fit with orange line, measured \(T_1^{{\mathrm{DQ}}}\) ≈ 3.4 ms) T1 measurements for estimating relaxation rates Ω (1/\(T_1^{{\mathrm{SQ}}}\) = 3Ω) and γ (1/\(T_1^{{\mathrm{DQ}}}\) = Ω + 2γ), which are illustrated in the inset

Full size image

The noise spectrum of deep NV centres can be analysed by a single Lorentzian36. For our data (see Fig. 4b), since the cut-off frequency eludes us, we fixed it as the highest probed frequency (thus τc ≤ 0.25 μs, the intracorrelation time of the bath spins) and fitted to find the minimum for Δ (Δ ≥ 0.1 MHz, the average coupling strength of the bath to the NV centre’s spin). The minimum density of the paramagnetic impurities/defects npara was derived from Δ under the assumption that the noise source originates from dipolar interaction between these and the NV centre only (npara ≈ Δ/α with α ≈ 3.3 × 10−13 s−1 cm331), giving 3 × 1017 cm−3.

For a Lorentzian bath, in the limit of very short correlation times (\(\tau _{\mathrm{c}} \ll T_2\)), the dynamical-decoupling sequence is inefficient and there is no improvement with the number of pulses36. In addition, there is a limitation to the π-pulse duration, and their spacing restricts the maximum CPMG filter frequency38. We consider that these explain why the decoupling technique is not very effective for the extension of T2.

As for the contribution of nuclear spins, it is shown theoretically39 and experimentally15 that the concentration of nuclear spins inversely proportionally affects the T2 of the electron spin. From the extrapolation of their results for the concentration of nuclear spins in our sample, the contribution of the nuclear spin to the decoherence is considered to be very small. From the applied external magnetic field (1.8 mT), the Larmor frequencies of the nuclear spins of 14N, 15N, 13C, 31P, and 1H were calculated and they are indicated in Fig. 4b. They were not detected in the noise spectrum, which indicates as well that the contribution of the nuclear spins to the decoherence is small. For 13C, this is consistent with its expected density (0.002%).

Additionally, to infer an effect of electric-field noise, T1 is measured with single and double quantum measurements38. The relaxation rates Ω (between ms = 0 and ms = ±1, related to the magnetic noise) and γ (between ms = −1 and ms = +1, related to the electrical noise) were derived by fitting as shown in Fig. 4c. From fitting of the results of the NV centre that shows the longest T2, the rates are Ω ≈ 45 s−1 and γ ≈ 1.2 × 102 s−1. In addition, we measured the rates of the NV centres that show shorter T2 in several phosphorus-doped samples (see Supplementary Note 7). In contrast to the previously reported rates for shallow NV centres38, they show 3Ω > γ, which indicates that magnetic noise is more prevalent in our samples, since for NV centres the actual single quantum 1/T1 = 3Ω + γ. Please note that this is the T1 limiting T2, which is actually just 3.9 ms for this NV centre, not to confuse with the T1 as given earlier (6 ms20, 7.5 ms2, and in our NV centre 7.4 ms), which means our T2,dd is about 85% of the limiting T1.

In conclusion, in our phosphorus-doped n-type diamond sample, we were able to measure the longest \(T_2^ \ast\) and T2, which leads to the best magnetic field sensitivities (among others such as temperature), which we confirmed for AC magnetic fields. The sensitivity improvements were not only due to the longer coherence times but also due to additional effects of our n-type diamond (increased Rabi contrast and photon count). From the above results, the main decoherence source is considered to be electron spins of impurities/defects. Analysing the noise spectrum estimates a minimum concentration of 3 × 1017 cm−3, which is larger than the phosphorus concentration. As shown in Fig. 1b, the longest measured T2 in diamond with [P] = 1 × 1017 atoms cm−3 is shorter than that in diamond with [P] = 6 × 1016 atoms cm−3, potentially because the phosphorus becomes the more dominant source of noise at higher concentrations. Therefore, elongation of T2 could be realised by optimising the phosphorus concentration and by continuing to decrease the paramagnetic impurities and defects. Thus our research opens a new avenue for further extension of coherence times of NV centres using new synthesis techniques of quantum-grade diamond. Moreover, the elongation of coherence times in n-type semiconductor diamond paves the way to the development and application of diamond-based quantum-information, sensing, and spintronics devices.

Methods

Phosphorus-doped diamond growth

The films of phosphorus-doped diamond were grown by MW plasma-enhanced CVD (PECVD) in a 5-kW magnetron generator equipped with a load-lock system. The base pressure of the main reactor was <2 × 10−8 Torr before CVD growth. Source gases were hydrogen (purity: N9), 12C-enriched methane (enrichment level: 99.998%, purified by a zirconium absorber), and phosphine (N6, dilution ratio PH3/H2 = 1000 ppm). The CH4/H2 gas flow rate was at a constant value of 0.4%, and the PH3/CH4 ratio was varied from 12.5 to 2000 ppm. The gas pressure, total gas flow, and MW power were 150 Torr, 1000 sccm, and 3600 W, respectively. During PECVD growth, the plasma and substrate temperatures were measured by optical pyrometry and confirmed to be stable. The incorporation of phosphorus was evaluated using secondary ion mass spectrometry. N-type conductivity, with a phosphorus donor level of 570 meV, and the electron mobilities were characterised by Hall-effect measurements. The electrodes were fabricated using the Van-der-Pauw contact configurations, and the details of the processes were the same as the ones reported previously. The mobilities depend on the phosphorus concentration and showed a scatter, but they were about 800 cm2 V−1 s−1 at 300 K, which are almost the same as the highest ones reported previously28.