Abstract
One of the central problems in quantum theory is to characterize, detect, and quantify quantumness in terms of classical strategies. Dephasing processes, caused by non-dissipative information exchange between quantum systems and environments, provides a natural platform for this purpose, as they control the quantum-to-classical transition. Recently, it has been shown that dephasing dynamics itself can exhibit (non)classical traits, depending on the nature of the system-environment correlations and the related (im)possibility to simulate these dynamics with Hamiltonian ensembles–the classical strategy. Here we establish the framework of detecting and quantifying the nonclassicality for pure dephasing dynamics. The uniqueness of the canonical representation of Hamiltonian ensembles is shown, and a constructive method to determine the latter is presented. We illustrate our method for qubit, qutrit, and qubit-pair pure dephasing and describe how to implement our approach with quantum process tomography experiments. Our work is readily applicable to present-day quantum experiments.
Similar content being viewed by others
Introduction
The boundary between the quantum and the classical world has always been a fundamental issue in quantum mechanics1,2,3,4. An operationally viable way to demonstrate the genuine quantum nature of an experiment relies on the impossibility to mimic certain statistical properties of interest by using a “classical strategy”. According to this logic, the quantum nature of an experiment is only convincingly demonstrated if the experimental statistics cannot be mimicked by the classical strategy; thus excluding any loophole to explain the statistics with a classical model.
For example, under the assumptions of realism and locality, Bell5 derived an inequality for correlations between the statistics of measurements on a bipartite system. Whenever the inequality is violated, one cannot reproduce the correlations by using a local hidden variable model, the latter serving as the classical strategy for mimicking the measurement statistics. Another important paradigm is the quantumness of a boson field, which is formulated in terms of the Wigner function or the Glauber–Sudarshan P representation6,7,8. Whenever these functions exhibit negative values, the classical explanation in terms of a probability distribution over phase space fails to represent the boson field.
Following this spirit, one may ask for a classical strategy to frame the “quantumness” of open system dynamics. This question has been addressed in different ways. In these approaches, specific properties of system states, e.g., Wigner functions with negativities, violation of Leggett–Garg inequality, non-stochasticity of dynamical processes, or detection of quantum coherence, are identified as indicators of nonclassicality and monitored during the temporal evolution9,10,11,12,13,14,15,16.
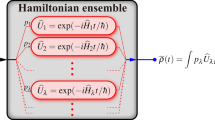
Alternatively, we propose to take the presence or absence of quantum correlations between system and environment as a signature for the quantum nature of the open system dynamics. As was shown recently17, such presence or absence of nonclassical system–environment correlations is intimately linked to the (im)possibility to simulate the open system dynamics with a Hamiltonian ensemble (HE), which may thus serve as the classical strategy to witness the nonclassicality of the open system dynamics. HEs, which are also used to describe disordered quantum systems, attribute to each member of a collection of (time-independent) Hamiltonians a probability of occurrence, giving rise to an effective average dynamics.
Finding a simulating HE certifies that the open dynamics is classical. The nonexistence of a simulating HE, on the other hand, can be proven by the necessity to resort to a HE accompanied by negative quasi-distributions. Although being conceptually clear, as was shown in ref. 17 for the example of an extended spin-boson model, this is technically highly nontrival in general; especially for high dimensions. For example, the closely related problem of random-unitary decomposition can in general merely be numerically implemented18. An efficient approach appears desirable.
On the other hand, analyzing dephasing is essential for the improvements of quantum information science and quantum technologies. Besides its fundamental relevance for the quantum-to-classical transition19,20,21, classicality of the dynamics, reflected by the existence of a simulating HE, can then be related to the in-principle possibility to correct errors caused by the HE22. Furthermore, it also constitutes one of the main obstacles in the fabrication and manipulation of quantum information devices23,24,25,26,27,28. Different implementations for the simulation of controlled pure dephasing29,30,31 and its mitigation32,33,34,35,36 exist. Other experiments highlight the potential of decoherence or pure dephasing to contribute positively to certain quantum information tasks, such as entanglement stabilization37 or entanglement swap38.
Here, we introduce a measure of nonclassicality for pure dephasing dynamics, i.e., we focus on situations where dephasing constitutes the sole dynamical agent. We begin with recasting any HE into a canonical form; within this framework, each HE is composed of the same canonical set of Hamiltonians, such that the accompanying (quasi-)distribution fully characterizes the HE. Let us remark that one can interpret the resulting representation as a random rotation model, since it is a (quasi-)distribution of rotations induced by the Hamiltonians. We also prove its existence and uniqueness. This promotes it to a faithful representation of the pure dephasing dynamics and allows us to unambiguously quantify the nonclassicality. Additionally, we outline a systematic procedure to retrieve (quasi-)distributions for pure dephasing and elaborate our ideas for qubit, qutrit, and qubit-pair examples. Finally, we also discuss the implementation of our approach with the quantum process tomography experiments to show the ready applicability to present-day quantum experiments.
Results
Averaged dynamics of Hamiltonian ensembles
A HE \(\{ {( {p_\lambda ,{\widehat{H}}_\lambda } )} \}_\lambda\) is a collection of Hermitian operators \({\widehat{H}}_\lambda\) acting on the same system17,39, where each member Hamiltonian is drawn according to the probability distribution pλ ≥ 0. A system ρ0, isolated from any environment, is sent into a unitarily-evolving channel \(\rho_\lambda \left( t \right) = \widehat{U}_\lambda \rho _0\widehat{U}_\lambda ^\dagger\), with \(\widehat{U}_\lambda = exp\left[ { - i{\widehat{H}}_\lambda t/\hbar } \right]\) for a chosen \({\widehat{H}}_\lambda\) according to pλ. Then, the dynamics of the averaged state \(\overline \rho \left( t \right)\) is given by the unital map
Even though each single realization ρλ(t) evolves unitarily, the averaged state \(\overline \rho \left( t \right)\) exhibits incoherent behavior39,40,41,42. A seminal and intriguing example is a single qubit subject to spectral disorder with HE given by \(\left\{ {\left( {p\left( \omega \right),\hbar \omega \hat \sigma _z/2} \right)} \right\}_\omega\), then the averaged dynamics describes pure dephasing:
with the dephasing factor \(\phi \left( t \right) = {\int} {p\left( \omega \right)e^{ - i\omega t}d\omega }\) being the Fourier transform of the probability distribution p(ω).
The pure dephasing in Eq. (2) is a consequence of the commuting member Hamiltonian \(\hbar \omega \hat \sigma _z/2\) in the ensemble. Each Hamiltonian induces a unitary rotation about the z-axis of the Bloch sphere at angular velocity ω. This gives rise to an intuitive interpretation of pure dephasing in terms of random phases: each component rotates at different angular velocity ω and hence possesses its own time-evolving phase. Consequently, the phase of the averaged system gradually blurs out.
Note that p(ω) is the probability distribution of the angular velocity and qualitatively characterizes the “randomness” of the random rotation. Whenever p(ω) is specified, the dynamics is uniquely determined via the Fourier transform in Eq. (2). This is also in line with our classification of such pure dephasing as classical17 since it is a statistical mixture of rotations at different angular velocities. Meanwhile, the experimental simulation of pure dephasing is implemented in a similar spirit29,30,31.
Canonical Hamiltonian-ensemble representation
Although p(ω) is particularly representative for characterizing qubit pure dephasing, it is obvious that, in general cases with non-commuting or higher dimensional member Hamiltonians \({\widehat{H}}_\lambda\), the Fourier transform in Eq. (2) is not applicable. We are, therefore, spurred to explore the canonical Hamiltonian-ensemble representation (CHER) as a generalized representation of an averaged dynamics.
To fully understand the CHER, we first observe that, since both \({\widehat{H}}_\lambda\) and density matrices ρ are Hermitian, they are elements in the Lie algebra \({{\mathfrak{u}}(n)}={{\mathfrak{u}}(1)}\oplus{{\mathfrak{su}}(n)}\), which are spanned by the identity \(\{ {\hat I} \}\) and \(\{ {\widehat{L}_m} \}_m\) of n2 − 1 traceless Hermitian generators, respectively. Then \({\widehat{H}}_\lambda \in {\frak{u}}\left( n \right)\) is a linear combination \({\widehat{H}}_\lambda = \lambda_0 \hat{I} + \mathop {\sum}\nolimits_{m = 1}^{n^2 - 1} {\lambda _m\widehat{L}_m = \lambda_0 \hat{I} + {\boldsymbol{\lambda }} \cdot {\widehat{\mathbf{L}}}}\), where \(\lambda _0 \in {\Bbb R}\) and \({\boldsymbol{\lambda }} = \left\{ {\lambda _m} \right\}_m \in {\Bbb R}^{n^2 - 1}\).
Since the dynamics is a linear map acting on ρ, invoking to the adjoint representation (see Methods and Supplementary Note 1), we can assign each generator \(\widehat{L}_m\) a linear map \(\widehat{L}_m \mapsto \widetilde{L}_m \in {\frak{g}}{\frak{l}}\left( {{\frak{u}}\left( n \right)} \right)\), with its action \(\widetilde L_m\left( \bullet \right) = [ {\widehat L_m, \bullet } ]\) defined in terms of the commutator.
With the above mathematical setup, given a HE \(\{ {( {p_\lambda ,{\widehat{H}}_\lambda } )} \}_\lambda\), one can consider the probability distribution pλ as a CHER of an averaged dynamics \({\mathcal{E}}_t\), in the sense that Eq. (1) can always be recast into a Fourier transform from pλ, on a locally compact group \({\cal{G}}\) characterized by the parameter space λ = {λ0, λ}, to the dynamical linear map \({\mathcal{E}}_t^{\left( {\widetilde L} \right)}\):
Note that we have set ℏ = 1 for symbolic abbreviation. Similarly, we can also express \(\rho = n^{ - 1}\hat I + {\boldsymbol{\rho }} \cdot {\widehat{\mathbf{L}}}\) in terms of a column vector \(\rho = \left\{ {n^{ - 1},{\boldsymbol{\rho }}} \right\}\), the action of \({\mathcal{E}}_t\) on ρ is then the usual matrix multiplication \({\mathcal{E}}_t\left\{ \rho \right\} = {\mathcal{E}}_t^{\left( {\widetilde L} \right)} \cdot \rho\) [see Supplementary Note 2 for the proof of Eq. (3)].
We emphasize that, compared with Eq. (1), the Fourier transform formalism (3) is a powerful tool in the following proof of uniqueness and establishment of our procedure. It also highlights our exclusive focus on the dynamics alone, regardless of the system state. Additionally, it provides further insights into the nature of CHER and the connection to the process nonclassicality, in terms of a random rotation model. In such interpretation, different components rotate about different axes, defined by the generators \(\left \{ {\widehat L_m} \right \}_m\). Moreover, pλ is the distribution function of the random rotations over the n2-dimensional Euclidean space. This interpretation is consistent with the random phase model in the case of qubit pure dephasing (2).
HE simulation and process nonclassicality
So far we have discussed the averaged dynamics of an isolated system, in the absence of any environment, governed by a HE. Conversely, to discuss the nonclassicality of an open system dynamics reduced from a system–environment arrangement, we should construct a simulating \(\{ {( {\wp _\lambda ,{\widehat{H}}_\lambda } )} \}_\lambda\) for a given unital dynamics.
An autonomous system–environment arrangement is characterized by a time-independent total Hamiltonian \({\widehat{H}}_{\mathrm{T}}\) and evolves unitarily with \(\widehat U_{\mathrm{T}} = exp[ { - i{\widehat{H}}_{\mathrm{T}}t} ]\). We have shown that17, if the total system \(\rho _{\mathrm{T}}\left( t \right) = \widehat U_{\mathrm{T}}\rho _{\mathrm{T}}\left( 0 \right)\widehat U_{\mathrm{T}}^\dagger\) remains at all times classically correlated between the system and its environment, displaying neither quantum discord43,44 nor entanglement, then the reduced system dynamics \(\rho _{\mathrm{S}}\left( t \right) = {\mathcal{E}}_t\{ {\rho _{\mathrm{S}}\left( 0 \right)} \} = {\mathrm{Tr}}_{\mathrm{E}}[ {\rho _{\mathrm{T}}\left( t \right)} ]\) can be described by a time-independent HE equipped with a legitimate (i.e., non-negative and normalized to unity) probability distribution. Moreover, such ensemble description under classical environments in the absence of back-action has also been discussed in the literature45,46,47.
However, given exclusively the knowledge on the reduced system dynamics \({\mathcal{E}}_t\), it is impossible to fully verify the correlations between the system and its environment. Counter-intuitively, even if we have limited access to the system alone, the emergence of nonclassical correlations can be witnessed, whenever one has no way to simulate the dynamics with any HEs equipped with a legitimate probability distribution. Such impossibility to simulate arises from the buildup of nonclassical correlations. On the other hand, if such simulation is possible, one can explain \({\mathcal{E}}_t\) as a classical random rotation model. We, therefore, define the negative values of the quasi-distribution \(\wp _\lambda\) within the simulating HE as an indicator of process nonclassicality17.
Existence and uniqueness of the CHER for pure dephasing
Here we promote the \(\wp _\lambda\) within the simulating HE as a CHER for a reduced system dynamics. In particular, by further investigating the underlying algebraic structures, we can show that such CHER for pure dephasing is even faithful, provided diagonal member Hamiltonians. More precisely, for any pure dephasing dynamics, there always exists a unique simulating HE of diagonal member Hamiltonians, equipped with either a legitimate or quasi-distribution.
The proof will become intelligible only after introducing our procedure to find the CHER below. We postpone it to Supplementary Note 8.
Since \(\wp _\lambda\) is a distribution function over the parameter space of diagonal member Hamiltonians, along with the Fourier transform on the group \({\cal{G}}\) in Eq. (3), this endows the CHER with a geometric interpretation of pure dephasing in terms of random rotation model. Consequently, the CHER is particularly competent in characterization of the nonclassicality of pure dephasing.
The nonclassicality measure for pure dephasing dynamics
Having characterized the HE simulation of pure dephasing and its representation, we are now ready to propose the measure of nonclassicality of dynamics. The measure aims to provide an operational quantification on the nonclassicality of a pure dephasing dynamics. Due to the existence and uniqueness, every pure dephasing \({\mathcal{E}}_t\) can be assigned a unique (quasi-)distribution \(\wp _\lambda\). We emphasize that it is the distribution \(\wp _\lambda\) which gives the characterization of the nonclassicality: unless they correspond to legitimate probabilities, no HE exists for the exact simulation.
The nonclassicality measure for a dynamics \({\mathcal{E}}_t\) assigned with a unique (quasi-)distribution \(\wp _\lambda\) is as follows,
where the infimum runs overall classical probability distributions pλ over the parameter space \({\cal{G}}\) of the diagonal member Hamiltonians. The variational distance \(D\left( {p_{\mathrm{\lambda }},p_\lambda{\hskip -3pt}\prime} \right)\) has an operational meaning as the single-shot distinguishability: it quantifies the highest success probability of distinguishing two probabilistic systems pλ and \(p_\lambda{\hskip -3pt}\prime\), such that \(p_{{\mathrm{success}}} = \left[ {1 + D\left( {p_{\mathrm{\lambda }},p_\lambda{\hskip -3pt}\prime} \right)} \right]/2\).
The measure proposed in Eq. (4) contains advantages and useful properties for the quantification. First, the measure has a clear operational meaning. It tells how well a dynamics \({\mathcal{E}} _t\) can be simulated by a HE. The possibility of making success or failure in the simulation with a HE can be found. Second, the measure is monotonic that the larger it is, the harder a classical simulation is. This follows from the fact that the classical dynamics of pure dephasing forms a convex set, i.e., their probabilistic mixture is also classical. The proof is presented in Supplementary Note 3. It is noteworthy that the convexity can be constructed by considering (quasi-)probabilities of dynamics, but not dynamics per se. Finally, we also note that the measure shares some similarities with the quantification of non-Markovianity48.
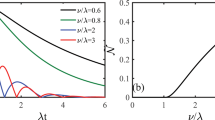
In what follows, we consider the nonclassicality of pure dephasing dynamics on a single qubit reduced from the extended spin-boson model17 with a relative phase between the coupling constants, i.e., \(g_{2,{\mathbf{k}}} = g_{1,{\mathbf{k}}}e^{i\varphi }\). The quasi-distribution \(\wp _{{\mathrm{o1}}}^{\left( {\mathrm{X}} \right)}\left( \omega \right)\) represents the single qubit pure dephasing and, consequently, its nonclassicality varies with φ. The results are shown in Fig. 1.
The nonclassicality of the qubit pure dephasing. We consider the qubit pure dephasing reduced from the extended spin-boson model, wherein φ (in unit of π) is the relative phase between the coupling constants of the qubit-pair to the common boson environment. The nonclassicality \({\cal{N}}\) is quantified according to Eq. (4). In this example, the Ohmic spectral density \({\cal{J}}(\omega ) = \omega exp( - \omega /\omega _{\mathrm{c}})\) with cut-off ωc = 1 and the zero-temperature limit are considered
Retrieval of the (quasi-)distribution
Given a HE, it is, in principle, straightforward to calculate the averaged dynamics of an isolated system, according to Eq. (1) [or, equivalently, to Eq. (3)]. Nevertheless, to find the solution to the inverse transform of Eq. (3), i.e., retrieval of the (quasi-)distribution within the simulating HE for a given reduced dynamics, is formidable in general, in contrast to the conventional inverse Fourier transform. Consequently, to establish a systematic procedure to find the CHER of pure dephasing dynamics is very desirable.
In view of the qubit pure dephasing in Eq. (2), to simulate any higher dimensional pure dephasing dynamics, we focus on the traceless and diagonal member Hamiltonian such that \({\widehat{H}}_\lambda = \lambda \widehat L\) belongs to the Cartan subalgebra (CSA) \({\frak{H}}\) of \({\frak{s}}{\frak{u}}\left( n \right)\) (see Methods). The tracelessness is due to the fact that the trace plays no role in describing the dynamics. Additionally, since the adjoint representation preserves the structure of commutator, the adjoint representation of \({\frak{H}}\) is also a CSA of \({\frak{s}}{\frak{l}}\left( {{\frak{u}}\left( n \right)} \right)\). We, therefore, have the following commutativity \([ {{\lambda}\widehat L,{\lambda}\prime \widehat L} ] = 0 \Leftrightarrow [ {{\lambda}\widetilde{L},{\lambda}^\prime \widetilde{L}} ] = 0\).
It should be noted that, even if \({\lambda}\widehat L \in {\frak{H}}\) can be chosen to be diagonal, \(\lambda\widetilde L\) itself may not necessarily be diagonal as well since the generators of \({\frak{u}}(n)\) are not the suitable bases for diagonalizing it. As we will see below, the diagonalization of the adjoint representation is a critical step to the retrieval of the (quasi-)distribution for pure dephasing.
Furthermore, the conventional inverse Fourier transform does not work because we are now dealing with linear maps in the \({\frak{s}}{\frak{l}}\left( {{\frak{u}}\left( n \right)} \right)\) space. To efficiently establish a set of equations governing the CHER of pure dephasing, we inevitably encounter increasingly many mathematical terminologies, especially those specifying the intrinsic algebraic structures within the CHER. To make our procedure transparent, we instead demonstrate several examples, each of which reveals the central concepts of our procedure, rather than elaborate the mathematical tutorial. Our approach can be easily generalized to higher dimensional pure dephasing.
Procedure towards the CHER of pure dephasing
We begin with the case of qubit pure dephasing. Although this problem has been discussed17, it relies on the conventional Fourier transform and Bochner’s theorem49 and cannot be generalized to higher dimensional systems. Here we recast it into Eq. (3). This helps us to establish a systematic procedure for higher dimensional problems.
Within a properly chosen basis, a qubit pure dephasing, reduced from a system–environment arrangement, can be expressed in the same form as Eq. (2). Unlike the one resulting from ensemble average, the dephasing factor ϕ(t) = exp[−iθ(t) − Φ(t)] is determined by the system–environment interaction, where θ(t) (Φ(t)) is a real odd (even) function on time t, respectively, such that ϕ(0) = 1, |ϕ(t)| ≤ 1, and ϕ(−t) = ϕ*(t). The dynamical linear map \({\mathcal{E}}_t^{\left( {\tilde \sigma } \right)}\) can be constructed by applying \({\mathcal{E}}_t\left\{ {\hat \sigma _m} \right\} = {\sum}_{l = 0}^3 {\hat \sigma _l [ {{\mathcal{E}}_t^{\left( {\tilde \sigma } \right)}} ]_{lm}}\) on each generator, where \(\hat \sigma _0 = \hat I\) is the identity and \(\hat \sigma _{1,2,3}\) denotes the three Pauli matrices.
To find the CHER, we mean to find a (quasi-)distribution \(\wp \left( \omega \right)\) encapsulated within the simulating HE \(\{ {( {\wp ( \omega ),{\widehat{H}}_\omega = \omega \hat \sigma _z/2} )} \}_\omega\) satisfying
The same conclusion \(exp\left[ { - i\theta \left( t \right) - \Phi \left( t \right)} \right] = {\int}_{\Bbb R} {\wp \left( \omega \right)e^{ - i\omega t}d\omega }\) is easily seen after diagonalizing Eq. (5) (see Supplementary Note 4 for more details). Finally, performing the conventional inverse Fourier transform leads to the desired result \(\wp \left( \omega \right)\).
To understand the deeper insight behind the diagonalization, we observe that the diagonalization changes the basis from the three pauli matrices into raising and lowering operators and leaves \(\hat \sigma _z\) invariant; namely, \(\left\{ {\hat \sigma _ + ,\hat \sigma _ - ,\hat \sigma _z} \right\}\), which are the generators of \({\frak{s}}{\frak{l}}\left( 2 \right)\). In other words, they are the common “eigenvectors” of \({\widehat{H}}_\omega\) with “eigenvalues” ±1 in the sense of the adjoint representation, \(\widetilde H_\omega \left( {\hat \sigma _ \pm } \right) = \left[ {\omega \hat \sigma _z/2,\hat \sigma _ \pm } \right] = \pm \!{1} \cdot \omega \hat \sigma _ \pm\) (see Supplementary Note 5 for more details). The eigenvalues ±1 are referred to as the roots (denoted by α1,2) associated to the root spaces \({\mathrm{span}}\left\{ {\hat \sigma _ \pm } \right\}\), spanned by the operators \(\hat \sigma _ \pm\), respectively. However, for higher dimensional systems, the roots are no longer real scalars but vectors in an Euclidean space. This can be better seen as follow.
A qutrit pure dephasing can be written as
To guarantee the Hermicity of ρ(t), the dephasing factors must further satisfy \(\phi _1\left( t \right) = \phi _2^ \ast \left( t \right)\), and so on.
To expand ρ as a nine-dimensional column vector, it is natural to use the Gell-Mann matrices (denoted by \(\hat \sigma _m\), m = 1, …, 8) as the generators of \({\frak{s}}{\frak{u}}\left( 3 \right)\). However, after the diagonalization, the basis is changed into that of \({\frak{g}}{\frak{l}}\left( 3 \right)\) (e.g., \({\widehat { K }}_0 = \hat I\), \({\widehat { K }}_1 = {\widehat { K }}_2^\dagger = \left( {\hat \sigma _1 + i\hat \sigma _2} \right)/2\), and \({\widehat { K }}_3 = \widehat L_3 = \hat \sigma _3\)). Within this basis, the dynamical linear map \({\mathcal{E}}_t^{\left( {\widetilde L} \right)}\) is diagonalized, i.e., \({\mathcal{E}}_t\{ {{\widehat { K }}_m} \} = {\widehat { K }}_m\phi _m\left( t \right)\).
In this case, we consider the member Hamiltonian \({\widehat{H}}_{\boldsymbol{\lambda }} = ( {{\lambda}_3\widehat L_3 + {\lambda}_8\widehat L_8} )/2 \in {\frak{H}}\) and \({\boldsymbol{\lambda }} = \left( {\lambda _3,\lambda _8} \right) \in {\Bbb R}^2\). After estimating all the commutators \([ {{\widehat{H}}_{\boldsymbol{\lambda }},{\widehat { K }}_m} ] = \left( {{\boldsymbol{\alpha }}_m \cdot {\boldsymbol{\lambda }}} \right){\widehat { K }}_m\), we obtain its adjoint representation \(\widetilde H_{\boldsymbol{\lambda }} = \left( {{\lambda}_3\widetilde L_3 + {\lambda}_8\widetilde L_8} \right)/2\), which is diagonal in the \({\frak{g}}{\frak{l}}\left( 3 \right)\) basis.
Finally, according to Eq. (3) \({\mathcal{E}}_t^{\left( {\widetilde L} \right)} = {\int}_{{\Bbb R}^2} {\wp \left( {{\lambda}_3,{\lambda}_8} \right)e^{ - i\widetilde H_{\boldsymbol{\lambda }}t}d{\lambda}_3d{\lambda}_8}\), we conclude that the (quasi-)distribution \(\wp \left( {{\lambda}_3,{\lambda}_8} \right)\) is governed by the following simultaneous Fourier transforms:
We can collect the six non-zero root vectors αm. They are two-dimensional vectors of equal length in the λ3-λ8 plane forming the root system R of \({\frak{s}}{\frak{u}}\left( 3 \right)\). We plot them in Fig. 2. Further details are given in Supplementary Note 6.
The root system R of \({\frak{s}}{\frak{u}}\left( 3 \right)\). It consists of six non-zero root vectors on the λ3−λ8 plane. Among them, α1 (blue), α4 (green), and α6 (blue) are positive and the other three (red) are negative since roots are always come in pair with opposite directions. Also, α1 and α6 are simple because α4 = α1 + α6 is a combination of simple roots
Similarly, for n-dimensional pure dephasing, each member Hamiltonian \({\widehat{H}}_{\boldsymbol{\lambda }}\), taken from the \({\frak{H}}\) of \({\frak{s}}{\frak{u}}\left( n \right)\), possesses n − 1 free parameters \({\boldsymbol{\lambda }} = \left\{ {{\mathrm{\lambda }}_{k^2 - 1}} \right\}_{k = 2,3, \ldots \! \! ,n}\); meanwhile, the (quasi-)distribution \(\wp \left( {\boldsymbol{\lambda }} \right)\) is defined on the (n−1)-dimensional Euclidean space. Moreover, the action of \({\widehat{H}}_{\boldsymbol{\lambda }}\) on the n2 − n root spaces \({\mathrm{span}}\{ {{\widehat { K }}_m} \}\) is described by the root system R = {αm}m, consisting of n2 − n real vectors of (n − 1)-dimension. Further properties of R reduce the complexity of our procedure (see Methods).
Consequently, combining the techniques, i.e., the adjoint representation, the Fourier transform on groups, and the root space decomposition, we can concisely formulate our procedure to find the CHER \(\wp \left( {\boldsymbol{\lambda }} \right)\) for the n-dimensional pure dephasing. We restrict ourselves to the diagonal member Hamiltonians (in \({\frak{H}}\)) and establish its root system R. The (quasi-)distribution \(\wp \left( {\boldsymbol{\lambda }} \right)\) is characterized by the (n2 − n)/2 Fourier transforms with respect to positive roots and its corresponding dephasing factor ϕm(t) associated to the root space \({\mathrm{span}}\{ {{\widehat { K }}_m} \}\):
Furthermore, the simple roots define a new set of random variables xm = αm⋅λ, for simple roots αm, and their corresponding equations define the marginals of \(\wp \left( {\boldsymbol{\lambda }} \right)\) along xm. The other equations describe the correlations among xm.
Example: qubit pair pure dephasing
As an instructive paradigm demonstrating our procedure to find the CHER of pure dephasing, we consider the extended spin-boson model consisting of a non-interacting qubit pair coupled to a common boson bath (Fig. 3a) with total Hamiltonian \({{\widehat{H}}} _{\mathrm{T}} = \mathop {\sum}\nolimits_{j = 1,2} {\omega _j\hat \sigma _{z,j}/2 + \mathop {\sum}\nolimits_{\mathbf{k}} {\omega _{\mathbf{k}}\hat b_{\mathbf{k}}^\dagger \hat b_{\mathbf{k}} + \mathop {\sum}\nolimits_{j,{\mathbf{k}}} {\hat \sigma _{z,j} \otimes \left( {g_{j,{\mathbf{k}}}\hat b_{\mathbf{k}}^\dagger + g_{j,{\mathbf{k}}}^ \ast \hat b_{\mathbf{k}}} \right)} } }\). We now focus on the pure dephasing of the qubit pair as a 4 × 4 system. The full dynamics has been given in ref. 17.
Nonclassicality of the qubit pair pure dephasing. a A schematic illustration of our extended spin-boson model, describing a pair of non-interacting qubits coupled to a common boson environment. b To simulate the qubit pair pure dephasing, \(\wp \left( {\boldsymbol{\lambda }} \right)\) is a (quasi-)distribution over \({\Bbb R}^3\) space spanned by λ3, λ8, and λ15. Here we show the six positive root vectors of \({\frak{s}}{\frak{u}}(4)\). Three simple root vectors (blue) define a new set of random variables. The other three non-simple root vectors (green) can be expressed as a combination of simple ones, e.g., α9 = α1 + α6 + α13. c The function \(\wp _{1,13}\left( {x_1,x_{13}} \right)\) distributes over the plane spanned by x1 and x13. For the case of Ohmic spectral density in the zero-temperature limit and ωc = 1, it shows manifest negative regions and therefore indicates the nonclassicality of the qubit pair pure dephasing
To simulate the qubit pair pure dephasing, the diagonal member Hamiltonian is taken from the \({\frak{H}}\) of \({\frak{s}}{\frak{u}}\left( 4 \right)\) \({{\widehat{H}}}_{\boldsymbol{\lambda }} = \left( {{\lambda}_3\widehat L_3 + {\lambda}_8\widehat L_8 + {\lambda}_{15}\widehat L_{15}} \right)/2\) and \(\wp ({\boldsymbol{\lambda }})\) is a (quasi-)distribution over \({\Bbb R}^3\) space with λ3, λ8, and λ15 being its axes. Note that the \({\frak{s}}{\frak{u}}\left( 4 \right)\) has six positive root vectors and three among them are simple, and all positive root vectors can be obtained by combining simple ones (Fig. 3b). We perform the change of variables xm = αm⋅λ, m = 1, 6, 13. Then, the (quasi-)distribution changes as \(\wp \left( {\boldsymbol{\lambda }} \right) \mapsto \wp^\prime \left( {x_1,x_6,x_{13}} \right)\). The three axes of \(\wp^\prime \left( {\boldsymbol{x}} \right)\) are defined by the three simple root vectors.
Additionally, since ϕ6(t) = 1, by observing the special correspondences between root vectors and dephasing factors, we can assume that
is separable into two parties. The Fourier equation for ϕ6(t) leads to the result that \(\wp _6\left( {x_6} \right) = \delta\left( {x_6} \right)\) and those for ϕ1(t) and ϕ13(t) specify the marginals of \(\wp _{1,13}\left( {x_1,x_{13}} \right)\) along the direction α1 and α13, respectively; meanwhile the one for ϕ9(t)
describes the correlation between x1 and x13.
For the case of Ohmic spectral density \({\cal{J}}\left( \omega \right) = \omega exp\left( { - \omega /\omega _{\mathrm{c}}} \right)\) in the zero-temperature limit, Eq. (12) can be recast into a conventional two-dimensional Fourier transform by a simple ansatz. Then, \(\wp _{1,13}\left( {x_1,x_{13}} \right)\) can be easily obtained by conventional inverse transform and the numerical result is shown in Fig. 3c. It exhibits manifest negative regions and illustrates the nonclassical nature of the qubit pair pure dephasing. Detailed calculations are given in Supplementary Note 7.
Finally, having introducing our procedure to find the CHER, we combine it with the investigation on the intrinsic algebraic structure. Then the uniqueness of the CHER for pure dephasing is intelligible and the detailed proof is given in Supplementary Note 8.
It is worthwhile to recall that similar models, in which several qubits were coupled identically to a common bath, had been considered50,51,52, wherein the suppression of decoherence within certain Hilbert subspace had been discovered. These studies spurred the development of the theory of decoherence-free-subspace53,54, which is conceived as a promising solution to circumvent the obstacle of decohernece in quantum information science. The phenomenon of coherence-preserving can be observed in our paradigm as well and is related to the delta component \(\wp _6\left( {x_6} \right) = \delta\left( {x_6} \right)\) on x6. Consequently, our procedure provides a potential application in the detection of decoherence-free-subspace in terms of delta components in the (quasi-)distribution.
Proposed experimental realization
Finally, to underpin the practical feasibility of our approach, here we explain how to recover the dynamical linear map \({\mathcal{E}}_t^{\left( {\widetilde L} \right)}\) from the measurable χ matrix, which is a typical way to characterize arbitrary dynamics. The matrix elements χl,m(t) are measured following the quantum process tomography technique, which has been applied in various architectures, e.g., optics55,56,57, trapped ions58,59, and superconductors60,61.
Note that \({\mathcal{E}}_t^{\left( {\widetilde L} \right)}\) on the left-hand side of Eq. (3) describes the complete time evolution of the system, i.e., we need to generate raw data of χl,m(t) as a time sequence. While this implies repeating the experiment for different time intervals, it does in principle not impose additional technical difficulty. Finally, \({\mathcal{E}}_t^{\left( {\widetilde L} \right)}\) can be reconstructed by combining the measured χl,m(t) (see Methods).
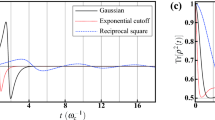
Here, we also demonstrate a numerical simulation of the quantum state tomography experiment in the S-T0 qubit24,25. With spin relaxation on the order of milliseconds62, the qubit dynamics is well approximated as pure dephasing on the time scale of tens of nanoseconds. The qubit state is detected by measuring the return probabilities, i.e., projective measurements onto each axis of the Bloch sphere, after a free induction decay time τs, as shown in Fig. 4a (see Methods).With the measured return probabilities, we can depict the trajectories in the Bloch sphere (Fig. 4b). This allows us to fully reconstruct the dynamics εt of the qubit. Then applying our procedure outlined above, we can obtain the resulting \(\wp \left( \omega \right)\) shown in Fig. 4c. They reflect the fact that the |S〉 possesses a lower eigenenergy than |T0〉, and the physical intuition that the shorter the coherence time, the broader the \(\wp \left( \omega \right)\). Having recovered \(\wp \left( \omega \right)\), the nonclassicality values can be estimated according to Eq. (4). To achieve realistic experimental conditions, we dress the theoretical model with statistical fluctuations (Fig. 4d). This confirms the robustness of the nonclassicality detection against experimental errors (see Supplementary Note 9).
Numerical simulation of the S-T0 qubit pure dephasing. a The return probabilities \(P_{|j\rangle }\left( {\tau _{\mathrm{s}}} \right)\) are measured by projecting the states onto each axis after a free induction decay time τs. Here, we show two numerical simulations at different J values. b The trajectories can be depicted in the Bloch sphere and the dynamics are therefore clearly visualized. The axes of rotation, as well as the angle Ω between the |S〉-axis, are identified by the normal vectors. c According to the rotation axes identified in (b), a unitary rotation \(\widehat R_\Omega\) recovers the standard form in Eq. (2). Then our procedure is applicable. The resulting \(\wp \left( \omega \right)\)’s reflect several physical intuitions, as explained in the main text. d The corresponding nonclassicality \({\cal{N}}\) at different J can be estimated according to Eq. (4). It increases with J in our simulation. In line with a realistic experimental modeling, statistically fluctuating noise is taken in account. The average nonclassicalities (brown dots) are reduced due to the noise. The brown error bars are the standard deviations of the series of nonclassicality \({\cal{N}}\) values obtained by repeatedly performing the noise simulation. More details are given in Supplementary Note 9
Discussion
The studies on unveiling genuine quantum properties are very important since these discover the fundamental principle of nature and spur the growth of different branches in physics and technologies. Particularly, in the field of quantum information science, highly quantum-correlated systems are critical resources for prominent quantum information tasks which can hardly be accomplished efficiently by classical computers.
By genuine quantum properties, we refer to those that can never be resembled by classical strategies. For example, Bell’s inequality is derived based on the assumption of realism and locality, while the Wigner function explain a boson field in terms of classical phase space. Inspired by these works, our characterization of process nonclassicality stems from the correspondence between the averaged dynamics of a HE and the dynamics reduced from a system–environment arrangement17.
By introducing the CHER, the role of classical strategy played by the simulating HE for a dynamics is even more apparent. The (quasi-)distribution is endowed with an explanation in terms of a random rotation model. This also implies that the nonclassical properties of a dynamics can be well-characterized by a (quasi-)distribution.
Our main achievement here lies in the establishment of a constructive procedure to retrieve the (quasi-)distributions for pure dephasing of any dimension. Additionally, along with the analysis of the underlying algebraic structure, we also achieve to prove its existence and uniqueness provided commuting member Hamiltonians. Therefore, the CHER of pure dephasing is faithful. Accordingly, based on our studies, we propose a measure of nonclassicality of pure dephasing by comparing the (quasi-)distributions in terms of variational distance. We also show that our measure is reasonable due to its convexity.
In order to make our procedure viable, we discuss how to implement our approach with the raw data measured by quantum process tomography. Furthermore, we also demonstrate a numerical simulation of the S-T0 qubit quantum state tomography, with which we implement our approach step by step.
Finally, let us remark that the generalization to the cases beyond pure dephasing or even nonunital dynamics invokes nonabelian algebraic structures. The Baker–Campbell–Hausdorff formula is then required and therefore complicates the formulation here. On the other hand, our approach highlights an inherent difference between dephasing and dissipative dynamics in terms of their underlying algebras. This may provide a new route toward the theory of open systems. Additionally, we also find that it would be interesting to investigate how the notion of dynamical process nonclassicality is related to other quasi-distributions63.
Methods
Adjoint representation
The adjoint representation is a particularly important tool in the theory of Lie algebra. It assigns each element in a Lie algebra \({\frak{L}}\) an endomorphism in \({\frak{g}}{\frak{l}}\left( {\frak{L}} \right)\) (i.e., a homomorphism from \({\frak{L}}\) to itself) in terms of Lie bracket. Therefore, \({\frak{g}}{\frak{l}}\left( {\frak{L}} \right)\) is a Lie algebra consisting of linear maps acting on \({\frak{L}}\), wherein \({\frak{L}}\) plays the role of a vector space with the generators being its basis. The adjoint representation of each generator is constructed in terms of structure constants cklm. See Supplementary Note 1 for more details.
Cartan subalgebra
The structure of a Lie algebra \({\frak{L}}\) is largely determined by its Lie bracket, i.e., the commutator acting on \({\frak{L}}\). A Lie algebra is said to be abelian if all its elements are mutually commutative. Let \({\frak{H}}\) be a Lie subalgebra of \({\frak{L}}\). \({\frak{H}}\) is said to be the CSA of \({\frak{L}}\) if \({\frak{H}}\) is the maximal abelian (and semisimple) subalgebra. A very important property is that, for a Lie algebra consists of matrices, the elements in its CSA are all simultaneously diagonalizable for a suitably chosen basis.
In our case, to simulate pure dephasing dynamics, we deal with traceless and diagonal member Hamiltonians, taken from \({\frak{H}}\) of \({\frak{s}}{\frak{u}}(n)\). To be noted, since the adjoint representation preserves the Lie bracket, the adjoint representation of \({\frak{H}}\) is also a CSA of \({\frak{s}}{\frak{l}}({\frak{u}}(n))\). However, even if \({\frak{H}}\) is diagonal, its adjoint representation may not necessarily be diagonal as well since the generators of \({\frak{u}}(n)\) are not the suitable basis for diagonalizing it.
Root system
For n-dimensional systems, there are (n − 1) generators in the \({\frak{H}}\) of \({\frak{s}}{\frak{u}}(n)\). Therefore, each member Hamiltonian possesses (n − 1) parameters \({\widehat{H}}_{\boldsymbol{\lambda }} = \mathop {\sum}\nolimits_{k = 2}^n {{\lambda}_{k^2 - 1}\widehat L_{k^2 - 1}/2}\), with \(\{ {\widehat L_{k^2 - 1}} \}_{k = 2,3, \ldots \!\! ,n}\) being the generators of \({\frak{H}}\). Additionally, the (n2 − n) roots αm, associated to each root space \({\mathrm{span}}\{ {{\widehat { K }}_m} \}\), are (n−1)-dimensional vectors, forming the root system R = {αm}m of \({\frak{s}}{\frak{u}}(n)\). Besides, according to the theory of root space decomposition, the root system possesses the following critical properties: (1) the roots come in pairs in the sense that, if αm is a root, then −αm is a root as well. This reduces the number of equations half since we are sufficient to consider the positive roots alone. (2) Among the (n2 − n)/2 positive roots, (n − 1) simple roots provide the marginal of \(\wp\) along different directions and the others provide the information on the correlations between them. (3) For \({\frak{s}}{\frak{u}}(n)\), the angle between any two non-pairing roots must be either π/3, π/2, or 2π/3. Furthermore, with the Fourier transform on groups, an n-dimensional pure dephasing is characterized by (n2 − n)/2 complex functions ϕm(t), which are the dephasing factors associated to each root space \({\mathrm{span}}\{ {{\widehat { K }}_m} \}\).
Reconstructing \({\mathcal{E}}_t^{\left( {\widetilde L} \right)}\) from the χ matrix
In our approach, the reduced system dynamics is fully characterized by the dynamical linear map \({\mathcal{E}}_t^{\left( {\widetilde L} \right)}\), which is an n2 × n2 matrix acting on a state column vector \(\rho = \left\{ {n^{ - 1},{\boldsymbol{\rho }}} \right\} \in {\Bbb R}^{n^2}\). On the other hand, in a quantum process tomography experiment, the dynamics is characterized by the measurable χ matrix representation, with the matrix elements defined according to
Note that we have used the Hermiticity \(\widehat L_m^\dagger = \widehat L_m\) in the above expression.
Now we demonstrate how to reconstruct \({\mathcal{E}}_t^{\left( {\widetilde L} \right)}\) from the measured χl,m(t). For a given dynamics εt, the matrix elements \(\left[ {{\mathcal{E}}_t^{\left( {\widetilde L} \right)}} \right]_{jk}\) are defined by applying
on each generator \({\widehat L}_k\). On the other hand, according to the measured χl,m(t) in Eq. (13), we have
From the above two equations, we can deduce that
and
In the above equations, we have used the facts that \(\widehat L_0 = \hat I\) and \({\mathrm{Tr}}\widehat L_j^2 = 2\) for j ≠ 0.
Recovering the S-T0 trajectory from measured data
For a double-quantum-dot S-T0 qubit, the three axes of the Bloch sphere are conventionally defined as \(|{\mathrm{X}}\rangle = \left( {|{\mathrm{S}}\rangle + |{\mathrm{T}}_0\rangle } \right)/\sqrt 2 = | \uparrow \downarrow \rangle\), \(|{\mathrm{Y}}\rangle = \left( {|{\mathrm{S}}\rangle - i|{\mathrm{T}}_0\rangle } \right)/\sqrt 2\), and \(|{\mathrm{Z}}\rangle = |{\mathrm{S}}\rangle = \left( {| \uparrow \downarrow \rangle - | \downarrow \uparrow \rangle } \right)/\sqrt 2\) being the singlet state, as shown in Fig. 4b. The free Hamiltonian in the S-T0 basis is
where J = 0.37 μeV (red) and 1.5 μeV (blue) is the exchange energy between two dots, \(\Delta {\mathrm{B}}_{{\mathrm{nuc}}}^z = 10.5\) mT is the hyperfine field gradient, g = −0.44 is the g-factor for GaAs, and μB = 57.8 μeVT−1 is Bohr’s magneton. Various kinds of initial states can be prepared with carefully designed pulse by controlling the voltage detuning between the quantum dots. After the initialization, the qubit undergoes a free induction decay for a time period τs. Finally, projective measurements onto each axis are performed.
We numerically simulate the return probabilities \(P_{| \uparrow \downarrow \rangle }\left( {\tau _{\mathrm{s}}} \right)\), \(P_{|{\mathrm{Y}}\rangle }\left( {\tau _{\mathrm{s}}} \right)\), and \(P_{|{\mathrm{S}}\rangle }\left( {\tau _{\mathrm{s}}} \right)\) to each axis (Fig. 4a). Then the density matrix \(\rho \left( {\tau _{\mathrm{s}}} \right) = \left[ {\hat I + \mathop {\sum}\nolimits_{j = {\mathrm{X}},{\mathrm{Y}},{\mathrm{Z}}} {r_j\left( {\tau _{\mathrm{s}}} \right)\hat \sigma _j} } \right]/2\) can be determined by
And one can depict the trajectory r(τs) = {rX(τs), rY(τs), rZ(τs)} in the Bloch sphere (Fig. 4b). This helps us to identify the axis of rotation with bare rotation frequencies \(\omega = \sqrt {J^2 + \left( {2g\mu _{\mathrm{B}}\Delta {\mathrm{B}}_{{\mathrm{nuc}}}^z} \right)^2} /\hbar\) and the angle Ω between the |S〉-axis.
Finally, a unitary rotation \(\widehat R_\Omega \rho \left( {\tau _{\mathrm{s}}} \right)\widehat R_\Omega^\dagger\) with \(\widehat R_\Omega = exp\left[ {i\Omega \hat \sigma _{\mathrm{Y}}/2} \right]\) recover the standard form in Eq. (2). Our procedure is then applicable and leads to

The numerical solutions are shown in Fig. 4c.
Further schematic illustration of the simulation and detailed analysis of the effects of noise are given in Supplementary Note 9.
Data availability
The data analyzed during the current study are available from the corresponding authors on reasonable request.
References
Ballentine, L. E. The statistical interpretation of quantum mechanics. Rev. Mod. Phys. 42, 358–381 (1970).
Zurek, W. H. Decoherence, einselection, and the quantum origins of the classical. Rev. Mod. Phys. 75, 715–775 (2003).
Schlosshauer, M. Decoherence, the measurement problem, and interpretations of quantum mechanics. Rev. Mod. Phys. 76, 1267–1305 (2005).
Modi, K., Brodutch, A., Cable, H., Paterek, T. & Vedral, V. The classical-quantum boundary for correlations: Discord and related measures. Rev. Mod. Phys. 84, 1655–1707 (2012).
Bell, J. S. On the Einstein Podolsky Rosen paradox. Physics 1, 195–200 (1964).
Wigner, E. P. On the quantum correction for thermodynamic equilibrium. Phys. Rev. 40, 749–759 (1932).
Glauber, R. J. Coherent and incoherent states of the radiation field. Phys. Rev. 131, 2766–2788 (1963).
Sudarshan, E. C. G. Equivalence of semiclassical and quantum mechanical descriptions of statistical light beams. Phys. Rev. Lett. 10, 277–279 (1963).
Rahimi-Keshari, S. et al. Quantum process nonclassicality. Phys. Rev. Lett. 110, 160401 (2013).
Sabapathy, K. K. Process output nonclassicality and nonclassicality depth of quantum-optical channels. Phys. Rev. A 93, 042103 (2016).
Lambert, N., Emary, C., Chen, Y.-N. & Nori, F. Distinguishing quantum and classical transport through nanostructures. Phys. Rev. Lett. 105, 176801 (2010).
Xiong, H.-N., Lo, P.-Y., Zhang, W.-M., Feng, D. H. & Nori, F. Non-Markovian complexity in the quantum-to-classical transition. Sci. Rep. 5, 13353 (2015).
Hsieh, J.-H., Chen, S.-H. & Li, C.-M. Quantifying quantum-mechanical processes. Sci. Rep. 7, 13588 (2017).
Milz, S., Sakuldee, F., Pollock, F. A. & Modi, K. Kolmogorov extension theorem for (quantum) causal modelling and general probabilistic theories. Preprint at https://arxiv.org/abs/1712.02589 (2017).
Knee, G. C., Marcus, M., Smith, L. D. & Datta, A. Subtleties of witnessing quantum coherence in nonisolated systems. Phys. Rev. A 98, 052328 (2018).
Smirne, A., Egloff, D., Daz, M. G., Plenio, M. B. & Huelga, S. F. Coherence and non-classicality of quantum markov processes. Quantum Sci. Technol. 4, 01LT01 (2019).
Chen, H.-B., Gneiting, C., Lo, P.-Y., Chen, Y.-N. & Nori, F. Simulating open quantum systems with Hamiltonian ensembles and the nonclassicality of the dynamics. Phys. Rev. Lett. 120, 030403 (2018).
Audenaert, K. M. R. & Scheel, S. On random unitary channels. New J. Phys. 10, 023011 (2008).
Zurek, W. H. Decoherence and the transition from quantum to classical. Phys. Today 44, 36–44 (1991).
Joos, E. et al. Decoherence and the Appearance of a Classical World in Quantum Theory, 2nd ed (Springer, New York, p2003).
Schlosshauer, M. Decoherence and the Quantum-to-Classical Transition (Springer, Berlin, 2007).
Buscemi, F., Chiribella, G. & Mauro D’Ariano, G. Inverting quantum decoherence by classical feedback from the environment. Phys. Rev. Lett. 95, 090501 (2005).
Vandersypen, L. M. K. et al. Experimental realization of Shor’s quantum factoring algorithm using nuclear magnetic resonance. Nature 414, 883–887 (2001).
Petta, J. R. et al. Coherent manipulation of coupled electron spins in semiconductor quantum dots. Science 309, 2180–2184 (2005).
Foletti, S., Bluhm, H., Mahalu, D., Umansky, V. & Yacoby, A. Universal quantum control of two-electron spin quantum bits using dynamic nuclear polarization. Nat. Phys. 5, 903–908 (2009).
Ladd, T. D. et al. Quantum computers. Nature 464, 45–53 (2010).
Buluta, I., Ashhab, S. & Nori, F. Natural and artificial atoms for quantum computation. Rep. Prog. Phys. 74, 104401 (2011).
Georgescu, I. M., Ashhab, S. & Nori, F. Quantum simulation. Rev. Mod. Phys. 86, 153–185 (2014).
Myatt, C. J. et al. Decoherence of quantum superpositions through coupling to engineered reservoirs. Nature 403, 269–273 (2000).
Liu, B.-H. et al. Experimental control of the transition from Markovian to non-Markovian dynamics of open quantum systems. Nat. Phys. 7, 931–934 (2011).
Liu, Z.-D. et al. Experimental implementation of fully controlled dephasing dynamics and synthetic spectral densities. Nat. Commun. 9, 3453 (2018).
Veldhorst, M. et al. An addressable quantum dot qubit with fault-tolerant control-fidelity. Nat. Nanotechnol. 9, 981–985 (2014).
Shulman, M. D. et al. Suppressing qubit dephasing using real-time hamiltonian estimation. Nat. Commun. 5, 5156 (2014).
Delbecq, M. R. et al. Quantum dephasing in a gated gaas triple quantum dot due to nonergodic noise. Phys. Rev. Lett. 116, 046802 (2016).
Balasubramanian, G. et al. Ultralong spin coherence time in isotopically engineered diamond. Nat. Mater. 8, 383–387 (2009).
Bar-Gill, N., Pham, L. M., Jarmola, A., Budker, D. & Walsworth, R. L. Solid-state electronic spin coherence time approaching one second. Nat. Commun. 4, 1743 (2013).
Shankar, S. et al. Autonomously stabilized entanglement between two superconducting quantum bits. Nature 504, 419–422 (2013).
Nakajima, T. et al. Coherent transfer of electron spin correlations assisted by dephasing noise. Nat. Commun. 9, 2133 (2018).
Kropf, C. M., Gneiting, C. & Buchleitner, A. Effective dynamics of disordered quantum systems. Phys. Rev. X 6, 031023 (2016).
Gneiting, C., Anger, F. R. & Buchleitner, A. Incoherent ensemble dynamics in disordered systems. Phys. Rev. A 93, 032139 (2016).
Gneiting, C. & Nori, F. Quantum evolution in disordered transport. Phys. Rev. A 96, 022135 (2017).
Gneiting, C. & Nori, F. Disorder-induced dephasing in backscattering-free quantum transport. Phys. Rev. Lett. 119, 176802 (2017).
Ollivier, H. & Zurek, W. H. Quantum discord: A measure of the quantumness of correlations. Phys. Rev. Lett. 88, 017901 (2001).
Dakić, B., Vedral, V. & Brukner, C. Necessary and sufficient condition for nonzero quantum discord. Phys. Rev. Lett. 105, 190502 (2010).
Lo Franco, R., Bellomo, B., Andersson, E. & Compagno, G. Revival of quantum correlations without system-environment back-action. Phys. Rev. A 85, 032318 (2012).
Xu, J.-S. et al. Experimental recovery of quantum correlations in absence of system-environment back-action. Nat. Commun. 4, 2851 (2013).
D’Arrigo, A., Lo Franco, R., Benenti, G., Paladino, E. & Falci, G. Recovering entanglement by local operations. Ann. Phys. 350, 211–224 (2014).
Breuer, H.-P., Laine, E.-M. & Piilo, J. Measure for the degree of non-Markovian behavior of quantum processes in open systems. Phys. Rev. Lett. 103, 210401 (2009).
Bochner, S. Monotone Funktionen, Stieltjessche Integrale und harmonische Analyse. Math. Ann. 108, 378–410 (1933).
Palma, G. M., Suominen, K.-A. & Ekert, A. K. Quantum computers and dissipation. Proc. Roy. Soc. Lond. Ser. A 452, 567–584 (1996).
Duan, L.-M. & Guo, G.-C. Preserving coherence in quantum computation by pairing quantum bits. Phys. Rev. Lett. 79, 1953–1956 (1997).
Zanardi, P. & Rasetti, M. Noiseless quantum codes. Phys. Rev. Lett. 79, 3306–3309 (1997).
Lidar, D. A., Chuang, I. L. & Whaley, K. B. Decoherence-free subspaces for quantum computation. Phys. Rev. Lett. 81, 2594–2597 (1998).
Lidar, D. A. Review of decoherence-free subspaces, noiseless subsystems, and dynamical decoupling. Adv. Chem. Phys. 154, 295–354 (2014).
O’Brien, J. L. et al. Quantum process tomography of a controlled-not gate. Phys. Rev. Lett. 93, 080502 (2004).
Kiesel, N., Schmid, C., Weber, U., Ursin, R. & Weinfurter, H. Linear optics controlled-phase gate made simple. Phys. Rev. Lett. 95, 210505 (2005).
Pogorelov, I. A. et al. Experimental adaptive process tomography. Phys. Rev. A 95, 012302 (2017).
Riebe, M. et al. Process tomography of ion trap quantum gates. Phys. Rev. Lett. 97, 220407 (2006).
Monz, T. et al. Realization of the quantum Toffoli gate with trapped ions. Phys. Rev. Lett. 102, 040501 (2009).
Bialczak, R. C. et al. Quantum process tomography of a universal entangling gate implemented with josephson phase qubits. Nat. Phys. 6, 409–413 (2010).
Yamamoto, T. et al. Quantum process tomography of two-qubit controlled-z and controlled-not gates using superconducting phase qubits. Phys. Rev. B 82, 184515 (2010).
Johnson, A. C. et al. Triplet-singlet spin relaxation via nuclei in a double quantum dot. Nature 435, 925–928 (2005).
Wootters, W. K. A Wigner-function formulation of finite-state quantum mechanics. Ann. Phys. 176, 1–21 (1987).
Acknowledgements
This work is supported partially by the National Center for Theoretical Sciences and Ministry of Science and Technology, Taiwan, Grants No. MOST 107-2628-M-006-002-MY3, MOST 107-2627-E-006-001, MOST 106-2811-M-006-044, MOST 107-2811-M-006-017, and MOST 107-2811-M-009-527, and Army Research Office (Grant No. W911NF-19-1-0081). J.B. is supported by an Institute of Information and Communications Technology Promotion (IITP) grant funded by the Korean government (MSIP) (Grant No. 2019-0-00831, EQGIS), the KIST Institutional Program (2E29580-19-148), and ITRC Program(IITP2018-2019-0-01402). F.N. is supported in part by the MURI Center for Dynamic Magneto-Optics via the Air Force Office of Scientific Research (AFOSR) (FA9550-14-1-0040), Army Research Office (ARO) (Grant No. W911NF-18-1-0358), Asian Office of Aerospace Research and Development (AOARD) (Grant No. FA2386-18-1-4045), Japan Science and Technology Agency (JST) (Q-LEAP program and CREST Grant No. JPMJCR1676), Japan Society for the Promotion of Science (JSPS) (JSPS-RFBR Grant No. 17-52-50023, and JSPS-FWO Grant No. VS.059.18N), RIKEN-AIST Challenge Research Fund, and the John Templeton Foundation.
Author information
Authors and Affiliations
Contributions
H.-B.C. conceived the research and carried out the calculations, with help from P.-Y.L. and C.G., under the supervision of Y.-N.C. J.B. proposed the idea of variational distance. Y.-N.C. and F.N. were responsible for the integration among different research units. All authors contributed to the discussion of the central ideas and to the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Peer review information: Nature Communications thanks the anonymous reviewers for their contribution to the peer review of this work. Peer reviewer reports are available.
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Chen, HB., Lo, PY., Gneiting, C. et al. Quantifying the nonclassicality of pure dephasing. Nat Commun 10, 3794 (2019). https://doi.org/10.1038/s41467-019-11502-4
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-019-11502-4
This article is cited by
-
On Markovianity and classicality in multilevel spin–boson models
Scientific Reports (2023)
-
Effects of symmetry breaking of the structurally-disordered Hamiltonian ensembles on the anisotropic decoherence of qubits
Scientific Reports (2022)
-
Faint trace of a particle in a noisy Vaidman three-path interferometer
Scientific Reports (2021)
-
Canonical Hamiltonian ensemble representation of dephasing dynamics and the impact of thermal fluctuations on quantum-to-classical transition
Scientific Reports (2021)
-
A scheme for direct detection of qubit–environment entanglement generated during qubit pure dephasing
Quantum Information Processing (2021)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.