Abstract
Deep decarbonization of electricity production is a societal challenge that can be achieved with high penetrations of variable renewable energy. We investigate the potential of energy storage technologies to reduce renewable curtailment and CO2 emissions in California and Texas under varying emissions taxes. We show that without energy storage, adding 60 GW of renewables to California achieves 72% CO2 reductions (relative to a zero-renewables case) with close to one third of renewables being curtailed. Some energy storage technologies, on the other hand, allow 90% CO2 reductions from the same renewable penetrations with as little as 9% renewable curtailment. In Texas, the same renewable-deployment level leads to 54% emissions reductions with close to 3% renewable curtailment. Energy storage can allow 57% emissions reductions with as little as 0.3% renewable curtailment. We also find that generator flexibility can reduce curtailment and the amount of energy storage that is needed for renewable integration.
Similar content being viewed by others
Introduction
Due to cost decreases1,2, renewable energy is experiencing greater use (https://www.eia.gov/outlooks/steo/pdf/steo_full.pdf). Many jurisdictions have policies in place to incentivize renewable use (http://www.dsireusa.org/). These policies are often intended to decrease the carbon-intensity of electricity production.
The role of energy storage in aiding the integration of renewable energy into electricity systems is highly sensitive to the renewable-penetration level3. California, for instance, is experiencing days during which demand is too low to accommodate all of the solar energy that is available midday4. This overgeneration-related renewable curtailment can be exacerbated by thermal generators having limited flexibility in how quickly they can adjust their production or how low their production levels can go5.
The development and deployment of grid-scale energy storage is advancing due to technology development and policy actions, such as California’s energy storage mandate6,7. Energy storage can provide a variety of services and its economic rationale is highly application-dependent8. Numerous studies optimize the size and operation of energy storage within a specific power system to achieve the best economic or environmental outcome. However, there are no studies in the extant literature that investigate systematically the economic viability of using energy storage to alleviate renewable curtailment for the purposes of decarbonizing electricity production. Moreover, the existing literature does not examine the impacts of emissions policy, such as a carbon tax, on the economics of energy storage for mitigating renewable curtailment. Detailed analysis is required to estimate the value of energy storage that is used for different applications, including renewable integration9. This study addresses this gap by optimizing the investment in and operation of nine currently available energy storage technologies to minimize cost of the California and Texas power systems. We assume varying renewable penetrations and different CO2-tax policies.
Energy storage technologies have different characteristics and potential applications10,11,12,13. As such, no single technology excels on all characteristics. Integrating energy storage into the grid can have different environmental and economic impacts, which depend on performance requirements, location, and characteristics of the energy storage system14,15,16. The cost of energy storage systems and regulatory challenges are major obstacles to their adoption13,17,18,19. Braff et al.20 examine the value of using energy storage to increase the price at which wind and solar energy can be sold in wholesale markets. They find that many energy storage technologies are currently too costly for this application and determine the cost reductions that are needed to make this application economically viable. Other works21,22,23,24,25 examine the environmental impacts of energy storage, showing that it depends upon how it is operated and the technical characteristics of the power system into which it is integrated.
Thus, there is a need to optimize the operation of energy storage to achieve desired economic and environmental outcomes. Many studies optimize the operation and size of an energy storage system for a given grid application based on economic criteria26,27. Others propose optimization models for sizing and operating energy storage to minimize total electricity cost or to maximize investor profits28,29,30. Another set of studies model emissions and economic considerations in optimizing energy storage use31,32,33.
Our study extends the existing literature by evaluating the role of energy storage in allowing for deep decarbonization of electricity production through the use of weather-dependent renewable resources (i.e., wind and solar). The model optimizes the power and energy capacities of the energy storage technology in question and power system operations, including renewable curtailment and the operation of generators and energy storage. This is done to minimize total system costs, which consist of the capital cost of energy storage, generator-operations costs, and CO2-emissions costs. Technical constraints in the model include operating limits of generators and energy storage and load-balance requirements. We examine nine currently available energy storage technologies: pumped-hydroelectric storage (PHS), adiabatic (ACAES), and diabatic (DCAES) compressed air energy storage (CAES), and lead-acid (PbA), vanadium-redox (VRB), lithium-ion (Li-ion), sodium-sulfur (NaS), polysulfide bromide (PSB), and zinc-bromine (ZNBR) batteries. Our model allows us to determine which energy storage technologies are most cost-effective in aiding renewable integration and the extent to which the cost of a currently uneconomic technology must come down to make it cost-effective. We use two case studies, which are based on the California and Texas power systems in 2010–2012, and consider up to 20 GW of wind and 40 GW of solar capacity added to the system. We also consider the impact of a CO2 tax of up to $200 per ton.
Our analysis of the cost reductions that are necessary to make energy storage economically viable expands upon the work of Braff et al.20, who examine the combined use of energy storage with wind and solar generation assuming small marginal penetrations of these technologies. Conversely, we examine their economics at significant renewable penetrations that are necessary for deep decarbonization of electricity production.
Our findings show that renewable curtailment and CO2 reductions depend greatly on the capital cost of energy storage. Moreover, increasing the renewable penetration or CO2 tax makes energy storage more cost-effective. This is because higher renewable penetrations increase the opportunities to use stored renewable energy to displace costly generation from non-renewable resources. Among the energy storage technologies that we consider, PHS and DCAES are deployed in more of the scenarios that we examine. This is due to the lower capital costs of these technologies. Other technologies see deployment under some scenarios. We also find that relatively modest reductions in the capital costs of other energy storage technologies can make them cost-effective for this proposed application.
Results
Energy storage deployment
Supplementary Table 1 summarizes the energy capacity of the energy storage technologies that are installed with different wind- and solar-penetration levels and CO2 emissions-tax regimes in 2012 in the base case with a 7.0-GW minimum-dispatchability requirement in the California Independent System Operator (CAISO) system. Supplementary Table 2 summarizes the same for the Electric Reliability Council of Texas (ERCOT) system under the base-case 8.2-GW minimum-dispatchability requirement. The tables show that higher renewable penetrations or emissions taxes tend to improve the economics of energy storage deployment. Due to their relatively low capital costs, PHS and DCAES are deployed in more scenarios and with greater capacity than most of the other technologies. Conversely, a technology that is currently more-expensive but has a higher round-trip efficiency, such as Li-ion batteries, is not deployed in any of the scenarios that are summarized in these two tables. Table 1 shows the results of a sensitivity analysis, in which lower cost assumptions for Li-ion batteries lead to significant Li-ion deployment and resultant curtailment and emissions reductions. Supplementary Data 1 summarizes the amounts of energy storage that are installed in the other years and with the other minimum-dispatchability requirements that we analyze.
Supplementary Tables 1 and 2 show that irrespective of the carbon-tax level, energy storage is not cost-effective in California for the application that we model without added renewables. This is because California’s fossil-fueled generators are all natural gas-fired. Thus, there is limited value in using energy storage for energy arbitrage, because of small differences between on- and off-peak marginal generation costs. In California, the value of energy storage stems primarily from its ability to reduce renewable curtailment, thereby displacing fossil-fueled generation. This benefit is greater with a higher carbon tax, because fossil-fueled generation is more costly in the presence of a tax. Recent estimates from the California Energy Commission show that as of October 2017, California has 5.6 GW of wind and 16.2 GW of solar installed (https://www.energy.ca.gov/almanac/renewables_data/wind/). Thus, California is approaching renewable-penetration levels at which a number of energy storage technologies are cost-effective for mitigating renewable curtailment.
Even in the absence of renewables, deploying some energy storage technologies in Texas is cost-effective under higher emissions-tax rates. This is because the ERCOT system has a more mixed generation fleet, with both coal- and natural gas-fired units that have very different generation costs. Moreover, the differences in the carbon contents of coal and natural gas gives larger differences in marginal generation costs between coal- and natural gas-fired units with higher CO2-tax rates.
Renewable curtailment
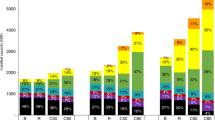
Figure 1 shows total annual renewable curtailment with and without access to energy storage with different amounts of renewable capacity and CO2-emissions taxes in 2012 in California under the base case 7.0-GW minimum-dispatchability requirement. Figure 2 shows the same for Texas under its 8.2-GW base case minimum-dispatchability requirement. The curtailment results for other minimum-dispatchability requirements and years are provided in Supplementary Data 1. The figures show that California has much higher renewable-curtailment rates relative to Texas. This is because California has much higher outputs from inflexible resources (e.g., nuclear, geothermal, biomass, and hydroelectric units) and energy imports compared to Texas. This greater inflexibility makes it more challenging for the CAISO system to absorb wind and solar generation. The figures show that with relatively low emissions taxes (i.e., $50 per ton or less), PHS and CAES are the only economically viable technologies for averting renewable curtailment. However, with higher emissions taxes, all of the energy storage technologies (except for Li-ion batteries) become cost-effective for this application. This is consistent with Supplementary Tables 1 and 2, which show that most of the energy storage technologies are deployed in some of the renewable-penetration scenarios if the CO2-emissions tax is sufficiently high.
Annual renewable curtailment as a percentage of potential renewable production in California for the year 2012 in the base case with a 7.0-GW minimum-dispatchability requirement. Figure panels correspond to different wind- and solar-penetration levels, which are indicated at the left-hand side and bottom, respectively, of the figure. Source data are provided as a Source Data file
Annual renewable curtailment as a percentage of potential renewable production in Texas for the year 2012 in the base case with an 8.2-GW minimum-dispatchability requirement. Figure panels correspond to different wind- and solar-penetration levels, which are indicated at the left-hand side and bottom, respectively, of the figure. Source data are provided as a Source Data file
Consistent with real-world experience4, renewable curtailment is greatest in the spring. This is due to the spring having relatively low electricity demand and many days with good midday solar availability. California has experienced recently an increasing number of spring days on which these factors require solar curtailment.
CO2 emissions
Figure 3 summarizes the benefits of energy storage in decarbonizing in-state electricity production in California in 2012, under the base case 7.0-GW minimum-dispatchability requirement. Figure 4 shows the same in Texas under the base case 8.2-GW minimum-dispatchability requirement. Results for other minimum-dispatchability requirements and years are provided in Supplementary Data 1. Without any added renewables or energy storage, California can achieve negligible 0.2% CO2-emissions reductions with a sufficiently high carbon tax through dispatch switching. In Texas, dispatch switching can decrease emissions by 24% without added renewables. California’s fossil-fueled generators have negligible emissions-rate differences. With a carbon tax, generating loads can be switched to units that have higher operating costs and lower emissions rates. Texas, conversely, has a mix of coal- and natural gas-fired generating units. A sufficiently high carbon tax switches the merit order between these units.
Annual CO2 emissions (million ton) in California for the year 2012 in the base case with a 7.0-GW minimum-dispatchability requirement. Figure panels correspond to different wind- and solar-penetration levels, which are indicated at the left-hand side and bottom, respectively, of the figure. Source data are provided as a Source Data file
Annual CO2 emissions (million ton) in Texas for the year 2012 in the base case with an 8.2-GW minimum-dispatchability requirement. Figure panels correspond to different wind- and solar-penetration levels, which are indicated at the left-hand side and bottom, respectively, of the figure. Source data are provided as a Source Data file
Without any access to energy storage, California’s 2012 CO2 emissions could have been reduced by 72%, through deployment of renewables with a 7.0-GW minimum-dispatchability requirement and a $200 per ton CO2 tax. However, energy storage decarbonizes electricity production to a greater extent by reducing renewable curtailment. Li-ion batteries would have provided essentially no emissions improvements in 2012, due to their high capital costs. Conversely, DCAES yields the greatest emissions reductions in California in 2012. Texas shows similar trends. Without energy storage, renewable deployment, in conjunction with a $200 per ton CO2-emissions tax, can reduce CO2 emissions by 54% in 2012 with the base case 8.2-GW minimum-dispatchability level. As in California, DCAES yields the greatest emissions reductions in Texas.
Figure 5 summarizes energy storage’s impacts on renewable curtailment and CO2 emissions in California in the 3 years that we analyze. The results that are shown in the figure assume 20-GW and 40-GW wind- and solar-penetration levels, respectively, a $200 per ton CO2-emissions tax, and the base-case 7.0-GW minimum-dispatchability requirement. The results are similar for other minimum-dispatchability requirements. Renewable curtailments are shown as percentages of potential renewable production while emissions reductions are reported as percentages relative to a no-renewables case. The figure shows significant interannual variability in renewable-curtailment rates, which stem from differences in electric loads. 2012 has significantly higher loads compared to 2010, meaning that California can accept more renewable generation in 2012. Each of the energy storage cases that is shown in the figure corresponds to the technology that achieves the greatest curtailment or emissions reduction. PHS achieves the greatest curtailment reductions in all of the years that are analyzed and the greatest emissions reductions in 2010. However, DCAES achieves greater emissions reductions in the other 2 years. These results suggest that if curtailment reduction is the goal of deploying energy storage, PHS is a relatively stable technology choice in California. Conversely, if emissions reduction is the policy priority, there is less technology robustness.
Annual renewable curtailment and CO2-emissions reductions in California assuming 20-GW and 40-GW wind- and solar-penetration levels, respectively, $200 per ton CO2-emissions tax, and base case 7.0-GW minimum-dispatchability requirement. Renewable curtailment reported as a percentage of potential renewable production and CO2-emissions reductions are reported relative to a no-renewables case. Storage cases show results for a the technology that achieves the lowest curtailment and b highest emissions reductions in each year. Source data are provided as a Source Data file
DCAES is, conversely, a more robust technology in Texas, achieving the greatest curtailment and emissions reductions in all of the years and with all of the minimum-dispatchability requirements that we examine. However, energy storage delivers smaller incremental benefits in reducing Texas’s CO2 emissions. Figure 5 shows that without energy storage, adding 60 GW of renewables yields emissions reductions that range between 71 and 92% across the years that are analyzed. Energy storage increases these emissions reductions to between 90 and 97%. ERCOT achieves 52–56% emissions reductions from adding 60 GW of renewables without energy storage. DCAES increases these emissions reductions to 56–59%. This relatively small impact of energy storage in Texas is because there is relatively little renewable curtailment compared to California. As such, energy storage has a more limited role in increasing the use of renewable energy in Texas relative to California. Instead, the emissions-reduction benefits of DCAES in Texas largely stem from helping to shift some generating loads from coal- to natural gas-fired generators.
Discussion
Our case study shows that energy storage can play a non-trivial role in decarbonizing California’s electricity production through greater use of renewables. Some technologies (e.g., PHS, CAES, and VRB and PSB batteries) can eliminate cost-effectively over 90% of CO2 emissions relative to a no-renewables case. Without energy storage, massive renewable deployment can only achieve about 72% CO2-emissions reductions (with the base-case 7.0-GW minimum-dispatchability requirement and a $200 per ton CO2-emissions tax). In Texas, energy storage deployment yields 57% CO2-emissions reductions compared to a no-renewables case (assuming an 8.2-GW minimum-dispatchability requirement and a $200 per ton emissions tax). Without energy storage, 60 GW of renewables reduce emissions by 54% relative to a no-renewables case. Recent analyses1,34 show that Texas had over 22 GW of wind installed as of 2017. Thus, the case with 60 GW of renewables represents a significant increase in solar capacity and an already-achieved wind-penetration level.
California has less supply-side flexibility (i.e., more output from nuclear, geothermal, biomass, and hydroelectric units and energy transactions) compared to Texas, resulting in relatively high renewable curtailment in California. Thus, energy storage is valuable in reducing renewable curtailment and displacing fossil-fueled generation. Conversely, even without added renewables, energy storage is cost-effective in Texas with a carbon tax, as it can be used to shift generating loads away from coal-fired units toward natural gas-fired generation.
Our results represent a lower bound on energy storage’s role in renewable integration and electricity decarbonization. This is because at high renewable penetrations, energy storage may play other roles that are not captured in our model3. For instance, energy storage can be a low-cost source of flexibility to accommodate subhourly or minute-to-minute variability in wind and solar availabilities. Because our model assumes an hourly temporal resolution, such a benefit of energy storage is not captured.
Our results show that its capital cost is the primary factor in determining the scale at which an energy storage technology is deployed. Even with ambitious renewable penetrations and a high emissions tax, a relatively expensive (but high-efficiency) technology, such as Li-ion batteries, has a limited role to play. Our results suggest, however, that modest reductions in Li-ion-battery costs may increase their deployment. We determine this by examining the reduced cost of energy storage capacity, which is obtained from solving our optimization model. In the context of our model, the reduced cost can be interpreted as indicating how much the capital cost of an uneconomic energy storage technology must change before it is cost-effective to build35. Our results show that in scenarios in which Li-ion batteries are not built, capital cost reductions of between $1 per kWh and $40 per kWh are sufficient to make the technology economically viable. Given the major reductions in battery-manufacturing costs over the past decade, such cost reductions may be possible. This would mean that energy storage technologies that appear uneconomic in our case study may well be viable in the near future. The reduced costs results for other storage technologies are provided in Supplementary Data 1.
Given the wide range of costs for Li-ion, NaS, and PSB batteries that are reported in the literature (https://www.lazard.com/media/450774/lazards-levelized-cost-of-storage-version-40-vfinal.pdf), we conduct a sensitivity analysis, in which the capital costs of Li-ion batteries are reduced to $259 per kWh and $59 per kW, the costs of NaS batteries are increased to $350 per kW and $350 per kWh, and the costs of PSB batteries are reduced to $200 per kW and $90 per kWh. Table 1 summarizes the impacts of these changed capital costs. Specifically, the table reports changes in renewable curtailments and CO2 emissions relative to the levels that are achieved with the baseline costs, as a percentage of the baseline curtailment and emissions impacts of Li-ion, NaS, and PSB. The results that are in the table are for 2012, assuming 20 GW of wind and 40 GW of solar are added to each system, a $200 per ton CO2-emissions tax, and the base-case minimum-dispatchability requirement for each system. The amounts of energy storage added, renewable curtailments, and CO2 emissions that are achieved in other scenarios are provided in Supplementary Data 1.
Our results demonstrate that increasing the CO2-emissions tax makes energy storage more cost effective. Yong and McDonald36 show that an emissions-tax regime that is set by a government with a willingness to commit to it, has a positive influence on the size and the direction of firm-level investment in clean technologies. Thus, adding a strong emissions tax to the already-established energy storage mandate in California may have beneficial economic, policy, and technology-development impacts. We also show that greater generator flexibility, which is represented through a lower minimum-dispatchability requirement, reduces renewable curtailment and the amount of energy storage that is needed.
There are some important limitations of our analysis that can be examined in future research. The only environmental impact of electricity production and energy storage use that we examine is CO2 emissions. There may be other important impacts. Our results show that PHS holds great promise, due to its relatively low cost. There are concerns around other environmental impacts of PHS, such as land and water use, species mortality, and impacts on biological production, however. Moreover, PHS is location-dependent and requires sites with specific characteristics12. The deployment of CAES is also limited, as specific underground formations are needed to store the compressed air12. Further examination of these limitations would provide a more comprehensive understanding of the deployment potential of these technologies.
Our optimization model could be applied to other case studies, with different generation mixes. We assume no degradation of energy storage throughout its operation. Arbabzadeh et al.37 show that its degradation does not change significantly the environmental impacts of using energy storage for generation-shifting. Nevertheless, future work could examine the impact of such degradation on the cost-effectiveness of using energy storage for alleviating renewable curtailment. We also assume that energy storage can operate between 0 and 100% state of charge. Future analyses can define technology-specific operational windows for energy storage.
Methods
Optimization model
Our analysis uses an optimization model with an hourly time resolution over a T-h optimization horizon. The model determines the size of the energy storage system as well as the hourly operation of the power system. Specifically, we let \(\bar Q\) and \(\bar S\) denote the power and energy capacities of the energy storage, which are measured in MW and MWh, respectively. We let gt,i represent the hour-t production level (measured in MW) of generator i, where \(i \in {\cal{I}}\), the set of natural gas- and coal-fired, nuclear, biomass, hydroelectric, and geothermal generators. We let \(\bar R_t\) and Rt denote the total amount of renewable production that is available and the amount of renewable production that is used in hour t, respectively. Both of these quantities are measured in MW. The difference, \((\bar R_t - R_t)\), gives hour-t renewable curtailment. Finally, we let \(q_t^c\) and \(q_t^d\) denote MW that are charged into and discharged from energy storage, respectively, in hour t. We also let st denote the ending hour-t state of charge (SoC) of storage, which is measured in MWh.
The optimization model is formulated as:
Eq. (1) minimizes the total cost of operating the system. The first two terms in the objective function, \(\kappa ^Q\bar Q + \kappa ^S\bar S\), reflect the cost of building energy storage. Energy storage is assumed to have a capital cost that can depend on its power and energy capacities, with κQ denoting the power-capacity cost (given in $ per MW) and κS the energy-capacity cost (given in $ per MWh). The remaining term in the objective function denotes the hourly operating costs. Some energy storage technologies (e.g., DCAES) use a fuel, such as natural gas, when discharging stored energy. cS denotes the direct cost (in $ per MWh) of discharging stored energy for such technologies (i.e., cS = 0 for technologies that do not consume fuel when discharging) while the term, EρS, denotes any CO2-related costs. Specifically, E represents the $ per ton CO2 tax and ρS is the CO2-emissions rate (in ton MWh−1) of discharging stored energy. ci is the direct cost (in $ per MWh) of producing energy from generator i and ρi is the CO2-emissions rate (in ton MWh−1) of generator i.
Constraints (2) ensure that load is exactly met in each hour. We let Lt denote the hour-t load, in MW. Constraints (3) enforce the minimum-dispatchability requirement, where ϕt represents the hour-t requirement in MW. If real-time renewable availability is sufficiently high, renewable generation is curtailed to ensure that the minimum-dispatchability requirement is met4. This dispatchability requirement can be met using generators (other than wind and solar), as well as energy storage. Constraints (4) and (5) impose generation limits on non-renewable and renewable generators, respectively. We let Ki denote generator i's production capacity in MW. Constraints (6) define the ending hour-t SoC of energy storage to be the SoC at the end of hour (t − 1), plus any energy that is charged and less any energy that is discharged in hour t. We apply an efficiency factor, ηc ∈ (0, 1), to the energy that is charged, which is a typical method of accounting for the round-trip efficiency losses of storing energy38. Constraints (7)–(9) impose the energy- and power-capacity constraints on the SoC and charging and discharging of energy storage, respectively.
The model is formulated using version 20170902 of the AMPL mathematical programming language and solved using version 12.7.1.0 of the CPLEX linear program solver.
Annualization of capital cost of energy storage
The capital costs of building each energy storage technology are annualized using a capital charge rate39. This annualization makes the capital costs comparable to the power system operating costs, which are modeled over a single-year period, in the optimization model. The capital charge rate takes into account the service life of each energy storage technology. In essence, a longer service life yields a lower capital charge rate, because the capital cost of building the energy storage can be amortized over a longer period. The capital charge rate, γ, is computed as:
where Y is the service life of the technology and δ is the discount rate, which we take to be 10%. This yields capital charge rates ranging between 10% (for the technologies with 60-year service lives) and 16% (for ZNBR batteries, which have 10-year service lives).
Wind and solar modeling
The scenarios that we model vary the penetration of wind and photovoltaic solar exogenously. We consider cases with up to 20 GW and 40 GW of added wind and solar, respectively. The hourly generation that is available from the added wind plants are modeled using the Wind Integration National Dataset Toolkit (WIND Toolkit)40. The WIND Toolkit provides modeled historical wind-availability data for more than 126000 sites across the United States for the years 2007–2013. Because our other case study data are for the years 2010 through 2012, we use wind-availability data for the same years.
To capture the impacts of spatial diversification of the added wind, we compute hourly wind capacity factors that are averaged across each of the states of California and Texas. To do this, we let \({\cal{W}}\) denote the set of wind sites in each state that are in the WIND Toolkit. Then, we let At,w denote the MW of wind that is available at location w in hour t. We compute the state-average wind capacity factor in hour t, Wt, as:
where \(\bar A_w\) is the assumed nameplate capacity of the wind generator at location w in the WIND Toolkit dataset. The amount of wind that is available in hour-t (in our optimization model) is computed as:
where \(\bar W\) is the aggregate amount of wind that is added to the system (i.e., \(\bar W\) equals either 0 GW, 10 GW, or 20 GW).
Hourly solar availability is modeled in the same way, using modeled historical solar data that are obtained from the National Solar Radiation Database (NSRDB)41,42. The NSRDB data are processed using version 5 of the PVWatts software tool43. PVWatts simulates the output of a photovoltaic system, given solar and other weather-condition data. We assume that the added photovoltaic plants are fixed axis with a 180° azimuth and a tilt that is equal to each location’s latitude. To account for geographic diversification of where solar can be added within each state, we compute state-average hourly solar capacity factors. To do this, we let \({\cal{P}}\) denote the set of 5636 and 1751 sites within the states of California and Texas, respectively, that are represented in the NSRDB dataset. Then, we define the state-average solar capacity factor in hour t, Pt, as:
where Bt,p and \(\bar B_p\) are the photovoltaic output that is available in hour t and the assumed nameplate capacity of the photovoltaic generator at location p, respectively, in the NSRDB data. We then model available solar in hour t (in our optimization model) as:
where \(\bar P\) is the aggregate amount of solar that is added to the system. We compute the total amount of renewable energy that is available in each hour as:
Case studies—overview
We examine using energy storage to ease the integration and reduce the curtailment of renewable energy in California and Texas. California makes for an interesting case study because it has limited ability to decarbonize through fuel switching (the fossil-fueled fleet in the state is almost entirely natural gas-fired). Concurrently, the state is pursuing ambitious renewable portfolio standards with the aim of decarbonization and is promoting more recently energy storage through policy measures. Given this context, Solomon et al.44 evaluate the opportunities for increased use of renewable energy in California with and without energy storage. Eichman et al.45 examine the value of California’s energy storage mandate with high penetrations of renewable energy. They do not, however, endogenize the sizing of energy storage nor do they examine the range of technologies, renewable penetrations, and carbon-related policies that we do.
A second case study examines Texas, specifically focusing on the ERCOT system. ERCOT is largely electrically isolated from the rest of North America46. ERCOT makes for an interesting case relative to California, because it has greater variety in the mix of thermal generation, including coal- and natural gas-fired units, meaning that there is potential for fuel switching to achieve CO2 reductions. Texas also has excellent renewable resources46.
Case studies—data
Due to limited data availability, our case studies cover 20 April 2010 until 31 December 2012. During this period, California had about 237 natural gas-fired generating units whereas ERCOT had about 39 coal- and 234 natural gas-fired units installed. Table 2 summarizes the installed capacity of other generation technologies and the annual-average loads in the two systems.
The natural gas- and coal-fired generators are assumed to be dispatchable (i.e., their production levels can be varied to achieve supply/demand balance). The capacities and heat and CO2-emissions rates of these generators are obtained from United States Environmental Protection Agency Air Markets Program Data (https://ampd.epa.gov/ampd/) and Form EIA-860 and EIA-923 data from the United States Energy Information Administration (EIA). The nuclear, biomass, hydroelectric, and geothermal generators (that were installed in the study years) are treated as being non-dispatchable. The outputs of these units are fixed based on historical hourly production levels that are reported by the CAISO and ERCOT. Table 3 summarizes the fuel prices that we use for the dispatchable natural gas- and coal-fired units, which are obtained from Form EIA-923 data (these are reported in $ per MMBTU, as MMBTU is the unit that is used most commonly in the United States for reporting fuel prices). Fuel prices for other generating technologies are not needed, because these units are modeled as being non-dispatchable.
California exchanges energy with neighboring states. We assume these exchanges to be fixed in our case study, based on historical CAISO data. ERCOT has extremely limited energy exchanges, due to its being electrically isolated from the rest of North America. Thus, we model the ERCOT system as having no energy exchanges. CAISO and ERCOT also provide hourly historical load data, which we use in our analysis. We assume that the two systems have dispatchability requirements that the total output of the natural gas-fired, coal-fired, nuclear, biomass, hydroelectric, and geothermal generators plus the amount of energy that could be provided by energy storage be above some minimum value. This requirement reflects the limited flexibility of the non-renewable generators in reducing their output as well as the desire by system operators to maintain some dispatchable generation to accommodate unanticipated system contingencies47. We define the minimum-dispatchability requirement for the CAISO system based on an analysis of its flexibility4 and generation and curtailment data that are published by CAISO. On this basis, we consider four different minimum-dispatchability requirements of 0.0 GW (i.e., the system is fully flexible with no minimum-dispatchability requirement), 5.4, 7.0, and 12.6 GW, with 7.0 GW as the base case. We set the minimum-dispatchability requirements for the ERCOT system by scaling on a pro rata basis compared to the values that are used for the CAISO system. This gives minimum-dispatchability requirements of 0.0, 6.3, 8.2, and 14.8 GW, with 8.2 GW as the base case, for the ERCOT system.
We examine nine energy storage technologies that have suitable characteristics for renewable integration- and curtailment-related applications: PHS, ACAES, DCAES, and PbA, VRB, Li-ion, NaS, PSB, and ZNBR batteries8,37. These technologies are characterized by their round-trip efficiencies, service lives, and capital costs, which are summarized in Table 4 and obtained from a comprehensive literature review8,10,11,12,13,29,37,48,49,50,51,52. The service lives of the technologies are accounted for when annualizing their capital costs. This annualization makes the capital costs of the technologies comparable to the cost of power system operations, which are modeled over a single-year period for each year that is studied. Because we only have data starting from 20 April 2010, we subannualize the capital cost in this year to make the capital and operating costs comparable.
The round-trip efficiency of DCAES is modeled differently than those of the other energy storage technologies. The other technologies are pure energy storage, in the sense that they each use electricity as the sole energy input. DCAES uses electricity when charging but combusts natural gas when discharged. Each MWh of electricity that is stored in a DCAES system is assumed to produce 1.39 MWh of electricity when discharged but uses 4.20 MMBTU of natural gas in doing so13,53. This natural gas combustion is assumed to result in CO2 emissions of 0.058 ton MMBTU−1 37. The direct cost of the natural gas that is consumed by the DCAES is computed using the values that are reported in Table 3.
Case studies—scenarios
For each energy storage technology, we model its optimal investment level and hourly operation of the power system in 36 scenarios that correspond to different renewable-penetration levels and carbon policies. These cases are examined in the CAISO and ERCOT systems for each of the years 2010–2012. Specifically, we examine three wind-penetration levels, which are cases with 0, 10, and 20 GW of wind total, three solar-penetration levels, with 0, 20, and 40 GW of photovoltaic solar total, and four carbon-tax regimes, with tax rates of $0, $50, $100, and $200 per ton. The outputs of the wind and solar plants can be curtailed, as required by the constraints of the optimization model to achieve hourly supply/demand balance.
Code availability
The optimization code that supports the analysis within this paper and other findings of this study are available from the corresponding author upon reasonable request.
Change history
26 August 2019
An amendment to this paper has been published and can be accessed via a link at the top of the paper.
References
Wiser, R. & Bolinger, M. 2016 Wind Technologies Market Report. Technical Report No. DOE/GO-102917-5033. (U.S. Department of Energy, Washington D.C., 2017).
Feldman, D. & Margolis, R. Q1/Q2 2018 Solar Industry Update. Technical Report No. NREL/PR-6A20-72036. (National Renewable Energy Laboratory, Golden, 2018).
Denholm, P., Ela, E., Kirby, B. & Milligan, M. R. The Role of Energy Storage with Renewable Electricity Generation. Technical Report No. NREL/TP-6A2-47187. (National Renewable Energy Laboratory, Golden, 2010).
Denholm, P., O’Connell, M., Brinkman, G. & Jorgenson, J. Overgeneration from Solar Energy in California: A Field Guide to the Duck Chart. Technical Report No. NREL/TP-6A20-65023. (National Renewable Energy Laboratory, Golden, 2015).
Denholm, P. & Margolis, R. The Potential for Energy Storage to Provide Peaking Capacity in California under Increased Penetration of Solar Photovoltaics. Technical Report. No. NREL/TP-6A20-70905. (National Renewable Energy Laboratory, Golden, 2018).
Roberts, B. & Harrison, J. Energy Storage Activities in the United States Electricity Grid. (Electricity Advisory Committee, U.S. Department of Energy, Washington D.C., 2011)
Luo, X., Wang, J., Dooner, M. & Clarke, J. Overview of current development in electrical energy storage technologies and the application potential in power system operation. Appl. Energy 137, 511–536 (2015).
Eyer, J. M. & Corey, G. Energy Storage for the Electricity Grid: Benefits and Market Potential Assessment Guide. Technical Report No. SAND2010-0815. (Sandia National Laboratories, Albuquerque, 2010).
Denholm, P. et al. The Value of Energy Storage for Grid Applications. Technical Reportt No. NREL/TP-6A20-58465. (National Renewable Energy Laboratory, Golden, 2013).
Dunn, B., Kamath, H. & Tarascon, J.-M. Electrical energy storage for the grid: a battery of choices. Science 334, 928–935 (2011).
Aneke, M. & Wang, M. Energy storage technologies and real life applications—a state of the art review. Appl. Energy 179, 350–377 (2016).
Kyriakopoulos, G. L. & Arabatzis, G. Electrical energy storage systems in electricity generation: energy policies, innovative technologies, and regulatory regimes. Renew. Sustain. Energy Rev. 56, 1044–1067 (2016).
Gallo, A. B., Simões-Moreira, J. R., Costa, H. K. M., Santos, M. M. & Moutinho dos Santos, E. Energy storage in the energy transition context: a technology review. Renew. Sustain. Energy Rev. 65, 800–822 (2016).
Arbabzadeh, M., Johnson, J. X., Keoleian, G. A., Rasmussen, P. G. & Thompson, L. T. Twelve principles for green energy storage in grid applications. Environ. Sci. Technol. 50, 1046–1055 (2016).
Lin, Y., Johnson, J. X. & Mathieu, J. L. Emissions impacts of using energy storage for power system reserves. Appl. Energy 168, 444–456 (2016).
Fisher, M. J. & Apt, J. Emissions and economics of behind-the-meter electricity storage. Environ. Sci. Technol. 51, 1094–1101 (2017).
Abeygunawardana, A. M. A. K. & Ledwich, G. Estimating benefits of energy storage for aggregate storage applications in electricity distribution networks in Queensland. In Proc. 2013 IEEE Power & Energy Society General Meeting (Institute of Electrical and Electronics Engineers, Vancouver, 2013).
Chang, J. et al. The Value of Distributed Electricity Storage in Texas: Proposed Policy for Enabling Grid-Integrated Storage Investments. (The Brattle Group, Maryland, 2014).
Sardi, J., Mithulananthan, N., Gallagher, M. & Hung, D. Q. Multiple community energy storage planning in distribution networks using a cost-benefit analysis. Appl. Energy 190, 453–463 (2017).
Braff, W. A., Mueller, J. M. & Trancik, J. E. Value of storage technologies for wind and solar energy. Nat. Clim. Change 6, 964–969 (2016).
Carson, R. T. & Novan, K. The private and social economics of bulk electricity storage. J. Environ. Econ. Manag. 66, 404–423 (2013).
Hiremath, M., Derendorf, K. & Vogt, T. Comparative life cycle assessment of battery storage systems for stationary applications. Environ. Sci. Technol. 49, 4825–4833 (2015).
Hittinger, E. & Azevedo, I. M. L. Bulk energy storage increases united states electricity system emissions. Environ. Sci. Technol. 49, 3203–3210 (2015).
Hittinger, E. & Azevedo, I. M. L. Estimating the quantity of wind and solar required to displace storage-induced emissions. Environ. Sci. Technol. 51, 12988–12997 (2017).
Goteti, N. S., Hittinger, E. & Williams, E. How much wind and solar are needed to realize emissions benefits from storage. Energy Syst. 10, 437–459 (2019).
Ho, W. S. et al. Optimal scheduling of energy storage for renewable energy distributed energy generation system. Renew. Sustain. Energy Rev. 58, 1100–1107 (2016).
Parra, D., Norman, S. A., Walker, G. S. & Gillott, M. Optimum community energy storage system for demand load shifting. Appl. Energy 174, 130–143 (2016).
Korpaas, M., Holen, A. T. & Hildrum, R. Operation and sizing of energy storage for wind power plants in a market system. Int. J. Electr. Power Energy Syst. 25, 599–606 (2003).
Zafirakis, D., Chalvatzis, K. J., Baiocchi, G. & Daskalakis, G. The value of arbitrage for energy storage: evidence from European electricity markets. Appl. Energy 184, 971–986 (2016).
Chau, C.-K., Zhang, G. & Chen, M. Cost minimizing online algorithms for energy storage management with worst-case guarantee. IEEE Trans. Smart Grid 7, 2691–2702 (2016).
Hemmati, R., Saboori, H. & Jirdehi, M. A. Multistage generation expansion planning incorporating large scale energy storage systems and environmental pollution. Renew. Energy 97, 636–645 (2016).
de Sisternes, F. J., Jenkins, J. D. & Botterud, A. The value of energy storage in decarbonizing the electricity sector. Appl. Energy 175, 368–379 (2016).
Arciniegas, L. M. & Hittinger, E. Tradeoffs between revenue and emissions in energy storage operation. Energy 143, 1–11 (2018).
Wiser, R. & Bolinger, M. 2017 Wind Technologies Market Report. Techical Report No. DOE/EE-1798. (U.S. Department of Energy, Washington D.C., 2018).
Sioshansi, R. & Conejo, A. J. Optimization in Engineering: Models and Algorithms, Vol. 120 of Springer Optimization and Its Applications. (Springer Nature, Cham, 2017).
Yong, S. K. & McDonald, S. Emissions tax and second-mover advantage in clean technology R&D. Environ. Econ. Policy Stud. 20, 89–108 (2018).
Arbabzadeh, M., Johnson, J. X. & Keoleian, G. A. Parameters driving environmental performance of energy storage systems across grid applications. J. Energy Storage 12, 11–28 (2017).
Sioshansi, R., Denholm, P., Jenkin, T. & Weiss, J. Estimating the value of electricity storage in PJM: arbitrage and some welfare effects. Energ. Econ. 31, 269–277 (2009).
Denholm, P. & Sioshansi, R. The value of compressed air energy storage with wind in transmission-constrained electric power systems. Energy Policy 37, 3149–3158 (2009).
Draxl, C., Clifton, A., Hodge, B.-M. & McCaa, J. The Wind Integration National Dataset (WIND) Toolkit. Appl. Energy 151, 353–366 (2015).
Sengupta, M. et al. A Physics-Based GOES Satellite Product for Use in NREL’s National Solar Radiation Database. Technical Report No. NREL/CP-5D00-62237. (National Renewable Energy Laboratory, Golden, 2014).
Sengupta, M. et al. A Physics-Based GOES Product for Use in NREL’s National Solar Radiation Database. Technical Report No. NREL/CP-5D00-62776. (National Renewable Energy Laboratory, Golden, 2014).
Dobos, A. P. PVWatts Version 5 Manual. Technical Report No. NREL/TP-6A20-62641. (National Renewable Energy Laboratory, Golden 2014).
Solomon, A. A., Kammen, D. M. & Callaway, D. The role of large-scale energy storage design and dispatch in the power grid: a study of very high grid penetration of variable renewable resources. Appl. Energy 134, 75–89 (2014).
Eichman, J., Denholm, P., Jorgenson, J. & Helman, U. Operational Benefits of Meeting California’s Energy Storage Targets. Technical Reportt No. NREL/TP-5400-65061. (National Renewable Energy Laboratory, Golden, 2015).
Denholm, P. & Hand, M. Grid flexibility and storage required to achieve very high penetration of variable renewable electricity. Energy Policy 39, 1817–1830 (2011).
Jenkins, J. D. et al. The benefits of nuclear flexibility in power system operations with renewable energy. Appl. Energy 222, 872–884 (2018).
Schoenung, S. Energy Storage Systems Cost Update. Technical Report. No. SAND2011-2730. (Sandia National Laboratories, Albuquerque, 2011).
Kintner-Meyer, M. C. W. et al. National Assessment of Energy Storage for Grid Balancing and Arbitrage: Phase 1, WECC. Technical Report No. PNNL-21388. (Pacific Northwest National Laboratory Richland, Washington, 2012).
Zakeri, B. & Syri, S. Electrical energy storage systems: a comparative life cycle cost analysis. Renew. Sustain. Energy Rev. 42, 569–596 (2015).
Cole, W. J., Marcy, C., Krishnan, V. K. & Margolis, R. Utility-scale Lithium-Ion Storage Cost Projections for Use in Capacity Expansion Models. In Proc. 2016 North American Power Symposium (Institute of Electrical and Electronics Engineers, Denver, 2016).
Schmidt, O., Hawkes, A., Gambhir, A. & Staffell, I. The future cost of electrical energy storage based on experience rates. Nat. Energy 2, 1–8 (2017).
Drury, E., Denholm, P. & Sioshansi, R. The value of compressed air energy storage in energy and reserve markets. Energy 36, 4959–4973 (2011).
Acknowledgements
This work was supported by National Science Foundation Grants 1230236 and 1548015, the Dow Sustainability Fellows Program, and the University of Michigan Rackham Predoctoral Fellowship Program. We thank Y. Zerehsaz, H. Tavafoghi, and A. Sarabi (University of Michigan) for their valuable contributions on this project, the Center for Sustainable System at the University of Michigan for intellectual support, and A. Sorooshian (University of Arizona) for helpful discussions.
Author information
Authors and Affiliations
Contributions
M.A. and R.S. developed the model, designed the study, conducted the analysis, and co-wrote the paper. J.J. and G.K. participated in the study design and edited the paper.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Peer review information: Nature Communications thanks Soo. Keong Yong and other anonymous reviewer(s) for their contribution to the peer review of this work. Peer reviewer reports are available.
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Source data
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Arbabzadeh, M., Sioshansi, R., Johnson, J.X. et al. The role of energy storage in deep decarbonization of electricity production. Nat Commun 10, 3413 (2019). https://doi.org/10.1038/s41467-019-11161-5
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-019-11161-5
This article is cited by
-
An integrated high-throughput robotic platform and active learning approach for accelerated discovery of optimal electrolyte formulations
Nature Communications (2024)
-
Synergy level measurement and optimization models for the supply-transmission-demand-storage system for renewable energy
Annals of Operations Research (2024)
-
Keystones of green smart city—framework, e-waste, and their impact on the environment—a review
Ionics (2024)
-
The Influence of Beam Shape on the Single-Track Formation of Pure Zn Towards the Additive Manufacturing of Battery Electrodes
Lasers in Manufacturing and Materials Processing (2024)
-
Economic evaluation of energy storage integrated with wind power
Carbon Neutrality (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.