Abstract
Silicon spin qubits have emerged as a promising path to large-scale quantum processors. In this prospect, the development of scalable qubit readout schemes involving a minimal device overhead is a compelling step. Here we report the implementation of gate-coupled rf reflectometry for the dispersive readout of a fully functional spin qubit device. We use a p-type double-gate transistor made using industry-standard silicon technology. The first gate confines a hole quantum dot encoding the spin qubit, the second one a helper dot enabling readout. The qubit state is measured through the phase response of a lumped-element resonator to spin-selective interdot tunneling. The demonstrated qubit readout scheme requires no coupling to a Fermi reservoir, thereby offering a compact and potentially scalable solution whose operation may be extended above 1 K.
Similar content being viewed by others
Introduction
The recent years have witnessed remarkable progress in the development of semiconductor spin qubits1,2,3,4 with an increasing focus on silicon-based realizations5,6,7,8. Access to isotopically enriched 28Si has enabled the achievement of very long spin coherence times for both nuclear and electron spins9,10,11. In addition, two-qubit gates with increasing high fidelities were demonstrated in electrostatically defined electron double quantum dots12,13,14.
While further improvements in single- and two-qubit gates can be expected, growing research efforts are now being directed to the realization of scalable arrays of coupled qubits15,16,17,18,19. Leveraging the well-established silicon technology may enable facing the scalability challenge, and initiatives to explore this opportunity are on the way20. Simultaneously, suitable qubit device geometries need to be developed. One of the compelling problems is to engineer scalable readout schemes. The present work addresses this important issue.
It has been shown that a microwave excitation applied to a gate electrode drives Rabi oscillations via the electric-dipole spin resonance mechanism4,5,6,21,22,23. The possibility of using a gate as sensor for qubit readout would allow for a compact device layout, with a clear advantage for scalability. Gate reflectometry probes charge tunneling transitions in a quantum dot system through the dispersive shift of a radiofrequency (rf) resonator connected to a gate electrode24,25,26,27. Jointly to spin-selective tunneling, e.g. due to Pauli spin blockade in a double quantum dot (DQD), this technique provides a way to measure spin states.
In a similar fashion, the phase shift of a superconducting microwave resonator coupled to the source of an InAs nanowire has enabled spin qubit dispersive readout22. In Si, recent gate reflectometry experiments have shown single-shot electron spin detection28,29,30.
Here, we combine coherent spin control and gate dispersive readout in a compact qubit device. Two gates tune an isolated hole DQD, and two distinct electric rf tones (one per gate) allow spin manipulation and dispersive readout. Spin initialization and control are performed without involving any charge reservoir; qubit readout relies on the spin-dependent phase response at the DQD charge degeneracy point. We assess hole single spin dynamics and show coherent spin control, validating a protocol for complete qubit characterization exploitable in more complex architectures.
Results
Double quantum dot dispersive spectroscopy
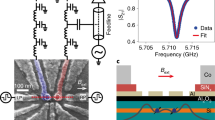
The experiment is carried out on a double-gate, p-type Si transistor fabricated on a silicon-on-insulator 300-mm wafer using an industry-standard fabrication line6. The device, nominally identical to the one in Fig. 1c, has two parallel top gates, GR and GC, wrapping an etched Si nanowire channel. The gates are defined by e-beam lithography and have enlarged overlapping spacers to avoid doping implantation in the channel. The measurement circuit is shown in Fig. 1a. At low temperature (we operate the device at 20 mK using a dilution refrigerator), DC voltages VC and VR are applied to these gates to induce two closely spaced hole quantum dots. The control gate GC delivers also sub-μs pulses and microwave excitation in the GHz range to manipulate the qubit. The readout gate, GR, is wire-bonded to a 220 nH surface-mount inductor. Along with a parasitic capacitance and the device impedance, the inductor forms a tank circuit resonating at f0 = 339 MHz. Figure 1b shows the phase ϕ and attenuation A of the reflected signal as a function of the resonator driving frequency fR. From the slope of the phase trace at f0 we extract a quality factor Qloaded ≃ 18. The qubit device acts as a variable impedance load for the resonator, and the resonant frequency f0 undergoes a dispersive shift according to the state of the qubit.
Device layout and circuitry for qubit dispersive sensing and manipulation. a False-color transmission electron micrograph of a double-gate Si device. The 11-nm-thick, 35-nm-wide Si nanowire (light blue) connects p-type, boron-doped source-drain contacts (dark blue) and lies on a 140-nm-thick SiO2 buffer layer (pink). The two 35-nm-wide gates (grey) are spaced by 35 nm. Si3N4 spacers (cyan) prevent dopant implantation in the Si channel. At 20 mK, proper gate voltages induce the accumulation of two hole quantum dots: one can be used as a spin qubit, the other as a helper dot for qubit readout. One gate is connected to a lumped-element resonator excited at frequency fR for dispersive readout. A ultra-high frequency digital lock-in demodulates the reflected signal after a directional coupler, separating the incoming and outgoing waves, and a low-noise amplifier at 4 K. The other gate applies square pulses and GHz radiation to drive controlled coherent rotations of the hole spin qubit. At the bottom, DQD energy diagram with Ev as valence band edge and EF as Fermi energy. b Phase response (ϕ) and attenuation (A) of the resonator at base temperature. c Scanning electron micrograph of the device
To determine the charge stability diagram of our DQD, we probe the phase response of the resonator while sweeping the DC gate voltages VR and VC (see Supplementary Note 2 and Supplementary Fig. 2).
The diagonal ridge in Fig. 2a denotes the interdot charge transition we shall focus on hereafter. Along this ridge, the electrochemical potentials of the two dots line up enabling the shuttling of a hole charge from one dot to the other. This results in a phase variation Δϕ in the reflected signal. Quantitatively, Δϕ is proportional to the quantum capacitance associated with the gate voltage dependence of the energy levels involved in the interdot charge transition. Interdot tunnel coupling results in the formation of molecular bonding (+) and anti-bonding (−) states with energy levels E+ and E−, respectively. These states have opposite quantum capacitance since CQ,± = −α2(∂2E±/∂ε2)27. Here ε is the gate-voltage detuning along a given line crossing the interdot charge transition boundary, and α is a lever-arm parameter relating ε to the energy difference between the electrochemical potentials of the two dots (we estimate α ≃ 0.58 eV V−1 along the detuning line in Fig. 2a). The width of the Δϕ ridge, once translated into energy, gives the interdot tunnel coupling, t. We estimate t between 6.4 and 8.5 μeV, depending on whether thermal fluctuations contribute or not to the dispersive response (see Supplementary Note 3).
Magnetospectroscopy of the double quantum dot. a Phase shift of the reflected signal as a function of VC and VR near the interdot transition line under study. The arrow indicates ε detuning axis. b Interdot dispersive signal as a function of a magnetic field B oriented along the nanowire axis. The phase response diminishes with B, denoting a interdot charge transition of (0, 2) ↔ (1, 1) type. Inset: theoretical prediction of the dispersive response for a DQD model taking into account thermal spin populations, see Supplementary Note 3. c Line cuts of the plot in panel b) at the position of the dashed lines. Data are offset for clarity. d Schematic of the DQD energy levels close to a (0, 2) ↔ (1, 1) transition at finite B and for \(|g_{\mathrm{L}}^ \ast - g_{\mathrm{R}}^ \ast | = 0.5\). e Thermally-averaged phase response 〈Δϕ〉i with Teff = 0.25 K. 〈Δϕ〉i is second derivative of the energy-level dispersion of state i in d), weighted by the occupation probability. Here i labels the different DQD states, i.e. the singlets Sg (green) and Se (black), and the triplets T0 (blue), T− (red), and T+ (red). f Qualitative phase shift resulting from the sum of all 〈Δϕ〉i from e). A double-peak structure emerges at sufficiently high B in qualitative agreement with the experimental data in c)
The total charge parity and the spin character of the DQD states can be determined from the evolution of the interdot ridge in an applied magnetic field, B31. Figure 2b shows the B-dependence of the phase signal at the detuning line indicated in Fig. 2a. Four representative traces taken from this plot are shown in Fig. 2c. The interdot phase signal progressively drops with B. At B = 0.355 T the line profile is slightly asymmetric, while a double-peak structure emerges at B = 0.46 T. The two peaks move apart and weaken by further increasing B, as revealed by the trace at B = 0.85 T.
The observed behavior can be understood in terms of an interdot charge transition with an even number of holes in the DQD, in a scenario equivalent to a (0, 2) ↔ (1, 1) transition. We shall then refer to a “(0, 2)” and a “(1, 1)” state, even if the actual number of confined holes is larger (we estimate around ten, see Supplementary Note 2). The ε dependence of the DQD states at finite B is presented in Fig. 2d. Deeply in the positive detuning regime, different g-factors for the left (\(g_{\mathrm{L}}^ \ast\)) and the right dot (\(g_{\mathrm{R}}^ \ast\)) result in four non-degenerate (1, 1) levels corresponding to the following spin states: |⇓⇓〉, |⇑⇓〉, |⇓⇑〉, |⇑⇑〉22,32,33. At large negative detuning, the ground state is a spin-singlet state S(0,2) and the triplet states T(0,2) lie high up in energy. Around zero detuning, the |⇑⇓〉, |⇓⇑〉 states hybridize with the S(0, 2) state forming an unpolarized triplet T0(1, 1) and two molecular singlets, Sg and Se, with bonding and anti-bonding character, respectively (Supplementary Note 3).
We use the spectrum of Fig. 2d to model the evolution of the interdot phase signal in Fig. 2b, c. Importantly, we make the assumption that the average occupation probability of the available excited states are populated according to a Boltzmann distribution with an effective temperature Teff, which is used as a free parameter. Because the reflectometry signal is averaged over many resonator cycles, \({\mathrm{\Delta }}\phi = \mathop {\sum}\nolimits_i {\langle {\mathrm{\Delta }}\phi \rangle _i}\), where 〈Δϕ〉i is the phase response associated to state i weighted by the respective occupation probability31 (here i labels the DQD levels in Fig. 2d). Figure 2e shows 〈Δϕ〉i as a function of ε for Teff = 250 mK. The spin polarized triplet states T− and T+ (i.e. |⇓⇓〉 and |⇑⇑〉, respectively) are linear in ε and, therefore, they do not cause any finite phase shift; Sg, Se, and T0(1, 1), on the other hand, possess a curvature and are sensed by the reflectometry apparatus (Supplementary Note 3). We note that the phase signal for T0(1, 1) has a peak-dip line shape whose minimum lies at positive ε (blue trace), partly counterbalanced by the positive phase signal due to Se. The Sg state causes a pronounced dip at negative ε (green trace), dominating over the peak component of T0. The overall net result is a phase signal with an asymmetric double-dip structure consistent with our experimental observation.
This simple model, with the chosen Teff = 250 mK, qualitatively reproduces the emergence of the double-dip structure at B~0.4 T, as well as its gradual suppression at higher B, as shown in the inset to Fig. 2b and in Fig. 2f (increasing the Zeeman energy results in the depopulation of the Sg and T0 excited states in favor of the T−(1,1) ground state, for which Δϕ = 0).
Dispersive detection of electric-dipole spin resonance
Now that we have elucidated the energy-level structure of the DQD, we can discuss the operation of the device as a single-hole spin qubit with electrical control and dispersive readout. Electric-dipole spin resonance (EDSR)6,23,34 is induced by a microwave voltage modulation applied to gate GC. To detect EDSR dispersively, the resonating states must have different quantum capacitances. The DQD is initially tuned to the position of the red star in Fig. 2c, where the DQD is in a “shallow” (1,1) configuration, i.e. close to the boundary with the (0,2) charge state (more details in Supplementary Note 4 and Supplementary Fig. 4).
Figure 3a shows the dispersive measurement of an EDSR line. The microwave gate modulation of frequency fC is applied continuously and B is oriented along the nanowire axis. We ascribe the resonance line to a second-harmonic driving process where 2hfC = gμBB (h the Planck’s constant, μB the Bohr magneton and g the effective hole g-factor). From this resonance condition we extract g = 1.735 ± 0.002, in agreement with previous works6,23. The first harmonic signal, shown in the inset to Fig. 3a, is unexpectedly weaker. Though both first and second harmonic excitations can be expected35, the first harmonic EDSR line (inset to Fig. 3a) is unexpectedly weaker. A comparison of the two signal intensities requires the knowledge of many parameters (relaxation rate, microwave power, field amplitude) and calls for deeper investigations.
Experimental detection of electric-dipole spin resonance (EDSR). a Phase response as a function of B and microwave frequency fC. B is oriented along the y direction with respect to the frame of Fig. 1a. The linear phase ridge denoted by a red arrow is a characteristic signature of EDSR. It corresponds to a second-harmonic signal, while the much weaker first harmonic is shown in the lower inset. b Stability diagram at B = 0.52 T (orientation β = 55° and θ = 90° according to the diagram in upper inset of a) with fC = 7.42 GHz and microwave power PC ≈ −80 dBm. EDSR between T−(1, 1) and T0(1, 1) (purple arrows in inset) is driven at point I. In the stability diagram, the change of population induced by EDSR is visible as a localized phase signal at point I/R. c Phase shift at VR = 1039.9 mV as a function of VC without microwave irradiation (dark), and under on-resonance and off-resonance excitation at fC = 7.42 and 7.60 GHz, respectively. EDSR-stimulated transitions appear as a pronounced peak whose position and line shape are compatible with our model (inset)
The visibility of the EDSR signal can be optimized by a fine tuning of the gate voltages. Figure 3b shows a high-resolution measurement over a narrow region of the stability diagram around the interdot charge transition boundary at B = 0.52 T; the interdot line has a double-peak structure, consistently with the data in Fig. 2b, c. The measurement is performed while applying a continuous microwave tone fC = 7.42 GHz. EDSR appears as a distinct phase signal around VC ≃ 362.5 mV and VR ≃ 1040 mV, i.e. slightly inside the (1,1) charge region, pinpointed by the black arrow as I/R. Such EDSR feature is extremely localized in the stability diagram reflecting the gate-voltage dependence of the hole g-factor23.
Figure 3c displays line cuts across the interdot transition line at fixed VR and different microwave excitation conditions. With no microwaves excitation, we observe the double-peak line shape discussed above. With a microwave gate modulation at fC = 7.42 GHz, the spin resonance condition is met at VC ≃ 362.45 mV, which results in a pronounced EDSR peak, the same observed at point I/R in Fig. 3b (see also Supplementary Fig. 4). The peak vanishes when fC is detuned by 20 MHz (cyan trace).
At point I/R, resonant microwave excitation enables the spectroscopy of the T0(1, 1) state. The inset to Fig. 3c shows the signal we expect from our model (Supplementary Note 4). In a small detuning window, the populations of T−(1, 1) and T0(1, 1) are assumed to be balanced by EDSR (see the energy levels in the inset to Fig. 3b); this results in a phase signal dramatically enhanced resembling the feature centered at I/R in the main panel. A further confirmation that the spin transitions are driven between T−(1, 1) and T0(1, 1) is given by the extrapolated intercept at 0 T of the EDSR transition line in Fig. 3a, found much smaller (<100 MHz) than t. In the following, we shall use point I/R to perform qubit initialization and readout.
Qubit control and readout
The device is operated as a spin qubit implementing the protocol outlined in Fig. 4a. The voltage sequence in the upper part of Fig. 4a tunes the DQD at the control point C (≃1 mV deep in the (1, 1) region) where holes are strongly localized in either one or the other dot with negligible tunnel coupling. A microwave burst of duration τburst and frequency fC drives single spin rotations between |⇓⇓〉 and |⇑⇓〉; the system is then brought back to I/R in the “shallow” (1, 1) regime for a time twait for readout and initialization. The dispersive readout eventually relies on the spin-resolved phase shift at I/R, though the reflectometry tone fR is applied during the whole sequence period TM and the reflected signal is streamed constantly to the acquisition module.
Single spin control and dispersive sensing. a The pulse sequence alternating between “deep” (1, 1) regime (C) for spin manipulation and “shallow” (1, 1) regime (I/R), close to the (0, 2) ↔ (1, 1) transition, for the readout and resetting of the spin system. A microwave burst rotates the hole spin during the manipulation stage. The readout tone is continuously applied throughout the sequence period TM. b Phase shift as a function of twait for a ≃1 mV pulse on VC with τburst = 100 ns and fC = 12.865 GHz, with B = 0.512 T along β = 0° and θ = 60°. The phase signal approaches 0 when twait ≫ T1. A simple model yields T1 = 2.7 ± 0.7 μs. c Dispersive signal Δϕ(fC, τburst), measured with the detuning pulses of a) with twait = 1 μs. Four maps have been averaged. d Phase response as a function of EDSR burst time at fC = 12.865 GHz. The plot shows Rabi oscillations with 15 MHz frequency due to coherent spin rotations. Each data point is integrated for 100 ms and then averaged over 30 traces
First, we determine the lifetime T1 of the excited spin state at the readout point I/R by sweeping twait after a π-burst at point C. The results are shown in Fig. 4b. The phase signal rapidly diminishes with increasing twait because spin relaxation depopulates the excited spin state in favor of the non-dispersive T−(1, 1) ground state. The estimated spin lifetime at the readout position is T1 = 2.7 ± 0.7 μs (see Supplementary Note 5). By shifting the position of a 100 ns microwave burst within a 12 μs pulse, no clear decay of the dispersive signal is observed, which suggests a spin lifetime at manipulation point longer than 10 μs.
We demonstrate coherent single spin control in the chevron plot of Fig. 4c. The phase signal is collected as a function of microwave burst time τburst and driving frequency fC. The spin state is initialized at point I/R (twait~T1). In Fig. 4d the phase signal is plotted as a function of τburst with fC set at the Larmor frequency fLarmor. The Rabi oscillations have 15 MHz frequency, consistent with Refs. roro and gtensor. The non-monotonous envelope is attributed to random phase accumulation in the qubit state by off-resonant driving at fLarmor ± fR due to up-conversion of microwave and reflectometry tones during the manipulation time. Data in Fig. 4d have been averaged over 30 measurements though the oscillations are easily distinguishable from single scans where each point is integrated over 100 ms. Figure 4 witnesses the success of using electrical rf signals both for coherent manipulation by EDSR and for qubit-state readout by means of gate reflectometry.
Discussion
The measured T1 is compatible with the relaxation times obtained for hole singlet-triplet states in acceptor pairs in Si36 and in Ge/Si nanowire double quantum dots37; in both cases T1 has been measured at the charge degeneracy point with reflectometry setups similar to ours. Nonetheless, charge detector measurements have shown T1 approaching 100 μs for single hole spins in Ge hut wire quantum dots38 and ≲1 ms for Ge/Si singlet-triplet systems39. This suggests that despite the intrinsic spin-orbit coupling single spin lifetimes in the ms range might be achievable in Si too. Strategies to boost T1 at the readout point may consist of inserting rf isolators between the coupler and the amplifier to reduce the backaction on the qubit and avoiding high-κ dielectric in the gate stack to limit charge noise.
We note that T1 could depend on the orientation of the magnetic field as well40. Future studies on magnetic field anisotropy will clarify whether T1, along with the effective g-factors (and hence the dispersive shift for readout) and Rabi frenquency, can be maximized at once along a specific direction. Technical improvements intended to enhance the phase sensitivity, like resonators with higher Q-factor and parametric amplification, could push the implemented readout protocol to distinguish spin states with a micro-second integration time, enabling single shot measurement as reported in a recent experiment with a gate-connected superconducting resonant circuit41. Lastly, the resonator integration in the back-end of the industrial chip could offer the possibility to engineer the resonant network at a wafer scale, guaranteeing controlled and reproducible qubit-resonator coupling.
The gate-based dispersive sensing demonstrated here does not involve local reservoirs of charges or embedded charge detectors. This meets the requirements of forefront qubit architectures (e.g. Ref. 16), where the spin readout would be performed at will by any gate of the 2D quantum dot array by frequency multiplexing.
Dispersive spin detection by Pauli blockade has a fidelity not constrained by the temperature of the leads. As recently shown42, isolated DQDs can serve as spin qubits even if placed at environmental temperatures exceeding the spin splitting, like 1 K or more. This should relax many cryogenic constraints and support the co-integration with classical electronics, as required by a scale-up perspective19.
Methods
Device fabrication
The fabrication process of the device was carried out in a 300 mm CMOS platform and is described in Ref. 6.
Experimental set-up
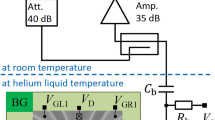
The experiment is performed by exciting the resonator input at fR = f0 = 339 MHz and power PR ≈ −110 dBm. We measure the phase variation Δϕ of the reflected signal isolated from the incoming wave by a directional coupler, amplified by 35 dB at 4 K and demodulated to baseband using homodyne detection. The complete circuit diagram of the experimental setup for qubit manipulation and dispersive readout is provided in Supplementary Note 1 and Supplementary Fig. 1.
Data availability
The data that support the findings of this study are available from the corresponding author upon reasonable request.
References
Petta, J. R. et al. Coherent manipulation of coupled electron spins in semiconductor quantum dots. Science 309, 2180–2184 (2005).
Laird, E. A., Pei, F. & Kouwenhoven, L. A valley–spin qubit in a carbon nanotube. Nat. Nanotech. 8, 565–568 (2013).
Dutt, M. G. et al. Quantum register based on individual electronic and nuclear spin qubits in diamond. Science 316, 1312–1316 (2007).
Watzinger, H. et al. A germanium hole spin qubit. Nat. Commun. 9, 3902 (2018).
Kawakami, E. et al. Electrical control of a long-lived spin qubit in a si/sige quantum dot. Nat. Nanotech. 9, 666–670 (2014).
Maurand, R. et al. A CMOS silicon spin qubit. Nat. Comm. 7, 13575 (2016).
Reed, M. et al. Reduced sensitivity to charge noise in semiconductor spin qubits via symmetric operation. Phys. Rev. Lett. 116, 110402 (2016).
Thorgrimsson, B. et al. Extending the coherence of a quantum dot hybrid qubit. npj Quant. Inform. 3, 32 (2017).
Veldhorst, M. et al. An addressable quantum dot qubit with fault-tolerant control-fidelity. Nat. Nanotech. 9, 981–985 (2014).
Muhonen, J. T. et al. Storing quantum information for 30 s in a nanoelectronic device. Nat. Nanotech. 9, 986–991 (2014).
Yoneda, J. et al. A quantum-dot spin qubit with coherence limited by charge noise and fidelity higher than 99.9%. Nat. Nanotech. 13, 102–106 (2018).
Zajac, D. M. et al. Resonantly driven cnot gate for electron spins. Science 359, 439–442 (2018).
Watson, T. et al. A programmable two-qubit quantum processor in silicon. Nature 555, 633–637 (2018).
Huang, W. et al. Fidelity benchmarks for two-qubit gates in silicon. Preprint at, https://arxiv.org/abs/1805.05027 (2018).
Veldhorst, M., Eenink, H., Yang, C. & Dzurak, A. Silicon CMOS architecture for a spin-based quantum computer. Nat. Commun. 8, 1766 (2017).
Li, R. et al. A crossbar network for silicon quantum dot qubits. Sci. Adv. 4, eaar3960 (2018).
Jones, C. et al. Logical qubit in a linear array of semiconductor quantum dots. Phys. Rev. X 8, 021058 (2018).
Zajac, D., Hazard, T., Mi, X., Nielsen, E. & Petta, J. Scalable gate architecture for a one-dimensional array of semiconductor spin qubits. Phys. Rev. Appl. 6, 054013 (2016).
Vandersypen, L. et al. Interfacing spin qubits in quantum dots and donors—hot, dense, and coherent. npj Quant. Inform. 3, 34 (2017).
Hutin, L. et al. Si MOS technology for spin-based quantum computing. In Proc. 2018 48th ESSDERC, 12–17 (IEEE, Dresden, Germany, 2018).
Nowack, K., Koppens, F., Nazarov, Y. V. & Vandersypen, L. Coherent control of a single electron spin with electric fields. Science 318, 1430–1433 (2007).
Petersson, K. et al. Circuit quantum electrodynamics with a spin qubit. Nature 490, 380–383 (2012).
Crippa, A. et al. Electrical spin driving by g-matrix modulation in spin-orbit qubits. Phys. Rev. Lett. 120, 137702 (2018).
Ciccarelli, C. & Ferguson, A. Impedance of the single-electron transistor at radio-frequencies. New J. Phys. 13, 093015 (2011).
Colless, J. et al. Dispersive readout of a few-electron double quantum dot with fast rf gate sensors. Phys. Rev. Lett. 110, 046805 (2013).
Gonzalez-Zalba, M., Barraud, S., Ferguson, A. & Betz, A. Probing the limits of gate-based charge sensing. Nat. Commun. 6, 6084 (2015).
Crippa, A. et al. Level spectrum and charge relaxation in a silicon double quantum dot probed by dual-gate reflectometry. Nano. Lett. 17, 1001–1006 (2017).
Pakkiam, P. et al. Single-shot single-gate rf spin readout in silicon. Phys. Rev. X 8, 041032 (2018).
West, A. et al. Gate-based single-shot readout of spins in silicon. Nat. Nanotech. 14, 437–441 (2019).
Urdampilleta, M. et al. Gate-based high fidelity spin read-out in a CMOS device. Preprint at https://arxiv.org/abs/1809.04584 (2018).
Schroer, M., Jung, M., Petersson, K. & Petta, J. Radio frequency charge parity meter. Phys. Rev. Lett. 109, 166804 (2012).
Nadj-Perge, S., Frolov, S., Bakkers, E. & Kouwenhoven, L. P. Spin-orbit qubit in a semiconductor nanowire. Nature 468, 1084–1087 (2010).
Nadj-Perge, S. et al. Spectroscopy of spin-orbit quantum bits in indium antimonide nanowires. Phys. Rev. Lett. 108, 166801 (2012).
Venitucci, B., Bourdet, L., Pouzada, D. & Niquet, Y.-M. Electrical manipulation of semiconductor spin qubits within the g-matrix formalism. Phys. Rev. B 98, 155319 (2018).
Scarlino, P. et al. Second-harmonic coherent driving of a spin qubit in a si/sige quantum dot. Phys. Rev. Lett. 115, 106802 (2015).
van der Heijden, J. et al. Spin-orbit dynamics of single acceptor atoms in silicon. Sci. Adv. 4, eaat9199 (2018).
Higginbotham, A. P. et al. Hole spin coherence in a Ge/Si heterostructure nanowire. Nano. Lett. 14, 3582–3586 (2014).
Vukušić, L., Kukučka, J., Watzinger, H., Schäffler, F. & Katsaros, G. Single-shot readout of hole spins in ge. Nano. Lett. 18, 7141–7145 (2018).
Hu, Y., Kuemmeth, F., Lieber, C. M. & Marcus, C. M. Hole spin relaxation in ge–si core–shell nanowire qubits. Nat. Nanotech. 7, 47–50 (2012).
Weber, B. et al. Spin–orbit coupling in silicon for electrons bound to donors. npj Quant. Inform. 4, 61 (2018).
Zheng, G. et al. Rapid high-fidelity gate-based spin read-out in silicon. Preprint at https://arxiv.org/abs/1901.00687 (2019).
Yang, C. et al. Silicon quantum processor unit cell operation above one kelvin. Preprint at https://arxiv.org/abs/1902.09126 (2019).
Acknowledgements
We thank K.D. Petersson, M.L.V. Tagliaferri, M.F. Gonzalez-Zalba and Y.-M. Niquet for fruitful discussions. The work was supported by the European Union’s Horizon 2020 research and innovation program under Grant Agreement No. 688539 MOS-QUITO (http://mos-quito.eu) and by the ERC Project No. 759388 LONGSPIN.
Author information
Authors and Affiliations
Contributions
A.C. and R.E. performed the experiments with help from R.M., A.C., R.M., and S.D.F. designed the experiment. R.L., L.H., B.B., M.V. fabricated the sample. A.C. analyzed the results with inputs from R.E., A. Aprá, A. Amisse, M.U., T.M., M.S., X.J., R.M., and S.D.F., A.C., R.M., and S.D.F. wrote the paper. M.S., X.J., M.V., and S.D.F. initiated the project.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Peer review information: Nature Communications thanks the anonymous reviewers for their contribution to the peer review of this work. Peer reviewer reports are available.
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Crippa, A., Ezzouch, R., Aprá, A. et al. Gate-reflectometry dispersive readout and coherent control of a spin qubit in silicon. Nat Commun 10, 2776 (2019). https://doi.org/10.1038/s41467-019-10848-z
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-019-10848-z
This article is cited by
-
Non-symmetric Pauli spin blockade in a silicon double quantum dot
npj Quantum Information (2024)
-
Strong coupling between a microwave photon and a singlet-triplet qubit
Nature Communications (2024)
-
High-fidelity spin qubit operation and algorithmic initialization above 1 K
Nature (2024)
-
Compilation and scaling strategies for a silicon quantum processor with sparse two-dimensional connectivity
npj Quantum Information (2023)
-
Noisy intermediate-scale quantum computers
Frontiers of Physics (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.