Abstract
Topological superconductor is attracting growing interest for its potential application to topological quantum computation. The superconducting proximity effect on the topological insulator surface state is one promising way to yield topological superconductivity. The superconductivity realized at the interface between Bi2Te3 and non-superconductor FeTe is one such candidate. Here, to detect the mutual interaction between superconductivity and topological surface state, we investigate nonreciprocal transport; i.e., current-direction dependent resistance, which is sensitive to the broken inversion symmetry of the electronic state. The largely enhanced nonreciprocal phenomenon is detected in the Bi2Te3/FeTe heterostructure associated with the superconducting transition. The emergent nonreciprocal signal at low magnetic fields is attributed to the current-induced modulation of supercurrent density under the in-plane magnetic fields due to the spin-momentum locking. The angular dependence of the signal reveals the symmetry of superconductivity and indicates the existence of another mechanism of nonreciprocal transport at high fields.
Similar content being viewed by others
Introduction
Topological superconductivity (TSC) is extensively sought for in contemporary condensed matter physics1,2,3. In a conventional superconductor, spin-up and spin-down electrons form a spin-singlet Cooper pair, and even-parity s-wave superconductor is realized. However, in a spinless superconductor, i.e., paired systems with only one active fermionic species, an odd-parity p + ip-wave superconductor is induced because of Pauli’s exclusion principle. Such a superconductor is topologically non-trivial and supports Majorana zero modes at the boundary or at the vortex core, which can act as building blocks of topological quantum computation owing to their non-abelian statistics1,2,3. To realize a non-degenerate spinless mode, one has to fight against the Kramers degeneracy: One way to deal with the Kramars degeneracy is time-reversal symmetry breaking as discussed in superfluid 3He-A phase4 and superconducting Sr2RuO45. Another strategy is to utilize spin-splitting by inversion symmetry breaking as proposed in the synthetic topological superconductors, such as superconducting–proximity coupled Rashba wires6,7,8 and topological insulator (TI) surface states9,10,11,12,13,14. Spin splitting caused by relativistic spin–orbit coupling and the inversion symmetry breaking yields a spin non-degenerate band, as exemplified by the spin–momentum-locked topological surface state. In these systems, the understanding of the superconducting property on the spin-splitted band structure is a prerequisite for the realization of TSC.
Recently, nonreciprocal charge transport measurement has been developed as a new probe to detect the spin-splitting in inversion symmetry-broken systems15,16,17,18,19,20,21,22,23,24. Reflecting the asymmetric nature of the electronic band structure with spin splitting, the electrical resistivity is expected to vary depending on the current and magnetic field direction. For example, nonreciprocal resistance is experimentally observed in materials with Rashba-type spin splitting, such as a bulk Rashba semiconductor15, interfaces16,17,18,19, and TI surfaces20,21,22. Under the in-plane magnetic field perpendicular to the current, the resistance value depends on the spin accumulation direction, either parallel or antiparallel to the external magnetic field15,18,19,20,21,22. Hence, this method works as an alternative to angle-resolved photoemission spectroscopy (ARPES)13 and scanning tunneling microscope (STM)14 to discuss the effect of spin splitting via transport measurement. Furthermore, nonreciprocal transport is also observed in non-centrosymmetric superconductors, such as a chiral nanotube23 and a transition metal dichalcogenide24, demonstrating that this probe is also applicable to inversion symmetry broken superconductors.
In this study, we target the emergent superconductivity at the interface between Bi2Te3 and FeTe25. The interface superconductivity is induced when a three-dimensional TI Bi2Te326 is grown on a parent compound of iron-based superconductor FeTe as schematically shown in Fig. 1a. Since the topological surface state locates at the interface, the interaction between them makes this system a strong candidate of TSC. However, it has remained unclear how the spin–momentum locking of the surface state affects the superconducting property25. To study the interplay between them, we here employ nonreciprocal charge transport. The nonreciprocal transport is especially effective to this system because surface-sensitive methods, such as ARPES and STM is not applicable to such a buried interface. The large nonreciprocal transport is observed to be associated with the superconducting transition of Bi2Te3/FeTe. This is revealed to originate from the current-induced-modulation of supercurrent density due to spin–momentum locking, which represents the close connection between superconductivity and topological surface state.
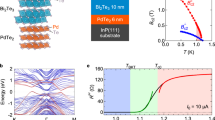
Nonreciprocal transport in a Bi2Te3/FeTe heterostructure. a The illustration of a Bi2Te3/FeTe heterostructure (Bi2Te3: blue, FeTe: green). The interface of Bi2Te3 and FeTe shows superconductivity (yellow region). The nonreciprocal transport is measured with current I along x-direction under the in-plane magnetic field B (along y-direction) perpendicular to the current. The mutual interaction between spin–momentum-locked topological surface state and superconductivity (as represented by ΔSC) is expected at the interface as expressed in momentum space in the right circle. σ represents the spin direction of the electron. b Temperature dependence of resistance in FeTe(18 nm)/CdTe(100) (green), Bi2Te3(15 nm)/InP(111) (blue) and Bi2Te3(15 nm)/FeTe(18 nm)/CdTe(100) (red) thin films. The superconductivity and topological surface state appear at the interface between Bi2Te3 and FeTe as denoted by the yellow allow. c The temperature dependence of resistance in Bi2Te3/FeTe heterostructure under in-plane magnetic field B = 0, 2, 4, 6, 8, 10, 12, and 14 T. The resistance is measured under I = 1 μA. d The magnetic field dependence of R2ω in Bi2Te3/FeTe heterostructure at T = 12 K (blue, normal state) and at T = 9.5 K (light blue, below the superconducting onset temperature) measured with a current magnitude of I = 200 μA
Result
Sample and basic characterization
We grew the heterostructure of Bi2Te3/FeTe using molecular-beam epitaxy (MBE) on CdTe(100) substrate. Van der Waals nature of Bi2Te3 and FeTe allows the sharp interface despite the difference in the lattice symmetry. The scanning transmission electron microscopy and energy-dispersive x-ray spectroscopy images demonstrate the high quality of the interface without discernable interdiffusion (see Supplementary Fig. 1 and Supplementary Note 1). Figure 1b shows the temperature dependence of resistance for the respective samples, FeTe(18 nm), Bi2Te3(15 nm), and Bi2Te3(15 nm)/FeTe(18 nm) bilayer thin films. FeTe thin film shows a semi-metallic behavior with a kink at around 50 K associated with the transition to the bicollinear antiferromagnetic state27, while Bi2Te3 shows a metallic behavior due to its electron-doped nature. The resistance of Bi2Te3/FeTe behaves as parallel conduction of these two materials except for the resistance drop to zero at around Tc0 = 10.7 K (Fig. 1c), indicating the appearance of superconductivity at the interface25. The fitting of the temperature dependence of resistivity with the Berezinskii–Kosterlitz–Thouless (BKT) transition28,29,30 and the jump in the power law of current–voltage characteristics (Supplementary Fig. 2 and Supplementary Note 2) verifies the two-dimensional nature of superconductivity25, where the binding of the vortex–antivortex pairs realizes the zero-resistance state. Because of the two-dimensional nature of superconductivity, the superconducting order parameter appears at Tc0, but finite resistance exists in the intermediate state because of the current-induced motion of vortex and antivortex. When vortex and antivortex form a pair at TBKT, zero-resistance state, i.e., the superconducting state is realized.
Nonreciprocal transport in Bi2Te3/FeTe
If inversion symmetry of the electronic system is broken, the electrical voltage V under the in-plane magnetic field is phenomenologically described up to a linear order in the magnetic field B and second order of current I as16
Here, we define the direction normal to the plane as z-axis and γ is a coefficient representing the nonlinear and nonreciprocal transport. When the current is perpendicular to the in-plane magnetic field, Eq. (1) becomes V = R0I + γR0BI2. If the second term is finite, the resistance value depends on the current direction, namely the nonreciprocal transport appears. Since the second term is proportional to I2, measurements of the second harmonic resistance \(R^{2\omega } = \frac{{R_0}}{{\sqrt 2 }}\gamma BI\) under ac current can detect the nonreciprocal transport (see Supplementary Note 3 for the derivation). We fabricated a Hall bar of 100 μm width and measured R2ω with a lock-in amplifier18,19,20,21,22,23,24 under the ac current of I = 200 μA (i = 2 A/m in current density) unless otherwise noted. Figure 1d displays the magnetic field dependence of R2ω in the normal and the intermediate states. In the normal state (T = 12 K), R2ω is almost zero. On the other hand, B-linear R2ω appears at T = 9.5 K in the intermediate region as the superconducting order parameter develops.
In contrast to the first harmonic resistance Rω, which is independent of the current magnitude, R2ω is proportional to the current as shown in Fig. 2a, b, which is consistent with Eq. (1). Thus, the γ value can be derived from the slope of the magnetic field dependence of R2ω/Rω as shown in Fig. 2c. To see the correspondence between the temperature dependence of Rω and γ value (Fig. 2d, e), we categorize them into three regions: normal, intermediate, and superconducting region. In the normal region, R2ω is not observed within the measurement noise level. In the superconducting region, R2ω vanishes with the disappearance of Rω (see Supplementary Fig. 3 and Supplementary Note 4). On the other hand, γ becomes finite in the intermediate region. Especially, γ value shows a divergent behavior towards the BKT transition temperature, TBKT, since R2ω drops to zero more slowly than Rω. The maximum of γ is 6.5 × 10−3 T−1 A−1 m at T = 6.9 K, which is more than five orders of magnitude larger than the reported value of γ = 6 × 10−8 T−1 A−1 m in TI without superconductivity22. The large enhancement of γ associated with the superconducting transition can be qualitatively explained as follows: The energy scale governing the system changes from the Fermi energy EF (~a few hundred meV) to the much smaller superconducting gap ΔSC (~1 meV) along with the superconducting transition. Consequently, the relative energy scale of spin–orbit interaction and magnetic field gets larger, resulting in the enhancement of nonreciprocal transport24.
Current-magnitude and temperature dependence of nonreciprocal transport. a The current-magnitude dependence of second harmonic resistance R2ω at T = 9.5 K, and B = 0.5 K deduced from the data shown in b. The black dotted line is the fitting line. b The magnetic field dependence of R2ω at T = 9.5 K measured under I = 40, 80, 120, 160, and 200 μA. c The magnetic field dependence of R2ω/Rω measured under I = 200 μA at T = 6.9, 7.2, 7.5, 7.8, 8.1, 8.5, 9, 9.5, and 10 K. d The temperature dependence of resistance measured under I = 200 μA. The black curve is the fitting of the Berezinskii–Kosterlitz–Thouless (BKT) transition using Halperin–Nelson formula, \(R = R_0\,{\mathrm{exp}}\left( { - 2b\left( {\frac{{T_{{\mathrm{c}}0} - T}}{{T - T_{{\mathrm{BKT}}}}}} \right)^{0.5}} \right)\), where R0 and b are material parameters. Tc0 is the temperature at which the finite amplitude of the order parameter develops and TBKT is the BKT transition temperature. The fitting gives the values, Tc0 = 10.7 K and TBKT = 6.0 K. The blue, green, and red regions correspond to normal, intermediate, and superconducting regions, respectively. e The temperature dependence of γ-value measured under I = 200 μA derived from c. The red points are the measurement on Bi2Te3(15 nm)/FeTe(18 nm) sample (denoted as BT(15 nm)/FT). The green point are the measurement on Bi2Te3(1.5 nm)/FeTe(18 nm) sample (denoted as BT(1.5 nm)/FT). Note that all the measurements, except for Fig. 1b, and the green curve of Fig. 2e, are done on the BT(15 nm)/FT sample. The purple curve is the fitting of the red points with the formula γ = β\((T - T_{{\mathrm{BKT}}})^{ - 1.5}\), where β = 5.3 × 10−3 T−1 A−1 m. Note that the BKT model and the fitting is valid only at around TBKT, which is represented by the solid purple curve. The purple dotted curve is out of the applicable range of theory
Surface state origin of nonreciprocal transport
Because of the following two reasons, it is natural to guess that topological surface state plays a vital role in nonreciprocal transport: (i) spin–orbit coupling is an essential source of nonreciprocal transport31 and (ii) topological surface state with strong spin–orbit coupling coexists with superconductivity at the interface where nonreciprocal transport appears. To substantiate this argument, we study the nonreciprocal transport of Bi2Te3(1.5 nm)/FeTe(18 nm) with much thinner Bi2Te3 thickness. Although the normal state resistance and the BKT transition temperature is almost the same in the two samples (Supplementary Figs 4 and 5, and Supplementary Notes 5 and 6), the γ-value for Bi2Te3(1.5 nm)/FeTe(18 nm) is about an order of magnitude smaller than that of Bi2Te3(15 nm)/FeTe(18 nm) as shown in the green points in Fig. 2e. This dramatic change is attributed to the suppressed spin polarization of the surface state in the ultrathin limit because of the hybridization between the top and surface states32,33. Thus, the large suppression of the signal points to the surface state origin of nonreciprocal transport.
On the basis of the above observation, we theoretically treat the superconducting-proximity-coupled surface state to discuss the temperature dependence of γ. A recent theoretical study34 suggests that spin–momentum locking of the surface state causes the renormalization of supercurrent density under the current in superconducting-proximity-coupled TI. As a result, the BKT transition temperature is modulated as T′BKT = TBKT(1 + αBI). Interestingly, this equation means that resistance in this system can decrease for a specific current direction, different from the conventional superconductors, where resistance increases by the excitation with large current. By substituting T′BKT to the standard BKT model which is valid at around BKT transition temperature, we get
Here, we employed perturbative expansion about αBI, which is justified because R2ω is several orders of magnitude smaller than Rω as shown in Fig. 2c. Comparing the result with Eq. (1), the γ-value is expected to diverge as (T − TBKT)−1.5 34. In fact, the fitting of the γ-value by the formula (T − TBKT)−1.5 in Fig. 2e well reproduces the divergent behavior toward TBKT (see Supplementary Fig. 7 and Supplementary Note 8 for the reproducibility in another sample). The good consistency between the theory and the experiment supports that the enhancement of nonreciprocal transport can be understood in terms of the current-induced modulation of supercurrent density in the superconducting-proximity-coupled surface state.
High field behavior and angular dependence of nonreciprocal transport
In the above, we have considered the second harmonic resistance at a low magnetic field region, we next discuss R2ω at higher fields. Figure 3a, b show the magnetic field dependence of Rω and R2ω for T = 9.5 and 10 K. The breaking of superconductivity with the application of the magnetic field is clearly discerned in Fig. 3a. At low magnetic fields, the linear-positive slope of R2ω with respect to the magnetic field is observed. The positive slope can be explained in terms of the modulation of supercurrent density as discussed earlier. At high magnetic fields, however, R2ω shows a sign reversal. With the further application of the magnetic field, R2ω goes to zero along with the breaking of superconductivity, which is clearly discerned at T = 10 K at around B = 14 T. The B–T diagrams for Rω and R2ω are displayed as contour plots in Fig. 3c, d, respectively. We can again see that R2ω appears positively at low fields and negatively at high fields at the intermediate temperature region. To discuss the origin of the negative component, we investigate the magnetic field direction dependence of R2ω. Figure 3e, f show the xy plane (in-plane) and zy plane (out-of-plane) magnetic-field directional dependence of R2ω, respectively. R2ω becomes almost zero at B||x (φ = 0°, 180°, 360°) and B||z (θ = 0°, 180°, 360°), consistent with the symmetry of a superconducting-proximity-coupled TI20,21,22 (see Supplementary Fig. 9 and Supplementary Discussion 1 for the discussion on the disappearance of R2ω under B||z). In xy plane (Fig. 3e), R2ω shows sin φ dependence both at 2 and 9 T, meaning that the signal is scaled with the y component of the magnetic field, consistent with Eq. (1). Similarly, in the zy plane (Fig. 3f), R2ω shows sinθ behavior at 2 T, and the signal at 9 T basically follows sinθ behavior with the same sign as the 2 T signal. Remarkably, however, a sudden sign reversal of the signal is observed at θ = 90° and 270°, namely the negative component appears only when B is almost exactly aligned to in-plane (see Supplementary Figs. 6 and 8, and Supplementary Notes 7 and 8 for further analysis and reproducibility). In fact, the negative component almost vanishes at θ = 70°, leaving only the positive component, as shown in Fig. 3g. These results imply that the positive and the negative components are governed by the different origins. The sudden appearance of the negative component under the in-plane magnetic field indicates that it originates from the in-plane magnetic vortex along the y-direction35. The current-induced renormalization of supercurrent density may result in the modulation of the nucleation/annihilation energy barrier of the in-plane vortex, which can appear as nonreciprocal resistance35. Further theoretical and experimental investigation is required to fully reveal the origins of the negative component.
Nonreciprocal transport at high magnetic fields. a The magnetic field dependence of first harmonic resistance Rω at T = 9.5 K (light blue) and T = 10 K (gray) measured under I = 200 μA. b The magnetic field dependence of second harmonic resistance R2ω. at T = 9.5K and T = 10 K measured under I = 200 μA. The red and blue triangles represent the positive and negative peaks at around B = 2 T and B = 9 T, respectively. c The contour plot of Rω in the plane of magnetic field and temperature at θ = 90° (B || y, defined in f) measured under I = 200 μA. The superconducting onset and R = 1 Ω are shown in circle and triangle, respectively. d The contour plot of R2ω in the plane of magnetic field and temperature at θ = 90° measured under I = 200 μA. e The in-plane magnetic-field direction dependence of R2ω at B = 2 T (red) and B = 9 T (blue) within xy plane measured under I = 200 μA. φ is defined as an angle in xy plane measured from the x-axis. f The out-of-plane magnetic-field direction dependence of R2ω at B = 2 T (red) and B = 9 T (blue) within zy plane measured under I = 200 μA. θ is defined as an angle in zy plane measured from the z-axis. g The contour plot of R2ω in the plane of magnetic field and temperature at θ = 70° measured under I = 200 μA
Discussion
The large nonreciprocal charge transport in the superconducting interface of Bi2Te3/FeTe can be utilized as a magnetically controllable superconducting diode24 and as a rectenna at low temperatures35. The nonreciprocal transport can be well-explained by the modulation of supercurrent density due to spin–momentum locking, exemplifying the close connection between superconductivity and topological surface state. Thus, tuning the Fermi level to the surface state36 will make the present system a desirable platform to study TSC and the associated formation of Majorana fermion. The nonreciprocal transport measurement is also applicable to other TSC candidates, such as LaAlO3/SrTiO3 interface37,38, superconducting-proximity coupled Rashba wire7,8, and topological surfaces10,11,12,13,14, which will help to discuss the effect of spin splitting on the superconducting properties.
During the final revision of the manuscript, we noticed the independent ARPES study of Bi2Te3/FeTe, which suggests that charge transfer from FeTe to Bi2Te3 induces the interfacial superconductivity in hole-doped FeTe39. The interfacial superconductivity induces the proximity effect on the surface state of Bi2Te3, which is in line with the discussion of our present study.
Methods
MBE thin film growth
Thin films were grown by MBE on insulating CdTe(100) and InP(111) substrates. The growth temperatures for FeTe and Bi2Te3 were 400 and 180 °C, respectively. CdTe(100) substrates were etched with bromine–methanol (bromine 0.01%) for 5 min before the deposition. For FeTe, the flux ratio was fixed at Fe:Te = 1:30 and the growth rate was about 0.7 nm/min. For Bi2Te3, the flux ratio was fixed at Bi:Te = 1:2 and the growth rate was about 0.2 nm/min. To suppress the degradation of the film, AlOx capping layer with a thickness of about 3 nm was deposited at room temperature with an atomic layer deposition system immediately after taking out the samples from the MBE vacuum chamber.
Device fabrication
The Hall-bar device pattern was defined by a photolithography technique and wet etching processes with HCl:H3PO4:H2O = 1:1:8. For Ohmic-contact electrodes, 5 nm Ti/45 nm Au were deposited with an electron-beam evaporator.
Transport measurements
The first and second harmonic resistances, Rω and R2ω, were measured using a current source (Keithley: Model 6221) and lock-in amplifiers (SRS: SR830). The measurement current and frequency were fixed at 200 μA (root mean square) unless otherwise noted and at 13 Hz, respectively. The measurements were done in Physical Property Measurement System (Quantum Design: PPMS). R2ω was anti-symmetrized with respect to B.
Data availability
The data that support plots within this paper and other findings of this study are available from the corresponding author upon reasonable request.
References
Kitaev, A. Y. Anyons in an exactly solved model and beyond. Ann. Phys. 321, 2–111 (2006).
Wilczek, F. Majorana returns. Nat. Phys. 5, 614–618 (2009).
Alicea, J. New directions in the pursuit of Majorana fermions in solid state systems. Rep. Prog. Phys. 75, 076501 (2012).
Leggett, A. J. A theoretical description of the new phases of liquid 3He. Rev. Mod. Phys. 47, 331–414 (1975).
Mackenzie, A. P. & Maeno, Y. The superconductivity of Sr2RuO4 and the physics of spin-triplet pairing. Rev. Mod. Phys. 75, 657–712 (2003).
Oreg, Y., Refael, G. & Oppen, F. V. Helical liquids and Majorana bound states in quantum wires. Phys. Rev. Lett. 105, 177002 (2010).
Mourik, V. et al. Signatures of Majorana fermions in hybrid superconducto–semiconductor nanowire devices. Science 25, 1003–1007 (2012).
Nadj-Perge, S. et al. Observation of Majorana fermions in ferromagnetic atomic chains on a superconductor. Science 346, 602–607 (2014).
Fu, L. & Kane, C. L. Superconducting proximity effect and majorana fermions at the surface of a topological insulator. Phys. Rev. Lett. 100, 096407 (2008).
Wiedenmann, J. et al. 4π-periodic Josephson supercurrent in HgTe-based topological Josephson junctions. Nat. Commun. 7, 10303 (2016).
He, Q. L. et al. Chiral Majorana fermion modes in a quantum anomalous Hall insulator–superconductor structure. Science 357, 294–299 (2017).
Xu, J.-P. et al. Experimental detection of a Majorana mode in the core of a magnetic vortex inside a topological insulator–superconductor Bi2Te3/NbSe2 heterostructure. Phys. Rev. Lett. 114, 017001 (2015).
Yao, M.-Y. et al. The coexistence of superconductivity and topological order in the Bi2Se3 thin films. Science 336, 52–55 (2012).
Xu, S.-Y. et al. Momentum-space imaging of Cooper pairing in a half-Dirac-gas topological superconductor. Nat. Phys. 10, 943–950 (2014).
Ideue, T. et al. Bulk rectification effect in a polar semiconductor. Nat. Phys. 13, 578–583 (2017).
Rikken, G. L. J. A. & Wyder, P. Magnetoelectric anisotropy in diffusive transport. Phys. Rev. Lett. 94, 016601 (2005).
Olejník, K., Novák, V., Wunderlich, J. & Jungwirth, T. Electrical detection of magnetization reversal without auxiliary magnets. Phys. Rev. B 91, 180402 (2015).
Avci, C. O. et al. Unidirectional spin Hall magnetoresistance in ferromagnet/normal metal bilayers. Nat. Phys. 11, 570–575 (2015).
He, P. et al. Observation of out-of-plane spin texture in a SrTiO3 (111) two-dimensional electron gas. Phys. Rev. Lett. 120, 266802 (2018).
Yasuda, K. et al. Large unidirectional magnetoresistance in a magnetic topological insulator. Phys. Rev. Lett. 117, 127202 (2016).
Lv, Y. et al. Unidirectional spin-Hall and Rashba−Edelstein magnetoresistance in topological insulator-ferromagnet layer heterostructures. Nat. Commun. 9, 111 (2018).
He, P. et al. Bilinear magnetoelectric resistance as a probe of three-dimensional spin texture in topological surface states. Nat. Phys. 14, 495–499 (2018).
Qin, F. et al. Superconductivity in a chiral nanotube. Nat. Commun. 8, 14465 (2017).
Wakatsuki, R. et al. Nonreciprocal charge transport in noncentrosymmetric superconductors. Sci. Adv. 3, e1602390 (2017).
Zhang, H. et al. Topological insulators in Bi2Se3, Bi2Te3 and Sb2Te3 with a single Dirac cone on the surface. Nat. Phys. 5, 438–442 (2009).
He, Q. L. et al. Two-dimensional superconductivity at the interface of a Bi2Te3/FeTe heterostructure. Nat. Commun. 5, 4247 (2014).
Bao, W. et al. Tunable (δπ, δπ)-type antiferromagnetic order in α-Fe(Te,Se) superconductors. Phys. Rev. Lett. 102, 247001 (2009).
Berezinskii, V. L. Destruction of long-range order in one-dimensional and two-dimensional systems possessing a continuous symmetry group. II. Quantum systems. Sov. Phys. JETP 34, 610–616 (1972).
Kosterlitz, J. M. & Thouless, D. J. Ordering, metastability and phase transitions in two-dimensional systems. J. Phys. C 6, 1181–1203 (1973).
Halperin, B. I. & Nelson, D. R. Resistive transition in superconducting films. J. Low Temp. Phys. 36, 599–616 (1979).
Tokura, Y. & Nagaosa, N. Nonreciprocal responses from non-centrosymmetric quantum materials. Nat. Commun. 9, 3740 (2018).
Li, Y.-Y. et al. Intrinsic topological insulator Bi2Te3 thin films on Si and their thickness limit. Adv. Mater. 22, 4002–4007 (2010).
Neupane, M. et al. Observation of quantum-tunnelling-modulated spin texture in ultrathin topological insulator Bi2Se3 films. Nat. Commun. 5, 3841 (2014).
Hoshino, S., Wakatsuki, R., Hamamoto, K. & Nagaosa, N. Nonreciprocal charge transport in two-dimensional noncentrosymmetric superconductors. Phys. Rev. B 98, 054510 (2018).
Lustikova, J. et al. Vortex rectenna powered by environmental fluctuations. Nat. Commun. 9, 4922 (2018).
Zhang, J. et al. Band structure engineering in (Bi1−xSbx)2Te3 ternary topological insulators. Nat. Commun. 2, 574 (2011).
Mohanta, N. & Taraphder, A. Topological superconductivity and Majorana bound states at the LaAlO3/SrTiO3 interface. Europhys. Lett. 108, 60001 (2014).
Wakatsuki, R. & Nagaosa, N. Nonreciprocal current in noncentrosymmetric Rashba superconductors. Phys. Rev. Lett. 121, 026601 (2018).
Owada, K. et al. Electronic structure of Bi2Te3/FeTe heterostructure: implications for unconventional superconductivity. Preprint at http://arxiv.org/abs/1905.05899 (2019).
Acknowledgements
We thank Y. Saito, T. Ideue, M. Kawamura, and S. Hoshino for fruitful discussions and experimental supports. K.Y. is supported by the Japan Society for the Promotion of Science (JSPS) through a research fellowship for young scientists (No. 16J03476). This research was supported by Nos. JP15H05853, JP17H04846, JP18H04229, JP18H03676, and 26103006 from JSPS/MEXT, and No. JPMJCR16F1 from CREST, JST.
Author information
Authors and Affiliations
Contributions
Y.T. conceived the project. H.Y., K.Y. and R.Y. grew the thin films with the help of A.T., K.S.T. and M.K. K.Y., H.Y., and T.L. fabricated the device and performed the measurement. K.Y., H.Y., A.T., N.N., and Y.T. analyzed and interpreted the data. K.Y., A.T., and Y.T. jointly wrote the manuscript with contributions from all authors.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Peer review information: Nature Communications thanks the anonymous reviewers for their contribution to the peer review of this work. Peer reviewer reports are available.
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Yasuda, K., Yasuda, H., Liang, T. et al. Nonreciprocal charge transport at topological insulator/superconductor interface. Nat Commun 10, 2734 (2019). https://doi.org/10.1038/s41467-019-10658-3
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-019-10658-3
This article is cited by
-
Two-fold symmetric superconductivity in the Kagome superconductor RbV3Sb5
Communications Physics (2024)
-
Light-induced giant enhancement of nonreciprocal transport at KTaO3-based interfaces
Nature Communications (2024)
-
The supercurrent diode effect and nonreciprocal paraconductivity due to the chiral structure of nanotubes
Nature Communications (2023)
-
The superconducting diode effect
Nature Reviews Physics (2023)
-
Controlled large non-reciprocal charge transport in an intrinsic magnetic topological insulator MnBi2Te4
Nature Communications (2022)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.