Abstract
Beryllium oxides have been extensively studied due to their unique chemical properties and important technological applications. Typically, in inorganic compounds beryllium is tetrahedrally coordinated by oxygen atoms. Herein based on results of in situ single crystal X-ray diffraction studies and ab initio calculations we report on the high-pressure behavior of CaBe2P2O8, to the best of our knowledge the first compound showing a step-wise transition of Be coordination from tetrahedral (4) to octahedral (6) through trigonal bipyramidal (5). It is remarkable that the same transformation route is observed for phosphorus. Our theoretical analysis suggests that the sequence of structural transitions of CaBe2P2O8 is associated with the electronic transformation from predominantly molecular orbitals at low pressure to the state with overlapping electronic clouds of anions orbitals.
Similar content being viewed by others
Introduction
Due to the broad technological applications of beryllium oxocompounds1,2,3, their structure and chemical bonding became a focus of a number of recent experimental and theoretical studies. Small atomic radius and high ionization energy of beryllium make covalent interactions playing the important role in stabilizing beryllium compounds, unlike other alkaline-earth elements. In contrast to MgO, CaO, SrO, and BaO, at ambient conditions BeO crystallizes in the hexagonal wurtzite structure, featuring tetrahedrally coordinated Be2+ and O2− ions4. Bonding of beryllium to four oxygen atoms with the formation of BeO46− tetrahedra is also exclusive for its natural occurrence5. Various molecular oxygen-rich composition compounds (BeO2, Be2O2, Be2O4, BeO4, and Be(O3)2) demonstrating diverse Be–O bonding situations have been recently isolated within solid noble-gas matrices6. Cases with Be in coordination higher than four have not been observed experimentally for inorganic compounds, though recent ab initio calculation studies on BeO27 and BeO8 have predicted the formation of BeO6 octahedra with ionic Be–O bonding at high pressures.
Recent advances at third-generation synchrotron facilities made the in situ high-pressure X-ray diffraction a powerful tool in simultaneous synthesis and structural characterization of new compounds9,10,11. High-pressure can effectively overcome reaction energy barriers and reorder atomic orbital energy levels so that new phases could reveal properties and stoichiometries unexpected from the viewpoint of conventional solid-state chemistry. Pressure-induced densification of matter is accompanied by the rearrangement of atomic bonds and structural units in order to fill the available space as effective as possible, which usually results in the increase of the atomic coordination numbers (see, e.g., reports on five- and six-fold coordination of silicon in glasses and melts12,13,14,15,16 as well as in a number of crystalline silicates17,18,19,20,21,22,23).
Recent discovery of five- and six-fold coordinated silicon in the high-pressure phases of CaB2Si2O819 has inspired us to probe high-pressure behavior of structurally similar compound CaBe2P2O8. The question whether beryllium could experience the same increase in coordination number is of general chemical interest as well as of particular importance for the understanding the nature of Be–O and P–O bonding. While the first experimental observations of P[V] and P[VI] have been recently reported for high-pressure phases of TiPO49 and AlPO424, the current study appears to the first reporting on the experimental observation of five- and six-fold coordinated beryllium. Here, we present results of high-pressure single-crystal X-ray diffraction (SCXRD) experiments conjoined with ab initio density functional theory (DFT) calculations that evidence a step-wise transition of Be and P coordination from tetrahedral to octahedral through trigonal bipyramidal.
Results
Pressure-induced formation of hurlbutite-II with Be[V]
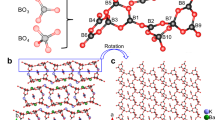
At ambient conditions hurlbutite, CaP2Be2O8, possesses a monoclinic symmetry (space group P21/c) with a = 7.798(3), b = 8.782(2), c = 8.299(1) Å, β = 90.50(5)˚25. The asymmetric unit of hurlbutite contains four tetrahedrally coordinated T cations (two P and two Be), eight oxygen and one calcium atoms. Polymerization of PO4 and BeO4 tetrahedra through common vertices results in the formation of framework with four- and eight-membered channels running along the a-axis (Fig. 1). The eight-membered rings are occupied by Ca atoms that are seven-fold coordinated (for Ca–O bonds shorter than 3 Å).
Crystal structure of hurlbutite, CaBe2P2O8, at ambient conditions25. BeO4 and PO4 tetrahedra are given in blue and yellow, respectively. Ca and O atoms are given as blue and red spheres, respectively. Black solid line outlines a unit cell
Conventional continuous contraction of unit-cell parameters and atomic bonds is observed up to 7.5 GPa (Fig. 2). The compression of the unit cell is anisotropic so that the c-axis is the most and the a axis is the least compressible (Supplementary Fig. 1). In agreement with earlier reports on the compression of similar frameworks26, the compression of hurlbutite is controlled up to 7.5 GPa by changes in T–O–T angles of the tetrahedral framework, while the TO4 tetrahedra stay as rigid units.
The unexpected response of the crystal structure on pressure treatment is observed above 7.5 GPa. While the b and c axes continue to decrease, the a-axis reveals an anomalous increase upon compression indicating a change in the compression mechanism (Fig. 2, Supplementary Fig. 1). Indeed half of the TO4 units start to undergo pressure-induced geometrical distortion. The progressive deviation of P1O4 and Be2O4 tetrahedra from the ideal tetrahedral geometry above ~7.5 GPa is perfectly visible on plots showing quadratic elongation and bond angular variance parameters as a function of pressure27 (Supplementary Fig. 2). Such a distortion results from the closure of eight-membered rings and progressive approach of the fifth oxygen to the P1 and Be2 atoms across the rings (Supplementary Fig. 3).
At pressures above 20 GPa the crystal structure again experiences conventional contraction with the preservation of the most (c-axis) and least (a-axis) compressible directions. The evolution of the new-forming contacts P1–O8* and Be2–O2* is shown in Supplementary Fig. 4. The shortening of the Be2–O2* contact is smooth however distribution of Be–O bonds indicates that the Be[IV] to Be[V] transition occurs between 70 and 75 GPa (Supplementary Tables 1 and 2). At 75 GPa BeO5 polyhedra possesses trigonal bipyramidal geometry with two long apical (1.70 and 1.92 Å) and three short equatorial bonds (1.50–1.53 Å), while P1 still preserves tetrahedral coordination. Upon further compression of hurlbutite-II, BeO5 evolves towards more regular trigonal bipyramid geometry by pronounced shortening of the Be–O2* bond.
Crystal structure of hurlbutite-III with Be[V] and P[V]
At ~83 GPa the crystal structure undergoes another phase transition, which is reflected in an abrupt change of the unit-cell parameters (Fig. 2, Supplementary Fig. 1). The high-pressure phase hurlbutite-III preserves initial P21/c symmetry. The phase transition to hurlbutite-III is displacive and induced by the final incorporation of O8* atoms into the coordination sphere of P1. At 83.2 GPa polyhedra of penta-coordinated P1 and Be2 possess trigonal bipyramidal geometry (Fig. 3) with two long apical (1.662–1.813 Å for P1 and 1.711–1.798 Å for Be2) and three short equatorial bonds (1.471–1.506 Å for P1 and 1.492–1.545 Å for Be2; Supplementary Table 2). The O–T–O apical bond angles are 10.5˚ and 11.5˚ away from the 180˚ required for the regular trigonal bipyramid for P1 and Be2, respectively. The P2 and Be1 atoms remain tetrahedrally coordinated up to 82 GPa, so that the framework of hurlbutite-III is built upon TO4 and TO5 polyhedra sharing common vertices. The structure of hurlbutite-III contains distorted elements of both hexagonal and cubic packings (HCP and CCP, respectively), where the P1 and Be2 atoms fill trigonal bipyramidal voids and the P2 and Be1 atoms fill tetrahedral voids. Ca has 11-fold coordination manifesting distortion from an ideal close packing.
Crystal structure of hurlbutite-IV with Be[VI] and P[VI]
Upon the compression above 90 GPa, new reflections appear in the diffraction patterns indicating the occurrence of another phase, coexisting with hurlbutite-III. The structure of this new phase, named hurlbutite-IV, was solved and refined in the P-1 space group (Supplementary Table 1). The asymmetric unit of hurlbutite-IV contains four crystallographically independent P, four Be, two Ca and 16 O atoms. The P21/c → P-1 phase transition is reconstructive in character and involves rearrangement of the bonding network with the accompanying increase of coordination numbers for all cations. At 89.5 GPa, all P atoms are octahedrally coordinated with the distribution of P–O bond distances varying in the range 1.49-1.77 Å (Supplementary Table 3). Be–O bond distances vary in the range 1.50–1.92 Å for Be1, Be2, and Be3 atoms that are octahedrally coordinated as well. The Be4 atom has five neighboring oxygens within the distance of 1.50–1.81 Å while the sixth Be4–O7 contact is of 2.09 Å. This distribution indicates that the coordination polyhedron of Be4 should better be described as a square pyramid. The geometry of individual P and Be polyhedra is shown in Fig. 4. The dense structure of hurlbutite-IV is built on the TO6 and TO5 polyhedra sharing common edges. The Ca and O atoms form distorted by stacking faults CCP arrangement, where P and Be atoms are filling octahedral voids and Ca atoms are 12-fold coordinated (Supplementary Fig. 5).
Ab initio calculations of the transformation route
In order to check whether experimentally observed behavior of CaP2Be2O8 may be reproduced by theory we have performed ab initio simulations (See Methods) and found an excellent agreement between measured and calculated unit-cell parameters, volume, atomic coordinates and interatomic distances (Supplementary Figs. 6 and 7) as a function of pressure. Calculated pressure dependence of the interatomic distances (Supplementary Fig. 7) and enthalpy of high-pressure phases of hurlbutite (Supplementary Fig. 8) reproduce the experimentally observed sequence of transitions. According to the ab initio simulations, hurlbutite transforms to hurlbutite-II at 58 GPa, while hurlbutite-II to hurlbutite-III at calculated transition pressure of 67.5 GPa (slight underestimation of the transition pressure is typical for DFT calculations employing semilocal functionals, like GGA in our case, see Methods). Interestingly, these two transitions occur without any barrier as a result of relaxation of atomic positions in the unit cell. These three phases correspond to the topologically same enthalpy minimum that evolves with pressure smoothly but in a way that qualitatively modifies the local coordination of atoms in the unit cell at the corresponding transition pressures. On the contrary, calculated atomic configuration of hurlbutite-IV has its own enthalpy minimum, and the transition to this phase is of the first order, in agreement with experimental observation of coexistence of the phases III and IV. In fact, according to calculations hurlbutite-IV is the most thermodynamically stable phase at pressures above 65 GPa. Even though this pressure is most probably somewhat underestimated, it is very close to calculated transition pressure from hurlbutite-II to hurlbutite-III. Thus, theoretical analysis indicates that experimentally observed hurlbutite-III is likely a metastable phase of CaBe2P2O8.
Discussion
To the best of our knowledge, hurlbutite-II, -III, and -IV are the first examples of experimentally observed inorganic compounds possessing beryllium in coordination higher than four. Moreover, it appears to be the first structural report on an element of the second period manifesting such increase of coordination number. In a framework of classical Pauling’s model28 the sp3d and sp3d2 hybridization and, respectively, five- and six-fold coordination would not be expected for beryllium due to the absence of d atomic orbitals. Despite the advances in the quantum chemistry in the second half of XX century and, particularly, introduction of a multicenter bonding model29,30,31, there are still recent reports questioning whether the absence of d orbitals prohibits the increased coordination of the elements of the second period32.
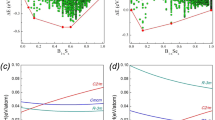
Close agreement between our experimental observations and ab initio calculations make us confident that our theoretical approach should also adequately describe driving forces behind pressure-induced transformations in CaP2Be2O8 as well as reasons for formation of phases with unusual coordinations of phosphorus and beryllium. In order to gain this knowledge, we have investigated the behavior of the electronic structure of CaP2Be2O8 upon compression. Figure 5 summarizes calculated total electronic density of states (DOS) of different phases of hurlbutite. Analysis of the partial local DOS (Supplementary Fig. 9) demonstrates that all the occupied states of CaP2Be2O8 are of s- and p-character: the electronic states corresponding to d orbitals are well above the highest occupied state at all the studied pressures, and therefore are not relevant for the phase transitions observed in this work. At the same time, one can clearly see in Fig. 5a that the electronic structure of hurlbutite is characterized by well localized electronic states (peaks of the DOS are sharp and separated from each other by energy gaps). Upon compression, the states become broader, and the energy gaps between them disappear, starting from the high-energy part of the spectrum in hurlbutite-II, and proceeding all the way to the low-energy part of the spectrum in hurlbutite-IV. We, therefore, conclude that the sequence of structural transitions observed in the present study is associated with the electronic transitions from predominantly molecular orbitals at low pressure to the state with overlapping electronic clouds of anions orbitals. Both experimental observations of the BeO5/BeO6 configurations and ab initio calculations are in line with previous quantum chemical calculations33,34,35,36 and demonstrate that the involvement of d orbitals is not mandatory for the formation of species with trigonal–bipyramidal and octahedral geometries. Instead, an electron-deficient multicenter bonding can be proposed as a mechanism of formation of such exotic configurations and, generally, as a densification mechanism for the CaP2Be2O8 crystal structure adopting to high-pressure conditions37,38.
Pressure-induced increase of cation coordination number is repeatedly observed tendency38,39,40 that was outlined as a general rule of high-pressure crystal chemistry in reviews of Prewitt and Downs41 and Grochala et al. (2007)27. In inorganic oxocompounds this tendency is typically realized along with evolution of the oxygen sublattice toward the close packing arrangements41. This is also the case for hurlbutite: upon pressurizing O and Ca cations firstly arrange into close packing assembly consisting both of distorted HCP and CCP elements (with P and Be occupying tetrahedral and trigonal bipyramidal voids in hurlbutite-II and -III) and later into ABCACABCBCAB arrangement (with P and Be filling octahedral voids in hurlbutite-IV). While the cation coordination and oxygen sublattice are traditional determinants of a crystal structure, the alternative view on the crystal chemistry of oxides was proposed by O’Keeffe and Hyde by introducing terms cation packing and anion coordination42,43,44. While this approach was found to be effective for a number of cases (e.g., elaborating on Al coordination in AlVI2O3 and AlIVPO4, describing olivine → spinel transition), we find that the classical way of structure representation is more appropriate for our cases. By studying high-pressure behavior of a group of isotopological compounds with general formulae MT12T22O8 (M = Ca, Ba, Sr; T = Si, B, Be, P), we conclude that the crystal structure response (and particularly formation of TO5 species) is governed by interplay of two factors: compressibility of TO4 tetrahedra and size of large M cation. The chemistry of the T site governs T[IV] → T[V] transition pressure (e.g., compare Be[V] and P[V] between 70–75 and 82–85 GPa in CaBe2P2O8, respectively, and Si[V] at c.a. 22 GPa in CaB2Si2O819). The size of the M cation is responsible for formation of close packing arrangement with trigonal bipyramidal voids, i.e., TO5 species. Thus, in contrast to CaB2Si2O8, Si site in the structure of SrB2Si2O8 does not change coordination to five-fold upon pressurizing but instead undergoes a splitting into two sites45. Further increase of M cation size results in complete absence of Si[V]: the high-pressure polymorphism is realized via direct Si[IV] → Si[VI] transition in the crystal structure of BaB2Si2O845. In the upcoming review article on high-pressure behavior of MT12T22O8 compounds we are going to elaborate on the crystal chemical regularities in detail.
The present study further proves the powerful capabilities of high pressure as a tool for tuning chemical properties of matter. Growing interest of the chemical community in high-pressure SCXRD techniques using diamond anvil cells (DACs) ensures that the upcoming studies will bring further examples of unique phases as well as provide a solid experimental basis for the future development of novel high-pressure crystal chemistry.
Methods
High-pressure SCXRD experiments
The natural samples of hurlbutite, CaBe2P2O8, originating from Viitaniemi pegmatite (Eräjärvi area, Orivesi, Western and Inner Finland Region, Finland46) have been provided by Mineralogical Museum, CeNak, University of Hamburg. Three separate in situ high-pressure SCXRD were performed at the experimental station P02.2 (extreme conditions beamline) at synchrotron Petra III (Hamburg, Germany). Symmetric DACs with culets diameter of 300, 200, and 150 μm were used for pressure generation in experiments #1, #2, and #3, respectively. The sample chambers with approximate diameters of 150, 100, and 85 μm were obtained by drilling the preindented rhenium gasket. Hurlbutite crystals were placed inside the sample chambers along with a ruby sphere for pressure estimation (Supplementary Fig. 10)47. The DACs were loaded with neon as pressure-transmitting medium using the in-house gas loading system at Petra III. Monochromatic X-ray diffraction experiments were performed using X-rays with wavelength of ~0.2905 Å. The X-ray beam was focused to less than 10 × 10 μm by Kirkpatrick–Baez mirrors for experiments #1 and #3 and by Compound Reflective Lenses for experiment #248. Diffraction patterns were collected using Perkin Elmer detector. Before each experiment the detector-sample distance was calibrated with a CeO2 standard using the procedure implemented in the program Dioptas49.
At each pressure both a wide-scan and a stepped ω-scan were collected for each crystal. Wide scans consisted of 40 s exposures during rotations of ±20° of the DAC. Step scans consisted of individual exposures taken over 0.5° intervals to constrain the ω angle of maximum intensity of each peak. Collected diffraction images were analyzed using the program CrysAlis Pro[©50. The SHELXL program package was used for all structural determinations51. The high-pressure structural behavior of hurlbutite has been followed up to 91 GPa by performing SCXRD experiments at every pressure step of 3–5 GPa. In total 26 high-pressure structural refinements have been performed, the representative ones are given in Supplementary Tables 1 and 2.
Ab initio DFT calculations
Calculations of the electronic structure, total energies and structural parameters for all phases of hurlbutite were performed in the framework of the DFT using the Vienna ab initio simulation package52,53. The interaction between ions and electrons were described using the projector augmented-wave method54,55 through recommended potentials for Ca, Be, P and O. A plane-wave basis set cutoff energy was set to 600 eV. The generalized gradient approximation (GGA) in the Perdew–Burke–Ernzerhof (PBE)56 parametrization was selected to treat the exchange and correlation effects. PBE-GGA belongs to the so-called semilocal DFT functionals, which are known to slightly underestimate bonding strength in solids and significantly underestimate band gaps in semicinductors and insulators. However, it is numerically efficient and provides accuracy, which is sufficient for the purposes of the present study. The integration over the Brillouin zone was performed using a gamma-centered mesh with a k-points grid 6 × 6 × 6. All the calculations were carried out using the Gaussian smearing with a broadening of σ = 0.05 eV. All properties were calculated at a given volumes (pressures) after the ion positions and cell shape were relaxed to achieve forces action on ions smaller then 10−2 eV/Å and hydrostatic conditions: |p − px|, |p − py|, |p − pz| < 0.5 kbar.
Data availability
The X-ray crystallographic coordinates for structures reported in this article have been deposited at the Inorganic Crystal Structure Database (ICSD) under deposition numbers CSD 1913366-1913370. These data can be obtained from CCDC’s and FIZ Karlsruhe’s free service for viewing and retrieving structures (https://www.ccdc.cam.ac.uk/structures/).
References
Snead, L. L. Use of beryllium and beryllium oxide in space reactors. AIP Conf. Proc. 746, 768–775 (2005).
Marder, J. M. Beryllium—technology and applications. JOM 36, 45–47 (1984).
Shinde, R. & Tayade, M. Remarkable hydrogen storage on beryllium oxide clusters: first-principles calculations. J. Phys. Chem. C 118, 17200–17204 (2014).
McKeehan, L. W. The crystal structure of beryllium and of beryllium oxide. Proc. Natl Acad Sci. 8, 270–274 (1922).
Hawthorne, F. & Huminicki, D. The crystal chemistry of beryllium. Rev. Mineral. Geochem. 50, 333–403 (2002).
Zhang, Q., Jerabek, P., Chen, M., Zhou, M. & Frenking, G. The oxygen-rich beryllium oxides BeO4 and BeO6. Angew. Chem. 55, 10863–10867 (2016).
Zhang, S., Li, F., Xu, H. & Yang, G. Pressure-induced stable beryllium peroxide. Inorg. Chem. 56, 5233–5238 (2017).
Li, D., Zhang, P. & Yan, J. Ab initio molecular dynamics study of high-pressure melting of beryllium oxide. Sci. Rep. 4, 4707 (2015).
Bykov, M. et al. High-pressure phase transformations in TiPO4: a route to pentacoordinated phosphorus. Angew. Chem. 55, 15053–15057 (2016).
Zhang, W. et al. Unexpected stable stoichiometries of sodium chlorides. Science 342, 1502–1505 (2013).
Bykova, E. et al. Structural complexity of simple Fe2O3 at high pressures and temperatures. Nat. Commun. 7, 10661 (2016).
Stebbins, J. F. & McMillan, P. Compositional and temperature effects on five-coordinated silicon in ambient pressure silicate glasses. J. Non-Cryst. Solids 160, 116–125 (1993).
Prescher, C. et al. Beyond sixfold coordinated Si in SiO2 glass at ultrahigh pressures. Proc. Natl Acad. Sci. 114, 10041–10046 (2017).
Xue, X., Kanzaki, M., Trønnes, R. G. & Stebbins, J. F. Silicon coordination and speciation changes in a silicate liquid at high pressures. Science 245, 962–964 (1989).
Stebbins, J. F. & McMillan, P. Five- and six-coordinated Si in K2Si4O9 glass quenched from 1.9 GPa and 1200 °C. Am. Mineral. 74, 965–968 (1989).
Petitgirard, S. et al. Magma properties at deep Earth’s conditions from electronic structure of silica. Geochem. Perspect. Lett. 9, 32–37 (2019).
Plonka, A. M. et al. β-diopside, a new ultrahigh-pressure polymorph of CaMgSi2O6 with six-coordinated silicon. Geophys. Res. Lett. 3, L24307 (2012).
Hu, Y., Kiefer, B., Bina, C. R., Zhang, D. & Dera, P. K. High-pressure γ-CaMgSi2O6: does penta-coordinated silicon exist in the earth’s mantle? Geophys. Res. Lett. 44, 11340–11348 (2017).
Pakhomova, A. et al. A closer look into close packing: pentacoordinated silicon in a high-pressure polymorph of danburite. IUCrJ 4, 671–677 (2017).
Pakhomova, A. et al. A new high-pressure phase transition in clinoferrosilite: in situ single-crystal X-ray diffraction study. Am. Mineral. 102, 666–673 (2017).
Solomatova, N. V. et al. High-pressure single-crystal X-ray diffraction and synchrotron Mössbauer study of monoclinic ferrosilite. C R Geosci. 351, 129–140 (2018).
Bykova, E. et al. Metastable silica high pressure polymorphs as structural proxies of deep Earth silicate melts. Nat. Commun. 9, 4789 (2018).
Gorelova, L. A., Pakhomova, A. S., Aprilis, G., Dubrovinsky, L. S. & Krivovichev, S. V. Pentacoordinated silicon in the high-pressure modification of datolite, CaBSiO4(OH). Inorg. Chem. Front. 5, 1653–1660 (2018).
Pellicer-Porres, J., Saitta, A. M., Polian, A., Itié, J. P. & Hanfland, M. Six-fold-coordinated phosphorus by oxygen in AlPO4 quartz homeotype under high pressure. Nat. Mater. 6, 698–702 (2007).
Lindbloom, J. T., Gibbs, G. V. & Ribbe, P. H. The crystal structure of hurlbutite: a comparison with danburite and anorthite. Am. Mineral. 59, 1267–1271 (1974).
Hackwell, T. P. & Angel, R. J. The comparative compressibility of reedmergnerite, danburite and their aluminium analogues. Eur. J. Miner. 4, 1221–1228 (1992).
Robinson, K., Gibbs, G. V. & Ribbe, P. H. Quadratic elongation: a quantitative measure of distortion in coordination polyhedra. Science 172, 567–570 (1971).
Pauling, L. The nature of the chemical bond. Application of results obtained from the quantum mechanics and from a theory of paramagnetic susceptibility to the structure of molecules. J. Am. Chem. Soc. 53, 1367–1400 (1931).
Pimentel, G. C. The bonding of trihalide and bifluoride ions by the molecular orbital method. J. Chem. Phys. 19, 446–448 (1951).
Rundle, R. E. Electron deficient compound. J. Phys. Chem. 61, 45–50 (1957).
Kutzelnigg, W. Chemical bonding in higher main group elements. Angew. Chem. 23, 272–295 (1984).
Sean McGrady, G. & Steed, J. W. Hypervalent compounds. In Encyclopedia of Inorganic Chemistry, first ed. (eds. King, R. B., Crabtree, R. H., Lukehart, C. M., Atwood, D. A. & Scott, R. A.) 1–21 (John Wiley & Sons, Ltd., Hoboken, New Jersey, 2006).
Hoffmann, R., Howell, J. M. & Muetterties, E. L. Molecular orbital theory of pentacoordinate phosphorus. J. Am. Chem. Soc. 94, 3047–3058 (1972).
Bentrude, W. G., Johnson, W. D. & Khan, W. A. Cyclic pentacovalent phosphoranes from reaction of trivalent phosphorus compounds with dimethylketene. J. Am. Chem. Soc. 94, 3058–3067 (1972).
Cheung, Y.-S., Ng, C.-Y., Chiu, S.-W. & Li, W.-K. Application of three-center-four-electron bonding for structural and stability predictions of main group hypervalent molecules: the fulfillment of octet shell rule. J. Mol. Struct. 623, 1–10 (2003).
Lein, M. & Frenking, G. Chemical bonding in octahedral XeF6 and SF6. Aust. J. Chem. 57, 1191 (2004).
Grochala, W., Hoffmann, R., Feng, J. & Ashcroft, N. W. The chemical imagination at work in very tight places. Angew. Chem. 46, 3620–3642 (2007).
Gao, G., Liang, X., Ashcroft, N. W. & Hoffmann, R. Potential semiconducting and superconducting metastable Si3C structures under pressure. Chem. Mater. 30, 421–427 (2018).
Feng, J. et al. Structures and potential superconductivity in SiH4 at high pressure: en route to “Metallic Hydrogen”. Phys. Rev. Lett. 96, 017006 (2006).
Naumov, I. I., Hemley, R. J., Hoffmann, R. & Ashcroft, N. W. Chemical bonding in hydrogen and lithium under pressure. J. Chem. Phys. 143, 064702 (2015).
Prewitt, C. T. & Downs, R. T. Chapter 9. High pressure crystal chemistry. In Ultrahigh Pressure Mineralogy (ed. Hemley, R. J.) 283–318 (De Gruyter, Davis, California, 1998).
O’Keeffe, M. & Hyde, B. G. 10—The role of nonbonded forces in crystals. in Structure and Bonding in Crystals (eds. O’keeffe, M. & Navrotsky, A.) 227–254 (Academic Press, New York, 1981).
O’Keeffe, M. & Hyde, B. G. Anion coordination and cation packing in oxides. J. Solid State Chem. 44, 24–31 (1982).
O’Keeffe, M. & Hyde, B. G. An alternative approach to non-molecular crystal structures with emphasis on the arrangements of cations. In Cation Ordering and Electron Transfer 61, 77–144 (Springer, Berlin, Heidelberg, 1985).
Gorelova, L. et al. Comparative crystal chemistry of danburite-group minerals, MB2Si2O8: the high-pressure behaviour of maleevite, BaB2Si2O8, and pekovite, SrB2Si2O8. Am. Mineral. In Press (2019).
Sandström, F., Lahti, S. I. Viitaniemipegmatiten i Eräjärvi, Orivesi, Finland. Litiofilen 26, 11–38 (2009).
Mao, H. K., Xu, J. & Bell, P. M. Calibration of the ruby pressure gauge to 800 kbar under quasi-hydrostatic conditions. J. Geophys. Res. 91, 4673 (1986).
Liermann, H.-P. et al. The extreme conditions beamline P02.2 and the extreme conditions science infrastructure at PETRA III. J. Synchrotron Radiat. 22, 908–924 (2015).
Prescher, C. & Prakapenka, V. B. DIOPTAS: a program for reduction of two-dimensional X-ray diffraction data and data exploration. High. Press. Res 35, 223–230 (2015).
Agilent, 2014. CrysAlis PRO. (Agilent Technologies Ltd., Yarnton, Oxfordshire, England).
Sheldrick, G. M. A short history of SHELX. Acta Crystallogr A 64, 112–122 (2008).
Kresse, G. & Hafner, J. Ab initio molecular-dynamics simulation of the liquid-metal—amorphous-semiconductor transition in germanium. Phys. Rev. B 49, 14251–14269 (1994).
Kresse, G. & Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 54, 11169–11186 (1996).
Blöchl, P. E. Projector augmented-wave method. Phys. Rev. B 50, 17953–17979 (1994).
Kresse, G. & Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 59, 1758–1775 (1999).
Perdew, J. P., Burke, K. & Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865–3868 (1996).
Acknowledgements
Prof. Dr. Jochen Schlüter (Mineralogisches Museum, Centrum für Naturkunde (CeNak), Universität Hamburg, Grindelallee 48, 20146 Hamburg) is highly acknowledged for providing the samples. This research was carried out at the light source PETRA III at DESY, a member of the Helmholtz Association (HGF). Theoretical calculations of structural properties were supported by the Ministry of Science and High Education of the Russian Federation in the framework of Increase Competitiveness Program of NUST “MISIS” (No. K2-2019-001) implemented by a governmental decree dated 16 March 2013, No. 211. Theoretical analysis of the electronic structure was supported by the Russian Foundation for Basic Research (Grant 19-02-00871). Financial support from the Swedish Research Council (VR) through Grant no. 2015-04391 and the Swedish Government Strategic Research Areas in Materials Science on Functional Materials at Linköping University (Faculty Grant SFO-Mat-LiU No. 2009-00971) and SeRC are gratefully acknowledged.
Author information
Authors and Affiliations
Contributions
A.P., G.A., M. Byk, and L.G. conducted the high-pressure single-crystal X-ray diffraction experiments. A.P. analyzed the X-ray diffraction data. M. Bel. and I.A. conducted ab initio calculations. A.P., L.D., M. Bel, I.A. and S.K. interpreted the results and wrote the paper with the contribution of all authors.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Peer review information: Nature Communications thanks Gernot Frenking, Paul McMillan and other anonymous reviewer(s) for their contribution to the peer review of this work. Peer reviewer reports are available.
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Pakhomova, A., Aprilis, G., Bykov, M. et al. Penta- and hexa-coordinated beryllium and phosphorus in high-pressure modifications of CaBe2P2O8. Nat Commun 10, 2800 (2019). https://doi.org/10.1038/s41467-019-10589-z
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-019-10589-z
This article is cited by
-
Polymorphism of feldspars above 10 GPa
Nature Communications (2020)
-
Compressibility of hingganite-(Y): high-pressure single crystal X-ray diffraction study
Physics and Chemistry of Minerals (2020)
-
High pressure phase transitions of paracelsian BaAl2Si2O8
Scientific Reports (2019)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.