Abstract
The discovery of superconductivity at 260 K in hydrogen-rich compounds like LaH10 re-invigorated the quest for room temperature superconductivity. Here, we report the temperature dependence of the upper critical fields μ0Hc2(T) of superconducting H3S under a record-high combination of applied pressures up to 160 GPa and fields up to 65 T. We find that Hc2(T) displays a linear dependence on temperature over an extended range as found in multigap or in strongly-coupled superconductors, thus deviating from conventional Werthamer, Helfand, and Hohenberg (WHH) formalism. The best fit of Hc2(T) to the WHH formalism yields negligible values for the Maki parameter α and the spin–orbit scattering constant λSO. However, Hc2(T) is well-described by a model based on strong coupling superconductivity with a coupling constant λ ~ 2. We conclude that H3S behaves as a strong-coupled orbital-limited superconductor over the entire range of temperatures and fields used for our measurements.
Similar content being viewed by others
Introduction
The ongoing scientific endeavor to stabilize superconductivity at room temperature led to the discovery of superconductivity, with a very high critical temperature Tc = 203 K, in sulfur hydride H3S under high pressures of p = 155 GPa1. H3S along with other hydrides2,3 seems to be the closest compound, so far, to metallic hydrogen, which is predicted to be a high temperature superconductor4,5,6. H3S forms as the result of the chemical instability of H2S under high pressures, where H2S decomposes into elemental sulfur S and H3S7,8,9,10. The structure of H3S is believed to be body-centered cubic with Im-3m symmetry above 150 GPa10, and characterized by H atoms symmetrically situated midway between two body-centered S atoms. Tc shows a sharp increase from 95 K to 203 K in the pressure range of 110–155 GPa, but decreases with further increasing the pressure due to the pressure-induced phase transition from the R-3m to the Im-3m phase of H3S1,10.
The superconductivity in H3S is believed to be conventional, or whose pairing is mediated by phonons characterized by high-frequency optical modes due to the motion of hydrogen1,11,12,13,14. The high Tc arises from both the metallization of the strongly covalent bonds in H3S15 and the high phonon frequencies displayed by its light elements16. Band structure calculations indicate that H3S is a multiband metal17 having a large Fermi surface (broad energy dispersive bands) as the result of the hybridization between the H 1s and the 3p orbitals of sulfur8,9,13,16,18,19. Band structure calculations also yield small Fermi surface pockets for the high-Tc phase of H3S17.
Despite the very high Tcs reported for H3S, the studies of Hc2(T) are limited to a narrow range of temperatures close to Tc due to the inherent experimental difficulties in performing ultrahigh pressure measurements under very high magnetic fields. The behavior of Hc2(T) provides valuable information such as an estimation of the Cooper pair coherence length, the strength of the electron–phonon coupling, the role of the spin–orbit coupling, and the dominant mechanism breaking the Copper pairs.
In type-II superconductors, the orbital and the spin-paramagnetic pair-breaking effects are the two main mechanisms depairing electrons under high magnetic fields. The orbital pair-breaking effect explains the suppression of superconductivity via the formation of Abrikosov vortices20 in the presence of a field. The superconductivity is suppressed when the kinetic energy associated with vortex currents exceeds the condensation energy of the paired electrons. When the magnetic field approaches a critical value \(H_{{\mathrm{c2}}}^{{\mathrm{orb}}} = \phi _0/2\pi \xi ^2\), referred to as the orbital limiting field, the vortex cores overlap and the system returns to the normal state. Here, ϕ0 is the flux quantum and ξ is the coherence length. The spin-paramagnetic effect explains the effect of the magnetic field on the spin of the electron based on the work by Clogston21 and Chandrasekhar22. When the magnetic energy exceeds the superconducting gap, i.e. \(1/2\chi _{\mathrm{p}}H_{\mathrm{p}}^2 = 1/2N(E_{\mathrm{F}}){\mathrm{\Delta }}^2\), superconductivity will be suppressed, where χp, N(EF), and Δ are the normal state paramagnetic susceptibility, the density of states at the Fermi level, and the superconducting gap, respectively. If we only consider the spin-paramagnetic effect, the zero-temperature Pauli limiting field (Chandrasekhar-Clogston limit) for a weakly coupled superconductor is approximately μ0Hp(0) = 1.86 Tc, where \(2{\mathrm{\Delta }}(T = 0)\sim 3.52 \ k_{\mathrm{B}}T_{\mathrm{c}}\) (for a conventional Bardeen-Cooper-Schrieffer (BCS) superconductor) and \(\chi _{\mathrm{p}} = g\mu _{\mathrm{B}}^2N(E_{\mathrm{F}})\) (g is the Landé g factor and μB is the Bohr magneton). Hp can be renormalized by the strength of the electron–phonon coupling or by electronic correlations. In many superconductors Hc2(T) is affected by both pair-breaking mechanisms. The Maki23 parameter \(\alpha = \sqrt 2 H_{{\mathrm{c2}}}^{{\mathrm{orb}}}(0)/H_{\mathrm{p}}(0)\) is a measure of the relative strength between the orbital and the paramagnetic pair-breaking mechanisms for a given type-II superconductor. The WHH theory24 includes both pair-breaking effects through the Maki parameter and the spin–orbit constant.
Here, we report measurements of the upper critical field in H3S samples under extremely high pressures and high magnetic fields. The ultrahigh pressures can only be obtained through the use of a diamond anvil cell (DAC), however, measurements on samples contained by a DAC are quite challenging, particularly in pulsed fields due to the narrow magnet bore and the large magnetic-field induced currents which heat the cell. The small diameter of the DAC1 employed in our study allows us to perform transport measurements up to 65 T without heating the sample significantly. Our pulsed field measurements under p > 150 GPa represent a significant pressure increase over a previous pulsed field study under 10 GPa25. We find that H3S is an orbital-limited superconductor over the entire temperature range and likely a multigap or strongly coupled superconductor.
Results
Temperature dependence of the resistance
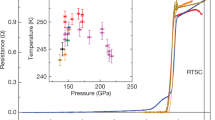
Figure 1 displays the resistance as a function of the temperature T for H3S samples pressurized up to 155 GPa and 160 GPa. The onset, i.e., the first deviation from the normal state resistivity, of the superconducting transitions are estimated to be Tc = 201 K for the sample under 155 GPa, and Tc = 174 K for the other sample under 160 GPa. The drop in Tc for the higher pressure sample is consistent with the results in ref. 1. The width of these transitions are ΔTc = 5.5 K and 26 K for the samples under 155 GPa and 160 GPa, respectively, indicating that the latter sample is less homogeneous, or that it is subjected to stronger pressure gradients. The value of Tc for the sample under 155 GPa increases slightly over time, indicating an evolution towards a more homogeneous sample or weaker pressure gradients. Notice that the superconducting transition displayed by this sample shows a step around 195 K indicating that its superconducting state indeed is inhomogeneous. For samples synthesized within the confines of the DAC a certain degree of inhomogeneity is inevitable. The multiple SC transition steps merge into a single one above a moderate field of 3 T in the 155 GPa sample (Supplementary Fig. 1).
Resistive transition towards the superconducting state. Resistance R as a function of the temperature T for two DACs containing H3S samples under pressures p = 155 GPa and 160 GPa. Red line is a fit to R = R0 + AT2. Notice that the Tc for the 155 GPa sample shifts slightly to higher values while its resistance decreases between July and September 2018. Source data are provided as a Source Data file
We find that R(T) exhibits supralinear behavior in both samples, which is well described by a R ∝ T2 leading term. A quadratic temperature dependence for the resistivity is usually ascribed to the inelastic electron–electron scattering in Fermi liquid theory. While our estimates point to a predominantly electron–phonon transport scattering at high temperatures (Supplementary Fig. 2), a linear temperature dependence for the resistivity is typically expected for this regime, hence R ∝ T2 is quite unusual. Spectroscopic studies on H3S attribute the supralinear behavior of R(T) to strong coupling between electrons and a very high energy optical phonon26. A similar explanation was given for the supralinear R(T) observed in MgB2, which is another BCS superconductor characterized by a strong coupling to an optical phonon mode27.
Hall resistance as a function of the temperature
Figure 2a displays the Hall resistance Rxy for the sample under p = 155 GPa as a function of the magnetic field μ0H near the superconducting transition. The Rxy(μ0H) do not reveal any non-linearity as a function of μ0H all the way up to 35 T. This indicates that near and above Tc the electrical transport in H3S is dominated by a single type of carrier (electrons) despite H3S being predicted to be a multiband metal17. Most likely, this indicates that electrons display a considerably higher carrier mobility than holes at these temperatures. The temperature dependence of the Hall coefficient RH is shown in Fig. 2b, obtained by multiplying the slope of Rxy(μ0H) at high fields by the sample thickness, estimated to be t = (2 ± 1) μm. We observed a noticeable decrease in RH(T) by as much as 20% as the temperature is decreased, corresponding to an increase in the effective carrier density n = 1/eRH. The smaller values of the Hall coefficient at lower temperatures could come from a decrease in electron mobility, a progressive increase in hole mobility, or from an evolution in their relative densities. If one assumes that only one band contributed to the transport of carriers, the Hall coefficient would yield an electron density n = 1/eRH = (8.5 ± 4.3) × 1022 cm−3 at room temperature, which is relatively close to known values for transition metals such as copper.
Hall-effect as a function of the field and for several temperatures. a Hall resistance Rxy as a function of the magnetic field μ0H at a temperatures T = 160, 205, and 250 K for 155 GPa sample. For the trace collected at 160 K, the sample remains superconducting below 20 T, but recovers its linear-in-field behavior in the normal state above Hc2. Magenta and red lines are linear fits to the 160 K and 205 K curves, respectively. b Normal state Hall coefficient RH as a function of T for the H3S sample pressurized under 155 GPa. Source data are provided as a Source Data file
Superconducting phase diagram
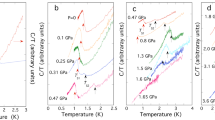
To determine the temperature dependence of Hc2, we measured the isothermal resistance as a function of the magnetic field μ0H at selected temperatures ranging from T = 55 K to 200 K. Figure 3a, b show the magnetic field dependence of the resistance for the samples under 155 GPa and 160 GPa at fixed temperatures. At each temperature the resistance changes from zero to a finite value as μ0H increases due to the field-induced suppression of the superconductivity. Hc2 is defined as the intersection between an extrapolation of the resistance in the normal state and a line having the slope of the resistive transition at its middle point28. The same criterion is used across DC and pulsed field traces. The field value at the intersect with R = 0 axis, H*, marks the onset of dissipation associated with melting of the vortex lattice. In contrast to the unconventional high-temperature superconductors (HTS), vortex melting field in H3S closely follows the upper critical filed, particularly in the more homogeneous 155 GPa sample (Supplementary Fig. 3).
Upper critical fields for H3S as a function of the temperature. Resistance as a function of the field μ0H for the H3S samples under a p = 155 GPa and b 160 GPa and for several temperatures. This data was collected under continuous and pulsed fields. Two black dashed lines extrapolate the resistance in the normal state and the slope at the middle point of the resistive transition. The open circle symbol at the intersection of the two black dashed lines illustrates the position of Hc2. The open circle symbol at the intersect of the x-axis and the black dashed line illustrates the position of H* which marks the onset of dissipation. Source data are provided as a Source Data file
The resistive onset has been found to match the thermodynamic Hc2 obtained through other experimental probes29,30,31. The resistive transition shifts to higher fields as the temperature is lowered while broadening slightly. The Hc2(T) values obtained from pulsed field measurements agree with the curvature and the values extracted under DC fields. At very high pulsed magnetic fields the self-heating of the metallic DACs by the magnetic-field induced currents becomes noticeable at temperatures below 55 K.
Figure 4 shows the extracted Hc2 as a function of T for both samples under p = 155 GPa and 160 GPa as a function of the reduced temperature t = T/Tc. To avoid the influence of possible superconducting vortex phases, we plot just the onset of their resistive transition. These phase boundaries were obtained from both isothermal field scans and from temperature scans under fixed magnetic fields. For both samples Hc2(T) increases almost linearly upon decreasing the temperature under fields all the way up to 60 T yielding the slopes \(|{\mathrm{d}}H_{{\mathrm{c2}}}/{\mathrm{d}}T|_{T_{\mathrm{c}}} = 0.62\) and 0.50 T K−1 for the samples under 155 GPa and 160 GPa, respectively.
Superconducting phase diagram of H3S. Upper critical fields Hc2 as a function of the reduced temperature t = T/Tc for the H3S samples under pressures p = 155 GPa (filled circles) and 160 GPa (open circles). Solid lines are fits to theoretical models: Ginzburg-Landau (GL), Werthamer, Helfand and Hohenberg (WHH), and a strong-coupling model using λ = 2 for the coupling strength parameter (reproduced from a prediction based on strong-coupling theory40,41). Although the GL formalism is mainly valid near Tc, we extrapolated the corresponding fit to T = 0 K to allow a visual comparison between all models. Error bars are standard deviation in the linear extrapolation of the resistance in the normal state and the slope of the resistive transition used to determine Hc2. Inset: upper critical fields for H3S and for two different pressures plotted in reduced variables. The vertical axis is re-scaled by the product of Tc and the slope of Hc2(T) at Tc as derived from the WHH fits for each sample. Red line is a linear fit. Source data are provided as a Source Data file
Discussion
HTS hydrides are considered to be conventional BCS-type superconductors. At the same time, the linear Hc2(T) dependence reported here is quite unusual for a weakly coupled BCS superconductor. The linear dependence of Hc2(T) over an extended range of temperatures was also observed in the two-band superconductor MgB232,33 and in the multigap Fe-pnictide superconductors for fields along certain, but not for all crystallographic orientations, and claimed to result from the orbital limiting effect34,35,36. Multigap effects might explain our phase diagram for H3S in analogy with those systems. However, this multiband scenario contrasts with the linear in field Hall data in Fig. 2a, which indicates conduction dominated by a single type of carrier. Measurements of, for example, the penetration depth as a function of T should help clarify the nature of the superconducting state in this system. The estimated weak coupling Pauli limiting fields for the samples under 155 GPa and 160 GPa are Hp(0) ≃ 374 T and 324 T, respectively. In the dirty limit, the Hc2(0) values derived from the slope of the H–T phase boundary at Tc are, \(H_{{\mathrm{c2}}}^{{\mathrm{orb}}}(0) = 0.69 {\mathrm{d}}H_{{\mathrm{c2}}}/{\mathrm{d}}T|_{T_{\mathrm{c}}} \times T_{\mathrm{c}} = 86\,{\mathrm{T}}\) for the sample under 155 GPa and 60 T for the one under 160 GPa. These latter values are much closer to the extrapolation of our experimental Hc2(T) towards zero-temperature, when compared to the Pauli limiting values which differ by a factor of ~5, thus indicating that H3S is an orbital-limited superconductor.
Subsequently, we fit our experimentally determined phase boundary to two different expressions in order to estimate the value of Hc2 at T = 0 K (see Methods). At temperatures near Tc, our experimental Hc2 values seem to follow the GL-expression, which is used to estimate Hc2(0) in hydrides from the low field data1,2, but at low temperatures they deviate from it considerably. This is particularly apparent for the sample under 160 GPa, for which we were able to reach smaller t values, given that the GL theory is formulated for \((1 - t) \ll 1\). Fitting the upper critical fields to the WHH expression yields very small values for α which points again to rather small orbital limiting fields relative to the Pauli limiting ones, with no apparent saturation in Hc2(t) at low ts. We obtained the best fits to the WHH formula for α values ranging between 0.0 and 0.3 for the sample under 155 GPa and α = 0–0.2 for the sample under 160 GPa. For such small values of α, the WHH formula is almost insensitive to the strength of the spin–orbit interaction. We obtained the superconducting coherence length by extrapolating the WHH fit to zero-temperature. This extrapolation of the Hc2(T)s yields Hc2(T = 0) = 88 T and 70 T for the H3S samples pressurized up to 155 GPa and 160 GPa, respectively. Thus, we find coherence lengths of ξ = 1.84 nm and 2.12 nm for the samples under 155 GPa and 160 GPa, respectively, which are smaller than the initial estimate ξ ≃ 4 nm from first-principles calculations15. As for the effect of pressure on the H3S samples, our experimental upper critical fields do not reveal any change in the relative strength of both pair-breaking mechanisms between both pressures. As seen in the inset of Fig. 4, the superconducting phase diagrams for both samples fall into a single curve when plotted in reduced units. What is remarkable is the linearity of the phase boundary as a function of t all the way down to t ~ 0.3. Again, this resembles behavior reported, for example, for the Fe based superconductors36.
This deviation from the conventional WHH formalism could be explained by the fact that it was formulated for the weak limit of electron–phonon coupling or for a coupling constant λ ≪ 1 . Recent ab initio calculations report substantial enhancement of λ in H3S due to the proximity to a structural instability between the Im-3m and the R3m crystal symmetries37. As the phonon frequencies ωp soften near this instability, the Cooper pairing becomes weaker at elevated temperatures by the thermal phonons, while it remains robust in the T → 0 limit, leading to a relative enhancement in Hc2(T) at low temperatures. The calculated λ ~ 29,37 would correspond to a nearly linear Hc2(T) for t > 0.3 within the framework of the strong coupling model40,41, which was also found to be applicable to the unusually strong electron–phonon coupled case of Bi-III38. Coincidentally, the strong coupling model also predicts a very high Tc ~ 300 K–400 K for a lattice containing light atoms like H40. The fact is that our experimental Hc2(T) values display a much better agreement with the temperature dependence predicted by the strong coupling model40 with an electron–phonon coupling constant λ = 2.
In summary, we have investigated the temperature dependence of the upper critical fields of H3S under magnetic fields up to 65 T. At lower fields the phase boundary separating normal and superconducting states is relatively well described by the Werthamer, Helfand, and Hohenberg formula. Pronounced deviations from the WHH formula are observed at lower temperatures due to the linearity of Hc2(T). Overall, the phase boundary between superconducting and metallic states indicates that the orbital-effect suppresses superconductivity over the entire temperature range. The linearity of Hc2(T) observed over an extended range of reduced temperatures suggests that this system might indeed be a multigap superconductor as predicted theoretically and in analogy with similar results for the Fe-based superconductors. Alternatively, enhanced electron–phonon coupling and softening of hydrogen vibrational modes in the vicinity of a structural instability could also explain the deviation from the WHH predictions. We extract values for the coherence length ξ ranging between ξ = 1.84 nm and 2.12 nm. Above the transition temperature the Hall-effect remains linear up to high magnetic fields indicating that H3S is a very good metal and that at high temperatures carrier conduction is dominated by electrons.
Methods
Sample preparation
Two samples of H3S were synthesized in-situ inside the DACs using two different techniques. The first sample was prepared from condensed liquid H2S via a disproportionation reaction as described in ref. 1, the final pressure inside the sample was as high as 160 GPa. We refer to this sample as the 160 GPa sample. The second sample was synthesized directly from elemental sulfur and hydrogen at high pressures. For this sample a small piece of elemental sulfur (purity of 99.98%) with a lateral dimension of about 20 μm and a thickness of ~3 μm–5 μm was placed in a DAC having diamonds with culets of ~60 μm–70 μm. Excess hydrogen was introduced in the DAC at a gas pressure of ~130 MPa–150 MPa. Subsequently, the DAC was pressurized up to 150 GPa and then heated up to 1000 K with a YAG laser at room temperature to initiate the chemical reaction. The pressure increased slightly up to 155 GPa after the synthesis. The vibrational properties of the pressurized initial reactants, and of the synthesized products, were probed using a triple grating Raman spectrometer equipped with a HeNe laser having a wavelength of 633 nm. Sputtered gold electrodes were thoroughly isolated from the metal gasket by a layer made from magnesium oxide, calcium fluorite, and an epoxy glue mixture. This layer also prevented hydrogen penetration into the rhenium gasket. The pressure was estimated using the Raman shift of stressed diamond39 and the H2 vibron’s wavenumber, previously calibrated in a separate experiment42. The uncertainty in these pressure values is estimated to be ±10%. Both scales indicated a pressure of 155 GPa after the laser heating. Both DACs with H3S samples remain under pressure after initial synthesis throughout the duration of the study. The sample under 155 GPa experienced slight decrease in resistance and increase in Tc between July and September 2018 (Fig. 1), but no further change was noted.
Magnetotransport measurements
The magnetoresistance and the Hall signal was recorded using a conventional 4-probe configuration. Under continuous fields up to μ0H = 35 T the resistance of the sample is measured using a commercial low-frequency (~13 Hz AC resistance bridge). A high-frequency (345 kHz) lock-in amplifier technique is used under pulsed fields up μ0H = 65 T as follows. An AC current of 5 × 10−4 (RMS) is applied to one pair of sample leads through an isolating radio-frequency transformer. The voltage drop across the second pair of leads was amplified using instrumentation amplifier and recorded at 30 MSPS rate with a high speed digitizer, which is synchronized with the AC current source. The corresponding in-phase and quadrature components of the AC signal are extracted from the recorded waveform by a software lock-in.
Theoretical models for the upper critical fields
First, the Hc2(T) were fit to a conventional Ginzburg–Landau (GL) expression:
where ϕ0 is the quantum of flux and \(\bar \xi (0)\) is an average Ginzburg–Landau coherence length at T = 0.
Subsequently to the WHH formalism where the temperature dependence of Hc2(T) defined by orbital and spin-paramagnetic effects in the dirty limit is given by24:
where, \(\bar h = (4/\pi ^2)[H_{{\mathrm{c2}}}(T)/( - {\mathrm{dH}}_{{\mathrm{c2}}}/{\mathrm{d}}T)_{T_{\mathrm{c}}}]\), α is the Maki parameter, and λSO is the spin–orbit constant. The results of the fits are summarized in Table 1.
References
Drozdov, A. P., Eremets, M. I., Troyan, I. A., Ksenofontov, V. & Shylin, S. I. Conventional superconductivity at 203 Kelvin at high pressures in the sulfur hydride system. Nature 525, 73–76 (2015).
Drozdov, A. P. et al. Superconductivity at 250 K in lanthanum hydride under high pressures. Nature 569, 528–531 (2019).
Somayazulu, M. et al. Evidence for superconductivity above 260 K in lanthanum superhydride at megabar pressures. Phys. Rev. Lett. 122, 027001 (2019).
Ashcroft, N. W. Metallic hydrogen: a high-temperature superconductor? Phys. Rev. Lett. 21, 1748–1749 (1968).
Ginzburg, V. L. Superfluidity and superconductivity in the Universe. Sov. Phys. Usp. 12, 241–251 (1969).
Maksimov, E. & Savrasov, D. Lattice stability and superconductivity of the metallic hydrogen at high pressure. Solid State Commun. 119, 569–572 (2001).
Li, Y., Hao, J., Liu, H., Li, Y. & Ma, Y. The metallization and superconductivity of dense hydrogen sulfide. J. Chem. Phys. 140, 174712 (2014).
Duan, D. et al. Pressure-induced metallization of dense (H2S)2H2 with high-Tc superconductivity. Sci. Rep. 4, 6968 (2014).
Errea, I. et al. High-pressure hydrogen sulfide from first principles: a strongly anharmonic phonon-mediated superconductor. Phys. Rev. Lett. 114, 157004 (2015).
Einaga, M. et al. Crystal structure of the superconducting phase of sulfur hydride. Nat. Phys. 12, 835–838 (2016).
Gor’kov, L. P. & Kresin, V. Z. Pressure and high-Tc superconductivity in sulfur hydrides. Sci. Rep. 6, 25608 (2016).
Flores-Livas, J. A., Sanna, A. & Gross, E. K. U. High temperature superconductivity in sulfur and selenium hydrides at high pressure. Eur. Phys. J. B 89, 63 (2016).
Akashi, R., Kawamura, M., Tsuneyuki, S., Nomura, Y. & Arita, R. First-principles study of the pressure and crystal-structure dependences of the superconducting transition temperature in compressed sulfur hydrides. Phys. Rev. B 91, 224513 (2015).
Gor’kov, L. P. & Kresin, V. Z. Colloquium: high pressure and road to room temperature superconductivity. Rev. Mod. Phys. 90, 011001 (2018).
Bernstein, N., Hellberg, C. S., Johannes, M. D., Mazin, I. I. & Mehl, M. J. What superconducts in sulfur hydrides under pressure and why. Phys. Rev. B 91, 060511 (2015).
Quan, Y. & Pickett, W. E. Van Hove singularities and spectral smearing in high-temperature superconducting H3S. Phys. Rev. B 93, 104526 (2016).
Bianconi, A. & Jarlborg, T. Superconductivity above the lowest earth temperature in pressurized sulfur hydride. Europhys. Lett. 112, 37001 (2015).
Heil, C. & Boeri, L. Influence of bonding on superconductivity in high-pressure hydrides. Phys. Rev. B 92, 060508 (2015).
Flores-Livas, J. A. et al. Superconductivity in metastable phases of phosphorus-hydride compounds under high pressure. Phys. Rev. B 93, 020508 (2016).
Abrikosov, A. A. Nobel lecture: type-II superconductors and the vortex lattice. Rev. Mod. Phys. 76, 975–979 (2004).
Clogston, A. M. Upper limit for the critical field in hard superconductors. Phys. Rev. Lett. 9, 266–267 (1962).
Chandrasekhar, B. S. A note on the maximum critical field of high–field superconductors. Appl. Phys. Lett. 1, 7–8 (1962).
Maki, K. Effect of Pauli paramagnetism on magnetic properties of high-field superconductors. Phys. Rev. 148, 362–369 (1966).
Werthamer, N. R., Helfand, E. & Hohenberg, P. C. Temperature and purity dependence of the superconducting critical field, Hc2 III. electron spin and spin-orbit effects. Phys. Rev. 147, 295–302 (1966).
Millot, M., Broto, J.-M. & Gonzalez, J. High-field Zeeman and Paschen-Back effects at high pressure in oriented ruby. Phys. Rev. B 78, 155125 (2008).
Capitani, F. et al. Spectroscopic evidence of a new energy scale for superconductivity in H3S. Nat. Phys. 13, 859–863 (2017).
Tajima, S. et al. Experimental study of electron–phonon interaction in MgB2. Phys. C Supercond. 388–389, 103–104 (2003).
Meier, W. R. et al. Anisotropic thermodynamic and transport properties of single-crystalline CaKFe4As4. Phys. Rev. B 94, 064501 (2016).
Mielke, C. et al. Superconducting properties and fermi-surface topology of the quasi-two-dimensional organic superconductor λ-(BETS)2GaCl4. J. Phys. Condens. Matter 13, 8325–8345 (2001).
Altarawneh, M. M. et al. Determination of anisotropic Hc2 up to 60 T in Ba0.55K0.45Fe2As2 single crystals. Phys. Rev. B 78, 220505 (R) (2008).
Grissonnanche, G. et al. Direct measurement of the upper critical field in cuprate superconductors. Nat. Commun. 5, 3280 (2014).
Lee, S. et al. Growth, structure analysis and anisotropic superconducting properties of MgB2 single crystals. J. Phys. Soc. Jpn 70, 2255–2258 (2001).
Gurevich, A. Enhancement of the upper critical field by nonmagnetic impurities in dirty two-gap superconductors. Phys. Rev. B 67, 184515 (2003).
Zhang, Q. R., Rhodes, D., Zeng, B., Johannes, M. D. & Balicas, L. Non-Ising-like two-dimensional superconductivity in a bulk single crystal. Phys. Rev. B 94, 094511 (2016).
Jaroszynski, J. et al. Comparative high-field magnetotransport of the oxypnictide superconductors RFeAsO1−xFx (R = La, Nd) and SmFeAsO1−δ. Phys. Rev. B 78, 064511 (2008).
Yuan, H. Q. et al. Nearly isotropic superconductivity in (Ba,K)Fe2As2. Nature 457, 565–568 (2009).
Errea, I. et al. Quantum hydrogen-bond symmetrization in the superconducting hydrogen sulfide system. Nature 532, 81–84 (2016).
Brown, P. et al. Strong coupling superconductivity in a quasiperiodic host-guest structure. Sci. Adv. 4, eaao4793 (2018).
Eremets, M. I. Megabar high-pressure cells for Raman measurements. J. Raman Spectrosc. 34, 515–518 (2003).
Bulaevskii, L. N., Dolgov, O. V. & Ptitsyn, M. O. Properties of strong-coupled superconductors. Phys. Rev. B 38, 11290–11295 (1988).
Thomas, F. et al. Strong coupling effects on the upper critical field of the heavy-fermion superconductor Ube13. J. Low Temp. Phys. 102, 117–132 (1996).
Eremets, M. I. & Troyan, I. A. Conductive dense hydrogen. Nat. Mater. 10, 927–931 (2011).
Acknowledgements
We acknowledge A.V. Gurevich, H.H. Wen, and T. Timusk for useful discussions. This work was performed at the National High Magnetic Field laboratory, which is supported by National Science Foundation Cooperative Agreement No. DMR-1644779, and the State of Florida. S.M. acknowledges support from the FSU Provost Postdoctoral Fellowship Program. L.B. is supported by DOE-BES through award DE-SC0002613. This study was supported by JSPS KAKENHI, Specially Promoted Research (26000006). M.I.E. is thankful to the Max Planck community for the invaluable support and U. Pöschl for the constant encouragement.
Author information
Authors and Affiliations
Contributions
F.F.B., L.B. and M.I.E. designed the research; V.S.M., A.P.D., D.K., M.E., K.S. and M.I.E. prepared the samples, S.M., D.S., J.B.B., F.F.B., L.B. and M.I.E. performed high field measurements; S.M., F.F.B. and L.B. analyzed the data, and wrote the paper. All authors helped in writing the paper.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Journal peer review information: Nature Communications thanks Alain Polian and other anonymous reviewer(s) for their contribution to the peer review of this work. Peer reviewer reports are available.
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Source data
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Mozaffari, S., Sun, D., Minkov, V.S. et al. Superconducting phase diagram of H3S under high magnetic fields. Nat Commun 10, 2522 (2019). https://doi.org/10.1038/s41467-019-10552-y
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-019-10552-y
This article is cited by
-
Quantum symmetrization transition in superconducting sulfur hydride from quantum Monte Carlo and path integral molecular dynamics
npj Computational Materials (2024)
-
Full-bandwidth anisotropic Migdal-Eliashberg theory and its application to superhydrides
Communications Physics (2024)
-
High-pressure synthesis of a ternary yttrium-sulfur hydride superconductor with a high Tc of approximately 235 K
Science China Physics, Mechanics & Astronomy (2024)
-
Magnetic flux trapping in hydrogen-rich high-temperature superconductors
Nature Physics (2023)
-
The effect of critical coupling constants on superconductivity enhancement
Scientific Reports (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.