More efficient North Atlantic carbon pump during the Last Glacial Maximum

Abstract

During the Last Glacial Maximum (LGM; ~20,000 years ago), the global ocean sequestered a large amount of carbon lost from the atmosphere and terrestrial biosphere. Suppressed CO₂ outgassing from the Southern Ocean is the prevailing explanation for this carbon sequestration. By contrast, the North Atlantic Ocean—a major conduit for atmospheric CO₂ transport to the ocean interior via the overturning circulation—has received much less attention. Here we demonstrate that North Atlantic carbon pump efficiency during the LGM was almost doubled relative to the Holocene. This is based on a novel proxy approach to estimate air–sea CO₂ exchange signals using combined carbonate ion and nutrient reconstructions for multiple sediment cores from the North Atlantic. Our data indicate that in tandem with Southern Ocean processes, enhanced North Atlantic CO₂ absorption contributed to lowering ice-age atmospheric CO₂.

Introduction

The North Atlantic Ocean (>~35°N, including the Nordic Seas and Arctic Ocean) is a major atmospheric CO₂ sink, which has been mitigating anthropogenic atmospheric CO₂ increases¹. Preindustrial North Atlantic surface water partial pressure of CO₂ (pCO₂) was up to ~100 μatm lower than the contemporary atmospheric pCO₂ of ~280 μatm, which caused substantial atmospheric CO₂ invasion^2,3. Despite its modest area, the North Atlantic Ocean accounts for at least ~30% of the global ocean CO₂ uptake today and during preindustrial times^1,4. Over longer timescales, large-scale oceanic carbon sequestration also occurred during Plio-Pleistocene glaciations^5,6,7. This is commonly attributed to reduced glacial Southern Ocean CO₂ outgassing^6,8,9, while even the sign of past North Atlantic CO₂ uptake efficiency changes remains unconstrained. Here, we present a novel proxy approach to trace atmospheric CO₂ invasion in the North Atlantic and thereby evaluate its role in carbon sequestration in ice-age oceans. We find that the last glacial North Atlantic carbon absorption became more efficient, highlighting a critical role of the North Atlantic Ocean in regulating glacial–interglacial atmospheric CO₂ changes.

Results

Air–sea CO₂ exchange tracers

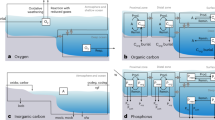
Any effect of ocean processes on atmospheric pCO₂ must occur via air–sea CO₂ exchange. In the North Atlantic, high-nutrient utilization decreases surface-water dissolved inorganic carbon (DIC) and causes surface-water pCO₂ to be lower than atmospheric pCO₂ (Supplementary Fig. 1). This leads to net air-to-sea CO₂ transfer, creating an air–sea exchange signature of DIC (DIC_as). DIC_as signals can be distinguished by accounting for within-ocean DIC redistributions that are heavily mediated by biology (Fig. 1). Biological cycling of organic matter depletes DIC and nutrients such as phosphate (PO₄) in surface waters and enriches them at depth. Seawater mixing also affects DIC and PO₄ concentrations in the ocean. Nevertheless, PO₄ variations are ultimately determined by biological processes: without biology, PO₄ should be the same everywhere in the ocean regardless of ocean circulation (ignoring the small effect from salinity change). Because marine biology incorporates and releases PO₄ and DIC in a relatively fixed proportion following Redfield stoichiometry^3,10 and because PO₄ is not affected by air–sea exchange, PO₄ can be used to estimate biology-driven within-ocean DIC redistributions (Fig. 1). Any within-ocean DIC redistribution associated with CaCO₃ cycling can be accounted for using alkalinity (ALK) and nitrate.

Fig. 1

Concepts to distinguish DIC_as. For simplicity, only CO₂ invasion associated with organic matter cycling is considered. In the ocean box, vertical solid and dashed lines (a–d) represent mean PO₄ (blue) and DIC (red) in an abiotic ocean (a). Biology redistributes DIC and PO₄ following Redfield stoichiometry (curves; b). This decreases surface-ocean DIC and pCO₂, and hence causes air-to-sea CO₂ transfer (c). Through mixing and ocean circulation, CO₂ invasion raises water-column DIC, i.e., shifting dashed curve (equals the red-solid curve in b) to red-solid curve (c). The shaded region in c represents air–sea exchange DIC_as signatures. After removing carbon redistribution by biology based on PO₄-related curvature of the profiles (b), DIC_as can be revealed by the shaded region in d

Following the established method³ to account for within-ocean DIC redistributions by soft-tissue and CaCO₃ cycling, we calculate preindustrial Atlantic DIC_as using the GLODAP dataset² (Fig. 2a). See Methods for details to calculate DIC_as. More positive DIC_as values indicate a greater degree of atmospheric CO₂ invasion. At basin-scale, the preindustrial DIC_as of North Atlantic deep water (NADW) is ~50–80 µmol/kg higher than for Antarctic bottom water (AABW) and Antarctic intermediate water (AAIW). This difference reflects North Atlantic CO₂ uptake and Southern Ocean release^3,11. North Atlantic CO₂ absorption is driven by (i) an efficient solubility pump due to strong cooling of northward-flowing Gulf Stream waters and (ii) a strong biological pump associated with high nutrient utilization^12,13,14. NADW thus represents an efficient pathway for atmospheric CO₂ sequestration^6,15. Through global deep ocean circulation, CO₂ absorbed in the North Atlantic is transported throughout the world ocean^1,3, with profound implications for the global carbon cycle.

Fig. 2

Preindustrial Atlantic air–sea exchange tracers. a DIC_as. b [CO₃²⁻]_as. Circles represent studied sediment cores. Inset: GLODAP hydrographic data² used to generate the sections⁹⁶. NADW North Atlantic deep water, AABW Antarctic bottom water, AAIW Antarctic intermediate water. See Methods for calculation details

No proxy exists to reconstruct past seawater DIC and ALK at acceptable precision for direct application, so we employ a linked carbonate system parameter for palaeoceanographic studies. Everything else being equal, atmospheric CO₂ invasion would decrease seawater carbonate ion concentration ([CO₃²⁻]), because CO₂ reacts with carbonate ion to form bicarbonate¹⁶. We thus develop a new tracer, [CO₃²⁻]_as, which essentially reflects seawater [CO₃²⁻] contrasts for the same biological (i.e., PO₄) and physical (i.e., temperature–salinity–pressure; T–S–P) conditions (Fig. 2b; see Methods for calculation details). To extract air–sea exchange signals, it is necessary to compare [CO₃²⁻] at the same PO₄–T–S–P conditions because we must first remove influences on [CO₃²⁻] from (i) within-ocean DIC and ALK redistributions by biology and (ii) T−S–P variations via their effects on CO₂ system dissociation constants¹⁶. In the preindustrial Atlantic, the strong negative correlation between [CO₃²⁻]_as and DIC_as (Fig. 2, Supplementary Fig. 2) indicates that [CO₃²⁻]_as variations are affected only by DIC_as, and thus are ultimately linked to air–sea CO₂ exchange.

The Gulf Stream is a major NADW source¹⁷; thus, comparing the [CO₃²⁻]_as gradient between the Gulf Stream and NADW can provide a measure of CO₂ sequestration intensity during transformation of Gulf Stream waters into NADW. Because Gulf Stream waters are more or less in equilibrium with atmospheric pCO₂ from ~10°N to 35°N^1,2, the Gulf Stream−NADW [CO₃²⁻]_as gradient mainly reflects North Atlantic (>~35°N) air–sea CO₂ exchange (Supplementary Fig. 3). Physical oceanographers have shown that the path of Gulf Stream waters, rather than being a direct conveyor to the polar North Atlantic, is instead a “corkscrew”, where Gulf Stream waters are recirculated south in the subtropical gyre and subduct after being made more dense by air–sea heat loss (e.g., refs. ^18,19). However, our interest lies in net CO₂ uptake by the North Atlantic region, and variations in spatial pathways from Gulf Stream to NADW formation sites^18,19 should not significantly complicate our conclusion. The greater the [CO₃²⁻]_as gradient between Gulf Stream and NADW (instead of their absolute [CO₃²⁻]_as values), the more efficient air–sea CO₂ absorption by the North Atlantic. Linked to large-scale overturning circulation, Gulf Stream−NADW [CO₃²⁻]_as gradient changes regulate long-term CO₂ sequestration into the deep ocean.

Downcore reconstructions

Next, we reconstruct past Gulf Stream–NADW [CO₃²⁻]_as gradients to investigate North Atlantic carbon pump efficiency during the LGM (18–27 ka). Previous work suggests that most of North Atlantic subtropical gyre water circulates through the Caribbean Sea before being transported to the subpolar North Atlantic via the Gulf Stream²⁰. We, therefore, use Caribbean Sea ODP Site 999 (12.8°N, 78.7°W) to constrain past Gulf Stream physicochemical conditions (Fig. 3, Supplementary Figs. 4 and 5). The feasibility of using ODP Site 999 to reflect the first-order Gulf Stream carbonate chemistry changes between the Holocene and LGM is supported by observations that (i) Caribbean surface waters have similar [CO₃²⁻]_as values to hydrographic sites located within Gulf Stream during the preindustrial (Supplementary Fig. 3), and (ii) cores from the broader western subtropical Atlantic show comparable Holocene and LGM [CO₃²⁻]_as signatures as those from ODP 999 (Supplementary Fig. 6). Surface-water T and S are estimated from Globigerinoides ruber Mg/Ca and sea level fluctuations, respectively^21,22. Previously published G. ruber δ¹¹B (ref. ²¹) is used to calculate surface-water pH, while ALK is estimated from S using the modern relationship between S and ALK^21,22. Along with T, S, and ALK estimates, pH is then used to calculate surface-water [CO₃²⁻] and DIC. Given the constraint from pH, seawater ALK and DIC must vary systematically within the ocean carbonate system (Supplementary Fig. 5). This allows precise estimation of [CO₃²⁻], because even large ALK uncertainties (100 μmol/kg; ± 2σ, used throughout) only have a minor effect on [CO₃²⁻] (~14 μmol/kg). Given its oligotrophic setting, past surface-water PO₄ at ODP 999 is assumed to be zero^2,21,22.

Fig. 3

Down core reconstructions. a ODP 999. b BOFS 17 K. c BOFS 14 K. d BOFS 11 K. Seawater [CO₃²⁻] values are derived from benthic B/Ca (empty circles) and δ¹¹B (solid circles). Light gray envelopes and error bars: 2σ. Note different y-scales for surface- (ODP 999) and deep-water (BOFS cores) reconstructions. See Methods for reconstruction details

Three cores are used to reconstruct deep-water conditions of northern-sourced waters (Fig. 3). BOFS 17 K (58°N, 16.5°W, 1150 m) and BOFS 14 K (58.6°N, 19.4°W, 1756 m) are located close to the previously surmised center of Glacial North Atlantic intermediate water (GNAIW)²³, while BOFS 11 K (55.2°N, 20.4°W, 2004 m) is thought to be affected by glacial Nordic Sea overflows²⁴. We employ benthic foraminiferal δ¹¹B and B/Ca to reconstruct deep-water [CO₃²⁻] with an uncertainty of ~10 μmol/kg²⁵. δ¹¹B and B/Ca give consistent downcore [CO₃²⁻] reconstructions. Benthic Cd/Ca is used to estimate deep-water Cd and PO₄ based on an established approach (Supplementary Fig. 7)^26,27. Past deep-water T and S changes are estimated from foraminiferal δ¹⁸O and sea level fluctuations; use of other methods negligibly affects our conclusion. In total, we present 180 new measurements for benthic foraminiferal δ¹¹B, B/Ca, and Cd/Ca. Details of core materials, methods, new and compiled data, and fully propagated uncertainties are given in Methods and Supplementary Data 1–9.

A pragmatic recipe to estimate [CO₃ ²⁻]_as change

Surface-water [CO₃²⁻] at ODP 999 is ~150 μmol/kg higher than deep-water values at BOFS cores (Fig. 3), but this [CO₃²⁻] contrast includes influences from physical (via dissociation constants) and biological (via within-ocean DIC and ALK redistributions) changes in addition to any air–sea CO₂ changes between surface and deep waters. Below, we present a pragmatic recipe to estimate [CO₃²⁻]_as gradients between water masses. We take advantage of well-defined sensitivities of [CO₃²⁻] to T–S–P (Fig. 4) to calculate normalized seawater [CO₃²⁻] ([CO₃²⁻]_Norm) at conditions of T = 3 °C, S = 35‰, and P = 2500 dbar (Methods). Any variation in T–S–P would affect seawater [CO₃²⁻] via (i) changing CO₂ system dissociation constants, and (ii) altering the solubility pump and thereby air–sea exchange component CO₂ concentrations in seawater. Calculation of [CO₃²⁻]_Norm only corrects for influences from (i), without affecting any air–sea CO₂ signal. After normalization to constant T–S–P conditions and assuming no net air–sea exchange, biological activity drives changes in both [CO₃²⁻]_Norm and PO₄ along the biological trend (green curves in Fig. 5; Methods). Note that along a certain biological trend, seawater [CO₃²⁻]_Norm and PO₄ are only affected by within-ocean DIC and ALK redistributions (Fig. 1b). A net air–sea CO₂ change would cause changes in [CO₃²⁻]_Norm and PO₄ across biological curves. At the same PO₄, [CO₃²⁻]_Norm contrasts reflect [CO₃²⁻]_as gradients due to air–sea CO₂ exchange between water masses.

Fig. 4

Carbonate system sensitivities to various changes. a Salinity effect. b Temperature effect. c Pressure effect. d Biological effect. e Air–sea CO₂ exchange effect. Calculations are based on GLODAP² (n = 55,399; blue) and a LGM output from LOVECLIM⁵⁸ (n = 71,768; gray). For a–d, calculations assume no net air–sea CO₂ change. Best fits of data are shown by red curves. See Methods for calculation details

Fig. 5

[CO₃²⁻]_Norm vs. PO₄. a Preindustrial Atlantic surface (<100 m, north of 10°N) and deep (>1000 m, 65°N–65°S) water data². b Holocene and LGM data. Error bars, 2σ

A plot of [CO₃²⁻]_Norm vs. PO₄ greatly facilitates investigation of air–sea CO₂ exchange from combined [CO₃²⁻] and PO₄ measurements/reconstructions. Compared to the biological trend, preindustrial North Atlantic surface waters have a steeper trend (Fig. 5a), which reflects CO₂ absorption during northward transport. Deep-water data lie on a shallower trend, consistent with mixing between low-[CO₃²⁻]_as (high DIC_as) NADW and high-[CO₃²⁻]_as (low DIC_as) AABW in the deep Atlantic (Fig. 2).

For our downcore reconstructions, benthic Cd/Ca suggests that deep-waters at the BOFS sites had PO₄ values of ~1.2 and ~0.8 μmol/kg during the Holocene and LGM, respectively (Fig. 5b; Supplementary Fig. 8). Assuming no air–sea CO₂ exchange, [CO₃²⁻]_Norm of ODP 999 surface waters at elevated PO₄ due to biological processes can be estimated straightforwardly using the H→H′ and G→G′ trajectories in Fig. 5b for the Holocene and LGM, respectively. For the Holocene, ODP 999 [CO₃²⁻]_Norm is ~56 ± 8 μmol/kg higher than [CO₃²⁻]_Norm of BOFS cores at PO₄ = 1.2 μmol/kg. For the LGM, ODP 999 [CO₃²⁻]_Norm is ~114 ± 9 μmol/kg higher than [CO₃²⁻]_Norm of BOFS cores at PO₄ = 0.8 μmol/kg. This suggests a Holocene-to-LGM increase of ~58 ± 12 μmol/kg in the ODP 999−BOFS [CO₃²⁻]_as gradient.

We also present a second approach to calculate [CO₃²⁻]_as gradients, which involves frequent use of the CO₂sys program²⁸ and intermediate-step ALK and DIC parameters (Supplementary Note 1; Supplementary Figs. 9 and 10). The approach gives similar results as the above pragmatic recipe, because both methods are essentially based on the same principle, which is to compare [CO₃²⁻] of water masses at the same physical and biological conditions.

Enhanced CO₂ uptake in the glacial North Atlantic

What caused the greater ODP 999−BOFS [CO₃²⁻]_as gradient during the LGM? We consider influences from biogenic matter composition variations, surface-water ALK and PO₄ changes, ocean circulation changes, and North Atlantic air–sea exchange. In Fig. 5, we have used a soft-tissue Redfield C/PO₄ of 127 and a rain ratio (R, = C_organic:${\mathrm{C}}_{{{\rm{CaCO}}_3}}$) of 4 (refs. ^3,10,29,30) to predict the biological trend. Raising LGM C/PO₄ to 140 (the high end value in today’s North Atlantic³⁰) and R to 8 (doubling of the modern value) could lower the LGM [CO₃²⁻]_as gradient by ~16 μmol/kg (Supplementary Fig. 15), still leaving ~42 μmol/kg [CO₃²⁻]_as gradient increase to be explained by other processes. Evidence for such large biological changes is lacking. Importantly, any increase in C/PO₄ and R would implicitly sequester more atmospheric CO₂ via an enhanced soft-tissue pump and weakened carbonate pump¹⁵. Inclusion of a whole ocean ALK inventory change⁶ or any increased glacial surface-water PO₄ at ODP 999 would raise the LGM [CO₃²⁻]_as gradient (Supplementary Figs. 16 and 17).

Regarding ocean circulation changes, most AAIW upwells in the tropics and less than ~25% of today’s NADW is fed directly by AAIW without surfacing at low latitudes¹⁷. Northward AAIW transport is thought to have been reduced substantially in the glacial Atlantic^23,31,32,33 in the face of vigorous GNAIW production³⁴. Assuming a constant total carbon uptake by the North Atlantic, a complete shutdown of AAIW contribution would only raise the ODP 999−BOFS [CO₃²⁻]_as gradient by ~30%, which is much smaller than the ~100% increase from the Holocene (~56 μmol/kg) to LGM (~114 μmol/kg) (Fig. 5b). Any increased mixing of glacial AABW at BOFS sites would reduce the ODP 999−BOFS [CO₃²⁻]_as gradient during the LGM. Given the proximity of our deep-water sites to the core of GNAIW and Nordic Sea overflow waters^{23,24,31,35,36}, the larger LGM [CO₃²⁻]_as gradient between ODP 999 and BOFS cores likely reflects a greater DIC_as increase from Gulf Stream to GNAIW. North Atlantic CO₂ invasion was responsible for the preindustrial Gulf Stream-NADW [CO₃²⁻]_as gradient (Fig. 2). Therefore, we ascribe the increased ODP 999−BOFS [CO₃²⁻]_as gradient during the LGM to more efficient atmospheric CO₂ uptake via air–sea exchange and subsequent transport to at least ~2 km depth (BOFS 11 K core depth) in the glacial North Atlantic.

Quantification of North Atlantic CO₂ uptake

With reconstructed ODP 999−BOFS [CO₃²⁻]_as gradients, we further quantify North Atlantic air–sea CO₂ absorption changes between the Holocene and LGM. [CO₃²⁻]_as/DIC_as sensitivities can be precisely estimated (Fig. 4e), making [CO₃²⁻]_as gradients a useful proxy to calculate DIC_as changes. The 58 ± 12 μmol/kg Holocene-to-LGM [CO₃²⁻]_as increase (Fig. 5b) indicates a DIC_as increase of 91 ± 20 μmol/kg due to enhanced North Atlantic air–sea CO₂ absorption (Methods). Compared to the preindustrial Gulf Stream-NADW DIC_as gradient of ~90 μmol/kg (Fig. 2, Supplementary Fig. 3), this suggests a doubling of CO₂ uptake efficiency in the LGM North Atlantic.

Beside DIC_as gradient changes, which indicate air–sea CO₂ uptake efficiency, knowledge of northern-sourced-water volumes in the global deep ocean is required to determine total North Atlantic carbon sequestration. Figure 6 shows the total extra carbon absorbed by the LGM North Atlantic for a range of northern-sourced-water volumes (Methods). Sedimentary Pa/Th, radiocarbon, neodymium isotopes, and paired benthic Cd/Ca–δ¹³C suggest^32,34,35,37 vigorous glacial northern-sourced intermediate water production and subsequent transport to the remaining world ocean. Based on previous estimates^35,36,38,39, we tentatively assume that NADW- and GNAIW-derived waters occupy ~50% and ~30%, respectively, of the global deep ocean volume (1 × 10¹⁸ m³ for >1 km). In this case, our ~91 μmol/kg Holocene-to-LGM DIC_as increase yields ~100 Petagrams of carbon (PgC; 1 Pg = 1 × 10¹⁵ g) greater CO₂ sequestration by the LGM North Atlantic (Fig. 6; Methods). To maintain similar total carbon uptake between the Holocene and LGM, GNAIW would need to be less than ~50% of NADW in volume, which we consider unlikely given evidence for intensive GNAIW export to the global ocean^{23,32,34,35,37}. We acknowledge uncertainties associated with our calculations, and encourage future work to better constrain volumes and carbonate chemistry changes of various water masses in the past.

Fig. 6

North Atlantic CO₂ budget. The LGM–Holocene extra carbon uptake is based on Holocene-to-LGM DIC_as increase of 91 μmol/kg. The large red square represents our best estimate of ~100 PgC, assuming that NADW and GNAIW occupied ~50% and ~30% of the global deep ocean (>1 km), respectively^35,36,38,39. See Methods for calculation details

Discussion

Previous work^40,41,42 has tried to constrain air–sea CO₂ exchange by reconstructing surface conditions. This requires reconstructions of the air–sea pCO₂ difference (influenced by T, S, and nutrient utilization), the gas transfer velocity (a power function of wind speed), solubility of CO₂ in seawater (mainly affected by T), and the area and contact time of surface waters available for air–sea exchange¹. Sea ice cover⁴³ possibly expanded, reducing glacial North Atlantic CO₂ absorption. A larger LGM meridional surface temperature gradient^43,44 would enhance the North Atlantic solubility pump¹³. Existing planktonic δ¹⁵N and Cd/Ca data^40,45 show conflicting results regarding the glacial North Atlantic nutrient conditions, perhaps due to complications associated with surface-water proxies and spatial/seasonal nutrient variations in the North Atlantic. A decreased preformed nutrient in the glacial North Atlantic might be inferred from a lower GNAIW PO₄ (Fig. 3), but faster ventilation and/or reduced glacial AAIW could also cause a nutrient decline in GNAIW^23,34,46. Little is known about past wind intensity and air–sea contact time changes. Consequently, potential North Atlantic glacial CO₂ invasion remains poorly understood. Bypassing the necessity to reconstruct surface-water conditions for which some proxies are still lacking (e.g., wind), our new approach, to our knowledge, offers the first proxy-based quantitative estimate of air–sea CO₂ uptake efficiency in the glacial North Atlantic.

In contrast to previous calculations^47,48,49 which concern combined biological (i.e., within-ocean DIC redistribution) and air–sea exchange carbon changes (Fig. 1c), our total North Atlantic carbon uptake estimate only represents the net air–sea CO₂ change that is more directly relevant to atmospheric and terrestrial carbon inventory variations. Our estimated ~100 PgC sequestration constitutes ~15% of the Holocene-LGM ~600 PgC change associated with the atmosphere (~200 PgC) and terrestrial biosphere (~400 PgC)^5,6. Given this global carbon budget context, our work reinforces the role of other polar regions (e.g., Southern Ocean) in controlling the glacial–interglacial carbon cycle. However, if there were no efficiency enhancement for the LGM North Atlantic, a 40% shrinkage of NADW volume would decrease air–sea component CO₂ sequestration by ~240 PgC in the deep ocean (Methods). Therefore, by overcoming this opposing “volume effect”, the improved glacial North Atlantic efficiency increased DIC_as values of northern-sourced deep waters (termed the “endmember effect”) and thereby contributed substantially to air–sea CO₂ sequestration in the LGM deep ocean.

Atmospheric pCO₂ is controlled by both CO₂ gains (e.g., via Southern Ocean outgassing) and losses (e.g., via North Atlantic absorption)^2,3,11. Growing evidence indicates that processes outside the Southern Ocean may have affected past atmospheric CO₂ variations^50,51,52. Our proxy-based results indicate that the North Atlantic CO₂ pump efficiency during the LGM was almost doubled relative to the Holocene. This increased efficiency and associated “endmember effect” effectively outcompeted the opposing “volume effect” due to any shrinkage of northern-sourced deep waters in the world ocean. In addition to the well-recognized role of reduced outgassing in the Southern Ocean^{6,8,9,47,53,54}, we therefore suggest that variations in the uptake and sequestration of atmospheric CO₂ via the North Atlantic Ocean were important contributors to glacial/interglacial carbon cycling.

Methods

CO₂ system calculations

For both the preindustrial ocean and down-core CO₂ system calculations, seawater carbonate system variables were calculated using the CO₂sys.xls program²⁸ with dissociation constants K₁ and K₂ according to Mehrbach et al.⁵⁵ and ${K}_{{{\mathrm{SO}}_4}}$ according to Dickson⁵⁶. Seawater total boron concentration was calculated from the boron–salinity relationship of Lee et al.⁵⁷. For the GLODAP dataset, the anthropogenic CO₂ contribution was subtracted from the measured DIC to obtain preindustrial DIC values².

Preindustrial Atlantic DIC_as and [CO₃ ²⁻]_as

The GLODAP dataset² is used to calculate preindustrial ocean CO₂ system variables. Following the established method of Broecker and Peng³, we account for DIC anomalies created by (1) freshwater addition or removal based on S, (2) soft-tissue carbon creation and respiration based on PO₄, and (3) CaCO₃ formation and dissolution based on ALK and nitrate (NO₃). See Fig. 1 for the simplified concept. We adopt the term DIC_as to represent net air–sea exchange component DIC signatures from:

$$ {\hskip-10pt}{{\mathrm{DIC}}_{\rm{as}}} = {{\mathrm{DIC}}_{\rm{s}}} - ({{\mathrm{PO}}_{\rm{4s}}} - {{{\mathrm{{PO}}}_4}^{\rm{mo}}}) \times {{\mathrm{C/PO}}_4}\\ - {\ }^{1}{\hskip-2.5pt} {\hbox{/}}{\ }_{{\hskip-5pt} 2}\times \left( {{\mathrm{ALK}}_{\mathrm{s}}-{\mathrm{ALK}}^{{\mathrm{mo}}} + {\mathrm{NO}}_{{\mathrm{3s}}}-{{\mathrm{{NO}}}_3}^{\rm{mo}}} \right)-{\mathrm{DIC}}_{{\mathrm{constant}}}$$

(1)

where the subscript “s” represents values normalized to S of 35 (e.g., DIC_s = DIC × 35/S); the superscript “mo” denotes mean ocean values at S = 35 (PO₄^mo = 2.2 μmol/kg, ALK^mo = 2383 μmol/kg, DIC^mo = 2267 μmol/kg, and NO₃^mo = 31 μmol/kg)²⁹; C/PO₄ represents the soft-tissue stoichiometric Redfield ratio; and the arbitrary DIC_constant ( = 2285 μmol/kg) is designed to bring zero DIC_as close to the NADW–AABW boundary (Fig. 2). The term (PO_4s − PO₄^mo) × C/PO₄ corrects for DIC changes due to photosynthesis and soft-tissue degradation, and the term ½ × (ALK_s − ALK^mo + NO_3s − NO₃^mo) accounts for DIC changes caused by CaCO₃ formation and dissolution. To be consistent with previous work^3,30, we used C/PO₄ = 127 to calculate DIC_as and [CO₃²⁻]_as in Fig. 2. Using other C/PO₄ values¹⁰ does not significantly affect spatial DIC_as and [CO₃²⁻]_as patterns (Supplementary Figs. 11 and 12). Neither are their patterns affected by using other PO₄–ALK–NO₃ values to replace global mean values in Eq. (1) (Supplementary Figs. 13 and 14). Ideally, DIC_constant would be the mean DIC value of an abiotic ocean (Fig. 1), but this value cannot be simply determined from modern observations. Because our interest lies in spatial DIC_as contrasts instead of absolute values, the choice of DIC_constant has no effect on our interpretation.

To obtain [CO₃²⁻]_as, we first calculate [CO₃²⁻]_{PO4–T–S–P} using (DIC_as + DIC_constant), ALK^mo, and PO₄^mo at T = 3 °C, S = 35, and P = 2500 dbar. [CO₃²⁻]_as is then calculated by [CO₃²⁻]_as = [CO₃²⁻]_{PO4–T–S–P} − [CO₃²⁻]_constant, where [CO₃²⁻]_constant ( = 78 μmol/kg, calculated using DIC_constant and ALK^mo) is designed to bring zero [CO₃²⁻]_as close to the NADW–AABW boundary. In essence, the [CO₃²⁻]_as distribution reflects the variation of [CO₃²⁻] when normalized to the same PO₄−T−S−P conditions.

CO₂ system sensitivities and calculation of [CO₃ ^{2 −}]_Norm

Because the seawater CO₂ system is nonlinear, there is currently no simple way to derive these sensitivities based on CO₂ system equations¹⁶. We use GLODAP preindustrial data² to calculate numerically [CO₃²⁻] sensitivities to various physiochemical parameters. Use of LGM outputs from the LOVECLIM model⁵⁸ yields comparable sensitivities. We first use hydrographic data, including T, S, P, DIC, ALK, PO₄, and SiO₃ to calculate [CO₃²⁻]. We then change S to 35‰ and other chemical concentrations proportionally. For example, ALK and DIC will change as follows:

$${\mathrm{ALK}}_{{\mathrm{s = 35}}}={\mathrm{ALK} \,\times 35/S,}\,{\mathrm{and}}$$

(2)

$${\mathrm{DIC}}_{{\mathrm{s = 35}}} = {\mathrm{DIC}} \; \times {{35/S}}{.}$$

(3)

We use S = 35‰, ALK_S=35, DIC_S=35, [PO₄]_S=35, and [SiO₃]_S=35 along with hydrographic T and P to calculate [CO₃²⁻]_S=35. The [CO₃²⁻] to S sensitivity (Sen_{_S}) is calculated by:

$${\mathrm{Sen}}_{\_{\mathrm{S}}} = \left( {\left[ {{{\mathrm{CO}}_{\mathrm{3}}}^{{\mathrm{2 - }}}} \right]-\left[ {{{\mathrm{CO}}_{\mathrm{3}}}^{{\mathrm{2 - }}}} \right]_{{\mathrm{S = 35}}}} \right)/\left( {{S}-{\mathrm{35}}} \right){.}$$

(4)

To estimate temperature effects, we calculate [CO₃²⁻]_{S=35, T=3 °C} using S = 35‰, ALK_S=35, DIC_S=35, [PO₄]_S=35, [SiO₃]_S=35, T = 3 °C, and hydrographic P. The sensitivity of [CO₃²⁻]_S=35 to temperature (Sen_{_T}) is defined by:

$${\mathrm{Sen}}_{\_{\mathrm{T}}}\,{\mathrm{ = }}\,\left( {\left[ {{{\mathrm{CO}}_{\mathrm{3}}}^{{\mathrm{2 - }}}} \right]_{{\mathrm{S = 35,}}\,{\mathrm{T}} = {\mathrm{3}}^ {\circ} {\mathrm{C}}}-\left[ {{{\mathrm{CO}}_{\mathrm{3}}}^{{\mathrm{2 - }}}} \right]_{{\mathrm{S}} = {\mathrm{35}}}} \right)/\left( {{\mathrm{3}}-{T}} \right){.}$$

(5)

Regarding pressure effects, we calculate [CO₃²⁻]_{S=35, T=3 °C, P=2500 dbar} using S = 35‰, ALK_S=35, DIC_S=35, [PO₄]_S=35, [SiO₃]_S=35, T = 3°C, and P = 2500 dbar. The sensitivity of [CO₃²⁻]_{S=35, T=3°C} to P (Sen_{_P}) is defined by:

$${\mathrm{Sen}}_{\_{\mathrm{P}}} = \,\left( {\left[ {{{\mathrm{CO}}_{\mathrm{3}}}^{{\mathrm{2 - }}}} \right]_{{\mathrm{S= 35, }}\,{\mathrm{T}} = {\mathrm{3}}^ {\circ} {\mathrm{C,}}\,{\mathrm{P}} = {\mathrm{2500}}\,{\mathrm{dbar}}}} \right. \\ \left. {-\left[ {{{\mathrm{CO}}_{\mathrm{3}}}^{{\mathrm{2 - }}}} \right]_{{\mathrm{S}} = {\mathrm{35,}}\,{\mathrm{T}} = {\mathrm{3}}^ {\circ} {\mathrm{C}}}} \right)/\left( {{\mathrm{2500}}-{P}} \right){\mathrm{ \times 100}}.$$

(6)

To estimate the influence on [CO₃²⁻] from within-ocean ALK–DIC redistributions by biological processes, we assume a 0.1 μmol/kg increase in PO₄ (i.e., ΔPO₄ = 0.1 μmol/kg) due to biological respiration (photosynthesis has an opposite effect). The resultant ALK (ALK_{S=35+respiration}) and DIC (DIC_{S=35+respiration}) can then be calculated from:

$${\mathrm{ALK}}_{{\mathrm{S}} = {\mathrm{35}} + {\mathrm{respiration}}} = {\,} {\mathrm{ALK}}_{{\mathrm{s = 35}}} + {\mathrm{\Delta PO}}_{\mathrm{4}} \times {\mathrm{C/PO}}_{\mathrm{4}}\\ \div \, {R} \times {\mathrm{2}}-{\mathrm{\Delta PO}}_{\mathrm{4}} \times {\mathrm{N/PO}}_{\mathrm{4}}.$$

(7)

$${\mathrm{DIC}}_{{\mathrm{S}} = {\mathrm{35}} + {\mathrm{respiration}}} = {\mathrm{DIC}}_{{\mathrm{s}} = {\mathrm{35}}} + {\mathrm{\Delta PO}}_{{\mathrm{4}}} \times {\mathrm{C/PO}}_{\mathrm{4}} + {\mathrm{\Delta PO}}_{{\mathrm{4}}} \times {\mathrm{C/PO}}_{\mathrm{4}} \div {R}{.}$$

(8)

Resultant [CO₃²⁻] ([CO₃²⁻]_{Norm+respiration}) values are calculated using DIC_{S=35+respiration}, ALK_{S=35+respiration}, and ([PO₄]_S=35 + ΔPO₄) at constant physical conditions of T = 3 °C, S = 35, and P = 2500 dbar. The sensitivity of [CO₃²⁻]_Norm to PO₄ is defined by:

$$ \left[ {{{\mathrm{CO}}_{\mathrm{3}}}^{{\mathrm{2 - }}}} \right]_{{\mathrm{Norm}}}{\mathrm{/PO}}_{\mathrm{4}}\,{\mathrm{sensitivity}} = \\ \left( {\left[ {{{\mathrm{CO}}_{\mathrm{3}}}^{{\mathrm{2 - }}}} \right]_{{\mathrm{Norm}} + {\mathrm{respiration}}}{\mathrm{- }}\left[ {{{\mathrm{CO}}_{\mathrm{3}}}^{{\mathrm{2 - }}}} \right]_{{\mathrm{Norm}}}} \right)/{\mathrm{\Delta PO}}_{\mathrm{4}}.$$

(9)

We consider four Redfield stoichiometric scenarios: C/PO₄ = 127, R = 4 (the reference composition; Fig. 4d); C/PO₄ = 140, R = 4; C/PO₄ = 127, R = 8; and C/PO₄ = 140, R = 8 (Supplementary Fig. 15). In all cases, strong exponential correlations exist between [CO₃²⁻]_Norm/PO₄ sensitivities and [CO₃²⁻]_Norm. The correlations may reflect the buffering effect of the seawater CO₂ system: for seawater with high DIC (low [CO₃²⁻] and high buffering capability), [CO₃²⁻] would be relatively less sensitive to biological DIC and ALK disturbances. All of the above sensitivity calculations assume no net air–sea CO₂ change.

To calculate air–sea exchange sensitivities, we assume a 10 μmol/kg increase in DIC_S=35 due to atmospheric CO₂ invasion (i.e., ΔDIC_as = 10 μmol/kg). We calculate [CO₃²⁻]_Norm+as using S = 35‰, ALK_S=35, DIC_S=35+as ( = DIC_S=35 + ΔDIC_as), [PO₄]_S=35, [SiO₃]_S=35, T = 3 °C, and P = 2500 dbar. The sensitivity of [CO₃²⁻]_as to DIC_as is defined by:

$$ \left[ {{{\mathrm{CO}}_{\mathrm{3}}}^{{\mathrm{2 - }}}} \right]_{{\mathrm{as}}}{\mathrm{/DIC}}_{{\mathrm{as}}}\,{\mathrm{sensitivity}} = \\ \left( {\left[ {{{\mathrm{CO}}_{\mathrm{3}}}^{{\mathrm{2 - }}}} \right]_{{\mathrm{Norm}} + {\mathrm{as}}}-\left[ {{{\mathrm{CO}}_{\mathrm{3}}}^{{\mathrm{2 - }}}} \right]_{{\mathrm{Norm}}}} \right)/\Delta {\mathrm{DIC}}_{{\mathrm{as}}}.$$

(10)

Using sensitivities shown in Fig. 4, [CO₃²⁻]_Norm can be calculated by:

$$\left[ {{{\mathrm{CO}}_{\mathrm{3}}}^{{\mathrm{2 - }}}} \right]_{{\mathrm{Norm}}} \,= \,\left[ {{{\mathrm{CO}}_{\mathrm{3}}}^{{\mathrm{2 - }}}} \right] + \left( {{\mathrm{35}}-{S}} \right) \times {{\mathrm{Sen}}_{\_{\mathrm{S}}}} + \left( {{\mathrm{3}}-{T}} \right)\\ \times \, {{\mathrm{Sen}}_{\_{\mathrm{T}}}} + \left( {{\mathrm{2500}}-{P}} \right){\mathrm{/100}} {\hskip1pt}\times {{\mathrm{Sen}}_{\_{\mathrm{P}}}}.$$

(11)

Excel spreadsheets are provided in Supplementary Data 7–8 to calculate [CO₃²⁻]_Norm and the biological curves shown in Fig. 5.

LGM–Holocene North Atlantic carbon budget

The total extra carbon increase (Δ∑C_{LGM−Holocene}) in Fig. 6 is calculated by Δ∑C_{LGM−Holocene} = V × density × %GNAIW × ([CO₃²⁻]_{as_ODP999-BOFS}^LGM/0.61) × 12 − V × density × %NADW × ([CO₃²⁻]_{as_ODP999-BOFS}^Holocene/0.59) × 12, where V is the global deep ocean volume (>1 km water depth) at 100.8 × 10¹⁶ m³, density = 1027.8 kg/m³ (ref. ²⁹), %GNAIW and %NADW, respectively, represent their volume fractions in the deep ocean, [CO₃²⁻]_{as_ODP999-BOFS}^Holocene = 56 μmol/kg, [CO₃²⁻]_{as_ODP999-BOFS}^LGM = 114 μmol/kg (Fig. 5), terms 0.61 and 0.58, respectively, represent the absolute LGM and Holocene [CO₃²⁻]_as/DIC_as sensitivities (Fig. 4e) used to transfer [CO₃²⁻]_{as_ODP999-BOFS} into ODP999–BOFS DIC_as contrasts (LGM: 186 μmol/kg; Holocene: 95 μmol/kg), and the number 12 converts C from moles into weight. Based on previous estimates, %NADW is thought to be ~50% (refs. ^38,39), while %GNAIW remained roughly similar to %NADW or shrank (refs. ^35,36). These estimates are debated and have large uncertainties, and we thus calculate Δ∑C_{LGM−Holocene} for a range of %NADW and %GNAIW values (Fig. 6). Any influence from AAIW is ignored because of its similar [CO₃²⁻]_as signals to Gulf Stream during the Holocene (Supplementary Fig. 3) and much reduced northward advection during the LGM^23,31,32,33. We tentatively treat Δ∑C_LGM-Holocene of ~100 PgC using %NADW = 50% and %GNAIW = 30% as our best estimate. Assuming no Holocene–LGM DIC_as gradient change (i.e., the same CO₂ uptake efficiency) and everything else being equal, Δ∑C_{LGM–Holocene} would be −240 PgC at %NADW = 50% and %GNAIW = 30%.

Cores, age models, samples, and analytical methods

We used ODP Site 999 for Gulf Stream surface-water reconstructions (Fig. 2). The age model is from Schmidt et al.⁵⁹. Planktonic foraminiferal Globigerinoides ruber (sensu stricto, white variety) δ¹⁸O, Mg/Ca, and δ¹¹B data are from refs. ^21,22,59. Briefly, about 25 and 55 shells from the 250–350 μm size fraction were used for δ¹⁸O and Mg/Ca analyses, respectively. Samples for δ¹⁸O analyses were sonicated in methanol for 5–10 s, roasted under vacuum at 375 ^oC for 30 min, and analyzed on a Fisons Optima IRMS with a precision of <0.06‰. Shells for Mg/Ca were cleaned following the reductive cleaning procedure⁶⁰ and measured on an inductively-coupled plasma mass spectrometer (ICP–MS) with a precision of ~1.7%. For δ¹¹B analyses, about 100–120 G. ruber (w) shells from the 300–355 μm size fraction were cleaned following the “Mg-cleaning” procedure⁶¹, to minimize material loss during cleaning⁶². G. ruber (w) δ¹¹B was measured on a Neptune multicollector (MC)–ICP–MS with an analytical error in δ¹¹B of about ±0.25‰ (ref. ²¹).

Three cores (BOFS 17, BOFS 11, and BOFS 14 K) from the polar North Atlantic Ocean are used for deep-water reconstructions (Fig. 3). Their age models are based on published chronologies^24,63,64,65. For each sample (~2 cm thickness), ~10–20 cm³ of sediment was disaggregated in de-ionized water and was wet sieved through 63 μm sieves. To facilitate analyses, we picked the most abundant species for measurements. For each B/Ca analysis, ~10–20 monospecific shells of the benthic foraminifera C. mundulus (BOFS 17 K) and C. wuellerstorfi (BOFS 14, 11 K) were obtained from 250 to 500 μm size fraction. The shells were double checked under a microscope before crushing to ensure that consistent morphologies were used throughout the core. On average, following this careful screening the starting material for each sample was ~8–12 shells, which is equivalent to ~300–600 μg of carbonate. For benthic B/Ca analyses, foraminiferal shells were cleaned with either the “Mg-cleaning” method⁶¹ or the “Cd-cleaning” protocol⁶¹, to investigate cleaning effects on trace element/Ca in foraminiferal shells^62,66. No discernable B/Ca difference is observed between the two cleaning methods^25,62. Benthic B/Ca ratios were measured on an ICP–MS using procedures outlined in ref. ⁶⁷, with an analytical error better than ~5%.

For each benthic Cd/Ca analysis, ~10–20 shells of the benthic foraminiferal taxa C. mundulus (BOFS 17 K), C. wuellerstorfi (BOFS 14 K, 11 K), and Uvigerina spp. (BOFS 17 K) were picked from the 250–500 μm size fraction. Previous studies^26,27,68 showed similar Cd/Ca ratios between infaunal Uvigerina spp. and epifaunal Cibicidoides, and we thus combined Cd/Ca data from these taxa to obtain continuous downcore PO₄ records. We used the “Cd-cleaning” method^60,69 to clean benthic shells for Cd/Ca measurements. Cd/Ca ratios were measured on an ICP–MS with an analytical error better than ~5% (ref. ⁶⁷)

For δ¹¹B measurements, about 20 benthic shells from the 250–500 μm size fraction were picked for each sample. Shells used for δ¹¹B analyses were cleaned using the “Mg-cleaning” method, to minimize loss of shell material⁶¹. After cleaning, shells were dissolved and pure boron was extracted using column chemistry as described by Foster²¹. Benthic δ¹¹B was measured on a Neptune multi-collector (MC)–ICP–MS following ref. ²¹. The analytical error in δ¹¹B is about ± 0.25‰. Due to the relatively large sample size requirement, shell availability, and lengthy chemical treatments for δ¹¹B, we present low-resolution δ¹¹B for C. mundulus from BOFS 17 K and for C. wuellerstorfi from BOFS 11 K. Note that consistent [CO₃²⁻] results from B/Ca and δ¹¹B strengthen the reliability of our reconstructions (Fig. 3).

Published benthic Cd/Ca and B/Ca results are included in Fig. 3. Altogether, we generated 180 new measurements of benthic δ¹¹B, B/Ca, and Cd/Ca. All data are listed in Supplementary Data 1–9.

ODP 999 reconstructions

ODP Site 999 was used to constrain past physical conditions and carbonate chemistry of the Gulf Stream (Supplementary Fig. 4). Following previous approaches^21,22, surface water temperature (T_surface) and salinity (S_surface) were estimated based on G. ruber Mg/Ca (ref. ⁵⁹) and sea level changes^21,22,59, respectively. We first convert G. ruber δ¹¹B to borate δ¹¹B (δ¹¹B_borate), following the conversion method of ref. ²². Surface water pH (pH_surface) was calculated from seawater δ¹¹B_borate along with T_surface and S_surface. To constrain the CO₂ system, two CO₂ system variables are necessary¹⁶. In addition to δ¹¹B-derived pH, literature studies^21,22,41 generally estimate past surface-water ALK (ALK_surface) changes. Following refs. ^21,22, we estimate ALK_surface from S_surface using the modern S_surface–ALK_surface relationship (ALK_surface = 59.19 × S_surface + 229.08, R² = 0.99)²¹. Together with T_surface and S_surface, pH_surface, and ALK_surface were used to calculate other CO₂ system variables including surface-water [CO₃²⁻] ([CO₃²⁻]_surface) and DIC (DIC_surface) using the CO₂sys program²⁸. Surface-water PO₄ concentration at ODP 999 is assumed to be zero over the last 27 ka.

Following refs. ^21,22,59, errors are estimated to be 1 °C, 1‰, 100 μmol/kg, and ~0.43‰ for T_surface, S_surface, ALK_surface, and δ¹¹B_borate, respectively. Integrated average uncertainties in [CO₃²⁻]_surface and DIC_surface for a single reconstruction are, respectively, ~20 (Holocene: ~18, LGM: ~24) and ~90 μmol/kg, based on quadratic addition of all individual errors sourced from T_surface ([CO₃²⁻]_surface: 2 μmol/kg, DIC_surface: 3 μmol/kg), S_surface ([CO₃²⁻]_surface: 2 μmol/kg, DIC_surface: 5 μmol/kg), ALK_surface ([CO₃²⁻]_surface: 14 μmol/kg, DIC_surface: 86 μmol/kg), and δ¹¹B_borate ([CO₃²⁻]_surface: 16 μmol/kg, DIC_surface: 24 μmol/kg; note that δ¹¹B_borate leads to an error in [CO₃²⁻] via pH). Uncertainties for calculated CO₂ system variables at ODP 999 are tabulated in Supplementary Data 1. Use of other methods to estimate ALK would have little impact on our conclusions (Supplementary Figs. 16 and 17).

From pH to [CO₃ ²⁻]

For palaeo-studies, surface-water pH is generally obtained from planktonic foraminiferal δ¹¹B. To calculate [CO₃²⁻], a second CO₂ system variable is needed¹⁶. Following the previous approach^21,22, past ALK_surface at ODP 999 have been estimated from S using the S_surface–ALK_surface relationship. Due to limited knowledge about the past S_surface–ALK_surface relationship, a generous uncertainty has been assigned to ALK_surface at ±100 μmol/kg (ref. ^21,22), which is about half of the entire ALK range in the present global ocean². Using ALK_surface and pH_surface along with T_surface and S_surface, [CO₃²⁻]_surface and DIC_surface can be calculated using the CO₂sys program²⁸. Because of the large uncertainty in ALK_surface, large errors in DIC_surface might be expected (Supplementary Fig. 4). However, given the constraint from pH_surface, seawater ALK_surface and DIC_surface variations are not random but must vary systematically within ALK–DIC space (Supplementary Fig. 5). Because of the close relationship between pH and [CO₃²⁻] (i.e., roughly parallel patterns of pH and [CO₃²⁻] within ALK−DIC space; Supplementary Fig. 5), this systematic ALK−DIC variation allows us to confine [CO₃²⁻] with acceptable uncertainty. For a given pH at ODP 999, an error of 100 μmol/kg in ALK only leads to an error of about ±14 μmol/kg in [CO₃²⁻] (Supplementary Fig. 5).

For clarity, Supplementary Fig. 5a, b only consider the effect of ALK errors on [CO₃²⁻] estimates assuming constant pH and T–S–P conditions. To fully propagate errors from various sources including T_surface, S_surface, ALK_surface, and pH_surface, we use a Monte Carlo approach (n = 10,000) to calculate the integrated error in [CO₃²⁻] (ref. ⁷⁰). As can be seen from Supplementary Fig. 5c–f, the final errors (~20–25 μmol/kg) in an individual [CO₃²⁻] reconstruction based on the Monte-Carlo are similar to those (~18–24 μmol/kg) based on quadratic addition of individual errors, justifying our major error estimation approach (i.e., quadratic addition).

Subtropical western North Atlantic surface [CO₃ ²⁻]

Because most of North Atlantic subtropical gyre waters circulate through the Caribbean Sea before being transported to the subpolar North Atlantic via the Gulf Stream, ODP 999 from Caribbean Sea is used to constrain past Gulf Stream carbonate chemistry²⁰. To further test the feasibility of using ODP 999 to represent the first-order Gulf Stream [CO₃²⁻] changes during the Holocene and LGM, we have estimated surface-water [CO₃²⁻] for four sites from the wider subtropical western Atlantic region (latitude: 12–33°N, longitude: 61–91°W). Among these sites, KNR140–51GGC (33°N, 76°W) is located within the Gulf Stream today⁷¹. Because subtropical surface waters cycle multiple times through the upper ocean gyre circulations, it is possible that surface waters have been close to equilibrium with past atmospheric pCO₂ (refs. ^21,22). Therefore, we assume surface-water pCO₂ of 270 and 194 ppm for the Holocene and LGM, respectively⁷². We assign a ±15 ppm error to surface-water pCO₂ to account for any potential air–sea CO₂ disequilibrium. For these sites, we use surface temperature and salinity reconstructions from previous publications^71,73,74,75. ALK is calculated based on the same approach for ODP 999. The reconstructed in situ [CO₃²⁻] values show some differences between cores, due to local T–S conditions. Since we are interested in air–sea CO₂ exchange signals, we convert reconstructed in situ [CO₃²⁻] into [CO₃²⁻]_Norm using Eq. (11). As can be seen from Supplementary Fig. 6 and Supplementary Data 2, these cores show similar [CO₃²⁻]_Norm values for the Holocene (~260 μmol/kg) and LGM (~300 μmol/kg) as ODP 999. Therefore, we argue that ODP 999 sufficiently records first-order Gulf Stream air–sea exchange carbonate chemistry for the Holocene and LGM. Because we aim to obtain a proxy-based estimates, we use ODP 999 data for calculations in the main text.

Benthic B/Ca and δ¹¹B to deep-water [CO₃ ²⁻]

Most deep-water [CO₃²⁻] values are reconstructed using benthic B/Ca (refs. ^25,47) from [CO₃²⁻]_downcore = [CO₃²⁻]_PI + ΔB/Ca_{downcore–coretop}/k, where [CO₃²⁻]_PI is the preindustrial (PI) deep-water [CO₃²⁻] value estimated from the GLODAP dataset², ΔB/Ca_{downcore–coretop} represents the deviation of B/Ca of down-core samples from the core-top value, and k is the B/Ca–[CO₃²⁻] sensitivity of C. wuellerstorfi (1.14 μmol/mol per μmol/kg) or C. mundulus (0.69 μmol/mol per μmol/kg)²⁵. We use a reconstruction uncertainty of ±10 μmol/kg in [CO₃²⁻] based on global core-top calibration samples^25,76.

For cores BOFS 17 K and BOFS 11 K, new monospecific epifaunal benthic δ¹¹B values were converted into deep-water [CO₃²⁻] following the approach detailed in ref. ⁷⁷. Briefly, benthic δ¹¹B is assumed to directly reflect deep-water borate δ¹¹B, as suggested by previous core-top calibration work⁷⁸. Deep-water pH is calculated using benthic δ¹¹B along with T_deep and S_deep, similar to the approach to calculate surface-water pH at ODP 999 (refs. ^21,22). We assume constant ALK at the studied sites (2313 μmol/kg at BOFS 17 K and 2310 μmol/kg at BOFS 11 K) in the past. Following ref. ⁷⁷, a generous error of 100 μmol/kg is assigned to ALK estimates. We then calculate deep-water [CO₃²⁻] from pH and ALK using the CO₂sys program²⁸. The integrated average uncertainty in deep-water [CO₃²⁻] is ~±10 μmol/kg, based on quadratic addition of individual errors of ~±2 μmol/kg sourced from T_deep (±1 °C), ~±2 μmol/kg from S_deep (±1‰), ~±5 μmol/kg from ALK (±100 μmol/kg), and ~±8 μmol/kg from δ¹¹B_borate (~±0.25‰). As demonstrated by Supplementary Fig. 5, the large ALK error only contributes a small uncertainty to the final [CO₃²⁻] estimate. As shown in Fig. 3, benthic B/Ca and δ¹¹B yield consistent deep-water [CO₃²⁻] reconstructions for the Holocene and LGM.

Benthic Cd/Ca to deep-water PO₄

We follow the established approach^26,46,79 to convert benthic (C. wuellerstorfi, C. mundulus, and Uvigerina spp.) foraminiferal Cd/Ca into deep-water Cd concentrations. Partition coefficients (D_Cd) are used to calculate deep water Cd from: Cd (nmol/kg) = [(Cd/Ca)_foram/D_Cd] × 10. Bertram et al.⁶⁵ used empirical D_Cd values of 2.3, 2.2, and 2.7 for BOFS 17, 14, and 11 K, respectively. However, these D_Cd values would result in Holocene Cd of 0.3–0.4 nmol/kg, higher than the observed value of ~0.25 nmol/kg from modern hydrographic measurements (Supplementary Fig. 7)⁸⁰. This offset may suggest higher D_Cd values for the North Atlantic Ocean, which has been acknowledged recently⁸¹. We thus adjust D_Cd (~25% increase) so that the calculated Holocene deep-water Cd concentrations match modern measurements. This adjustment is supported by consistent Cd reconstructions from this study and previous reconstructions based on Cd/Ca measurements for Hoeglundina elegans. Compared to Cibicidoides, D_Cd into H. elegans is far less variable⁷⁹. As can be seen from Supplementary Fig. 8, for cores with similar benthic δ¹³C from similar water depths (i.e., bathed in similar water masses), our Cd reconstructions match favorably with those based on H. elegans measurements⁸². Deep water Cd is converted into PO₄ using the relationship based on the latest North Atlantic Ocean measurements (Supplementary Fig. 7)⁸⁰. Using older published Cd–PO₄ relationships^26,83 only marginally affects our PO₄ estimates.

Uncertainties associated with Cd and PO₄ reconstructions are estimated as follows. Error for Cd is estimated using 2σ_Cd = $\sqrt{(2\sigma _{D_{\mathrm{Cd}}})^2 + (2\sigma _{{\mathrm{Cd}}/{\mathrm{Ca}}})^2}$, where $2\sigma _{D_{\mathrm{Cd}}}$ and $2\sigma _{\mathrm{Cd}/\mathrm{Ca}}$ (=5%) are errors for D_Cd and Cd/Ca, respectively. Due to poorly defined uncertainty for D_Cd from the literature, we assume an error of 50%, and then compare our final errors with literature estimates to assess the appropriateness of our calculations. Seawater PO₄ is calculated from Cd using: PO₄ = $\frac{{\mathrm{Cd} - b \pm (2\sigma _b)}}{{a \pm (2\sigma _a)}}$, where 2σ_a and 2σ_b, respectively, represent 95% confidence errors associated with a and b (Supplementary Fig. 7b). The PO₄ uncertainty was calculated from: $2\sigma _{{{\rm{PO}}_4}} = \sqrt {\left( {\partial _{{{\rm{PO}}_4}}{\mathrm{/}}\partial _a \cdot 2\sigma _a} \right)^2 + \left( {\partial _{{{\rm{PO}}_4}}{\mathrm{/}}\partial _b \cdot 2\sigma _b} \right)^2 + \left( {\partial _{{{\rm{PO}}_4}}/\partial _{\mathrm{Cd}} \cdot 2\sigma _{\mathrm{Cd}}} \right)^2}$, where $\partial _{{{\rm{PO}}_4}}/\partial _a$ = $\frac{{ - (\mathrm{Cd} - b)}}{{a^2}}$, $\partial _{{{\rm{PO}}_4}}/\partial _b$ = $\frac{{ - 1}}{a}$, and $\partial_{{{\rm{PO}}_4}}/\partial _{\mathrm{Cd}}$ = $\frac{1}{a}$. Our final errors on individual Cd and PO₄ are ~0.12 nmol/kg (~55%) and ~0.5 μmol/kg (~50%), respectively. When compared with previously published uncertainties (~0.08 nmol/kg for Cd and ~0.17 μmol/kg for PO₄)^46,68, our error estimates are possibly too generous. Here we use ~50% error to be conservative. We encourage future work to improve uncertainty estimates for the benthic Cd/Ca proxy.

The oceanic residence time of PO₄ is ~100,000 years⁸⁴. The LGM deep ocean was possibly more reducing⁸⁵, which might have facilitated sediment organic matter preservation, and, thus, PO₄ removal from the ocean. However, this effect might have been compensated by decreased organic burial on continental slopes due to shallower LGM sea levels^86,87. Considering the short (~10,000 years) last deglacial⁸⁴, we assume that global PO₄ and Cd reservoirs remained constant between the Holocene and LGM. Our reconstructions (Fig. 3) are consistent with high benthic δ¹³C and low benthic Cd/Ca at numerous glacial North Atlantic mid-depth sites^{23,31,46,65,88,89}.

Deep-water temperature and salinity estimates

Deep-water temperature (T_deep) is estimated from the ice volume corrected benthic δ¹⁸O (δ¹⁸O_IVC) and the δ¹⁸O-temperature equation of Marchitto et al.⁹⁰ from T_deep = 2.5 − (δ¹⁸O_IVC − 2.8)/0.224, where δ¹⁸O_IVC = δ¹⁸O_benthic − δ₁₈O_{global_sealevel}. δ¹⁸O_{global_sealevel} was estimated from sea level curves^86,87 with a global δ¹⁸O_seawater−sea level scaling of 0.0085‰/m (ref. ⁹¹). Deep-water salinity (S_deep) is calculated by: S_deep = S_{core_top} + 1.11 × δ¹⁸O_{global_sealevel}, where S_{core_top} is the modern S_deep (35.06, 34.926, and 34.893 at BOFS 17 , 11 , and 14 K, respectively²) and the term 1.11 is the scaling term for a global S−δ¹⁸O_{global_sealevel} relationship^29,91. We assume ±1 °C and ±1‰ uncertainties in T_deep and S_deep, respectively. Use of other methods to estimate T_deep and S_deep negligibly affects our conclusions, due to relatively weak sensitivities of [CO₃²⁻]_Norm to T and S changes (Fig. 4).

Uncertainties and statistical analyses

Uncertainties associated with [CO₃²⁻] and PO₄ were evaluated using a Monte-Carlo approach^92,93. Errors associated with the chronology (x-axis) and [CO₃²⁻] and PO₄ reconstructions (y-axis) are considered during error propagation. Age errors are assumed to be ±3000 years for the three BOFS cores. Methods to calculate errors associated with individual [CO₃²⁻] and PO₄ reconstructions (y-axis) are given above. All data points were sampled separately and randomly 5000 times within their chronological and [CO₃²⁻] or PO₄ uncertainties and each iteration was then interpolated linearly. At each time step, the probability maximum and data distribution uncertainties of the 5000 iterations were assessed. Figure 3 shows probability maxima (bold curves) and ±95% (light gray; 2.5−97.5th percentile) probability intervals for the data distributions, including chronological and proxy uncertainties. For details, see refs. ^92,93.

For a time period (e.g., Holocene) where multiple analyses are available, uncertainties are calculated following the method from ref. ⁹⁴ by 2σ = $\sqrt {[\mathop {\sum }\nolimits_{i = 1}^n (2\sigma _i)^2]/n}$, where n is the number of reconstructions and 2σ_i is the error associated with individual reconstruction. For [CO₃²⁻] or [CO₃²⁻]_Norm offsets between the Holocene and LGM, 2σ = $\sqrt {(2\sigma _{\mathrm{Holocene}})^2 + (2\sigma _{\mathrm{LGM}})^2}$, where $2{\sigma} _{\mathrm{Holocene}}$ and $2{\sigma} _{\mathrm{LGM}}$ are 2σ of Holocene and LGM values, respectively. Other methods (e.g., weighted mean)⁹⁵ would give similar results.

When using Eq. (11) to calculate [CO₃²⁻]_Norm, errors from various sensitivities are <1.5 μmol/kg (see Supplementary Data 8 for crosschecking). Because [CO₃²⁻] is normalized to a constant condition (i.e., no error with final T–S–P), the error in [CO₃²⁻]_Norm is largely sourced from [CO₃²⁻] reconstruction uncertainties. For surface water [CO₃²⁻]_Norm calculations, T and S errors are already included in surface [CO₃²⁻] reconstructions. For calculations associated with deep waters, [CO₃²⁻]_Norm errors are ~0.5, ~3.5, and ~0.1 μmol/kg from ± 1 °C in T, ±1‰ in S, and ±50 dbar in P, respectively. Therefore, these uncertainties (already included in error calculations) are relatively less important compared to the reconstruction error of ±10 μmol/kg for deep water [CO₃²⁻].