Abstract
Magneto-elastic distortions are commonly detected across magnetic long-range ordering (LRO) transitions. In principle, they are also induced by the magnetic short-range ordering (SRO) that precedes a LRO transition, which contains information about short-range correlations and energetics that are essential for understanding how LRO is established. However these distortions are difficult to resolve because the associated atomic displacements are exceedingly small and do not break symmetry. Here we demonstrate high-multipole nonlinear optical polarimetry as a sensitive and mode selective probe of SRO induced distortions using CrSiTe3 as a testbed. This compound is composed of weakly bonded sheets of nearly isotropic ferromagnetically interacting spins that, in the Heisenberg limit, would individually be impeded from LRO by the Mermin-Wagner theorem. Our results show that CrSiTe3 evades this law via a two-step crossover from two- to three-dimensional magnetic SRO, manifested through two successive and previously undetected totally symmetric distortions above its Curie temperature.
Similar content being viewed by others
Introduction
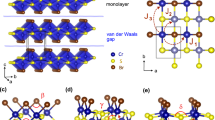
Ferromagnetic (FM) semiconductors belonging to the transition metal trichalcogenide family have recently been shown to be promising starting materials for realizing monolayer ferromagnets by exfoliation1,2. However predicting the viability of the ferromagnetic long-range ordered state in the 2D limit relies on first understanding how FM long-range ordering (LRO) is established in the 3D bulk crystals, which is often unclear. A case in point is CrSiTe33,4,5,6,7,8, which consists of ABC stacked sheets of Cr3+ (spin-3/2) moments arranged in a honeycomb network (Fig. 1). Each Cr atom is coordinated by six Te atoms that form an almost perfect octahedron7, giving rise to a near isotropic (Heisenberg) spin state and dominant FM nearest neighbor exchange interactions (Jab < 0) owing to the near 90° Cr–Te–Cr bond angle. This is corroborated by inelastic neutron scattering experiments7 on bulk CrSiTe3, which report a relatively feeble easy-axis (Ising) anisotropy strength (D/Jab < 2 %). According to the Mermin-Wagner theorem9, LRO should be forbidden in a strictly 2D Heisenberg system. Therefore the finite value of the Curie temperature (Tc ~ 31 K) in bulk CrSiTe3 (Fig. 1) must either be driven by the weak spin anisotropy or by a weak interlayer coupling that mediates a crossover from 2D to 3D character. A dimensional crossover can in principle be uncovered by tracking the spatial anisotropy of short-range spin correlations using magnetic neutron and X-ray scattering techniques. However the requirement of nearly ideal bulk crystals and the difficulty of detecting and integrating diffuse magnetic scattering is restrictive and currently renders these techniques inoperable on exfoliated nanoscale thick sheets. Hence this mechanism is yet to be verified in CrSiTe3 or related compounds1.
Characterization of long-range spin ordering in CrSiTe3. Temperature dependence of the a c-axis thermal expansion coefficient, b magnetic susceptibility and (left inset) magneto-optical Kerr rotation angle from a bulk single crystal of CrSiTe3 showing the clear onset of long-range magnetic order at Tc ~ 31 K. Note the absence of any features above Tc in all of these measurements. Right inset shows the crystal structure of CrSiTe3. In the FM phase, the Cr3+ spins all point parallel to the c-axis
An alternative route to measuring short-range spin correlations is through their effects on the crystal lattice. The magnetic energy of an insulating system is given by the thermal expectation value of its magnetic Hamiltonian \({\cal{H}}_m = J_{ij}\mathop {\sum }\nolimits_{i,j} \vec S_i \cdot \vec S_j\) which contains the short-range spin correlator \(\langle\vec S_i \cdot \vec S_j\rangle\) as well as the exchange interaction Jij between spins at sites i and j. Upon onset of magnetic short-range ordering (SRO), it may be energetically favorable for the system to re-adjust the distances and bonding angles between atoms that mediate Jij in order to lower its magnetic energy, at the expense of some gain in elastic energy. Measuring such magneto-elastic distortions therefore yields information about spin correlations along various directions and, for simple low dimensional Hamiltonians, can even provide quantitative values of the \(\langle\vec S_i \cdot \vec S_j\rangle\) function10, which is difficult to obtain by neutron scattering because only a limited range of its spatio-temporal Fourier components are accessed. However, SRO induced distortions are extremely hard to resolve because they are minute by virtue of \(\langle\vec S_i \cdot \vec S_j\rangle\) being small, and because they generally do not break any lattice symmetries. A suitable probe must therefore be sensitive to and able to distinguish between different totally symmetric distortions (i.e., different basis functions of the totally symmetric irreducible representation). This suggests that examining the nonlinear high rank tensor responses of a crystal may be a promising approach.
Optical second harmonic generation (SHG), a frequency doubling of light produced by its nonlinear interactions with a material, is governed by high rank (>2) susceptibility tensors that are sensitive to many degrees of freedom in a crystal. Traditionally SHG has been exploited as a symmetry sensitive probe because the leading order electric dipole susceptibility necessarily vanishes if the system possesses a center of inversion. This makes SHG particularly powerful for studying surfaces of centrosymmetric crystals11, and for identifying bulk symmetry breaking phase transitions through the appearance of additional, high symmetry forbidden, tensor elements12,13,14,15. In principle, SHG can also be utilized to study symmetry preserving distortions16 by examining their subtle effects on the existing symmetry allowed tensor elements. However this potential capability is highly underexplored, in part due to the technical demand of simultaneously tracking small changes across an entire set of allowed tensor elements.
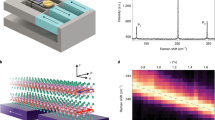
Recently we managed to surmount this challenge by developing a rotating scattering plane based SHG polarimetry technique17. In these experiments, linear (either P or S) polarized light of frequency ω is focused obliquely onto the surface of a bulk single crystal. The intensity of either the P or S component of reflected light at frequency 2ω is then measured as a function of the angle (φ) that the scattering plane is rotated about the c-axis (Fig. 2a), which allows a multitude of SHG susceptibility tensor elements to be sampled. By collecting these rotational anisotropy (RA) patterns with different polarization combinations, a complete set of SHG susceptibility tensor elements can typically be uniquely determined. Here we apply this technique to track the magnitudes of all of the symmetry allowed SHG susceptibility tensor elements of CrSiTe3 as a function of temperature. Evidence of previously undetected structural distortions are observed above Tc at T2D ~ 110 K and T3D ~ 60 K. Using a hyper-polarizable bond model, we are able to attribute the distortions at T2D and T3D to displacements along different totally symmetric normal mode coordinates, which are consistent with an onset of intralayer and interlayer spin correlations respectively.
Temperature dependence of the SHG rotational anisotropy. a Experimental geometry of the RA SHG experiment. The φ = 0° direction coincides with the crystallographic a-axis. b Image plots of the raw temperature dependent RA SHG data acquired in SS, PP, and PS polarization configurations, where the first and second labels denote the selected incident (ω) and detected (2ω) polarization components. The horizontal black line indicates the Tc of our sample (see Fig. 1). c A zoom-in on the RA SHG image plot acquired in SP configuration. Cuts at select temperatures displayed as polar plots (open circles) are shown to emphasize the changes in shape of the RA patterns taking place above Tc. Blue curves are best fits to the expected EQ SHG response from a \(\bar 3\) point group as described in the text
Results
SHG polarimetry results
The full temperature evolution of the RA patterns acquired from the (001) surface of CrSiTe3 under select polarization geometries is displayed in Fig. 2b. We first note that a finite weak SHG intensity is present at all temperatures despite previous work showing that CrSiTe3 always retains a centrosymmetric structure with \(\bar 3\) point group symmetry18. This suggests that the SHG originates from a higher multipole process such as electric quadrupole (EQ) radiation, which is governed by a fourth rank susceptibility tensor \(\chi _{ijkl}\) that has only eight independent non-zero elements (\(\chi _{xxxz}\), \(\chi _{xxyy}\), \(\chi _{xxzz}\), \(\chi _{yxxx}\), \(\chi _{yyyz}\), \(\chi _{zzxx}\), \(\chi _{zzxy}\), \(\chi _{zzzz}\)) after accounting for the symmetries of the \(\bar 3\) point group and the degeneracy of the incident electric fields19. Expressions for the RA SHG intensity \(I\left( {2\omega } \right) \propto \left| {\hat e_i^{2\omega }\left( \varphi \right)\chi _{ijkl}\hat e_j^\omega \left( \varphi \right)\kappa _k\left( \varphi \right)\hat e_l^\omega \left( \varphi \right)} \right|^2I_0^2\left( \omega \right)\) derived under these conditions (here \(\hat e\) are the polarization directions, \(\kappa\) is the incident wave vector and \(I_0\) is the incident intensity; see Supplementary Note 1) indeed produce excellent fits to our set of RA patterns at any given temperature and allow us to uniquely determine the values of \(\chi _{ijkl}\) at each temperature. In contrast, other possible allowed SHG processes such as surface electric dipole or bulk magnetic dipole radiation cannot reproduce the RA data and are thus treated as negligibly small (see Supplementary Note 2).
From the raw RA data (Fig. 2b) we can clearly discern the bulk three-fold rotational symmetry of CrSiTe3 and, as expected, we observe no change in symmetry as a function of temperature. Yet the absolute and relative intensities of the various features do undergo changes upon cooling, which must encode symmetry preserving distortions. Most notably, there is a dramatic increase of intensity below Tc that, as we will show later on, arises from LRO induced magneto-elastic distortions that have previously been detected by optical absorption20, Raman scattering20, and X-ray diffraction18, and are also captured by our dilatometry measurements (Fig. 1a). Surprisingly however, we find that the RA patterns continue to subtly evolve even far above Tc. In SP polarization geometry for example (Fig. 2c), representative RA patterns at 140, 80, and 40 K have qualitatively different shapes, indicating that the magnitude of the \(\chi _{ijkl}\) elements change non-uniformly with temperature.
Temperature dependence of the nonlinear susceptibility
The temperature (T) dependence of each of the eight individual \(\chi _{ijkl}\) elements was extracted through the aforementioned fitting procedure (Fig. 2c). From every \(\chi _{ijkl}\left( T \right)\) curve, we subtracted a high temperature background using the data above 150 K, where the shapes of the RA patterns have ceased evolving (see Supplementary Note 3). Figure 3 shows the complete set of background subtracted curves \({\mathrm{\Delta }}\chi _{ijkl}\left( T \right)\) that have all been normalized to their low temperature values. Three distinct sets of behavior are clearly resolved. Below a characteristic temperature T2D ~ 110 K, the xxxz and yyyz elements alone start to grow in tandem (Fig. 3a). Then below a second characteristic temperature T3D ~ 60 K, a solitary zzzz element begins to grow (Fig. 3b). The temperature dependence of the former and latter set of elements are sub-linear above Tc and scale with classical calculations of the nearest neighbor intralayer and interlayer spin correlators respectively (see Supplementary Note 5). By contrast, below Tc the remaining five elements turn up with an order parameter like temperature dependence indicative of a phase transition (Fig. 3c), with a critical exponent twice that reported7 for the magnetization (2β ≈ 0.3). Since magneto-elastic distortions scale like the square of the magnetic order parameter, this further confirms that \(\chi _{ijkl}\) is probing the lattice degrees of freedom. This also shows that \(\chi _{ijkl}\) is a time-reversal invariant i-tensor19, which naturally explains why our measurements are insensitive to magnetic domains21.
Temperature evolution of individual susceptibility tensor elements. The values of the a xxxz, yyyz, b zzzz and c remaining elements of the SHG susceptibility tensor \(\chi _{ijkl}\) at each temperature extracted through simultaneous fitting to all four polarization configurations of the RA data (see text). For every element, a high temperature background derived from the data above T = 150 K was subtracted off. The background subtracted curves (\(\Delta \chi _{ijkl}\)) were then each normalized to their values at T = 7 K. Error bars are the least squared errors of the fits, which are smaller than the data symbols in panel a. Solid lines in panels a and b are the calculated intralayer and interlayer spin correlator respectively. The line in panel c is the function \(\left| {T - T_c} \right|^{ - 2\beta }\), where β is the critical exponent of the magnetization. The two elements zzxx and zzxy are not displayed in c for clarity because their fitted values are very small, resulting in much larger error bars. However their trend follows that of the xxyy, xxzz and yxxx elements shown in c (see Supplementary Note 4). Diffuse magnetic neutron scattering data from CrSiTe3 reproduced from ref. 7 is shown in the inset of a. The inset of b shows the frequency of the Eu phonon (top) and amplitude of the Eg phonon (bottom), which are respectively reproduced from ref. 20 and measured using impulsive stimulated Raman scattering (see Supplementary Note 7)
Microscopic origin of the susceptibility change
To understand the microscopic origin of the features in \({\mathrm{\Delta }}\chi _{ijkl}\left( T \right)\), we appeal to a simplified hyper-polarizable bond model22, which treats the crystal as an array of charged anharmonic oscillators centered at the chemical bonds and constrained to only move along the bond directions. The nonlinear polarizability of each oscillator is calculated by solving classical equations of motion, and then appropriately summed together to form the total nonlinear susceptibility. Recently an expression for the EQ SHG susceptibility was derived using this model23 and was found to take the form \(\chi _{ijkl} \propto \mathop {\sum }\nolimits_n \alpha _\omega \alpha _{2\omega }\left( {\hat b_n \otimes \hat b_n \otimes \hat b_n \otimes \hat b_n} \right)_{ijkl}\), where \(\alpha _\omega\) and \(\alpha _{2\omega }\) are the first-order (linear) and second-order (hyper) polarizabilities, \(\hat b_n\) is a unit vector that points along the nth bond, and all bond charges are assumed equal. Using this expression, we investigated how distortions along each of the four totally symmetric normal mode coordinates allowed in the \(\bar 3\) point group (i.e., the four basis functions \(A_g^1\), \(A_g^2\), \(A_g^3\) and \(A_g^4\) of its totally symmetric irreducible representations) change the individual \(\chi _{ijkl}\) elements.
For simplicity, we considered only the nearest neighbor intralayer Cr–Te bonds and the nearest neighbor interlayer Cr–Cr bonds, which is reasonable because the states accessed by our photon energy (2ħω = 3 eV) are predominantly composed of Cr and Te orbitals24,25. Remarkably, our hyper-polarizable bond model shows that under a small distortion along the \(A_g^1\) normal coordinate δ, which we implement by changing the \(\hat b_n\) while keeping the \(\alpha _\omega \alpha _{2\omega }\) values constant, only the xxxz and yyyz elements are affected (Fig. 4a), in perfect agreement with our observations below T2D (Fig. 3a). Since motion along \(A_g^1\) deforms the Te octahedra and can bring the Cr–Te–Cr bond angle closer to 90° to strengthen Jab, it is natural to associate this distortion with the development of FM in-plane spin correlations. This is further supported by neutron scattering experiments7, which show a rise in magnetic diffuse scattering around T2D (inset Fig. 3a) indicative of a growing in-plane correlation length \(\xi _{ab}\).
Hyper-polarizable bond model and dimensional crossover. Plots show hyper-polarizable bond model calculations of the change in each of the eight allowed SHG susceptibility tensor elements relative to their undistorted values (\({\mathrm{\Delta }}\chi _{ijkl}\)) under totally symmetric distortions along the a, \(A_g^1\), b, \(A_g^2\), c, \(A_g^3\) and d, \(A_g^4\) normal coordinates. Schematics in the insets show the bonds (springs) used in our model and depict how each distortion is parameterized. Both vertical and horizontal axes are plotted on a linear scale. Tensor elements that change in the same way are represented as multi-colored curves. e Illustration of the spin ordering process in CrSiTe3 deduced from our data. The light blue regions represent an absence of spin-spin correlations and the dark blue regions represent FM correlations, which are dynamic above Tc and static below Tc
To uncover a mechanism that would exclusively affect the zzzz element below T3D (Fig. 3b), we note that the distortion along the \(A_g^2\) normal coordinate involves a pure out-of-plane displacement of the Cr atoms. Although this motion does not change the \(\hat b_n\) of the interlayer Cr–Cr bonds since they remain parallel to the z-axis, it will change their polarizabilities by virtue of their altered bond length. Assuming that it is these Cr–Cr bonds that primarily contribute to the observed changes at T3D (see Supplementary Note 6), our model indeed shows that tuning either \(\alpha _\omega\) or \(\alpha _{2\omega }\) of the Cr–Cr bond will exclusively affect the zzzz element (Fig. 4b). This naturally suggests an association of the \(A_g^2\) distortion with the development and enhancement of FM interlayer spin correlations, and hence an identification of T3D as the 2D to 3D dimensional crossover temperature. Independent evidence for a structural distortion at T3D was also found via anomalies in the Eg and Eu phonons using impulsive stimulated Raman scattering (see Supplementary Note 7) and infrared absorption measurements20 respectively (inset Fig. 3b), which likely arise from their nonlinear coupling to the \(A_g^2\) distortion.
As a further consistency check, we note that one expects interlayer correlations to onset when \(\xi _{ab}\) grows to a size where the total interlayer exchange energy becomes comparable to the temperature. In a mean field approximation, this condition is expressed as \(T = N\left( T \right)J_cS\left( {S + 1} \right)/3k_B\), where N is the number of in-plane correlated spins of magnitude S that are interacting with the next layer, Jc is the interlayer Cr–Cr exchange and \(k_B\) is Boltzmann’s constant. Using the values of \(\xi _{ab}\left( T \right)\) and Jc determined from neutron scattering7, we find a solution to the mean field equation at T ~ 70 K (see Supplementary Note 8), which is reasonably close to T3D. Displacements along the remaining two \(A_g^3\) and \(A_g^4\) normal coordinates are found from our model to affect all eight of the tensor elements (Fig. 4c, d) and are therefore not measurably induced at either T2D or T3D. It is possible that they occur below Tc where we observe all elements to change (Fig. 3), but details of LRO induced distortions are outside the scope of this work.
Discussion
Our EQ SHG data and analysis taken together provide a comprehensive picture of how the quasi-2D Heisenberg ferromagnet CrSiTe3 evades the Mermin-Wagner theorem via a multiple stage process to establish long-range spin order (Fig. 4e), and shows that interlayer interactions are vital to stabilizing LRO at such high temperatures. More generally, our results demonstrate that the nonlinear optical response is a highly effective probe of short-range spin physics and their associated totally symmetric magneto-elastic distortions, which are typically unresolvable by capacitance dilatometry10 (Fig. 1a) or lower rank optical processes like linear reflectivity and Raman scattering due to their limited degrees of freedom (see Supplementary Note 9), and are challenging to detect by diffraction based techniques limited to pico-meter resolution18. This technique will be particularly useful for studying anisotropic or geometrically frustrated magnetic systems, which tend to display interesting short-range spin correlations. It will also be useful for uncovering magnetic ordering mechanisms in monolayer or few layer ferromagnetic and antiferromagnetic nanoscale flakes and devices26,27,28,29, which are often unclear because of their inaccessibility by neutron diffraction. We anticipate that access to this type of information may offer new strategies to control magnetism based on manipulating SRO induced distortions through chemical synthesis, static perturbations or even out-of-equilibrium excitations30.
Methods
Sample growth and characterization
The CrSiTe3 crystals used in this study were grown using a Te self-flux technique20. High purity Cr (Alfa Aesar, 99.999%), Si (Alfa Aesar 99.999%), and Te (Alfa Aesar 99.999%) were weighed in a molar ratio of 1:2:6 (Cr:Si:Te) and loaded into an alumina crucible sealed inside a quartz tube. The quartz ampoule was evacuated and backfilled with argon before sealing. Plate-like crystals up to 5 mm thick with flat, highly reflective surfaces were then removed from the reaction crucible. X-ray diffraction (XRD) data collected on crushed crystals using an Emperyan diffractometer (Panalytical) confirmed the correct \(R\bar 3\), space group 148, CrSiTe3 phase. Measurements of the temperature and field-dependence of the magnetization were carried out using a Magnetic Property Measurement System (MPMS, Quantum Design). The samples were mounted with the field applied parallel to the ab-plane of the crystals for magnetization and susceptibility measurements. The thermal expansion coefficient was measured using the Quantum Design dilatometer option in a PPMS DynaCool. Dilation was measured along the c-axis; sample thickness in this direction was 0.41 mm. Data were collected under a ramp rate of 0.1 K/min.
RA SHG measurements
Incident light with <100 fs pulse width and 800 nm center wavelength was derived from a ti:sapph amplified laser system (Coherent RegA) operating at 100 kHz. Specular reflected second-harmonic light at 400 nm was selected using short-pass and narrow bandpass filters and measured with a two-dimensional EM-CCD camera (Andor iXon Ultra 897). Both the sample and detector remained fixed while the scattering plane is rapidly mechanically spun about the central beam axis. The angle of incidence was fixed at 10°. A detailed description of the RA SHG apparatus used can be found in ref. 17. The fluence of the beam was maintained at ~340 μJ cm−2 with a spot size of ~30 μm FWHM. The close agreement between the Tc values measured using RA SHG and magnetic susceptibility indicates negligible average heating by the laser beam. Each complete RA pattern was acquired with a 5 min exposure time. Samples (~1 mm × 2 mm × 0.1 mm) were cleaved prior to measurement and immediately pumped down in an optical cryostat to a pressure better than 10−6 Torr.
Data availability
The datasets generated are/or analyzed during the current study are available from the corresponding author on reasonable request.
References
Gong, C. et al. Discovery of intrinsic ferromagnetism in two-dimensional van der Waals crystals. Nature 546, 265–269 (2017).
Huang, B. et al. Layer-dependent ferromagnetism in a van der Waals crystal down to the monolayer limit. Nature 546, 270–273 (2017).
Carteaux, V., Moussa, F. & Spiesser, M. 2D Ising-like ferromagnetic behaviour for the lamellar Cr2Si2Te6 compound: a neutron scattering investigation. EPL Europhys. Lett. 29, 251 (1995).
Li, X. & Yang, J. CrXTe3 (X = Si, Ge) nanosheets: two dimensional intrinsic ferromagnetic semiconductors. J. Mater. Chem. C 2, 7071–7076 (2014).
Chen, X., Qi, J. & Shi, D. Strain-engineering of magnetic coupling in two-dimensional magnetic semiconductor CrSiTe3: competition of direct exchange interaction and superexchange interaction. Phys. Lett. A 379, 60–63 (2015).
Lin, M.-W. et al. Ultrathin nanosheets of CrSiTe3: a semiconducting two-dimensional ferromagnetic material. J. Mater. Chem. C 4, 315–322 (2015).
Williams, T. J. et al. Magnetic correlations in the quasi-two-dimensional semiconducting ferromagnet CrSiTe3. Phys. Rev. B 92, 144404 (2015).
Liu, B. et al. Critical behavior of the quasi-two-dimensional semiconducting ferromagnet CrSiTe3. Sci. Rep. 6, 33873 (2016).
Mermin, N. D. & Wagner, H. Absence of ferromagnetism or antiferromagnetism in one- or two-dimensional isotropic Heisenberg models. Phys. Rev. Lett. 17, 1133–1136 (1966).
Zapf, V. S. et al. Direct measurement of spin correlations using magnetostriction. Phys. Rev. B 77, 020404 (2008).
Shen, Y. R. Surface second harmonic generation: a new technique for surface studies. Annu. Rev. Mater. Sci. 16, 69–86 (1986).
Fiebig, M., Pavlov, V. V. & Pisarev, R. V. Second-harmonic generation as a tool for studying electronic and magnetic structures of crystals: review. JOSA B 22, 96–118 (2005).
Denev, S. A., Lummen, T. T. A., Barnes, E., Kumar, A. & Gopalan, V. Probing ferroelectrics using optical second harmonic generation. J. Am. Ceram. Soc. 94, 2699–2727 (2011).
Zhao, L. et al. Evidence of an odd-parity hidden order in a spin–orbit coupled correlated iridate. Nat. Phys. 12, 32–36 (2016).
Harter, J. W., Zhao, Z. Y., Yan, J.-Q., Mandrus, D. G. & Hsieh, D. A parity-breaking electronic nematic phase transition in the spin-orbit coupled metal Cd2Re2O7. Science 356, 295–299 (2017).
Matsubara, M. et al. Optical second- and third-harmonic generation on the ferromagnetic semiconductor europium oxide. J. Appl. Phys. 109, 07C309 (2011).
Harter, J. W., Niu, L., Woss, A. J. & Hsieh, D. High-speed measurement of rotational anisotropy nonlinear optical harmonic generation using position-sensitive detection. Opt. Lett. 40, 4671–4674 (2015).
Carteaux, V., Ouvrard, G., Grenier, J. C. & Laligant, Y. Magnetic structure of the new layered ferromagnetic chromium hexatellurosilicate Cr2Si2Te6. J. Magn. Magn. Mater. 94, 127–133 (1991).
Birss, R. R. Symmetry and Magnetism. (North-Holland Pub. Co., Amsterdam, Netherlands, 1964).
Casto, L. D. et al. Strong spin-lattice coupling in CrSiTe3. APL Mater. 3, 041515 (2015).
Wu, S. et al. The direct observation of ferromagnetic domain of single crystal CrSiTe3. AIP Adv. 8, 055016 (2018).
Powell, G. D., Wang, J.-F. & Aspnes, D. E. Simplified bond-hyperpolarizability model of second harmonic generation. Phys. Rev. B 65, 205320 (2002).
Bauer, K.-D. & Hingerl, K. Bulk quadrupole contribution to second harmonic generation from classical oscillator model in silicon. Opt. Express 25, 26567–26580 (2017).
Siberchicot, B., Jobic, S., Carteaux, V., Gressier, P. & Ouvrard, G. Band structure calculations of ferromagnetic chromium tellurides CrSiTe3 and CrGeTe3. J. Phys. Chem. 100, 5863–5867 (1996).
Sivadas, N., Daniels, M. W., Swendsen, R. H., Okamoto, S. & Xiao, D. Magnetic ground state of semiconducting transition-metal trichalcogenide monolayers. Phys. Rev. B 91, 235425 (2015).
Li, X., Cao, T., Niu, Q., Shi, J. & Feng, J. Coupling the valley degree of freedom to antiferromagnetic order. Proc. Natl Acad. Sci. USA 110, 3738–3742 (2013).
Sivadas, N., Okamoto, S. & Xiao, D. Gate-controllable magneto-optic Kerr effect in layered collinear antiferromagnets. Phys. Rev. Lett. 117, 267203 (2016).
Jiang, S., Li, L., Wang, Z., Mak, K. F. & Shan, J. Controlling magnetism in 2D CrI3 by electrostatic doping. Nat. Nanotechnol. 13, 549–553 (2018).
Huang, B. et al. Electrical control of 2D magnetism in bilayer CrI3. Nat. Nanotechnol. 13, 544–548 (2018).
Basov, D. N., Averitt, R. D. & Hsieh, D. Towards properties on demand in quantum materials. Nat. Mater. 16, 1077–1088 (2017).
Acknowledgements
This work was supported by ARO MURI Grant No. W911NF-16–1–0361. D.H. also acknowledges support for instrumentation from the David and Lucile Packard Foundation and from the Institute for Quantum Information and Matter, an NSF Physics Frontiers Center (PHY-1733907). A.R. acknowledges support from the Caltech Prize Fellowship. The MRL Shared Experimental Facilities are supported by the MRSEC Program of the NSF under Award No. DMR 1720256; a member of the NSF-funded Materials Research Facilities Network. S.D.W. acknowledges support from the Nanostructures Cleanroom Facility at the California NanoSystems Institute (CNSI). We thank Tom Hogan for performing the dilatometry measurements and Liangbo Liang, David Mandrus, Jan Musfeldt, Kai Xiao, and Houlong Zhuang for helpful discussions.
Author information
Authors and Affiliations
Contributions
A.R. and D.H. conceived the experiment. A.R. performed the optical measurements. A.R., D.H., and L.B. analysed the data. L.B. performed the classical Heisenberg model calculations. E.Z. and S.D.W. prepared and characterized the sample. A.R. and D.H. wrote the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Journal peer review information: Nature Communications thanks the anonymous reviewers for their contribution to the peer review of this work. Peer reviewer reports are available.
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Ron, A., Zoghlin, E., Balents, L. et al. Dimensional crossover in a layered ferromagnet detected by spin correlation driven distortions. Nat Commun 10, 1654 (2019). https://doi.org/10.1038/s41467-019-09663-3
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-019-09663-3
This article is cited by
-
Electric quadrupole second-harmonic generation revealing dual magnetic orders in a magnetic Weyl semimetal
Nature Photonics (2024)
-
Abnormal thickness-dependent magneto-transport properties of vdW magnetic semiconductor Cr2Si2Te6
npj 2D Materials and Applications (2023)
-
Selection rules in symmetry-broken systems by symmetries in synthetic dimensions
Nature Communications (2022)
-
Mirror symmetry breaking in a model insulating cuprate
Nature Physics (2021)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.