Abstract
In a cavity quantum electrodynamics (QED) system, where atoms coherently interact with photons in a cavity, the eigenstates of the system are the superposition states of atoms and cavity photons, the so-called dressed states of atoms. When two cavities are connected by an optical fiber with negligible loss, the coherent coupling between the cavities gives rise to photonic normal modes. One of these normal modes is the fiber-dark mode, in which photons are delocalized in the two distant cavities. Here we demonstrate the setting of coupled-cavities QED, where two nanofiber cavity-QED systems are coherently connected by a meter-long low-loss channel in an all-fiber fashion. Specifically, we observe dressed states of distant atoms with delocalized photons of the fiber-dark normal mode. Our system will provide a platform for the study of delocalized atomic and photonic states, photonic many-body physics, and distributed quantum computation.
Similar content being viewed by others
Introduction
When atoms are coherently coupled to each other via their interaction with a common mode of the electromagnetic field, they form collective states, the dynamics of which can be drastically different from that of independent atoms. For the case of atoms in free space, collective effects become observable, as a change in radiative decay rates, when inter-atomic separations are smaller than a few wavelengths1,2,3,4. Recently, such super-radiance and sub-radiance phenomena have been observed for atoms interacting with a common guided mode of a photonic crystal waveguide5 and an optical nanofiber6, where atoms are separated by a macroscopic distance up to several hundred microns, much larger than the wavelength. On the other hand, in the setting of cavity quantum electrodynamics (QED), where coherent atom−atom coupling is mediated by the confined mode of the cavity, the collective effects can be observed as coherent, reversible dynamics of the system, which is evident as a structural change in the energy spectra, in contrast to changes in atomic dissipation rates as for the above cases. For example, the vacuum Rabi splitting for the dressed states of an atom in the Jaynes−Cummings model7,8,9,10 is enhanced by a factor of \(\sqrt N\) for the collective dressed states in the N-atom Tavis−Cummings model11,12,13,14. These coherent collective effects may be extended to a configuration of coupled, but distant, cavity QED systems. In particular, when two cavities are connected via a channel whose loss is negligible compared to the coupling between each cavity and the channel, photons can deterministically propagate back and forth between the cavities many times before being lost. Such coherent coupling between two cavities gives rise to normal modes, or superpositions in certain combinations of the two cavities and the connecting fiber, each of which extends to the whole system nonlocally. Notably, one of these normal modes is a superposition of the two cavity modes but has no contribution from the connecting fiber (fiber-dark mode)15.
Here, we demonstrate an all-fiber, coupled-cavities QED system in which either a single ensemble or two distantly separated ensembles of several tens of atoms coherently interact with the delocalized normal modes of coherently coupled, distant cavities, and we observe collective dressed states of atoms with the fiber-dark mode. This is the demonstration of coherent, reversible coupling between distant atoms, with a separation of the order of a meter, which is made possible by the all-fiber nature of the connection between the two cavities, with a loss as low as 2%. Our achievement is an important step towards the physical implementation of cavity QED-based distributed quantum computation15,16,17,18 and a quantum network19,20, where a large number of cavity QED systems are coherently connected by low-loss fiber channels. In such systems, quantum entanglement over the whole network can be created deterministically21,22, instead of probabilistically23. Our achievement also paves the way for the study of many-body physics with atoms and photons in a coupled-cavities QED system, such as quantum phase transitions of light24,25,26,27,28,29,30,31.
Results
Theory
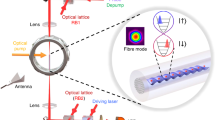
As illustrated in Fig. 1, our system consists of two nanofiber cavity QED systems32 connected in an all-fiber fashion. In each cavity, an ensemble of several tens of atoms interacts with the cavity field through the evanescent field of a nanofiber, both ends of which are connected to standard optical fibers through tapered regions and sandwiched by a pair of fiber-Bragg-grating mirrors. A probe laser at the frequency ωp is input from mirror 1 (left mirror of cavity 1), and the output from mirror 4 (right mirror of cavity 2) is measured.
Schematic of the coupled-cavity QED system. Cavity 1 of length L1 and cavity 2 of length L2 are coupled to a connecting fiber of length Lf with coupling rates of v1 and v2, respectively. Atomic ensembles are coupled to Cavities 1 and 2 with atom-cavity coupling rates of g1 and g2, respectively. Probe beam is input from the left mirror of cavity 1 (Mirror 1), and its output from the right mirror of cavity 2 (Mirror 4) is measured
For simplicity, we first consider the system with one atom for each cavity, which is modeled by the following Hamiltonian (ℏ = 1) in a frame rotating at ωp:
where we assume, for simplicity, that the cavity and connecting-fiber modes (a1, a2, b) have the same frequency ωc so that Δc = ωc − ωp (see Supplementary Note 1). The atom-probe detuning is given by Δa = ωa − ωp, where ωa is the atomic transition frequency. The coupling rates of cavities 1 and 2 with the connecting fiber are given by
where c is the speed of light in the fiber and Ti, Li, and Lf are the transmittance of the mirror i, length of the cavity i, and length of the connecting fiber, respectively. The atoms are coupled to their respective cavity modes with strengths g1 and g2.
Considering just the cavities and connecting fiber, we can move to a normal-mode picture, with normal-mode operators given by
where
Note that the normal mode d has no contribution from the connecting-fiber mode b. Rather, it has only contributions from the two cavity modes a1 and a2, and it has the frequency ωc. On the other hand, the normal modes c± have contributions from the two cavities and the connecting fiber, and they are shifted in frequency by \(\pm \sqrt 2 \tilde v\) from ωc. If \(\sqrt 2 \tilde v\) is sufficiently large, the atomic transition frequency is close to the bare cavity resonance, \(\omega _{\mathrm{a}} \simeq \omega _{\mathrm{c}}\), and the frequency of the probe laser is scanned only in this vicinity, then it is possible to focus on the system dynamics involving only the mode d. That is, we can focus on the reduced Hamiltonian
where
This Hamiltonian is identical to the Hamiltonian for a standard single-cavity QED system with a cavity mode d and two atoms (Tavis−Cummings Hamiltonian11) having single-atom coupling strengths of gd1 and gd2. The eigenstates of this system are the collective dressed states of atoms in distant cavities and of photons in the delocalized normal mode d. In other words, each atom interacts with both cavities simultaneously and collectively, but not with the connecting fiber. Indeed, the atom-field coupling strengths, gd1 and gd2, do not depend on the length of the connecting fiber.
For a general case of the system with many atoms in each cavity, the linear optical response in the weak-driving limit is identical to the single-atom model discussed above, with replacements of single-atom coupling strengths gi with the collective coupling strengths \(g_{i,{\mathrm{eff}}} = g_{i,(0)}\sqrt {N_{i,{\mathrm{eff}}}}\), where gi,(0) is the single-atom coupling strength for an atom located at a potential minimum of the atomic trap in cavity i and Ni,eff is the effective number of atoms in cavity i (see Supplementary Note 1).
Experiments
In order to investigate the interaction between atoms and the normal modes of the coupled-cavities system, we measure transmission spectra with different atom-loading conditions and various lengths of the connecting fiber.
Each cavity QED system is similar to the previous setup described in ref. 32. The transmittances of the mirrors are (T1, T2, T3, T4) = (0.13, 0.39, 0.33, 0.06). The single-pass losses inside the cavities and that for the connecting fiber are all 0.02, which are dominated by the splicing losses (two splices for each cavity and the connecting fiber). The cavity lengths are (L1, L2) = (0.92, 1.38) m. Atoms are trapped in a state-insensitive, two-color, evanescent-field optical trap32,33,34,35,36.
Firstly, we fix the length of the connecting fiber as Lf = 1.23 m and measure the transmission spectra of the coupled-cavities QED system with different atom-loading conditions, in which the atoms are not loaded, loaded in either cavity, or loaded in both cavities. In Fig. 2a, the blue solid line shows the measured transmission spectrum normalized to the maximum transmission for the case without atoms. Three peaks for the normal modes d and c± are clearly observed. The red dashed line shows the corresponding theoretical curve (see Supplementary Note 1) with no free fitting parameter, which agrees well with the experimental data. In particular, the splittings of the side peaks from the center peak match with the theoretical value of the frequency difference of the modes c± from the fiber-dark mode d given by \(\sqrt 2 \tilde v = 2\pi \times 12.1\,{\mathrm{MHz}}\). The slight broadening in linewidths and the asymmetry of the spectral shape in the experiments are, we believe, due to the instability of the detunings of the cavity and fiber modes (a1, a2, and b) from the atomic frequency ωa during the measurement. Figure 2b, c shows the spectra for the cases of atoms loaded only in cavities 1 and 2, respectively. It can be clearly seen that the interaction of atoms with the fiber-dark mode d causes a splitting of the center peak in Fig. 2a, which is the signature of the dressed states of atoms with delocalized photons of the fiber-dark mode. On the other hand, the (off-resonant) interaction of atoms with the modes c± causes the frequency shifts of the side peaks. It can be seen that the spectra agree reasonably well with the theoretical curves of a linearized model with the atom-cavity coupling strengths (g1,eff, g2,eff) = 2π × (7.2 ± 1.0, 7.3 ± 1.0) MHz ((gd1, gd2) = 2π × (4.3 ± 0.6, 5.8 ± 0.8) MHz) as the only free parameters. Figure 2d shows the spectrum for the case of atoms loaded in both cavities. The measured spectra clearly also agree quite well with the theoretical curves with no additional free parameters. Note that the splitting of the center peak is larger than that observed in Fig. 2b, c and agrees with the theoretical value of \(\sqrt {g_{d1}^2 + g_{d2}^2} = 2\pi \times 7.3\,{\mathrm{MHz}}\), which is the signature of the collective dressed states of distant atoms with delocalized photons of the fiber-dark mode.
Transmission spectra with different atom-loading conditions. a No atoms are loaded. b Atoms are loaded in cavity 1 only. c Atoms are loaded in cavity 2 only. d Atoms are loaded in both cavities. Blue solid lines represent experimental data, while red dashed lines and pink shaded bands are theoretical curves for (g1,eff, g2,eff) = 2π × (7.2, 7.3) MHz and (g1,eff, g2,eff) = 2π × (7.2 ± 1.0, 7.3 ± 1.0) MHz, respectively. When no atoms are loaded (a), formation of normal modes for three coupled empty cavities results in the clear triplet spectrum. The central peak corresponds to the fiber-dark mode d, while the two side peaks correspond to the other two normal modes c±. When atoms are loaded in one of the two (b, c), or both cavities (d), coupling between atoms and the fiber-dark mode results in the splitting of the central peak observed in (a). In particular, the splitting observed in (d) is the signature of the dressed states of distant atoms with delocalized photons in the fiber-dark mode
Secondly, we measure transmission spectra of the coupled-cavities QED system with different lengths of the connecting fiber. Figure 3a, b shows the spectra without atoms for the cases of Lf = 0.83 m and 2.27 m, respectively. The measured spectra (blue solid lines) reasonably agree with the theoretical curves (red dashed lines). A change of splittings between the center and side peaks from that in Fig. 2a (Lf = 1.23 m) is clearly observed. Specifically, the observed splittings roughly match the theoretical values of \(\sqrt 2 \tilde v = 2\pi \times 14.7\,{\mathrm{MHz}}\) and 2π × 8.9 MHz for Lf = 0.83 m and 2.27 m, respectively. Figure 3c, d shows the spectra with atoms for the cases of Lf = 0.83 m and 2.27 m, respectively. Again, the measured spectra (blue solid lines) reasonably agree with the theoretical curves (red dashed lines). Note that the splittings of the center peak associated with the coupling of atoms to the fiber-dark mode do not change for different lengths of the connecting fiber, in agreement with the above theory.
Transmission spectra with different connecting-fiber lengths. Blue solid lines represent experimental data, while red dashed lines and pink shaded bands are theoretical curves for (g1,eff, g2,eff) = 2π × (7.2, 7.3) MHz and (g1,eff, g2,eff) = 2π × (7.2 ± 1.0, 7.3 ± 1.0) MHz, respectively. The small peaks at Δa ≈ 2π × 25 MHz in (a, c) correspond to a mode with different polarization, which appears because of imperfect polarization compensation in the connecting fiber (see Supplementary Note 2). The dependence of the cavity-fiber coupling rates v1 and v2 on the connecting-fiber length is clearly observed as the change of the splitting in the triplet structure in (a, b). In contrast, the splitting of the central peak in (c, d) remains unchanged. This is because the coupling rate between atoms and the delocalized photons in the fiber-dark mode does not depend on the connecting-fiber length
Lastly, we investigate saturation behaviors of the coupled-cavities QED system to confirm that the above measurements are conducted in the weak-driving regime. Specifically, we load atoms in either of the cavities and measure transmission as a function of the input probe power. The length of the connecting fiber is fixed at Lf = 1.23 m. Figure 4a, b shows the normalized transmission at zero detuning Δa = 0 for atoms loaded in cavities 1 and 2, respectively. It can be clearly seen that the system is in the weak-driving regime at the input power of 210–310 pW for the above measurement and that the transmission starts to saturate as the input power exceeds ~103 pW.
Saturation behavior of the on-resonance transmission. Normalized transmission is plotted as a function of input probe power for atoms loaded in a cavity 1 and b cavity 2. Red curves are semiclassical state equations with (g1,(0), g2,(0)) = 2π × (0.75, 1.2) MHz and (N1,eff, N2,eff) = (92, 37). The corresponding saturation photon numbers are (n1,sat, n2,sat) = (6.9, 2.7), and thus, our system shows strong nonlinearity at the few-photon level
We further compare the measured saturation behaviors with semiclassical state equations for the many-atom coupled-cavities QED system (see Supplementary Note 1). The red solid lines in Fig. 4a, b are the theoretical curves with (g1,(0), g2,(0)) = 2π × (0.75, 1.2) MHz, from which we obtain (N1,eff, N2,eff) ≡ ((g1,eff/g1,(0))2, (g2,eff/g2,(0))2) = (92, 37). It can also be seen that these curves reasonably agree with the experimental results. Saturation behavior of a cavity QED system can be characterized with the so-called saturation photon number, which is a measure of the system nonlinearity. Note that the corresponding saturation photon numbers are (n1,sat, n2,sat) = (6.9, 2.7) (see Supplementary Note 1), and thus, our system shows strong nonlinearity at the few-photon level.
Discussion
In summary, we have demonstrated the setting of a coupled-cavities QED system in which two nanofiber cavity QED systems are coherently connected via a meter-long, low-loss fiber channel. Specifically, we have observed the collective dressed states of distant atoms with delocalized photons of a fiber-dark normal mode. We note that the delocalization of photons for the fiber-dark mode would be explicitly demonstrated by the inability to drive or detect this mode through the connecting fiber, which could be facilitated by inserting a fiber beam splitter in the connecting fiber. Also, while in the present study the coherent coupling between distant atoms has been observed in the steady-state spectra, it will be possible, and very interesting, to also investigate transient dynamics of this system, where deterministic, reversible exchange of excitation between distant atoms would be observable.
It is straightforward to increase the number of coupled-cavities in our system, and by driving the atoms from the side of the cavities with classical fields, it will be possible to realize a system of strongly interacting polaritons25. Since the cavities are coupled via optical fibers, it is also possible to design a system with arbitrary geometry of connections. Note that ensembles of atoms \(\gtrsim 10^3\) are routinely loaded into the optical traps around nanofibers34,36,37. By reducing the number of atoms in each cavity to one32, on the other hand, it will be possible to construct a fiber network of single-atom-cavity QED systems19,20. With such a system, deterministic creation of quantum entanglement over the whole network21,22, instead of probabilistic creation23, will be possible. Furthermore, provided that the normal-mode description is valid, i.e., if the coherent coupling rate between each cavity and the fiber is larger than the loss rates, the interaction of atoms with the resulting fiber-dark mode can be utilized in quantum gates for distributed quantum computation15. In order to extend our work to the construction of a fiber network of coherently coupled single-atom-cavity QED systems, we are currently making technical improvements to the setup, for example, further reduction of the internal losses in the cavities, active stabilization of the cavities, and extending the lifetime of the atomic traps38.
Methods
Experimental methods
Each experimental sequence starts with cooling and collecting Cs atoms in standard magneto-optical traps (MOTs). We use the D2-line F = 4 → F′ = 5 transition for cooling and the F = 3 → F′ = 4 transition for repumping in the MOT. The numbers of atoms in the MOTs are 7 × 106 and 3.3 × 107 for cavities 1 and 2, respectively. The positions of the MOTs are intentionally shifted from the cavities, and atoms are not coupled to the cavities at this stage. After the numbers of atoms in the MOTs are saturated, we scan the lengths of the cavities and the connecting fiber with different frequencies and monitor the transmission of a laser with the frequency ωa (atomic F = 4 → F′ = 5 transition). The transmission varies with the lengths of the cavities and the connecting fiber, i.e., the detunings of the modes a1, a2, and b from ωa, and takes the maximum value when all the three modes are resonant to ωa. When the transmission reaches a certain threshold value, we assume that this resonance condition is satisfied and proceed to the next step, in which we switch off the monitor laser and change the detuning and intensity of the cooling laser for 32 ms to further cool the atoms down to 20 μK. Subsequently, we move the MOTs to overlap with the cavities to load atoms in the optical traps in the evanescent fields of the nanofibers.
Atoms are trapped in a state-insensitive, two-color evanescent-field optical trap32,33,34,35,36. We use counterpropagating red-detuned beams (λred = 937 nm), which form a one-dimensional optical lattice, and a blue-detuned beam (λblue = 688 nm). The trap depth of the lattice well is about 260 μK.
After loading atoms in the optical traps, we measure the transmission spectrum of the system by sending a probe pulse with the atom-probe detuning Δa scanned over ±30 MHz within 4 ms and by detecting the transmitted probe beam from the system by an avalanche photodiode after removing unwanted stray light with filters. The power of the input probe is 210–310 pW. Next, we optically pump the atoms into the F = 3 state, which is sufficiently off-resonant from the cavity modes, by irradiating a pumping laser resonant to the atomic F = 4 → F′ = 3 transition from the sides of the cavities for 1 ms, and we send a frequency-scanned probe pulse again to measure the transmission spectrum of the coupled empty cavities, i.e., the system without atoms. We then switch on the cooling and repumping lasers for 4 ms to cool and load the atoms into the optical trap again. We repeat the above procedure for spectroscopy and re-cooling five times per MOT loading sequence, and we use the average of the second, third, and fourth data for each sequence (see Supplementary Note 2 for details).
Data availability
The data that support the findings of this study are available from the corresponding author on reasonable request.
References
Dicke, R. H. Coherence in spontaneous radiation processes. Phys. Rev. 93, 99 (1954).
Scully, M. O. & Svidzinsky, A. A. The super of superradiance. Science 325, 1510–1511 (2009).
DeVoe, R. G. & Brewer, R. G. Observation of superradiant and subradiant spontaneous emission of two trapped ions. Phys. Rev. Lett. 76, 2049 (1996).
Guerin, W., Araújo, M. O. & Kaiser, R. Subradiance in a large cloud of cold atoms. Phys. Rev. Lett. 116, 083601 (2016).
Goban, A. et al. Superradiance for atoms trapped along a photonic crystal waveguide. Phys. Rev. Lett. 115, 063601 (2015).
Solano, P., Barberis-Blostein, P., Fatemi, F. K., Orozco, L. A. & Rolston, S. L. Super-radiance reveals infinite-range dipole interactions through a nanofiber. Nat. Commun. 8, 1857 (2017).
Jaynes, E. T. & Cummings, F. W. Comparison of quantum and semiclassical radiation theories with application to the beam maser. Proc. IEEE 51, 89 (1963).
Thompson, R. J., Rempe, G. & Kimble, H. J. Observation of normal-mode splitting for an atom in an optical cavity. Phys. Rev. Lett. 68, 1132 (1992).
Boca, A. et al. Observation of the vacuum Rabi spectrum for one trapped atom. Phys. Rev. Lett. 93, 233603 (2004).
Maunz, P. et al. Normal-mode spectroscopy of a single-bound-atom-cavity system. Phys. Rev. Lett. 94, 033002 (2005).
Tavis, M. & Cummings, F. W. Exact solution for an N-molecule-radiation-field Hamiltonian. Phys. Rev. 170, 379 (1968).
Kaluzny, Y., Goy, P., Gross, M., Raimond, J. M. & Haroche, S. Observation of self-induced Rabi oscillations in two-level atoms excited inside a resonant cavity: the ringing regime of superradiance. Phys. Rev. Lett. 51, 1175 (1983).
Raizen, M. G., Thompson, R. J., Brecha, R. J., Kimble, H. J. & Carmichael, H. J. Normal-mode splitting and linewidth averaging for two-state atoms in an optical cavity. Phys. Rev. Lett. 63, 240 (1989).
Ruddell, S. K., Webb, K. E., Herrera, I., Parkins, A. S. & Hoogerland, M. D. Collective strong coupling of cold atoms to an all-fiber ring cavity. Optica 4, 576 (2017).
Serafini, A., Mancini, S. & Bose, S. Distributed quantum computation via optical fibers. Phys. Rev. Lett. 96, 010503 (2006).
Yang, C.-P., Su, Q.-P. & Nori, F. Entanglement generation and quantum information transfer between spatially-separated qubits in different cavities. New J. Phys. 15, 115003 (2013).
Koshino, K. et al. Theory of deterministic entanglement generation between remote superconducting atoms. Phys. Rev. Appl. 7, 064006 (2017).
Cao, Y., Wang, G. C., Liu, H. D. & Sun, C. F. Implementation of a Toffoli gate using an array of coupled cavities in a single step. Sci. Rep. 8, 5813 (2018).
Kimble, H. J. The quantum internet. Nature 453, 1023–1030 (2008).
Reiserer, A. & Rempe, G. Cavity-based quantum networks with single atoms and optical photons. Rev. Mod. Phys. 87, 1379–1418 (2015).
Pellizzari, T., Gardiner, S. A., Cirac, J. I. & Zoller, P. Decoherence, continuous observation, and quantum computing: a cavity QED model. Phys. Rev. Lett. 75, 3788–3791 (1995).
Cirac, J. I., Zoller, P., Kimble, H. J. & Mabuchi, H. Quantum state transfer and entanglement distribution among distant nodes in a quantum network. Phys. Rev. Lett. 78, 3221–3224 (1997).
Ritter, S. et al. An elementary quantum network of single atoms in optical cavities. Nature 484, 195–200 (2012).
Törmä, P. Transitions in quantum networks. Phys. Rev. Lett. 81, 2185–2189 (1998).
Hartmann, M. J., Brandao, F. G. S. L. & Plenio, M. B. Strongly interacting polaritons in coupled arrays of cavities. Nat. Phys. 2, 849–855 (2006).
Greentree, A. D., Tahan, C., Cole, J. H. & Hollenberg, L. C. L. Quantum phase transitions of light. Nat. Phys. 2, 856–861 (2006).
Rossini, D. & Fazio, R. Mott-insulating and glassy phases of polaritons in 1D arrays of coupled cavities. Phys. Rev. Lett. 99, 186401 (2007).
Angelakis, D. G., Santos, M. F. & Bose, S. Photon-blockade-induced Mott transitions and XY spin models in coupled cavity arrays. Phys. Rev. A 76, 031805(R) (2007).
Cho, J., Angelakis, D. G. & Bose, S. Fractional quantum Hall state in coupled cavities. Phys. Rev. Lett. 101, 246809 (2008).
Irish, E. K., Ogden, C. D. & Kim, M. S. Polaritonic characteristics of insulator and superfluid states in a coupled-cavity array. Phys. Rev. A 77, 033801 (2008).
Hartmann, M. J., Brandão, F. G. S. L. & Plenio, M. B. Quantum many-body phenomena in coupled cavity arrays. Laser Photon. Rev. 2, 527 (2008).
Kato, S. & Aoki, T. Strong coupling between a trapped single atom and an all-fiber cavity. Phys. Rev. Lett. 115, 093603 (2015).
Kien, F. Le, Balykin, V. I. & Hakuta, K. State-insensitive trapping and guiding of cesium atoms using a two-color evanescent field around a subwavelength-diameter fiber. J. Phys. Soc. J. 74, 910 (2005).
Vetsch, E. et al. Optical interface created by laser-cooled atoms trapped in the evanescent field surrounding an optical nanofiber. Phys. Rev. Lett. 104, 203603 (2010).
Lacroûte, C. et al. A state-insensitive, compensated nanofiber trap. New J. Phys. 14, 023056 (2012).
Goban, A. et al. Demonstration of a state-insensitive, compensated nanofiber trap. Phys. Rev. Lett. 109, 033603 (2012).
Béguin, J.-B. et al. Generation and detection of a sub-Poissonian atom number distribution in a one-dimensional optical lattice. Phys. Rev. Lett. 113, 263603 (2014).
Meng, Y., Dareau, A., Schneeweiss, P. & Rauschenbeutel, A. Near-ground-state cooling of atoms optically trapped 300 nm away from a hot surface. Phys. Rev. X 8, 031054 (2018).
Acknowledgements
This work was supported by JST CREST Grant Number JPMJCR1771, JSPS KAKENHI Grant Numbers 16H01055, 18H04293, 18H05207, JST PRESTO Grant Number JPMJPR1662, Japan, and Institute for Advanced Theoretical and Experimental Physics, Waseda University. S.P. acknowledges support from the Marsden Fund of the Royal Society of New Zealand (Contract No. UOA1328).
Author information
Authors and Affiliations
Contributions
T.A. planned the research. S.K., K.S., S.M., and X.H. constructed the setup. S.K. performed the experiment. N.N. and S.P. formulated the theory. S.K., N.N., S.P., and T.A. analyzed the data. All authors discussed the results. S.K., S.P., and T.A. prepared the manuscript. All work was supervised by T.A.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Journal peer review information: Nature Communications would like to thank the anonymous reviewers for their contribution to the peer review work. Peer review reports are available.
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Kato, S., Német, N., Senga, K. et al. Observation of dressed states of distant atoms with delocalized photons in coupled-cavities quantum electrodynamics. Nat Commun 10, 1160 (2019). https://doi.org/10.1038/s41467-019-08975-8
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-019-08975-8
This article is cited by
-
Demonstration of a MOT in a sub-millimeter membrane hole
Scientific Reports (2021)
-
Atoms in separated resonators can jointly absorb a single photon
Scientific Reports (2020)
-
Measurement and simulation of atomic motion in nanoscale optical trapping potentials
Applied Physics B (2020)
-
Fabrication of optical nanofibre-based cavities using focussed ion-beam milling: a review
Applied Physics B (2020)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.