Abstract
Quantum memories are essential for quantum information processing. Techniques have been developed for quantum memory based on atomic ensembles. The atomic memories through optical resonance usually suffer from the narrow-band limitation. The far off-resonant Raman process is a promising candidate for atomic memories due to broad bandwidths and high speeds. However, to date, the low memory efficiency remains an unsolved bottleneck. Here, we demonstrate a high-performance atomic Raman memory in 87Rb vapour with the development of an optimal control technique. A memory efficiency of above 82.0% for 6 ns~20 ns optical pulses is achieved. In particular, an unconditional fidelity of up to 98.0%, significantly exceeding the no-cloning limit, is obtained with the tomography reconstruction for a single-photon level coherent input. Our work marks an important advance of atomic memory towards practical applications in quantum information processing.
Similar content being viewed by others
Introduction
Quantum memory is a necessary component for quantum communications and quantum computing. A practical quantum memory should be efficient, low-noise, broadband, and as simple as possible to operate1,2,3,4,5,6. Using several approaches, including electromagnetically induced transparency (EIT), gradient echo memory (GEM), the off-resonant Faraday effect, and far off-resonant Raman memory, optical memory has been demonstrated in cold atomic ensembles2,7,8,9, atomic vapors10,11,12,13,14, and solids15,16,17,18,19. Hsiao et al.20 reported a 92.0% memory efficiency for a coherent light pulse in a cold atomic ensemble using EIT. Hosseini et al.21 used GEM to realize a 78% memory efficiency for weak coherent states with 98% fidelity. Polzik’s group12 demonstrated a quantum memory with a fidelity of 70% based on the off-resonant Faraday effect. These examples12,20,21 successfully demonstrated the capability to store optical states with high efficiency and/or fidelity exceeding the classical limit22,23,24 and sub-megahertz bandwidths. However, the bandwidth is important for the practical application of quantum memory25. Quantum sources with bandwidth at the GHz level have been used in long-distance quantum communication26,27 and quantum computers28.
Unlike these protocols, far-off-resonant atomic Raman memory can store short-time pulses corresponding to high bandwidths and can operate at high speeds. In addition, the far-off-resonance characteristic makes the atomic Raman memory10,29,30 robust against inhomogeneities in the ensemble and facilitates controlling the frequency of the output state. All of these properties indicate that atomic Raman memory has great potential in practical quantum information processing. The first experimental realization of an atomic Raman memory was demonstrated29 in 2010. This indeed represented significant progress in the field of Raman memory, but the limitations with low efficiency (<30%) and significant noise from the spontaneous four-wave mixing (FWM) process persist. Recently, Raman memory using photonic polarized entanglement30 was reported in a cold atomic ensemble with a fidelity of 86.9 ± 3.0%, but still an efficiency of only 20.9 ± 7.7%. An efficiency exceeding 50% and a fidelity exceeding 2/3 are necessary to store and retrieve an optical state within the no-cloning regime without post-selection22,23,24,31. Therefore, so far, low efficiency has appeared to exclude the broadband Raman memory as an unconditional quantum memory.
In this paper, we present an optimal control technique where the atomic vapor is performed a real-time optimal response on an input signal pulse. With a 87Rb atomic vapor in paraffin-coated cell at T = 78.5 °C, we achieve a Raman quantum memory on a coherent input of 6–20 ns duration with above 82.0% memory efficiency, and more importantly, with 98% unconditional fidelity at single photon level (n ≈ 1).
Results
Experimental setup
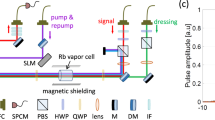
The experimental setup and atomic levels are depicted in Fig. 1. The 87Rb atomic vapor in the paraffin-coated glass cell is the core component of the current Raman memory. The atomic cell is 10.0 cm long, has a diameter of 1.0 cm, and is heated to 78.5 °C. Our Raman memory starts with a large ensemble of atoms that were initially prepared in the |m〉 = |52S1/2, F = 2〉 state by a 44-μs-long optical pumping pulse (OP). Then, the input signal pulse Ein is stored as atomic spin excitation SW induced by the strong off-resonant write pulse (W) with the Rabi frequency ΩW(t) and detuning ΔW. After a certain delay τ, the atomic excitation can be retrieved into optical state ER by the strong off-resonant read pulse (R) with the Rabi frequency ΩR(t) and detuning ΔR. The waists of the laser beams (W, R, and Ein) are all 600 μm. The two strong driving beams, W and R, can be generated by the same or different semiconductor lasers (Toptica, DLPro + Boosta) and are coupled into the same single-mode fiber. Their intensities and temporal shapes are controlled by acousto-optic modulators (AOMs). The input Ein signal comes from another semiconductor laser (Toptica, DLPro) phase-locked on the W laser. The temporal shape is controlled by a Pockels cell (Conoptics, Model No. 360-80). The shortest pulse duration of the Pockels cell is 6 ns. The W and Ein fields are two-photon resonant and spatially overlapped after passing through a Glan polarizer with 94% spatial visibility in the atomic vapor. The output signals can be separated from the strong driving pulses by another Glan polarizer with an extinction ratio of 40 dB, and detected, respectively, by intensity detection to calibrate the memory efficiency, by homodyne detection combining with tomography reconstruction to determine the memory fidelity, and by single-photon detection to analyze the excess noise in storage process. The total optical transmittance including the atomic cell and all optical elements in homodyne detection is about 89%. The four etalons with 33% transmission can filter the leaked driving photons at 115 dB.
Raman memory. a Schematic, atomic energy levels and frequencies of the optical fields. |g, m〉: hyperfine levels |52S1/2, F = 1, 2〉; |e1〉 and |e2〉: excited states |52P1/2, F = 2〉 and |52P3/2〉. W write field, Ein input signal, Eleak leaked signal, SW collective atomic spin wave, R read field, ER retrieved signal. b Experimental setup. The polarizations of the weak signal beams, Ein and ER, are perpendicular to the strong driving beams, W and R. The signals can be detected by homodyne detection. OP optical pumping laser, SMF single-mode fiber, BS beam splitter, PZT piezoelectric transducer. D1 photo-detector, D2 and D3 photo-diode, D4 single-photon detector, FM1 and FM2 flip mirror. The flip mirrors FM1,2 allow alternative selection of detections via intensity, homodyne, and single photon. Intensity detection is chosen to calibrate the memory efficiency by flipping FM1 up, homodyne detection combining with tomography reconstruction to determine the memory fidelity by flipping FM1 down and FM2 up, and single-photon detection to measure and analyze the excess noise in storage process by flipping FM1,2 both down
Efficiency
The Raman write process is a type of coherent absorption induced by a strong write pulse. As shown in Fig. 2a, when the write pulse is switched off, owing to the far-off-resonant frequency, almost 100% of the Ein pulse passes through the atomic vapor. Below, we use the total energy of such an Ein pulse to normalize the write and retrieve efficiencies. When the write pulse is turned on, part of the energy of the Ein pulse is converted coherently as the atomic spin wave SW(z) near the two-photon resonance frequency. The rest of the Ein energy passes through the atoms as Eleak, as shown in Fig. 1a. The full width at half maximum (FWHM) of the absorption spectrum is approximately 100 MHz, as shown in Fig. 2a.
Efficient Raman memory. a Absorption rate of the weak input-signal pulse as a function of the Raman detuning frequency. ΔW is fixed at 3.0 GHz. The input signal pulse is 10 ns long. b Theoretical efficiency as a function of the energy of the strong control pulse. The input optical pulse is a 10 ns near-square pulse. All optical fields detune 3.0 GHz from atomic transition and the optical depth d = 1100 (see Methods section for details). In the write process, the efficiency is always much smaller than 1.0 when using a non-optimal write pulse (10 ns Gaussian shape), but it can approach 1.0 with the optimal write pulse when the write pulse is larger than 1.5 nJ. In the read process, the curves with Gaussian and square read pulses coincide with each other. The retrieval efficiency is waveform-independent and increases with the energy of the read pulse until approaching 1.0. c Temporal modes of the strong driving (blue, experimental shape of write pulse \(W_{{\mathrm{exp}}}^{{\mathrm{opt}}}\), read pulse R; dashed purple, theoretical shape of optimal write pulse \(W_{{\mathrm{theory}}}^{{\mathrm{opt}}}\)), input signal (black, Ein), leaked signal (orange, Eleak), and output signal (red, ER) pulses. d Waveform of the leaked signal with the \(W_{{\mathrm{exp}}}^{{\mathrm{opt}}}(t)\) (orange circle) and \(W_{{\mathrm{exp}}}^{{\mathrm{opt}}}(t + 1ns)\) (gray square) write pulse. The lines are the corresponding theoretical fits. e Storage efficiency (ηW) and retrieval efficiency (ηR) as function of the energy of the driving pulse (W and R) with the shape of \(W_{{\mathrm{exp}}}^{{\mathrm{opt}}}\) and R as shown in (c). Square represents experimental data and solid line is theoretical fitting. The error bars correspond to one standard deviation caused by the statistical uncertainty of measurement. f The write-in efficiency as a function of the width of the Ein pulse
According to the theoretical analysis in ref. 32, the spatial-distributed atomic spin wave in a far-off-resonant Raman write process is given by
where \(q(z,t) = i\frac{{\sqrt d }}{{{\mathrm{\Delta }}_{\mathrm{W}}}}{\mathrm{\Omega }}_{\mathrm{W}}^ \ast (t)e^{i\frac{{dz + h(t,t_{\mathrm{W}})}}{{{\mathrm{\Delta }}_{\mathrm{W}}}}}J_0\left( {\frac{{2\sqrt {h(t,t_{\mathrm{W}})dz} }}{{{\mathrm{\Delta }}_{\mathrm{W}}}}} \right)\), tW is the duration of the write process, d is the optical depth of atomic ensemble, and \(h(t,t_{\mathrm{W}}) = {\int}_t^{t_{\mathrm{W}}} \left| {{\mathrm{\Omega }}_{\mathrm{W}}(t^\prime )} \right|^2dt^\prime\) with t′ is the integration variable from t to tW in the co-moving frame. Eq. (1) is an iterative function that is determined by the matching between the temporal shapes of the input Ein(t) and the write pulse ΩW(t)32,33,34. Therefore, to achieve efficient conversion, it is crucial to perform real-time control on ΩW(t) or Ein(t) to make the atoms coherently absorb as much energy Ein(t) as possible. The optimal control of Ein(t) has been used to achieve efficient memory in an EIT-based process20, where the shape of the input signal Ein(t) was adjusted according to atomic memory system. Here, we prefer the dynamical control ΩW(t) because a quantum memory system should have the ability to store and preserve quantum information of an input optical signal with an arbitrary pulse shape. To obtain the optimal ΩW(t), denoted \(\Omega _{\mathrm{W}}^{{\mathrm{opt}}}(t)\), we first use the iterative methods mentioned in ref. 32 to calculate the optimal spin wave, corresponding to the minimum Eleak. Then, the optimal spin wave establishes a one-to-one correspondence between Ein(t) and \(\Omega _{\mathrm{W}}^{{\mathrm{opt}}}(t)\) via Eq. (1). Thus, for any given shape of Ein(t), \(\Omega _{\mathrm{W}}^{{\mathrm{opt}}}(t)\) can be obtained from Eq. (1) via the optimal spin wave. Moreover, the corresponding optimal efficiency \(\eta _{\mathrm{W}}^{{\mathrm{opt}}}\) depends only on the optical depth d and the total energy of the write pulse. Figure 2b shows the theoretical efficiencies as the function of the energy of the strong driven pulses. Using a 10 ns near-square pulse as the input Ein, the write efficiency with \(\Omega _{\mathrm{W}}^{{\mathrm{opt}}}(t)\) is approximately equal to 1 when the energy of a write pulse with 10 ns duration is larger than 1.5 nJ, while the maximum write-in efficiency with a non-optimized ΩW(t) (a 10 ns Gaussian-shaped ΩW(t) is used in Fig. 2) is much smaller than one. In the read process (see Fig. 1), the spin wave SW(z) is retrieved back to the optical field ER(t) by the read pulse ΩR(t). Unlike ηW, the retrieval efficiency ηR is independent of the temporal waveform32, and a read pulse whose duration is 10 ns with strong power but without temporal optimization is sufficient for ηR ~ 1. This can be seen in Fig. 2b. ηR increases with the total energy of the read pulse, whether Gaussian or square-shaped until ηR ~ 1. Thus, with the above optimal control on ΩW(t), the total efficiency of the Raman memory process is ηT = ηW × ηR ~ 1 in principle.
Here, we experimentally demonstrate a break of the efficiency in Raman memory with dynamic control over the temporal shape of the write pulse. In the experiment, the given Ein pulse is mapped in a forward-retrieval configuration. We derive \(\Omega _{\mathrm{W}}^{{\mathrm{opt}}}(t)\) using the iteration-based optimization strategy based on the given short Ein(t) pulse and experimentally control the temporal profile of the write pulse by using an intensity modulator (here, an AOM). The theoretical shape of optimal write pulse \(W_{{\mathrm{theory}}}^{{\mathrm{opt}}}\) and the experimentally-optimized shape \(W_{{\mathrm{exp}}}^{{\mathrm{opt}}}\) are given in Fig. 2c. The experimental shape is much longer than the theoretical one before the Ein pulse is turned on due to the limitation of the bandwidth of our intensity modulator, but two curves match well within the Ein duration effectively guaranteed high write-in efficiency. Furthermore, to show the definite improvement of optimization control, two write pulses are given, the optimal \(W_{{\mathrm{exp}}}^{{\mathrm{opt}}}(t)\) and an optimal write pulse delayed by 1.0 ns, \(W_{{\mathrm{exp}}}^{{\mathrm{opt}}}\left( {t + 1\,{\mathrm{ns}}} \right)\). The corresponding leaked optical pulses and the theoretical fits are shown in Fig. 2d. The leaked energy for the sub-optimal curve is twice that for the optimal one. Through the optimal control, the leaked energy of the input signal is greatly reduced. The storage efficiency ηW, calculated by \((\overline N _{E_{{\mathrm{in}}}} - \overline N _{E_{{\mathrm{leak}}}})/\overline N _{E_{{\mathrm{in}}}}\), reaches ~84% when the atomic temperature T is 78.5 °C and the power of the write pulse is 10.6 nJ (Fig. 2e). Such high a write-in efficiency can be achieved when the signal duration changes from 6 to 20 ns, and ηW always remains above 83.5% by optimal control, as shown in Fig. 2f. The retrieval efficiency ηR, calculated by \(\left( {\overline N _{E_{\mathrm{R}}}/(\overline N _{E_{{\mathrm{in}}}} - \overline N _{E_{{\mathrm{leak}}}})} \right)\), can reach 98.5% when the read laser is 10.6 nJ, with 3.0 GHz frequency detuning (Fig. 2e). Here, Ein, Eleak, and ER pulses are all measured through the intensity detection as shown in Fig. 1b. The optical paths for these pulses are arranged in the way that they are subject to the same optical losses. This allows the storage efficiency to be calibrated to characterize the atomic memory process alone. The total memory efficiency, ηT = ηW × ηR, is above 82.0% when the input signal pulse contains an average number of photons ranging from 0.4 to 104; thus, this Raman memory is a good linear absorber. The 82.0% memory efficiency is the best performance reported to date for Raman-based memory and far exceeds the no-cloning limit.
In principle, ηT = ηW × ηR ~ 1. With ηR = 98.5%, further improvement of ηT mainly depends on ηW, which could be improved by better experimental conditions. According to our theoretical analysis, larger atomic optical depth through increasing the atomic temperature or lengthening the cell could lead to about 3% improvement. Better temporal-mode control on the W pulse may bring about 6% increase. Improving the spatial-mode match between the Ein and W beams can contribute about 5%.
Fidelity
Fidelity is the ultimate performance criterion for quantum memory and reflects the maintenance of the quantum characteristics of the optical signal during the memory process. At the few-photon level, fidelity is readily degraded by excess noise and is mainly caused by the FWM process10 and spontaneous emission. Spontaneous noise comes from the spontaneous Raman scattering between the strong write pulse and the atoms populating the |g〉 = |52S1/2, F = 1〉 state. Having fewer |g〉 atoms helps suppress the spontaneous excess noise. In our paraffin-coated cell, more than 98% of the atoms populate the |m〉 state. The spontaneous emission noise intensity is measured by determining the photon number using the single-photon detection as shown in Fig. 1b when the Ein pulse is turned off. On average, the spontaneous noise is approximately 0.02 photons per memory process at the end of the atomic cell for two strong driving pulses with a power of 10.6 nJ at a detuning frequency of 3.0 GHz. The FWM excess noise is mainly attributed to anti-Stokes (ASFWM, with same frequency of ER) and Stokes (SFWM) photons with the same intensity. We can deduce the proportion of ASFWM in retrieved ER pulse by measuring the intensity of SFWM using single-photon detection. Our results show that the ASFWM noise is less than 10% in ER. Such low excess noise effectively guarantees the fidelity of the quantum memory process.
To achieve the fidelity performance of the current Raman quantum memory, we measure the fidelity using the equation \(F = \left| {Tr\left( {\sqrt {\sqrt {\rho _{{\mathrm{in}}}} \rho _{{\mathrm{out}}}\sqrt {\rho _{{\mathrm{in}}}} } } \right)} \right|^2\)35, where ρin and ρout are the reconstructed density matrices of Ein and ER, respectively. We record the quadrature amplitudes of the Ein and ER signals using homodyne measurement, and we then reconstruct the density matrices by tomographic reconstruction36. The setup used for homodyne detection is shown in Fig. 1b. To stabilize the phase difference between the Ein and ER pulses and simplify the homodyne setup, the write and read pulses are generated by the same laser and are controlled using one intensity modulator. In the measurement, the two weak signals, Ein and ER, are both short pulses. Matching the temporal modes of short pulses is difficult. Therefore, we use a strong continuous laser beam with the same frequency as the signal pulses Ein and ER as the local oscillator for homodyne detection (the detailed strategy can be found in refs. 36,37). We recorded 105 sets of quadrature amplitudes of the Ein and ER pulses while varying the phase of the local oscillator between 0 and 2π by scanning the piezoelectric transducer, multiplying the quadrature amplitudes of each pulse by the temporal shapes of the corresponding signals, and finally, integrating the product over the signal pulse duration. The temporal shape functions of the Ein and ER pulses are obtained by pointwise variance method. The integrated quadrature amplitude, which is normalized with the vacuum, as a function of the local oscillator phase is shown in Fig. 3a, where the mean number of photons contained in the Ein pulse is 7.9. The phase of the retrieved ER signal pulse closely follows that of the input Ein pulse. Insets in Fig. 3a are the probability distributions of amplitude quadratures of the Ein and ER pulses showing good Gaussian distributions.
Fidelity of the Raman memory. a Quadrature amplitudes of the input and output signal pulses at an average of 7.9 photons/pulse. Insets are the probability distributions of the Ein and ER quadrature values at the indicated phase. The density matrices of the input and output signal pulses at 4.2 (b) and 0.76 (c) photons/pulse on average. d Fidelity as a function of the number of photons contained in the input signal pulse. The red squares show the experimental data, and the black line shows the theoretical result. The error bars correspond to one standard deviation caused by the measurement noise
The density matrix elements of the Ein and ER pulses are obtained based on the quadrature-amplitude results using the maximum-likelihood reconstruction method36,38. Then on the basis of the diagonal density matrix elements, the photon distributions of the input and output pulses can be achieved to calculate the average photon numbers. The results are plotted in Fig. 3b, c, with the input pulses containing, on average, 4.2 and 0.76 photons, corresponding to unconditional fidelities of 0.915 and 0.98, respectively. The fidelities significantly exceed the no-cloning limit, indicating that the current Raman memory is a quantum-memory process and does not introduce significant excess noise during the memory process.
As mentioned above, the current Raman memory is a good linear absorber and allows the storage and retrieval of coherent optical signals at the single-photon level for up to 104 photons with the same memory efficiency. Unlike the efficiency, the unconditional fidelity of the quantum memory of the coherent field is related to the average photon number contained in the input signal \(\left( {\overline N _{E_{{\mathrm{in}}}}} \right)\) and efficiency (ηT) by \(F = 1/\left[ {1 + \overline N _{E_{{\mathrm{in}}}}(1 - \sqrt {\eta _{\mathrm{T}}} )^2} \right]\)24, which shows that if ηT < 1, the fidelity will rapidly decrease with \(\overline N _{E_{{\mathrm{in}}}}\) owing to the worse overlap between ρin and ρout. In Fig. 3d, the fidelity is shown as a function of \(\overline N _{E_{{\mathrm{in}}}}\) with ηT = 82.0%. The experimental F value is slightly smaller than the theoretical F value because of the excess noise in the experiment. F exceeds the no-cloning limit22,23,24 at \(\overline N _{E_{{\mathrm{in}}}} \le 49\) in the current Raman memory process.
Bandwidth and coherence time
Far off-resonant Raman memory is a genuine broadband memory. The ability to store and retrieve broadband pulses was successfully demonstrated in ref. 29, where a bandwidth larger than 1 GHz of the retrieved signal was obtained using a 300 ps and 4.8 nJ read pulse. In a practical Raman memory, the bandwidth is generated dynamically by the strong driving pulses. In Fig. 2, the shortest Ein pulse has a FWHM of 6 ns and a bandwidth of 170 MHz. The FWHM of the ER signal pulse which mainly depends on the rise time of the R pulse is 13 ns, corresponding to a bandwidth of 77 MHz. The bandwidth in the current memory is dozens or hundreds of times larger than the values reported based on the EIT20, Faraday12, and GEM21 approaches, thus demonstrating the broadband memory ability of the current quantum memory scheme.
In our experiment, the memory bandwidth is limited by the currently available intensity modulators (AOM and Pockels cell) and the corresponding electronics controllers (arbitrary wave generators) in our lab. The duration limit of the Pockels cell is 6 ns. As shown in Fig. 2f, the write-in efficiencies remain above 83.5% as the signal duration is larger than 6 ns. Shorter Ein and ER pulses corresponding larger bandwidths need faster intensity modulators and electronics controllers.
The decoherence time, which is another essential criterion for good quantum memory, is measured to be approximately 1.1 μs. The delay-bandwidth product at 50% memory efficiency, an appropriate figure of merit, is defined as the ratio of the memory time to the duration of the signal pulse and is 86 in this work. In the present atomic system, the decoherence time is mainly limited by the atomic diffusion out of the laser beam39. The delay-bandwidth product could be increased to ~103 by using a shorter signal pulse and an anti-relaxation-coated cell with the same diameter of the millimeter order as the laser beams. This can lead to a typical decoherence time of approximately several microseconds40.
Discussion
In summary, we have demonstrated a high-performance broadband quantum optical memory via pulse-optimized Raman memory in free space. The 82.0% memory efficiency is the highest value obtained to date for far-off-resonant Raman memory. The unconditional fidelity of 98% for an input pulse containing an average of approximately one photon significantly exceeds the classical limit. The 77 MHz bandwidth of the current memory is dozens or hundreds of times larger than the reported bandwidths for memories based on the EIT, Faraday, and GEM approaches. The delay-bandwidth product at 50% memory efficiency is 86. These attractive properties demonstrate that the Raman memory is a high-performance broadband quantum memory. Additionally, our memory is implemented in an atomic vapor system that can be easily operated and could become the core of a scalable platform for quantum information processing, long-distance quantum communication and quantum computation.
Methods
Optical depth
The formula of the optical depth is d = g2NL/(γc)32, where g is the atom-field coupling constant, N is the number of atoms, L is the length of atomic ensemble, γ is the decay rate of the |e1〉, and c is the speed of light. The values of these parameters are: g = 6.79 × 104 s−1 and γ = 3.613 × 107 s−1 for 87Rb D1 line, L = 10 cm, c = 3 × 108 m ⋅ s−1. The number of atoms varies with the temperature of the vapor cell. According to fluorescence measurement in experiment41, N ~ 2.58 × 1010 at the cell temperature of 78.5 °C.
Data availability
The data that support the findings of this study are available from the corresponding authors upon reasonable request.
References
Fleischhauer, M. & Lukin, M. D. Dark-state polaritons in electromagnetically induced transparency. Phys. Rev. Lett. 84, 5094–5097 (2000).
Liu, C., Dutton, Z., Behroozi, C. H. & Hau, L. V. Observation of coherent optical information storage in an atomic medium using halted light pulses. Nature 409, 490–493 (2001).
Phillips, D. F., Fleischhauer, A., Mair, A., Walsworth, R. L. & Lukin, M. D. Storage of light in atomic vapor. Phys. Rev. Lett. 86, 783–786 (2001).
Mair, A., Hager, J., Phillips, D. F., Walsworth, R. L. & Lukin, M. D. Phase coherence and control of stored photonic information. Phys. Rev. A 65, 031802(R) (2002).
Honda, K. et al. Storage and retrieval of a squeezed vacuum. Phys. Rev. Lett. 100, 093601 (2008).
Appel, J., Figueroa, E., Korystov, D., Lobino, M. & Lvovsky, A. I. Quantum memory for squeezed light. Phys. Rev. Lett. 100, 093602 (2008).
Zhao, R. et al. Long-lived quantum memory. Nat. Phys. 5, 100–104 (2008).
Bao, X.-H. et al. Efficient and long-lived quantum memory with cold atoms inside a ring cavity. Nat. Phys. 8, 517–521 (2012).
Parniak, M. et al. Wavevector multiplexed atomic quantum memory via spatially-resolved single-photon detection. Nat. Commun. 8, 2140 (2017).
Reim, K. F. et al. Single-photon-level quantum memory at room temperature. Phys. Rev. Lett. 107, 053603 (2011).
Hosseini, M., Sparkes, B. M., Campbell, G., Lam, P. K. & Buchler, B. C. High efficiency coherent optical memory with warm rubidium vapour. Nat. Commun. 2, 174 (2011).
Julsgaard, B., Sherson, J., Cirac, J. I., Fiurasek, J. & Polzik, E. S. Experimental demonstration of quantum memory for light. Nature 432, 482–486 (2004).
van der Wal, C. H. et al. Atomic memory for correlated photon states. Science 301, 196–200 (2003).
Pu, Y.-F. et al. Experimental realization of a multiplexed quantum memory with 225 individually accessible memory cells. Nat. Commun. 8, 15359 (2017).
Longdell, J. J., Fraval, E., Sellars, M. J. & Manson, N. B. Stopped light with storage times greater than one second using electromagnetically induced transparency in a solid. Phys. Rev. Lett. 95, 063601 (2005).
Chaneliere, T., Ruggiero, J., Bonarota, M., Afzelius, M. & Le Gouët, J.-L. Efficient light storage in a crystal using an atomic frequency comb. New J. Phys. 12, 023025 (2010).
Bigelow, M. S., Lepeshkin, N. N. & Boyd, R. W. Superluminal and slow light propagation in a room-temperature solid. Science 301, 200–202 (2003).
Clausen, C. et al. Quantum storage of photonic entanglement in a crystal. Nature 469, 508–511 (2011).
England, D. G. et al. Storage and retrieval of THz-bandwidth single photons using a room-temperature diamond quantum memory. Phys. Rev. Lett. 114, 053602 (2015).
Hsiao, Y.-F. et al. Highly efficient coherent optical memory based on electromagnetically induced transparency. Phys. Rev. Lett. 120, 183602 (2018).
Hosseini, M., Campbell, G., Sparkes, B. M., Lam, P. K. & Buchler, B. C. Unconditional room-temperature quantum memory. Nat. Phys. 7, 794–798 (2011).
Grosshans, F. & Grangier, P. Quantum cloning and teleportation criteria for continuous quantum variables. Phys. Rev. A 64, 010301 (2001).
Hétet, G., Peng, A., Johnsson, M. T., Hope, J. J. & Lam, P. K. Characterization of electromagnetically-induced-transparency-based continuous-variable quantum memories. Phys. Rev. A 77, 012323 (2008).
He, Q. Y., Reid, M. D., Giacobino, E., Cviklinski, J. & Drummond, P. D. Dynamical oscillator-cavity model for quantum memories. Phys. Rev. A 79, 022310 (2009).
Simon, C. et al. Quantum memories. Eur. Phys. J. D 58, 1–22 (2010).
Halder, M. et al. High coherence photon pair source for quantum communication. New J. Phys. 10, 023027 (2008).
Rakher, M. T. et al. Simultaneous wavelength translation and amplitude modulation of single photons from a quantum dot. Phys. Rev. Lett. 107, 083602 (2011).
Lounis, B. & Orrit, M. Single-photon sources. Rep. Prog. Phys. 68, 1129–1179 (2005).
Reim, K. F. et al. Towards high-speed optical quantum memories. Nat. Photonics 4, 218–221 (2010).
Ding, D.-S. et al. Raman quantum memory of photonic polarized entanglement. Nat. Photonics 9, 332–338 (2015).
Varnava, M., Browne, D. & Rudolph, T. Loss tolerance in one-way quantum computation via counterfactual error correction. Phys. Rev. Lett. 97, 120501 (2006).
Gorshkov, A. V., André, A., Lukin, M. D. & Sørensen, A. S. Photon storage in Λ-type optically dense atomic media. II. Free-space model. Phys. Rev. A 76, 033805 (2007).
Nunn, J. et al. Mapping broadband single-photon wave packets into an atomic memory. Phys. Rev. A 75, 011401(R) (2007).
Wasilewski, W. & Raymer, M. G. Pairwise entanglement and readout of atomic-ensemble and optical wave-packet modes in traveling-wave Raman interactions. Phys. Rev. A 73, 063816 (2006).
Nielsen, M. A. & Chuang, I. L. Quantum Computation and Quantum Information. (Cambridge University Press, UK, 2000).
Paris, M. & Řeháček, J. Quantum State Estimation. (Springer-Verlag Berlin Heidelberg, New York, 2004).
MacRae, A., Brannan, T., Achal, R. & Lvovsky, A. I. Tomography of a high-purity narrowband photon from a transient atomic collective excitation. Phys. Rev. Lett. 109, 033601 (2012).
Lvovsky, A. I. Iterative maximum-likelihood reconstruction in quantum homodyne tomography. J. Opt. B: Quantum Semiclass. Opt. 6, S556–S559 (2004).
Camacho, R. M., Vudyasetu, P. K. & Howell, J. C. Four-wave-mixing stopped light in hot atomic rubidium vapour. Nat. Photonics 3, 103–106 (2009).
Klein, M. et al. Slow light in narrow paraffin-coated vapor cells. Appl. Phys. Lett. 95, 091102 (2009).
Zhao, M., Zhang, K. & Chen, L. Q. Determination of the atomic density of rubidium-87. Chin. Phys. B 24, 094206 (2015).
Acknowledgements
This work was supported by the National Key Research and Development Program of China under Grant number 2016YFA0302001, the National Natural Science Foundation of China (Grant numbers 11874152, 91536114, 11474095, 11654005, and 11234003), the Natural Science Foundation of Shanghai (Grant no. 17ZR1442800), and Quantum Information Technology, Shanghai Science and Technology Major Project.
Author information
Authors and Affiliations
Contributions
L.Q.C. and W.Z. planned the experiment and supervised the project. J.G., X.F., P.Y., and Z.Y. performed the experiment. J.G., X.F., and L.Q.C. analyzed the data. L.Q.C., J.G., C.-H.Y., and W.Z. wrote the paper.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Journal peer review information: Nature Communications thanks the anonymous reviewers for their contributions to the peer review of this work.
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Guo, J., Feng, X., Yang, P. et al. High-performance Raman quantum memory with optimal control in room temperature atoms. Nat Commun 10, 148 (2019). https://doi.org/10.1038/s41467-018-08118-5
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-018-08118-5
This article is cited by
-
Fast, noise-free atomic optical memory with 35-percent end-to-end efficiency
Communications Physics (2023)
-
Coherent optical two-photon resonance tomographic imaging in three dimensions
Communications Physics (2023)
-
Anti-relaxation coating-induced velocity-dependent population re-distribution in electromagnetically induced transparency
Applied Physics B (2023)
-
Ancilla-assisted protection of information: application to atom–cavity systems
Quantum Information Processing (2023)
-
Optimizing Raman quantum memory with dynamic phase
Science China Information Sciences (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.