Abstract
H2O2 is a sacrificial reductant that is often used as a hole scavenger to gain insight into photoanode properties. Here we show a distinct mechanism of H2O2 photo-oxidation on haematite (α-Fe2O3) photoanodes. We found that the photocurrent voltammograms display non-monotonous behaviour upon varying the H2O2 concentration, which is not in accord with a linear surface reaction mechanism that involves a single reaction site as in Eley–Rideal reactions. We postulate a nonlinear kinetic mechanism that involves concerted interaction between adions induced by H2O2 deprotonation in the alkaline solution with adjacent intermediate species of the water photo-oxidation reaction, thereby involving two reaction sites as in Langmuir–Hinshelwood reactions. The devised kinetic model reproduces our main observations and predicts coexistence of two surface reaction paths (bi-stability) in a certain range of potentials and H2O2 concentrations. This prediction is confirmed experimentally by observing a hysteresis loop in the photocurrent voltammogram measured in the predicted coexistence range.
Similar content being viewed by others
Introduction
Photoelectrochemical (PEC) water splitting is an elegant route to store radiant solar power in chemical bonds by producing hydrogen1. Haematite (α-Fe2O3) is an attractive model material for the photoanode in the PEC cell given its visible light absorption2, abundance, non-toxicity, high catalytic activity for water oxidation3, and, most importantly, stability in alkaline solutions4. Recent advances in haematite photoanodes have led to significant progress in improving their performance, with most of the progress focused on enhancing the photocurrent, reaching over 4 mA cm−2 for champion haematite photoanodes5,6,7,8. The photocurrent records were achieved at electrode potentials of over 1.4 VRHE (Volts vs. the reversible hydrogen electrode)5,6,7,8, which is well above the flat-band potential of haematite photoanodes (0.3−0.4 VRHE)9. Enhancing the photocurrent and reducing the applied bias (potential) are required to compete with the efficiency of PV-powered electrolysis systems10. Achieving these goals would benefit from detailed understanding of the underlying processes that govern the photo-generation, recombination, and charge transfer at the semiconductor electrode|electrolyte interface9,11,12,13,14,15.
PEC reactions, such as water splitting and other fuel production reactions, involve three components that give rise to physicochemical processes spanning a wide range of spatiotemporal scales16,17,18. The first component is the semiconductor photoelectrode, where the light absorption, charge carrier generation, separation and transport toward the photoelectrode|electrolyte interface occur. Material properties that control these processes and competing processes that lead to charge recombination play a central role in the photoelectrode operation and performance. The second component is the electrolyte, which supplies the chemical reactants for the fuel production reaction and maintains the ionic conductivity required to close the electrical circuit between the electrodes. The third component is the photoelectrode|electrolyte interface, where the charge transfer reaction occurs (from electronic charges within the photoelectrode to ionic charges within the electrolyte). All three components are cross-linked by feedback loops that follow matter and charge conservation laws.
The oxygen evolution reaction which occurs at the photoanode|electrolyte interface is a complex four-electron process that requires multiple surface intermediates that facilitate interfacial charge transfer with the reactants from the electrolyte19,20. On the other hand, those intermediates can also serve as recombination centres for photo-generated charge carriers21. Thus, surface intermediates display intriguing and rich dynamics that have a strong influence on the PEC performance of semiconductor electrodes14,22, which on haematite photoanodes are still under debate23,24,25. Numerous experimental and theoretical reports have suggested the existence of a stable Fe = O intermediate species24,25,26. The existence of this intermediate was recently confirmed by operando infrared spectroscopy26. The formation of this long-lived intermediate is the first step in the multi-step water photo-oxidation process on haematite photoanodes26, but it also serves as a centre for recombination of electrons and holes, which results in large overpotential and efficiency losses14,22.
One way of suppressing the effects of surface recombination in order to study bulk processes within the photoanode is through the use of sacrificial reductants, such as H2O227. At high concentrations (typically about 0.5 M), H2O2 serves as a hole scavenger that collects the photo-generated holes much faster than the surface recombination reaction28. Therefore, it provides an upper limit for the bulk-limited photocurrent. Consequently, H2O2 is mostly exploited at high concentrations to gain insights into photoanode properties, such as charge carrier collection and charge transfer efficiencies27, and it is often considered a surrogate substrate to assess the potential effectiveness of water oxidation co-catalysts29,30. However, the mechanism by which H2O2 extracts the photo-generated holes remains elusive. The understanding of this mechanism may lead to rational design of photoanode|electrolyte interfaces and co-catalysts that enhance hole collection and reduce deleterious surface recombination in closely related processes, such as water photo-oxidation.
Here we study the H2O2 photo-oxidation mechanism on a model haematite photoanode. By combining experimental studies at different H2O2 concentrations in alkaline solution together with theoretical modelling of the reaction kinetics, we postulate that the overall H2O2 photo-oxidation reaction, H2O2 + 2 h+ + 2OH−→2H2O + O2, begins with deprotonation of H2O2 to HOO− in the alkaline solution31, followed by adsorption of HOO− ions and interaction with adjacent surface intermediates (Fe = O) of the water photo-oxidation reaction26. Thereby, the H2O2 photo-oxidation reaction involves a concerted interaction of two sites, as in Langmuir–Hinshelwood (LH) reactions32. The H2O2 photo-oxidation reaction competes with the water photo-oxidation reaction for the holes that arrive at the surface33, and for the available surface sites and the intermediate species that facilitate both reactions. The consequences of this competition are unfolded by a nonlinear kinetic model that not only reproduced the experimental observations but also gave rise to unexpected predictions that were subsequently verified by further experiments. Unlike the linear models of water photo-oxidation on haematite that consider a multi-step reaction on a single surface site24,25,26,34,35, as in Eley–Rideal (ER) reactions, our work suggests that splitting the reaction into two sites, as in LH reactions, enabled here by the presence of H2O2 in the electrolyte, gives rise to nonlinear behaviour and facilitates the collection of photo-generated holes by oxidized surface species that help to level the potential of the elementary steps involved in the reaction20. The knowledge gained from this work may explain the behaviour observed for some common water oxidation co-catalysts based on cobalt36,37,38, and be also used to rationally design co-catalysts that facilitate water oxidation via a two-site process20.
In what follows, we first discuss photocurrent vs. potential voltammetry measurements and intensity-modulated photocurrent spectroscopy (IMPS) measurements carried out at different H2O2 concentrations ranging from 0 to 0.5 M in alkaline solution (1 M NaOH in deionized water). Secondly, we model and analyse the underlying surface reactions and calculate the photocurrent as a function of potential and H2O2 concentration. Thirdly, we show that the calculated results qualitatively reproduce the empirical observations and finally, we verify experimentally the model prediction that is related to hysteresis.
Results
PEC measurements
The photocurrent (j) vs. potential (U) voltammograms are shown in Fig. 1a; the measurements were done under white light-emitting diode (LED) illumination of 80 mW cm−2 (see Methods section for details) at H2O2 concentrations ranging from 0 to 500 mM in alkaline solution (1 M NaOH in deionized water). The photocurrent density, j, is the current measured under illumination after subtraction of the dark current (at the same potential), divided by the aperture area of the PEC cell. At low H2O2 concentrations (5 mM), the photocurrent voltammograms display three regions distinguished by their slope, i.e., weak increase in j with increased U up to point (i), rapid increase from point (i) to point (ii), and moderate increase from point (ii) onwards. At higher H2O2 concentrations (10 mM) j increases almost linearly with U, indicating that the flux of photo-generated holes arriving at the surface is proportional to the applied potential. To distinguish the bias-dependent interfacial charge transfer at the photoanode|electrolyte interface from the bias-dependent hole flux from the bulk to the surface, the photocurrent voltammograms were normalized by the photocurrent obtained at the highest H2O2 concentration (500 mM), for which the surface reaction no longer limits the photocurrent27. The normalized photocurrent voltammograms are depicted in Fig. 1b. They display an unexpected non-monotonous behaviour at low H2O2 concentrations (from 1 to 5 mM) wherein the normalized photocurrent first increases at low potentials, secondly decreases at moderate potentials, thirdly exhibits a steep rise at the onset potential around 1.1 VRHE, and finally converges with the water photo-oxidation current at about 1.5 VRHE.
Photocurrent voltammograms and intensity-modulated photocurrent spectra at varied H2O2 concentrations. a Photocurrent density as a function of the applied potential under white LED illumination (80 mW cm−2) at different H2O2 concentrations as indicated in the legend. b Normalized photocurrent voltammograms obtained by dividing the photocurrent voltammograms in a by the photocurrent measured at [H2O2]= 500 mM, j500. Bottom IMPS spectra correspond to: (i) [H2O2]=0 mM, U= 1.05 VRHE, (ii) [H2O2]=0 mM, U= 1.25 VRHE, (iii) [H2O2]= 5 mM, U= 1.05 VRHE, (iv) [H2O2]= 5 mM, U= 1.25 VRHE, (v) [H2O2]= 500 mM, U= 1.05 VRHE, (vi) [H2O2]= 500 mM, U=1.25 VRhe
To shed more light into the photocurrent behaviour at different H2O2 concentrations, IMPS measurements were carried out at potentials and H2O2 concentrations marked by points (i) to (vi) in Fig. 1a, b. The IMPS spectra of the complex photocurrent admittance, Y(ω) = j(ω)/Φ(ω), where ω is the ac frequency and Φ is the light intensity, display two main features: upper (positive imaginary part) and lower (negative imaginary part) semicircles. The diameter of a lower semicircle corresponds to hole flux to the surface, whereas the diameter of the upper semicircle corresponds to surface recombination39. In the absence of H2O2 in the electrolyte, the upper semicircle at low potentials (point (i)) is large, indicating strong surface recombination. Notably, the Y(ω) vanishes when ω → 0, indicating that all photo-generated holes arriving at the surface recombine with electrons such that an increase in light intensity does not lead to an increase in photocurrent. At higher potentials (point (ii)), the upper semicircle shrinks, indicating lower surface recombination as usually observed in haematite photoanodes in alkaline solution (without H2O2) at high potentials39. The spectra obtained at a high H2O2 concentration (500 mM, points (v) and (vi)), display only the lower semicircle, whereas the upper semicircle disappears both at low and high potentials. This indicates that at high concentrations, H2O2 serves as an effective hole scavenger that suppresses surface recombination as expected27. However, at a low H2O2 concentration (5 mM, points (iii) and (iv)) surface recombination is strong at low potentials (point (iii)) and is suppressed at higher potentials (point (iv)), similarly to the situation without H2O2 (points (i) and (ii), respectively). These analogies indicate that in points (iii) and (iv), Y(ω) is dominated by water photo-oxidation rather than by H2O2 photo-oxidation. This implies that at low H2O2 concentrations, the photocurrent below the onset of water photo-oxidation is limited by the supply of H2O2 to the surface.
The transition from H2O2-limited photocurrent at low potentials to H2O2-independent photocurrent at high potentials implies a competition between H2O2 photo-oxidation and water photo-oxidation for the available holes, surface reaction sites and intermediate species33. To test this hypothesis, we examine the effect of light intensity, which controls the photo-generation rate of excess charge carriers (holes), at a low H2O2 concentration of 2.5 mM. The results are shown in Fig. 2. The pronounced nonlinear behaviour observed at high light intensities becomes linear as the light intensity is decreased. This shows that at low light intensity, the photo-generation rate is low enough to enable hole scavenging even at low H2O2 concentrations. Another observation that supports our hypothesis is the saturation of the photocurrent density with increasing light intensities at potentials lower than 1.1 VRHE, which indicates that the photocurrent is limited by H2O2 rather than by the flux of photo-generated holes.
Modelling of the reaction kinetics
The experimental results presented in the previous section suggest that the fate of the photo-generated holes arriving from the bulk (where they are created) to the surface of the photoanode (where they vanish) involves different possible paths: H2O2 photo-oxidation, water photo-oxidation and recombination with electrons (surface recombination). The competition between these paths depends on control parameters such as the H2O2 concentration, light intensity and applied potential, thereby affecting the photocurrent. In order to understand the mechanisms of the respective reactions and the competition between them that determines the fate of the photo-generated holes, and thereby the performance of the photoanode, we construct a kinetic model. Our model extends the water photo-oxidation mechanism presented by Zandi and Hamann26 and Zandi and co-workers40, by adding additional steps that account for H2O2 photo-oxidation. The model yields kinetic equations, which we solve numerically in order to analyse the fate of the photo-generated holes as a function of the control parameters, aiming for qualitative agreement between the calculations and the experimental results in the entire parameter space examined. Since we aim for qualitative rather than quantitative agreement, our model is not so sensitive to the selection of the parameters (rate constants) in the kinetic equations, unlike multi-parametric fitting that aims for quantitative agreement by fitting the unknown parameters to reproduce the experimental results precisely. Instead, the essence of our model is in capturing the nonlinearity of the PEC kinetics that gives rise to the non-trivial behaviour observed in the experimental results presented in Figs. 1, 2. Therefore, the model depends on the phenomenological structure of the nonlinear kinetic equations rather than on the parameters within those equations.
We start with the widely accepted model of water photo-oxidation mechanism on haematite in alkaline solution26,40,41:





where boxed ( ) species correspond to surface intermediates and ki are the respective rate constants. The reaction path from steps (1) to (5) is illustrated on the left side of Fig. 3. According to this mechanism, the water photo-oxidation current is given by the net summation of all the reaction rates, that is, the sum of the forward charge transfer rates (steps (1) and (3)–(5)) minus the backward reaction rate (step (2)). When both reactions (1) and (2) occur successively, their combination forms effectively a surface recombination step. It is noteworthy that steps (1)–(5) give rise to a set of linear kinetic equations, see Model equations and numerical computations in Methods.
) species correspond to surface intermediates and ki are the respective rate constants. The reaction path from steps (1) to (5) is illustrated on the left side of Fig. 3. According to this mechanism, the water photo-oxidation current is given by the net summation of all the reaction rates, that is, the sum of the forward charge transfer rates (steps (1) and (3)–(5)) minus the backward reaction rate (step (2)). When both reactions (1) and (2) occur successively, their combination forms effectively a surface recombination step. It is noteworthy that steps (1)–(5) give rise to a set of linear kinetic equations, see Model equations and numerical computations in Methods.
Next, incorporating the H2O2 photo-oxidation reaction requires accounting for the following observations: (a) At low and intermediate potentials, the photocurrent depends on the H2O2 concentration, whereas at high potentials it coincides with the water photo-oxidation current (without H2O2), see Fig. 1a, b. This suggests that the H2O2 photo-oxidation reaction competes with the water photo-oxidation reaction33. (b) Comparison of the IMPS spectra in points (i) and (iii) in Fig. 1 shows a deviation of the upper semicircle from a perfect shape in the presence of H2O2 in the electrolyte, which suggests that the H2O2 photo-oxidation reaction competes with the recombination reaction (step (2)). (c) Since the stable surface intermediate in the water photo-oxidation reaction is Fe = O26,40,41, it is expected that the competing step in the H2O2 photo-oxidation reaction should involve Fe = O intermediates. (d) In the presence of H2O2 in the electrolyte the photocurrent at low potentials is due to H2O2 photo-oxidation rather than water photo-oxidation. Under these conditions, the Fe = O intermediates are short-lived and the stable surface species is Fe-OH26. Thus, for H2O2 photo-oxidation to occur, an adsorption step that involves the long-lived Fe-OH species is expected to precede the step in which the adions interact with the Fe = O intermediates, as suggested in (c).
Accordingly, we postulate that the water photo-oxidation reaction (steps (1)–(5)) is complemented by the following steps to account for the H2O2 photo-oxidation reaction:


Step (6) describes the deprotonation reaction of H2O2 in the alkaline solution31, which occurs spontaneously since a pKa of 11.7 for H2O2 deprotonation42 yields [HOO−]/[H2O2]≃100 at pH = 13.6. Due to the fast nature of deprotonation reactions, step (6) is expected to occur much faster than the other steps, thus it does not affect the overall kinetics. Its product, HOO−, is postulated to weakly (physically) adsorb to Fe-OH surface sites in the next step, as described in step (7), in accordance with (d) above. Empirical evidence supporting this adsorption step was obtained by infrared spectroscopy (see Supplementary Figure 1 and related discussion in the Supplementary Information). It is also supported by previous works showing the adsorption of (non-deprotonated) H2O2 to Fe-OH surface sites in haematite43 (and similarly in other transition metal oxides44). Finally, step (8) postulates that the adsorbates from step (7) are oxidized by photo-generated holes coupled with proton transfer to adjacent Fe = O surface intermediates that were produced in step (1) of the water photo-oxidation reaction. Thus, step (8) represents a concerted interaction between two different surface species, one from the water photo-oxidation reaction and the second from H2O2 adsorption. It couples both reactions and gives rise to nonlinearity in the kinetic equations that depend on the concentration of the respective species (see Model equations and numerical computations in Methods for details). It is noted that the exact molecular identity of the surface species involved in the reaction is beyond the scope of this work, and it remains to be verified by spectroelectrochemical studies45. However, this specific detail is not crucial to the results that follow, and alternative surface species may be considered without affecting the qualitative results of the analysis. The salient point is that the H2O2 photo-oxidation reaction mechanism involves a concerted interaction of two surface sites, as in LH reactions, consuming two holes and yielding an oxygen molecule. The postulated reaction path is schematically illustrated on the right side of Fig. 3.
To uncover the nonlinear nature of the elementary steps in the water and H2O2 photo-oxidation reactions that result in the measured non-monotonic photocurrents for certain H2O2 concentrations (see Fig. 1), we derive kinetic equations (see Model equations and numerical computations in Methods for details) and supplement them by the hole flux from the surface to the electrolyte that is given by the sum of the forward chemical reactions (1), (3)–(5), and (8):
where p1 is the hole flux from the surface to the electrolyte46, which in general depends on the illumination intensity and potential, and p4 is the OH− concentration in the electrolyte, which depends on the electrolyte composition, θx is the fractional surface coverage of species x, and σh corresponds to the surface density of holes at reacting sites. It is useful to regard eq. 9 as the charge conservation constraint46. In addition to the charge conservation constraint, we also employ a standard surface site conservation constraint:
Next, we define the normalized photocurrent that is related to the flux of holes across the surface (p1) minus the flux of holes consumed by the surface recombination reaction (step (2)):46
where p2 is the electron density at the surface. We emphasize that this form regards only the reaction kinetics at the surface and it does not account for bulk processes that control the hole flux to the surface. From experiments, it is evident that p1 is often potential dependent, but the dependence is relatively weak. For instance, in the results presented in Fig. 1 the dependence is essentially linear (see j500 in Fig. 1). In contrast to p1, p2 displays strong dependence on the applied potential, p2∝exp(-φ), where φ is dimensionless potential (see Model equations and numerical computations in Methods section for details). Thus Eq. (11) comprises an empirical normalization by p1 (similarly to the normalization by j500 in Fig. 1b). Notably, the shape of the calculated voltammograms of the normalized photocurrent is essentially robust with respect to the potential dependence of p1, as shown here by comparing Fig. 4a, b in which p1 is taken to be linearly proportional to U or independent of U, respectively. This implies a generic mechanism that is hidden in this physicochemical process that we unfold, in what follows, by using a bifurcation theory via keeping p1 as constant for simplified analysis purposes, \(p_1 = p_1^{\mathrm{c}}\).
Numerically computed normalized photocurrent voltammograms at different H2O2 concentrations (p3). All the observables are dimensionless. The photocurrents are calculated for two cases in which p1 is a with linear dependence on the applied potential, or b constant (see text and Model equations and numerical computations in Methods section for details)
The qualitative similarity between the calculated curves in Fig. 4 and the experimental results in Fig. 1b is clearly evident. Specifically, the calculated curves capture the non-monotonous behaviour of the normalized photocurrent at low H2O2 concentrations and potentials below the onset of water photo-oxidation, and the convergence of the photocurrent at high potentials towards the water photo-oxidation limit. It is noted that the non-monotonous behaviour displayed by the cyan (p3 = 0.01) curve in Fig. 4 emerges from the nonlinearity in the kinetic equations, as a result of the concerted interaction of two different surface sites as in step (8) above.
Bi-stability, competing kinetics and hysteresis
Analysis of the solutions shows that while for low H2O2 concentrations there is only one solution (mono-stable regime), above a certain threshold concentration there is a limited potential range in which stable solutions coexist, as shown in Fig. 5a, c. The coexistence of stable solutions implies that hysteresis in the photocurrent should be expected in this range of potentials and H2O2 concentrations. The hysteresis onset is at a generic cusp bifurcation47 (marked by Qc in Fig. 5a) in the two-parameter projection of the normalized photocurrent as a function of the potential (φ) and H2O2 concentration (p3), see Fig. 5a. The shaded region between the curves in Fig. 5a is where coexistence of bi-stable solutions exists. Above p3 ≃ 0.144 (marked by the bold dashed line in Fig. 5a), although the coexistence persists, it cannot be observed experimentally because one of the stable solution branches spans the entire relevant potential range. In this case, an unstable solution connects the two stable solutions only at infinite potential, a known and universal (model independent) property of the cusp bifurcation47. Thus, our calculations predict a stable unique behaviour at low and high H2O2 concentrations, whereas at intermediate concentrations bi-stable solutions and hysteresis are expected (in a certain potential range). It is noted that additional calculations (not shown here) demonstrate the same qualitative behaviour with similar features of hysteresis and multiplicity of solutions (i.e., bi-stable regimes) over a wide range of parameters spanning orders of magnitude of the respective rate constants, confirming the robustness of our model predictions. Moreover, the simple ER mechanism typically used to describe water photo-oxidation on haematite photoanodes24,25,34,35 cannot yield such hysteresis because it lacks nonlinearity in the kinetic equations of its elementary steps (see Model equations and numerical computations in Methods for details).
Bi-stability and hysteresis. a Coexistence parameter space for the computed normalized photocurrent voltammograms showing the distinct regions of coexisting solutions. 2D projection of the manifold describing the computed normalized photocurrent voltammograms (j/jmax) as a function of the applied dimensionless potential (φ) and H2O2 concentration (p3), showing the coexistence (bi-stability) regime of the normalized photocurrent (the grey shaded area). The bold dashed line indicates the threshold between observable and non-observable hysteresis. b, c Simulated normalized photocurrent voltammograms at p3 = 0.5 and 0.1, respectively. Solid lines indicate stable solutions, whereas dashed lines indicate unstable ones. The transition points from stable to unstable solutions and vice versa in b, c are, respectively, marked in a
The hysteresis predicted by the model calculations was validated by linear sweep voltammetry measurements, as shown in Fig. 6. Consistent with the model predictions, hysteresis was observed only at intermediate H2O2 concentrations (5 mM; Fig. 6b) but not at low and high concentrations (Fig. 6a, c, respectively). The hysteresis mechanism is consistent with the proposed reaction path (Fig. 3) through examination of the potential dependence (and therefore dependence on the potential sweep direction) of the distinct surface species involved in the reaction. Specifically, we focus on the evolution of the Fe = O, Fe-OH, and Fe-OH···−OOH species. At low potentials, for example, U = 0.6 VRHE, the concentration of electrons at the surface is high (because the photoanode is donor-doped) and the recombination rate (step (2)) is fast, and therefore the surface is covered mostly by the long-lived Fe-OH and Fe-OH···−OOH species, whereas the short-lived Fe = O intermediates are minority species. Thus, the photocurrent at low potentials is dominated by the reaction path associated with the formation of Fe-OH···−OOH adions with increasing potentials, that is, in the 0.8 VRHE ≤ U ≤ 1.3 VRHE range, the electron concentration at the surface decreases due to band bending, thereby prolonging the lifetime of the Fe = O intermediates. Consequently, the surface concentration of Fe = O increases, leading to comparable contributions to the photocurrent from both the water and H2O2 photo-oxidation reactions. At high potentials, U ≥ 1.3 VRHE, the surface recombination becomes negligible and the surface is covered mostly by long-lived Fe = O intermediates. If the potential is then swept in the opposite direction, that is from high to low potentials, the surface coverage of Fe = O decreases progressively. Unlike during the potential sweep from low to high potentials, the time scale that is required to form a significant coverage of Fe-OH···−OOH adions is much larger than in the reverse direction, consequently the H2O2 photo-oxidation reaction dominates. Thus, the different time scales that are associated with the evolution of different surface intermediates are manifested as hysteresis in the case of H2O2 photo-oxidation that involves concerted interaction of different intermediate specie.
Experimental realization of hysteresis. Forth and back linear sweep voltammetry scans at different H2O2 concentrations in alkaline solution (1 M NaOH) under white LED illumination of 80 mW cm−2: a 1 mM, b 5 mM and c 500 mM. Hysteresis is observed only at [H2O2]=5 mM. The arrows indicate the direction of potential sweep from low to high potentials and then back to low potentials
Discussion
The two-site interaction postulated here belongs to the LH class of surface reactions, where two different surface species mutually interact. This mechanism is inherently different from the single-site, multi-step process that accounts for the reported reaction mechanism of water photo-oxidation on haematite24,25,26,34,35, as in ER reactions. Our two-site/LH reaction mechanism provides a favourable photo-oxidation path by splitting the charge transfer steps across two sites rather than the single-site/ER water photo-oxidation reaction, thereby helping to level the potential of the elementary steps involved in the reaction20. In a broader context, the nonlinear photocurrent voltammograms observed at certain H2O2 concentrations (see Fig. 1) correspond to a class of systems exhibiting negative differential resistance, typical of competing mechanisms with different time scales47,48, as discussed above. Notably, the LH-like nature of the H2O2 photo-oxidation reaction bares similarity to catalytic CO oxidation49, where bi-stability was observed and related to the generic character of LH reactions. This suggests that an appropriate spatiotemporal framework should be considered to account for concerted interaction between two sites, especially in cases where the simple single-site reaction scheme fails, as in the case of the H2O2 photo-oxidation reaction presented in this work.
It is noteworthy that two-site reactions on oxidized metal and metal oxide surfaces were previously suggested in the context of photocatalysis50,51 and water photo-oxidation20,32,52,53,54,55,56. Particularly, hydroperoxide (HOO) adsorbed on metal sites participating in two-site LH-like reactions was suggested as part of the water oxidation mechanism on noble metals (Pt and Au) as well as Co3O436,57. Oxo-bridged and peroxo-bridged Fe dimers (FeIV−O−FeIV and FeIV−O−O−FeIV) were found on haematite surface in alkaline solution, but were reported not to participate in water oxidation24,26. The mechanism presented here, however, assumes the interaction of non-dimerized surface intermediates to form the O−O bond. The interaction of two non-dimerized surface intermediates in an LH-like mechanism has been suggested by Bockris19 to take part in the water oxidation mechanism. Such a mechanism was indeed reported for water photo-oxidation on haematite at high light intensities and high potentials, where the photocurrent saturates58. The behaviour was attributed to conditions where the hole flux to the surface is high enough to allow the oxidation of nearest-neighbour sites, thereby reducing the surface recombination, consistent with our conclusion.
Given the ability of H2O2 to act as a hole scavenger, it often serves as a surrogate substrate that can be used to assess the effectiveness of co-catalysts for water photo-oxidation29,30. Thus, understanding the mechanism by which H2O2 extracts photo-generated holes may further provide insight into the effect of water oxidation co-catalysts on haematite photoanodes (and possibly other photoanode materials) and assist in rational design of better performing co-catalysts. In this context, it has been reported that sub-monolayer coverage of cobalt on haematite photoanodes has improved their water photo-oxidation performance, with no further enhancement as a result of additional co-catalyst loading36. Another study reported that the kinetic bottleneck that limits the water photo-oxidation performance of haematite photoanodes decorated with cobalt-phosphate (Co-Pi) water oxidation co-catalyst overlayers is effectively suppressed by sparse deposition on the haematite surface37. Trivial assignment of the detrimental effect observed with thicker layers to parasitic light absorption within the co-catalyst overlayer59 was ruled out in this case by comparing back and front illumination measurements that were found to display similar trends38. These counter-intuitive observations cannot be accounted for by the “adaptive junction” mechanism that often prevails in thicker ion-permeable co-catalyst overlayers60,61, or by alternative mechanisms suggested by other researchers, such as the formation of a Schottky-type heterojunction at the haematite/Co-Pi interface62. Thus, the mechanism by which ultrathin/sparse co-catalyst overlayers improve the water photo-oxidation performance of haematite photoanodes remains elusive38,63,64. The current work provides a possible insight to this enigma by considering that the water photo-oxidation reaction in the presence of sparse co-catalysts may proceed by a concerted interaction that involves two sites, one site from the photoanode and another site from the co-catalyst, similarly to the two-site H2O2 photo-oxidation reaction. Consistent with this view are the observations that ultrathin/sparse cobalt co-catalysts are more effective in enhancing water photo-oxidation at low potentials than at high potentials36,37, indicating that the reaction proceeds via the co-catalyst at low potentials and via the haematite surface at high potentials38. This is similar to the effect of H2O2 reported in this work, suggesting a possible link between the respective photo-oxidation schemes. In view of these examples, we conclude that a LH-like mechanism in PEC reactions may be a general phenomenon and should be considered as a possible route for enhanced collection of photo-generated charge carriers.
To conclude, this work shows that the photo-oxidation mechanism of hydrogen peroxide (H2O2) on haematite photoanodes proceeds via a concerted interaction between two different surface species, one from the water photo-oxidation reaction and the other from H2O2 adsorption. This two-site LH-like reaction occurs in parallel with the single-site ER-like water photo-oxidation reaction. Splitting the photo-oxidation reaction into two sites instead of one facilitates the collection of photo-generated holes by the oxidized species by helping to level the potential of the elementary steps involved in the reaction, thereby reducing kinetic barriers. Moreover, we show that the competition between the H2O2 and water photo-oxidation reactions for holes, intermediate species and surface sites, involves processes with different time scales, thereby giving rise to bi-stability phenomena that may lead to negative differential resistance and hysteresis in the photocurrent voltammograms. Our findings suggest that the concerted interaction of two surface intermediates should be considered as a possible path towards improving the photoelectrode performance. This may shed light on the effect of ultrathin/sparse co-catalysts for water oxidation on haematite as well as other photoanodes.
Methods
Haematite photoanode
The samples consisted of a heteroepitaxial (110)-oriented Sn-doped (1%) haematite thin film photoanode (thickness ~30 nm) on Nb-doped SnO2 (NTO) transparent electrode (thickness ~350 nm) deposited on an a-plane sapphire substrate. Details of the fabrication process and the microstructural characteristics of the photoanode can be found elsewhere65.
PEC measurements
All measurements were conducted at ambient temperature in alkaline aqueous solutions (1 M NaOH in deionized water). For varying the H2O2 content, a 1 M NaOH + 0.5 M H2O2 solution was prepared in deionized water and diluted with 1 M NaOH in deionized water to reach the desired H2O2 concentrations. The pH of the electrolyte solution was kept fixed throughout the study. Linear sweep voltammetry measurements were carried out in a so-called cappuccino cell, as described in ref. 66 with the photoanode serving as the working electrode, Pt mesh as the counter electrode and an Hg/HgO reference electrode in 1 M NaOH aqueous solution. The reference electrode has a potential of 0.930 VRHE. The measurements were carried out with a Zahner Zennium electrochemical workstation equipped with a CIMPS system67. The light source was a high power white LED (Zahner WLC02, 4300 K) with a maximum intensity of 120 mW cm−2. The spectrum of this light source is shifted toward shorter wavelength than the AM1.5G solar spectrum, resulting in slightly higher photo-generation rate compared to proper solar simulators. To compensate for the spectral mismatch of our light source with respect to the AM1.5G solar spectrum, we reduced the light intensity to 80 mW cm−2 instead of 100 mW cm−2 in conventional solar simulators. Potential sweeps were performed by increasing the potential from 0.6 to 1.8 VRHE and subsequently decreasing it back to 0.6 VRHE with a sweep rate of 20 mV s−1.
IMPS spectra were obtained by measuring both PEC impedance spectroscopy (PEIS) and intensity-modulated voltage spectroscopy (IMVS) at the corresponding operating point and then calculating the IMPS spectrum. This was done because of the better accuracy compared to direct IMPS measurement, as reported elsewhere39. The frequency was scanned from 10 kHz to 0.7 Hz and the perturbation amplitude was 10 mV for PEIS and 20 mV for IMVS.
Spectroscopic characterization
For Fourier transformed infrared spectroscopy (FTIR) measurements, samples were soaked for 30 min in a NaOH (1 M) aqueous solution or in a NaOH (1 M) + H2O2 (0.5 M) aqueous solution, then washed in DI water (18 MOhm) and dried in a gentle air flow. The FTIR spectra of the electrolyte solutions were recorded by a drop placed on an attenuated total reflection diamond crystal using a Nicolet 8700 FTIR spectrometer with a DTGS detector, with the background recorded on the clean diamond crystal. The spectra were recorded in the range from 4000 to 700 cm−1, at 2 scanning resolution (0.24 cm−1) and 36 scans. The FTIR spectra of the samples were recorded using an iN-10 FTIR microscope (Thermo Scientific) spectrometer equipped with a narrow-band liquid nitrogen-cooled MCTA detector. All single-beam spectra were measured against a background recorded from gold, with subtraction of the measured FTIR spectrum of the bare NTO/sapphire substrate. The spectra were recorded in the range from 4000 to 700 cm−1, at 8 scanning resolution (1 cm−1) and 128 scans; detection area was 100 × 100 μm2. The FTIR data were collected using the OMNIC-Picta software.
Model equations and numerical computations
The rates of the reaction steps of the water and H2O2 photo-oxidation reactions, see eqs. (1)–(8), depend on the fractional surface coverage of species x, θx, which are dimensionless by definition. The units of the electron and hole surface densities, σe and σh, respectively, are given by their number surface density [σe] = [σh] = mol m−2. The units of the rate constants are given according to the corresponding reaction orders: [k1] = [k2] = [k3] = [k4] = m5 mol−2 s−1, [k5] = m3 mol−1 s−1, and [k−1] = [k6] = m2 mol−1 s−1, and thus the units of other parameters read as mol m−2 s−1 for p1, mol m−2 for p2 and mol m−3 for p3 and p4; p1—the flux of photo-generated holes from the surface to the electrolyte; p2—the electron density at the surface; p3—the HOO− concentration in the electrolyte (which is directly proportional to the concentration of H2O2); and p4—the OH− concentration in the electrolyte (related to the pH).
Introducing rescaled variables and parameters, \(\hat t = t/\tau ,\) with \(\tau = 1/p_4k_5\), \(\hat p_1 = p_1/k_6\), \(\hat p_2 = p_2/\sigma _0\), with \(\sigma _0 = k_6^{ - 1}\tau ^{ - 1} = p_4k_5/k_6\), \(\hat p_3 = p_3/p_4,\) \(\hat \sigma _{\mathrm{h}} = \sigma _{\mathrm{h}}/\sigma _0\), \(\hat k_1 = k_1p_4/k_6\), \(\hat k_2 = k_2p_4/k_6\), \(\hat k_3 = k_3p_4/k_6\), \(\hat k_4 = k_4p_4/k_6\), \(\hat k_{ - 1} = k_{ - 1}/k_6\), we obtain a combined set of dimensionless kinetic equations for reactions (1)–(8). For ease of reading the hat signs were removed in what follows and in Table 1:
We note that our model addresses the working conditions of haematite photoanodes at high pH levels4,5,6,7,8,9.
For analysis, we first solve numerically the model equations under the charge and site conservation constraints described by Eqs. (9) and (10), respectively, and examine all the possible steady-state solutions (fix points) to Eqs. (12) through (16). The equations have been numerically solved by continuation method using the publically available package AUTO68. To determine the temporal stability of each steady-state solution, we linearize Eqs (12)–(16) about the fix points and solve the standard eigenvalue problem, while correlating the negative eigenvalues with stable solutions.
The dimensionless parameters p1,2,3,4 for Eqs (12)–(16) are unknown, and thus the results are qualitative in nature. Consequently, we compute and compare only the qualitative trends. The dimensionless rate constants were chosen such that their ratios are in accord with reported values for water photo-oxidation on haematite24. The rate constants for the H2O2 photo-oxidation are rationalized in points (a) through (d) in the Results. The linear potential dependence of p1 is chosen to be significantly smaller than 1, as most photo-generated holes do not arrive at the surface, see Table 1. The dimensionless OH− concentration, p4, was set to be equal to 1. We cannot derive a simple relation between σh and p2, though such relation is expected from steps (1) and (2). The model parameters are summarized in Table 1. Additionally, we use a dimensionless potential scaled by kBT/q and also normalized, i.e., φ = U/Usat, where Usat = 12 is the minimal potential for which all photocurrents for different H2O2 concentrations are considered to be saturate, kB is Blotzmann constant,T is temperature, and q is elementary charge.
To test the validity of the LH-like mechanism proposed herein, a possible ER-like mechanism for H2O2 photo-oxidation was also considered. The alternative mechanism excludes reaction (7) and instead involves a direct interaction between HOO− and Fe = O, implying that k5p3(θFe-OH−θFe-OH···OOH) → 0 and k6θFe = OσhθFe-OH···OOH → k6p3σhθFe = O. The latter can then be combined with the linear k2p4σhθFe = O term in Eq. (13), thereby removing the qualitative nonlinear nature of the solutions. Therefore, the resulting photocurrent based upon the ER-like mechanism fails to capture the non-monotonous behaviour observed in Fig. 1.
Data availability
All data generated or analysed during this study are included in this published article (and its Supplementary Information Files).
References
Heller, A. Hydrogen-evolving solar cells. Science 223, 1141–1148 (1984).
Marusak, L. A., Messier, R. & White, W. B. Optical absorption spectrum of hematite, α-Fe2O3 near IR to UV. J. Phys. Chem. Solids 41, 981–984 (1980).
Smith, R. D. L. et al. Photochemical route for accessing amorphous metal oxide materials for water oxidation catalysis. Science 340, 60–63 (2013).
Dias, P., Vilanova, A., Lopes, T., Andrade, L. & Mendes, A. Extremely stable bare hematite photoanode for solar water splitting. Nano Energy 23, 70–79 (2016).
Warren, S. C. et al. Identifying champion nanostructures for solar water-splitting. Nat. Mater. 12, 842–849 (2013).
Dotan, H. et al. Resonant light trapping in ultrathin films for water splitting. Nat. Mater. 12, 158–164 (2013).
Kim, J. Y. et al. Single-crystalline, wormlike hematite photoanodes for efficient solar water splitting. Sci. Rep. 3, 2681 (2013).
Guo, X., Wang, L. & Tan, Y. Hematite nanorods Co-doped with Ru cations with different valence states as high performance photoanodes for water splitting. Nano Energy 16, 320–328 (2015).
Sivula, K., Le Formal, F. & Grätzel, M. Solar water splitting: progress using hematite (α-Fe2O3) photoelectrodes. ChemSusChem 4, 432–449 (2011).
Rothschild, A. & Dotan, H. Beating the efficiency of photovoltaics-powered electrolysis with tandem cell photoelectrolysis. ACS Energy Lett. 2, 45–51 (2017).
Iandolo, B., Wickman, B., Zorić, I. & Hellman, A. The rise of hematite: origin and strategies to reduce the high onset potential for the oxygen evolution reaction. J. Mater. Chem. A 3, 16896–16912 (2015).
Zandi, O. & Hamann, T. W. The potential versus current state of water splitting with hematite. Phys. Chem. Chem. Phys. 17, 22485–22503 (2015).
Shen, S., Lindley, S. A., Chen, X. & Zhang, J. Z. Hematite heterostructures for photoelectrochemical water splitting: rational materials design and charge carrier dynamics. Energy Environ. Sci. 9, 2744–2775 (2016).
Sivula, K. Metal oxide photoelectrodes for solar fuel production, surface traps, and catalysis. J. Phys. Chem. Lett. 4, 1624–1633 (2013).
Grave, D. A., Yatom, N., Ellis, D. S., Caspary Toroker, M. & Rothschild, A. The ‘rust’ challenge: on the correlations between electronic structure, excited state dynamics and photoelectrochemical performance of hematite photoanodes for solar water splitting. Adv. Mater. https://doi.org/10.1002/adma.201706577 (2018).
Kemppainen, E., Halme, J. & Lund, P. Physical modeling of photoelectrochemical hydrogen production devices. J. Phys. Chem. C 119, 21747–21766 (2015).
Zhang, X. & Bieberle-Hütter, A. Modeling and simulations in photoelectrochemical water oxidation: from single level to multiscale modeling. ChemSusChem 9, 1223–1242 (2016).
Pham, T. A., Ping, Y. & Galli, G. Modelling heterogeneous interfaces for solar water splitting. Nat. Mater. 16, 401–408 (2017).
Bockris, J. O. Kinetics of activation controlled consecutive electrochemical reactions: anodic evolution of oxygen. J. Chem. Phys. 24, 817–827 (1956).
Dau, H. et al. The mechanism of water oxidation: from electrolysis via homogeneous to biological catalysis. ChemCatChem 2, 724–761 (2010).
Shockley, W. & Read, W. T. Jr Statistics of the recombinations of holes and electrons. Phys. Rev. 87, 835–842 (1952).
Prévot, M. S. & Sivula, K. Photoelectrochemical tandem cells for solar water splitting. J. Phys. Chem. C 117, 17879–17893 (2013).
Klahr, B., Gimenez, S., Fabregat-Santiago, F., Hamann, T. & Bisquert, J. Water oxidation at hematite photoelectrodes: the role of surface states. J. Am. Chem. Soc. 134, 4294–4302 (2012).
Yatom, N., Neufeld, O. & Caspary Toroker, M. Toward settling the debate on the role of Fe2O3 surface states for water splitting. J. Phys. Chem. C 119, 24789–24795 (2015).
Braun, A. et al. The electronic, chemical and electrocatalytic processes and intermediates on iron oxide surfaces during photoelectrochemical water splitting. Catal. Today 260, 72–81 (2016).
Zandi, O. & Hamann, T. W. Determination of photoelectrochemical water oxidation intermediates on haematite electrode surfaces using operando infrared spectroscopy. Nat. Chem. 8, 778–783 (2016).
Dotan, H., Sivula, K., Grätzel, M., Rothschild, A. & Warren, S. C. Probing the photoelectrochemical properties of hematite (α-Fe2O3) electrodes using hydrogen peroxide as a hole scavenger. Energy Environ. Sci. 4, 958–964 (2011).
Itoh, K. & Bockris, J. O. Thin film photoelectrochemistry: iron oxide. J. Electrochem. Soc. 131, 1266–1271 (1984).
Zhong, D. K., Choi, S. & Gamelin, D. R. Near-complete suppression of surface recombination in solar photoelectrolysis by “Co-Pi” catalyst-modified W:BiVO4. J. Am. Chem. Soc. 133, 18370–18377 (2011).
Abdi, F. F. et al. Efficient solar water splitting by enhanced charge separation in a bismuth vanadate-silicon tandem photoelectrode. Nat. Commun. 4, 2195 (2013).
Boehme, K. & Brauer, H. D. Generation of singlet oxygen from hydrogen peroxide disproportionation catalyzed by molybdate ions. Inorg. Chem. 31, 3468–3471 (1992).
Fang, Y.-H. & Liu, Z.-P. Mechanism and Tafel lines of electro-oxidation of water to oxygen on RuO2(110). J. Am. Chem. Soc. 132, 18214–18222 (2010).
Klotz, D., Grave, D. A., Dotan, H. & Rothschild, A. Empirical analysis of the photoelectrochemical impedance response of hematite photoanodes for water photo-oxidation. J. Phys. Chem. Lett. 9, 1466–1472 (2018).
Zhang, X., Klaver, P., van Santen, R., van de Sanden, M. C. M. & Bieberle-Hütter, A. Oxygen evolution at hematite surfaces: the impact of structure and oxygen vacancies on lowering the overpotential. J. Phys. Chem. C 120, 18201–18208 (2016).
English, N. J., Rahman, M., Wadnerkar, N. & MacElroy, J. M. D. Photo-active and dynamical properties of hematite (Fe2O3)–water interfaces: an experimental and theoretical study. Phys. Chem. Chem. Phys. 16, 14445–14454 (2014).
Kay, A., Cesar, I. & Grätzel, M. New benchmark for water photooxidation by nanostructured α-Fe2O3 films. J. Am. Chem. Soc. 128, 15714–15721 (2006).
Zhong, D. K. & Gamelin, D. R. Photoelectrochemical water oxidation by cobalt catalyst (‘Co-Pi’)/α-Fe2O3 composite photoanodes: oxygen evolution and resolution of a kinetic bottleneck. J. Am. Chem. Soc. 132, 4202–4207 (2010).
Carroll, G. M., Zhong, D. K. & Gamelin, D. R. Mechanistic insights into solar water oxidation by cobalt-phosphate-modified α-Fe2O3 photoanodes. Energy Environ. Sci. 8, 577–584 (2015).
Klotz, D. et al. Empirical in operando analysis of the charge carrier dynamics in hematite photoanodes by PEIS, IMPS and IMVS. Phys. Chem. Chem. Phys. 18, 23438–23457 (2016).
Young, K. M. H., Klahr, B. M., Zandi, O. & Hamann, T. W. Photocatalytic water oxidation with hematite electrodes. Catal. Sci. Technol. 3, 1660–1671 (2013).
Hellman, A., Iandolo, B., Wickman, B., Grönbeck, H. & Baltrusaitis, J. Electro-oxidation of water on hematite: effects of surface termination and oxygen vacancies investigated by first-principles. Surf. Sci. 640, 45–49 (2015).
Goor, G., Glenneberg, J. & Jacobi, S. in Ullmann’s Encyclopedia of Industrial Chemistry Vol. 1, 131–139 (Wiley-VCH, Weinheim, Germany, 2007).
Lin, S.-S. & Gurol, M. D. Catalytic decomposition of hydrogen peroxide on iron oxide: kinetics, mechanism, and implications. Environ. Sci. Technol. 32, 1417–1423 (1998).
Lousada, C. M., Johansson, A. J., Brinck, T. & Jonsson, M. Mechanism of H2O2 decomposition on transition metal oxide surfaces. J. Phys. Chem. C 116, 9533–9543 (2012).
Zhang, M. & Frei, H. Water oxidation mechanisms of metal oxide catalysts by vibrational spectroscopy of transient intermediates. Annu. Rev. Phys. Chem. 68, 209–231 (2017).
Klotz, D., Grave, D. A. & Rothschild, A. Accurate determination of the charge transfer efficiency of photoanodes for solar water splitting. Phys. Chem. Chem. Phys. 19, 20383–20392 (2017).
Krischer, K., Mazouz, N. & Grauel, P. Fronts, waves, and stationary patterns in electrochemical systems. Angew. Chem. Int. Ed. 40, 850–869 (2001).
Kalaev, D., Rothschild, A. & Riess, I. Negative differential resistance and hysteresis in Au/MoO3-δ/Au devices. RSC Adv. 7, 38059–38068 (2017).
Imbihl, R. & Ertl, G. Oscillatory kinetics in heterogeneous catalysis. Chem. Rev. 95, 697–733 (1995).
Bahnemann, D. W., Hilgendorff, M. & Memming, R. Charge carrier dynamics at TiO2 particles: reactivity of free and trapped holes. J. Phys. Chem. B 101, 4265–4275 (1997).
Draper, R. B. & Fox, M. A. Titanium dioxide photooxidation of thiocyanate: (SCN)2—studied by diffuse reflectance flash photolysis—breaks. J. Phys. Chem. 94, 4628–4634 (1990).
Nakamura, R. & Nakato, Y. Primary intermediates of oxygen photoevolution reaction on TiO2 (Rutile) particles, revealed by in situ FTIR absorption and photoluminescence measurements. J. Am. Chem. Soc. 126, 1290–1298 (2004).
Salvador, P. Mechanisms of water photooxidation at n-TiO2 rutile single crystal oriented electrodes under UV illumination in competition with photocorrosion. Prog. Surf. Sci. 86, 41–58 (2011).
Henderson, M. A. A surface science perspective on TiO2 photocatalysis. Surf. Sci. Rep. 66, 185–297 (2011).
Zhang, M., de Respinis, M. & Frei, H. Time-resolved observations of water oxidation intermediates on a cobalt oxide nanoparticle catalyst. Nat. Chem. 6, 362–367 (2014).
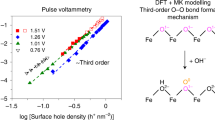
Zhang, Y. et al. Rate-limiting O–O bond formation pathways for water oxidation on hematite photoanode. J. Am. Chem. Soc. 140, 3264 (2018).
Rossmeisl, J., Logadottir, A. & Nørskov, J. K. Electrolysis of water on (oxidized) metal surfaces. Chem. Phys. 319, 178–184 (2005).
Le Formal, F. et al. Rate law analysis of water oxidation on a hematite surface. J. Am. Chem. Soc. 137, 6629–6637 (2015).
Trotochaud, L., Mills, T. J. & Boettcher, S. W. An optocatalytic model for semiconductor–catalyst water-splitting photoelectrodes based on in situ optical measurements on operational catalysts. J. Phys. Chem. Lett. 4, 931–935 (2013).
Lin, F. & Boettcher, S. W. Adaptive semiconductor/electrocatalyst junctions in water-splitting photoanodes. Nat. Mater. 13, 81–86 (2014).
Nellist, M. R., Laskowski, F. A. L., Lin, F., Mills, T. J. & Boettcher, S. W. Semiconductor–electrocatalyst interfaces: theory, experiment, and applications in photoelectrochemical water splitting. Acc. Chem. Res. 49, 733–740 (2016).
Barroso, M. et al. The role of cobalt phosphate in enhancing the photocatalytic activity of α-Fe2O3 toward water oxidation. J. Am. Chem. Soc. 133, 14868–14871 (2011).
Qiu, J. et al. Direct in situ measurement of charge transfer processes during photoelectrochemical water oxidation on catalyzed hematite. ACS Cent. Sci. 3, 1015–1025 (2017).
Gamelin, D. R. Catalyst or spectator? Nat. Chem. 4, 965–967 (2012).
Grave, D. A. et al. Effect of orientation on bulk and surface properties of Sn-doped hematite (α-Fe2O3) heteroepitaxial thin film photoanodes. J. Phys. Chem. C 120, 28961–28970 (2016).
Deo Malviya, K. et al. Systematic comparison of different dopants in thin film hematite (α-Fe2O3) photoanodes for solar water splitting. J. Mater. Chem. A 4, 3091–3099 (2016).
Zahner. CIMPS—Controlled Intensity Modulated Photo Spectroscopy http://www.zahner.de/pdf/CIMPS.pdf.33 (2011).
Doedel, E. J. et al. AUTO07p: continuation and bifurcation software for ordinary differential equations. http://indy.cs.concordia.ca/auto (2011).
Acknowledgements
This research was supported by the Ministry of National Infrastructures, Energy and Water Resources of Israel (grant no. 3-11430), the Ministry of Science and Technology of Israel (grant no. 3-14423), the European Research Council under the European Union’s Seventh Framework programme (FP/200702013)/ERC (grant agreement no. 617516), and the Adelis Foundation. Y.Y.A. acknowledges support by the Kreitman Fellowship, B.G. acknowledges the support of the Blaustein Centre for Scientific Cooperation’s postdoctoral fellowship and D.A.G. acknowledges support by Marie-Sklodowska-Curie Individual Fellowship no. 659491. The experiments were performed using central facilities at the Technion’s Hydrogen Technologies Research Laboratory (HTRL) supported by the Adelis Foundation and the Solar Fuels I-CORE program of the Planning and Budgeting Committee and the Israel Science Foundation (grant no. 152/11). We thank Maytal Caspary Toroker for useful comments on the manuscript.
Author information
Authors and Affiliations
Contributions
A.Y. and H.D. conceived the idea. H.D., D.K., A.T., and B.G. designed and performed the experiments. S.K. performed the FTIR analysis. D.A.G. provided the haematite photoanodes. Y.Y.A., H.D., I.V.-F., A.R., and A.Y. designed the chemical modelling. Y.Y.A. and A.Y. performed the theoretical analysis and wrote the first draft. A.Y., I.V.-F. and A.R. supervised the research. All co-authors contributed to the analysis and to the writing of the final manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Avital, Y.Y., Dotan, H., Klotz, D. et al. Two-site H2O2 photo-oxidation on haematite photoanodes. Nat Commun 9, 4060 (2018). https://doi.org/10.1038/s41467-018-06141-0
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-018-06141-0
This article is cited by
-
Inductive effect of Ti-doping in Fe2O3 enhances the photoelectrochemical water oxidation
Science China Chemistry (2023)
-
Binary dopant segregation enables hematite-based heterostructures for highly efficient solar H2O2 synthesis
Nature Communications (2022)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.