Abstract
Termination of the terminal Cryogenian Marinoan snowball Earth glaciation (~650–635 Ma) is associated with the worldwide deposition of a cap carbonate. Modeling studies suggest that, during and immediately following deglaciation, the ocean may have experienced a rapid rise in pH and physical stratification followed by oceanic overturn. Testing these predictions requires the establishment of a high-resolution sequence of events within sedimentary records. Here we report the conspicuous occurrence of pyrite concretions in the topmost Nantuo Formation (South China) that was deposited in the Marinoan glacial deposits. Sedimentary facies and sulfur isotope data indicate pyrite precipitation in the sediments with H2S diffusing from the overlying sulfidic/euxinic seawater and Fe (II) from diamictite sediments. These observations suggest a transient but widespread presence of marine euxinia in an ocean characterized by redox stratification, high bioproductivity, and high-fluxes of sulfate from chemical weathering before the deposition of the cap carbonate.
Similar content being viewed by others
Introduction
The Sturtian (~717–660 Ma) and Marinoan (~650–635 Ma) snowball Earth events in the Cryogenian Period1,2,3,4,5 represent the most severe pan-glaciation climate experienced over the past 2 billion years, and possibly over the entire Earth history2,6,7. Climatic and geochemical models show that the termination of a snowball Earth glaciation requires a high level of atmospheric CO2 (pCO2 > 0.2 bar)8,9,10,11,12 in order to overcome the high albedo from global ice cover. Such a high pCO2 atmosphere will result in a rapid meltdown of glaciers13 and an extreme greenhouse climate9,10. Rapid deglaciation may lead to the shutdown of thermohaline circulation and the intensification of ocean stratification14,15, with warmer and dysoxic freshwater in the surface ocean overlying cold and anoxic seawater in the deep13,15.
Such a catastrophic end of a snowball Earth glaciation is expected to drive drastic perturbations in ocean chemistry16,17,18,19. Globally, sedimentary sequences during deglaciation are mostly manifested as a cap carbonate sharply overlying glacial diamictites2,7,20,21. Although the cap carbonate is often assumed to have been deposited immediately after the onset of deglaciation, a window of time is required to allow atmospheric pCO2 drawndown and seawater alkalinity buildup9,20. This necessarily means that deglaciation and associated continental weathering must have started before the initiation of cap carbonate deposition. This time lag is supported by recent work exploring Mg isotopes within post-Marinoan sequences20 and may be on the order of 105 years9.
Because this time lag cannot be resolved using currently available geochronometric tools, we are forced to carry out high-resolution analysis of sedimentary sequence in order to test models about the termination of snowball Earth glaciation22. Here, we report the occurrence of abundant pyrite concretions from the topmost Nantuo Formation5,23,24, a sedimentary sequence deposited during the terminal Cryogenian Marinoan glaciation in the Yangtze Block of South China (Fig. 1 and Supplementary Fig. 1, see Supplementary Note 1). These pyrite concretions lie immediately beneath the cap carbonate of the basal Doushantuo Formation deposited in the Ediacaran Period, and they present opportunities to investigate the atmospheric, oceanic, and biological events during the termination of the Marinoan glaciation.
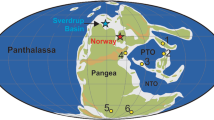
Paleogeographic map and depositional model of the Yangtze Block. a Paleogeographic map, modified from Jiang et al.21 showing the distribution of pyrite concretions in the topmost Nantuo Formation. Inset showing the geographic locality of the Yangtze Block. b Depositional model. The height of the columns indicates the maximum size of pyrite nodules observed in field. 1: Yazhai, 2: Tongle, 3: Silikou, 4: Yangxi, 5: Yuanjia, 6: Huakoushan, 7: Bahuang, 8: Siduping, 9: Tianping, 10: Songlin, 11: Youxi, 12: Huajipo, 13: Shennongjia
In this paper, we explore the origin of these pyrite concretions based on an integrated analysis of sedimentary facies, thin-section petrography, and multiple sulfur stable isotopes. We show that there was a transient marine euxinia before the deposition of the cap carbonate.
Results
Stratigraphic distribution and petrography
Pyrite concretions are abundantly distributed in the top 0.5–10 m of the Nantuo Formation (Fig. 2). The concretions include spheroidal-ellipsoidal nodules and aggregates with irregular outlines (Supplementary Fig. 2a–g). The pyrite nodules are randomly distributed and aligned parallel or subparallel to the bedding plane, whereas the pyrite aggregates are parallel to the bedding plane (Supplementary Fig. 2c). Individual concretions are isolated from each other, and there is no connection between nodules or between a nodule and an aggregate.
Sulfur isotopic compositions of pyrite concretions (red symbols) and disseminated pyrite (blue symbols) in the Nantuo Formation. a Limited variations of δ34Spy and variable Δ33S values of pyrite concretions from open shelf environment. b Variable δ34Spy and slightly positive Δ33S values of pyrite concretions and disseminated pyrite from slope environment. c Limited variations of δ34Spy and variable Δ33S values of pyrite concretions from basin environment. DST: Doushantuo Formation
The pyrite concretions are present in all studied sections except those in proximal inner shelf environment of the Yangtze Block (Figs. 1, 2). Both the size and abundance of pyrite concretions display depth gradients. In the basinal sections, most pyrite nodules are 10–30 cm in size (Supplementary Fig. 2), whereas pyrite aggregates can be >1 m in length and >30 cm in thickness (Supplementary Fig. 2c). In these settings, pyrite concretions account for ~5 vol% (ranging from 2 to 10 vol%, n = 5, Supplementary Table 1) of the concretion-bearing strata. In the slope depositional environment, most pyrite nodules vary between 5 and 15 cm in size (Supplementary Fig. 2f), and pyrite concretions account for 2~5 vol% (average value of 3.1 vol%, n = 5, Supplementary Table 1). In the shallower outer shelf sections, pyrite concretions occur only sporadically (<0.5 vol%) as small nodules less than 3 cm in size in gravelly siltstone layers immediately below the Doushantuo cap carbonate (Supplementary Fig. 2g). No pyrite concretions are found in the most proximal inner shelf sections (Fig. 1).
Both the nodules and aggregates are composed of euhedral pyrite, which normally range from 50 to 500 μm with occasional occurrences of mega-crystals >1 mm in size (Supplementary Fig. 3a–d). No framboidal pyrite has been identified using reflective microscopy (Supplementary Fig. 3d), nor are framboidal cores present in euhedral pyrite under back-scatter electron microscopy (Supplementary Fig. 3e, f), suggesting that the euhedral crystals were not derived from overgrowths of framboidal pyrite. Pyrite nodules are composed of densely packed euhedral pyrite and interstitial space is filled with fine sands/silts and/or cemented by silica (Supplementary Fig. 3a–d). Within a single nodule, there is no rim to core differentiation in either pyrite content or crystal size. On the other hand, pyrite aggregates are texturally supported by siliciclasts that are identical to the host rock in composition, and thus have less (15–30 vol%) pyrite content than the nodules (40–60 vol%). Pyrite crystals may contain abundant siliciclastic inclusions (Supplementary Fig. 3), and small pebbles up to 2 cm in size are observed in some aggregates and large nodules (Supplementary Fig. 2a and d).
Sulfur isotopic compositions
Individual pyrite concretions have limited variations in sulfur isotope composition (δ34Spy), but δ34Spy may vary substantially between different concretions or between different sections. In basinal sections, concretions display a smaller range of variation in δ34Spy [Tongle (13.5–19.3‰, mean = 16.5‰), Yuanjia (15.7–19.9‰, 18.5‰), Yazhai (13.6–23.7‰, mean = 19.4‰)]. Concretions from the slope sections have higher δ34Spy than those from the basinal sections, and δ34Spy values display a wider range of variation [Huakoushan (16.1–37.1‰, mean = 26.7‰) and Bahuang (21.0–28.2‰, mean = 25.2‰)]. δ34S values of disseminated pyrite extracted from gravelly siltstone in the top Nantuo Formation shows greater fluctuation (13.7–48.1‰, mean = 28.9‰) in the Taoying section but limited variation (–5.0‰ to –5.7‰, mean = –5.4‰) in the Bahuang section. In the outer shelf sections, pyrite concretions from the gravelly siltstone layers have the lowest δ34Spy values [Songlin (8.1–12.6‰, mean = 11.1‰), Youxi (−5.5‰ to −2.5‰, mean = −4.0‰)]. Δ33S (defined as Δ33S = δ33S − 1000([1 + δ34S/1000]0.515 − 1)) also exhibits a wide but overlapping range of variation among different concretions or among different facies [basin (–0.008‰ to 0.072‰, mean = 0.027‰), slope (–0.010‰ to 0.067‰, mean = 0.032‰), shelf (0.018‰ to 0.098‰, mean = 0.057‰)] (Fig. 2, Supplementary Tables 2, 3).
Discussion
Pyrite can be generated by hydrothermal activities during late-stage diagenesis, precipitated directly from seawater column, or formed within sediment porewater during early diagenesis. Postdepositional hydrothermal origin of the Nantuo pyrite concretions can be ruled out on the basis of the following sedimentological, petrological, and geochemical observations. First, the stratigraphic distribution of pyrite concretions is controlled by depositional environment (Fig. 1). Pyrite concretions can be observed both in gravelly siltstone and massive diamictite in the slope environment, whereas in the shallow water facies pyrite nodules only occur in gravelly siltstone. Second, no fluid conduits or hydrothermal veins are observed in connection with pyrite concretions (Supplementary Fig. 2). Third, although the diamictite-cap carbonate interface could serve as a conduit for fluid circulation, pyrite nodules also occasionally occur in the overlying cap carbonate (Supplementary Fig. 2e). Pyrite nodules are preserved in the matrix of cap carbonate and predating the early diagenetic sheet crack structures and arguing against a late diagenetic or hydrothermal origin. Finally, highly positive δ34Spy (>10‰) and variable Δ33S values are not characteristics of hydrothermal pyrite25,26,27 (Fig. 2). Direct pyrite precipitation from seawater is also inconsistent with observed euhedral pyrite (Supplementary Fig. 2), because sedimentary pyrite formed in the water column is typically framboidal in morphology28. Although euhedral pyrite could be generated by the overgrowth of framboidal pyrite29, no framboidal cores have been identified (Supplementary Fig. 3e, f).
Petrological evidence suggest that the Nantuo pyrite concretions were formed in sediment during early diagenesis. Pyrite crystals are tightly packed with interstitial spaces filled with clasts or cemented by silica, or float within a siliciclastic matrix, suggesting early concretion formation before sediment compaction (Supplementary Figs. 2d and 3a, b). Furthermore, the matrix of pyrite-bearing diamictite and gravelly siltstone also contains some disseminated euhedral pyrite, (Supplementary Fig. 3g, h), suggesting an authigenic origin. Thus, the euhedral pyrite in the Nantuo concretions most likely precipitated from porewater within sediment.
In modern nonsulfidic oceans, authigenic pyrite precipitation is fueled by dissimilatory sulfate reduction (DSR) in sediment porewater, and DSR is sustained by sulfate diffusion from seawater30 (Supplementary Fig. 4a). Alternatively, DSR may occur in a sulfidic water column, and authigenic pyrite can precipitate from porewater within sediment, with H2S diffusing from the overlying euxinic seawater (Supplementary Fig. 4b). In order to differentiate these two scenarios, we develop numerical models to simulate the sulfur isotope systematics of pyrite formation. In the first scenario, DSR in sediment porewater is sustained by continuous diffusion of seawater sulfate, which is driven by a sulfate concentration gradient that results from porewater sulfate consumption by DSR. Here we simulate the processes utilizing a one-dimensional diffusion-advection-reaction (1D-DAR) model. Assuming a seawater sulfate sulfur isotopic composition (δ34Ssw) of +30‰31 and biological fractionation (ΔDSR) in DSR at 40‰32, our modeling results indicate a maximum δ34Spy value of +8‰ (Fig. 3a, b), and the amount of pyrite formation is variably controlled by sedimentation rate, reaction rate of DSR, and seawater sulfate concentrations (Fig. 3c, Supplementary Figs. 5–9, and Supplementary Table 4). Therefore, DSR in sediment porewater cannot explain the high δ34Spy values of the pyrite concretions in slope and basinal sections (Fig. 2).
Modeling results. a The Rayleigh distillation model (dashed lines, with different sulfur isotope fractionations or ΔDSR) showing the relationship between δ34Spy and pyrite content with DSR occurring within sediment porewater under a closed system. The 1D-DAR model result (solid lines, with different sedimentation rates) showing the relationship between δ34Spy and pyrite content when DSR occurs in sediment porewater with sulfate supply by diffusion from the overlying seawater (an open system). b and c The maximum values of δ34Spy and pyrite content are ~+8‰ and 6.99 vol% within sediments. The default parameters for Ds, s, R, and [SO4]0 are 3.61 × 10−6 cm2 s−1, 0.01 cm year−1, 1 year−1, and 3 mM L−1, respectively. d The Rayleigh distillation model quantifying the δ34S of H2S with DSR occurring in seawater. Assuming δ34Ssw is 30‰, sulfur isotope fractionation for DSR is 40‰, variable δ34S values of the Nantuo pyrite concretions indicates the different degree of DSR (1 − f, f is the fraction of sulfate remaining). e The 1D-DR model result (black lines) showing DSR in water column followed by pyrite formation in sediment porewater fueled by H2S diffusion from sulfidic seawater. This process can explain high δ34Spy and high pyrite content in the basin and slope sections, indicating high degree of sulfate reduction in water column. f δ34Spy−Δ33Spy cross-plot37. Individual contour lines represent modeled sulfur isotopic compositions of pyrite formed from a sulfate pool with an initial sulfur isotope at the right end of the lines. Modeled values in the blue field require a bacterial sulfur disproportionation (BSD), whereas the yellow field indicate pyrite formed by DSR only. Measured data from pyrite in the top Nantuo Formation fall in the yellow field, suggesting that the pyrite was precipitated in an anoxic environment where DSR but not BSD occurs
Heavy (34S-enriched) pyrite could be generated by DSR in a closed porewater system (i.e., without sulfate supply from seawater), which can be simulated by a Rayleigh distillation model (see Supplementary Note 2 and Supplementary Table 5). However, the Rayleigh process can only account for <0.1 vol% of pyrite (Fig. 3a), and thus cannot explain the high pyrite content in the top Nantuo Formation (Fig. 3a, Supplementary Table 1). On the other hand, pyrite precipitation in porewater, driven by H2S diffusion from sulfidic seawater, can be simulated by a combination of DSR in the water column and H2S diffusion/pyrite formation in sediments. We simulated these processes using a Rayleigh distillation model and a 1D-DR model (see Supplementary Note 2 and Supplementary Table 6). Our modeling result indicates that δ34Spy values are predominantly controlled by DSR with high δ34Spy values resulting from a high degree of DSR in the water column (Fig. 3d, e). In contrast, H2S diffusion controls the pyrite content but not δ34Spy value (Supplementary Fig. 10), because the reaction between H2S and reactive Fe to generate pyrite is associated with negligible isotopic fractionation (~1‰)33. Our modeling results indicate that precipitation of 34S-enriched pyrite in the basin and slope sections was driven by a higher degree of sulfate reduction than in outer shelf settings (Fig. 3d, e).
Because δ34Spy mirrors the isotopic composition of H2S in seawater33, the spatial variation in δ34Spy reflects the isotopic heterogeneity of seawater H2S. The relatively consistent δ34Spy values observed in the basinal samples suggest that the H2S concentration was more or less homogenous in most distal seawaters. For the same reason, the more variable δ34Spy values of the slope sections reflect a rapid oscillation of seawater H2S concentrations.
Given high reactive Fe contents of siliciclastic sediments34,35,36, the amount of pyrite formation was controlled by the availability of H2S in seawater, which was a function of seawater H2S concentrations and the volume of seawater. Thus, abundant pyrite in the top Nantuo Formation implies vigorous DSR and a high concentration of dissolved H2S in the seawater, which is also consistent with the lack of bacterial sulfate disproportionation as shown in the Δ33S–δ34S plot (Fig. 3f)37. The decrease of pyrite content from deep to shallow settings is attributed to the bathymetric differences of the depositional environments38. Deeper water in the basin may have a thicker sulfidic water layer, resulting in more pyrite precipitation. While the absence of pyrite concretions in the inner shelf setting is the consequence of an absence of sulfidic seawater in the near shore, shallow, and more oxic waters39,40.
Abundant pyrite concretions in the top Nantuo Formation imply the development of oceanic euxinia before the precipitation of cap carbonate41. Oceanic euxinia can only be sustained by sufficient supplies of sulfate and organic matter36,42,43. Riverine influx is the major source of nutrients (e.g., P) and seawater sulfate30,44,45. We hypothesize that, during the deglaciation of the Marinoan glaciation, enhanced continental weathering20 could have delivered abundant nutrients and sulfate into the ocean. Because the deglacial continental weathering may predate oceanic euxinia20 due to the delayed recovery of productivity in acidified seawater, both nutrients and sulfate might be accumulated in seawater from riverine inputs. Once surface ocean productivity was resumed at high levels, high nutrient content could sustain high productivity, while DSR in water column would be fueled by sufficient supplies of organic matter and sulfate, driving oceanic euxinia.
The pyrite-rich interval in the topmost Nantuo Formation marks a brief yet widespread euxinic condition in the aftermath of the Marinoan glaciation immediately before cap carbonate precipitation. It is an interval with rising sulfate levels17, and high nutrient fluxes from the continents. This is also an interval characterized by redox stratified oceans where a large quantity of H2S was scavenged by Fe(II) in the glacial diamictite sediments. Importantly, this is also an interval prior to the deposition of the well-known cap carbonates, a time when seawater pH values or alkalinity were still below the threshold of carbonate precipitation or pCO2 levels were sufficiently high in the atmosphere12,46. The current study extends previous efforts to reconstruct from sedimentary records the sequence of events in the aftermath of the Marinoan meltdown47 in order to test the predictions of snowball Earth glaciations2.
Methods
Sample preparation and sulfur isotope analysis
Pyrite concretions were first split by a rock saw and then slabs were polished before sampling. Pyrite samples were collected by a hand-held micromill from the polished slabs. To capture the isotopic variations within a single pyrite concretion, multiple samples were sequentially collected from rim to core. Sulfur isotopic compositions of pyrite were measured at the Oxy-Anion Stable Isotope Consortium in Louisiana State University, at the EPS Stable Isotope Laboratory in McGill University, and at the Geochemistry laboratory in University of Maryland.
For δ34S analysis, about 0.05 mg pyrite-rich powder was mixed with 1–2 mg V2O5, and was analyzed for S isotopic compositions on an Isoprime 100 gas source mass spectrometer coupled with a Vario Microcube Elemental Analyzer. Sulfur isotopic compositions are expressed in standard δ-notation as permil (‰) deviations from the Vienna-Canyon Diablo Troilite standard. The analytical error is <0.2‰ based on replicate analyses of samples and laboratory standards. Samples were calibrated on two internal standards: LSU-Ag2S-1: −4.3‰; LSU-Ag2S-2: +20.2‰.
Multiple sulfur isotope analyses were conducted by converting pyrite samples to H2S(g) via the chromium reduction method. H2S gas was then carried through a N2 gas stream to a Zn acetate solution where it precipitated as ZnS. ZnS was then converted to Ag2S through addition of AgNO3. Samples were then filtered and dried at 80 °C. Ag2S samples were converted to SF6(g) through reaction with F2(g) in heated Ni bombs. Generated gas was then purified through a series of cryo-focusing steps followed by gas chromatography. The purified samples were then analyzed on a Thermo MAT-253 on dual-inlet mode. The total error on the entire analytical procedure is less than (1σ) 0.1‰ for δ34S and 0.01‰ for ∆33S.
Geochemical models of pyrite formation
Sedimentary or authigenic pyrite can precipitate either from sediment porewater or water column. In sediment porewater, pyrite formation can occur in a closed or an open porewater system. For a closed system, DSR occurs within sediment porewater with no additional sulfate supply from seawater. In contrast, open system DSR refers to sulfate supply via diffusion from the overlying seawater and pyrite formation in sediment porewater (Supplementary Fig. 4).
The close system reaction can be simulated by the Rayleigh distillation model, whereas the open system pyrite formation can be modeled by the 1D-DAR or the 1D-DR model.
Rayleigh distillation model. The Rayleigh distillation model can be expressed as follows:
where δ34Ssw is the isotopic composition of seawater, δ34Sr is the isotopic composition of remaining sulfate in sediment porewater or in water column. f is the fraction of sulfate remaining, and α is the fractionation factor for DSR. The isotopic composition of H2S (δ34SH2S) or pyrite (δ34Spy, assuming negligible fractionation between H2S and pyrite) can be described as:
The amount of pyrite (Mpy) formation can be calculated by:
where ∅ is the porosity of sediment (estimated at 60%), ρpy is the density of pyrite (4.9 g cm–3), Mr is the relative molecular mass of pyrite, [SO4] is seawater/porewater sulfate concentration (mol L–1).
1D-DAR model. The 1D-DAR model can be applied to quantify the geochemical profiles in sediment porewater. The DAR model describes three physio-chemical processes: molecular diffusion, advection, and chemical reaction. During DSR in porewater, sulfate is supplied from seawater by diffusion. The diffusion is driven by the sulfate concentration gradient between seawater and sediment porewater, which is generated by sulfate consumption in sediment porewater by DSR. To model sulfur isotopic profiles of porewater, we treat 34S and 32S separately. The 1D-DAR model is expressed as:
where [3iSO4] is the porewater concentration of 34SO4 and 32SO4, z is the depth below the redox boundary of DSR, Ds is the vertical diffusivity coefficient of bulk sediment (m2 year−1), s is the sedimentation rate (cm ky−1), R is the first-order rate constant during DSR.
Sulfur isotopic fractionation during DSR can be regard as the different reaction rate constant between 34S and 32S. Assuming a steady state (\(\frac{{\partial \left[ {\,^{3\mathrm{i}}{\mathrm{SO}}_4} \right]}}{{\partial t}} = 0\), with invariant D, s, R), the solution of Eq. (4) is given by:
The porewater sulfur isotope (\({\mathrm{\updelta }}^{34}{{{\rm{SO}}_4}}_{{\mathrm{pw}}}\)) profile can be calculated by:
The subscript std denotes the standard. At any depth below the upper bound of DSR zone, the sulfur isotope of instantaneous H2S formation can be calculated by:
where ΔDSR is the biological sulfur isotope fractionation during DSR between sulfate and H2S.
Pyrite precipitation within sediment is a continuous process within the DSR zone with the lower bound marked by the depletion of porewater sulfate. To calculate the instantaneous sulfur isotope of pyrite within the DSR zone, we divide sediments into different depth slices (i) starting from the upper bound of DSR zone (i = 0). Assuming no sulfur isotope fractionation during pyrite precipitation between H2S and pyrite, δ34Spy at depth z can be calculated by:
The depth z of the slice i can be calculated as z = i × h, where h is the thickness of each slice. Assuming all H2S is precipitated as pyrite, the cumulative amount of pyrite formation within DSR (Mz) can expressed as:
1D-DR model. Pyrite can precipitate in porewater with H2S diffusion from overlying water column. This process can be quantified by the one-dimensional diffusion-reaction (1D-DR) model. This model includes two processes: H2S diffusion and pyrite precipitation. The sulfide diffusion is driven by the H2S concentration gradient between sulfidic seawater and sediment porewater, which is generated by pyrite precipitation in sediment porewater. The 1D-DR model is expressed as:
Where the [H3iS] is the porewater concentration of H34S and H32S, z is the depth below the water-sediment surface, Ds is the vertical diffusivity coefficient of bulk sediment (m2 year−1), R is the first-order rate constant for pyrite formation via H2S reaction with reactive Fe.
Assuming a steady state, the solution for this equation is,
δ34SH2S profile can be calculated by:
[3iS]std represents the standard of 34S or 32S. The instantaneous δ34Spy can be calculated by:
where Δpy represents the sulfur isotope fractionation during pyrite precipitation. The δ34Spy at depth z below water-sediment surface can be calculated by:
The cumulative amount of pyrite formation can be calculated by Eq. (9).
Sulfur isotope model for Δ33Spy–δ34Spy plot. Assuming all the Nantuo pyrite were formed within ferruginous porewater and pyrite formation was rapid and irreversible. δ34Spy was modeled by a sulfate concentration model37. In a steady state, sulfate concentration at specific depth can be expressed as:
where, \({\rm{SO}}_{{4}_{z}}\) represents sulfate concentration at any given depth z, \({\rm{SO}}_{{4}_{0}}\) represents the initial sulfate concentration, \({\rm{SO}}_{{4}_{\infty}}\) represent sulfate concentration at infinitive depth, i.e., sulfate left after DSR, k is sulfate reduction rate constant, s is the sedimentation rate.
As the little mass of 36S, here the equation of total mass of sulfate can be simplified as \({\rm{SO}}_{{4}_{{\rm{total}}}} = {\,}^{32}{\rm{SO}}_{{4}_{z}} + {\,}^{33}{\rm{SO}}_{{4}_{z}} + {\,}^{34}{\rm{SO}}_{{4}_{z}}\).
For sulfur isotope, Eq. (15) can be rewritten as:
Here, i equals 3 or 4.
δ3iS of porewater sulfate is controlled by the initial seawater sulfate δ3iS, sulfate reduction rate constant k, sedimentation rate s and sulfur isotope fractionation factor (α) for DSR37. Defined α as the ratio of sulfate reduction rate (SRR) of 33S or 34S over the 32S normalized with corresponding isotope concentration:
Then, Δ33S of porewater sulfate can be calculated:
where, 33λ is the slope of terrestrial mass fractionation line.
The instantaneous H2S sulfur isotopic compositions can be calculated by the ratios of DSR rate at corresponding depth:
Pyrite sulfur isotopic compositions can be calculated by the accumulated δ3iH2S.
Determination of pyrite concretion content
Pyrite concretion content was determined by using the photograph area proportion method. Pyrite concretion-bearing Nantuo diamictite and siltstone layer were photographed in field. For each field photograph, pyrite concretion content (Cpy) can be calculated by:
where Apy is pyrite concretion area in the photo and AT is the total area of host rock in the photo.
The average content of pyrite concretion in each section can be calculated by:
where n is the total number of analyzed field photographs.
Data availability
The data that support the findings of this study are available from the corresponding author upon reasonable request.
Change history
03 September 2018
This Article was originally published without the accompanying Peer Review File. This file is now available in the HTML version of the Article; the PDF was correct from the time of publication.
References
Hoffman, P. F., Kaufman, A. J., Halverson, G. P. & Schrag, D. P. A neoproterozoic snowball Earth. Science 281, 1342–1346 (1998).
Hoffman, P. F. et al. Snowball Earth climate dynamics and Cryogenian geology–geobiology. Sci. Adv. 3, e1600983 (2017).
Rooney, A. D., Strauss, J. V., Brandon, A. D. & Macdonald, F. A. A Cryogenian chronology: two long-lasting synchronous neoproterozoic glaciations. Geology 43, 459–462 (2015).
Macdonald, F. A. et al. Calibrating the Cryogenian. Science 327, 1241–1243 (2010).
Condon, D. et al. U-Pb ages from the neoproterozoic Doushantuo formation, China. Science 308, 95–98 (2005).
Kirschvink, J. L. Late proterozoic low-latitude global glaciation: the snowball Earth. The Proterozoic Biosphere: A Multidisciplinary Study. 51–52 (Cambridge University Press, New York, 1992).
Hoffman, P. F. & Schrag, D. P. The snowball Earth hypothesis: testing the limits of global change. Terra Nova 14, 129–155 (2002).
Bao, H., Fairchild, I. J., Wynn, P. M. & Spötl, C. Stretching the envelope of past surface environments: neoproterozoic Glacial Lakes from Svalbard. Science 323, 116–119 (2009).
Le Hir, G., Goddéris, Y., Donnadieu, Y. & Ramstein, G. A geochemical modelling study of the evolution of the chemical composition of seawater linked to a “snowball” glaciation. Biogeosciences 5, 253–267 (2008).
Pierrehumbert, R. T. High levels of atmospheric carbon dioxide necessary for the termination of global glaciation. Nature 429, 646–649 (2004).
Le Hir, G., Ramstein, G., Donnadieu, Y. & Goddéris, Y. Scenario for the evolution of atmospheric pCO2 during a snowball Earth. Geology 36, 47–50 (2008).
Cao, X. & Bao, H. Dynamic model constraints on oxygen-17 depletion in atmospheric O2 after a snowball Earth. Proc. Natl Acad. Sci. 110, 14546–14550 (2013).
Yang, J., Jansen, M. F., Macdonald, F. A. & Abbot, D. S. Persistence of a freshwater surface ocean after a snowball Earth. Geology 45, 615–618 (2017).
Stouffer, R. J. et al. Investigating the causes of the response of the thermohaline circulation to past and future climate changes. J. Clim. 19, 1365–1387 (2006).
Shields, G. A. Neoproterozoic cap carbonates: a critical appraisal of existing models and the plumeworld hypothesis. Terra Nova 17, 299–310 (2005).
Higgins, J. A. & Schrag, D. P. Aftermath of a snowball Earth. Geochem. Geophys. Geosyst. 4, 1–20 (2003).
Crockford, P. W. et al. Triple oxygen and multiple sulfur isotope constraints on the evolution of the post-Marinoan sulfur cycle. Earth Planet. Sci. Lett. 435, 74–83 (2016).
Lang, X. et al. Ocean oxidation during the deposition of basal Ediacaran Doushantuo cap carbonates in the Yangtze Platform, South China. Precambrian Res. 281, 253–268 (2016).
Sahoo, S. K. et al. Ocean oxygenation in the wake of the Marinoan glaciation. Nature 489, 546–549 (2012).
Huang, K.-J. et al. Episode of intense chemical weathering during the termination of the 635-Ma Marinoan glaciation. Proc. Natl Acad. Sci. 113, 14904–14909 (2016).
Jiang, G., Shi, X., Zhang, S., Wang, Y. & Xiao, S. Stratigraphy and paleogeography of the Ediacaran Doushantuo Formation (ca. 635–551Ma) in South China. Gondwana Res. 19, 831–849 (2011).
Crockford, P. W. et al. Linking paleocontinents through triple oxygen isotope anomalies. Geology 46, 179–182 (2017).
Zhang, Q. R., Chu, X. L. & Feng, L. J. Chapter 32 Neoproterozoic glacial records in the Yangtze Region, China. Geol. Soc. 36, 357–366 (2011).
Zhang, S., Jiang, G. & Han, Y. The age of the Nantuo Formation and Nantuo glaciation in South China. Terra Nova 20, 289–294 (2008).
Labidi, J., Cartigny, P., Hamelin, C., Moreira, M. & Dosso, L. Sulfur isotope budget (32S, 33S, 34S and 36S) in Pacific–Antarctic ridge basalts: a record of mantle source heterogeneity and hydrothermal sulfide assimilation. Geochim. Cosmochim. Acta 133, 47–67 (2014).
Seal, R. R. Sulfur isotope geochemistry of sulfide minerals. Rev. Mineral. Geochem. 61, 633–677 (2006).
Peters, M. et al. Sulfur cycling at the mid-atlantic ridge: a multiple sulfur isotope approach. Chem. Geol. 269, 180–196 (2010).
Wilkin, R. T. & Barnes, H. L. Formation processes of framboidal pyrite. Geochim. Cosmochim. Acta 61, 323–339 (1997).
Soliman, M. F. & El Goresy, A. Framboidal and idiomorphic pyrite in the upper Maastrichtian sedimentary rocks at Gabal Oweina, Nile Valley, Egypt: Formation processes, oxidation products and genetic implications to the origin of framboidal pyrite. Geochem. Cosmochim. Acta 90, 195–220 (2012).
Bottrell, S. H. & Newton, R. J. Reconstruction of changes in global sulfur cycling from marine sulfate isotopes. Earth Sci. Rev. 75, 59–83 (2006).
Canfield, D. E. The evolution of the Earth surface sulfur reservoir. Am. J. Sci. 304, 839–861 (2004).
Habicht, K. S. & Canfield, D. E. Sulfur isotope fractionation during bacterial sulfate reduction in organic-rich sediments. Geochim. Cosmochim. Acta 61, 5351–5361 (1997).
Böttcher, M. E., Smock, A. M. & Cypionka, H. Sulfur isotope fractionation during experimental precipitation of iron(II) and manganese(II) sulfide at room temperature. Chem. Geol. 146, 127–134 (1998).
Poulton, S. W. & Raiswell, R. The low-temperature geochemical cycle of iron: From continental fluxes to marine sediment deposition. Am. J. Sci. 302, 774–805 (2002).
Raiswell, R. & Canfield, D. E. Sources of iron for pyrite formation. Am. J. Sci. 298, 219–245 (1998).
Poulton, S. W. & Canfield, D. E. Ferruginous conditions: a dominant feature of the ocean through Earth’s history. Elements 7, 107–112 (2011).
Kunzmann, M. et al. Bacterial sulfur disproportionation constrains timing of Neoproterozoic oxygenation. Geology 45, 207–210 (2017).
Wang, J. & Li, Z. X. History of Neoproterozoic rift basins in South China: implications for Rodinia break-up. Precambrian Res. 122, 141–158 (2003).
Xiao, S. et al. Integrated chemostratigraphy of the Doushantuo Formation at the northern Xiaofenghe section (Yangtze Gorges, South China) and its implication for Ediacaran stratigraphic correlation and ocean redox models. Precambrian Res. 192-195, 125–141 (2012).
Li, C. et al. A stratified redox model for the Ediacaran ocean. Science 328, 80–83 (2010).
Hurtgen, M. T., Halverson, G. P., Arthur, M. A. & Hoffman, P. F. Sulfur cycling in the aftermath of a 635-Ma snowball glaciation: evidence for a syn-glacial sulfidic deep ocean. Earth Planet. Sci. Lett. 245, 551–570 (2006).
Lyons, T. W., Anbar, A. D., Severmann, S., Scott, C. & Gill, B. C. Tracking Euxinia in the Ancient Ocean: a multiproxy perspective and proterozoic case study. Annu. Rev. Earth Planet. Sci. 37, 507–534 (2009).
Lyons, T. W. & Gill, B. C. Ancient sulfur cycling and oxygenation of the early biosphere. Elements 6, 93–99 (2010).
Planavsky, N. J. et al. The evolution of the marine phosphate reservoir. Nature 467, 1088–1090 (2010).
Fike, D. A., Bradley, A. S. & Rose, C. V. Rethinking the ancient sulfur cycle. Annu. Rev. Earth Planet. Sci. 43, 593–622 (2015).
Bao, H., Lyons, J. R. & Zhou, C. Triple oxygen isotope evidence for elevated CO2 levels after a neoproterozoic glaciation. Nature 453, 504–506 (2008).
Zhou, C., Bao, H., Peng, Y. & Yuan, X. Timing the deposition of 17O-depleted barite at the aftermath of Nantuo glacial meltdown in South China. Geology 38, 903–906 (2010).
Acknowledgments
This study is supported by the Strategic Priority Research Program (B) of Chinese Academy of Sciences (Grant number XDB18000000), Natural Science Foundation of China (41322021) and State Key Laboratory of Palaeobiology and Stratigraphy (Nanjing Institute of Geology and Paleontology, CAS) (No. 183114). P.W.C. acknowledges funding from an NSERC PGS-D fellowship, and the Agouron Institute Postdoctoral Fellow Program.
Author information
Authors and Affiliations
Contributions
B.S. designed the project. X.L., B.S., K.H. and H.M. conducted field work. X.L., A.J.K., P.W.C. and Y.P. analyzed data. X.L., W.T. and B.S. performed modeling analyses. X.L., B.S., Y.P., S.X., C.Z., H.B. and Y.L. led data interpretation and developed the manuscript. All authors contributed to discussion and manuscript revision.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Lang, X., Shen, B., Peng, Y. et al. Transient marine euxinia at the end of the terminal Cryogenian glaciation. Nat Commun 9, 3019 (2018). https://doi.org/10.1038/s41467-018-05423-x
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-018-05423-x
This article is cited by
-
Cryogenian and Ediacaran integrative stratigraphy, biotas, and paleogeographical evolution of the Qinghai-Tibetan Plateau and its surrounding areas
Science China Earth Sciences (2024)
-
Mid-latitudinal habitable environment for marine eukaryotes during the waning stage of the Marinoan snowball glaciation
Nature Communications (2023)
-
Neoproterozoic Diamictite of the Luoquan Formation from the North China Block and Their Implications
Journal of Earth Science (2023)
-
Pyrite Concretions in the Lower Cambrian Niutitang Formation, South China: Response to Hydrothermal Activity
Journal of Earth Science (2023)
-
Active methanogenesis during the melting of Marinoan snowball Earth
Nature Communications (2021)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.