Abstract
The Bloch–Siegert shift is a phenomenon in NMR spectroscopy and atomic physics in which the observed resonance frequency is changed by the presence of an off-resonance applied field. In NMR, it occurs especially in the context of homonuclear decoupling. Here we develop a practical method for homonuclear decoupling that avoids inducing Bloch–Siegert shifts. This approach enables accurate observation of the resonance frequencies of decoupled nuclear spins. We apply this method to increase the resolution of the HNCA experiment. We also observe a doubling in sensitivity for a 30 kDa protein. We demonstrate the use of band-selective Cβ decoupling to produce amino acid-specific line shapes, which are valuable for assigning resonances to the protein sequence. Finally, we assign the backbone of a 30 kDa protein, Human Carbonic Anhydrase II, using only HNCA experiments acquired with band-selective decoupling schemes, and instrument time of one week.
Similar content being viewed by others
Introduction
In driven two-level quantum systems, the Bloch–Siegert shift is a perturbation of the observed resonance frequency caused by an off-resonance field1,2,3,4,5. The observed spin is subjected to its intrinsic Larmor precession as well as an oscillating field. After dynamical averaging of the oscillatory field, the resulting average Hamiltonian contains an apparent shift in the Larmor frequency, compared with its intrinsic value6. In nuclear magnetic resonance (NMR) spectroscopy, simultaneous application of radiofrequency (RF) pulses at a range of frequencies is common, especially for decoupling purposes. When the coupled spin is nearby in frequency to the observed spin, the decoupling pulse induces a Bloch–Siegert shift7,8. This prevents accurate observation of the resonance frequencies and causes severe phase distortions to the observed resonance peaks9. However, decoupling has important benefits: increased signal-to-noise ratio and improved resolution due to the collapse of multiplet line shapes. Decoupling is especially important in protein spectroscopy, because of the large number of resonances in limited spectral space.
The HNCA is a prototypical NMR triple-resonance experiment. It is necessary for sequential assignment of protein backbones10,11,12. For large proteins, its TROSY version13 is the most sensitive of the triple-resonance experiments that yield sequential connectivities14. For comparison, the sensitivity of the HNCACB experiment, typically used to resolve assignment ambiguities, is ~25% of the HNCA for high-molecular-weight proteins at high field14. In principle, the HNCA alone provides enough information for complete sequence-specific assignment. In practice, however, there is insufficient dispersion of Cα chemical shifts. This leads to degeneracies in peak position, which prevent unambiguous assignment.
Deuteration of the protein slows the Cα relaxation and increases the achievable resolution15. For large (≥ 30 kDa) deuterated proteins in high fields, resolution of 4–8 Hz in the Cα dimension is possible based on the relaxation rates16. However, with uniform sampling of the Nyquist grid, collecting sufficient indirect increments for this level of resolution would require instrument time on the order of months. However, high resolution is readily accessible, in feasible acquisition time (i.e., 2–3 days), using non-uniform sampling (NUS)17,18,19. In contrast, Cβ-encoding incurs relaxation losses due to longer delays for magnetization transfer and CO spins suffer from a large chemical shift anisotropy and relax quickly in high fields. Therefore, the achievable resolution is poor and the sensitivity is low for experiments that encode or transfer through Cβ or CO. This suggests that the ability to assign challenging proteins using only the HNCA is of considerable interest.
The Cα–Cβ coupling splits the peaks into doublets in the Cα dimension. This J-splitting is undesirable because it halves the sensitivity and the larger footprint contributes to crowding and overlaps. There are several ways to decouple this splitting; however, each technique has its own difficulties. The constant time experiment20,21 lets the Cα evolve for a multiple of 1/J, so that the coupling modulation envelope refocuses. However, the Cα needs to be transverse for long times even to encode short indirect increments. To obtain high resolution, indirect time periods of up to 100 ms are needed and the peaks are almost completely lost to relaxation under a multiple constant time approach16. It is also possible to remove the splitting computationally, known as virtual decoupling22. The algorithm must be tuned to a specific coupling magnitude. However, any given protein can contain a range of couplings (33–42 Hz) and differences between the deconvolution setting and the actual coupling values lead to poor line shapes in the case of long indirect acquisition times16. A third scheme is to apply weak trains of decoupling pulses to the Cβ regions. This produces singlets;7 however, the decoupling pulses generate Bloch–Siegert shifts. Correcting the peak list by approximately removing the effect (after acquisition) is possible by calibrating a best-fit model of the theoretical shift. However, this is cumbersome. Another significant problem with this technique is that, in practice, it does not produce the expected doubled peak height from collapsing a doublet into a singlet7,22, due to off-resonance effects from the decoupling field.
In this work, we use a single, optimized shaped pulse in the middle of the indirect encoding period to simultaneously refocus the Cα–Cβ and Cα–CO couplings. The key insight is that decoupling can be done without causing any Bloch–Siegert shift in the Cα resonance frequency, by explicitly optimizing the pulse for the desired Cα behavior. As we require a different response from the Cα and nearby Cβ resonances, we have used optimal control theory the design the shaped pulses23,24,25,26,27.
During the optimized decoupling pulses, the Cα spins precess according to their chemical shift frequencies, whereas the Cβ and CO spins are inverted. The coupling refocuses during the second half of the encoding period. This approach is robust to different magnitudes of J couplings. We set up a cost/reward function that encourages Cα to follow its natural precession in the transverse plane while Cβ and CO transition from + Iz to − Iz. Pulsing on Cβ necessarily perturbs the trajectory of the nearby Cα spins; however, Bloch–Siegert shifts can be avoided by incorporating a target final Cα state into the optimization. This approach avoids the severe phase distortions that arise if Cβ is selectively inverted without controlling the behavior of Cα. Phase distortions caused by the Bloch–Siegert shift are problematic even for inversion of the relatively isolated CO resonances, which is why the standard HNCA pulse program contains Bloch–Siegert compensation pulses9.
The shaped pulses we have designed here are named gradient optimized CO decoupling pulse (GOODCOP) and beta/alpha decoupling pulse (BADCOP). The latter has three variations targeted to specific Cβ chemical shifts, BADCOP1, BADCOP2, and BADCOP3.
We have tested GOODCOP and BADCOP1–3 on two protein samples. The first is Protein G, B1 domain (GB1). The second is 30 kDa Human Carbonic Anhydrase II (HCAii) measured at 25 °C. By comparing the standard HNCA pulse program with our new method, we demonstrate that we induce no Bloch–Siegert shifts or phase distortions, and decoupled Cα peaks exhibit the expected doubling in sensitivity. Partially decoupled peaks, with Cβ near the edge of the inversion bandwidth, also exhibit sensitivity gains. The sensitivity gain available by using BADCOP1 decoupling and the absence of any Bloch–Siegert shifts are demonstrated on HCAii in Fig. 1. Finally, we demonstrate that by using several different decoupling pulses (BADCOP1–3), we can extract sufficient residue-specific information for backbone assignment, without the need for additional triple-resonance experiments. We demonstrate 85% assignment of HCAii using only HNCA experiments, with GOODCOP and BADCOP1–3 decoupling pulses.
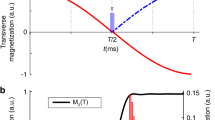
Sensitivity gain using BADCOP1. HN-Cα planes of HNCA were acquired on a 700 μM sample of HCAii, using the standard pulse program as well as with optimized decoupling of Cβ below 35 p.p.m. and CO using BADCOP1. a Overlay of a section of the two spectra, showing that with BADCOP1 some peaks have collapsed into singlets in the Cα dimension, whereas some remain doublets, depending on Cβ chemical shift. The full spectrum is in Supplementary Fig. 6. b 1D carbon trace through point H = 8.66 p.p.m. Decoupled peaks show the expected twofold gain in sensitivity, but not all peaks are decoupled. The decoupling pulse BADCOP1 has not caused any Bloch–Siegert shifts. c Skyline projection onto the 1 H axis (minus 1.2 arbitrary units to put the baseline at 0). The area under the curve is 48% larger for the version using BADCOP1. d Scatter plot to compare the two skyline projections. Two broad trends are visible: along the line y = x, the sensitivities are equal. Along the line y = 2x, the sensitivity is doubled by using BADCOP1. Partial decoupling, for Cβ near the boundary of the inversion bandwidth, produces points between the two trend lines. Anything above the line y = x indicates a gain in sensitivity. All acquisition, processing, and display settings are the same for the two spectra
Results
In this section we describe the newly developed pulse design methods, the experimental tests, and the assignment of HCAii using only the HNCA experiment.
Design of GOODCOP for CO inversion with C α encoding
GOODCOP is designed to have a different effect on Cα vs. CO spins. That is, all CO spins will be inverted, whereas the Cα spins will each precess at a rate proportional to their respective chemical shifts. The initial density matrix of any Cα spin, ρ(0), reaches a final state ρ(T) at the end of the pulse that has evolved under the unitary dynamics U = exp(− iωaTIz). Here, T is the pulse duration, ω is the chemical shift, Iz is the appropriate su(2) basis element for rotation about the z-axis (e.g., a Pauli matrix), and a is a constant that scales the rate of evolution. T′ = aT can be thought of as a contracted time, during which the spin evolves in the transverse plane at its intrinsic chemical shift frequency ω.
If a = 1 then there is no contraction; T′ = T and the Cα spins evolve at their natural chemical shift frequencies (as although there were no off-resonance pulse at all). However, provided that a is a constant we can ensure that there is no Bloch–Siegert shift by calculating the indirect increment accounting for the contracted time T′ = aT. In fact, other homonuclear decoupling methods also scale down the speed of the evolution in a similar way28,29 and a similar approach can be used to scale up J-splittings30. In our case, the scaling is only present during the relatively short pulse duration, not during the entire encoding period. Thus, the total (unscaled) time to encode a desired increment is only increased by a few microseconds because of the contracted time (which causes negligible relaxation compared with a maximum encoding time of up to 100 ms). As off-resonance pulsing on the coupled spin will interfere with the Cα dynamics during the pulse, setting a to a value < 1 allows the optimization some freedom for the Cα to deviate from their natural trajectory, as long as they end up at the desired final state at the end of the pulse. The desired behavior of the Cα is a universal rotation; we need the pulse to take any input state and produce the corresponding rotated output state.
In contrast, the required CO behavior is a point-to-point rotation. Specifically, if 165 < ω < 185 p.p.m., then we require only that longitudinal magnetization is inverted (i.e., ρ(0) = Iz is inverted to ρ(T) = − Iz). Regardless of the initial spin state of the CO (e.g., transverse or longitudinal), this point-to-point specification is necessary and sufficient for decoupling.
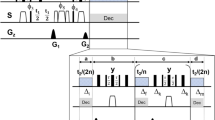
Based on numerical experimentation and on hardware requirements, we chose a pulse duration of 150 μs, a maximum RF amplitude of 15 kHz, and set a = 0.9. This means that the Cα will acquire phase of ωT′ = ω(0.9T) during the pulse, i.e., T′ = 135 μs of evolution time at the intrinsic chemical shift frequency ω. Therefore, for a desired indirect evolution period of t1, we should let the spins evolve for d0 = 0.5(t1 − aT), then run the shaped pulse, then evolve a further d0. This takes t1 + 15 μs in real time, but only produces t1 worth of chemical shift encoding. There is 15 μs of overhead. The coupling changes sign in the middle of t1, when we run the pulse, and therefore refocuses exactly at the end of the encoding period. The minimum possible evolution time with the GOODCOP pulse is 135 μs, which occurs when d0 = 0. A conditional statement (“if statement”) skips the pulse for shorter indirect increments. Pulse sequence diagrams for this scheme, for regular HNCA as well as TROSY-HNCA, are given in Supplementary Fig. 1 and Supplementary Fig. 2.
The pulse shape optimization was conducted by sampling a set of 100 chemical shifts uniformly spaced in the Cα range ω ∈ [35,75] p.p.m. We alternate their initial states between Ix and Iy, and set their desired final states to ρ(T) = Uρ(0)U† where U = exp(− iωaTIz), a = 0.9, and T = 150 μs. By linearity, we can expect appropriate input/output behavior for any initial state in the transverse plane. We can also expect that any longitudinal magnetization will be preserved for these chemical shifts, since the net rotation is constrained to the z-axis. We further sampled 30 chemical shifts from the CO range ω ∈ [165, 185] p.p.m. and set their initial states to Iz and desired final states to − Iz. We randomized the initial pulse shape and ran the GRAPE algorithm. We used our new implementation of GRAPE, set up in a toggling frame, to ensure that optimization converged quickly31. This speed helped a great deal when experimenting numerically with pulse duration and other parameters.
Experimentally, the pulse decouples the CO without producing any Bloch–Siegert shifts in the Cα resonance frequency (Supplementary Fig. 3). In contrast, using an off-resonance decoupling pulse such as WURST or hyperbolic secant leads to clear Bloch–Siegert shifts (Supplementary Fig. 4). Spectra recorded with GOODCOP on HCAii and GB1 are essentially identical to spectra acquired with a standard HNCA pulse program (although we note that our approach saves 576 μs of Cα relaxation compared with the standard method, which uses an intricate system of extra pulses and delays to address the Bloch–Siegert shift). In particular, the sensitivity is the same and the peaks appear in the same (unshifted) locations, without any phase distortions. Next, we expand the method to include Cβ inversion, which is far more useful.
BADCOP for CO and C β inversion during C α encoding
In this subsection, we explain the BADCOP1 design method. Specifically, we add the requirement that Cβ is inverted during the pulse, so that the Cα–Cβ coupling can be refocused.
We chose a pulse duration of 1 ms. In general, longer pulse durations could produce more selective decoupling. Note that this 1 ms of pulsing occurs during the Cα encoding delay, and therefore it does not contribute additional time or relaxation losses to the experiment. Instead, the overhead is (1 − a)T (i.e., < 100 μs) due to the slightly slowed encoding of Cα during the pulse. This slowed encoding is uniform across the Cα bandwidth and is accounted for by adjusting the indirect evolution time as described above; therefore, it creates no Bloch–Siegert shift.
We sampled 100 chemical shifts ω ∈ [40,72] p.p.m., alternated their initial states between Ix and Iy, and set their desired final states to ρ(T) = Uρ(0)U† where U = exp(− iaωTIz), a = 0.91, and T = 1 ms. Further chemical shifts were sampled, 30 from ω ∈ [165, 185] p.p.m. and 60 from ω ∈ [5,37] p.p.m., and for these the optimization was set up to require that longitudinal magnetization is inverted. The value of a = 0.91 was determined by numerical exploration, but other values a close to a = 1 also work well. The resulting optimized pulse is BADCOP1, which is depicted in Fig. 2 along with spin-dynamics simulations. The trajectories of individual spins are given in Supplementary Fig. 5. In particular, the Cα spins take a highly irregular trajectory during the pulse, but at the end of the pulse they end up in the same state as if they had evolved without any decoupling pulse for the contracted time T′ = 910 μs. At the same time, the Cβ and CO spins take different trajectories, but end up inverted at the end of the pulse. The spin trajectories during the pulse are all highly intricate, in order to simultaneously achieve the various desired spin-state transitions for Cα, Cβ, and CO with high fidelity.
RF profile and simulation of BADCOP1. a The shaped pulse “BADCOP1” RF amplitude and phase profiles. Note that there are no abrupt changes in amplitude or phase. On an 800 Mhz spectrometer the maximum power is 5.94 kHz (100% amplitude) and the duration is 1 ms. For other field strengths, these values can be scaled appropriately to maintain the same bandwidths and flip angles. b Simulation assuming an initial state of ρ(0) = Ix. We see sinusoidal chemical shift encoding in the transverse plane for the Cα region. This behavior was explicitly built into the optimization. Outside of the Cα region off-resonance effects take over and the encoding is lost. c Simulation assuming an initial state of ρ(0) = Iy also shows encoding. By linearity, the pulse is producing a universal rotation about the z-axis for the Cα region, with rotation angle proportional to chemical shift frequency. d Simulation assuming an initial state of ρ(0) = Iz. The longitudinal magnetization is inverted for all CO and for Cβ below about 35 p.p.m. This leads to selective decoupling of resonances in these two regions. The pulse can be run in the middle of an arbitrary-duration indirect encoding period to refocus resonances, without inducing any Bloch–Siegert shifts
Band-selective C β decoupling with CO inversion
Two additional BADCOP pulses were designed to selectively invert subsets of the Cβ bandwidth. Specifically, we follow the general setup of the previous subsection, but vary the chemical shift range that is inverted. We also specifically optimize the pulses to not invert (i.e., to preserve) longitudinal magnetization for Cβ outside of the desired selective decoupling bandwidth. The idea is to encode information about the Cβ from the Cα line shapes in the HNCA, instead of from the HNCACB experiment. As the additional transfer time in the HNCACB (compared with the HNCA) results in large relaxation losses, selective decoupling of certain Cβ is a viable alternative to transferring magnetization to and from Cβ, especially for high-molecular-weight systems.
Table 1 summarizes the pulses we have tested, including GOODCOP and the various versions of BADCOP. In particular, the pulse BADCOP3 inverts chemical shifts ω ∈ [10,45] p.p.m. This includes Cβ for most amino acids. The exception is the two downfield shifted Cβ of serine and threonine. However, for this pulse the desired Cα behavior (precession in the transverse plane) is achieved only above ~47 p.p.m., which excludes the glycine Cα. As a result, glycine Cα are perturbed (i.e., they have reduced amplitude and/or are poorly phased) with BADCOP3.
The benefit of this suite of decoupling pulses is that by acquiring multiple spectra, and examining which resonances are doublets or singlets in each, we can identify the approximate Cβ frequency and narrow the choice of sequential candidates during the assignment procedure. Figure 3 shows examples of line shapes that we observe using the various BADCOP pulses and how these line shapes encode Cβ chemical shift frequencies. It is worth mentioning that splitting patterns and line shapes are always identical in the internal peak and its sequential match. That is, if a certain peak is a singlet under one decoupling pulse and doublet for another decoupling pulse, then it can only be matched to a peak that follows the same pattern. In particular, this is true right at the boundary of the inversion bandwidth where we can see partially decoupled peaks with distinctive line shapes (i.e., with some narrowing and sensitivity gain). In general, true matches have a high correlation coefficient (between the internal and sequential line shape) irrespective of decoupling sequence32,33. In cases of chemical shift degeneracy, correct matches must correlate well for all decoupling pulses. If there is any exception, then they have different Cβ frequencies and are therefore not a correct match. We show examples of how matching across multiple spectra, acquired with different decoupling pulses BADCOP1–3, resolves ambiguities in Fig. 4 and Supplementary Fig. 6. Specifically, some candidate sequential matches can be excluded, because their appearance using BADCOP1 is not the same as the appearance of the internal peak, even though the Cα resonance frequency is identical. This is analogous to resolving ambiguities using the HNCACB. Examples of how the additional information can be used to assign sequential matches onto the primary sequence are given in Fig. 5. Generating different line shapes in order to dramatically reduce the number of possible assignments can also be approached biochemically, using selective Cβ isotope labeling16.
Experimental observation of amino acid-specific line shapes using BADCOP1–3. a Simulated Cβ inversion profiles with the three decoupling pulses BADCOP1–3. The initial state is ρ(0) = Iz, and the final longitudinal magnetization is depicted. The mean Cβ chemical shift from the BMRB is indicated for the various amino acids. b Peaks selected from four 2D HNCA planes of HCAii, acquired with the standard pulse program (left column) and with the three different optimized decoupling pulses (columns 2–4; BADCOP1–3). The same peak is represented in each row. The peaks are either singlets or doublets depending on Cβ chemical shift. Therefore, the patterns code for the Cβ and indirectly for the amino acid type. The selectivity is not perfect in all cases (due to secondary shifts moving the Cβ). Note that there are no Bloch–Siegert shifts; all peaks appear at the correct Cα position (i.e., the same as the standard sequence in the leftmost column). Of particular interest is the loss of upfield glycine Cα (row 6) using BADCOP3 and the slightly different line shape patterns between the two aspartic acid Cα, indicating different Cβ chemical shifts (rows 2 and 3). The alanine pattern is unique (row 5). All acquisition, processing, and display settings are the same for the four spectra
Using BADCOP1–3 line shapes and splitting patterns for sequential matching. In the 3D HNCA of HCAii, tyrosines 190Y and 40Y are overlapped in the Cα dimension, as are the sequential peaks in their respective i + 1 residues. This produces an ambiguity in the sequential assignment, which could be resolved using an HNCACB experiment. a The four HNCA strips, recorded using GOODCOP. All peaks are doublets and the chemical shifts are the same, generating an ambiguity in the sequential assignment. b Using BADCOP1, two of the peaks are partially decoupled and become broad singlets. The other two remain doublets. This resolves the ambiguity in the sequential matching process and implies that 190Y and 40Y have different Cβ chemical shifts. c Using BADCOP2, the same decoupling pattern appears in this case. In some cases (depending on Cβ shift), different line shapes are observed with BADCOP1 vs. BADCOP2. d With BADCOP3, all the peaks appear as singlets with doubled height compared with the doublets. The sequential peak for 190Y at 55.4 p.p.m. is more clearly visible above the noise. All acquisition, processing, and display settings are the same for the four spectra
Using BADCOP1–3 line shapes and splitting patterns for sequential assignment. a Strips from a 3D HNCA experiment of HCAii. Glycines appear as singlets and have Cα chemical shifts around 45 p.p.m. The strip identified as “82 G” has an internal and a sequential glycine peak, and the sequential is matched to the strip “81 G”. Two neighboring glycines only occur once in the primary sequence, so these strips can be unambiguously assigned. b In contrast, most peaks appear as doublets because of the Cα–Cβ coupling. These can be be sequentially matched, but assignment onto the primary sequence is difficult without further data or long chains of sequential correlations. c Using three BADCOP decoupling pulses gives residue-specific information. The three leftmost strips (the same strips as in b) show a particular sequence of different splitting patterns under the various decoupling pulses, as described in Fig. 3a. This pattern is only consistent with one location on the primary sequence of HCAii and so these can be unambiguously assigned. Further sequential matches show splitting patterns consistent with the primary sequence and the expected splitting patterns based on Fig. 3a. This gives many opportunities to make or confirm assignments. All acquisition and processing settings are the same for the four spectra, while strip contour levels are set individually for visual clarity. An expanded version of this figure is included as Supplementary Fig. 8
In the next section, we show that these homonuclear decoupling pulses perform well in experiments on simple (GB1) and challenging (HCAii) protein samples. In particular, we show that the Cβ-specific information is sufficient for assignment.
Experimental validation on GB1
We have applied the optimized homonuclear decoupling pulses in HNCA experiments, and compared the results with the standard implementation. The decoupled Cα peaks do indeed become singlets and that the sensitivity gain is substantial (i.e., double).
GB1 is well known as a simple NMR model system. We recorded HN-Cα planes using the HNCA pulse program, in order to observe the resulting line shapes and verify the basic operation of the optimized decoupling pulses. We tested GOODCOP by collecting two-dimensional (2D) HN − Cα planes with no decoupling at all vs. with GOODCOP. The results are as expected; the 55 Hz coupling to the CO is removed. Moreover, no Bloch–Siegert shifts are present (Supplementary Fig. 3). Next, Cβ decoupling was tested by applying BADCOP. We acquired 2D HN − Cα planes with various selective Cβ decoupling schemes. In Supplementary Fig. 6, we show how the resulting line shape depends on the Cβ chemical shift. This can be used to resolve ambiguous sequential correlations and narrow the choice of possible assignments.
Backbone assignment of HCAii using BADCOP
The protein HCAii has a molecular weight of 30 kDa with a correlation time of 18 ns at 25 °C, which represent reasonably challenging conditions on which to test the GOODCOP and BADCOP decoupling pulses.
Initially, we acquired 2D HN − Cα of the HNCA. We collected four 2D planes: one plane using the regular HNCA pulse program and the other three planes using Cα − Cβ decoupling pulses BADCOP1–3. To measure the overall sensitivity we took skyline projections onto the 1H axis. Figure 1c shows these projections for the regular pulse program as well as for one of our decoupling pulses, BADCOP1. It is clear that a majority of peaks display higher intensity in the presence of decoupling using BADCOP1. To roughly quantify the overall sensitivity gains, we can calculate the area under the skyline projections. Compared with the regular pulse program, we see an overall enhancement of 48%. A more nuanced measure of the sensitivity improvement is to compare the skylines point-by-point, as in Fig. 1d (and also Supplementary Fig. 7E–G). In these scatter plots, two broad trends are readily apparent. Along the line y = x the two skylines are approximately equal, indicating no sensitivity gain. Along the line y = 2x, BADCOP1 decoupling has collapsed doublets into singlets for a twofold improvement. Similar analyses were done for the other BADCOP pulses and all these spectra showed substantial improvements in sensitivity (Supplementary Fig. 7). Depending on the decoupling pulse, we see different densities of points along the two trend lines (equal and doubled sensitivity).
In particular, BADCOP3 decouples Cβ up to about 43 p.p.m. This interferes with the glycine Cα encoding. Therefore, we see many instances of degraded performance (points below the line y = x), corresponding to affected glycines (Supplementary Fig. 7F). We also see that most other peaks have doubled intensity; the line y = 2x is densely populated. If we restrict the skyline projection to Cα > 47 p.p.m. then the glycines are excluded from the projection (Supplementary Fig. 7G). Most of the peaks from the other residues fall on the double-sensitivity line, y = 2x.
We also analyzed four three-dimensional (3D) HNCA spectra of HCAii. We obtained amino acid-specific information by examining the splitting patterns under different decoupling pulses and this allowed us to assign the backbone using only a set of HNCA experiments acquired in less than 1 week of total instrument time. We emphasize that our 3D spectra are recorded using NUS, in order to access high resolution in the Cα dimension.
The observed resonances were classified into possible amino acids using the coding of line shapes and splitting patterns (Fig. 3) and sequentially matched (Fig. 4). Short chains of sequential correlations could then be unambiguously located on the primary sequence (Fig. 5). Longer chains of correlations provide additional confidence in the assignments (Supplementary Fig. 8 and Supplementary Fig. 9). Proceeding in this manner, 85% of the sequence was assigned. Practically speaking, almost all the observed amide resonances were successfully assigned. However, only around 85% of the expected number of systems were observed in the spectrum. The missing peaks are largely from the core of the protein, suggesting that there has been incomplete back-exchange of deuterons during sample preparation. Our spectra are missing these peaks altogether, preventing complete assignment.
Comparison with existing decoupling pulses
Standard selective decoupling pulses shift the Cα resonances away from their intrinsic positions. However, we have designed our pulses to avoid such Bloch–Siegert shifts. A second drawback of selective dynamical decoupling using established shaped pulses is that the glycine Cα peaks are perturbed due to their proximity to the decoupling region7. This introduces strong cycling sideband artifacts, i.e., spurious satellite peaks that take magnitude away from the true peaks.
We have collected 2D HN − Cα planes of HCAii using the methods of Matsou et al.7, with the same acquisition and processing parameters that were used to test the GOODCOP and BADCOP pulses. We observe the strong decoupling sidebands on glycine, and also observe smaller sidebands for other (non-glycine) peaks (Supplementary Fig. 4 and Supplementary Fig. 10). These satellite peaks reduces the height of their respective main peaks and make the spectrum more difficult to interpret. Moreover, the magnitudes of the Bloch–Siegert shift are different depending on which sort of selective pulses is used (e.g., WURST or hyperbolic secant) and exactly where they are centered. This makes it difficult to compare various spectra recorded with different pulse sequences, magnetization transfer pathways, and field strengths. Furthermore, accurate 13C chemical shift data are required for bond angle determination in structure calculations34, so decoupling pulses that influence observed resonance frequencies are to be avoided.
In addition to the unwanted Bloch–Siegert shifts, we also compared the sensitivity of selectively dynamically decoupled spectra (using WURST and hyperbolic secant) to our approach using GOODCOP and BADCOP. For CO decoupling only, the sensitivities are almost identical for the standard pulse program, selective decoupling, and GOODCOP. However, selective decoupling using either WURST or hyperbolic secant (30 p.p.m. decoupling band, centered at 170 p.p.m.) introduces Bloch–Siegert shifts. These spectra are shown in Supplementary Fig. 4. When decoupling Cβ in addition to CO using WURST or hyperbolic secant, we do not observe the expected doubling of sensitivity. Unlike BADCOP, selective decoupling with WURST or hyperbolic secant suffers from sidebands and off-resonance effects, which diminish the heights of the real peaks and therefore lower sensitivity. We compared the empirical sensitivity for various attempts at selective decoupling and it is clear that spectra recorded with BADCOP have significantly higher overall sensitivity (Supplementary Fig. 11).
Discussion
We have presented practical methods for homonuclear decoupling pulse design that completely avoid Bloch–Siegert shifts. The pulses were designed using the methods of optimal control, aided by rapid convergence techniques. The same pulses are applicable for other experiments that encode Cα. For example, GOODCOP can be used to decouple Cα from CO in a 13C-HSQC and the series of BADCOPs can be used to remove the coupling from Cβ in addition to CO. The use of these decoupling pulses in 13C-HSQC will especially find use in residual dipolar coupling measurements.
More generally, the pulse design methods we have developed are readily applicable to other homonuclear decoupling applications, as long as there is some frequency separation between the observed and decoupled spins. For example, one can remove Cγ and Cβ couplings and record high-resolution 13C-HSQC for methyl resonances for amino acids such as alanine, isoleucine, and valine, where the methyl resonances are separated from the coupled side-chain resonance. This pulse design can also be used to remove 13C − 13C coupling of DNA/RNA bases and polysaccharides. In addition, similarly designed pulses can be used to remove 19F − 19F couplings without any Bloch–Siegert shift. Similar to GOODCOP and BADCOP, any such decoupling pulse can be transferred to any field strength by appropriate scaling of the duration and RF power level.
The decoupling pulses that we have designed perform very well for collapsing the Cα doublets in the HNCA. The Bloch–Siegert shift was removed by explicitly optimizing for Cα to continue precessing while Cβ and CO invert. By targeting the inversion to a few specific Cβ regions, we generated sufficient amino acid-specific information for assignment using only HNCA. Experimental tests show the expected doubling of sensitivity for decoupled spins, in contrast to previous efforts to dynamically decouple Cβ from Cα. Therefore, the new decoupling shaped pulses are highly suitable for NMR spectroscopy.
Methods
Sample preparation
First, we used a sample of 1 mM GB1. The sample is fully 13C, 15N labeled, and perdeuterated, and created following established protocols35.
Second, we used a 13C, 15N-labeled sample of the protein HCAii at a concentration of 700 μM. The correlation time is 18 ns at 298 K. We expressed and purified HCAii following established protocols36,37. Briefly, we transformed BL21(DE3)pLysS Escherichia coli cells (EMD Millipore) with a pACA plasmid containing the gene for HCAII (a kind gift from Carol Fierke and coworkers at the University of Michigan) and grew the transformed cells to an OD600 of 0.4–0.8 in M9 minimal medium (6 g/L Na2HPO4, 3 g/L KH2PO4, 0.5 g/L NaCl, 0.25 g/L MgSO4, 14 mg/L CaCl2, 100 M ZnSO4, 2 g/L d-13C-glucose (Cambridge Isotopes), 2 g/L 15NH4Cl (Cambridge Isotopes), and 100 mg/L ampicillin) in D2O. The medium was further supplemented with the trace elements (50 mg/L EDTA, 8 mg/L FeCl3, 0.1 mg/L CuCl2, 0.1 mg/L CoCl2, 0.1 mg/H3BO3, and 0.02 MnCl2) and the vitamins Biotin (0.5 mg/L, Sigma) and Thiamin (0.5 mg/L, Sigma). Protein expression was induced with 0.25 mM isopropyl β-d-1-hiogalactopyranoside and 450 mM ZnSO4 were added to ensure full Zn-ion occupancy in the HCAii active site. Protein expression was allowed to continue for 20–24 h after induction, at 25 °C.
We then collected the cells by centrifugation at 5000 r.p.m. for 15 min and purified 2H-, 13C-, and 15N-labeled HCAii following a previously described procedure38, with small modifications. Briefly, we re-suspended the cells into BPER protein extraction buffer (Thermo Scientific), containing 1 mM MgSO4, 1 mM N-p-tosyl-l-arginine methyl ester, 3 mM tris(2-carboxyethyl) phosphine, 2.5 mM ZnSO4, and 1 M phenylmethanesulfonyl fluoride. We then lysed the cells with a tip sonicator (VWR Scientific) at 70% amplitude, added 0.125 μg/mL lysozyme (Sigma) and 10 U/mL DNase I (Life Technology) to the lysed solution and incubated it in an incubator shaker for 2 h. HCAii was subsequently purified from cell lysate with (i) two rounds of precipitation with ammonium sulfate at room temperature (60% and 90% v/v with a solution of saturated ammonium sulfate, respectively), (ii) dialysis into Tris-SO4 buffer (50 mM in H2O, pH = 8.0) at 4 °C, (iii) anion exchange chromatography with a Q Sepharose Fast Flow resin (GE Healthcare), (iv) size-exclusion chromatography with a Superdex 75 resin (GE Healthcare), and (v) dialysis into NMR buffer (10 mM Na2HPO4/NaH2PO4 in H2O, pH = 7.6). Finally, we incubated HCAii overnight at 40 °C to exchange amide-bound deuterons to protons and added 5% D2O for NMR measurements. All measurements were recorded on a 700 μM sample.
NMR experiments
NMR data collection of GB1 samples was performed on a Bruker 800 MHz instrument equipped with a cryogenically cooled TXO probe. The 2D HN − Cα plane of a TROSY-HNCA pulse sequence in Supplementary Fig. 2 was used. Sweep widths for the 1H and 13C dimension were 12820 and 6036 Hz, respectively. Data collection on the HCAii sample was performed on a Bruker 750 MHz instrument equipped with a cryogenically cooled (TCI) probe. The TROSY-HNCA pulse sequence in Supplementary Fig. 2 was used. Sweep widths for the 1H, 15N, and 13C dimension were 12,019, 2735, and 4901 Hz, respectively. The indirect dimensions were sampled non-uniformly, selecting 458 out of a matrix of 40 × 300 (15N ×13C) complex points (4% sampling). The sampling schedule was selected based on the Poisson gap sine weighted protocol.
Code availability
The pulse sequences (Supplementary Fig. 1 and Supplementary Fig. 2), GOODCOP/BADCOP shaped pulse files, and parameter set (all for Bruker Spectrometers) can be obtained from http://artlab.dana-farber.org/downloads. This webpage also has instructions for implementing the pulses at any magnetic field strenth.
Data availability
Other data supporting the findings of this manuscript are available from the corresponding author upon reasonable request.
References
Bloch, F. & Siegert, A. Magnetic resonance for nonrotating fields. Phys. Rev. 57, 522–527 (1940).
Shirley, J. H. Solution of the Schrödinger equation with a Hamiltonian periodic in Time. Phys. Rev. 138, B979–B987 (1965).
Haeberlen, U. & Waugh, J. S. Coherent averaging effects in magnetic resonance. Phys. Rev. 175, 453–467 (1968).
Stenholm, S. Saturation effects in RF spectroscopy. I. General theory. J. Phys. B: At. Mol. Phys. 5, 878 (1972).
Ramsey, N. F. Resonance transitions induced by perturbations at two or more different frequencies. Phys. Rev. 100, 1191–1194 (1955).
Llor, A. Equivalence between dynamical averaging methods of the Schrödinger equation: average Hamiltonian, secular averaging, and Van Vleck transformation. Chem. Phys. Lett. 199, 383–390 (1992).
Matsuo, H., Kupce, E., Li, H. & Wagner, G. Increased sensitivity in HNCA and HN(CO)CA experiments by selective Cβ decoupling. J. Magn. Reson., Ser. B 113, 91–96 (1996).
Chevelkov, V., Chen, Z., Bermel, W. & Reif, B. Resolution enhancement in MAS solid-state NMR by application of 13C homonuclear scalar decoupling during acquisition. J. Magn. Reson. 172, 56–62 (2005).
Sattler, M., Schleucher, J. & Griesinger, C. Heteronuclear multidimensional NMR experiments for the structure determination of proteins in solution employing pulsed field gradients. Progress. Nucl. Magn. Reson. Spectrosc. 34, 93–158 (1999).
Kay, L. E., Ikura, M., Tschudin, R. & Bax, A. Three-dimensional triple-resonance NMR spectroscopy of isotopically enriched proteins. J. Magn. Reson. (1969) 89, 496–514 (1990).
Ikura, M., Kay, L. E. & Bax, A. A novel approach for sequential assignment of proton, carbon-13, and nitrogen-15 spectra of larger proteins: heteronuclear triple-resonance three-dimensional NMR spectroscopy. Appl. Calmodulin Biochem. 29, 4659–4667 (1990).
Cavanagh, J., Fairbrother, W. J., Palmer, A. G., Skelton, N. J. & Rance, M. Protein NMR Spectroscopy: Principles and Practice. 2nd edn (Academic Press, San Diego, 2006).
Salzmann, M., Pervushin, K., Wider, G., Senn, H. & Wüthrich, K. TROSY in triple-resonance experiments: new perspectives for sequential NMR assignment of large proteins. Proc. Natl Acad. Sci. USA 95, 13585–13590 (1998).
Senthamarai, R. R., Kuprov, I. & Pervushin, K. Benchmarking NMR experiments: a relational database of protein pulse sequences. J. Magn. Reson. 203, 129–137 (2010).
LeMaster, D. M. Uniform and selective deuteration in two-dimensional NMR of proteins. Annu. Rev. Biophys. Biophys. Chem. 19, 243–266 (1990).
Robson, S. et al. Mixed pyruvate labeling enables backbone resonance assignment of large proteins using a single experiment. Nature Communications 9, 356 (2018).
Rovnyak, D., Hoch, J., Stern, A. & Wagner, G. Resolution and sensitivity of high field nuclear magnetic resonance spectroscopy. J. Biomol. NMR 30, 1–10 (2004).
Hyberts, S. G., Milbradt, A. G., Wagner, A. B., Arthanari, H. & Wagner, G. Application of iterative soft thresholding for fast reconstruction of NMR data non-uniformly sampled with multidimensional Poisson Gap scheduling. J. Biomol. NMR 52, 315–327 (2012).
Hyberts, S. G., Arthanari, H., Robson, S. A. & Wagner, G. Perspectives in magnetic resonance: NMR in the post-FFT era. J. Magn. Reson. 241, 60–73 (2014).
Powers, R., Gronenborn, A. M., Clore, G. M. & Bax, A. Three-dimensional triple-resonance NMR of 13C/15N-enriched proteins using constant-time evolution. J. Magn. Reson. 94, 209–213 (1991).
Grzesiek, S. & Bax, A. An efficient experiment for sequential backbone assignment of medium-sized isotopically enriched proteins. J. Magn. Reson. 99, 201–207 (1992).
Shimba, N., Stern, A. S., Craik, C. S., Hoch, J. C. & Dötsch, V. Elimination of 13Cα splitting in protein NMR spectra by deconvolution with maximum entropy reconstruction. J. Am. Chem. Soc. 125, 2382–2383 (2003).
Conolly, S., Nishimura, D. & Macovski, A. Optimal control solutions to the magnetic resonance selective excitation problem. IEEE Trans. Med. Imaging 5, 106–115 (1986).
Mao, J., Mareci, T., Scott, K. & Andrew, E. Selective inversion radiofrequency pulses by optimal control. J. Magn. Reson. (1969) 70, 310–318 (1986).
Khaneja, N., Reiss, T., Kehlet, C., Schulte-Herbrueggen, T. & Glaser, S. J. Optimal control of coupled spin dynamics: design of NMR pulse sequences by gradient ascent algorithms. J. Magn. Reson. 172, 296–305 (2005).
Tošner, Z. et al. Optimal control in NMR spectroscopy: Numerical implementation in SIMPSON. J. Magn. Reson. 197, 120–134 (2009).
Asami, S. et al. Ultrashort broadband cooperative pulses for multidimensional biomolecular NMR experiments. Angew. Chem. Int. Ed. (2018).
Koroleva, V. D. M. & Khaneja, N. Homonuclear decoupling for liquid-state NMR. J. Chem. Phys. 137, 094103 (2012).
Yuan, H., Koroleva, V. D. M. & Khaneja, N. Reduced coupling with global pulses in quantum registers. New J. Phys. 16, 105013 (2014).
Glanzer, S. & Zangger, K. Visualizing unresolved scalar couplings by real-time J-upscaled NMR. J. Am. Chem. Soc. 137, 5163–5169 (2015).
Coote, P., Anklin, C., Massefski, W., Wagner, G. & Arthanari, H. Rapid convergence of optimal control in NMR using numerically-constructed toggling frames. J. Magn. Reson. 281, 94–103 (2017).
Harden, B. J., Nichols, S. R. & Frueh, D. P. Facilitated assignment of large protein NMR signals with covariance sequential spectra using spectral derivatives. J. Am. Chem. Soc. 136, 13106–13109 (2014).
Qingtao, W. et al. NMR backbone assignment of large proteins by using 13Cα only triple resonance experiments. Chem. A Eur. J. 22, 9556–9564.
Shen, Y., Delaglio, F., Cornilescu, G. & Bax, A. TALOS+: a hybrid method for predicting protein backbone torsion angles from NMR chemical shifts. J. Biomol. NMR 44, 213–223 (2009).
Gronenborn, A. et al. A novel, highly stable fold of the immunoglobulin binding domain of streptococcal protein G. Science 253, 657–661 (1991).
Goto, N. K. & Kay, L. E. New developments in isotope labeling strategies for protein solution NMR spectroscopy. Curr. Opin. Struct. Biol. 10, 585–592 (2000).
Cai, M. et al. An efficient and cost-effective isotope labeling protocol for proteins expressed in shape Escherichia coli. J. Biomol. NMR 11, 97–102 (1998).
Christianson, D. W. & Fierke, C. A. Carbonic anhydrase: evolution of the zinc binding site by nature and by design. Acc. Chem. Res. 29, 331–339 (1996).
Acknowledgements
This work is funded by NIH Grants GM047467, GM075879, and P41-EB002026 to G.W., A.B. thanks Fonds zur Förderung der wissenschaftlichen Forschung (FWF Project J3872-B21) for support. H.A. acknowledges funding from Claudia Adams Barr Program for Innovative Cancer Research. Maintenance of the NMR instruments used for this research was supported by NIH grant EB002026. We thank Kendra E. Leigh for helpful discussions during the preparation of this manuscript.
Author information
Authors and Affiliations
Contributions
P.W.C. designed the research, designed the optimized pulses, analyzed data, and wrote the manuscript. S.A.R., A.D. and A.B. prepared samples, acquired NMR spectra, and analyzed data. M.Z. prepared samples. G.W. and H.A. supervised the project. All authors provided critical feedback and helped shape the research, analysis, and manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Coote, P.W., Robson, S.A., Dubey, A. et al. Optimal control theory enables homonuclear decoupling without Bloch–Siegert shifts in NMR spectroscopy. Nat Commun 9, 3014 (2018). https://doi.org/10.1038/s41467-018-05400-4
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-018-05400-4
This article is cited by
-
Lactate regulates cell cycle by remodelling the anaphase promoting complex
Nature (2023)
-
Band-selective universal 90° and 180° rotation pulses covering the aliphatic carbon chemical shift range for triple resonance experiments on 1.2 GHz spectrometers
Journal of Biomolecular NMR (2022)
-
The structural basis of PTEN regulation by multi-site phosphorylation
Nature Structural & Molecular Biology (2021)
-
Nearest-neighbor NMR spectroscopy: categorizing spectral peaks by their adjacent nuclei
Nature Communications (2020)
-
NMR: an essential structural tool for integrative studies of T cell development, pMHC ligand recognition and TCR mechanobiology
Journal of Biomolecular NMR (2019)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.