Abstract
The evolution of burrowing animals forms a defining event in the history of the Earth. It has been hypothesised that the expansion of seafloor burrowing during the Palaeozoic altered the biogeochemistry of the oceans and atmosphere. However, whilst potential impacts of bioturbation on the individual phosphorus, oxygen and sulphur cycles have been considered, combined effects have not been investigated, leading to major uncertainty over the timing and magnitude of the Earth system response to the evolution of bioturbation. Here we integrate the evolution of bioturbation into the COPSE model of global biogeochemical cycling, and compare quantitative model predictions to multiple geochemical proxies. Our results suggest that the advent of shallow burrowing in the early Cambrian contributed to a global low-oxygen state, which prevailed for ~100 million years. This impact of bioturbation on global biogeochemistry likely affected animal evolution through expanded ocean anoxia, high atmospheric CO2 levels and global warming.
Similar content being viewed by others
Introduction
Most of the oxygenated seafloor within the present-day ocean is inhabited by benthic animals that influence sediment biogeochemistry due to movement, ingestion of food particles and the construction of burrows1,2,3. This faunal reworking of the seafloor is termed ‘bioturbation’ and, following its definition for present-day sediments, the process has two separate effects4: the upwards and downwards transport of solid phase minerals and particles (bio-mixing), and the exchange of pore water solutes with the overlying water (bio-irrigation).
Burrowing fauna appeared in the Cambrian5, marking a transition from the largely undisturbed microbial mat coverings of the Neoproterozoic to a colonised and reworked seafloor in the Cambrian2,3,6. Whilst it is still unclear when bioturbation reached modern-day mixing depths, recent work has indicated that this likely occurred gradually throughout the Palaeozoic3,7. The mixed layer depth through the early Palaeozoic was relatively shallow, around 1–3 cm on average7. Although these burrowing depths remain well below the tens of centimetres that are frequently encountered today8, this was a fundamental change from the Precambrian, when burrowing and sediment reworking was minimal5,6.
Bioturbation influences biogeochemical cycling in marine sediments in a number of ways. Foremost, bioturbation induces ‘redox oscillations’ in the upper sediment horizons, as bio-mixing transports deeper anoxic sediment back to the oxic zone near the sediment-water interface, thus re-exposing previously buried organic matter to oxygen. This continuous cycling between oxic and anoxic sediment horizons leads to a more complete breakdown of organic matter, thus reducing the rate of burial of organic carbon (Corg) on the seafloor9,10,11. Similarly, bio-irrigation introduces oxygen-rich water into deeper anoxic zones via burrow flushing, thus stimulating aerobic respiration12 and increasing the net carbon mineralisation rate13. Bioturbation also increases the oxygen exposure of other redox-sensitive species in the sediment, such as pyrite (FeS2), thus enhancing oxidative reaction pathways of sulphur and iron14,15,16. The resulting reduction in the burial rate of FeS2 has led to the suggestion that the advent of bioturbation caused an increase in oceanic sulphate concentrations in the Phanerozoic relative to the Precambrian16,17.
In addition to the carbon and sulphur cycles, bioturbation also influences the marine phosphorus cycle, with important consequences for oceanic productivity3. The enhanced oxygen influx from bio-irrigation substantially increases the oxic volume of sediment18, and hence expands the redox niche under which microbial polyphosphate synthesis occurs, while bio-mixing also diverts labile organic phosphorus away from aerobic sediment layers, thus leading to enhanced preservation of organic phosphorus (Porg)19. Therefore, in bioturbated sediments underlying oxic waters, Corg:Porg ratios are typically in the range of 30–115, which is lower than for laminated sediments underlying anoxic waters, where Corg:Porg ratios often amount to 200–700 in modern settings20, and up to 3500 in the geological record21. A recent model analysis of this phosphorus feedback suggests that the rise of bioturbation in the Cambrian period (541–485 million years ago, Ma) may have driven atmosphere and ocean de-oxygenation by increasing phosphorus preservation in sediments19,22.
Given the key role of the seafloor in constraining Earth’s geochemistry on geological timescales23,24, and the known impacts of bioturbation on sedimentary cycling, this has provoked the idea that the appearance of burrowing animals may have substantially changed the global geochemical cycles of carbon, sulphur, phosphorus and oxygen3,16,17,22. Although the qualitative nature of the feedback of bioturbation on global biogeochemical cycling is recognised3,5, the timing and magnitude of this feedback remain highly uncertain, which significantly limits our ability to reconstruct the chemical and biological response of the biosphere to early animal evolution. Conventionally, it has been assumed that the biogeochemical effect of bioturbation is more important when bioturbation parameters (the mixed layer depth and mixing intensity) reach near-modern values. As a consequence, it has been suggested that the major environmental impact of bioturbation was delayed until the Devonian, when major increases in burrowing occurred, more than 120 million years after the Cambrian ‘explosion’ of animal life7. Recently, however, both experimental25 and modelling studies16 have shown that biogeochemical processes respond non-linearly to bioturbation, and furthermore, that large biogeochemical impacts can occur even at shallow mixed layer depths and with low mixing intensities. Indeed, some of the most drastic changes in sediment biogeochemistry occur at low bioturbation levels16. This suggests that shallow bioturbation may have exerted a strong biogeochemical impact during the early Palaeozoic.
Here we present an evaluation of the global Earth system response to the rise of bioturbation, using a global biogeochemical model (COPSE)26,27 that simulates the coupled cycling of carbon, oxygen, phosphorus and sulphur. Based on the known impact of bioturbation in modern sediments, we implement a new parameterisation for bioturbation in the COPSE model that affects the cycles of carbon, oxygen and phosphorus. We then ground-truth our model outputs in relation to multiple types of geochemical data from the rock record. This allows us to reconcile contrasting views regarding the effects of bioturbation on global elemental cycles during the Cambrian, thus providing new insight into a significant potential driver of environmental change at a pivotal juncture in Earth history.
Results
Geochemical evolution of the early Palaeozoic Earth system
Geochemical data covering the late Neoproterozoic and early Phanerozoic (560–420 Ma) are summarised in Fig. 1. In general, there is evidence for considerable heterogeneity in the evolution of ocean redox chemistry from the late Neoproterozoic through to the mid-Cambrian, as might be expected in a pervasively low oxygen world. However, much of this apparent heterogeneity may be due to difficulties in adequately sampling sediments from a range of water depths in individual studies. For example, the existence of an anoxic oxygen minimum zone (OMZ) along productive continental margin settings has been advocated for the early Cambrian28. Samples from within the OMZ would give a very different redox signature compared to samples from oxic shallower and deeper waters. Nevertheless, an overall progression in ocean oxygenation across this period is now emerging, aided by the application of redox indicators that provide a more global indication of ocean redox chemistry29,30,31.
Compilation of geochemical data from the Neoproterozoic into the Palaeozic. a Mo abundances, as compiled by ref. 29. Higher oxygen levels lead to higher abundances of Mo. Note that other proxies providing support for the ocean oxygenation state outlined here are compiled in Supplementary Fig. 1. b Sulphate-S isotopes (δ34SSO4) as compiled by ref. 69. δ34SSO4 increases through the Cambrian, with a return to lighter values at the GOBE. c Pyrite fraction of sulphur burial (fpyr = pyrite burial/(pyrite burial + gypsum burial)), full range of estimates, as presented in ref. 44. d Carbonate-C isotopes (δ13Ccarb) as compiled by ref. 70. Higher values indicate a higher rate of organic carbon burial. e Mixed layer depth, reproduced from ref. 7. Black lines on panels b and d are local regression (LOESS) fits. Grey shaded areas indicate the Cambrian explosion (540–521 Ma) and the Great Ordovician Biodiversification Event (GOBE; 470–450 Ma). Blue shaded line indicates the Hirnantian glaciation
There is robust evidence for widespread deep ocean oxygenation in the late Neoproterozoic30,32,33,34,35. Building upon this, selenium isotope evidence30 also suggests progressive oxygenation through the Neoproterozoic. However, multiple lines of evidence demonstrate a short-lived return to widespread ocean anoxia at the Precambrian-Cambrian boundary (Fig. 1a and Supplementary Fig. 1)33,36,37,38. This anoxic episode was likely too short-lived to be captured by our modelling approach (see below), but evidence from sedimentary Mo concentrations and isotopes, U isotopes, and rare earth element concentrations suggests that the global ocean then became progressively oxygenated through the early Cambrian up until the height of the Cambrian explosion at ~520 Ma29,31,34. These same redox proxies demonstrate a subsequent return to more widespread anoxia after ~520 Ma (for simplicity we demonstrate this with Mo concentration data in Fig. 1, but other proxies are compiled in Supplementary Fig. 1), which is also consistent with evidence from S isotopes, Fe speciation, and trace metal concentrations indicating widespread euxinia in the later Cambrian ocean39.
Evidence from sulphur isotope systematics suggest this widespread euxinia continued during the early and mid-Ordovician40. Other geochemical records through the Ordovician are relatively sparse, although ocean redox conditions appear to have been subject to temporal variability, which is consistent with an overall low-oxygen world41. However, by the end of the Ordovician and during the Silurian (<460 Ma), oxygen started to increase27, coincident with the earliest instance of fossilised charcoal, indicating near-modern levels of atmospheric O242. This rise in oxygen has been attributed to the evolution of land plants, which culminated in the Devonian and Carboniferous with the development of roots and vasculature27,43.
The sedimentary record of oceanic sulphate δ34S shows significant variability (Fig. 1b), but the general trend suggests an increase in δ34SSO4 from the Ediacaran (25‰) to the mid Cambrian (39‰), followed by a recovery to pre-Palaeozoic values of 25‰, just before the Great Ordovician Biodiversification Event (GOBE). Increases in δ34SSO4 are often linked to increased rates of pyrite burial, but this may not necessarily be the case during the Early Palaeozoic44 (note the very large range in fpyr; the fraction of ocean sulphate that is buried as pyrite; Fig. 1c). A long-term perturbation during the Cambrian and Ordovician is apparent in the sedimentary carbonate δ13C record. While this record reveals fluctuations in the carbon cycle on short timescales of a few million years, on a longer time scale the δ13Ccarb record shows generally lower values from the middle Cambrian to the late Ordovician (~0‰) as compared to the late Ediacaran and early Cambrian (~4‰), with a return to higher values in the Silurian (~2‰). The shift in δ13Ccarb at around 521 Ma is consistent with a reduction in net organic carbon burial, and a resultant decrease in the production rate of O2. The recovery to more oxic conditions in the Silurian was likely coupled to increased organic carbon burial, as indicated by the more positive δ13Ccarb values (Fig. 1d).
The analysis of sediment fabric disturbance suggests early animals only reworked the seafloor superficially, with shallow burrowing appearing during the Cambrian and continuing into the Ordovician, whereas only towards the end of the Silurian do burrow systems become deeper (mixed layer depth shown in Fig. 1e)7. Various scalings of the biogeochemical response to bioturbation have been shown to be consistent with subsets of available geochemical proxies: a rapid and non-linear response at low bioturbation intensities may have increased phosphate retention in the sediment when the first shallow-burrowing animals appeared in the Cambrian22, leading to a decrease in the oxygen production source from organic carbon burial, and driving a return to anoxic ocean conditions after 520 Ma (Fig. 1a). In contrast, a more protracted response has been shown to be consistent with low sulphate concentrations throughout the Palaeozoic7. However, the proposed scenarios for the evolution of bioturbation have not been evaluated using multiple geochemical proxies or model simulations combining feedbacks between the carbon, oxygen, phosphorus and sulphur cycles.
The COPSE model
To obtain more robust constraints on the timing and environmental consequences of the rise of bioturbation, we modified the COPSE model26,27 (Carbon Oxygen Phosphorus Sulphur Evolution), which is a synthesis of the ‘Redfield’ model45 and the GEOCARB model46. The COPSE model simulates the coupled evolution of the major biogeochemical cycles over the Phanerozoic by describing burial, weathering and degassing processes, which transport chemical species between the atmosphere, oceans and sediments over geological timescales (Fig. 2). COPSE aims to capture trends in biogeochemical cycling over the timescale of 10–100 s of millions of years, but not shorter-term fluctuations on timescales of ~100,000 years. The model produces estimates for the global abundance of oxygen, carbon dioxide, phosphate and sulphate, alongside records of whole-ocean δ13Ccarb and δ34SSO4, which can be used to test hypotheses by comparison to data. For an overview of the biotic and tectonic controls covered by the current COPSE model, see ref. 47. The evolution of bioturbation and its feedback on global biogeochemistry has not been explicitly considered in COPSE: previous model versions have implicitly assumed that bioturbation is always active and that the bioturbation intensity remains independent of the oceanic oxygenation state.
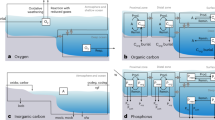
Diagram of key processes in the COPSE model. a Carbon cycle. Hydrospheric CO2 is transferred to sediments as organic C or carbonate by burial (B). Sedimentary C is returned to the ocean/atmosphere via weathering and metamorphism (W). Buried organic C is isotopically lighter than the carbon it is derived from. Burial of reduced organic carbon results in a net source of O2, whereas oxidative weathering of sedimentary organic carbon consumes O2. b Sulphur cycle. Burial of reduced pyrite is a net source of O2, whereas oxidative weathering of sedimentary pyrite consumes O2. c Oceanic phosphorus (P) cycle. Dissolved, bio-available P is delivered to the ocean by chemical weathering via rivers, and is buried either as organic phosphorus, or with iron or calcium minerals. Dashed lines show burial processes that are influenced by bioturbation (but are not considered so in the baseline model)
By using COPSE we employ a forward modelling approach, which enables a comparison of model predictions of δ13Ccarb and δ34SSO4 trends to the independent geological record. This contrasts with inverse modelling, where geological records are used as a model forcing, leaving no potential for quantitative testing of the model results. As with all models, comparison with the geological record requires some assumptions. Foremost, the model predicts δ13Ccarb and δ34SSO4 trends that are representative of the global marine dissolved inorganic carbon and sulphate reservoirs, reflecting the globally averaged operation of the long-term geochemical cycles (in essence changes in organic carbon and pyrite burial). However, changes in the geological isotope record are not solely dependent on changes in the global biogeochemical cycling of carbon and sulphur, but also incorporate possible effects of diagenesis, or evolutionary changes to the fractionation factors associated with photosynthesis and microbial sulphate reduction. Moreover, it is possible that some data represent regional signals rather than global trends. Nevertheless a quantitative comparison of our model predictions to the geological isotope record provides a useful test of the assumptions underlying the COPSE model.
For the late Ediacaran to mid Ordovician, the ‘baseline’ COPSE model (i.e., the model version as presented in ref. 27) generates stable conditions with high atmospheric CO2 (~15× Present Atmospheric Level (PAL)), a high degree of ocean anoxia (0.8, or 80% of the ocean surface resides under anoxic water) and δ13Ccarb around 0‰ (Fig. 3). Broadly, these results are driven by the absence of terrestrial productivity, and a suppression of silicate mineral weathering before land plant evolution (i.e., suppressed burial of both organic and inorganic carbon). The predictions of the baseline model reveal discrepancies with the available geochemical data, which suggest more dynamic ocean redox conditions in the early Palaeozoic and higher δ13Ccarb values in the late Ediacaran and early Cambrian (Fig. 1).
COPSE baseline model simulation. Simulation as presented in ref. 27. a Atmospheric CO2. b Average δ34SSO4 of seawater. c Pyrite fraction of sulphur burial. d Average δ13Ccarb of seawater. e Degree of ocean anoxia (1 = completely anoxic, 0 = completely oxic). f Summary of the evolution of sedimentary Mo concentrations over time. Model outcomes (in blue) are compared to δ13Ccarb and δ13SSO4 data and the sedimentary Mo concentrations, which is reflective of the extent of ocean oxygenation and is supported by multiple independent proxies (see Supplementary Note 1). Dotted lines in panels b and d represents a local regression (LOESS) fit to the data. Grey shaded areas indicate the Cambrian explosion (540–521 Ma) and the Great Ordovician Biodiversification Event (GOBE; 470–450 Ma). Blue shaded line indicates the Hirnantian glaciation
The effect of bioturbation on sedimentary elemental cycling
Here, we update the COPSE model parameterisation for the burial of organic carbon, pyrite sulphur and phosphorus to include a response to bioturbation. We introduce a bioturbation parameter, fbiot, which provides a single measure of the biogeochemical impact of bioturbation on sedimentary cycling (0 represents no bioturbation effect, 1 represents maximum bioturbation impact). This fbiot parameter must be expressed as a function of the strength of bioturbation, which is traditionally represented by the bio-mixing depth (Lb) and the bio-mixing intensity (Db) parameters, that feature in early diagenetic models48. As Db and Lb are essentially linked (Lb ~ √Db, see ref. 49 for a theoretical justification), the parameter fbiot may be expressed as some function of either one of these parameters (Fig. 4). Currently, there is a lack of data to constrain the exact nature of the relation between fbiot and bioturbation intensity.
The effect of bioturbation on sediment geochemistry. a The effect of bioturbation intensity (Db) on the sulphur cycling rate. Model results reproduced from ref. 16. b Solid line (Scenario 1): the bioturbation impact on geochemistry (fbiot) is linearly correlated with the depth and intensity of burrowing. Dashed line (Scenario 2): the bioturbation impact is maximal with shallow burrowing, but the areal expansion of bioturbation increases gradually throughout the early Palaeozoic. Dash-dotted line (Scenario 3): the bioturbation impact on geochemistry (fbiot) is already at full strength by the end of the Cambrian explosion. c Simplified conceptual model of the effect of bioturbation on the sedimentary cycles of carbon, phosphorus and sulphur. Arrow sizes denote relative changes in flux sizes
To examine the link between the emergence of bioturbation and global biogeochemistry, we describe three different formulations for the evolution of fbiot over time that are designed to represent the envelope of possibilities. In ‘Scenario 1’, the biogeochemical impact of bioturbation is assumed to be weak during the Cambrian and Ordovician, and becomes important when deeper and more intensively burrowing organisms evolve in the late Silurian and Devonian, increasing the mixing depth and creating larger burrow networks that are intensely flushed with overlying water (solid line in Fig. 4b). Throughout the Cambrian and Ordovician, the mixed layer depth may have been at least 5 times lower than the observed depths in the late Silurian and Devonian (Fig. 1d and ref. 7), and therefore we choose fbiot = 0.2 (thereby assuming a linear relationship between the effects of bioturbation and the mixed layer depth). Mixed layer depths likely increased to higher levels in the late Silurian and the Devonian7. Therefore, we allow fbiot to increase to 0.5 by the end of the Silurian, which implies that the biogeochemical impact of bioturbation only peaked after the Silurian (as suggested by ref. 7).
In Scenarios 2 and 3, we suggest that low depths of bioturbation mediate a disproportionally large response in sediment geochemistry. Both experimental25 and theoretical16 studies have proposed that geochemical state variables and rates (e.g., elemental cycling rates, partitioning of redox acceptors, stimulation of organic carbon breakdown) respond in a highly non-linear way to increasing levels of bioturbation, with 80–90% of the maximum response attained at low bioturbation intensities (Db < 1 cm2 yr−1 and Lb < 3 cm; see ref.16). For example, diagenetic modelling shows that the cycling rate of sulphur (the number of times a sulphur atom entering the sediment column is cycled between its oxidised and reduced states before it is eventually buried) rapidly increases from 5 to 10 when Db increases from 0 to 1 cm2 yr−1, to stabilise at 11 when Db values > 1 cm2 yr−1 (Fig. 4a). This increased redox cycling of sulphur potentially inhibits the rate at which reduced sulphur compounds are buried (by stimulating re-oxidation)14,17. Additionally, experimental work has shown that meiofauna (micron-scale animals that burrow ~1 cm) stimulate organic carbon breakdown as much as large animals (that burrow >10 cm depth)25.
During the Cambrian, the mixed layer depth increased from 0 to <0.5 cm 7, which may correlate with a significant biogeochemical response. In Scenario 3, the advent of shallow mixing thus invokes a large biogeochemical effect, and so the bioturbation impact (fbiot) increases exponentially from 0 to 1 during the Cambrian Explosion, and remains constant afterwards (dash-dotted line in Fig. 4b). We also define an intermediate situation (Scenario 2), in which we assume that shallow bioturbation has a large impact, but that the areal extent of bioturbation (and accordingly fbiot) gradually increases throughout the early Palaeozoic (dashed line in Fig. 4b). Furthermore, in all scenarios, two distinct options for the response of bioturbation towards anoxia have been tested; (i) no anoxia limitation, and (ii) anoxia limitation that scales with the fraction of the ocean that is anoxic (solid vs. dashed lines in model outputs, see Methods for more information).
The effect of bioturbation on the elemental cycling of C, P and S in marine sediments is summarised in Fig. 4c. Overall, the main effects of bioturbation are driven by the increase in oxygen exposure in the anoxic part of the sediment. In a sediment without bioturbation (e.g., the Ediacaran seafloor), organic matter is broken down less efficiently11,50,51 and sulphur is more efficiently sequestered as pyrite, leading to high burial rates of organic carbon and pyrite. With the introduction of burrowing fauna, organic matter mineralisation is enhanced and pyrite is more efficiently re-oxidised14, and so the burial of carbon and sulphur is reduced3,17. At the same time, bioturbation leads to an increase in polyphosphate sequestering, which then leads to an increase in organic phosphorus burial19. We implemented these relations between bioturbation and geochemical C, S and P cycling in COPSE by adapting the model equations for marine organic carbon burial, marine pyrite sulphur burial and marine organic phosphorus burial, and introduce new parameters that describe pre-bioturbation values for organic carbon, pyrite sulphur and organic phosphorus burial (see Methods).
Overall, this model description allows us to test the working hypotheses; (i) Scenario 1: the effect on global biogeochemical cycles scales with bioturbation depth and intensity, and increased only markedly in the Silurian–Devonian, (ii) Scenario 2: the effect on global biogeochemical cycles increased gradually throughout the Palaeozoic, and (iii) Scenario 3: the effect on global biogeochemical cycles was rapid and occurred in the Early Cambrian. We tested the validity of these hypotheses by comparing the quantitative model output to the geological record.
New model results
Under a protracted response to bioturbation (Scenario 1; Fig. 5a–g), δ13Ccarb values slightly decrease with the early development of bioturbation at the start of the Cambrian, and remain constant throughout the Cambrian and Ordovician. After rising in the late Ordovician, δ13Ccarb drops gradually during the Silurian, in response to decreased primary production and decreased carbon burial due to bioturbation (Fig. 5d). In the model simulation of ocean anoxia, the limited effects of bioturbation during the early Palaeozoic imply a high rate of organic carbon burial and therefore higher concentrations of atmospheric and oceanic oxygen, and a limited prevalence of anoxia (Fig. 5e). Both of these predictions are to some extent at odds with the geochemical record, which shows evidence for significant ocean anoxia after 520 Ma 31 until the middle Ordovician (470–460 Ma)40, and does not support high δ13Ccarb (~2‰) throughout this interval (Fig. 1).
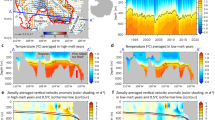
COPSE model with the addition of the evolution of bioturbation. Scenario 1 shows the effect of the sedimentary response that scales linearly with bioturbation intensity. Scenarios 2 and 3 assume that the effects of bioturbation on sediment geochemistry occur non-linearly (strong response for low levels of bioturbation), where Scenario 2 follows a gradual increase of the areal extent of bioturbation and Scenario 3 shows the maximum effect at the Ediacaran-Cambrian boundary (see panels g, n, u). a, h, o Atmospheric CO2. b, i, p Average sulphate δ34S of seawater. c, j, q Pyrite fraction of sulphur burial. d, k, r Average δ13C of carbonate. e, l, s Degree of ocean anoxia. Model outcomes (in red) are fitted to the δ13Ccarb and δ13SSO4 proxies (grey dotted line represents a LOESS fit), predictions for the relative importance of pyrite for the total sulphur burial rate (blue dotted lines represent the range of model results presented in ref. 44) and compared to a summary of the evolution of sedimentary Mo concentrations over time (f, m, t). Solid lines represent the model outcomes with anoxia feedback, dashed lines represent the model outcomes without anoxia feedback. Grey shaded areas indicate the Cambrian explosion (540–521 Ma) and the Great Ordovician Biodiversification Event (GOBE; 470–450 Ma). Blue shaded line indicates the Hirnantian glaciation
With a gradually increasing areal extent of bioturbation across the Palaeozoic (Scenario 2; Fig. 5h–n), organic matter burial gradually decreases, while sedimentary phosphate retention gradually increases, both leading to an increase in ocean anoxia (Fig. 5k, l). While the associated protracted decrease in δ13Ccarb values is not entirely at odds with the geochemical record, the gradual increase of ocean anoxia across the Palaeozoic does not fully agree with geochemical proxy evidence for an increase in ocean anoxia in the early Cambrian31. Furthermore, the absence of a transient increase in δ34SSO4 also disagrees with the geochemical record (Fig. 5i).
When the model simulations incorporate a strong biogeochemical response to shallow bioturbation in the early Cambrian (Scenario 3; Fig. 5o–u), the emergence of bioturbation results in significantly enhanced oxidation of marine organic carbon and pyrite, as well as benthic phosphate retention, which limits oceanic primary production. The initial decrease in marine organic carbon burial at 520 Ma (marked by the drop in δ13Ccarb from 2‰ to 0‰; Fig. 5r) is accompanied by an increase in ocean anoxia (Fig. 5s), which then provides a negative feedback and limits bioturbation. The resulting reduction in marine organic carbon burial results in increased atmospheric pCO2 (by >1000 ppm; Fig. 5o), and suggests that the evolution of burrowing organisms in the ocean could have triggered significant climate warming, consistent with the ‘greenhouse’ climate invoked for the Cambrian and early Ordovician, as indicated by elevated sea levels52 and oxygen isotope systematics53. We note that the direct effect of the organic carbon cycle on CO2 levels is not as widely discussed in the literature as the changes resulting from silicate weathering, but that it is an important part of the coupled C and O cycles54.
The increase in anoxia induced by bioturbation leads to an increase in δ34SSO4 (~30‰; Fig. 5p). We do not find, as previously suggested17, a rise in marine sulphate concentrations coincident with the evolution of bioturbation (Supplementary Fig. 2), because of our implementation of gypsum (CaSO4) burial. In COPSE, gypsum burial scales with the oceanic sulphate concentration, while gypsum burial was previously considered important only at higher sulphate concentrations17. Given the uncertainty over gypsum formation, it is difficult to make any strong conclusions regarding this effect. In general, the effect of the evolution of bioturbation on ocean sulphate concentration remains uncertain. Eventually, the effects of the evolution of bioturbation are largely reversed by the rise of early land plants in the late Ordovician, which increases net carbon burial and phosphate supply, as well as drawing down atmospheric CO2. Assumed high Palaeozoic erosion rates contribute to low δ13Ccarb in the model runs54, but it is unlikely that the rapid drop in δ13Ccarb at the end of the Cambrian explosion and the subsequent rise at the end of the Ordovician can be driven solely by rapid erosion and sedimentation, which continues into the Devonian. Overall, Scenario 3 brings the COPSE model predictions reasonably close to the available data from the geological record.
Caution is of course required, as bioturbation is likely not the only driver for variation in the isotope data, especially for variations on timescales <1 million years, which the model cannot capture. However, these limitations do not invalidate the hypothesis testing here, which shows that Scenario 3 (large geochemical effects due to shallow burrowing) can reproduce the broad changes seen in δ13Ccarb, δ34SSO4 and ocean anoxia, whilst Scenarios 1 and 2 (more protracted global biogeochemical responses) produce discrepant predictions for δ13Ccarb or δ34SSO4. Reversing these conclusions would require a very specific, and unlikely, set of additional forcing factors (see Supplementary Note 2 for further discussion). Nevertheless, many additional mechanisms were likely at work over the studied time interval. For example, nutrient stress and limited primary production were undoubtedly a factor in explaining the low-oxygen conditions in the early Palaeozoic. The COPSE model attempts to take into account such mechanisms: for example it includes process-based ocean nutrient cycles, including a representation of phosphorus removal with organic matter, calcium, and iron species and how these sinks may have varied with time26. However, as with all box models, these processes are greatly simplified, and apparent mismatches with geochemical data suggest that there are still processes missing or poorly represented (e.g., the P cycle). The COPSE model predictions are improved by our additional representation of bioturbation, suggesting that it was a major driver of biogeochemical cycling during the Palaeozoic.
Synthesis
By recognising that moderate levels of shallow bioturbation have a large impact on sediment geochemistry (Fig. 4a), our model results are able to broadly reconcile the bioturbation record (Fig. 1e) in relation to various proxies in the geochemical record (Fig. 5). We propose a significant bioturbation-driven step change in environmental conditions and geochemical cycling in the early Cambrian, well before benthic fauna reached their full capacity in terms of sediment reworking. This appears to have resulted in a ~100 Myr period of prevalent ocean anoxia and greenhouse climate conditions that is consistent with the available geological evidence. This transition period between the Cambrian explosion and the Great Ordovician Biodiversification Event (GOBE) was also marked by sizable fluctuations in δ13Ccarb values and variable ocean redox conditions (Fig. 1) on shorter timescales, alongside repetitive extinction and recovery events that sustained a radiation plateau55 which was eventually followed by the GOBE56.
There is a strong correlation between ocean anoxia, positive δ13Ccarb excursions and extinction events57, and it is possible that the interactions between burrowing macrofauna, biogeochemical cycling and ocean anoxia may have contributed to these patterns. The expansion of oceanic anoxia ultimately limits the habitable area of seafloor, and if anoxia resulted in an extinction event, the associated collapse of bioturbation would be expected to drive a positive carbon isotope excursion. In this way, the evolution of burrowing may have contributed to the diversification of Metazoa58, since the dynamic redox conditions that appear to be a feature of the Ediacaran and Cambrian (and potentially modified by the evolution of shallow bioturbation) would have led to enhanced ecological stress, thus paving the way for the next ‘explosion’ of diversity—the Great Ordovician Biodiversification Event59,60.
Methods
COPSE model equations and parameterisation
We update the COPSE model by including a feedback of bioturbation on the burial of marine organic carbon (mocb), marine organic phosphorus (mopb) and marine pyrite sulphur (mpsb). In the baseline model, marine organic carbon burial is quadratically dependent on primary production (newP), where mocb0 is an estimate for present-day marine organic carbon burial, and newP0 is an estimate of present-day primary production. We introduce a new parameter (CBbiot), which represents enhanced mineralisation by bioturbation and is defined as:
where fbiot is the bioturbated fraction of organic carbon and CBprebiot the mineralisation without bioturbation. The final expression is then:
Several experiments have shown that the presence of burrowing macrofauna reduces organic carbon burial by ~50%, which implies a significant reduction in organic C burial in bioturbated sediments11,61, leading to CBprebiot = 2 × CBbiot. This number is likely not applicable to the whole ocean, although the majority of carbon burial takes place in coastal areas and continental shelves62, which are also subject to the highest rates of bioturbation. About 80% of the global carbon burial takes place in the continental margin sediments (this takes into account the presence of relict sands that do not accumulate organic matter)62. Since about 5% of the near-shore seafloor is currently covered by hypoxic waters63, this restricts benthic activity to maximum 95% of the continental margin sediments. This gives CBprebiot = 1.6 × CBbiot (95% of 80% is increased by a factor 2, and the remaining 24 % is unaltered). As a more conservative estimate, we assume that only 40% of the continental shelf sediments are affected by bioturbation, which then leads to a CBprebiot = 1.2 × CBbiot. We tested these three values for the CBbiot parameter (see Supplementary Note 3), and found that the higher values caused unreasonably large changes in the model due to the global and nondimensional nature of the system, which does not capture regional feedbacks. Therefore we choose the more conservative value of CBprebiot = 1.2 × CBbiot for this work. It is common for processes measured at the local scale to cause overestimates when applied in global scale models, and this parameter choice does not affect our conclusions, which are based on the qualitative changes observed at different times in Earth history.
Marine organic phosphorus burial is dependent on the C:P ratio of organic carbon in bioturbated sediment (CPbiot) and non-bioturbated (or laminated) sediment (CPlam), and the burial rate of organic carbon (mocb). Equation (3) has been introduced before22 and represents the dependence of mopb on the bioturbated fraction of organic carbon:
We can trial again two extreme values for CPbiot (the Corg:Porg ratio of bioturbated organic matter). Following the reasoning from above (today, maximum 95% of 80% of the buried organic matter experiences bioturbation) and mean values for unbioturbated and bioturbated Corg:Porg ratios (450 and 73.5, respectively, derived from ref. 64), we arrive at a lower bound value of CPbiot = 160. Similarly, assuming only 40% of the 80% experiences bioturbation, we arrive at CPbiot = 330. We tested values of 150, 250 and 350 for CPbiot and values of 1000, 2000 and 3000 for CPlam (which compromises between higher palaeo data and lower modern estimates)19,22,64. For the model runs in the paper, we employed the conservative values CPbiot = 250 and CPlam = 1000.
A final adaptation is in the marine pyrite burial (mpsb). In the baseline model, mpsb is linearly dependent on the oceanic sulphate concentration and mocb, and inversely dependent on oxygen concentrations. We introduce an extra parameter which represents the enhanced recycling of sulphur (SCbiot), dependent on bioturbation, which has the same form as Eq. (1):
where SCprebiot is the rate of sulphur recycling without bioturbation. The final equation then becomes:
Bioturbation would enhance reduced sulphur reoxidation, thus stimulating sulphur recycling3,17. Together with decreasing organic carbon burial, this affects the Corg:Spyr ratio (organic carbon vs. pyrite) in the sediment14. Indeed, in unbioturbated sediments, pyrite formation is mainly driven by organic carbon availability, leading to fairly constant Corg:Spyr ratios65. Throughout the Phanerozoic however, the Corg:Spyr ratio changes, seemingly in sync with atmospheric oxygen66. Even though this effect on Corg:Spyr ratios is likely the consequence of increasing bioturbation levels throughout the Phanerozoic, the baseline model of COPSE already contains this dependency of pyrite sulphur burial in the form of the inverse dependency on oxygen concentrations26. Since in our model, bioturbation is also dependent on the oxygen content, we removed the direct effect of bioturbation on sulphur cycling from the more conservative model (by setting SCprebiot = 1) as the effect of bioturbation on pyrite burial is already implemented to some degree.
The present day values of CBbiot and SCbiot are set to 1 by means of reference, and scaling factors are introduced to set their values to ‘prebiotic’ conditions with no bioturbation (Table 1). The sensitivity tests for the alternative values for CBprebiot, SCprebiot, CPbiot and CPlam are shown in the Supplementary Note 3 (Supplementary Figs. 3, 4, 5) and the results are qualitatively robust to these choices.
Anoxia limitation
Oxygen is a key metabolic resource for animals67,68 but the oxygen concentrations at which macrofauna are excluded and bioturbation is impeded are presently not well constrained (even in modern oxygen minimum zones, where dissolved O2 is <9 µM, animals are found67, but these appear to display minimal bioturbation activity). Therefore, we explored two distinct options for the response of bioturbation towards anoxia; (i) fbiot is not dependent on the degree of oceanic anoxia and (ii) fbiot = fbiotref (1 − anox), where anox is the degree of ocean Anoxia, as in the original model:
The bioturbation parameter f biot
To parameterise the geochemical sediment response in our model, the bioturbation parameter has been described as a function of time, based on the three tested scenarios (see main text for more details); Scenario 1 (the effect of bioturbation on sediment geochemistry scales linearly with the depth and intensity of burrowing), Scenario 2 (low levels of bioturbation invoke a large response in sediment geochemistry, and the areal extent of bioturbation gradually increased throughout the Palaeozoic), Scenario 3 (low levels of bioturbation invoke a disproportionally large response in sediment geochemistry).
Data availability
The data presented in this manuscript can be freely accessed on ResearchGate [https://www.researchgate.net/publication/325361821_Data_from_van_de_Velde_et_al_Nature_Communications_2018].
References
Aller, R. C. The Influence of Macrobenthos on Chemical Diagenesis of Marine Sediments (Yale University, New Haven, CT, USA, 1977).
Meysman, F. J. R., Middelburg, J. J. & Heip, C. H. R. Bioturbation: a fresh look at Darwin’s last idea. Trends Ecol. Evol. 21, 688–695 (2006).
McIlroy, D. & Logan, Ga The impact of bioturbation on infaunal ecology and evolution during the Proterozoic-Cambrian transition. Palaios 14, 58–72 (1999).
Kristensen, E. et al. What is bioturbation? the need for a precise definition for fauna in aquatic sciences. Mar. Ecol. Prog. Ser. 446, 285–302 (2012).
Herringshaw, L. G., Callow, R. H. T. & McIlroy, D. Engineering the Cambrian explosion: the earliest bioturbators as ecosystem engineers. Geol. Soc. Lond. Spec. Publ. 448, 369–382 (2017).
Bottjer, D. J., Hagadorn, J. W. & Dornbos, S. Q. The Cambrian substrate revolution. GSA Today 10, 1–7 (2000).
Tarhan, L. G., Droser, M. L., Planavsky, N. J. & Johnston, D. T. Protracted development of bioturbation through the early Palaeozoic Era. Nat. Geosci. 8, 865–869 (2015).
Lecroart, P. et al. Bioturbation, short-lived radioisotopes, and the tracer-dependence of biodiffusion coefficients. Geochim. Cosmochim. Acta 74, 6049–6063 (2010).
Aller, R. C. Bioturbation and remineralization of sedimentary organic matter: effects of redox oscillation. Chem. Geol. 114, 331–345 (1994).
Hulthe, G., Hulth, S. & Hall, P. O. J. Effect of oxygen on degradation rate of refractory and labile organic matter in continental margin sediments. Geochim. Cosmochim. Acta 62, 1319–1328 (1998).
Kristensen, E. Organic matter diagenesis at the oxic/anoxic interface in coastal marine sediments, with emphasis on the role of burrowing animals. Hydrobiologia 426, 1–24 (2000).
Archer, D. & Devol, A. H. Benthic oxygen fluxes on the Washington shelf and slope: a comparison of in situ microelectrode and chamber flux measurements. Limnol. Oceanogr. 37, 614–629 (1992).
Aller, R. C. & Aller, J. Y. The effect of biogenic irrigation intensity and solute exchange on diagenetic reaction rates in marine sediments. J. Mar. Res. 56, 905–936 (1998).
Berner, R. A. & Westrich, J. T. Bioturbation and the early diagenesis of carbon and sulfur. Am. J. Sci. 285, 193–206 (1985).
Hines, M. E. & Jones, G. E. Microbial biogeochemistry and bioturbation in the sediments of Great Bay, New Hampshire. Estuar. Coast. Shelf Sci. 20, 729–742 (1985).
van de Velde, S. & Meysman, F. J. R. The influence of bioturbation on iron and sulphur cycling in marine sediments: a model analysis. Aquat. Geochem. 22, 469–504 (2016).
Canfield, D. E. & Farquhar, J. Animal evolution, bioturbation, and the sulfate concentration of the oceans. Proc. Natl Acad. Sci. USA 106, 8123–8127 (2009).
Glud, R. N. Oxygen dynamics of marine sediments. Mar. Biol. Res. 4, 243–289 (2008).
Dale, A. W., Boyle, R. A., Lenton, T. M., Ingall, E. D. & Wallmann, K. A model for microbial phosphorus cycling in bioturbated marine sediments: significance for phosphorus burial in the early Paleozoic. Geochim. Cosmochim. Acta 189, 251–268 (2016).
Ingall, E. & Jahnke, R. Influence of water-column anoxia on the elemental fractionation of carbon and phosphorus during sediment diagenesis. Mar. Geol. 139, 219–229 (1997).
Ingall, E. D., Bustin, R. M. & Van Cappellen, P. Influence of water column anoxia on the burial and preservation of carbon and phosphorus in marine shales. Geochim. Cosmochim. Acta 57, 303–316 (1993).
Boyle, R. A. et al. Stabilization of the coupled oxygen and phosphorus cycles by the evolution of bioturbation. Nat. Geosci. 7, 671–676 (2014).
Berner, R. A. Biogeochemical cycles of carbon and sulfur and their effect on atmospheric oxygen over phanerozoic time. Paleogeogr. Paleoclimatol. Paleoecol. 75, 97–122 (1989).
Lenton, T. M. & Watson, A. J. Redfield revisited 2. What regulates the oxygen content of the atmosphere? Glob. Biogeochem. Cycles 14, 249–268 (2000).
Nascimento, F. Ja, Naslund, J. & Elmgren, R. Meiofauna enhances organic matter mineralization in soft sediment ecosystems. Limnol. Oceanogr. 57, 338–346 (2012).
Bergman, N. M., Lenton, T. M. & Watson, A. J. COPSE: a new model of biogeochemical cycling over phanerozoic time. Am. J. Sci. 304, 397–437 (2004).
Lenton, T. M. et al. Earliest land plants created modern levels of atmospheric oxygen. Proc. Natl Acad. Sci. USA 113, 9704–9709 (2016).
Guilbaud, R. et al. Oxygen minimum zones in the early Cambrian ocean. Geochem. Perspect. Lett. 6, 33–38 (2018).
Chen, X. et al. Rise to modern levels of ocean oxygenation coincided with the Cambrian radiation of animals. Nat. Commun. 6, 7142 (2015).
Pogge von Strandmann, P. A. E. et al. Selenium isotope evidence for progressive oxidation of the Neoproterozoic biosphere. Nat. Commun. 6, 10157 (2015).
Dahl, T. W. et al. Reorganisation of Earth’s biogeochemical cycles briefly oxygenated the oceans 520 Myr ago. Geochemical Perspect. Lett. 3. 210–220 (2017).
Canfield, D. E., Poulton, S. W. & Narbonne, G. M. Late-Neoproterozoic deep-ocean oxygenation and the rise of animal life. Science 315, 92–95 (2007).
Canfield, D. E. et al. Ferruginous conditions dominated Neoproterozoic deep-water chemistry. Science 321, 949–952 (2008).
Wallace, M. W. et al. Oxygenation history of the Neoproterozoic to early Phanerozoic and the rise of land plants. Earth. Planet. Sci. Lett. 466, 12–19 (2017).
Sahoo, S. K. et al. Oceanic oxygenation events in the anoxic Ediacaran ocean. Geobiology 14, 457–468 (2016).
Kimura, H. & Watanabe, Y. Oceanic anoxia at the Precambrian-Cambrian boundary. Geology 29, 995 (2001).
Goldberg, T., Poulton, S. W. & Strauss, H. Sulphur and oxygen isotope signatures of late Neoproterozoic to early Cambrian sulphate, Yangtze Platform, China: diagenetic constraints and seawater evolution. Precambrian Res. 137, 223–241 (2005).
Goldberg, T., Strauss, H., Guo, Q. & Liu, C. Reconstructing marine redox conditions for the Early Cambrian Yangtze Platform: evidence from biogenic sulphur and organic carbon isotopes. Palaeogeogr. Palaeoclimatol. Palaeoecol. 254, 175–193 (2007).
Gill, B. C. et al. Geochemical evidence for widespread euxinia in the later Cambrian ocean. Nature 469, 80–83 (2011).
Thompson, C. K. & Kah, L. C. Sulfur isotope evidence for widespread euxinia and a fluctuating oxycline in Early to Middle Ordovician greenhouse oceans. Palaeogeogr. Palaeoclimatol. Palaeoecol. 313–314, 189–214 (2012).
Zou, C. et al. Ocean euxinia and climate change ‘double whammy’ drove the Late Ordovician mass extinction. Geology 46, 4–7 (2018).
Glasspool, I. J., Edwards, D. & Axe, L. Charcoal in the Silurian as evidence for the earliest wildfire. Geology 32, 381–383 (2004).
Berner, R. A. The Phanerozoic Carbon Cycle: CO 2 and O2 (Oxford University Press, New York, USA, 2004).
Wu, N., Farquhar, J., Strauss, H., Kim, S. T. & Canfield, D. E. Evaluating the S-isotope fractionation associated with Phanerozoic pyrite burial. Geochim. Cosmochim. Acta 74, 2053–2071 (2010).
Lenton, T. M. & Watson, A. J. Redfield revisited 1. Regulation of nitrate, phosphate, and oxygen in the ocean. Glob. Biogeochem. Cycles 14, 225–248 (2000).
Berner, R. A. A model for atmospheric CO2 over phanerozoic time. Am. J. Sci. 291, 339–376 (1991).
Lenton, T. M., Daines, S. J. & Mills, B. J. W. COPSE reloaded: an improved model of biogeochemical cycling over Phanerozoic time. Earth Sci. Rev. 178, 1–28 (2018).
Goldberg, E. D. & Koide, M. Geochronological studies of deep sea sediments by the ionium / thorium method. Geochim. Cosmochim. Acta 26, 417–450 (1962).
Boudreau, B. P. Mean mixed depth of sediments: the wherefore and the why. Limnol. Oceanogr. 43, 524–526 (1998).
Brasier, M. D. & McIlroy, D. Neonereites uniserialis from c. 600 Ma year old rocks in western Scotland and the emergence of animals. J. Geol. Soc. Lond. 155, 5–12 (1998).
Bianchi, T. S., Johansson, B. & Elmgren, R. Breakdown of phytoplankton pigments in Baltic sediments: effects of anoxia and loss of deposit-feeding macrofauna. J. Exp. Mar. Bio. Ecol. 251, 161–183 (2000).
Haq, B. U. & Schutter, S. R. A chronology of Paleozoic sea-level changes. Science 322, 64–68 (2008).
Trotter, J. A., Williams, I. S., Barnes, C. R., Lécuyer, C. & Nicoll, R. S. Did cooling oceans trigger Ordovician biodiversification? Evidence from conodont thermometry. Science 321, 550–554 (2008).
Shields, G. A. & Mills, B. J. W. Tectonic controls on the long-term carbon isotope mass balance. Proc. Natl Acad. Sci. USA 114, 4318–4323 (2017).
Bambach, R. K., Knoll, A. H. & Wang, S. C. Origination, extinction, and mass depletions of marine diversity. Paleobiology 30, 522–542 (2004).
Sepkoski Jr, J. The Ordovician radiations: diversification and extinction shown by global genus-level taxonomic data. Lethaia 26, 146 (1993).
Saltzman, M. R., Edwards, C. T., Adrain, J. M. & Westrop, S. R. Persistent oceanic anoxia and elevated extinction rates separate the Cambrian and Ordovician radiations. Geology 43, 807–811 (2015).
Erwin, D. H. & Tweedt, S. Ecological drivers of the Ediacaran-Cambrian diversification of Metazoa. Evol. Ecol. 26, 417–433 (2012).
Edwards, C. T., Saltzman, M. R., Royer, D. L. & Fike, D. A. Oxygenation as a driver of the Great Ordovician Biodiversification Event. Nat. Geosci. 10, 925–929 (2017).
Wood, R. & Erwin, D. H. Innovation not recovery: dynamic redox promotes metazoan radiations. Biol. Rev. 93, 863-873 (2017).
Papaspyrou, S., Kristensen, E. & Christensen, B. Arenicola marina (Polychaeta) and organic matter mineralisation in sandy marine sediments: in situ and microcosm comparison. Estuar. Coast. Shelf Sci. 72, 213–222 (2007).
Burdige, D. J. Preservation of organic matter in marine sediments: controls, mechanisms, and an imbalance in sediment organic carbon budgets? Chem. Rev. 107, 467–485 (2007).
Diaz, R. J. & Rosenberg, R. Spreading dead zones and consequences for marine ecosystems. Science 321, 926–929 (2008).
Slomp, C. P. & Van Cappellen, P. The global marine phosphorus cycle: sensitivity to ocean circulation. Biogeosciences 4, 155–171 (2007).
Berner, R. A. Sedimentary pyrite formation. Am. J. Sci. 268, 1–23 (1970).
Raiswell, R. & Berner, R. A. Pyrite and organic matter in Phanerozoic normal marine shales. Geochim. Cosmochim. Acta 50, 1967–1976 (1986).
Rosenberg, R., Johansson, B. & Hellman, B. Hypoxia tolerance of marine benthic fauna. Mar. Ecol. Prog. Ser. 79, 127–131 (1991).
Sperling, E. A. et al. Oxygen, ecology, and the Cambrian radiation of animals. Proc. Natl Acad. Sci. USA 110, 13446–13451 (2013).
Och, L. M. & Shields-Zhou, G. A. The Neoproterozoic oxygenation event: environmental perturbations and biogeochemical cycling. Earth Sci. Rev. 110, 26–57 (2012).
Saltzman, M. R. & Thomas, E. Carbon isotope stratigraphy. Geol. Time Scale 2012 1–2, 207–232 (2012).
Kump, L. R. & Garrels, R. M. Modeling atmospheric O2 in the global sedimentary redox cycle. Am. J. Sci. 286, 337–360 (1986).
Acknowledgements
Research was financially supported by the European Research Council under the European Union’s Seventh Framework Programme (FP/2007–2013) (ERC Grant 306933 to F.J.R.M.), the Netherlands Organisation for Scientific Research (VICI grant 016.VICI.170.072 to F.J.R.M.) and Research Foundation Flanders (FWO Aspirant PhD Fellowship to S.V.D.V.). B.J.W.M. is funded by a University of Leeds Academic Fellowship. S.W.P. and T.M.L. acknowledge support from Royal Society Wolfson Research Merit Awards and the NERC Biosphere Evolution, Transitions and Resilience (BETR) programme (NE/P013651).
Author information
Authors and Affiliations
Contributions
S.V.D.V. and F.J.R.M. conceived the hypothesis; S.V.D.V., B.J.W.M. and S.W.P. compiled the data; S.V.D.V. and B.J.W.M. altered the model and performed simulations; T.M.L. provided model code and advice; S.V.D.V., B.J.W.M. and S.W.P. wrote the paper, with significant contributions from all co-authors.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
van de Velde, S., Mills, B.J.W., Meysman, F.J.R. et al. Early Palaeozoic ocean anoxia and global warming driven by the evolution of shallow burrowing. Nat Commun 9, 2554 (2018). https://doi.org/10.1038/s41467-018-04973-4
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-018-04973-4
This article is cited by
-
Redox conditions of Early Cambrian Ocean as deciphered from multi-proxy geochemical and isotopic studies of Proto-Tethys carbonaceous sediments from Outer Lesser Himalaya, India
Journal of Earth System Science (2024)
-
Assessing the expansion of the Cambrian Agronomic Revolution into fan-delta environments
Scientific Reports (2022)
-
Alternation of stromatolites and vertical burrows controlled by storm processes and sea-level changes in the middle Cambrian carbonates of central China
Journal of Earth System Science (2022)
-
Microfossil Assemblages and Indication of the Source and Preservation Pattern of Organic Matter from the Early Cambrian in South China
Journal of Earth Science (2022)
-
Quantitative comparison of geological data and model simulations constrains early Cambrian geography and climate
Nature Communications (2021)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.