Abstract
Collective measurements on identically prepared quantum systems can extract more information than local measurements, thereby enhancing information-processing efficiency. Although this nonclassical phenomenon has been known for two decades, it has remained a challenging task to demonstrate the advantage of collective measurements in experiments. Here, we introduce a general recipe for performing deterministic collective measurements on two identically prepared qubits based on quantum walks. Using photonic quantum walks, we realize experimentally an optimized collective measurement with fidelity 0.9946 without post selection. As an application, we achieve the highest tomographic efficiency in qubit state tomography to date. Our work offers an effective recipe for beating the precision limit of local measurements in quantum state tomography and metrology. In addition, our study opens an avenue for harvesting the power of collective measurements in quantum information-processing and for exploring the intriguing physics behind this power.
Similar content being viewed by others
Introduction
Quantum measurements are the key for extracting information from quantum systems and for connecting the quantum world with the classical world. Understanding the power and limitation of measurements is of paramount importance not only to foundational studies, but also to many applications, such as quantum tomography, metrology, and communication1,2,3,4,5,6,7,8. An intriguing phenomenon predicted by quantum theory is that collective measurements on identically prepared quantum systems may extract more information than local measurements on individual systems, thereby leading to higher tomographic efficiency and precision9,10,11,12,13,14. The significance of collective measurements for multiparameter quantum metrology was also recognized recently15,16. This nonclassical phenomenon is owing to entanglement in the quantum measurements instead of quantum states. It is closely tied to the phenomenon of “nonlocality without entanglement”17. In addition, collective measurements are very useful in numerous other tasks, such as distilling entanglement18, enhancing nonlocal correlations19, and detecting quantum change point20. However, demonstrating the advantage of collective measurements in experiments has remained a daunting task. This is because most optimized protocols entail generalized entangling measurements on many identically prepared quantum systems, which are very difficult to realize deterministically.
Here we introduce a general method for performing deterministic collective measurements on two identically prepared qubits based on quantum walks, which extends the method for performing generalized measurements on a single qubit only21,22,23. By devising photonic quantum walks, we realize experimentally a highly efficient collective measurement highlighted in refs. 11,13,14. As an application, we realize, for the first time, qubit state tomography with deterministic collective measurements. The protocol we implemented is significantly more efficient than local measurements commonly employed in most experiments. Moreover, it can achieve near-optimal performance over all two-copy collective measurements with respect to various figures of merit without using adaptive measurements. Such high efficiency demonstrates the main advantage of collective measurements over separable measurements. Here, we encode the two qubits in the two degrees of freedom of a single photon24,25,26,27, but our method for performing collective measurements can be generalized to two-photon two-qubit states by combining the technique of quantum joining28 or teleportation29.
Results
Optimized collective measurements
In quantum theory, a measurement is usually represented by a positive-operator-valued measure (POVM), which is composed of a set of positive operators that sum up to the identity. In traditional quantum information-processing, measurements are performed on individual quantum systems one by one, which often cannot extract information efficiently. Fortunately, quantum theory allows us to perform collective measurements on identically prepared quantum systems in a way that has no classical analog, as illustrated in Fig. 1.
Individual and collective measurements. a Repeated individual measurements. b Single N-copy collective measurement. c Repeated two-copy collective measurements. d Realization of the collective SIC-POVM defined in Eqs. (1) and (2) using five-step quantum walks. The coin qubit and the walker in positions 1 and −1 are taken as the two-qubit system of interest, whereas the other positions of the walker act as an ancilla. Site-dependent coin operators C(x, t) are specified in the Methods section. Five detectors E1 to E5 correspond to the five outcomes of the collective SIC-POVM
In the case of a qubit, a special two-copy collective POVM was highlighted in refs.11,13,14, which consists of five POVM elements,
where \(\left| {{\mathrm{\Psi }}_ - } \right\rangle = \frac{1}{{\sqrt 2 }}\left( {\left| {01} \right\rangle - \left| {10} \right\rangle } \right)\) is the singlet, which is maximally entangled, and \(\left| {\psi _j} \right\rangle\) for j = 1, 2, 3, 4 are qubit states that form a symmetric informationally complete POVM (SIC-POVM), that is, \(\left| {\left\langle {\psi _j\left| {\psi _k} \right.} \right\rangle } \right|^2\) = (2δ jk + 1)/330,31. Geometrically, the Bloch vectors of the four states \(\left| {\psi _j} \right\rangle\) form a regular tetrahedron inside the Bloch sphere. For concreteness, here we choose
The POVM defined by Eqs. (1) and (2) is referred to as the collective SIC-POVM henceforth. If this POVM is performed on the two-copy state ρ⊗2, then the probability of obtaining outcome j is given by p j = tr(ρ⊗2E j ).
The collective SIC-POVM is distinguished because it is optimal in extracting information from a pair of identical qubits9,11. It is universally Fisher symmetric in the sense of providing uniform and maximal Fisher information on all parameters that characterize the quantum states of interest13,14,32. Moreover, it is unique such POVM with no more than five outcomes. Consequently, the collective SIC-POVM is significantly more efficient than any local measurement in many quantum information-processing tasks, including tomography and metrology. Moreover, its high tomographic efficiency is achieved without using adaptive measurements, which is impossible for local measurements. As far as two-copy collective measurements are concerned, surprisingly, more entangled measurements, such as the Bell measurements, cannot lead to higher efficiency. Although multi-copy (say three-copy) collective measurements can further improve the efficiency, the improvement is not so significant13,14.
Realization of the collective SIC-POVM via quantum walks
Recently, discrete quantum walks were proposed as a recipe for implementing general POVMs on a single qubit21, which have been demonstrated in experiments22,23. In a one-dimensional discrete quantum walk, the system state is characterized by two degrees of freedom \(\left| {x,c} \right\rangle\), where x = …, −1, 0, 1, … denotes the walker position, and c = 0, 1 represents the coin state. The dynamics of each step is described by a unitary transformation of the form U(t) = TC(t), where
is the conditional translation operator, and C(t) = \(\mathop {\sum}\nolimits_x \left| x \right\rangle \left\langle x \right| \otimes C(x,t)\) with C(x, t) being site-dependent coin operators. A general POVM on a qubit can be realized by engineering the coin operators C(x, t) followed by measuring the walker position after certain steps. However, little is known in the literature on realizing POVMs on higher-dimensional systems. Here, we propose a general method for extending the capabilities of quantum walks. For concreteness, we illustrate our approach with the collective SIC-POVM.
To realize the collective SIC-POVM using quantum walks, the coin qubit and the walker in positions 1 and −1 are taken as the two-qubit system of interest, whereas the other positions of the walker act as an ancilla. With this choice, the collective SIC-POVM can be realized with five-step quantum walks, as illustrated in Fig. 1d and discussed in more details in Supplementary Note 1. Here, the nontrivial coin operators C(x, t) are specified in the Methods section. The five detectors E1 to E5 marked in the figure correspond to the five POVM elements specified in Eqs. (1) and (2). Moreover, this proposal can be implemented using photonic quantum walks, as illustrated in Fig. 2 (see also Supplementary Fig. 1).
Experimental setup for realizing the collective SIC-POVM. The setup consists of two modules designed for two-copy state preparation (a, b) and two-copy collective measurement c, respectively. In the two-copy state-preparation module, a prepares the first copy (walker qubit) in the path degree of freedom; b prepares the second copy (coin qubit) in the polarization degree of freedom. The two-copy collective measurement module (c) performs the collective SIC-POVM via photonic quantum walks as illustrated in Fig. 1d. Here beam displacers (BDs) are used to realize the conditional translation operator T. Combinations of half wave plates (HWPs) and quarter wave plates (QWPs) with rotation angles specified in the embedded table are used to realize site-dependent coin operators C(x, t). Five single-photon detectors (SPDs) E1 to E5 correspond to the five outcomes of the collective SIC-POVM
Experimental setup
The experimental setup for realizing the collective SIC-POVM and its application in quantum state tomography is presented in Fig. 2. The setup is composed of two modules designed for two-copy state-preparation and collective measurements, respectively.
The two-copy collective measurement module performs the collective SIC-POVM based on quantum walks, as illustrated in Fig. 1d (cf. Supplementary Fig. 1). Here the conditional translation operator T is realized by interferometrically stable beam displacers (BDs)33,34,35,36, which displace the component with horizontal polarization (H) away from the component with vertical polarization (V). The coin operators C(x, t) are realized by suitable combinations of half wave plates (HWPs) and quarter wave plates (QWPs), with rotation angles specified in the table embedded in Fig. 2.
In the two-copy state-preparation module, we first prepare copy 1 in the path degree of freedom, i.e., the walker qubit encoded in positions 1 and −1 (see a in Fig. 2). A pair of 1-mm-long BBO crystals with optical axes perpendicular to each other, cut for type-1 phase-matched spontaneous parametric down-conversion (SPDC) process, is pumped by a 40-mW H-polarized beam at 404 nm. The polarization state of the beam is prepared as \({\mathrm{cos}}{\kern 1pt} 2\alpha _1\left| H \right\rangle\) + \({\mathrm{sin}}{\kern 1pt} 2\alpha _1\left| V \right\rangle\) when the deviation angle of the HWP at 404 nm is set at α1. After the SPDC process, a pair of photons with wave length λ = 808 nm is created in the state of \({\mathrm{sin}}{\kern 1pt} 2\alpha _1\left| {HH} \right\rangle\) + \({\mathrm{cos}}{\kern 1pt} 2\alpha _1\left| {VV} \right\rangle\)37. The two photons pass through two interference filters whose FWHM (full width at half maximum) is 3 nm, resulting in a coherence length of 270λ. One photon is detected by a single-photon detector acting as a trigger. After tracing out this photon, the other photon is prepared in the state \({\mathrm{sin}}^{\mathrm{2}}{\kern 1pt} 2\alpha _1\left| H \right\rangle \left\langle H \right|\) + \({\mathrm{cos}}^{\mathrm{2}}{\kern 1pt} 2\alpha _1\left| V \right\rangle \left\langle V \right|\), whose purity is controlled by α1. Two HWPs (not shown in Fig. 2) at the input and output ports of the single-mode fiber are used to maintain the polarization state of the photon. After passing a HWP and a QWP with deviation angles h1, q1, the photon is prepared in the desired state ρ. To encode the polarization state into the path degree of freedom, BD0 is used to displace the H-component into path 1, which is 4-mm away from the V-component in path −1; then a HWP with deviation angle h3 = 45° is placed in path 1. The resulting photon is described by the state \(\rho \otimes \left| V \right\rangle \left\langle V \right|\).
Then we encode the second copy of ρ into the polarization degree of freedom (coin qubit) using two HWPs, a quartz crystal with a decoherence length of 385λ, and a QWP (see b in Fig. 2). The first HWP with rotation angle α2 and the quartz crystal prepare the polarization state \({\mathrm{sin}}^2{\kern 1pt} 2\alpha _2\left| H \right\rangle \left\langle H \right|\) + \({\mathrm{cos}}^2{\kern 1pt} 2\alpha _2\left| V \right\rangle \left\langle V \right|\) with desired purity. Then the direction of the Bloch vector of the polarization state is adjusted by a HWP and a QWP with deviation angles h2 and q2. In this way, we can prepare the desired two-copy state ρ ⊗ ρ, the first copy of which is encoded in the path degree of freedom, whereas the second one in the polarization degree of freedom.
The two-copy state-preparation module described above is capable of preparing any two-copy state (see Supplementary Note 2 for more details). Next, the two-copy state ρ ⊗ ρ is sent into the two-copy collective measurement module, which performs the collective SIC-POVM based on quantum walks, as described before. It is worth pointing out that the collective SIC-POVM can also be applied to measure arbitrary two-qubit states, although we focus on two-copy qubit states in this work.
Verification and tomography of the collective SIC-POVM
To verify the experimental implementation of the collective SIC-POVM, we took the conventional method of measuring the probability distributions after preparing the input states as normalized POVM elements, i.e., \(\hat E_i = E_i{\mathrm{/tr}}\left( {E_i} \right)\) for i = 1, …, 5. These input states can be prepared by choosing proper rotation angles α1, h1, q1, h3, α2, h2, q2 as specified in Supplementary Table 1. The measurement probability distributions are shown in Fig. 3, which agree very well with the theoretical prediction.
Experimental verification of the collective SIC-POVM realized. Here each \(\hat E_i\) for i = 1, 2, 3, 4, 5 denotes an input state, which corresponds to the POVM element E i of the collective SIC-POVM after normalization. Each input state is prepared and measured 100,000 times. The frequencies of obtaining the five outcomes are plotted using different colors; here the error bars are too small to be visible. For comparison, the probabilities in the ideal scenario are plotted in gray shadow
To accurately characterize the POVM elements that were actually realized, we then performed quantum measurement tomography. Overall, 36 input states, the tensor products of the six eigenstates of three Pauli operators, were prepared and sent to the collective measurement module, with each setting repeated 35,000 times. Then the five POVM elements were estimated from the measurement statistics using the maximum likelihood method developed in ref.38. The fidelities of the five POVM elements estimated are 0.9991 ± 0.0001, 0.9979 ± 0.0007, 0.9870 ± 0.0008, 0.9927 ± 0.0002 and 0.9961 ± 0.0002, respectively; the overall fidelity of the POVM (cf. the Methods section) is 0.9946 ± 0.0002. Here, the error bars denote the standard deviations of 100 simulations from Poisson statistics. Such high fidelities demonstrate that the collective SIC-POVM was realized with very high quality. Detailed information about the five reconstructed POVM elements can be found in Supplementary Note 3 and Supplementary Fig. 2.
Quantum state tomography with the collective SIC-POVM
The experimental realization of the collective SIC-POVM enables us to achieve unprecedented efficiency in quantum state tomography. In this section we demonstrate the tomographic significance of the collective SIC-POVM and the power of collective measurements.
In the first experiment, we investigated the scaling of the mean infidelity 1 − F achieved by the collective SIC-POVM with the sample size N (the number of copies of the state available for tomography). Three pure states with Bloch vectors (0, 0, 1), \(\frac{1}{{\sqrt 2 }}\)(1, 0, 1), and \(\frac{1}{{\sqrt 3 }}\)(1, 1, 1) were considered (see Supplementary Note 4 and Supplementary Fig. 3 for additional results on mixed states). In each case, the probabilities of obtaining the outcomes of the collective SIC-POVM were estimated from frequencies of repeated measurements, from which we reconstructed the original state using the maximum likelihood method4; see Supplementary Note 5 and Supplementary Fig. 4.
The experimental result and simulation result are shown in Fig. 4. Also shown as benchmarks are the simulation results on two popular alternative schemes: one based on mutually unbiased bases (MUB) for a qubit39,40,41,42 and the other based on two-step adaptive measurements proposed in ref. 43 (cf. refs.44,45,46). The experimental result agrees very well with the theoretical predication14 and numerical simulation. The efficiency of the collective SIC-POVM is almost independent of the input state; the infidelity approximately scales as O(1/N) for all states investigated (cf. Supplementary Table 2). This high efficiency is tied to the fact that the probability of obtaining the outcome E5 in Eq. (1) is very sensitive to the purity of the input state, so that the purity can be estimated very accurately. By contrast, the scaling behavior is much worse for MUB except when the input state aligns with one of the POVM elements, which corresponds to “known state tomography”43. This is because the infidelity is very sensitive to inaccurate estimation of the purity, which is unavoidable for a fixed individual measurement. For a generic pure state, the infidelity achieved by the collective SIC-POVM for N = 2048 is ~ 12 (three) times smaller than that achieved by MUB (local adaptive measurements). The advantage of the collective SIC-POVM becomes more significant as the sample size increases.
Scaling of the mean infidelity in quantum state tomography with the collective SIC-POVM. Both experimental (coll-exp) and simulation (coll-ideal) results are plotted for the collective SIC-POVM. The performances of MUB and two-step adaptive measurements (simulation) are shown for comparison. a, b and c correspond to the tomography of three pure states with Bloch vectors s as specified; N is the sample size, ranging from 16 to 2048. Each data point is the average of 1000 repetitions, and the error bar denotes the standard deviation
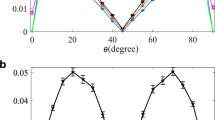
In the second experiment, we investigated the mean infidelity achieved by the collective SIC-POVM when the input states have the form \(\left| {\psi (\theta )} \right\rangle\) = \({\mathrm{sin}}{\kern 1pt} \theta \left| 0 \right\rangle + {\mathrm{cos}}{\kern 1pt} \theta \left| 1 \right\rangle\) with θ ranging from 0 to π/2. Here N is chosen to be 128 (that is, 64 pairs) or 1024 (512 pairs). The result shown in Fig. 5 further demonstrates that the efficiency of the collective SIC-POVM is almost independent of the input state. In addition, the infidelity in the worst scenario is much smaller than that achieved by MUB and local adaptive measurements. As in the first experiment, the advantage of the collective SIC-POVM becomes more significant when N increases.
Mean infidelities achieved by the collective SIC-POVM in estimating a family of pure states. These pure states have the form \(\left| {\psi (\theta )} \right\rangle\) = \({\mathrm{sin}}{\kern 1pt} \theta \left| 0 \right\rangle + {\mathrm{cos}}{\kern 1pt} \theta \left| 1 \right\rangle\). The performances of MUB and two-step adaptive measurements (simulation) are shown for comparison. The sample size is N = 128 in a and N = 1024 in b. Each data point is the average of 1000 repetitions, and the error bar denotes the standard deviation
In the third experiment, we considered two families of mixed states \(\rho = \frac{1}{2}\)(I + s ⋅ σ) with Bloch vectors along \(\widehat {\bf{s}}\) = (0, 0, −1) and \(\widehat {\bf{s}}\) = (0.490, −0.631, 0.602), respectively, and with s ranging from 0 to 1. The sample size N is chosen to be 256; both the mean infidelity and mean square error (MSE) are considered as figures of merit. The experimental result is shown in Fig. 6. The mean infidelity achieved by the collective SIC-POVM is not only smaller than that by MUB, but also smaller than the Gill-Massar (GM) bound13,44,47, which constrains the performance of any local measurement, even with adaptive choices. Moreover, the mean infidelity approximately saturates a bound derived in refs. 13,14, which represents the best performance that can be achieved by two-copy collective measurements; cf. the Methods section. In addition, the collective SIC-POVM is also nearly optimal with respect to the MSE for all states. Remarkably, such high efficiency is achieved without any adaptive measurement.
Performance of the collective SIC-POVM in the tomography of mixed qubit states. Two families of mixed states with Bloch vector direcitions specified in a and b are considered. The figures of merit are chosen as the mean infidelity and MSE. Also shown for comparison are the performance of MUB (simulation) as well as the Gill-Massar (GM) bound13,44,47 and a collective (coll) bound13,14 (see the Methods section). Here \({\hat{\mathbf s}}\) and s denote the direction and length of the Bloch vector; the sample size is N = 256; each data point is the average of 1000 repetitions, and the error bar denotes the standard deviation
Discussion
In summary, we introduced a general method for implementing deterministic collective measurements on two identically prepared qubits based on quantum walks. Using photonic quantum walks, we then realized experimentally the collective SIC-POVM with very high quality and thereby achieved unprecedented high efficiency in qubit state tomography. The collective SIC-POVM we realized is significantly more efficient than any local measurement. It improves the scaling of the mean infidelity in the worse scenario from \(O\left( {1{\mathrm{/}}\sqrt N } \right)\) to O(1/N). Moreover, it is nearly optimal over all two-copy collective measurements with respect to various figures of merit, including the mean infidelity and MSE, although no adaptive measurement is required. This high efficiency manifests the primary advantage of collective measurements over separable measurements.
Our work demonstrated a truly nonclassical phenomenon that is owing to entanglement in quantum measurements instead of quantum states. Moreover, it offers an effective recipe for exceeding the precision limit of local measurements in quantum state tomography. Similar idea can readily be applied to enhance the precision in multiparameter quantum metrology. For example, in the joint estimation of phase and phase diffusion, it was shown in ref. 15 that collective measurements can lead to higher precision than local measurements. Recently, this prediction was verified in a proof-of-principle experiment based on probabilistic Bell measurements16. Our technique for implementing deterministic collective measurements may help demonstrate the practical advantage of collective measurements in quantum metrology. More generally, our work opens an avenue for exploring the power of collective measurements in quantum information processing. In the future, it would be desirable to extend our approach to realize multi-copy collective measurements on qubits and systems of higher dimensions.
Methods
Coin operators for realizing the collective SIC-POVM
Here, we present the coin operators that appear in Fig. 1d; see Supplementary Note 1 for more details.
Fidelity between two POVMs
Consider two POVMs \(\left\{ {E_j} \right\}_{j = 1}^M\) and \(\left\{ {E_{j\prime }} \right\}_{j = 1}^M\) on a d-dimensional Hilbert space with the same number of elements, where \(E_{j\prime}\) is the counterpart of E j (for example, one is the experimental realization of the other). Construct two normalized quantum states as \(\sigma = \frac{1}{d}\mathop {\sum}\nolimits_{j = 1}^M {\kern 1pt} E_j \otimes \left( {\left| j \right\rangle \left\langle j \right|} \right)\) and \(\sigma {\prime} = \frac{1}{d}\mathop {\sum}\nolimits_{j = 1}^M {\kern 1pt} E_{j\prime} \otimes \left( {\left| j \right\rangle \left\langle j \right|} \right)\), where \(\left| j \right\rangle\) form an orthonormal basis for an ancilla system. The fidelity between the two POVMs \(\left\{ {E_j} \right\}_{j = 1}^M\) and \(\left\{ {E_{j\prime} } \right\}_{j = 1}^M\) is defined as the fidelity between the two states σ and σ′,
where \(w_j = \frac{{\sqrt {{\mathrm{tr}}\left( {E_j} \right){\mathrm{tr}}\left( {E_{j\prime} } \right)} }}{d}\), and \(F_j = F\left( {\frac{{E_j}}{{{\mathrm{tr}}\left( {E_j} \right)}},\frac{{E_{j\prime} }}{{{\mathrm{tr}}\left( {E_{j\prime }} \right)}}} \right)\) is the fidelity between the two normalized POVM elements \(\frac{{E_j}}{{{\mathrm{tr}}\left( {E_j} \right)}}\) and \(\frac{{E_{j\prime} }}{{{\mathrm{tr}}\left( {E_{j\prime }} \right)}}\).
GM bounds and collective bounds
In quantum state tomography with individual measurements (including local adaptive measurements), the precision achievable is constrained by the GM bound13,44,47 (see also ref. 48). In the case of a qubit, the GM bound is \(\frac{9}{{4N}}\) when the figure of merit is the mean infidelity (approximately equal to the mean square Bures distance), where N is the sample size (assuming N is not too small). When the figure of merit is the MSE \({\Bbb E}{\kern 1pt} {\mathrm{tr}}\left[ {\left( {\hat \rho - \rho } \right)^2} \right]\), the GM bound is \(\frac{{\left( {2 + \sqrt {1 - s^2} } \right)^2}}{{2N}}\), where s is the length of the Bloch vector of the qubit state.
When collective measurements on two identical qubits are allowed, the precision limit is constrained by a collective bound. According to Eqs. (6.73) and (6.74) in ref. 13 with t = 3/2, the collective bound for the mean infidelity (mean square Bures distance) is \(\frac{3}{{2N}}\) (cf. ref. 14), and the bound for the MSE is
The GM bound and collective bound for the mean infidelity may be violated when the state is nearly pure (with thresholds depending on N), in which case common estimators (including the maximum likelihood estimator) are biased due to the boundary of the state space. The precision limits with respect to the MSE are less sensitive to this influence.
Data availability
The data that support the results of this study are available from the corresponding authors upon request.
References
Helstrom, C. W. Quantum Detection and Estimation Theory. (Academic Press, NY, 1976).
Holevo, A. S. Probabilistic and Statistical Aspects of Quantum Theory. (North-Holland, Amsterdam, 1982).
Braunstein, S. L. & Caves, C. M. Statistical distance and the geometry of quantum states. Phys. Rev. Lett. 72, 3439–3443 (1994).
Paris, M. G. A & Řeháček, J. (eds). Quantum State Estimation, vol. 649 of Lecture Notes in Physics. (Springer, Berlin, 2004).
Lvovsky, A. I. & Raymer, M. G. Continuous-variable optical quantum-state tomography. Rev. Mod. Phys. 81, 299 (2009).
Riedel, M. F. et al. Atom-chip-based generation of entanglement for quantum metrology. Nature 464, 1170–1173 (2010).
Giovannetti, V., Lloyd, S. & Maccone, L. Advances in quantum metrology. Nat. Photonics 5, 222 (2011).
Szczykulska, M., Baumgratz, T. & Datta, A. Multi-parameter quantum metrology. Adv. Phys. 1, 621–639 (2016).
Massar, S. & Popescu, S. Optimal extraction of information from finite quantum ensembles. Phys. Rev. Lett. 74, 1259–1263 (1995).
Gisin, N. & Popescu, S. Spin flips and quantum information for antiparallel spins. Phys. Rev. Lett. 83, 432–435 (1999).
Vidal, G., Latorre, J. I., Pascual, P. & Tarrach, R. Optimal minimal measurements of mixed states. Phys. Rev. A. 60, 126 (1999).
Bagan, E., Ballester, M. A., Gill, R. D., Muñoz-Tapia, R. & Romero-Isart, O. Separable measurement estimation of density matrices and its fidelity gap with collective protocols. Phys. Rev. Lett. 97, 130501 (2006).
Zhu, H. Quantum State Estimation and Symmetric Informationally Complete POMs. Ph.D. thesis, National University of Singapore (2012).
Zhu, H. & Hayashi, M. Universally Fisher-symmetric informationally complete measurements. Phys. Rev. Lett. 120, 030404 (2018).
Vidrighin, M. D. et al. Joint estimation of phase and phase diffusion for quantum metrology. Nat. Commun. 5, 3532 (2014).
Roccia, E. et al. Entangling measurements for multiparameter estimation with two qubits. Quantum Sci. Technol. 3, 01LT01 (2018).
Bennett, C. H. et al. Quantum nonlocality without entanglement. Phys. Rev. A. 59, 1070–1091 (1999).
Bennett, C. H. et al. Purification of noisy entanglement and faithful teleportation via noisy channels. Phys. Rev. Lett. 76, 722–725 (1996).
Liang, Y.-C. & Doherty, A. C. Better Bell-inequality violation by collective measurements. Phys. Rev. A. 73, 052116 (2006).
Sents, G., Bagan, E., Calsamiglia, J., Chiribella, G. & Muñoz Tapia, R. Quantum change point. Phys. Rev. Lett. 117, 150502 (2016).
Kurzyński, P. & Wójcik, A. Quantum walk as a generalized measuring device. Phys. Rev. Lett. 110, 200404 (2013).
Bian, Z. et al. Realization of single-qubit positive-operator-valued measurement via a one-dimensional photonic quantum walk. Phys. Rev. Lett. 114, 203602 (2015).
Zhao, Y.-Y. et al. Experimental realization of generalized qubit measurements based on quantum walks. Phys. Rev. A. 91, 042101 (2015).
Englert, B.-G., Kurtsiefer, C. & Weinfurter, H. Universal unitary gate for single-photon two-qubit states. Phys. Rev. A. 63, 032303 (2001).
Fiorentino, M. & Wong, F. N. C. Deterministic controlled-not gate for single-photon two-qubit quantum logic. Phys. Rev. Lett. 93, 070502 (2004).
Barreiro, J. T., Wei, T.-C. & Kwiat, P. G. Beating the channel capacity limit for linear photonic superdense coding. Nat. Phys. 4, 282–286 (2008).
Rubino, G. et al. Experimental verification of an indefinite causal order. Sci. Adv. 3, e1602589 (2017).
Vitelli, C. et al. Joining the quantum state of two photons into one. Nat. Photonics 7, 521–526 (2013).
Ahnert, S. E. & Payne, M. C. All possible bipartite positive-operator-value measurements of two-photon polarization states. Phys. Rev. A. 73, 022333 (2006).
Zauner, G. Quantum designs: Foundations of a noncommutative design theory. Int. J. Quantum Inform. 09, 445–507 (2011).
Renes, J. M., Blume-Kohout, R., Scott, A. J. & Caves, C. M. Symmetric informationally complete quantum measurements. J. Math. Phys. 45, 2171 (2004).
Li, N., Ferrie, C., Gross, J. A., Kalev, A. & Caves, C. M. Fisher-symmetric informationally complete measurements for pure states. Phys. Rev. Lett. 116, 180402 (2016).
O’Brien, J. L., Pryde, G. J., White, A. G., Ralph, T. C. & Branning, D. Demonstration of an all-optical quantum controlled-not gate. Nature 426, 264–267 (2003).
Rahimi-Keshari, S. et al. Direct characterization of linear-optical networks. Opt. Express 21, 13450–13458 (2013).
Rab, A. S. et al. Entanglement of photons in their dual wave-particle nature. Nat. Commun. 8, 915 (2017).
Shalm, L. K. et al. Strong loophole-free test of local realism. Phys. Rev. Lett. 115, 250402 (2015).
Kwiat, P. G., Waks, E., White, A. G., Appelbaum, I. & Eberhard, P. H. Ultrabright source of polarization-entangled photons. Phys. Rev. A. 60, R773–R776 (1999).
Fiurášek, J. Maximum-likelihood estimation of quantum measurement. Phys. Rev. A. 64, 024102 (2001).
Wootters, W. K. & Fields, B. D. Optimal state–determination by mutually unbiased measurements. Ann. Phys. 191, 363 (1989).
Durt, T., Englert, B.-G., Bengtsson, I. & Życzkowski, K. On mutually unbiased bases. Int. J. Quantum Inform. 08, 535 (2010).
Adamson, R. B. A. & Steinberg, A. M. Improving quantum state estimation with mutually unbiased bases. Phys. Rev. Lett. 105, 030406 (2010).
Zhu, H. Quantum state estimation with informationally overcomplete measurements. Phys. Rev. A. 90, 012115 (2014).
Mahler, D. H. et al. Adaptive quantum state tomography improves accuracy quadratically. Phys. Rev. Lett. 111, 183601 (2013).
Hou, Z., Zhu, H., Xiang, G.-Y., Li, C.-F. & Guo, G.-C. Achieving quantum precision limit in adaptive qubit state tomography. npj Quantum Inf. 2, 16001 (2016).
Kravtsov, K. S. et al. Experimental adaptive Bayesian tomography. Phys. Rev. A. 87, 062122 (2013).
Qi, B. et al. Adaptive quantum state tomography via linear regression estimation: Theory and two-qubit experiment. npj Quantum Inf. 3, 19 (2017).
Gill, R. D. & Massar, S. State estimation for large ensembles. Phys. Rev. A. 61, 042312 (2000).
Hayashi, M. A linear programming approach to attainable Cramér-Rao type bounds. In: O. Hirota, A. S. Holevo, C. M. Caves (eds). Quantum Communication, Computing, and Measurement. (Plenum, NY, 1997).
Acknowledgements
The work at USTC is supported by the National Natural Science Foundation of China under Grants (Nos. 11574291, 11774334, 61327901, and 11774335), the National Key Research and Development Program of China (No.2017YFA0304100), Key Research Program of Frontier Sciences, CAS (No.QYZDY-SSW-SLH003), the Fundamental Research Funds for the Central Universities (No.WK2470000026), and China Postdoctoral Science Foundation (Grant No. 2016M602012). HZ acknowledges financial support from the Excellence Initiative of the German Federal and State Governments (ZUK 81) and the DFG. J.S. acknowledges financial support from the ERC (Consolidator Grant 683107/TempoQ), and the DFG.
Author information
Authors and Affiliations
Contributions
HZ developed the theoretical approach; GYX supervised the project; ZBH, JFT, JL, and GYX designed the experiment and the measurement apparatus for the collective measurement; ZBH built the instruments, performed the experiment and collected the data with assistance from GYX, JFT, YY, and KDW; JS developed the maximum likelihood algorithm for quantum state tomography with collective measurements. ZBH, JS, HZ, and GYX performed numerical simulations and analyzed the experimental data with assistance from CFL and GCG; HZ, ZBH, JS, and GYX prepared and wrote the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Hou, Z., Tang, JF., Shang, J. et al. Deterministic realization of collective measurements via photonic quantum walks. Nat Commun 9, 1414 (2018). https://doi.org/10.1038/s41467-018-03849-x
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-018-03849-x
This article is cited by
-
Verifying the security of a continuous variable quantum communication protocol via quantum metrology
npj Quantum Information (2024)
-
Fresh perspectives on the foundations of quantum physics
Nature Reviews Physics (2023)
-
Discriminating mixed qubit states with collective measurements
Communications Physics (2023)
-
Progress in quantum teleportation
Nature Reviews Physics (2023)
-
Approaching optimal entangling collective measurements on quantum computing platforms
Nature Physics (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.