Abstract
Measurements by the Genesis mission have shown that solar wind oxygen is depleted in the rare isotopes, 17O and 18O, by approximately 80 and 100‰, respectively, relative to Earth’s oceans, with inferred photospheric values of about −60‰ for both isotopes. Direct astronomical measurements of CO absorption lines in the solar photosphere have previously yielded a wide range of O isotope ratios. Here, we reanalyze the line strengths for high-temperature rovibrational transitions in photospheric CO from ATMOS FTS data, and obtain an 18O depletion of δ18O = −50 ± 11‰ (1σ). From the same analysis we find a carbon isotope ratio of δ13C = −48 ± 7‰ (1σ) for the photosphere. This implies that the primary reservoirs of carbon on the terrestrial planets are enriched in 13C relative to the bulk material from which the solar system formed, possibly as a result of CO self-shielding or inheritance from the parent cloud.
Similar content being viewed by others
Introduction
The light stable isotope compositions of meteorites, planets, and the Sun constrain how our solar system formed and the nature of the formation environment. Given that the protosun was the primary mass of the nascent solar system, its isotopic composition is of particular importance. The NASA Genesis mission succeeded in measuring O and N isotope ratios in returned solar wind samples1,2. Extrapolation of the solar wind results to the solar photosphere, by accounting for isotope fractionation due to ion collisions in the corona3, has demonstrated that Earth’s silicates, and by extension all terrestrial planet silicates, experienced a very different isotopic history compared to the bulk Sun. This result was predicted based on O isotope data from inclusions in primitive meteorites4,5, and it was suggested that photochemical processes in the solar nebula were responsible for the isotopic difference between the bulk Sun and planetary materials5,6,7.
Carbon isotopes are also of central importance to understanding solar system formation, and are essential to interpreting kinetic isotope fractionation in biochemical systems. Genesis has not yet reported C isotope values for the solar wind, due in part to the composition of the concentrator targets (SiC and diamond-like C). Measurement of solar wind implanted in lunar regolith silicate grains yielded a δ13C ~−105 ± 20‰, from which a bulk solar ratio of ~−150 to −100‰ was inferred8 (C isotope δ-values are computed relative to the Vienna Pee Dee Belemnite (VPDB) standard with 13C/12C = 0.0112372. All errors are 1σ, unless stated otherwise). Ion microprobe measurements9 of TiC grains in a CAI in the Isheyevo meteorite found δ13C = 1.1 ± 7‰, a value indistinguishable from Earth mantle C. TiC and CAIs are high-temperature condensates, so it was argued that the TiC isotope ratio represents the bulk solar nebula, and therefore the bulk Sun. Measurement of N isotopes in TiN grains in the same Isheyevo CAI yielded δ15N = −359 ± 5‰ relative to atmospheric N2 (15N/14N = 3.676 × 10−3), a value consistent with the bulk solar value inferred by Genesis2. Observations of CO absorption in the solar photosphere yielded C isotope ratios either consistent with terrestrial, δ13C ~ −30 ± 45‰ (ref. 10), or highly enriched relative to terrestrial, δ13C = 110 ± 14‰ (ref. 11). Thus, previously reported C isotope ratios for the Sun and bulk solar nebula span a range of ~200‰.
In order to resolve the discrepancies between astronomical observations of the photosphere and ion microprobe measurements of C isotopes in solar wind and TiC, we will first focus on solar O isotopes. Earlier measurements of the oxygen isotope ratios of the solar photosphere yielded ratios approximately consistent with terrestrial value (δ18O ~ 41 ± 59‰; ref. 10), or highly enriched in the rare isotopes (δ18O ~ 130 ± 15‰; ref. 11). Given the complexity of the solar atmosphere, and the potential for possible additional fractionation processes, it is important to reconcile the astronomically determined O isotope ratios of the photosphere with those inferred from Genesis. A recent reanalysis of shuttle-based observations of CO in the photosphere made significant progress to that end12 by eliminating line blends of CO isotopic species with the tails of 12C16O lines, and by using a 3D hydrodynamic model atmosphere13 of the photosphere to properly account for temperature variations within the footprint of the observations. However, the literature values for the oscillator strength (f-value) scale for CO rovibrational transitions left a 60‰ range of uncertainty, spanning the 18O/16O ratios from terrestrial values to those inferred for the photosphere from Genesis, precisely the range of most interest12. We resolve these differences in f-values, and present new photospheric O isotope ratios. We then derive a self-consistent 13C/12C ratio for the photosphere, which defines the C isotope ratio for the initial solar system.
Results
ATMOS Fourier transform spectrometer data and solar atmosphere model
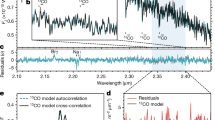
CO rovibrational transitions dominate the 2–5 micron spectral region of the photosphere. CO absorption line data were collected by the shuttle-borne ATMOS Fourier transform spectrometer (FTS) in the mid-1990s (ref. 14). The ATMOS FTS data contain thousands of CO fundamental (∆v = 1) and first-overtone (∆v = 2) lines (v is the vibrational quantum number) recorded at high signal-to-noise ratio (~102–103) and at high spectral resolution (ω/Δω ~ 150,000)14. Because of the high temperature of the photosphere and chromosphere, most of the transitions are between highly excited vibrational states (i.e., ‘hot’ bands). We define the lower energy level, also called the excitation energy, as Elow. To convert the ATMOS data into isotopic abundances in the photosphere, both highly accurate line strengths for CO isotopologues, and a physically representative photospheric model are needed. We have closely followed the radiative transfer and solar atmosphere modeling of Ayres et al.12, who constructed hybrid line profiles by co-adding absorption lines of CO isotopologues with similar excitation energy (Elow), wavenumber range, and absorption depth (Fig. 1). Overlap of line tails from the main isotopologue 12C16O onto the line peaks of the rare isotopologues was avoided, removing a major source of systematic error for the isotopologue abundances. Additional details of the ATMOS FTS data and the method for analyzing the CO absorption lines are given in Methods.
Lower energy levels versus line center frequency for co-added lines. Lines are constructed from ATMOS FTS data for all CO isotopologues analyzed12. The lower energy level is the energy of the lower state for a given transition. Most co-added lines consist of 3–6 individual lines of similar lower energy level and line center frequency. Overtone lines (Δv = 2, where v is the vibrational level) are used only for 12C16O. Analyses of rare isotopologues use only the fundamental transitions (Δv = 1). Comparison of the 12C16O abundance determined from Δv = 1 and Δv = 2 lines is used to make small corrections to the photospheric temperature profile
The CO5BOLD 3D radiation hydrodynamic model of the solar photosphere is used to capture convection-related temperature variations (both horizontal and vertical) associated with solar granulation13. Sixteen snapshots from the 3D hydrodynamic atmosphere model are used to capture the temperature variation associated with convection at the base of the photosphere, and to quantify the uncertainty in derived isotope abundances associated with the hydrodynamic model, as described in Ayres et al.12.
CO rovibrational spectroscopy
For a given rovibrational transition, involving a lower level (v″, J″) and an upper level (v′, J′), where v and J are the vibrational and rotational levels, the oscillator strength (or f-value) for the transition is given by15
Here σ is the frequency of the transition (line center frequency of Fig. 1), M is the rovibrational dipole moment, and SHL is the Hönl–London factor, which has a value of J″ for P branches and J″ + 1 for R branches. We employ a new dipole moment function16 and a spectroscopically determined potential energy function17 for the electronic ground state of CO to calculate a new set of vibration-rotational f-values for 12C16O, 12C17O, 12C18O, and 13C16O isotopologues.
Figure 2 shows the 12C16O f-value ratios of the new values compared to the old values of Hure et al.15 (HR96) and Goorvitch18 (G94). The 2–3% percent differences in the f-value ratios between the new f-values computed from Li et al.16, and the HR96 and G94 f-values are of opposite sign for the fundamental and first overtone transitions, which accounts for about 50‰ of the 60‰ difference in the 18O/16O ratios obtained in Ayres et al.12 for these HR96 and G94 f-value scales. This reduction in the uncertainty in f-values greatly reduces the uncertainty in our previously determined photospheric isotope ratios. The difference between the HR96 and G94 f-values is due to the dipole moment functions used. HR96 used a DMF from Langhoff and Bauschlicher19 and G94 used Chakerian et al.20, with the former showing better agreement to Li et al.16. The f-value ratios of Fig. 2 show only a slight dependence on isotope, and therefore the ratios for 12C17O, 12C18O, and 13C16O are quite similar to those of 12C16O, and are not shown here12,21. The work of Li et al.16 resolves a long-standing uncertainty in CO rovibrational f-values.
New 12C16O oscillator strengths. Strengths use the Li et al. dipole moment function16 for the co-added lines shown in Fig. 1. The oscillator strengths are shown multiplied by the multiplicity, g = 2J″ + 1 for lower state rotational quantum number J″, and are therefore designated as gf-values. The new gf-values are shown normalized to previously published (“old”) gf-values, where blue symbols are normalized by HR9615, and red symbols are normalized by G9418. Circles are for Δv = 1 transitions, and squares are for Δv = 2. This figure shows that the new gf-values are considerably closer to the gf-values of HR9615. The ratio of f-values moves in the opposite direction from Δv = 1 to Δv = 2 for HR96 and G94 f-values, causing the 5–6% difference in photospheric isotope ratios previously found12
Photospheric temperature perturbation
The solar hydrodynamic model does not perfectly capture the temperature profile of the Sun. As done previously12, three solar atmospheric temperature profiles are considered. One of the profiles, “baseline”, is the mean temperature profile from the hydrodynamic model13,22. A second profile is a 90 K enhancement of the photospheric temperature, applied from ~101 to 104 dyne cm−2 (ref. 12); i.e., from the middle photosphere to the lower chromosphere. The third profile, “Goldilocks”, is a 43 K enhancement of the photospheric temperature. Figure 3 shows the dependence of the determined O fraction on the three temperature models. Only the Goldilocks profile yields consistent O abundance results for both fundamental and first overtone 12C16O transitions. It is important to emphasize that we have not “tuned” the O isotope results to agree with the Genesis inferred ratios. We have enforced agreement between O abundances derived from fundamental and overtone transitions by applying a temperature perturbation of 43 K; the resulting O isotope ratios are consistent with Genesis1. The slightly higher photospheric temperature may result from heating associated with magnetic fields or due to wave motion, neither of which are included in the radiative hydrodynamic model. Ideally, the O fraction would be identical for all lines, but a small trend is visible in Fig. 3, which may indicate the presence of additional small errors in the f-values or in model temperature profiles.
Elemental oxygen fraction from ATMOS 12C16O data and for three different photospheric models. Elow is the energy of the lower rovibrational state for the transition. The “Goldilocks” model contains a mid-latitude photospheric temperature perturbation of 43 K that yields equality between the O fraction for Δv = 2 transitions (yellow diamonds) and Δv = 1 transitions (orange diamonds), with a linear fit to the data (black line). The Max (90 K) and Baseline (0 K) models yield less consistent results (small orange and green lines are for Δv = 1). (Figure after Ayres et al.12)
Solar photosphere isotope ratios
The C and O abundances are first determined from 12C16O lines, with the O abundance equal to twice the C abundance, εO = 2εC (ref. 23). Isotopic abundances are then computed separately for a given 16O abundance. The derived O abundance is 605–620 ppm, which is slightly low compared to the preferred value of 640–680 from helioseismology24. The derived isotope ratios are weakly dependent on the absolute O abundance, and we do not expect that this small elemental disparity will significantly affect our O isotope ratios. Our 18O abundance for the temperature-enhanced photosphere is δ18OSMOW = −50 ± 11‰, which is the same within errors as the inferred ratio from Genesis (Fig. 4). Our 17O value is δ17OSMOW = −65 ± 33‰, which does not distinguish between the Genesis photosphere value and a terrestrial value at the 2σ level due to the low signal to noise ratio (SNR) of the 12C17O lines. Our results provide the first accurate, directly determined 18O/16O isotope ratio for the solar photosphere, and provide support for the significant mass-dependent fractionation of O isotopes from the corona to the solar wind, most probably due to inefficient Coulomb drag (ICD)3. The predominant interpretation for the 60‰ difference in oxygen isotopes between the solar photosphere and the terrestrial planets is photochemical self-shielding of CO either in the solar nebula5,7 or in the parent molecular cloud in which the solar system formed6. The near unity slope of the δ17O-δ18O line defined by CAIs (Fig. 4) and of CO photolysis5,6,7,25 is diagnostic of an abundance-dependent, rather than mass-dependent, fractionation process such as self-shielding.
Directly measured oxygen isotope ratios of the photosphere from ATMOS observations of CO. Genesis solar wind and inferred photosphere values also shown, together with theoretical mass-dependent fractionated values for inefficient Coulomb drag for O6+ and O7+ ions in the solar corona42 (purple squares). The value for δ18O of the photosphere determined here (red square) is consistent with the inferred value from Genesis (black squares), and is distinct from a terrestrial value. All error bars are 1σ. OC is ordinary chondrite (yellow); CC is carbonaceous chondrite (gray); CAIs are calcium-aluminum inclusions (light blue); hibonites (blue); bulk silicate Earth (green circle); bulk silicate Mars (red circle). The terrestrial fractionation line describes the array of O isotope values for the vast majority of materials on Earth; it has a mass-dependent slope of about 0.52
Our analysis of the ATMOS CO data also yields the carbon isotope composition of the photosphere. For the same temperature profile, the photosphere is depleted in 13C relative to terrestrial carbonates (VPDB standard) by −48 ± 7‰ (Fig. 5). Mantle carbon is believed to have a mean δ13C ~−5‰ (ref. 26), suggesting that bulk terrestrial C is enriched in 13C by nearly as much as bulk terrestrial O is enriched in 18O. Terrestrial planet atmospheres are all enriched in 13C relative to the photosphere. Titanium carbide condensates in CAIs in the Isheyevo meteorite have δ13C ~1‰ (ref. 9), but the formation environment of these CAIs is unclear. Our photosphere ratio is near the −40‰ mean determined for Jupiter27, but the large error bars encompass the terrestrial mean mantle ratio also (Fig. 5).
Carbon isotope ratios in the solar system. The value for CO in the Sun (red squares, 1σ errors) reported here is among the lightest in the solar system for bulk materials, and lighter than previously reported values, AL13 (ref. 12) and SA06 (ref. 10). The computed values for C5+ and C6+ ions in the solar corona42 (in red) are similar to solar wind in lunar regolith8 and to ACE SWICS measurements29, but differ from the ratio in TiC from Isheyevo9. Other reservoirs include Earth mantle diamonds (mean and range)26 and core estimate58 (Earth atmosphere is about 2‰ lighter than mantle mean), Venus atmosphere59, Mars atmosphere60, Mars mantle from SNC silicates61, and SNC carbonates62. Enstatite chondritic (EC) bulk C, ordinary chondrite (OC) insoluble organic matter (IOM), and carbonaceous chondrite (CC) IOM overlap with Earth mantle values38. The Jupiter and interplanetary dust particle (IDP) ratios spans a wide range27,63. Dust form comet 81 P/Wild 2 had ratios clustering in a fairly tight range64. The heliocentric distances shown for TiC, ECs, OCs, CCs, and IDPs are illustrative only. Additional reservoirs not shown here include Earth organic carbon, terrestrial and marine carbonate, minor organic components in carbonaceous chondrites, and various poorly constrained reservoirs such as Saturn, Neptune, and most comets32. It should also be noted that the fraction of C in Earth’s core could be as much as 90% (ref. 65), in which case the bulk Earth C isotope ratio would be approximately the core value
The 1σ error bars in Figs 4 and 5 include contributions from several sources, as summarized in Table 1 for the determined elemental abundance of oxygen, εO, and the three elemental isotope ratios reported here. Error 1 is the uncertainty due to scaling the 1st overtone O abundance (εO) to the O abundance derived from the less numerous fundamental transitions in the calculation of isotopologue abundances12. Error 2 is the internal sample uncertainty (standard error of the mean), which is the dominant source of error for 16O/17O of the Sun, and which renders the δ17O value to be of limited use in this work. Error 3 is the uncertainty due to the ‘snapshot variability’ in 3D hydrodynamic model of the solar photosphere, as previously described12. Error 4 is the uncertainty in the oscillator strengths, taken to be ½ the difference between the results for HR9615 and Li et al.16. Errors 1 though 4 added in quadrature yield the column “1σ final” in Table 1, which for the isotope ratios correspond to the δ-value errors reported above. If we include in the quadrature sum the full range of photospheric temperature perturbations (i.e., “Baseline” and “Max” from Fig. 3, with temperature enhancements of 0 and 90 K, respectively), we obtain Error 5 in Table 1. Error 5, which characterizes a solar atmosphere modelization error, dominates the other 4 error terms in all cases except 16O/17O. However, this modelization error is removed by requiring that the Δv = 1 and 2 abundances for 12C16O are equivalent. We therefore reject the “Max” and “Baseline” results, and do not consider Error 5 in the reported error for O and C isotopes.
Gravitational settling of heavier isotopes into the solar radiative zone can slightly alter photospheric ratios over the age of the Sun. The convection zone has a vertically homogenous composition because of rapid turbulent mixing, while the chemical composition and the isotopic ratios in the photosphere are expected to be very close to the convective zone for heavier elements like oxygen and carbon. Downward convective overshoot into the radiative zone reduces gravitational settling effects. If convective overshoot into the radiative zone is neglected, the depletions in convective zone and photospheric δ13C, δ15N, and δ18O are −6.1, −4.4, and −9.1‰, respectively28. With convective overshoot present, the depletions in convective zone δ13C, δ15N, and δ18O are predicted to be −4.3, −3.1, and −6.4‰, respectively28. These predicted isotopic shifts are non-negligible, and are mass-dependent, but fall within the 1σ uncertainties of the photospheric O and C isotope results presented here. For this reason we have not shown isotopic shifts due to gravitational settling explicitly in either Figs 4 or 5.
For comparison to solar wind measurements, our O and C isotope ratios must account for isotope fractionation during transport from the photosphere to the corona, an environment in which collisional Coulomb drag is believed to operate3. Computing fractionation due to ICD yields δ13C values ~−75‰ and −95‰ for C6+ and C5+ ions, respectively (Fig. 5; “Methods”), which defines our predicted range for C isotopes in the solar wind. Reported values of C isotopes in solar wind implanted in lunar regolith grains8 are ~ −90 to −120‰, which overlaps with our predicted solar wind value for C5+ ions. The Advanced Composition Explorer Solar Wind Ion Composition Spectrometer (ACE SWICS) instrument29 has also determined an isotopically light mean δ13C value of ~−90‰, but with very large 1σ uncertainties (Fig. 5).
Enrichment in terrestrial planet 13C
The origin of the enrichment of the terrestrial planets in 13C is a central question which, as for the enrichment of O isotopes in planetary materials, bears on the formation environment of the solar system. We present here a preliminary evaluation of mechanisms that could produce enrichment of 13C in the inner solar system. The 13C enrichment could be a result of chemical processing in the solar nebula or parent molecular cloud, or could result from fractionation that accompanied accretion, differentiation, and atmospheric degassing during planet formation; here we focus on a nebular or parent cloud origin. Nebular C isotopes can be affected by many processes including CO self-shielding (as proposed for O isotopes), ion-molecule chemistry, CO ice formation in the outer nebula, and loss of CO in surface disk winds. Parent cloud C isotopes can be altered by similar processes, with the likely exclusion of surface winds.
Self-shielding during CO photodissociation, either in the solar nebula or parent molecular cloud, has been proposed5,6,7 to be responsible for the enrichment of planetary materials in 17O and 18O. Self-shielding was first observed in molecular clouds30, and more recently has been measured in the oxygen isotopologues of CO in young protoplanetary disks31. In self-shielding, 12C16O lines are saturated at dissociating wavelengths (~100 nm), while 12C17O and 12C18O remain unsaturated due to their much lower column abundances, resulting in a massive enrichment of 17O and 18O from CO dissociation. Oxygen enriched in the heavy isotopes can be sequestered in nebular water ice in cool regions of the nebula6,7. Precisely the same self-shielding effect occurs for C isotopes, with saturation of 12C16O and unsaturated 13C16O lines, resulting in C atoms highly enriched in 13C. However, it is less clear that 13C enrichment can be retained and sequestered in nebular materials. C atoms are ionized in a continuum at wavelengths ≤110 nm, so that ionization of atomic C accompanies CO dissociation (unless C is optically thick). Once ionized, a rapid ion-molecule exchange reaction32, 12CO + 13C+ ⇆ 13CO + 12C+ + 35 K, acts to erase any 13C excess in C+ at high temperatures, and at lower temperatures produces enrichments in 13CO and 12C+. CO photolysis also yields C atoms in the C(1D) excited electronic state. About 90% of CO photodissociation proceeds by the spin-allowed reaction, CO + hν → C(3P) + O(3P). Velocity-map imaging measurements show that approximately 8% of CO follows a spin-forbidden pathway33, CO + hν → C(1D) + O(3P) (see “Methods”). The C(1D) is highly reactive, forming CH radicals upon collision with H2, and therefore needs to be included in chemical models of the nebula.
Chemical timescales of C loss in the solar nebula
In order to assess possible chemical pathways for C species in the solar nebula, we estimate chemical loss timescales for the most relevant species due to a variety of reactions. We compute loss timescales at the FUV surface where optical depth is approximately unity for 12C16O. We employ a simple, analytical model for the number density of H nuclei in the solar nebula34. The FUV optical depth of CO is given by
where σCO is the CO absorption cross section, and fCO is the fraction of CO gas in the nebula. We assume the CO fraction is constant with Z with the value fCO = 2 × 10−4; this assumption allows an analytical evaluation of the vertical column density (“Methods”). The resulting values for Z at unit optical depth (in the vertical direction) are shown in Fig. 6 for a vertically isothermal nebula.
Height above midplane at which τCO = unity. Calculation assumes a CO absorption cross sections σCO = 1 × 10−16 cm2 and a CO fraction (relative to H2) fCO = 2 × 10−4 (i.e., a H2 column density of 1020 cm−2). The corresponding H2 number densities vary from ~1010 cm−3 at 0.1 AU to ~106 cm−3 at 100 AU. Vertically isothermal gas temperature is also shown (dashed line). Calculations use an analytical disk model34
For a 2nd-order reaction, A + B → C + D, the chemical loss timescale for species A is given by
where kA+B is the two-body rate coefficient, and [B] is the concentration of B. For 1-body reactions, such as photodissociation or radiative relation, described by A → B, the loss timescale is tA = 1/kA. Figure 7 shows the loss timescales for several carbon species, including C, C+, and several reactions for CH. One key point of the figure is that excited state carbon, C(1D), reacts rapidly with H2 to form CH. This allows C(1D) from CO photolysis to avoid photoionization and exchange of C+ with CO, which erases the isotope self-shielding isotope signature in the liberated carbon atoms. The chemistry of molecular carbon is quite complex in the solar nebula, and the fate of CH must be evaluated in a complete nebular chemical model. It is also not clear that a 5–10% production of C(1D) can play a significant role in altering enriching the 13C composition of planetary material; again, detailed models are needed to evaluate this.
Chemical loss timescales for several carbon species computed at the FUV surface of the nebula and as a function of heliocentric distance. The figure shows that excited state carbon, C(1D), is lost to reaction with H2 faster than for any other loss pathway. The C ionization reaction to form C+ is FUV radiation from the protosun; nearby O stars can also be a significant source of FUV radiation. The timescale for the reaction CH + H → C + H2 was computed assuming an H/H2 fraction = 0.01. This reaction returns C atoms to the gas in their ground state, allowing ionization and exchange to remove the C isotope self-shielding signature. Depending on the degree of dust settling and the CO fraction, the H/H2 ratio can be higher or lower by a factor of ~102 − 103 (ref. 66). A much lower H/H2 ratio allows the reaction CH + C → C2 + H to sequester the self-shielding signature in C2. Reaction of CH with H2 also becomes much faster inside of 1 AU, providing another possible pathway for sequestering a C isotope self-shielding signature in larger molecules
Also shown in Fig. 7 is the vertical mixing timescale,
where Hv is the vertical scale height of the solar nebula, and Dt is the turbulent diffusivity in the nebula. It has been standard to assume a turbulent diffusivity driven by magnetorotational instability (MRI), for which Dt ~αcsHv, where cs is the sound speed and α parameterizes the strength of turbulent mixing and has a value generally ~10−4 to 10−2. Figure 7 shows tv for α = 10−2. Recent work35 argues that the MRI is actually too dissipative to yield such vigorous turbulent mixing throughout the disk, so the plotted tv represents a maximum plausible degree of turbulence in the bulk nebula (see “Methods”).
The chemical reaction timescales in Fig. 7 show that reaction of C(1D) with H2 is faster by a factor ~103 than the next fastest process, radiative relaxation, in the inner solar nebula, and is comparable in timescale to radiative relaxation beyond ~50 AU. Subsequent reactions of CH may lead to sequestration of C in larger molecules, e.g., by the reaction CH + H2 → CH2 + H, or by CH + C → C2 + H, with possible preservation of the CO self-shielding isotope signature in the products. However, CH also reacts rapidly with H atoms, which returns C to its ground state, leaving it susceptible to ionization and exchange. The fate of CH is thus strongly dependent on the local H/H2 ratio. A full assessment of the effects of CO self-shielding on C isotopes requires detailed nebular chemistry modeling, including atomic excited states, but the results of Fig. 7 suggest that preservation of 13C enrichment in C atoms liberated by CO photodissociation may not necessarily occur at the surface of the nebula. Carbon isotopologues of CO in young protoplanetary disks often show a large depletion in 13CO in the gas phase, as expected for CO self-shielding, but the depletion is not generally correlated with depletions in the 12C17O and 12C18O isotopologues31. The lack of correlation is possibly a result of C+ formation, followed by exchange with CO, as discussed above. Thus, a self-shielding signature is very likely present in C isotopes initially, but is erased by exchange of C+ and CO.
It has been suggested that the 13C depletion observed in some protoplanetary disks may be a result of CO ice formation31. We briefly consider whether CO ice formation in the outer nebula can explain the difference between solar and planetary δ13C. Formation of a large fraction of CO ice, enough to account for a ~50‰ shift in δ13C in CO gas in the inner solar nebula, would also produce a mass-dependent fractionation in O isotopes. Assuming the CO ice remains sequestered in the outer solar nebula, the residual gas-phase CO in the nebula would have been mass-dependently shifted. In order to be consistent with meteoritic and solar photosphere data, the CO would have to be mass-dependently shifted onto the CAI mixing line (Fig. 8). This is required to explain the O isotope data of secondary magnetites36, which provide direct meteoritic evidence for CO self-shielding and formation of H2O from the product O atoms. We assume that isotope fractionation due to CO ice formation implies bulk CO (gas + ice) isotope ratios in the parent molecular cloud that are mass-dependently shifted by ~+50‰ in δ13C and δ18O relative to solar, if this process is to explain meteoritic data. Observations of 12CO and 13CO in protoplanetary disks and cloud cores do not clearly demonstrate isotopically enriched CO ice and depleted gas31. Instead, both CO gas and ice show 12C/13C ~60–160, with no clear anti-correlation in the two reservoirs, so the role of CO ice formation in protoplanetary disks is uncertain. About 50–100‰ shifts are easily incorporated within this large range of 12C/13C. But more problematic is that pre-existing nebular water would have to also need to reside near the O isotope CAI mixing line, as a result of water ice formation or the initial reservoir ratios of O isotopes (Fig. 8). Such a coincidence seems unlikely, and we therefore discard CO ice formation as an explanation for the δ13C difference between the Sun and terrestrial planets.
An illustration of how CO condensation in the outer solar nebula could qualitatively affect O isotope reservoirs. Assuming that condensed CO remains in the outer nebula, and is not mixed back into the O reservoir from which planets were formed, then there will be a mass-dependent enrichment in the CO ice relative to the bulk initial CO from the parent cloud. If CO self-shielding yielded H2O at the other end of the mixing line (H2Oss), the dissociated CO gas must have been on or close to the CAI mixing line. Residual (undissociated) CO gas (COss) would have been highly depleted in 17O and 18O (refs. 7,31). If the initial bulk reservoir of H2O was isotopically similar to CO initial bulk, then it too must have been mass-dependently fractionated until it resided on or near the CAI mixing line. This seems an unlikely occurrence, suggesting that perhaps the CO condensed phase was not large enough to substantially alter the O (and C isotopes) of the CO and from which planets were formed. Mixing lines for FUN inclusions are also shown, but the mass-dependent displacement that defines the lower end of the FUN inclusion mixing lines67 are mostly likely derived from melting and evaporation of precursor CAIs68, and not from the bulk initial CO and H2O reservoirs
Inheritance of terrestrial planet C isotopes from the parent cloud
The chemical loss timescales illustrated in Fig. 7 suggest that enrichment of 13C in planetary materials due to CO self-shielding in the solar nebula may not have occurred. Yet δ13C depletion is often observed in molecular clouds, and has been attributed to self-shielding by 12C16O (e.g., ref. 37). We suggest here a simple scenario for inheritance of C grains enriched in 13C from the parent molecular cloud from which the solar system formed. Grains that accreted to the outer nebula during infall would likely not be isotopically altered, or may have even been slightly enriched, during heating in the accretion shock. Accumulation of these grains in planetesimals just beyond the snowline, and subsequent delivery of H2O and C by these planetesimals, could have provided Earth with its observed C isotope reservoir38. This scenario must also account for the depletion in C in the inner solar system relative to solar elemental values. The high C depletion in terrestrial planets (~2 × 10−4 for Earth relative to solar), and the approximate positive gradient with distance of C concentration in enstatite, ordinary and carbonaceous chondrite meteorites, has been attributed to chemical erosion of carbon grains in the inner solar nebula by reactions with H, OH and/or O39,40. Mass-dependent fractionation of C isotopes will likely accompany these reactions, but at the high temperatures needed for graphite erosion (~1000 K), isotope fractionation will be small, and we therefore neglect C isotope fractionation associated with C grain oxidation in the inner solar nebula. Oxidation of C grains in the hot inner solar nebula would produce CO with a 13C/12C ratio similar to the grains (assuming complete conversion of grains to gas), suggesting that initial nebula CO was isotopically lighter than the Sun (Fig. 9).
Illustration of one possible explanation for the difference between solar and terrestrial planet and asteroidal C isotopes. If, in the parent molecular cloud, carbonaceous grains have a δ13CPDB values ~0‰ and CO has δ13CPDB ~−100‰, and C is approximately equally distributed between grains and CO gas, then formation of Jupiter from both grains and gas would yield δ13C ~−50‰. Terrestrial planets and asteroids, formed primarily from planetesimals with C from C grains, would have δ13C ~0‰. If C grains were converted to CO gas in the hot, inner solar nebula69, the total accreted CO gas would yield a solar δ13C ~−50‰, as reported here. The cause of the C isotopic ratio difference in grains and dust of the parent cloud may have been a result of self-shielding in the parent cloud exposed to a high FUV radiation field, as, e.g., observed in Ophiucus37
Discussion
We have determined the C isotope ratio of the solar photosphere by reanalyzing shuttle-borne ATMOS FTS data collected in the mid-1990s. Using a new DMF for ground state CO, we obtain a photospheric 18O/16O ratio consistent with the inferred value from Genesis solar wind measurements1,41. The corresponding 13C/12C ratio is light, with δ13C = −48 ± 7‰ VPDB. Using the ICD model we predict a solar wind δ13C ~−70 to −90‰ for C6+ and C5+ coronal ions, respectively. Our solar wind predictions for coronal C5+ agree with the range reported from ion microprobe analyses of solar wind implanted in lunar grain silicates8, but disagree with δ13C = 1 ± 7‰ from TiC grains in CAIs from the Isheyevo meteorite9. An examination of chemical loss timescales (in lieu of a full chemical model) of C isotope fraction due to CO photodissociation and self-shielding in the surface solar nebula, suggests that preservation of a 13C enrichment in planetary materials may not have occurred. We offer an alternative interpretation of inheritance of the 13C-enriched C grains from the parent molecular cloud, again derived from self-shielding of CO. We have not explored here the composition of the carbon-carrying grains, but both irradiated ices and polycyclic aromatic hydrocarbons are plausible carriers.
The Coulomb drag theory neglects the potential role of magnetohydrodynamic (MHD) waves in the solar atmosphere in modifying isotope fractionation during solar wind formation. Given the likely importance of MHD waves in heating the upper chromosphere and corona, it is possible that other isotope fractionation processes could be present42. Evidence for chromospheric heating by torsional Alfvenic waves has been found from Solar Dynamics Observatory observations by McIntosh et al.43. Elemental fractionation is well established as a function of first ionization potential (the FIP effect), and has been attributed to a ponderomotive force associated with Alfven wave propagation44. This force appears incapable of mass-independently fractionating isotopes of the same ion, but mass-dependent effects may be important.
Finally, we note that if self-shielding by CO in the solar nebula and/or in the parent cloud is responsible for the formation of 17O and 18O-rich water and 13C-rich C grains in quantities needed to enrich terrestrial planet isotope ratios relative to the Sun, then the chemical mass-independent fraction schemes45 involving SiOH or SiO are not necessary. Mass-independent fractionation of O isotopes in SiOH reactions presumably involve non-statistical effects, which are thought to be responsible for the mass-independent isotope effects seen in O3 formation46. Similar non-statistical effects in the chemical reactions that form C grains are unlikely to produce enrichment in 13C because of the complex set of pathways and products leading to grain formation.
Methods
Construction of co-added CO absorption lines
CO lines were co-added (hybridized) as described in Ayres et al.12. The full-width half-max of the CO absorption lines is ~4.4 km s−1, approximately the thermal Doppler broadening. All lines with a 12C16O line center within ~10 km s−1 were rejected. Saturated lines were also rejected. Co-added lines were constructed by combining lines of similar frequency and Elow. This was done to improve individual line SNR, but also to lessen the total computation time needed for radiative transfer calculations. For 12C16O, 36 hybrid lines (10 for Δv = 1, and 26 for Δv = 2) were constructed from 150 input transitions. For 13C16O, 12C17O, and 12C18O, 9, 4, and 4 hybrid lines, respectively, were constructed from 70 observed transitions. The O abundance was computed for a given solar model using the 12C16O hybrid lines by adjusting the O abundance to reproduce the observed equivalent widths. Rare isotope abundances were computed for a given O abundance and solar model, by adjusting the isotopic abundances to match the observed isotopic equivalent widths.
Solar model and radiative transfer
The solar atmosphere and radiative transfer models closely follow Ayres et al.12. The CO5BOLD radiative hydrodynamic model was used to simulate the solar atmosphere13,22, and uses 12 opacity bins and a Rosseland mean absorption. Full 3D simulations were required to reproduce continuum observations from 440 – 680 nm, with the continuum optical depth unity in the visible and IR at ~0.1 bars, deeper than the peak in CO at ~10−3 bars. Instantaneous equilibrium chemistry (ICE) has been previously shown to accurately simulate the composition of the middle photosphere47, and is used here. The neutral composition is dominated by atomics, H, O, C, and N, with CO the most abundant molecular species in the middle photosphere (at the CO peak near 10−3 bars, CO is 38% of the total carbon, with the rest atomic C). Radiative transfer modeling is used with isolated columns from the 3D model, but with angle-dependent visible scattering11,12,48. A Feautrier-based Hermitian solution scheme is employed49, with a black-body source term. With continuum source functions for each 3D column, specific intensities were computed along rays, reproducing the observed center-to-limb intensity variation. CO number density was calculated using ICE, and the O mole fraction was computed assuming ε = 2εC (ref. 23). CO line opacities were computed assuming thermal Doppler broadening, and for LTE conditions which are valid for CO in the middle photosphere50. 12C17O features are weak and are susceptible to errors in the local continuum level.
Calculation of new oscillator strengths
Oscillator strengths are computed with equation (1). The dipole moment matrix elements are given as
where μ(r) is the electric dipole moment at internuclear distance r. Expressing the dipole moment in a polynomial expansion of the deviation from the equilibrium internuclear distance, x = (r - re)/re
and the matrix elements become16
Li et al.16 used Level 8.2 software51 to determine the expectation values \(\left\langle {v\prime J\prime\prime \left| {x^i} \right|v\prime\prime J\prime\prime } \right\rangle\) and the coefficients M i . In the present work we computed the dipole moment matrix elements from the M i values from Li et al., and our line positions were computed from HITEMP21.
Inefficient Coulomb drag
The O isotope values measured in the solar wind samples collected by Genesis, δ17O = −80.8‰ and δ18O = −102.3‰ (ref. 1), differ from those of the photosphere due to isotopic fractionation during formation of the solar wind3. The most well studied process is ICD in which protons collide with highly ionized heavier elements in the solar corona, transferring momentum to the heavier ions after repeated collisions. ICD is most important in the ‘slow’ solar wind regime (<500 km s−1), and derives primarily from the gravitational separation of ions by mass. In the ‘fast’ solar wind, ICD is not an important source of fractionation. Neglecting pressure gradients, thermal diffusion, and Alfven wave forcing, the one-dimensional ion momentum equation due to collisions, gravity, and the radial ambipolar electric field, can be written as3
where mx and mp are the masses of the heavy ion and proton, respectively, νxp is the ion–proton collision frequency, ux and up are the vertical velocity components for ions and protons, Ax and Qx are the atomic mass and charge of the ions, and r is the heliocentric distance of the ion in the corona. The ion-collision frequency is proportional to \(Q_{\rm x}^2/m_{\rm x}\) (full expression is given in ref. 42). Solving for the ion velocity3,
where Cp is a constant dependent only on the proton temperature, Φp = npvpr2 is the proton flux integrated over full space, and the Coulomb drag factor Hx is
Isotopic fractionation of heavy ions in the fast and slow solar wind may be computed from the respective ion velocities for these two solar wind regimes. For two heavy ions, i and j, the fractionation factor fi,j is the ratio of the velocities
Because the factor C p /Φ p is not accurately known, measurements of a known fractionation, in this case H and 4He, are used to calibrate Coulomb drag fractionation between other ions. The equation for the fractionation factor may then be expressed as52
where \(f_{{}^4{\rm He,H}}\) is the ratio of 4He/H (mole fraction) in the slow solar wind to that in the fast solar wind. The validity of the ICD model has been established through measurements of noble gas isotopes (He, Ne, Ar) from Genesis samples of slow and fast regime solar wind. The photosphere value is taken to be the bulk solar value of 0.084, as determined by helioseismology53. The measured bulk solar wind value of 4He/H = 0.0402 with coronal mass ejection (CME) material included, and 4He/H = 0.037 if CMEs are not included52. This implies \(f_{{}^4{\rm He,H}} = 0.4786\) with CMEs, and \(f_{{}^4{\rm He,H}} = 0.4405\) not including CMEs. Because the Genesis O isotope data was collected with a bulk solar collector, we use the values that include CMEs. In the equation for the fractionation factor, \(H_{{}^4{\rm He}} = 1.3975\).
The resulting ICD parameters for several charge states of O and C in the solar corona are given in Supplementary Table 1 for 3 charge states of O and C. The mean charge state for O is thought to be Q = +6 in the acceleration region of the corona42. For C the mean charge state is thought to be Q = +5. The isotopic fractionation in permil is computed as 100(fi,j – 1). For Q = +6, 18O and 17O in the photosphere are enriched by 60 and 29‰ relative to 16O in the bulk solar wind measured by Genesis (Fig. 4). McKeegan et al.1 computed similar values from the ICD model, but then scaled their results to intersect the CCAM line; we are presenting the ICD model results without scaling. For Q = +5, 13C is predicted to be depleted by 44‰ relative to 12C compared to the photosphere value determined here (Fig. 5).
It should be recognized that many uncertainties are present in both the isotopic and elemental fractionation in the acceleration region of the corona52. In particular, it is unclear how well correlated isotope fractionation in the corona is to the elemental fractionation of 4He relative to H. Also, the charge state of a given ion in the corona is uncertain. For these reasons, the ICD results presented here are meant as an approximate guideline to the magnitude of isotope fractionation in the corona.
FUV surface of solar nebula
We employ an analytical model for the number density of H nuclei in the solar nebula34,
where n0 = 1.9 × 109 H nuclei cm−3, R and Z are the heliocentric distance and height above the midplane in AU, and \(a = \frac{{GM_{{\rm sun}}\mu m_{\rm H}}}{{kT\left( R \right)}}\). In the expression for a, μ = 2.37 is the mean molecular mass of the nebular gas, and mH is the mass of the H atom. T is the vertically isothermal gas temperature with T0 = 28 K, and L is the protosolar luminosity, which we assume here to be equal to Lsun. Equation 13 is an approximate form of the expression given by Aikawa and Herbst34, and is valid for Z2 « R2. At R = 100 AU, T = 28 K and a = 9055 AU, a value we define as a0. The exponential in equation 13 may be written as \(e^{ - 0.5b\left( R \right)Z^2}\), where
where R has units of AU and b has units of (AU)−2. To avoid a two-dimensional radiative transfer problem, we assume FUV radiation arriving normal to the disk midplane, even if it derives from the protostar. (This is a commonly made assumption7,32). The column density of H nuclei from the top of the nebula down to a height Z is then
where “erfc” is the complementary error function with its usual definition, \({\rm erfc}\left( x \right) = \frac{2}{{\sqrt \pi }}\mathop {\int }\limits_x^\infty e^{ - t^2}{\rm d}t\). The FUV optical depth of CO is given by
where σCO is the CO absorption cross section, and fCO is the fraction of CO gas in the nebula. Neglecting photodissociation of CO, we assume the CO fraction is constant with Z with the value fCO = 2 × 10−4. Solving this set of equations for Z at CO optical depth unity at a given wavelength, we find
The resulting values for Z are shown in Fig. 6. A similar analytical formulation was used by the first author in Antonelli et al.54.
Dissociation probabilities for C(1D) formation
The spin-forbidden reaction CO + hν → C(1D) + O(3P) arises due to coupling of a 1Π excited state to a 3Π valence state at wavelengths less than 100 nm33. The fraction of CO that yields C(1D) during photodissociation, χ C(1D) , may be approximated as
where \(\phi _i^{{\rm C}\left( {1{\rm D}} \right)}\) is the branching ratio for C(1D) production33, and \(\phi _i\) is the quantum yield for dissociation55,56. Using the CO band numbers defined in van Dishoeck and Black55, only bands 1, 3, 8, 16, 17, 20, 22–25 contribute to C(1D) production, yielding an 8.5% fraction of C(1D) from 91.2 to 108 nm. Absorption by H and H2 has been neglected in this estimate, and a uniform (interstellar-like) FUV radiation field has been assumed.
MRI and disk winds
Previous models of self-shielding of CO in the solar nebula have assumed vigorous turbulent mixing associated with the MRI. The potential importance of non-ideal MHD in protoplanetary disks has been recognized in the past few years35. Non-ideal MHD limits vigorous turbulent mixing due to the MRI to the FUV-active surface layer of the disk. In this active layer α ~ 10−1 to 10−2 is plausible. Deeper in the disk, a lower turbulent viscosity parameter is predicted, α ~ 10−4–10−3. This has two implications: (1) CO self-shielding in the outer solar nebula may become too slow to explain the enrichment in solar system O isotopes57; instead, self-shielding in the parent cloud core or in the inner nebula would have to be invoked6,40; (2) outer solar system disk winds become a significant source of mass loss35. These winds originate near the FUV surface of the solar nebula, and will preferentially carry away self-shielded CO (and N2), i.e., gas enriched in 12C16O and 28N2. Disk winds provide a natural mechanism for enrichment of the solar nebula in the rare isotopes of N and O, and possibly of C as well. Loss of CO by photoevaporation or in disk winds is a necessary process for removing CO highly enriched in 16O due to self-shielding from the solar nebula, although isotope fractionation during formation of tenuous disk winds is not likely to be significant.
Data availability
All relevant data are available from the authors.
References
McKeegan, K. D. et al. The oxygen isotopic composition of the Sun inferred from captured solar wind. Science 332, 1528–1532 (2011).
Marty, B., Chaussidon, M., Wiens, R. C., Jurewicz, A. J. G. & Burnett, D. S. A 15N-poor isotopic composition for the solar system as shown by Genesis solar wind samples. Science 332, 1533–1536 (2011).
Bodmer, R. & Bochsler, P. Influence of Coulomb collisions on isotopic and elemental fractionation in the solar wind acceleration process. J. Geophys. Res. 105, 47–60 (2000).
Clayton, R. N., Grossman, L. & Mayeda, T. K. Component of primitive nuclear composition in carbonaceous meteorites. Science 182, 485–488 (1973).
Clayton, R. N. Solar system: self-shielding in the solar nebula. Nature 415, 860–861 (2002).
Yurimoto, H. & Kuramoto, K. Molecular cloud origin for the oxygen isotope heterogeneity in the solar system. Science 305, 1763–1766 (2004).
Lyons, J. R. & Young, E. D. CO self-shielding as the origin of oxygen isotope anomalies in the early solar nebula. Nature 435, 317–320 (2005).
Hashizume, K., Chaussidon, M., Marty, B. & Terada, K. Protosolar carbon isotopic composition: implications for the origin of meteoritic organics. Astrophys. J. 600, 480–484 (2004).
Meibom, A. et al. Nitrogen and carbon isotopic composition of the sun inferred from a high-temperature solar nebular condensate. Astrophys 656, L33–L36 (2007).
Scott, P. C., Asplund, M., Grevesse, N. & Sauval, A. J. Line formation in solar granulation VII. CO lines and the solar C and O isotopic abundances. Astron. Astrophys. 456, 675–688 (2006).
Ayres, T. R., Plymate, C. & Keller, C. U. Solar carbon monoxide, thermal profiling, and the abundances of C, O, and their isotopes. Astrophys. J. Suppl. Ser. 165, 618–651 (2006).
Ayres, T. R., Lyons, J. R., Ludwig, H.-G., Caffau, E. & Wedemeyer-Böhm, S. Is the sun lighter than the earth? Isotopic CO in the photosphere, viewed through the lens of three-dimensional spectrum synthesis. Astrophys. J. 765, 46–71 (2013).
Freytag, B., Steffen, M., Ludwig, H.-G., Wedemeyer-Bohm, S., Schaffenberger, W. & Steiner, O. Simulations of stellar convection with CO5BOLD. J. Comp. Phys. 231, 919–959 (2012).
Abrams, M. C., Goldman, A., Gunson, M. R., Rinsland, C. P. & Zander, R. Observations of the infrared solar spectrum from space by the ATMOS experiment. Appl. Opt. 35, 2747–2751 (1996).
Hure, J. M. & Roueff, E. Analytic representations of rovibrational dipole matrix elements for the CO molecule and its isotopomers. Astron. Astrophys. Suppl. 117, 561–568 (1996).
Li, G. et al. Rovibrational line lists for nine isotopologues of the CO molecule in the X1Sigma+ ground electronic state. Astrophys. J. Suppl. Ser. 216, 15–32 (2015).
Coxon, J. A. & Hajigeorgiou, P. G. Direct potential fit analysis of the X 1∑+ ground state of CO. J. Chem. Phys. 121, 2992–3008 (2004).
Goorvitch, D. Infrared CO line list for the X 1∑+ state. Astrophys. J. Suppl. Ser. 95, 535–552 (1994).
Langhoff, S. R. & Bauschlicher, C. W. Global dipole-moment function for the X 1∑+ ground-state of CO. J. Chem. Phys. 102, 5220–5225 (1995).
Chackerian, C. Jr. et al. Experimental determination of the X 1∑+ state electric-dipole moment function of carbon monoxide up to a large internuclear separation. Can. J. Phys. 62, 1579–1585 (1984).
Gharib-Nezhad, E., Lyons, J. R., Ayres, T. R. CxO (x = 16,17,18) isotopologue ratios in the solar photosphere. Abstract 1592 presented at the 46th Lunar and Planetary Science Conference, The Woodlands, Texas, 16–20 March, 2015.
Cafau, E. et al. Solar chemical abundances determined with a CO5BOLD 3D model atmosphere. Sol. Phys. 268, 255–269 (2011).
Allende-Prieto, C., Lambert, D. L. & Asplund, M. A reappraisal of the solar photospheric C/O ratio. Astrophys. J. 573, L137–L140 (2002).
Basu, S. & Antia, H. M. Helioseismology and solar abundances. Phys. Rep. 457, 217–283 (2008).
Lyons, J. R. Isotope effects due to CO photodissociation in laboratory experiments and the solar nebula. Meteorit. & Planet. Sci. 49, 373–393 (2014).
Deines, P. The carbon isotope geochemistry of mantle xenoliths. Earth Sci. Rev. 58, 247–278 (2002).
Niemann, H. B. et al. The composition of the Jovian atmosphere as determined by the Galileo probe mass spectrometer. J. Geophys. Res. 103(22), 831–22,845 (1998).
Turcotte, S. & Wimmer-Schweingruber, R. F. Possible in situ tests of the evolution of elemental and isotopic abundances in the solar convection zone. J. Geophys. Res. 107, 1442 (2002).
R. F. Wimmer-Schweingruber, L. Berger, M. Köten1, P. Bochsler and G. Gloeckler et al. The 13C/12C isotopic ratio in the solar wind. 45th Lunar Planet. Sci. Conf., abstract 1114 (2014).
Bally, J. & Langer, W. D. Isotope-selective photodestruction of carbon monoxide. Astrophys. J. 255, 143–148 (1982).
Smith, R. L.et al Heterogeneity in 12CO/13CO abundance ratios toward solar-type young stellar objects. Astrophys. J. 813,16, 120 (2015).
Woods, P. M. & Willacy, K. Carbon isotope fractionation in protoplanetary disks. Astrophys. J. 693, 1360–1378 (2009).
Gao, H. et al. Branching ratio measurements for vacuum ultraviolet photodissociation of 12C16O. J. Phys. Chem. A 117, 6185–6195 (2013).
Aikawa, Y. & Herbst, E. Molecular evolution in protoplanetary disks. Astron. Astrophys. 351, 233–246 (1999).
Bai, X.-N. Toward a global evolutionary model of protoplanetary disks. Astrophys. J. 821, 80 (16 pp) (2016).
Sakamoto, N. et al. Remnants of the early solar system water enriched in heavy oxygen isotopes. Science 317, 231–233 (2007).
Federman, S. R. et al. Further evidence for chemical fractionation from ultraviolet observations of carbon monoxide. Astrophys. J. 591, 986–999 (2003).
Marty, B., Alexander, C. M. O. ’D. & Raymond, S. N. Primordial origins of Earth’s carbon. Rev. Min. Geochem 75, 149–181 (2013).
Gail, H.-P. Radial mixing in protoplanetary accretion disks I. Stationary disc models with annealing and carbon combustion. Astron. Astrophys. 378, 192–213 (2001).
Lee, J.-E., Bergin, E. A. & Lyons, J. R. Oxygen isotope anomalies of the Sun and the original environment of the solar system. Meteorit. Planet. Sci. 43, 1351–1362 (2008).
Burnett, D. S. et al. Solar composition from the Genesis Discovery Mission. Proc. Nat. Acad. Sci. 108, 19147–19151.
Bochsler, P. Abundances and charge states of particles in the solar wind. Rev. Geophys. 38, 247–266 (2000).
McIntosh, S. W., De Pontieu, B., Carlsson, M., Hansteen, V., Boerner, P. & Goossens, M. Alfvenic waves with sufficient energy to power the quiet solar corona and fast solar wind. Nature 475, 477–480 (2011).
Laming, J. M. The FIP and inverse FIP effects in solar and stellar coronae. Living Rev. Sol. Phys. 12(2), (76 pp) (2015).
Chakraborty, S., Yanchulove, P. & Thiemens, M. H. Mass-independent oxygen isotopic partitioning during gas-phase SiO2 formation. Science 342, 463–466 (2013).
Gao, Y. Q. & Marcus, R. A. Strange and unconventional isotope effects in ozone formation. Science 293, 259–263 (2001).
Wedemeyer-Bohm, S., Kamp, I., Bruls, J. & Freytag, B. Carbon monoxide in the solar atmosphere I. Numerical method and two-dimensional models. Astron. Astrophys. 438, 1043–1057 (2005).
Ayres, T. R. Solar forbidden oxygen, revisited. Astrophys. J. 686, 731–740 (2008).
Auer, L. An Hermitian method for the solution of radiative transfer problems. J. Quant. Spect. Rad. Transf. 16, 931–937 (1976).
Ayres, T. R. & Wiedemann, G. R. Non-LTE CO, revisited. Astrophys. J. 338, 1033–1046 (1989).
Le Roy, R. J. Level 8.2. http://leroy.uwaterloo.ca/programs/ (2014)
Heber, V. S., Baur, H., Bochsler, P., McKeegan, K. D., Neugebauer, M., Reisenfeld, D. B., Wieler, R. & Wiens, R. C. Isotopic mass fractionation of solar wind: evidence from fast and slow solar wind collected by the Genesis mission. Astrophys. J. 759(121), 13 (2012).
Basu, S. & Antia, H. M. Constraining solar abundances using helioseismology. Astrophys. J. 606, L85–L88 (2004).
Antonelli, M. A. et al. Early inner solar system origin for anomalous sulfur isotopes in differentiated protoplanets. Proc. Nat. Acad. Sci. 111, 17749–17754 (2014).
van Dishoeck, E. F. & Black, J. H. The photodissociation and chemistry of interstellar CO. Astrophys. J. 334, 771–802 (1988).
Visser, R., van Dishoeck, E. F. & Black, J. H. The photodissociation and chemistry of CO isotopologues: applications to interstellar clouds and circumstellar disks. Astron. Astrophys. 503, 323–343 (2009).
Lyons, J. R., Bergin, E., Ciesla, F., Davis, A., Desch, S., Hashizume, K. & Lee, J.-E. Timescales of oxygen isotope evolution in the solar nebula. Geochim. Cosmochim. Acta 73, 4998–5017 (2009).
Horita, J. & Pulyakov, V. B. Carbon-bearing iron phases and the carbon isotope composition of the deep Earth. Proc. Nat. Acad. Sci. 112, 31–36 (2015).
Istomin V. G., Grechnev K. V., Kochnev C. A. Mass spectrometry of the lower atmosphere of Venus: Krypton isotopes and other recent results of the Venera-11 and 12 data processing. 23rd COSPAR Meeting Budapest (1980).
Webster, C. R. et al. Isotope ratios of H, C, and O in CO2 and H2O of the Martian atmosphere. Science 341, 260–263 (2013).
Wright, I., Grady, M. M. & Pillinger, C. Chassigny and the nakhlites: carbon bearing components and their relationship to Martian environmental conditions. Geochim. Cosmochim. Acta 56, 817–826 (1992).
Niles, P. B. et al. Stable isotope measurements of Martian atmospheric CO2 at the Phoenix landing site. Science 329, 1334–1337 (2010).
Messenger, S., Stadermann, F. J., Floss, C., Nittler, L. R. & Mukhopadhyay, S. Isotopic signatures of presolar materials in interplanetary dust. Space Sci. Rev. 106, 155–172 (2003).
McKeegan, K. D. et al. Isotopic compositions of cometary matter returned by Stardust. Science 314, 1724–1728 (2006).
DePaolo, D. J. Sustainable carbon emissions: the geologic perspective. MRS Energy Sustain.: A Rev. J. 2, 1–16 (2015).
Bethell, T. J. & Bergin, E. A. The propagation of Ly-α in evolving protoplanetary disks. Astrophys. J. 739(78), 11 (2011).
Clayton, R. N. et al. Two forsterite-bearing FUN inclusions in the Allende meteorite. Geochim. Cosmochim. Acta 48, 535–548 (1984).
Krot, A. N. et al. Calcium-aluminum-rich inclusions with fractionation and unknown nuclear effects (FUN CAIs): I. Mineralogy, petrology, and oxygen isotopic compositions. Geochim. Cosmochim. Acta 145, 206–247 (2014).
Lee, J.-E., Bergin, E. A. & Nomura, H. The solar nebula on fire: a solution to the carbon deficit in the inner solar system. Astrophys. J. Lett. 710, L21–L25 (2010)
Acknowledgements
J.R.L. acknowledges support from the NASA Origins of Solar Systems program, grant NNX14AD49G to ASU. T.R.A. acknowledges support from NSF AST-0908293. Publication of this article was funded in part by the University of Colorado Boulder Libraries Open Access Fund.
Author information
Authors and Affiliations
Contributions
J.R.L. and T.R.A. conceived the project. E.G.N. and J.R.L. performed the oscillator strength calculations. T.R.A. performed the radiative transfer calculations. All authors contributed to writing the paper.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Additional information
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Lyons, J.R., Gharib-Nezhad, E. & Ayres, T.R. A light carbon isotope composition for the Sun. Nat Commun 9, 908 (2018). https://doi.org/10.1038/s41467-018-03093-3
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-018-03093-3
This article is cited by
-
Carbonate record of temporal change in oxygen fugacity and gaseous species in asteroid Ryugu
Nature Geoscience (2023)
-
Origin of life-forming volatile elements in the inner Solar System
Nature (2022)
-
Strong and selective isotope effect in the vacuum ultraviolet photodissociation branching ratios of carbon monoxide
Nature Communications (2019)
-
The tumultuous childhood of the Solar System
Nature Astronomy (2019)
-
Constraining the Evolutionary History of the Moon and the Inner Solar System: A Case for New Returned Lunar Samples
Space Science Reviews (2019)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.