Introduction

The superconducting phase diagram of LaAlO3/SrTiO3 interfaces defined by plotting the critical temperature Tc as a function of electrostatic doping has the shape of a dome. It ends into a quantum critical point, where the Tc is reduced to zero, as carriers are removed from the interfacial quantum well1,2,3,4. Despite a few proposals5,6,7, the origin of this carrier density dependence, and in particular the non-monotonic suppression of Tc, remains unclear. To investigate this issue, one must consider the two fundamental energy scales associated with superconductivity. On the one hand, the gap energy Δ measures the pairing strength between electrons that form Cooper pairs. On the other hand, the superfluid stiffness Js determines the cost of a phase twist in the superconducting condensate. In conventional superconductors, well described by Bardeen–Cooper–Schrieffer (BCS) theory, Js is much higher than Δ and the superconducting transition is controlled by the breaking of Cooper pairs. However, when the stiffness is strongly reduced, phase fluctuations play a major role and the suppression of Tc can be dominated by the loss of phase coherence8. Tunneling experiments in the low doping regime of LaAlO3/SrTiO3 interfaces evidenced the presence of a pseudogap in the density of states above Tc9. This can be interpreted as the signature of pairing surviving above Tc while superconducting coherence is destroyed by strong phase fluctuations, enhanced by a low superfluid stiffness10. Superconductor-to-insulator quantum phase transitions driven by gate voltage1 or magnetic field11 also highlighted the predominant role of phase fluctuations in the suppression of Tc.

The two-dimensional (2D) superfluid density derived from the stiffness \(\left( {n_{\mathrm{s}}^{{\mathrm{2D}}} = \frac{{4m}}{{\hbar ^2}}J_{\mathrm{s}}} \right)\) has to be analyzed within the context of the peculiar LaAlO3/SrTiO3 band structure. Under strong quantum confinement, the degeneracy of the t2g bands of SrTiO3 (dxy, dxz, and dyz orbitals) is lifted, generating a rich and complex band structure12,13. The emergence of superconductivity for a given carrier density suggests that it could be intrinsically related to orbital occupancy in the interfacial quantum well. Experiments performed on (110)-oriented LaAlO3/SrTiO3 interfaces, for which the ordering of the t2g bands is reversed from that of the conventional (001) orientation, revealed that superconductivity behaves differently14. Instead of following the usual dome shape and disappearing at low doping, Tc is only weakly affected by gating over a wide range of carrier density. This shows the important role of orbitals ordering and also suggests that only some specific bands could host superconductivity15. In particular, it has been emphasized that the dxz/dyz band lying at high energy in the quantum well could play an important role because of its large density of states6,7.

Here we use resonant microwave transport to measure the complex conductivity of the superconducting (001)-oriented LaAlO3/SrTiO3 interfaces. This allows us to directly extract the evolution of the superfluid stiffness in the phase diagram that we also convert into a gap energy through BCS theory in the dirty limit. Both energy scales are compared with theoretical predictions. The superfluid density ns deduced from Js is found to be close to the carrier density of the dxz/dyz band extracted from multiband Hall effect measurements, highlighting the key role of this band in the emergence of superconductivity.

Results

Resonant microwave transport experiment

In superconducting thin films, Js is usually assessed either from penetration depth measurements16,17 or from dynamic transport measurements18,19. This latter method was adapted in this work for the specific case of LaAlO3/SrTiO3 samples. While superconductors have an infinite dc conductivity, they exhibit a finite complex conductivity σ(ω) at non-zero frequency, which in 2D translates into a sheet conductance G(ω) = G1(ω) − iG2(ω). The real part G1(ω) accounts for the transport of unpaired electrons existing at T ≠ 0 and ω ≠ 0, and the imaginary part G2(ω) accounts for the transport of Cooper pairs20,21. In the low-frequency limit \(\hbar \omega \ll {\mathrm{\Delta }}\), a superconductor behaves essentially as an inductor and G2(ω) = \(\frac{1}{{L_{\mathrm{k}}\omega }}\), where Lk is the kinetic inductance of the superconductor due to the inertia of Cooper pairs22. The superfluid stiffness is directly related to the inductive response of the condensate through the relation \(J_{\mathrm{s}} = \frac{{\hbar ^2}}{{4e^2L_{\mathrm{k}}}}\).

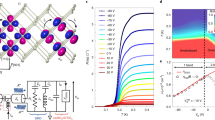
In this study, 8-uc-thick LaAlO3 epitaxial layers were grown on 3 × 3 mm2 TiO2-terminated (001) SrTiO3 single crystals by pulsed laser deposition (see Methods section). After the growth, a weakly conducting metallic back-gate of resistance ~100 kΩ is deposited on the backside of the 200-μm- thick substrate. Figure 1 gives a schematic description of our experimental setup, inspired by recent developments in the field of quantum circuits23,24. The LaAlO3/SrTiO3 heterostructure is inserted in a microwave circuit board, between the central strip of a coplanar waveguide guide (CPW) transmission line and its ground. It is embedded into an RLC resonant circuit whose inductor L1 and resistor R1 are surface mounted microwave devices (SMDs), and whose capacitor CSTO is due to the substrate in parallel with the 2D electron gas (2-DEG) (Fig. 1a, c). Because of the high dielectric constant of SrTiO3 at low temperature (i.e., \(\epsilon_{\mathrm{r}}\) ≃ 24,000), CSTO dominates the circuit capacitance. More information on the sample environment can be found in the Supplementary Note 1 and Supplementary Fig. 1. A directional coupler is used to guide the microwave signal from port 1 to the sample through a bias-tee, and to separate the reflected signal which is amplified by a low-noise cryogenic high electron mobility transistor amplifier before reaching port 2 (Fig. 1b). The complex transmission coefficient S21(ω) between the two ports is measured with a vector network analyzer. Standard microwave network analysis relates the reflection coefficient of the sample circuit Γ(ω) to S21(ω) through complex error coefficients, which are determined by a calibration procedure (see Methods section and Supplementary Fig. 5). For a transmission line terminated by a circuit load of impedance ZL(ω)25

$${\mathrm{\Gamma }}(\omega ) = \frac{{A^{{\mathrm{out}}}(\omega )}}{{A^{{\mathrm{in}}}(\omega )}} = \frac{{Z_{\mathrm{L}}(\omega ) - Z_0}}{{Z_{\mathrm{L}}(\omega ) + Z_0}},$$
(1)

where Ain and Aout are the complex amplitudes of incident and reflected waves, and Z0 = 50 Ω is the characteristic impedance of the CPW transmission line. A reflection measurement gives therefore a direct access to the load impedance ZL(ω) or equivalently its admittance GL(ω) = 1/ZL(ω), commonly called complex conductance. In the present case, ZL(ω) is the impedance of the RLC circuit represented in Fig. 1c, whose resonance frequency ω0 in the superconducting state is directly related to the kinetic inductance of the 2-DEG. Measuring ω0 as a function of gate voltage provides therefore a very direct method to determine the superfluid stiffness in the phase diagram. In addition, the setup of Fig. 1, which includes a bias-tee and protective capacitors in series with L1 and R1, allows measuring both the dc and ac microwave transport properties of the 2-DEG at the same time.

Fig. 1
figure 1

The LaAlO3/SrTiO3 sample and its microwave measurement setup. a LaAlO3/SrTiO3 sample inserted between the central strip and the ground of a CPW transmission line, in parallel with SMD inductors L1 and resistors R1. Cp are protective capacitors that avoid dc current to flow through L1 and R1 without affecting ω0. b Sample circuit of impedance ZL in its microwave measurement set-up that includes an attenuated input line and an amplified readout line separated by a directional coupler. A bias-tee allows dc biasing of the sample. c Equivalent electrical circuit of the sample circuit including the SMDs and the LaAlO3/SrTiO3 heterostructure modeled by an impedance Z2D in parallel with a capacitor CSTO. The reflection coefficient Γ(ω), taken at the discontinuity between the CPW line and the sample circuit, is defined as the ratio of the complex amplitude of the reflected wave Aout(ω) to that of the incident wave Ain(ω)

Full size image

Resonance in the normal and superconducting states

After cooling the sample to 450 mK, the back-gate voltage is first swept to its maximum value +50 V while keeping the 2-DEG at the electrical ground, to ensure that no hysteresis will take place upon further gating26. In the limit \(\omega \ll \tau ^{ - 1}\) (τ is the elastic scattering time) and for temperatures higher than Tc, the 2-DEG behaves as a metal whose Drude conductance is simply the inverse of the dc resistance (Fig. 2c). The circuit displays a resonance at frequency \(\omega _0 = \frac{1}{{\sqrt {L_1C_{{\mathrm{STO}}}} }}\). When ω ≈ ω0, ZL becomes purely real and the microwave signal is dissipated in the sample circuit. As a result, an absorption dip is observed in Γ(ω) along with a 2π phase shift (Fig. 2b). ω0 varies upon gating because of the electric-field-dependent SrTiO3 dielectric constant27 (Fig. 2a). Thus, the deduced substrate capacitance, CSTO, decreases with the absolute value of the gate voltage (Fig. 2c). Note that CSTO also includes a small contribution due to the circuit parasitic capacitance (≃3.5 pF) (see Methods section and Supplementary Fig. 2). According to the geometry of the sample, its value at VG = 0 V corresponds to a dielectric dielectric constant \(\epsilon _{\mathrm{r}}\) ≃ 23,700 (Supplementary Fig. 3). In the superconducting state, the 2-DEG conductance acquires an imaginary part \(G_2(\omega ) = \frac{1}{{L_{\mathrm{k}}(T)\omega }}\) that modifies ω0, since the total inductance of the circuit is now \(\frac{{L_1L_{\mathrm{k}}(T)}}{{L_1 + L_{\mathrm{k}}(T)}}\) (L1 in parallel with Lk(T)). The superconducting transition observed in dc resistance for positive gate voltages, VG, coincides with a shift of ω0 towards high frequency (Fig. 3b–d). We emphasize that this shift can already be detected in the uncalibrated S21(ω) coefficient (Supplementary Fig. 4). In the absence of superconductivity (for VG < 0 V), the resonance frequency remains unchanged as CSTO has no temperature dependence in the range of interest (Fig. 3a). In this experiment, the typical microwave current flowing into the sample circuit is <5 nA, which is much lower than the critical current of the superconducting 2-DEG (≃5 μA).

Fig. 2
figure 2

Resonance of the sample circuit in the normal state at T = 450 mK. a Magnitude of Γ(ω) in dB (color scale) as a function of ω and VG. b Magnitude and phase of Γ(ω) at VG = +24 V. c Capacitance CSTO extracted from the resonance frequency \(\omega _0 = 1{\mathrm{/}}\sqrt {L_1C_{{\mathrm{STO}}}}\) (left axis) and normal dc resistance Rn (right axis) as a function of VG. Square symbols indicate the values of VG used for calibration

Full size image
Fig. 3
figure 3

Resonance of the sample circuit in the superconducting state. Magnitude of Γ(ω) in dB (color scale) as a function of frequency and temperature for the selected gate values, VG = −34 V (a), VG = +14 V (b), VG = +24 V (c), and VG = +50 V (d). The corresponding dc resistance as a function of temperature is shown in gray solid lines (right axis)

Full size image

Superfluid stiffness and gap energy

In the following, we determine the gate dependence of the important energy scales in superconducting LaAlO3/SrTiO3 interfaces, and compare them with the BCS theory predictions. In Fig. 4a, we plot the gate dependence of the experimental superfluid stiffness \(J_{\mathrm{s}}^{{\mathrm{exp}}} = \frac{{\hbar ^2}}{{4e^2L_{\mathrm{k}}}}\) extracted from Lk at the lowest temperature T = 20 mK (≃0 K in the following). On the same logarithmic scale, we also show the gate dependence of the superconducting Tc defined as the temperature where Rdc = 0 Ω. The accuracy in the determination of the superfluid stiffness is limited by the uncertainty on the exact value of the circuit inductance L1 and the contribution of the sample geometrical inductance. The total error, corresponding to the gray outline on Fig. 4a, is estimated to be lower than 15% for all gate voltages (Supplementary Note 2).

Fig. 4
figure 4

Superfluid stiffness and phase diagram. a Experimental superfluid stiffness \(J_{\mathrm{s}}^{{\mathrm{exp}}}\left( {T \simeq 0} \right)\) (open triangles) as a function of VG compared with Tc taken at Rdc = 0 Ω (red open circles), and with the BCS theoretical stiffness JBCS expected from Eq. (2) assuming Δ(0) = 1.76kBTc (black open circles). The gray outline indicate the total error margin in the determination of \(J_{\mathrm{s}}^{{\mathrm{exp}}}(T \simeq 0)\). Inset) \(L_{\mathrm{k}}(T \simeq 0)\) as a function of VG and error margin (gray outline). b Superfluid stiffness converted into a gap energy \({\mathrm{\Delta }}_{\mathrm{s}}^{{\mathrm{exp}}}(T \simeq 0)\) as a function of VG (plain triangles) compared with the expected BCS gap energy 1.76kBTc (plain circles)

Full size image

The superconducting 2-DEG is in the dirty limit in which the elastic scattering time τ is much shorter than the superconducting gap Δ(T = 0) (\(\frac{{{\mathrm{\Delta }}(0)\tau }}{\hbar }\) ≃ 5.5 × 10−3). Within this limit and for \(\omega \ll {\mathrm{\Delta }}(0){\mathrm{/}}\hbar\), the zero-temperature superfluid stiffness of a single-band BCS superconductor can be expressed as a function of Δ(0)28:

$$J_{\mathrm{s}}(0) = \frac{{\pi \hbar }}{{4e^2R_{\mathrm{n}}}} \cdot {\mathrm{\Delta }}(0),$$
(2)

where Rn = Rdc(450 mK) is the normal state resistance (Fig. 2c) that accounts for the reduction of stiffness because of scattering.

\(J_{\mathrm{s}}^{{\mathrm{exp}}}\) increases continuously with gate voltage in the entire phase diagram in agreement with a previous report10. Moreover, a remarkable agreement is obtained between experimental data \(\left( {J_{\mathrm{s}}^{{\mathrm{exp}}}} \right)\) and BCS prediction (JBCS) in the overdoped (OD) regime defined by VG > \(V_{\mathrm{G}}^{{\mathrm{opt}}}\) ≃ 27 V, assuming a gap energy Δ(0) = 1.76kBTc in Eq. (2) (Fig. 4a). In this regime, the superfluid stiffness \(J_{\mathrm{s}}^{{\mathrm{exp}}}\) takes a value much higher than Tc in agreement with the BCS paradigm. However, in the underdoped (UD) regime, corresponding to VG < \(V_{\mathrm{G}}^{{\mathrm{opt}}}\), a discrepancy between the data and the BCS calculation is observed. The superfluid stiffness \(J_{\mathrm{s}}^{{\mathrm{exp}}}\) drops significantly while Tc and JBCS evolve smoothly before vanishing only when approaching closely the quantum critical point where Tc ≃ 0 K (VG = 4 V). This indicates that the loss of phase coherence of the superconducting condensate is stronger than what expected taking into account conventional scattering by defects, as encoded in Eq. (2). Such a behavior can then be ascribed to strong phase fluctuations probably reinforced by the presence of spatial inhomogeneities which has been proposed as an explanation for the observed broadening of the superconducting transitions29,30. In this context, it was shown that the 2-DEG in LaAlO3/SrTiO3 interfaces exhibits a behavior similar to the one of a Josephson junction array consisting of superconducting islands coupled through a metallic 2-DEG11,31. Whereas in the OD regime the islands are robust and tightly connected at T ≃ 0 K (homogeneous-like), in the UD regime, the charge carrier depletion makes the array more dilute. In this case, the system can maintain a rather high Tc (Rdc = 0 Ω) as long as the dc current can follow a percolating path through islands. However, the macroscopic stiffness \(J_{\mathrm{s}}^{{\mathrm{exp}}}\) is suppressed by phase fluctuations between islands and is therefore lower than that expected in a homogenous system of similar Tc.

We now convert \(J_{\mathrm{s}}^{{\mathrm{exp}}}\) into a superconducting gap energy \({\mathrm{\Delta }}_{\mathrm{s}}^{{\mathrm{exp}}}\) through Eq. (2) (Fig. 4b). Strikingly, these two characteristic energy scales of superconductivity evolve quite differently with doping. While \(J_{\mathrm{s}}^{{\mathrm{exp}}}\) continuously increases with VG (Fig. 4a), \({\mathrm{\Delta }}_{\mathrm{s}}^{{\mathrm{exp}}}\) has a dome-shaped dependence (Fig. 4b). More precisely, in the OD regime, \({\mathrm{\Delta }}_{\mathrm{s}}^{{\mathrm{exp}}}\) coincides with 1.76kBTc, and decreases like Tc while the superfluid stiffness increases: this is a clear indication that in this regime Tc is controlled by the pairing energy as in the BCS scenario. The maximum energy gap at optimal doping (\(V_{\mathrm{G}}^{{\mathrm{opt}}}\) ≃ 27 V) is \({\mathrm{\Delta }}_{\mathrm{s}}^{{\mathrm{exp}}}\) ≃ 23 μeV. This is in agreement with the BCS gap identified recently by Stornaiuolo et al.32 at optimal doping using spectroscopic Josephson junctions in LaAlO3/SrTiO3 interfaces of similar Tc. By using tunneling spectroscopy on planar Au/LaAlO3/SrTiO3 junctions, Richter et al.9 have reported an energy gap in the density of states of ≃40 μeV for optimally doped LaAlO3/SrTiO3 interfaces of higher Tc. In spite of this significantly higher gap energy, this corresponds to a \(\frac{{\mathrm{\Delta }}}{{k_{\mathrm{B}}T_{\mathrm{c}}}}\) ratio of 1.7, similar to our result. In the OD regime, we also checked that the gap value extracted from a BCS fit of the temperature dependence of \(J_{\mathrm{s}}^{{\mathrm{exp}}}\) matches \({\mathrm{\Delta }}_{\mathrm{s}}^{{\mathrm{exp}}}\) obtained by Eq. (2) (Supplementary Note 3 and Supplementary Fig. 6). In the UD regime of the phase diagram, \(\Delta _{\mathrm{s}}^{{\mathrm{exp}}}\) departs from 1.76kBTc which is in contradiction with BCS theory. This behavior is also different from that of the tunneling gap which was found to increase in the UD regime9. In addition, a pseudogap has been observed above Tc in this regime, as also reported in high-Tc superconducting cuprates33,34 or in strongly disordered films of conventional superconductors28,35,36. The results obtained by the two experimental approaches can be reconciled by considering carefully the measured quantities. In our case, the superconducting gap \({\mathrm{\Delta }}_{\mathrm{s}}^{{\mathrm{exp}}}\) probed by microwaves is directly converted from the stiffness of the superconducting condensate and is therefore only reflective of the presence of a true phase-coherent state. On the other hand, tunneling experiments probe the single particle density of states, and can evidence pairing even without phase coherence. The two experimental methods provide complementary informations which indicate that in the UD region of the phase diagram, the superconducting transition is dominated by phase coherence rather than by electron pairing. In this case, the energy gap cannot be extracted from Eq. (2), which is valid only for BCS superconductors. Notice that in the low carrier density region corresponding to VG < 0, some non-connected superconducting islands could already form without contributing to the macroscopic stiffness of the 2-DEG. Recently, preformed electron pairs without phase coherence has also been evidenced in SrTiO3-based nanostructures raising the question of a possible Bose–Einstein condensation mechanism where pairing precedes the formation of the superconducting state37.

Multiband transport

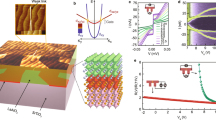
A simplified scheme of the band structure in the interfacial quantum well is presented in Fig. 5a, b38. The degeneracy of the three t2g bands is lifted by the confinement in the z direction, leading to a splitting that is inversely proportional to the effective masses mz along this direction. dxy subbands are isotropic in the interface plane with an effective mass mxy = 0.7m0, whereas the dxz/dyz bands are anisotropic with a corresponding average mass \(m_{{\mathrm{xz/yz}}} = \sqrt {m_{\mathrm{x}}m_{\mathrm{y}}}\) ≃ 3.13m0. At low carrier densities, we expect several dxy subbands to be populated, whereas at higher density (VG > 0 V), the Fermi energy should enter into the dxz/dyz bands. Multiband transport in LaAlO3/SrTiO3 and LaTiO3/SrTiO3 interfaces has been observed experimentally in various magneto-transport experiments including quantum oscillations39,40, magneto-conductance15,41, and Hall effect2,3,42,43,44. Yang et al. 39 recently showed that, in addition to a majority of low-mobility carriers (LMCs), a small amount of high-mobility carriers (HMCs) is also present, with an effective mass close to the mxz/yz one. Despite a band mass substantially higher than the mxy one, these carriers acquire a high mobility since dxz/yz orbitals extend deeper in SrTiO3 where they recover bulk-like properties, including reduced scattering, higher dielectric constant and better screening. In Hall effect measurements, the Hall voltage is linear in magnetic field B in the low doping regime corresponding to one-band transport, but this is not the case at high doping because of the contribution of a new type of carriers (the HMC)3. We performed a two-band analysis of the Hall effect data combined with gate capacitance measurements to determine the contribution of the two populations of carriers to the total density ntot (Fig. 5c)3. The first clear signature of multiband transport is seen when the Hall carrier density nHall, measured in the limit B → 0, drops with VG instead of following the charging curve of the gate capacitance (ntot in Fig. 5d). Figure 5d, e show that LMC of density nLM are always present, whereas a few HMC of density nHM are injected in the 2-DEG for positive VG, which corresponds to the region of the phase diagram where superconductivity is observed. In consistency with quantum oscillations measurements, we identify the LMC and the HMC as coming from the dxy and dxz/dyz bands, respectively, and we emphasize that the addition of HMC in the quantum well triggers superconductivity.

Fig. 5
figure 5

Superfluid density and Hall effect analysis. a Scheme of the interfacial quantum well showing the splitting of the t2g bands. b Simplified scheme of the band structure taking into account only the last filled dxy subband, the dxz band, and the dyz band. c Hall resistance as a function of magnetic field for different VG > 0 (open circles), fitted by at two-band model (black solid lines) (see Methods). d Hall carrier density \(n_{{\mathrm{Hall}}} = \frac{B}{{eR_{{\mathrm{Hall}}}}}\) extracted in the limit B → 0 (red open circles) and LMC density nLM extracted from the two-band analysis (green open squares). The total carrier density ntot is obtained by matching the charging curves of the gate capacitance with nHall at negative VG (black solid line). The unscaled Tc dome in the background indicates the region where superconductivity is observed. e Superfluid density \(n_{\mathrm{s}}^{{\mathrm{2D}}}\) calculated from \(J_{\mathrm{s}}^{{\mathrm{exp}}}\) using a mass mxz/yz (plain triangles), compared with the HMC density nHM (open squares)

Full size image

Discussion

To further outline the relation between HMC and superconductivity, we extract the superfluid density \(n_{\mathrm{s}}^{{\mathrm{2D}}}\) from \(J_{\mathrm{s}}^{{\mathrm{exp}}}\) assuming a mass mxz/yz for the electrons, and plot it as a function of the gate voltage (Fig. 5e). It increases continuously to reach \(n_{\mathrm{s}}^{{\mathrm{2D}}}\) ≃ 2 × 1012 e− cm−2 at maximum doping, which is approximately 1% of the total carrier density. The comparison of \(n_{\mathrm{s}}^{{\mathrm{2D}}}\) with nHM shows that, unexpectedly, both quantities have a very similar dependence with the gate voltage and almost coincide numerically (Fig. 5e). This suggests that the emergence of the superconducting phase is mainly related to the filling of dxz/dyz bands, whose high density of states is favorable to superconductivity. Nevertheless, in the presence of interband coupling, superconductivity may also be induced in some dxy subbands which would then slightly contribute to the total superfluid density.

Bert et al.10 measured the superfluid density in LaAlO3/SrTiO3 interfaces using a scanning SQUID technique. The overall gate dependence is similar in both experiments, including in the OD regime where the superfluid density keeps increasing while Tc is reduced. However, in our case \(n_{\mathrm{s}}^{{\mathrm{2D}}}\) is lower despite a much higher carrier density (n ≃ 1.8 × 1014e− cm−2 at maximum doping) which corresponds to the upper limit of the doping range commonly observed in LaAlO3/SrTiO3 interfaces. The fact that \(n_{\mathrm{s}}^{{\mathrm{2D}}} \simeq n_{{\mathrm{HM}}}\) may be somewhat intriguing as the dirty limit that we used in Eq. (2) implies that \(n_{\mathrm{s}}^{{\mathrm{2D}}}\) should correspond to a fraction of the total normal carrier density and not to nHM. To clarify this situation, it is needed to go beyond single-band superconductor models that cannot account correctly for the unusual t2g-based interfacial band structure of LaAlO3/SrTiO3 interfaces. Further investigations of recent experimental45 and theoretical46 developments on superconductors having two dissimilar bands (e.g., clean and dirty, weak, and strong coupling) should provide the starting framework to address this question.

In summary, we have measured the superfluid stiffness Js of LaAlO3/SrTiO3 interfaces by implementing a resonant microwave transport experiment. Whereas a good agreement with the BCS theory is observed at high carrier doping, we find that the suppression of Tc at low doping is controlled by the loss of macroscopic phase coherence instead of electron pairing strength as in standard BCS theory. The corresponding superfluid density represents only a small fraction of the total electrons density. We emphasize here that the monotonic raise of \(n_{\mathrm{s}}^{{\mathrm{2D}}}\) with gate voltage indicates that the decrease of Tc in the OD region of the phase diagram cannot be attributed to a loss of superfluid density. The gate dependence of \(n_{\mathrm{s}}^{{\mathrm{2D}}}\) agrees qualitatively with the density of HMCs extracted from multiband Hall effect. We therefore propose that the emergence of superconductivity upon gating is related to the weak filling of the dxz/dyz bands taking place at higher energy in the quantum well. In addition to having a larger density of states, these dxz/dyz bands also extends much deeper in the substrate due to their out-of-plane mass. Away from the interface, the dielectric constant, which is most probably a fundamental ingredient for electron pairing47, is less affected by the interfacial electric field and therefore closer to its nominal value. These delocalized electrons therefore recover properties similar to the ones found in bulk SrTiO3, including BCS superconductivity48. Our finding is consistent with the observation of a gate-independent superconductivity in (110)-oriented LaAlO3/SrTiO3 interfaces for which the dxz/dyz bands have a lower energy than the dxy subbands and are therefore always filled14.

Methods

Sample growth

In this study, we used 8-uc-thick LaAlO3 epitaxial layers grown on 3 × 3 mm2 TiO2-terminated (001) SrTiO3 single crystals by pulsed laser deposition. The substrates were treated with buffered hydrofluoric acid to expose TiO2-terminated surface. Before deposition, the substrate was heated to 830 °C for 1 h in an oxygen pressure of 7.4 × 10−2 mbar. The thin film was deposited at 800 °C in an oxygen partial pressure of 1 × 10−4 mbar. The LaAlO3 target was ablated with a KrF excimer laser at a rate of 1 Hz with an energy density of 0.56–0.65 J cm−2. The film growth mode and thickness were monitored using reflection high-energy electron diffraction (STAIB, 35 keV) during deposition. After the growth, a weakly conducting metallic back-gate of resistance ~100 kΩ (to avoid microwave shortcut of the 2-DEG) is deposited on the backside of the 200-μm-thick SrTiO3 substrate.

Calibration procedure

In this experiment, the resonance frequency shift and correspondingly Js can be extracted directly from the raw measurements of S21 in most of the regions of the phase diagram (Supplementary Fig. 4). Nevertheless, a calibration procedure can be applied to relate S21 measured with the Vector Network Analyzer to the reflection coefficient Γ = (ZL − Z0)/(ZL + Z0) of the sample circuit. This procedure also suppresses parasitic signals mainly due to wave interferences in the microwave setup, and improves the precision on the measurement as illustrated in Supplementary Fig. 4b. The microwave setup can be modeled using the scattering matrix formalism as shown in Supplementary Fig. 5. The relation between the transmission coefficient between port 1 and port 2 S21(ω) and the reflection coefficient of the sample circuit Γ(ω) is given by

$$S_{21} = \gamma + \frac{{\alpha {\prime}{\mathrm{\Gamma }}}}{{1 - \delta {\mathrm{\Gamma }}}},$$
(3)

where α′ = αβ, γ, and δ are three error complex coefficients. They can be determined using three known values of Γ = (ZL − Z0)/(ZL + Z0) which are obtained by imposing three different impedances ZL. It is customary to use an open, a short, and a matched load as standard impedances to calibrate microwave setup. However, such method is neither adapted to our very low temperature experiment nor to our sample circuit geometry. Instead, our setup was calibrated by directly varying the impedance ZL of the sample circuit with gate value. The main advantage of this method is that it fully takes into account the local microwave environment of the sample. The gate controls both the normal resistance of the 2-DEG whose value can be measured in dc and CSTO which can be extracted from ω0. In practice, we choose a set of three gate values which correspond to well-separated resonance frequencies. Other sets allow the accuracy of the calibration to be checked. Supplementary Fig. 4 shows a comparison between the raw measurement of S21 and the corresponding calibrated Γ coefficient both in the normal state and the superconducting state for VG = 50 V.

SrTiO3 dielectric constant

The dielectric constant of the SrTiO3 substrate can be retrieved from the value of CSTO plotted in Fig. 2c of the main text. For that, we performed numerical simulation using finite element method. We consider a 200-μm-thick 3 × 3 SrTiO3 substrate covered by two 100-μm-wide Au/Ti strips as represented in Supplementary Fig. 1. Supplementary Fig. 4a shows the distribution of the electrostatic potential when one volt is applied on one Au/Ti strip while the other one is at the ground. Arrows indicate the direction of the electric field. The numerical simulation provides the corresponding capacitance between the two Au/Ti strips for a given dielectric constant \(\epsilon _{\mathrm{r}}\). The gate dependence of \(\epsilon _r\) that corresponds to the value of (CSTO − Cpara) measured experimentally is shown in Supplementary Fig. 4b. At VG = 0 V, \(\epsilon _{\mathrm{r}}\) ≃ 23,700, which is consistent with the value found in the literature27.

Multiband Hall effect and gate capacitance

The dependence of the total carrier density ntot with VG is obtained by integrating the gate capacitance C(VG), measured by standard lock-in technique, over the gate voltage range

$$n_{{\mathrm{tot}}}\left( {V_{\mathrm{G}}} \right) = n_{{\mathrm{tot}}}\left( {V_{\mathrm{G}} = - 36\,{\mathrm{V}}} \right) + \frac{1}{{eA}}{\int}_{ - 36}^{V_{\mathrm{G}}} C(V){\mathrm{d}}V,$$
(4)

where A is the area of the sample and ntot(VG = −36 V) is matched to nHall since in this low doping regime the Hall effect is linear in magnetic field (single-band transport). In the multiband transport regime corresponding to VG > 0, the Hall resistance has been fitted with a two-band model

$$R_{{\mathrm{Hall}}} = \frac{B}{e}\frac{{\frac{{n_1\mu _1^2}}{{1 + \mu _1^2B^2}} + \frac{{n_2\mu _2^2}}{{1 + \mu _2^2B^2}}}}{{\left[ {\frac{{n_1\mu _1}}{{1 + \mu _1^2B^2}} + \frac{{n_2\mu _2}}{{1 + \mu _2^2B^2}}} \right]^2 + \left[ {\frac{{n_1\mu _1^2B}}{{1 + \mu _1^2B^2}} + \frac{{n_2\mu _2^2B}}{{1 + \mu _2^2B^2}}} \right]^2}},$$
(5)

where n1 and n2 are the 2D electron densities and, μ1 and μ2 the corresponding mobilities. Fits are performed with the two constraints: ntot = n1 + n2 and 1/Rdc = e(n1μ1 + n2μ2). The two populations of electrons are then identified as the LMC and the HMC.

Data availability

All data that support the findings of this study are available from the corresponding authors upon request.