Abstract
Double neutron star (DNS) merger events are promising candidates of short gamma-ray burst (sGRB) progenitors as well as high-frequency gravitational wave (GW) emitters. On August 17, 2017, such a coinciding event was detected by both the LIGO-Virgo gravitational wave detector network as GW170817 and Gamma-Ray Monitor on board NASA’s Fermi Space Telescope as GRB 170817A. Here, we show that the fluence and spectral peak energy of this sGRB fall into the lower portion of the distributions of known sGRBs. Its peak isotropic luminosity is abnormally low. The estimated event rate density above this luminosity is at least \(190_{ - 160}^{ + 440}\) Gpc−3 yr−1, which is close to but still below the DNS merger event rate density. This event likely originates from a structured jet viewed from a large viewing angle. There are similar faint soft GRBs in the Fermi archival data, a small fraction of which might belong to this new population of nearby, low-luminosity sGRBs.
Similar content being viewed by others
Introduction
Short-duration gamma-ray bursts (sGRBs) have long been proposed to be produced in systems involving the coalescence of double neutron stars (DNS)1, and the observations of sGRB afterglows and host galaxies are consistent with such a conjecture2,3,4. Based on the estimated event rate density derived from previously observed sGRBs at cosmological distances5, 6, the chance of detecting an sGRB within a small volume for detectable DNS mergers by advanced LIGO is very low7. Thus, GRB 170817A8/GW 1708179, as the first event in history showing a GRB associated with a gravitation wave signal from a compact binary merger, provides a unique opportunity to study its event rate, merger product, and implications of the GRB physics.
In this work, we performed a comprehensive analysis on GRB 170817A, mainly focusing on its prompt emission data in γ-ray energy band. Taking NGC 4993 as its host galaxy10, we find that its luminosity is abnormally low. We calculate the event rate of such sGRB event rate density and performed a comparison between such a rate density and the NS–NS merger event rate density. We also discussed the possible jet geometries, the physical implication of the time delay between GW signal and GRB signal, and the possible merger products of the event.
Results
Light curve structure
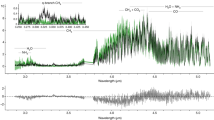
GRB 170817A (Fermi Trigger number 170817529) triggered Fermi GBM (8 keV–40 MeV)11 at T0 = 12:41:06.474598 UT on 17 August 20178. We processed the public Fermi/GBM data using the procedure as described in ref. 12. We selected two GBM/NaI detectors, n1 and n2, on board Fermi that are in good geometric configurations (e.g., angle <60°) with respect to the source position. By extracting the photon events from the Time-Tagged Event (TTE) data detected by these two detectors, we noticed that a sharp peak is present in the light curve between T0 − 0.26 s and T0 + 0.57 s with a signal-to-noise ratio (S/N) >5 (Methods). Such a signal is clearly identified in the two-dimensional (2-D) count map presented in Fig. 1. A weaker tail, which is also significant above the background with S/N >5, appears between T0 + 0.95 s and T0 + 1.79 s. The total span of GRB 170817A is about 2.05 s with a 0.38-s gap consistent with the background. The burst was also detected in the data of the SPI Anti-Coincidence System (ACS) on-board International Gamma-Ray Astrophysics Laboratory (INTEGRAL)13. We downloaded the pre-binned (50-ms bin) SPI-ACS light curve from http://isdc.unige.ch/Soft/ibas/ibas_acs_web.cgi, which is derived from 91 independent detectors with different lower energy thresholds (from 60 to 120 keV) and an upper threshold of ~10 MeV. The multi-channel GBM light curves and the SPI-ACS light curves are presented in Supplementary Fig. 1. We performed an extended search for signals before and after the burst using GBM data and no significant emission was found (Supplementary Note 5; Supplementary Figs. 9 and 10).
Spectral analysis
We first extract the time integrated spectrum in the first peak region (i.e., from T0 − 0.26 to T0 + 0.57 s). We select the NaI detectors n1 & n2 and BGO detector b0. The total number of photon counts is significantly above the background counts in NaI detectors (Supplementary Fig. 11). We used a software package developed by the first author, McSpecFit14, to perform spectral fitting. The energy channels at and around the iodine K-edge at 33.17 keV15 were excluded to better assess the quality of the fitting of spectral models. We find that the net spectrum can be successfully fitted by a power law function with an exponential high-energy cutoff (hereafter, cutoff power law or CPL model) with the goodness of statistics PGSTAT = 252.7 and degree of freedom DOF = 351 (Supplementary Note 1). The power law index is \(- {\mathrm{0}}{\mathrm{.61}}_{ - 0.60}^{ + 0.34}\) and the cutoff energy, parameterized as Ep, is \({\mathrm{149}}{\mathrm{.1}}_{ - 24.2}^{ + 229.4}\) keV. The corresponding average flux in this time interval is \(2.19_{ - 0.62}^{ + 3.76} \times 10^{ - 7}\) erg cm−2 s−1 between 10 keV and 10 MeV. The fluence is \(1.81_{ - 0.51}^{ + 3.11} \times 10^{ - 7}\) erg cm−2. For the second peak between T0 + 0.95 s and T0 + 1.79 s, we find that the net spectrum can be preferably fitted by a blackbody model with \(kT = 11.3_{ - 2.4}^{ + 3.8}\) keV (PGSTAT/DOF = 236.4/352) although we cannot rule out its non-thermal origin due to the large uncertainty of the lower spectral index when fitted by a CPL model (Supplementary Table 1). The corresponding average flux in this time interval is \(5.2_{ - 2.4}^{ + 4.7} \times 10^{ - 8}\) erg cm−2 s−1 between 10 keV and 10 MeV. The fluence in the same energy range is \(4.33_{ - 1.99}^{ + 3.95} \times 10^{ - 8}\) erg cm−2. Including both peaks, the total fluence is \(2.24_{ - 0.53}^{ + 3.51} \times 10^{ - 7}\) erg cm−2, corresponding to an isotropic energy of \(4.17_{ - 0.99}^{ + 6.54} \times 10^{46}\) erg. Using a 50-ms time resolution light curve, the peak luminosity at T0 ≃ −0.07 s is derived as \(1.6_{ - 0.4}^{ + 2.5} \times 10^{47}\) erg s−1. The best-fit parameters are presented in Supplementary Table 1. The spectral fitting plots as well as the parameter constraints are presented in Supplementary Figs. 2–4. No significant spectral evolution is observed (Supplementary Fig. 5).
Spectral lag analysis
Using the cross correlation function (CCF) method, we also calculate the spectral lag of the GRB between (25–50) keV and (50–100) keV, which is 0.03 ± 0.05 s, consistent with zero. This is consistent with the spectral lag distribution of sGRBs16.
Comparison with other GRBs
With the observed and derivative properties summarized in Table 1, one can compare GRB 170817A with other sGRBs. The following samples extracted from the Fermi/GBM catalog17 are considered for comparison: (a) the long GRB sample with Ep measured (1679 GRBs); (b) the short GRB sample (T90 < 2 s) with Ep measured (317 GRBs); and (c) the short GRB sample with S/N < 6 and Ep measured (66 “faint & short” GRBs). The latter is the faint sGRB sample to which GRB 170817A belongs (Supplementary Note 2 and Supplementary Fig. 6).
We first compare the observed properties of GRB 170817A with other GRBs. Figure 2 upper panel is the standard T90 − HR (hardness ratio) plot for GRBs. One can see that GRB 170817A falls in the boundary between short and long GRB populations. Since evidence has suggested that majority of sGRBs are consistent with the compact star merger origin, GRB 170817A, being associated with GW170817, belongs to the long and soft regime of this population. Figure 2 lower panel compares GRB 170817A and other GRBs in the fluence vs. Ep diagram. GRB 170817A seems to lie far away from the majority of the long GRBs. Based on γ-ray information only, this burst would be more likely regarded as one of those normal (but faint and soft) short GRBs if there was no gravitational wave trigger. Comparing the host galaxy NGC 4993 of GRB 170817A with the host galaxies of other sGRBs3, 18, we find that NGC 4993 falls into the distribution of sGRB hosts in terms of half-light radius, stellar mass, and afterglow offset from the host galaxy (Supplementary Note 3; Supplementary Fig. 7).
Comparisons between GRB 170817A and other GRBs. a A comparison between GRB 170817A and other Fermi long and short GRBs in the T90 − HR diagram. The hardness ratio (HR) is defined as ratio of the observed counts in the 50–100 keV band compared to the counts in the 25–50 keV band within the T90 region. b GRB 170817A in the fluence vs. Ep diagram against other sGRBs
We next investigate the intrinsic property of the burst. Taking into consideration the very small distance DL ~ 40 Mpc of the host galaxy NGC 499319, this burst is abnormally low in terms of luminosity and energy (throughout the paper, luminosity and energy are the isotropic-equivalent ones). The peak isotropic luminosity with 50 ms bin size is \(1.6_{ - 0.4}^{ + 2.5} \times 10^{47}\) erg s−1, and the isotropic energy is \(E_{{\mathrm{iso}}} = 4.17_{ - 0.99}^{ + 6.54} \times 10^{46}\) erg. Such low-luminosity sGRBs have never been observed before. Plotting it onto the intrinsic peak energy Ep,z = Ep(1 + z) vs. isotropic energy Eiso plane20, 21, we find that it is within the 2σ of the track of the sGRB population, but slightly deviates from the 1σ region of the track into the hard regime even if its Ep error is included (Fig. 3). The burst would be more normal if its isotropic luminosity was somewhat higher.
GRB 170817A in the Ep − Eiso correlation diagram. The solid lines are the best-fit correlations: logEp/(1 + z) = (3.24 ± 0.07) + (0.54 ± 0.04)log(Eiso/1052) for short GRBs, logEp/(1 + z) = (2.22 ± 0.03) + (0.47 ± 0.03)log(Eiso/1052) for long GRBs. Red dashed line represents GRB 170817A position if it were in different redshifts ranging from 0.009 to 3. All error bars represent 1−σ uncertainties
Event rate density of the 170817A-like GRBs
Based on previously known sGRBs, the event rate density (also called volumetric event rate) of sGRBs above then-minimum luminosity (~1050 erg s−1) is a few Gpc−3 yr−1 5, 6. For example, for a Gaussian distribution of the merger delay time22, the event rate density of sGRBs is \(4.2_{ - 1.0}^{ + 1.3}\) Gpc−3 yr−1 above 7 × 1049 erg s−1 6. This was significantly lower than the estimated DNS merger event rate density (ref. 9, see below). The discrepancy may be removed if one considers the beaming correction of sGRBs within the top-hat uniform jet model. Using the beaming factor fb ~ 0.04 inferred from the sparse sGRB jet break data collected in the past23, the beaming-corrected event rate density (counting for sGRBs not beaming toward us) was ~100 Gpc−3 yr−1. With the detection of GRB 170817A, the distribution of the sGRB isotropic peak luminosity extended down by ~three orders of magnitude. The revised event rate density of sGRB above 1.6 × 1047 erg s−1 becomes (Methods)
if one assumes only one such event within the GBM archives. This is comparable to (or somewhat higher than) the previously derived beaming-corrected sGRB event rate density, but could be still up to a factor of a few smaller than the DNS merger event rate density derived based on the detection of GW 170817A9, which is (Methods)
Figure 4 upper panel shows the sGRB event rate density as a function of luminosity threshold. The black power-law (PL) line with an index −0.7 was derived from the Swift sGRBs (black crosses with error included, peak luminosity derived with 64 ms time bin) with redshift measurements6. GRB 170817A (orange) extends the sGRB luminosity by three orders of magnitude in the low-Liso regime. Interestingly, the revised event rate density above 1.6 × 1047 erg s−1 follows the extension of the PL distribution derived by ref. 6. If one considers that there might be some sGRBs similar to GRB 170817A hidden in the GBM archives, the true event rate density could be higher, but has to be limited by the DNS merger event rate density (blue symbol). In Fig. 4 lower panel, we derive a new sGRB luminosity function across a wide range of luminosity, which is consistent with the extrapolation of the previous results that show a power law with \(L_{{\mathrm{iso}}}^{ - 1.7}\)6.
Distributions of local event rate density and luminosity function. a The local event rate density distribution of sGRBs including GRB 170817A. The orange symbol with error denotes the event rate density derived from GRB 170817A and the blue symbol with error denotes the DNS merger event rate density derived from GW170817. The black power-law line and other data points were derived from the Swift sGRB sample6. The vertical error bar represents the 1σ Gaussian errors derived from ref. 35. b Luminosity function distribution of sGRBs including GRB 170817A, with labels same as the upper panel. All error bars represent 1−σ uncertainties
Discussion
There are in principle two possibilities to produce a low-luminosity sGRB from a DNS merger. The first possibility is a bright sGRB jet viewed off-axis. Within this picture, the main jet (similar to the one observed from a more distant sGRB) beams toward a different direction. However, within such a scenario, one cannot have a sharp-edge conical jet viewed outside the jet cone. This is because the observed duration would be longer than the central engine activity time scale, inconsistent with its typical sGRB duration (Supplementary Note 6). Rather, one requires a structured jet viewed from a large wing24, 25 with emission powered by the low-luminosity wind along the line of sight. Within the sGRB context, such a jet configuration has been discussed in terms of a jet-cocoon geometry26, 27. A viewing angle θv ≤ 28° (or ≤36° depending on the assumed value of the Hubble constant28) has been inferred from the gravitational wave data. This is consistent with such a scenario. The second possibility is that the outflow of GRB 170817A may have an intrinsically low luminosity. However, the late rise of X-ray and radio flux29, 30 from the source suggests that the total energy budget of the source is higher. It disfavors this second possibility but favors the off-axis structured jet scenario (Supplementary Note 9).
The short duration of the burst is consistent with a prompt black hole or a hyper-massive neutron star that survived for a short (e.g., ~100 ms) period of time before collapsing to a black hole. We conduct a search of precursor or extended emission before and after the GRB trigger time and give a negative result (Supplementary Note 5). Even though the possibility of a long-live post-merger neutron star product cannot be ruled out from the GW31 and EM data, our non-detection of extended γ-ray emission is consistent with a BH post-merger product (Supplementary Note 7).
The merger time of the gravitational wave signal is at TGW = 12:41:04.430 ± 0.002 UTC on 17 August 2017 (GPS time TGW = 1187008882.430 ± 0.002 s)28. The beginning time of GRB 170817A (~ −0.3 s with respect to the Fermi/GBM trigger time T0 = 12:41:06.474598 UT on 17 August 20178) has an ~1.7-s delay with respect to the merger time. It is intriguing that this delay time scale has the same order as the burst duration itself. Such a delay offers a diagnostic of the emission site and energy dissipation process of GRBs. In particular, a scenario that invokes a magnetized jet dissipating in an optically thin region can interpret both time scales simultaneously without introducing an ad hoc jet-launching delay time as most other models do (Supplementary Note 8).
Assuming a standard radiative efficiency and standard shock microphysics parameters, the low isotropic energy of GRB 170817A suggests that the multi-wavelength afterglows of the burst should be very faint (Supplementary Note 6). We used the Javier Gorosabel 0.6 m robotic telescope at the BOOTES-5 station at Observatorio Nacional de San Pedro Martir (Mexico) to image the 15 galaxies in the GLADE Catalogue starting on Aug 18.21 UT. The optical counterpart (SSS17a) of GW 170817 was detected in the outskirts of the NGC 4993 galaxy, with a magnitude R = 18.20 ± 0.45, in agreement with other contemporaneous measurements. This is much brighter than the predicted flux of optical afterglow. As a result, this optical transient originates from a quasi-thermal kilonova32, 33, as suggested by independent modeling of many authors (e.g., ref. 34).
Within the Fermi GBM soft faint sGRB sample, there might be at most GRB 170817A-like events limited by the DNS merger rate. Some short, faint sGRB events are presented in Supplementary Fig. 6. However, identifying them turns out difficult without gravitational wave detections (Supplementary Note 10).
Methods
Determining GRB duration using 2-D energy vs. time count map
The GRB duration is usually defined by T90, which is the time span over which 5–95% of its total measured counts are measured17. The calculation of T90 is subject to the selection of energy band, the bin-size as well as the assumption of the model background (e.g., a 2nd or 3rd order polynomial function) of the GRB light curve. To minimize such an artificial effect for a faint GRB like GRB 170817A, we utilize the 2-D count map of the photon energy and photon arrival time directly from the Fermi/GBM TTE data and calculate the GRB duration. Our procedure is the following: (1) select the source region between the time interval [t1, t2] that includes the GRB signal. For GRB 170817A, [t1, t2] = [−1, 3]. (2) Select all the photon events between [t1, t2] in the Fermi/GBM TTE data. Note the selected data are a list of [time, energy] pairs. (3) Convert time vs. energy pairs to 2-D points in the time vs. energy plot, then use Kernel Density Estimation (KDE) to plot a 2-D source count map in the time vs. energy plot. This is the top panel in Fig. 1. (4) Select two background regions [t3, t4] and [t5, t6] that are before and after the burst region. For GRB 170817A, [t3, t4] = [−10, −2] and [t5, t6] = [5, 10]. Repeat steps (2) and (3) to get two 2-D count maps for the pre-burst and after-burst backgrounds. (5) Perform interpolation between those two background count maps to calculate the source-normalized background count map within [t1, t2] (middle panel of Fig. 2). Such a normalized and interpolated background within the source region can be used to calculate the standard derivation (STD) of the background. (6) Subtract the background count map from the source count map to get the net count map (bottom panel of Fig. 1). For each bin in the count map, define its signal-to-noise ratio as S/N = (net count)/STD. Overplotting the S/N = 1, 3, 5 in the net count map, we then define the burst duration region as where S/N ≥ 5.0 is satisfied.
sGRB event rate density
The abnormally low luminosity and extremely small distance of GRB 170817A suggest that the actual event rate density of short GRBs is large. With one detection, one can estimate the local event rate density ρ0,sGRB of short GRBs through
The field of view of GBM is approximatively taken as full sky with \({\mathrm{\Omega }}_{{\mathrm{GBM}}} \simeq 4\pi\). The working time of GBM is taken since 2008 with a duty cycle of ~50%, so that \(T_{{\mathrm{GBM}}} \simeq 4.5\,{\mathrm{yrs}}\). The maximum volume a telescope can detect for this low-luminosity event is \(V_{{\mathrm{max}}} = 4\pi D_{{\mathrm{L,max}}}^3{\mathrm{/}}3\). We simulate a set of pseudo-GRBs by placing GRB 170817A to progressively larger distances, and find that the signal would not be detectable at 65 Mpc (Supplementary Note 4; Supplementary Fig. 8). Taking this distance as DL,max, we derive the event rate density of sGRBs6
assuming only one such sGRB exists in the GBM archives. This number may be regarded as a lower limit if in reality there are other hidden ones.
The event rate density of DNS mergers may be also estimated based on one detection by aLIGO during O1 and O2. Since only one DNS merger event was detected9, one may write
Noticing Ω = 4π for GW detectors, taking DNS merger horizon ~60 and ~80 Mpc for O1 and O2, respectively, and adopting a duty cycle of ~40% for both O1 and O2, we estimate
This is consistent with the DNS merger event rate density derived by the LIGO-VIRGO team using more sophisticated simulations9.
The error bars in both Eqs. (4) and (6) show the 1σ Gaussian errors derived from ref. 35 by taking only one observational event into account. Comparing the two equations, one can see that even though the sGRB rate density may be consistent with the DNS merger rate density, it can be smaller than the latter by up to a factor of a few. This either suggests that there might be even less luminous sGRBs than GRB 170817A, or there might be GRB 170817A-like sGRBs hidden in the GBM archives. The number of these events is at most a few.
Data availability
The data that support the plots within this paper and other findings of this study are available from the corresponding author upon reasonable request.
References
Eichler, D., Livio, M., Piran, T. & Schramm, D. N. Nucleosynthesis, neutrino bursts and gamma-rays from coalescing neutron stars. Nature 340, 126–128 (1989).
Gehrels, N. et al. A short γ-ray burst apparently associated with an elliptical galaxy at redshift z = 0.225. Nature 437, 851–854 (2005).
Fong, W., Berger, E. & Fox, D. B. Hubble space telescope observations of short gamma-ray burst host galaxies: morphologies, offsets, and local environments. Astrophys. J. 708, 9–25 (2010).
Berger, E. Short-duration gamma-ray bursts. Annu. Rev. Astron. Astrophys. 52, 43–105 (2014).
Wanderman, D. & Piran, T. The rate, luminosity function and time delay of non-Collapsar short GRBs. Mon. Notices R. Astron. Soc. 448, 3026–3037 (2015).
Sun, H., Zhang, B. & Li, Z. Extragalactic high-energy transients: event rate densities and luminosity functions. Astrophys. J. 812, 33 (2015).
Ghirlanda, G. et al. Short gamma-ray bursts at the dawn of the gravitational wave era. Astron. Astrophys. 594, A84 (2016).
Goldstein, et al. An ordinary short gamma-ray burst with extraordinary implications: Fermi/GBM detection of GRB 170817A. Astrophys. J. Lett. 848, L14 (2017).
Abbott, B. P. et al. (LIGO Scientific Collaboration and Virgo Collaboration) GW 170817: observation of gravitational waves from a binary neutron star inspiral. Phys. Rev. Lett. 119, 161101 (2017).
Coulter, D. et al. Swope Supernova Survey 2017a (SSS17a), the optical counterpart to a gravitational wave source. Science https://doi.org/10.1126/science.aap9811 (2017).
Meegan, C. et al. The fermi gamma-ray burst monitor. Astrophys. J. 702, 791–804 (2009).
Zhang, B.-B., Uhm, Z. L., Connaughton, V., Briggs, M. S. & Zhang, B. Synchrotron origin of the typical GRB band function—a case study of GRB 130606B. Astrophys. J. 816, 72 (2016).
Savchenko, V. et al. INTEGRAL detection of the first prompt gamma-ray signal coincident with the gravitational wave event GW170817. Astrophys. J. Lett. 848, L15 (2017).
Zhang, B.-B. et al. Transition from fireball to poynting-flux-dominated outflow in three-episode GRB 160625B. Nat. Astron. 2, 69–75 (2018).
Goldstein, A. et al. The fermi GBM gamma-ray burst spectral catalog: the first two years. Astrophys. J. Suppl. Ser. 199, 19 (2012).
Gehrels, N. et al. A new γ-ray burst classification scheme from GRB060614. Nature 444, 1044–1046 (2006).
Narayana Bhat, P. et al. The third fermi GBM gamma-ray burst catalog: the first six years. Astrophys. J. Suppl. Ser. 223, 28 (2016).
Li, Y., Zhang, B. & Lü, H.-J. A comparative study of long and short GRBs. I. overlapping properties. Astrophys. J. Suppl. Ser. 227, 7 (2016).
Kopparapu, R. K. et al. Host galaxies catalog used in LIGO searches for compact binary coalescence events. Astrophys. J. 675, 1459–1467 (2008).
Amati, L. et al. Intrinsic spectra and energetics of BeppoSAX gamma-ray bursts with known redshifts. Astron. Astrophys. 390, 81–89 (2002).
Zhang, B. et al. Discerning the physical origins of cosmological gamma-ray bursts based on multiple observational criteria: the cases of z = 6.7 GRB 080913, z = 8.2 GRB 090423, and some short/hard GRBs. , Astrophys. J. 703, 1696 (2009).
Virgili, F. J. et al. Are all short-hard gamma-ray bursts produced from mergers of compact stellar objects? Astrophys. J. 727, 109 (2011).
Fong, W., Berger, E., Margutti, R. & Zauderer, B. A. A decade of short-duration gamma-ray burst broadband afterglows: energetics, circumburst densities, and jet opening angles. Astrophys. J. 815, 102 (2015).
Zhang, B. & Mészáros, P. Gamma-ray burst beaming: a universal configuration with a standard energy reservoir? Astrophys. J. 571, 876–879 (2002).
Rossi, E., Lazzati, D. & Rees, M. J. Afterglow light curves, viewing angle and the jet structure of γ-ray bursts. Mon. Notices R. Astron. Soc. 332, 945 (2002).
Lamb, G. P. & Kobayashi, S. Electromagnetic counterparts to structured jets from gravitational wave detected mergers. Preprint at http://arxiv.org/abs/1706.03000 (2017).
Lazzati, D. et al. Off-axis emission of short γ-ray bursts and the detectability of electromagnetic counterparts of gravitational-wave-detected binary merger. Mon. Notices R. Astron. Soc. 471, 1652 (2017).
Abbott, B. P. et al. (LIGO Scientific Collaboration and Virgo Collaboration) Gravitational waves and gamma rays from a binary neutron star merger: GW170817 and GRB 170817A. Astrophys. J. Lett. 848, L13 (2017).
Troja, E. et al. The X-ray counterpart to the gravitational-wave event GW170817. Nature 551, 71–74 (2017).
Hallinan, G. et al. A radio counterpart to a neutron star merger. Science 358, 1579–1583 (2017).
Abbott, B. P. et al. (LIGO Scientific Collaboration and Virgo Collaboration) Search for post-merger gravitational waves from the remnant of the binary neutron star merger GW170817. Preprint at http://arxiv.org/abs/1710.09320 (2017).
Li, L.-X. & Paczyński, B. Transient events from neutron star mergers. Astrophys. J. 507, L59 (1998).
Metzger, B. D. et al. Electromagnetic counterparts of compact object mergers powered by the radioactive decay of r-process nuclei. Mon. Notices R. Astron. Soc. 406, 2650 (2010).
Kasen, D., Metzger, B. & Barnes, J. et al. Origin of the heavy elements in binary neutron-star mergers from a gravitational-wave event. Nature 551, 80 (2017).
Gehrels, N. Confidence limits for small numbers of events in astrophysical data. Astrophys. J. 303, 336–346 (1986).
Acknowledgements
We acknowledge support from National Basic Research Program of China (973 Program, Grant No. 2014CB845800). B.-B.Z. and A.J.C.T. acknowledge support from the Spanish Ministry Projects AYA 2012-39727-C03-01 and AYA2015-71718-R. B.-B.Z. acknowledges the support from the National Thousand Young Talents program of China. This work is also supported by the Strategic Pioneer Program on Space Science, Chinese Academy of Sciences (Grant No. XDA15052100). B.Z., H.S., H.G., and X.F.W. are supported by the Strategic Priority Research Program of the Chinese Academy of Sciences “Multi-waveband Gravitational Wave Universe” (Grant No. XDB23040000). H.G. acknowledges the National Natural Science Foundation of China under grants Nos. 11722324, 11603003, 11633001, and 11690024. H.J.L. and E. W. L. acknowledge the National Natural Science Foundation of China under grant 11603006 and 11533003. Y.D.H. acknowledges the support by China Scholarships Council (CSC) under the Grant No. 201406660015. X.-F.W. acknowledges the National Natural Science Foundation of China under grant 11625312. L.S. acknowledges the support by the Joint NSFC-ISF Research Program (No. 11361140349), jointly funded by the National Natural Science Foundation of China and the Israel Science Foundation. X.F. was supported by Natural Science Foundation of China under Grants Nos. 11725314, 11673068, and 11433009. . The BOOTES-5/JGT observations were carried out at observatories Astronomico Nacional in San Pedro Martir (OAN-SPM, Mexico), operated by Instituto de Astronomia, UNAM, and with support from Consejo Nacional de Ciencia y Tecnologia (Mexico) through the Laboratorios Nacionales Program (Mexico), Instituto de Astrofisica de Andalucia (IAA-CSIC, Spain), and Sungkyunkwan University (SKKU, South Korea). We thank the staff of OAN-SPM for their support in carrying out the observations. We acknowledge the use of the public data from the Fermi and INTEGRAL data archives.
Author information
Authors and Affiliations
Contributions
B.-B.Z. led the Fermi data analysis and physical explanations of this particular event. B.Z., W.-H.L., H.G., X.-F.W., and E.-W.L. proposed the theoretical models to explain the data. B.-B.Z. and B.Z. wrote the manuscript with the contributions from W.-H.L. and H.G. H.S. calculated the event rate. Y.L. performed a statistical analysis of the host galaxy information. L.S. and B.-B.Z. worked on the short GRB sample study. H.-J.L. calculated the f parameters. All co-authors contributed to the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Additional information
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Zhang, BB., Zhang, B., Sun, H. et al. A peculiar low-luminosity short gamma-ray burst from a double neutron star merger progenitor. Nat Commun 9, 447 (2018). https://doi.org/10.1038/s41467-018-02847-3
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-018-02847-3
This article is cited by
-
An assessment of the association between a fast radio burst and binary neutron star merger
Nature Astronomy (2023)
-
Rates of compact object coalescences
Living Reviews in Relativity (2022)
-
A peculiarly short-duration gamma-ray burst from massive star core collapse
Nature Astronomy (2021)
-
Neutron star mergers and how to study them
Living Reviews in Relativity (2020)
-
The Giant Radio Array for Neutrino Detection (GRAND): Science and design
Science China Physics, Mechanics & Astronomy (2020)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.