Linkage disequilibrium under polysomic inheritance

Abstract

Linkage disequilibrium (LD) is the non-random association of alleles at different loci. Squared LD coefficients r² (for phased genotypes) and $r_{\Delta}^2$ (for unphased genotypes) will converge to constants that are determined by the sample size, the recombination frequency, the effective population size and the mating system. LD can therefore be used for gene mapping and the estimation of effective population size. However, current methods work only with diploids. To resolve this problem, we here extend the linkage disequilibrium measures to include polysomic inheritance. We derive the values of r² and $r_{\Delta}^2$ at equilibrium state for various mating systems and different ploidy levels. For unlinked loci, ${\mathrm{E}}( {\hat r}_{\Delta}^2) \approx \frac{1}{{3({N_e - \eta })}}$ for monoecious and dioecious (with random pairing) mating systems or $\frac{{3 + f}}{{3\left( {1 + f} \right)\left( {N_e - \eta } \right)}}$ for dioecious mating systems (with lifetime pairing), where f is the number of females in a half-sib family and η is a constant related to the ploidy level. We simulate the application of estimating N_e using unphased genotypes. We find that estimating N_e in polyploids requires similar sample sizes and numbers of loci as in diploids, with the main source of bias due to using 0.5 as the recombination frequency.

Introduction

Linkage disequilibrium (LD) is the non-random association of alleles at different loci within individuals in a given population (Slatkin 2008), and can be influenced by many factors, such as selection, mutation, recombination, genetic drift, and the mating system (Nei 1987). Linkage disequilibrium can be measured by several parameters, such as the correlation coefficient r, Lewontin’s (1964) D’, Hill’s (1975) Q, Maruyama’s (1982) D^*, Ohta’s (1980) F^*, and Brown et al.’s (1980) χ. The most frequently used measure of LD is the squared correlation coefficient r² (Hill and Weir 1994), which is the weighted sum of the squared correlation coefficient between alleles at two loci.

The influence of genetic drift on linkage disequilibrium in finite populations has been extensively studied in diploids (Ohta and Kimura 1969; Hill and Robertson 1968; Weir 1979; Weir and Cockerham 1979; Weir and Hill 1980; Sved and Feldman 1973; Hill 1974). In general, previous work has shown that the squared correlation coefficient r² (for phased genotypes) or $r_{\Delta}^2$ (for unphased genotypes) will converge to a constant after several generations of random mating for unlinked loci, whereas more generations are required to converge for linked loci. This constant is determined by the sample size n, recombination frequency c, effective population size N_e and the mating system. Based on these four factors, LD has been incorporated into two major applications: (i) gene mapping (Hill and Weir 1994; Devlin and Risch 1995; Jorde 1995; Hosking et al. 2002; Hästbacka et al. 1992) and (ii) the estimation of effective population size (England et al. 2006; Hill 1981; Waples et al. 2014; Hayes et al. 2003; Sved et al. 2013), which enable either c or N_e to be solved when the other three factors are known, respectively. However, current methods work only with organisms that are diploid.

Many plant species are polyploid, with 30–80% of angiosperm species being at least partially polyploid (Burow et al. 2001), with evidence for paleo-polyploidy in most plant lineages (Otto 2007). Although rare, polyploidy is also present in animals, such as in some salamanders, flatworms, leeches, brine shrimps, frogs and fishes. Polyploidy is also important in the evolution of both wild and cultivated plants, and plays a key role in plant breeding (Sattler et al. 2016; Udall and Wendel 2006). However, to date the effects of ploidy on LD has not been extensively studied.

Polysomic inheritance is expected in autopolyploids but not in allopolyploids, although complex mechanisms can lead to a mixture of disomic and polysomic inheritance in the same genome (segmental allopolyploids, Stift et al. 2008). There are at least three typical features in polysomic inheritances: (i) multivalents may be formed during meiosis (Rieger et al. 1968), resulting in a particular phenomenon in polysomic inheritance, termed the double-reduction (Butruille and Boiteux 2000), in which a gamete may inherit a single gene copy twice; (ii) the chromosomes are randomly paired and exchange their chromatid segments during meiosis, in which the recombination frequency c is 1−1/v if the corresponding loci are located on different chromosomes (v is the ploidy level), ≤ 0.5 (in bivalent pairing) or 0.75 (in multivalent pairing) if the corresponding loci are located on the same chromosome (Fisher 1947; Sved 1964); (iii) the decay coefficient of heterozygosity (i.e., the ratio of single non-identity coefficients in the next and the current generations in the absence of mutation and migration) is $1 - \frac{1}{{vN_e}}$ in polyploids (N_e is the effective population size).

Here, we extend both the linkage disequilibrium measure D and Burrow’s Δ statistic to account for polysomic inheritance, and calculate their corresponding squared correlation coefficients r² and $r_{\Delta}^2$. We also extend Weir and Hill’s (1980) double non-identity framework to account for polysomic inheritance, and derive the expressions of these double non-identity coefficients under five mating systems. On this basis, we are able to derive ${\text{E}}(\hat r^2)$ and ${\text{E}}({\hat r}_{\Delta}^2)$ at equilibrium state, and these two expectations are approximated by d² and δ², respectively. Both approximations are closely related to the mating system together with the effective population size N_e and the recombination frequency c. We study the behavior of the squared correlation coefficient estimators $\hat r^2$ and $\hat r_{\Delta}^2$ during genetic drift, investigate the influence of recombination frequency c on d² or δ², simulate the application for estimating effective population size N_e, and evaluate the statistical performance of estimating $\hat N_e$. We discuss the relationship between r² and c (or between $r_{\Delta}^2$ and c), and that between r² and v (or between $r_{\Delta}^2$ and v). We enable the estimation of Burrow’s Δ, the testing of linkage disequilibrium based on Burrow’s Δ, and the estimation of effective population size using our software package polygene V1.3 (Huang et al. 2020), which is freely available via http://github.com/huangkang1987/polygene.

Theory and modeling

LD measurements

We denote A and B for two alleles each from a different locus. The generalized LD measurement D between A and B is defined as the difference between the observed and the expected frequencies of the haplotype AB, where a haplotype is defined as a combination of alleles at multiple loci from a single set of chromosomes. We slightly revise the notations of both Weir and Cockerham (1979) and Weir and Hill (1980) and define five specific variants of D: (i) $D_s^{AB}$ (for the same haplotype), (ii) $D_d^{AB}$ (for two different haplotypes within the same individual), (iii) $D_w^{AB}$ (for the within-individual component), (iv) $D_b^{AB}$ (for the between-individual component) and (v) D_AB (for the usual LD measurement). These measurements can be defined by symbols as follows:

$$D_s^{AB}\mathop{=}\limits^{\rm{def}} P_s^{AB} - p_Aq_B,$$

$$D_d^{AB}\mathop{=}\limits^{\rm{def}} P_d^{AB} - p_Aq_B,$$

$$D_w^{AB}\mathop{=}\limits^{\rm{def}} P_s^{AB} - P_d^{AB},$$

$$D_b^{AB}\mathop{=}\limits^{\rm{def}} P_d^{AB} - p_Aq_B,$$

$$D_{AB}\mathop{=}\limits^{\rm{def}} D_w^{AB} + D_b^{AB},$$

where $P_s^{AB}$ is the probability that the alleles in the same haplotype are A and B, $P_d^{AB}$ is the probability that alleles in different haplotypes within the same individual are A and B, and p_A and q_B are respectively the probabilities of A and B.

According to these definitions, the following expressions hold:

$$D_w^{AB} = D_s^{AB} - D_d^{AB},\,D_b^{AB} = D_d^{AB}\,{{{\mathrm{and}}}}\,D_{AB} = D_s^{AB}.$$

The usual LD measurement D_AB is the covariance between A and B in the same haplotype, i.e., $D_{AB} = {\mathrm{Cov}}({\mathcal{B}}_A,{\mathcal{B}}_B )$, where ${{{\mathcal{B}}}}_A = 1$ if the first allele in the haplotype is A, otherwise ${{{\mathcal{B}}}}_A = 0$, and the meaning of ${{{\mathcal{B}}}}_B$ is analogous.

The values of D_AB may be negative, and its range is influenced by the probabilities of A and B. It is therefore more intuitive to use Pearson’s correlation coefficient r_AB to measure LD to convert the range to [−1,1]:

$$r_{AB} = \frac{{D_{AB}}}{{\sqrt {Q_{AB}} }} = \frac{{{{{\mathrm{Cov}}}}( {{{{\mathcal{B}}}}_A,{{{\mathcal{B}}}}_B} )}}{{\sqrt {{{{\mathrm{Var}}}}( {{{{\mathcal{B}}}}_A} ){{{\mathrm{Var}}}}( {{{{\mathcal{B}}}}_B} )} }}.$$

where $Q_{AB} = {{{\mathrm{Var}}}}\left( {{{{\mathcal{B}}}}_A} \right){{{\mathrm{Var}}}}\left( {{{{\mathcal{B}}}}_B} \right) = p_Ap_Xq_Bq_X$ (X represents any allele distinct from both A and B, and thus p_X = 1−p_A and q_X = 1−q_B).

The values of r_AB may also be negative. However, the squared correlation coefficient $r_{AB}^2$ ranges from 0 to 1. We will adopt the average value of $r_{AB}^2$ across all allele pairs to evaluate the LD between two loci for the situation of phased genotypes. For diallelic loci, the averaged $r_{AB}^2$ across all allele pairs is equal to that of any allele pair.

The above LD measurements are applicable for phased genotypes although unphased genotypes are more common. For unphased genotypes, Burrows’s Δ statistic (Cockerham and Weir 1977) can be used, and we will extend this to account for polysomic inheritance. By using $D_w^{AB}$ and $D_b^{AB}$, Burrows’s Δ statistic between A and B can be defined as ${\Delta}_{AB} \mathop{=}\limits^{\rm{def}} D_w^{AB} + v D_b^{AB}$, which is also equal to $D_s^{AB}+(v-1)D_b^{AB}$. Moreover, for two-locus unphased genotypes, Burrow’s Δ statistic can be expanded to:

$${\Delta}_{AB} = \left( {\mathop {\sum}\limits_{i = 1}^v {\mathop {\sum}\limits_{j = 1}^v {\frac{{ij}}{v}} } G_{B^jX^{v - j}}^{A^iX^{v - i}}} \right) - vp_Aq_B,$$

(1)

where X is an arbitrary allele distinct from both A and B, with each $G_{B_{j}X_{v - j}}^{A_{i}X_{v - i}}$ denoting a two-locus unphased genotypic frequency whose superscript (or subscript) is an unphased genotype containing exactly i copies of A (or j copies of B). In Supplementary Appendix A, we use triploids to illustrate how Δ_AB is expanded. Substituting the observed values of p_A, q_B and $G_{B^{j}X^{v - j}}^{A^{i}X^{v - i}}$ into Eq. (1), Δ_AB can be estimated.

Burrows’s Δ is also 1/v times the covariance between the allele dosages of A and B within individuals, i.e., ${\Delta}_{AB} = {{{\mathrm{Cov}}}}\left( {{{{\mathcal{C}}}}_A,{{{\mathcal{C}}}}_B} \right)/v$, where ${{{\mathcal{C}}}}_A$ and ${{{\mathcal{C}}}}_B$ are the allele dosages of A and B, respectively (Gao et al. 2008). In other words, ${{{\mathcal{C}}}}_A = \mathop {\sum}\nolimits_{i = 1}^v {{{{\mathcal{B}}}}_{A_i}}$ and ${{{\mathcal{C}}}}_B = \mathop {\sum}\nolimits_{i = 1}^v {{{{\mathcal{B}}}}_{B_i}}$, where i enumerates haplotypes within individuals. Similarly, it is more intuitive to use Pearson’s correlation coefficient r_ΔAB to measure LD for unphased data, which is also equal to the correlation coefficient between ${{{\mathcal{C}}}}_A$ and ${{{\mathcal{C}}}}_B$:

$$r_{{\Delta}AB} = \frac{{{\Delta}_{AB}}}{{\sqrt {R_{AB}} }} = \frac{{{{{\mathrm{Cov}}}}( {{{{\mathcal{C}}}}_A,{{{\mathcal{C}}}}_B} )/v}}{{\sqrt {{{{\mathrm{Var}}}}( {{{{\mathcal{C}}}}_A} ){{{\mathrm{Var}}}}( {{{{\mathcal{C}}}}_B} )} /v}}.$$

where ${{{\mathrm{Cov}}}}\left( {{{{\mathcal{C}}}}_A,{{{\mathcal{C}}}}_B} \right)$ and ${{{\mathrm{Var}}}}\left( {{{{\mathcal{C}}}}_A} \right)$ can be derived by

$$\begin{array}{l} {\mathrm{Cov}}( {\mathcal{C}}_A,{\mathcal{C}}_B ) = {\mathrm{E}}( {{\mathcal{C}}_A{\mathcal{C}}_B} ) - {\mathrm{E}}( {{\mathcal{C}}_A} ){\mathrm{E}}( {{\mathcal{C}}_B} ) \\ \qquad\qquad\,\,\,\, = {\left( {\mathop {\sum}\limits_{i = 1}^v {\mathop {\sum}\limits_{j = 1}^v {ijG_{B^jX^{v - j}}^{A^iX^{v - i}}} } } \right) - v^2p_Aq_B,} \end{array}$$

$$\begin{array}{l} {\mathrm{Var}}( {\mathcal{C}}_A ) = {\mathrm{E}}( {\mathcal{C}}_{A}^{2} ) - {\mathrm{E}}^{2}( {{\mathcal{C}}}_A ) \\ \qquad\quad\, = {\mathop {\sum}\limits_{i = 1}^v {\mathop {\sum}\limits_{j = 1}^v {{\mathrm{E}}( {{\mathcal{B}}_{Ai}{\mathcal{B}}_{Aj}} ) - v^{2}p_{A}^{2}} } } \\ \qquad\quad\,{ = \mathop {\sum}\limits_{i = 1}^v {\mathrm{E}}({\mathcal{B}}_{Ai}) + \mathop {\sum}\limits_{i \ne j} {\mathrm{E}}( {\mathcal{B}}_{Ai}{\mathcal{B}}_{Aj} ) - v^{2}p_{A}^{2}} \\ \qquad\quad\, { = vp_A + v( {v - 1} )[ {{{{\mathcal{F}}}}p_A + ( {1 - {{{\mathcal{F}}}}} )p_A^2} ] - v^2p_A^2.} \end{array}$$

In the expression of ${\mathrm{Var}}({\mathcal{C}}_A)$, ${{{\mathcal{F}}}}$ is the inbreeding coefficient and can be solved from the relation $P_{AA} = {\mathcal{F}}p_A + (1 - {\mathcal{F})}p_A^2$, where P_AA is the probability of sampling two copies of A within the same individual without replacement. ${{{\mathcal{F}}}}$ can be obtained by

$${{{\mathcal{F}}}} = \frac{{P_{AA} - p_A^2}}{{p_Ap_X}}.$$

Substituting the expression of ${{{\mathcal{F}}}}$ into r_ΔAB, a simplified expression of $\sqrt {R_{AB}}$ can be obtained

$$\begin{array}{l} {\sqrt {R_{AB}} = \sqrt {{{{\mathrm{Var}}}}( {{{{\mathcal{C}}}}_A} ){{{\mathrm{Var}}}}( {{{{\mathcal{C}}}}_B} )} /v} \\\qquad\,\,\, { = \sqrt {[ {p_Ap_X + ( {v - 1} )( {P_{AA} - p_A^2} )} ][ {q_Bq_X + ( {v - 1} )( {P_{BB} - q_B^2} )} ]} .} \end{array}$$

(2)

Likewise, r_ΔAB may be negative, but the squared correlation coefficient $r_{\Delta AB}^2$ ranges from 0 to 1, which can also be used to evaluate the LD between two loci for unphased genotypes.

In the following text, for simplicity, we will use D_w, D_b, D, Δ, Q, R, r and r_Δ to replace $D_w^{AB}$, $D_b^{AB}$, D_AB, Δ_AB, Q_AB, R_AB, r_AB and r_ΔAB in turn. Due to genetic drift, D² and Q (or Δ² and R) converge to zero after an infinite number of generations. However, the ratio r² of D² to Q (or the ratio $r_{\Delta}^2$ of Δ² to R) converges to a constant, whose value is determined by the mating system together with the recombination frequency c and the effective population size N_e (Weir and Hill 1980). Therefore, the effective population size can be estimated from $\hat r^2$ (or $\hat r_{\Delta}^2$) if the relationship between ${\text{E}}(\hat r^2)$ (or ${\text{E}}(\hat r_{\Delta}^2)$), mating system, c and N_e can be derived.

The values of $\hat r^2$ and $\hat r_{\Delta}^2$ can be calculated by

$$\hat r^2 = \frac{{\hat D^2}}{{\hat Q}}\quad{\mathrm{and}}\quad \hat r_{\Delta}^2 = \frac{{\hat {\Delta}^2}}{{\hat R}},$$

where ${\hat D},{\hat {\Delta}},{\hat Q}$, and $\hat R$ can be calculated from the samples. However, these statistics are correlated, such that ${\text{E}}(\hat r^2)$ and ${\text{E}}({\hat r}_{\Delta}^2)$ is hard to derive. If such correlations can be reduced or even eliminated (this can be done by some weighting scheme when multiple loci are used), then ${\text{E}}({\hat r}^2)$ and ${\text{E}}({\hat r}_{\Delta}^2)$ can be approximated by the ratio of two expectations, we denoted these ratios by d² and δ².

$${\mathrm{E}}({\hat r^2}) \approx \frac{{\mathrm{E}}( {\hat D^2} )}{{\mathrm{E}}( {\hat Q} )} = d^2\quad{\mathrm{and}}\quad{\mathrm{E}}( {\hat r_{\Delta}^2} ) \approx \frac{{\mathrm{E}}( {\hat {\Delta}^2} )}{{\mathrm{E}}( {\hat R} )} = \delta ^2.$$

(3)

In the following sections, we extend Weir and Hill’s (1980) double non-identity framework, to obtain the expressions of d² and δ².

Double non-identity coefficients

The double non-identity coefficients can be used to derive the moments of various LD measurements. The term identity means identical-by-descent (IBD), i.e., two alleles are identical because they are inherited from a common ancestor. Based on Weir and Hill (1980), we establish 22 two-locus allele configurations for polysomic inheritances (Table 1) The observed and expected frequencies of these 22 configurations are denoted by P_i and E_i, respectively; and E_i is derived by the non-identity coefficients assuming no initial LD (Table 1). The descriptions of the non-identity coefficients, and the derivations of E_i are provided in Supplementary Appendix B. The moments of LD measurements can be expressed by E_i (Supplementary Appendix C), and can be further expanded as linear combinations of the double non-identity coefficients (Table 2).

Table 1 Allele configurations and their expected frequencies.

Table 2 Essential factors of moment expressions.

The expressions of various moments can now be expressed uniformly by matrices. Let M be the row vector consisting of the 7 moments (header row of Table 2), and let Φ be the column vector consisting of the 13 double non-identity coefficients (header column of Table 2). Denote A as a 13 × 7 matrix, whose i^th column consists of the i^th column divided by the last column of Table 2. Then

$${{{\mathbf{M}}}} = {{{\mathbf{{\Phi}}}}}^{\boldsymbol{T}}{{{\mathbf{A}}}}.$$

(4)

We call M the moment vector, and Φ the double non-identity vector.

Transition matrix of double non-identity coefficients

The transition matrix of double non-identity coefficients can be used to describe the behavior of double non-identity coefficients due to genetic drift.

Let Φ be the double non-identity column vector in the current generation, and let Φ′ be that in the next generation and Φ′ can be expressed as Φ′ = ΩΦ. We call Ω the transition matrix from Φ to Φ′.

Let Φ₀ be the double non-identity vector in the founder generation and let Φ_t be that in the t^th generation. This gives Φ_t = Ω^tΦ₀. If a population is allowed to reproduce for several generations, the vector sequence is: Φ₀, Φ₁, Φ₂, …, Φ_t, … and will reach a steady state as t increases. In other words, this sequence will converge to a constant vector, denoted by Φ_∞. This limit vector Φ_∞ is independent to the initial vector Φ₀ if Φ₀ ≠ O.

To simplify the model for polysomic inheritance, we established a virtual mating system, named the haplotype sampling (HS) mating system. In this mating system, it is assumed that each individual is reproduced by randomly sampling v haplotypes with replacement from the previous generation. The genes in an offspring therefore come from a maximum of v parents. Because the haplotypes within (or among) individuals are randomly sampled, there is no difference among dihaplotypic, trihaplotypic and quadhaplotypic double non-identity coefficients, symbolically Θ₁ = Θ₂, Γ₁ = Γ₂ = Γ₃ = Γ₄ and Δ₁ = Δ₂ = … = Δ₇. Therefore, the transition matrix Ω in the HS mating system can be simplified as a 3 × 3 matrix, which is derived in Supplementary Appendix D. The full and simplified Ω are listed in Supplementary Table S3 and Table 3, respectively.

Table 3 Simplified Ω^T for HS mating system.

It is noteworthy that the sum of the combination coefficients of 1 in each column in Table 3 is exactly one, but the sum of each row of Ω is less than one. This indicates that the transition (i.e., a generation of random mating) will gradually reduce the double-nonidentity coefficients, and their values will eventually converge to zero, i.e., Ω^∞ = O. This also holds for the other mating systems and demonstrates the loss of heterozygosity and the fixation of alleles.

Although Φ_∞ will eventually converge to zero, the ratio of the moments ${\rm{E}}(\hat D^2)$ to ${\rm{E}}({\hat Q})$, and of the moments ${\rm{E}}({\hat \Delta^2})$ to ${\rm{E}}({\hat R})$ will converge to some constants. This can be considered as the double non-identity vector Φ reaches a relatively stable state so the direction of Φ is constant during reproduction, symbolically Φ′ = $\nu$Φ. The direction of Φ (say ω) and the scale factor $\nu$ can be solved by performing eigen-value decomposition for Ω, i.e., solving Ωω = $\nu$ω. It is also noteworthy that there are multiple eigenvalues, with the highest eigenvalue be of our interest. Therefore, d² and δ² can be calculated from Eq. (4) by substituting Ω with ω, i.e., M_ω = ω^TA. We denote the elements in M_ω as E_ω(⋅), e.g., ${\rm{E}}_\omega ({\hat D^2})$, then the exact d² and δ² are as follows:

$$d^2 = \frac{{{{{\mathrm{E}}}}_\omega ( {\hat D^2} )}}{{{{{\mathrm{E}}}}_\omega ( {\hat Q} )}}\quad{{{\mathrm{and}}}}\quad\delta ^2 = \frac{{{{{\mathrm{E}}}}_\omega ( {\hat {\Delta}^2} )}}{{{{{\mathrm{E}}}}_\omega ( {\hat R} )}}.$$

(5)

Approximations

Weir and Hill (1980) adopted a matrix decomposition technique to approximate $\nu$ and ω for disomic inheritance and also to approximate d² and δ². We follow this approach to derive the approximate expressions of d² and δ² for the HS mating system and four additional mating systems.

Let Ω be the simplified transition matrix for the HS mating system, as detailed in Table 3. If N is large enough, the values of the terms with N⁻² and N⁻³ in Table 3 will be small, then Ω can be decomposed to:

$${{{{\mathbf{\Omega}}}}} = {{{\mathbf{T}}}} + N^{ - 1}{{{\mathbf{S}}}} + {{{{{{\boldsymbol{\mathcal{O}}}}}}}}\left( {N^{ - 2}} \right).$$

For the matrices T and S in the principal part of Ω, with Ω given in Table 3 we obtain

$$\begin{array}{ll}{{{\mathbf{T}}}} = \left[ {\begin{array}{*{20}{c}} {c_1^2} & { - 2c_1c} & {c^2} \\ 0 & { - c_1} & c \\ 0 & 0 & 1 \end{array}} \right]\,{{{\mathrm{and}}}}\\ {{{\mathbf{S}}}} = \left[ {\begin{array}{*{20}{c}} {\frac{{c^2}}{{v_1}} - \frac{{1 + 2c_1c}}{v}} & {\frac{{4c\left( {2c - 1} \right)}}{v} - \frac{{2c^2}}{{v_1}}} & {\frac{{2c^2\left( {3 - 2v} \right)}}{{v_1v}}} \\ { - \frac{{c_1}}{v}} & {\frac{{6c - 3}}{v}} & { - \frac{{5c}}{v}} \\ 0 & {\frac{4}{v}} & { - \frac{6}{v}} \end{array}} \right],\end{array}$$

where c_i = c − i and v_i = v − i. Similarly, $\nu$ and ω can be decomposed to

$$\nu = 1 + N^{ - 1}r + {{{\mathcal{O}}}}\left( {N^{ - 2}} \right),$$

$${\mathbf{\omega}} = 1 + N^{ - 1}{{{\mathbf{x}}}} + {{{{{{\boldsymbol{\mathcal{O}}}}}}}}\left( {N^{ - 2}} \right),$$

where 1 = [1, 1, 1]^T and x = [x₁, x₂, x₃]^T. According to Ωω = $\nu$ω, we obtain a matrix equation as follows:

$${{{\mathbf{T1}}}} + N^{ - 1}{{{\mathbf{Tx}}}} + N^{ - 1}{{{\mathbf{S}}}}{\mathbf{1}} = {\mathbf{1}} + N^{ - 1}{{{\mathbf{x}}}} + N^{ - 1}{\boldsymbol{r1}} + {{{{{{\boldsymbol{\mathcal{O}}}}}}}}\left( {N^{ - 2}} \right).$$

Because T1 = 1, if the term ${{{\boldsymbol{{{{\mathcal{O}}}}}}}}\left( {N^{ - 2}} \right)$ is omitted, we obtain

$$\left( {{{{\mathbf{S}}}} - {\boldsymbol{r}}{{{\boldsymbol{I}}}}} \right){\boldsymbol{1}} = \left( {{{{\boldsymbol{I}}}} - {{{\mathbf{T}}}}} \right){{{\mathbf{x}}}}.$$

This matrix equation is a linear equation set with 3 equations and 4 unknowns, the solutions of which are as follows:

$$r = - 2/v,\,x_1 = \frac{{c^2v + \left( {1 - 2c} \right)v_1}}{{\left( {2 - c} \right)cv_1v}} + \zeta ,\,x_2 = \zeta ,\,x_3 = \zeta \, (\zeta \,{{{\mathrm{is}}}}\,{{{\mathrm{any}}}}\,{{{\mathrm{number}}}}).$$

If we let ζ = 0, we obtain a special solution: r = −2/v and ${{{\mathbf{x}}}} = \left[ {\frac{{c^2v + \left( {1 - 2c} \right)v_1}}{{\left( {2 - c} \right)cv_1v}},\,0,\,0} \right]^T.$ Replacing this solution into the expressions of $\nu$ and ω yields

$$\nu \approx \frac{{Nv - 2}}{{Nv}}\,{{{\mathrm{and}}}}\,{\boldsymbol{\omega}} \approx \left[ {1 + \frac{{c^2v + \left( {1 - 2c} \right)v_1}}{{\left( {2 - c} \right)cN_ev_1v}},\,1,\,1} \right]^T.$$

Now, by substituting Φ with ω and A with ${{{\mathbf{A}}}}_1 = \mathop{\lim}\limits_{n \to \infty }{{{\mathbf{A}}}}$ in Eq. (4), it can be calculated that

$${{{\mathrm{E}}}}_\omega \left( {\hat D^2} \right) = {{{\mathrm{E}}}}_\omega \left( {\hat {\Delta}^2} \right) \approx \frac{{c^2v + \left( {1 - 2c} \right)v_1}}{{\left( {2 - c} \right)cN_ev_1v}}\,{{{\mathrm{and}}}}\,{{{\mathrm{E}}}}_\omega \left( {\hat Q} \right) = {{{\mathrm{E}}}}_\omega \left( {\hat R} \right) \approx 1.$$

Therefore, the approximated d² and δ² are as follows:

$$d_{{{{\mathrm{HS}}}}}^2 \approx \frac{{c^2v + \left( {1 - 2c} \right)v_1}}{{\left( {2 - c} \right)cN_ev_1v}} \quad {{{\mathrm{and}}}} \quad \delta _{{{{\mathrm{HS}}}}}^2 \approx \frac{{c^2v + \left( {1 - 2c} \right)v_1}}{{\left( {2 - c} \right)cN_ev_1v}}.$$

To include the effect of finite sample size, higher order terms in A should be included. We derive the approximations of $d_{\rm{HS}}^2$ and $\delta _{\rm{HS}}^2$ by ignoring higher order terms of A, and find that $d_{\rm{HS}}^2$ and $\delta _{\rm{HS}}^2$ converge to

$$d_{{{{\mathrm{HS}}}}}^2 \approx \frac{{c^2v + ( {1 - 2c} )v_1}}{{( {2 - c} )cN_ev_1v}} + \frac{1}{{vn - 1}},$$

(6a)

$$\delta _{{{{\mathrm{HS}}}}}^2 \approx \frac{{c^2v + ( {1 - 2c} )v_1}}{{( {2 - c} )cN_ev_1v}} + \frac{1}{{n - 1}},$$

(6b)

where N_e and N are equivalent under the HS mating system, n is the sample size. The additional terms 1/(vn − 1) and 1/(n − 1) are corrections for finite sample size (see Supplementary Appendix E for details). The results from Eqs. (6a) and (6b) accord with those of Ohta and Kimura (1969) and Weir and Hill (1980) for the monoecious selfing mating system in diploids.

The transition of single non-identity coefficients satisfies the relations: $P^\prime = \frac{{Nv - 1}}{{Nv}}P$ and $\pi^{\prime} = \frac{{Nv - 1}}{{Nv}}\pi$. Moreover, if two loci are located at the two extremities on the same chromosome under bivalent pairing, and the thirteen double non-identity coefficients are all equal to P² and ${{{\mathbf{{\Phi}}}}}^{\prime} = \left( {\frac{{Nv - 1}}{{Nv}}} \right)^2{{{\mathbf{{\Phi}}}}}$, and thus also the corresponding eigenvalue $\nu = \left( {\frac{{Nv - 1}}{{Nv}}} \right)^2 \approx \frac{{Nv - 2}}{{Nv}}$. By comparing with the previous conclusion of $\nu \approx \frac{{Nv - 2}}{{Nv}}$ by substituting ζ = 0, we see that r = −2/v is a good approximation to the rate of loss of heterozygosity at the pairs of independent loci.

We follow Weir and Hill (1980) to establish four additional mating systems. Two are monecious mating systems: (i) selfing being allowed (termed MS), and (ii) selfing being excluded (termed ME). In both of these mating systems, the effective population size N_e is the same as the population size N. The other two mating systems we use are both dioecious systems: (i) dioecious with random pairing (termed DR), and dioecious with lifetime pairing (termed DH). In DR, each offspring is produced from a new pairing. In DH, each individual remains in a single reproductive unit for its entire lifetime. Moreover, in both DR and the DH, there are M males and F females in the population for each generation and F = fM, the effective population size is calculated by $N_e = \frac{{4MF}}{{M + F}}$.

The transition matrix Ω for each of the four additional mating systems (MS, ME, DR and DH) is a 13 × 13 matrix, whose element expressions are derived in Supplementary Appendices F–H. The matrices T and S in the principal part of Ω for all five mating systems are listed in Supplementary Appendix I. The approximate expressions of d² and δ² for additional mating systems can be derived with the same method (details can be found in Supplementary Appendix J) and are shown as follows:

$$d_{{{{\mathrm{MS}}}}/{{{\mathrm{ME}}}}/{{{\mathrm{DR}}}}}^2 \approx \frac{{8c_2c^2 - 4c_2cv\left( {5c - 1} \right) + 2v^2\left( {7c_2c^2 + c + 2} \right) - 3c_1^2v^3\left( {c + 1} \right)}}{{c_2c\left( {cv_2 + v} \right)\left( {3v - 4} \right)v^2N_e}} + \frac{1}{{vn - 1}},$$

$$\delta _{{{{\mathrm{MS}}}}/{{{\mathrm{ME}}}}/{{{\mathrm{DR}}}}}^2 \approx \frac{{v^2\left[ {4 - 3v + 8c^2 - 14c - cv\left( {2c^2 + 4c - 13} \right) + c_2cv^2\left( {c + 1} \right)} \right]}}{{c_2c\left( {cv_2 + v} \right)\left( {3v - 4} \right)v^2\left( {N_e - \eta } \right)}} + \frac{1}{{n - 1}};$$

$$\begin{array}{ll}d_{\mathrm{DH}}^2 \approx \Big\{ \left( {1 + f} \right)\left[ {cv\left( {3v^2 + 2v - 8} \right) - v^2\left( {3v - 4} \right)} \right] \\\qquad\qquad + c^2\left( {3v - 4} \right)\left[ {v^2 - 10v + 4 + f\left( {v^2 - 8v + 4} \right)} \right]\\ \qquad\qquad- c^3v_2\left[ {3v^2 - 10v + 4 + f\left( {3v^2 - 8v + 4} \right)} \right] \Big\}\\\qquad\qquad/\left[ {c_2c\left( {1 + f} \right)\left( {cv_2 + v} \right)\left( {3v - 4} \right)v^2N_e} \right] + \frac{1}{{vn - 1}},\end{array}$$

$$\begin{array}{ll}\delta _{\mathrm{DH}}^2 \approx v^2 \Big\{ c^3\left( {3 + f} \right)v_2v - \left( {1 + f} \right)\left( {3v - 4} \right) \\ \qquad\quad - c^2\left[ 3v^2 - 8 + f\left( {v^2 + 4v - 8} \right) \right] \\ \quad\qquad- c\left[f\left( {2v^2 - 13v + 14} \right) + 3\left( {2v^2 - 7v + 6} \right) \right] \Big\} \\ \quad\qquad/\left[c_2c\left( {1 + f} \right)\left( {cv_2 + v} \right)\left( {3v - 4} \right)v^2\left( {N_e - \eta } \right)\right] + \frac{1}{n - 1}.\end{array}$$

The approximate expressions of d² and δ² from disomic to decasomic are presented in Supplementary Tables S5 and S6. They follow a general pattern:

$$d^2 = \frac{{{{\mathcal{C}}}}}{{N_e}} + \frac{1}{{vn - 1}}\quad{{{\mathrm{and}}}}\quad\delta ^2 = \frac{{{{\mathcal{C}}}}}{{N_e - \eta }} + \frac{1}{{n - 1}}.$$

(7)

where η is equal to 0 for the HS mating system, $\frac{{2\left( {v - 2} \right)\left( {v - 1} \right)}}{{v^2}}$ for the MS mating system, or $\frac{{4\left( {v - 1} \right)^2}}{{v^2}}$ for the ME/DR/DH mating systems. The values of ${{{\mathcal{C}}}}$ for approximated d² and δ² between unlinked loci located on either the same chromosome (c = 0.5) or different chromosomes (c = 1 − 1/v) are presented in Table 4.

Table 4 Coefficient ${{{\mathbf{{{{\mathcal{C}}}}}}}}$ for approximated d² and $\delta ^2$.

Simulations and evaluations

Behaviors of $\hat r^2$ and $\hat r_{\Delta}^2$

In this section, we discuss the behaviors of the squared correlation coefficient estimators $\hat r^2$ and $\hat r_{\Delta}^2$ during reproduction and provide the exact and the approximate values of d² or δ² for reference.

Due to the correlation between $\hat D^2$ and $\hat Q$ (or between $\hat {\Delta}^2$ and $\hat R$), E($\hat r^2$) (or ${{{\mathrm{E}}}}\left( {\hat r_{\Delta}^2} \right)$) is not equal to d² (or δ²), which introduces some biases when few loci are used. To solve this problem, Waples (2006) used an empirical equation to adjust $\hat r_{\Delta}^2$ for di-allelic loci, which can be extended to multi-allelic loci by collapsing alleles. We use an alternative method to eliminate such correlations and bias. Assuming all locus pairs share the same parameters (c, n, N_e, v and mating system), then their d² (or δ²) are respectively the same, and their $\hat r^2$ (or $\hat r_{\Delta}^2$) can be weighted to approximate d² (or δ²). The multi-locus estimates of $\hat r^2$ and $\hat r_{\Delta}^2$ are calculated by

$$\hat r = \frac{{\mathop {\sum}\nolimits_{( {l_1,l_2} )} {\mathop {\sum}\nolimits_{A \in l_1,B \in l_2} {\hat D_{AB}^2} } }}{{\mathop {\sum}\nolimits_{( {l_1,l_2} )} {\mathop {\sum}\nolimits_{A \in l_1,B \in l_2} {\hat Q_{AB}} } }}\quad{{{\mathrm{and}}}}\quad\hat r_{\Delta}^2 = \frac{{\mathop {\sum}\nolimits_{( {l_1,l_2} )} {\mathop {\sum}\nolimits_{A \in l_1,B \in l_2} {\hat {\Delta}_{AB}^2} } }}{{\mathop {\sum}\nolimits_{( {l_1,l_2} )} {\mathop {\sum}\nolimits_{A \in l_1,B \in l_2} {\hat R_{AB}} } }},$$

(8)

where (l₁,l₂) is taken from all locus pairs, the symbol A ∈ l₁ (or B ∈ l₂) represents A (or B) is taken from all alleles at the first (or the second) locus in (l₁,l₂).

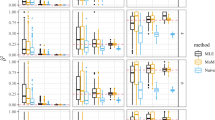
We adopt a Monte-Carlo method to simulate the behavior of $\hat r^2$ and $\hat r_{\Delta}^2$. During simulation, a population with the MS mating system is generated, which contains 40 or 80 individuals with a ploidy level of either 2 or 4. Next, the individuals generated are genotyped at 200 linked diallelic loci pairs, with a recombination frequency 0.1 for each locus pair. Although we generate 400 loci, only 200 loci pairs with c = 0.1 are used in calculating $\hat r^2$ and $\hat r_{\Delta}^2$. The population is then allowed to reproduce for 250 generations. For each generation, by using the data of genotypes of all individuals under various situations, $\hat r^2$ and $\hat r_{\Delta}^2$ are calculated by Eq. (8), and the exact and the approximate d² and δ² are also calculated by Eqs. (5) and (6a, 6b), respectively. This process is performed 300,000 times in total. The results are shown in Fig. 1.

Fig. 1: The behaviors of $\hat r^2$ and $\hat r_{\Delta}^2$ during reproduction for the MS mating system (set N_e = 40 or 80, v = 2 or 4, L = 200 and c = 0.1).

Each of the two columns shows the results of a different ploidy level, and each of the two rows shows the results of a different effective population size. Solid gray lines denote approximate d² or δ², dotted gray lines denote exact d² or δ², and solid lines denote $\hat r^2$ or $\hat r_{\Delta}^2$, where the lines representing δ² (or $\hat r_{\Delta}^2$) are above those representing d² (or $\hat r^2$) for each situation.

Figure 1 shows that the approximate d² or δ² are both slightly higher than their exact value, and both the exact and the approximate d² or δ² decrease as N_e or v increases. The values of $\hat r^2$ and $\hat r_{\Delta}^2$ are both initially 1, and reduce respectively to exact d² and δ² values after about 40 generations. Henceforth, $\hat r^2$ and $\hat r_{\Delta}^2$ both achieve a relatively stable state and remain around the exact values of d² and δ² for several generations. In particular, if the ploidy level is four, these values will both converge to the exact d² and δ² values as the number of generations increases.

Due to genetic drift, some loci become fixed and are excluded from the simulation, causing the number L of locus pairs used for genotyping to decline. The correlation between the numerator and the denominator in each of both formulas in Eq. (8) therefore increases, such that $\hat r^2$ and $\hat r_{\Delta}^2$ correspondingly decrease. The duration of a stable state depends on three factors: (i) ploidy level v, (ii) effective population size N_e and (iii) the number L of locus pairs. As the value of each of these factors increases, the longer the duration of the stable state of both $\hat r^2$ and $\hat r_{\Delta}^2$.

We also simulate the behaviors of $\hat r^2$ and $\hat r_{\Delta}^2$ during reproduction for five mating systems (including cases with f being set to either 2 or 5 for the DR and the DH mating systems). The simulation process is as follows. First, a population for each of the five mating systems is generated, which contains 40 individuals with a ploidy level of either 2, 4, 6 or 8. Next, these 40 individuals are genotyped as described for the previous simulation. Then, the population is allowed to reproduce for 50 generations. For each generation, by using data of the genotypes of all individuals under various situations, $\hat r^2$ and $\hat r_{\Delta}^2$ are calculated. The exact and approximate d² and δ² values are also calculated. The process is repeated 30,000 times. The results are shown in Supplementary Fig. S1, and are similar to those shown in Fig. 1. However, the approximate values of d² and δ² deviate more from their exact values for some mating systems.

Finally, we also simulate the behaviors of $\hat r^2$ and $\hat r_{\Delta}^2$ for the MS mating system under different recombination frequencies (set N_e = 80, v = 2 or 4, L = 200 and c = 0.001, 0.002, 0.004, 0.01, 0.02, 0.04, 1 or 2). The simulation process is similar to the previous method and is performed 20,000 times. The population is allowed to reproduce for 100 generations. For each generation, $\hat r^2$ and $\hat r_{\Delta}^2$ are calculated, with the results shown in Supplementary Fig. S2. This shows that the convergent rates for $\hat r^2$ or $\hat r_{\Delta}^2$ among different ploidy levels differ little as the number of generations increase, but are strongly affected by the recombination frequency: the higher the recombination frequency, the faster the rate of convergence.

Recombination frequency

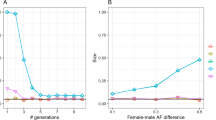
To investigate the influence of the recombination frequency c on d² and δ², the exact and the approximate d² and δ² are calculated for each mating system under different recombination frequencies (set N_e = 100, n = 100, v = 2, 4, 6 or 8, f = 1 for DR and f = 2 or 5 for DH). The recombination frequency c ranges from 0 to 1. The results for the MS mating system are shown in Fig. 2, and the results for all mating systems (including MS) are uniformly shown in Supplementary Fig. S3.

Fig. 2: The relationship between d² (or δ²) and the recombination frequency c for the MS mating system (set N_e = 100, n = 100 and v = 2, 4, 6 or 8).

The solid, dashed, dash-dotted and dotted lines denote the values for diploids, tetraploids, hexaploids and octoploids in turn, and the gray and the black lines denote the exact and the approximate values, respectively.

Figure 2 shows that d² or δ² are high at a low recombination frequency and decrease gradually to a relatively low value as c increases. The rate of decrease steepens as the ploidy level increases. However, after c reaches ~0.5, d² (at v = 2) or δ² (at all ploidy levels) both begin to increase. The approximate values of d² are close to their exact values, whilst the difference between the approximate and the exact values of δ² are more obvious, especially when c > 0.5.

The exact values for d² and δ² for the unlinked loci located on the same or different chromosomes are calculated for all five mating systems (set N_e = 100, n = 100, v = 2, 4, 6, 8 or 10, c = 0.5 or 1 − 1/v and f = 1, 2 or 5 for DR /DH). Moreover, the error rates for d² or δ² under different conditions are also calculated. The results are presented in Supplementary Table S7. It is clear that the difference between $\delta _{c = 0.5}^2$ and $\delta _{c = 1 - 1/v}^2$ is low under all conditions, but the difference between $d_{c = 0.5}^2$ and $d_{c = 1 - 1/v}^2$ is ~50 to 100 times higher. For example, for tetraploids, the error rate is about 13% for d² but only 0.13% for δ².

Estimation of effective population size

In this section, we estimate the effective population size N_e from unphased genotypes. We derived the relationships among v, c, n, N_e and δ² in the Theory and modeling section, e.g., Eq. (6b), where v and n are known, δ² can be substituted by $\hat r_{\Delta}^2$, $\hat N_e$ can be solved if c is known.

Close-linked loci take a long time to reach a mutation-drift equilibrium (Supplementary Fig. S2) and provide past information regarding N_e. Some estimators use this feature to estimate the time series of N_e, but need a priori information about recombination frequency (e.g., Tenesa et al. 2007; Santiago et al. 2020; Hollenbeck et al. 2016). For contemporary N_e, some estimators (e.g., England et al. 2006) assume that all loci are unlinked, and they use a recombination frequency 0.5 for all loci pairs. In polysomic inheritances, the recombination frequency is 1 − 1/v between two loci located on different chromosomes. Because $\delta _{c = 0.5}^2$ and $\delta _{c = 1 - 1/v}^2$ are close, with the error rate at most 1.5% (Supplementary Table S7), we assume the recombination frequency c = 0.5 between any two loci.

We preliminarily solve N_e using the approximated δ² by Eq. (7):

$$\hat N_{e\text{, initial}} = \frac{\mathcal{C}}{\hat r_\Delta^2-1/(n-1)}+\eta,$$

(9)

where $\hat r_{\Delta}^2$ is calculated by Eq. (8).

We further optimize the solution using the exact δ², i.e., Eq. (5). The exact δ² is related to the double non-identity coefficients and the effective population size N_e. Therefore, the exact δ² can be regarded as a function of N_e, denoted by δ²(N_e) such that $\hat N_e$ is the root of the following equation:

$$\delta ^2\left( {\hat N_e} \right) - \hat r_{\Delta}^2 = 0,$$

and we solve $\hat N_e$ with Newton’s method using $\hat N_{e,{{{\mathrm{initial}}}}}$ as the initial solution. This approach is denoted as newton’s approach. According to Eq. (8) and the central limit theorem, $\hat r_{\Delta}^2$ can be approximated with a normal distribution when there are many loci. Substituting δ² with $\hat r_{\Delta}^2$ and N_e with $\hat N_e$ in Eq. (7) and assuming $\hat r_{\Delta}^2\sim {{{\mathcal{N}}}}\left( {\mu ,\sigma ^2} \right)$, it can be found that $\left[ {\hat r_{\Delta}^2 - 1/\left( {n - 1} \right)} \right]/{{{\mathcal{C}}}}$ is accord with ${{{\mathcal{N}}}}\left( {\mu - 1/\left( {n - 1} \right),\sigma ^2/{{{\mathcal{C}}}}^2} \right)$ and is equal to 1/($\hat N_e$−η). Therefore, $\hat N_e$−η is in accordance with an inverse normal distribution whose expectation is undefined (Robert 1991). It is thus meaningless to evaluate the statistical performance of $\hat N_e$ because its expected value is not defined. To avoid this problem, we instead evaluate the statistical performance of 1/$\hat N_e$, which is approximately unbiased according to Eq. (9).

We use a Monte-Carlo method to simulate the estimation of effective population size N_e from unphased genotypes, and then evaluate the statistical performance of newton’s approach under different ploidy levels, numbers of loci, numbers of alleles and sample sizes. Two types of markers are used during simulation: (i) SNP (diallelic) and (ii) SSR (hexa-allelic). For simulation, first a founder population with 200 individuals all with a ploidy level of either 2, 4, 6 or 8 is created. To avoid the fixation of alleles, each allele in the founder generation is set as being unique. Second, the 200 individuals are genotyped at 100 or 200 diallelic SNPs, or at 20 or 40 hexa-allelic SSRs. These loci are assumed to be isometrically distributed on 10 chromosomes, and the length of each chromosome is 100 cM. Third, the founder population is allowed to reproduce for a fixed number of generations to reach the linkage equilibrium; the number of generations is 44 or 86 for SNP, and 11 or 19 for SSR; during meiosis, it is assumed that the chromosomes form bivalents. Fourth, after the final generation has been attained, to reduce the number of alleles k, we repeat collapsing two randomly selected alleles until the value of k is less than 2 (for SNP) or 6 (for SSR). Fifth, for the final generation, 400 individuals are created in total, and n individuals are randomly sampled from this generation, where n = 40, 80, …, 400 (interval 40). Finally, using the data of unphased genotypes of the n individuals sampled (n = 40, 80, …, 400), $\hat N_e$ can be estimated by using newton’s approach. We use the MS mating system as an example and performed 2000 replicates for each configuration. If we subsequently let ${\hat V}=1/{\hat N_e}$, the bias and the RMSE of $\hat V$ can be calculated, the results being shown in Fig. 3 and Supplementary Fig. S4. The simulated bias and RMSE of $\hat N_e$ are shown in Supplementary Fig. S4.

Fig. 3: The relationship between the bias of $\hat V$ and the sample size n (set N_e = 200, v = 2, 4, 6 or 8, L = 100 or 200 for SNP and L = 20 or 40 for SSR).

The results are obtained from the unphased genotypes of 40–400 individuals (interval 40). The solid, dashed, dash-dotted and dotted lines denote results for disomic, tetrasomic, hexasomic and octosomic inheritances in turn.

Figure 3 shows that the results for SNP are more biased than those for SSR, with $\hat V$slightly increasing as the number of loci L also increases. The bias of $\hat V$ is small, and is generally less than 2 × 10⁻³, especially less than 3 × 10⁻⁴ for the hexasomic and the octosomic inheritances, thus $\hat V$ is nearly unbiased, as expected.

Supplementary Fig. S5 shows that the RMSEs of $\hat V$ decrease as n increases, the values of which are similar among different ploidy levels. Moreover, the RMSEs for polyploids are slightly smaller than that for diploids. In general, the performances of SNPs and SSRs are similar.

Discussion

LD test

We here follow the method proposed by Weir and Cockerham (1979) to extend two LD measures, D and the Burrow’s Δ, to account for different levels of polysomic inheritance. These two measures can be used to perform the LD test. The null hypothesis of a LD test is that a pair of loci is under linkage equilibrium, which is equivalent to all D_AB (or all Δ_AB) values being equal to zero.

For a sample with n individuals, there are nv haplotypes. The observed and the expected occurrences of a haplotype AB are, respectively, nv$P_{s}^{AB}$ and nvp_Aq_B. Because D_AB = $P_{s}^{AB}$ P_s^AB−p_Aq_B, the χ² statistic for the LD measure D can be established as follows:

$$\chi _D^2 = nv\mathop {\sum}\limits_{AB} {\frac{{\hat D_{AB}^2}}{{p_Aq_B}}} \,{{{\mathrm{with}}}}\,{{{\mathrm{d}}}}.{{{\mathrm{f}}}}.\left( {k_1 - 1} \right) \times \left( {k_2 - 1} \right),$$

where d.f. is the number of degrees of freedom, k_i is the number of alleles among the allele copies in those haplotypes at the i^th locus (i = 1, 2), A is taken from all k₁ alleles at the first locus, and B is taken from all k₂ alleles at the second locus.

Next, for a sample with n individuals, there are nv² allele pairs, the observed and the expected occurrences of an allele pair AB are respectively nv$P_{s}^{AB}$ + nv(v − 1) $P_{d}^{AB}$ and nv²p_Aq_B. Because Δ_AB = $P_{s}^{AB}$ + (v − 1)$P_{d}^{AB}$−vp_Aq_B, the χ² statistic for Burrow’s Δ statistic can be established as follows:

$$\chi _{\Delta}^2 = n\mathop {\sum}\limits_{AB} {\frac{{\hat {\Delta}_{AB}^2}}{{p_Aq_B}}} \,{{{\mathrm{with}}}}\,{{{\mathrm{d}}}}.{{{\mathrm{f}}}}.\left( {k_1 - 1} \right) \times \left( {k_2 - 1} \right).$$

d ² and δ ²

In this study, various moments of LD measures are derived by extending Weir and Hill’s (1980) double non-identity coefficients, and thus the exact d² can be obtained by using the moments E($\hat D^2$) and E($\hat Q$) under various mating systems. The exact δ² can also be obtained by using the moments E($\hat {\Delta}^2$) and E($\hat R$). Hence the value of $\hat r^2$ (or $\hat r_{\Delta}^2$) can be approximately replaced by that of d² (or δ²) under each mating system at the equilibrium state. Moreover, the approximate expressions of d² and δ² under various mating systems are derived by using the transitional matrix, and several relationships are discussed, such as the relationship between $\hat r^2$ (or $\hat r_{\Delta}^2$) and the number of generations during reproduction, the relationship between d² (or δ²) and the recombination frequency c, and so on.

Figure 1 shows that after the population has been allowed to reproduce for about 40 generations, $\hat r^2$ (or $\hat r_{\Delta}^2$) reaches a relatively steady state, remaining close to the exact d² (or δ²) for several generations. Then, $\hat r^2$ (or $\hat r_{\Delta}^2$) begins to decrease again, due to both the fixation of alleles and the positive correlation between $\hat D^2$ and $\hat Q$ (or between $\hat {\Delta}^2$ and $\hat R$). As the number of loci decreases, the number of terms in the numerator or the denominator in Eq. (8) is reduced, due to the weighted scheme in Eq. (8) being unable to effectively eliminate the correlation. The number of generations at which $\hat r^2$ (or $\hat r_{\Delta}^2$) begins to decrease again depends on v, N_e, L and the initial heterozygosity.

Supplementary Fig. S2 shows that regardless of $\hat r^2$ or $\hat r_{\Delta}^2$, the smaller the recombination frequency, the slower the rate of convergence. Generally, $\hat r^2$ and $\hat r_{\Delta}^2$ decrease to a relatively steady state after about $- 4.21/\ln \left( {1 - c} \right)$ generations. Moreover, under the same recombination frequency, the convergent rates of $\hat r^2$ (or $\hat r_{\Delta}^2$) are similar for all levels of ploidy but differ markedly under different recombination frequencies.

Figure 2 (and Supplementary Fig. S3) shows that the relationship between d² (or δ²) and the recombination frequency c has two main features: (i) if c is small (e.g., <0.25), both d² and δ² for polysomic inheritance decreases more rapidly than those for disomic inheritance and (ii), the difference between $d_{c = 0.5}^2$ and $d_{c = 1 - 1/v}^2$ under polysomic inheritance is considerable (the error rate ranges from 10% to 23%), whereas the difference between $\delta _{c = 0.5}^2$ and $\delta _{c = 1 - 1/v}^2$ is negligible (the error rate is less than 1.5% for non-HS mating systems).

For (i), this infers that a higher density genetic map is required to detect any linkage in polyploids. A rough estimate would be the locus density in tetraploids (hexaploids or octoploids) to be 1.58 (2.16 or 2.67) times of that for diploids (estimated by the threshold δ² = 0.2, see Fig. 2). However, if the locus density is sufficient, the gene mapping in polyploids may be more accurate than that in diploids due to the steep slope of the curve at a low c.

For (ii) this indicates that it is unnecessary to distinguish whether two loci are located on the same chromosome or not if the effective population size N_e is estimated by $\hat r_{\Delta}^2$. From this reason, we can simply let the recombination frequency between any two loci be equal to 0.5, as is assumed in other methods (e.g., England et al. 2006). However, it is necessary to assume that two loci are located on different chromosomes if N_e is estimated by $\hat r^2$ using phased genotypes.

Effective population size

Among the parameters v, n, r², $r_{\Delta}^2$, N_e, c and f, the first two v and n are known, the next two r² and $r_{\Delta}^2$ can be estimated from the genotype data, and the mating system and the ratio f can be obtained from either a priori information, field observations or experiments. The remaining two parameters N_e and c are the parameters we usually need to estimate, and one can be estimated if the other is known.

After simulation, we evaluate the RMSE and the bias of $\hat V$ (i.e., 1/${\hat N}_e$). The curves of RMSE among different ploidy levels are similar, indicating that estimating N_e in polyploids requires similar numbers of samples and loci as in diploids. The performance of 100/200 diallelic SNPs is as good as that of 20/40 hexa-allelic SSRs (Supplementary Fig. S5), indicating that the RMSE is mainly determined by the number $\mathop {\sum}\nolimits_l^L {\left( {k_l - 1} \right)}$ of independent alleles. The results for polyploids may be better than for diploids due to smaller biases (Fig. 3).

Some possible sources of this bias of $\hat V$ are enumerated as follows. (i) According to Eq. (9), $\hat r_{\Delta}^2$−1/(n − 1) is proportional to 1/(N_e − η), not 1/N_e, indicating that the estimation of 1/(N_e − η) may be unbiased, but the estimation of 1/N_e is biased. (ii) The recombination frequency between two loci located on the same chromosome is less than 0.5, but it is assumed to be 0.5. (iii) The recombination frequency between two loci located on different chromosomes is 1 − 1/v, but it is also assumed to be 0.5.

We suggest that (ii) is the main source of this bias. This is because the bias is largely influenced by both the number L of loci used and the ploidy level v (Fig. 3). Because the length of each chromosome is 100 cM, the loci become denser at higher levels of L. The value of δ² between two close loci (implying smaller c) therefore increases in the deviation from $\delta _{c = 0.5}^2$ (Fig. 2). In addition, the simulation results for polyploids are less biased. This is because the curve of δ² at a higher ploidy level is flat for most situations (e.g., c > 0.2). To validate our prediction, we use unlinked loci to regenerate the results in Fig. 3, where the loci are on the same chromosome and the distance between two neighboring loci is long (10³⁰ cM). The results show the bias is reduced to 10⁻⁵ (Supplementary Fig. S6).

The bias sources (ii) and (iii) can be reduced if the a priori information is available: (i) if the combination frequency between any two loci is known, the exact δ² can be calculated between all loci pairs and averaged. In this case, Eq. (8) should use the arithmetic mean of $\hat r^2$ and $\hat r_{\Delta}^2$; (ii) if the lengths of chromosomes (in centimorgan) are known, assuming the loci are uniformly distributed on the chromosomes, then the exact δ² can be calculated; (iii) if the genome size and the number of chromosomes are both known, we can assume the length of the chromosomes accord with a particular distribution (e.g., triangular or uniform) and obtain the exact δ² (Waples et al. 2016); With newton’s approach as we described, the exact δ² can be considered a function of the true N_e, then N_e can be estimated; (iv) if the genetic data are sufficient, it is possible to cluster the loci into some linkage groups, and the loci in different lineage groups will be used to perform the estimation of N_e. This can be achieved using a specific software package designed for diploid N_e estimation, i.e., NeEstimator V2 (Do et al. 2014).

Non-independent samples

Non-independent samples can also be a potential bias source (Waples, personal communications). For non-independent samples due to random sampling, there is not extra bias. For non-independent samples due to non-random sampling, e.g., the relatives are more likely to be together sampled, extra bias is introduced.

We performed a simple simulation to show such bias, the results with different sampling strategies (random sampling, pair sampling of relatives) are compared. The bias of $\hat V$ is increased under non-random sampling at a low sample size and approaches that under random sampling as n increases (Supplementary Fig. S6). Such bias is mainly due to the overestimation of $\hat r_{\Delta}^2$ and $\hat {\Delta}^2$ .

We derived the LD moments under pair sampling of clones in Supplementary Appendix K. The LD moments under non-random sampling are related to the sample size, the probability of non-random sampling, the types of relatives, the single and the double non-identity coefficients, the allele probability product pq, and the heterozygosities. Therefore, d² and δ² cannot be derived by the method used in this manuscript, i.e., Eq. (5), and the elimination of such bias can be a direction of future studies.