Abstract
Inference of demographic histories using whole-genome datasets has provided insights into diversification, adaptation, hybridization, and plant–pathogen interactions, and stimulated debate on the impact of anthropogenic interventions and past climate on species demography. However, the impact of repetitive genomic regions on these inferences has mostly been ignored by masking of repeats. We use the Populus trichocarpa genome (Pop_tri_v3) to show that masking of repeat regions leads to lower estimates of effective population size (Ne) in the distant past in contrast to an increase in Ne estimates in recent times. However, in human datasets, masking of repeats resulted in lower estimates of Ne at all time points. We demonstrate that repeats affect demographic inferences using diverse methods like PSMC, MSMC, SMC++, and the Stairway plot. Our genomic analysis revealed that the biases in Ne estimates were dependent on the repeat class type and its abundance in each atomic interval. Notably, we observed a weak, yet consistently significant negative correlation between the repeat abundance of an atomic interval and the Ne estimates for that interval, which potentially reflects the recombination rate variation within the genome. The rationale for the masking of repeats has been that variants identified within these regions are erroneous. We find that polymorphisms in some repeat classes occur in callable regions and reflect reliable coalescence histories (e.g., LTR Gypsy, LTR Copia). The current demography inference methods do not handle repeats explicitly, and hence the effect of individual repeat classes needs careful consideration in comparative analysis. Deciphering the repeat demographic histories might provide a clear understanding of the processes involved in repeat accumulation.
Similar content being viewed by others
Introduction
Identification of the genetic variability between individuals of a species will enable reconstruction of their past relationships. While the type of DNA markers used for identifying genetic variation has changed with technological advances, the coalescent theory is the fundamental tool for studying gene genealogies in a population genetic framework. In this framework, changes in coalescence time and genetic diversity along the genome serve as a record of the population history over time. Estimation of demographic histories using whole-genomic datasets has proven to be particularly useful in addressing diverse evolutionary concepts such as host–parasite coevolution (Hecht et al. 2018), the effect of anthropogenic interventions (Dong et al. 2021), the impact of past climate change on the population dynamics (Bai et al. 2018), hybridization (Vijay et al. 2016), speciation events and split times between species (Cahill et al. 2016), history of inbreeding (Prado-Martinez et al. 2013), mutational meltdown (Rogers and Slatkin 2017), population decline, and threats of extinction (Mays et al. 2018).
The genomic distribution of repeat elements themselves, their population-level dynamics (Blumenstiel et al. 2014; Kofler et al. 2015; Ruggiero et al. 2017; Stritt et al. 2018), and their deviations from the neutral expectations (Arkhipova 2018; Riba et al. 2020) have received considerable attention. In contrast to the weak role attributed to different forms of selection, demographic forces strongly influence repeat diversity patterns (Lockton et al. 2008; Kofler et al. 2015; Bourgeois et al. 2020). The between-species variation in repeat content is thought to be due to variation in population sizes (Koonin 2009). Variation in the repeat content within the genome of a species is driven by variation in recombination rates (Wright et al. 2003; Jensen-Seaman et al. 2004; Pan et al. 2011). In addition to the population frequency of repeats, the overall abundance of different repeat types is also known to contain a phylogenetic signal with utility for taxa having low genetic divergence levels (Dodsworth et al. 2015). At much more recent evolutionary timescales, the use of microsatellite markers has provided higher resolving power while reconstructing population lineage histories (Behar et al. 2003).
The use of orthologous repeats to infer phylogenetic relationships across large numbers of species has served as a complementary source of phylogenetic information (Bashir et al. 2005; Zhang et al. 2014). Repeat regions contain a record of the evolutionary history at various evolutionary timescales and provide information complementary to that inferred from polymorphisms in non-repeat genomic regions. Despite the information available in repeat regions, whole-genome analysis tends to mask them due to uncertainty in the quality of the variant calls. The availability of longer read lengths combined with recent sequencing technologies has resulted in more contiguous genomes with a better assembly of repeat regions. Further improvements in technology, such as reduced sequencing error rates, lower costs, and more sophisticated variant-calling software, would allow widespread inclusion of genetic variation within repeat regions. In this context, it would be essential to understand how variants located within repeat regions contribute to the inference of demographic histories.
The early Sequentially Markovian Coalescent (SMC)-based methods (McVean and Cardin 2005; Li and Durbin 2011) for inference of demographic history relied upon a single whole-genomic dataset and has seen widespread usage with bird (Nadachowska-Brzyska et al. 2013, 2015, 2016; Hung et al. 2014; Natesh et al. 2020; Dong et al. 2021), marsupial (Feigin et al. 2018; Patton et al. 2019), Monotremata (Martin et al. 2018), placental (Prado-Martinez et al. 2013; Orlando et al. 2013; Freedman et al. 2014; Palkopoulou et al. 2015), and diverse plant datasets (Ibarra-Laclette et al. 2013; Project et al. 2013; Holliday et al. 2016; Bai et al. 2018; Patil et al. 2021). Despite the introduction of more sophisticated methods, PSMC continues to be used for non-model organisms with limited population-level sampling (Fitak et al. 2016; Jaiswal et al. 2018) and ancient genomes (Lord et al. 2020). A well-known limitation that has recently reduced the use of the PSMC method is its inability to distinguish changes in population structure from actual changes in population size (Mazet et al. 2015, 2016).
The use of information from the genomes of multiple individuals has resulted in improvements in the resolution and robustness of the inferences (Sheehan et al. 2013; Schiffels and Durbin 2014). The use of site frequency spectrum (SFS)-based information for demographic inference has been another popular approach (Gutenkunst et al. 2009; Liu and Fu 2015). However, the inferences from the SFS- and SMC-based methods are known to differ, especially when the number of genomes sampled is limited (Beichman et al. 2017). Hence, programs that incorporate information from both the SFS and the genomic distribution of the time to most recent common ancestor (TMRCA) can overcome some of these limitations (Terhorst et al. 2016; Palamara et al. 2018). However, these methods require population-level sampling of whole-genomic datasets (Zhou et al. 2017; Vijay et al. 2018; Cornejo et al. 2018).
These demographic inference methods are known to be affected by data quality, and efforts to reduce such effects are considered necessary (Schraiber and Akey 2015). Demographic history inference is affected by low-coverage regions, ascertainment bias, and hyperdiverse sequences (Li and Durbin 2011; Nadachowska-Brzyska et al. 2016). Repeat regions are prone to a high risk of assembly errors, collapsed segmental duplications, and mismapping of short reads. Challenges to the reliable genotyping of single-nucleotide polymorphisms (SNPs) within repeat regions have limited our understanding of the processes that determine genetic diversity in repeat regions. Erroneous variant calls contribute to altered effective population size (Ne) estimates. Overestimation of the genetic diversity due to variant calls resulting from incorrect read mapping and underestimation of the genetic diversity due to noncallable genomic regions can both bias the Ne estimates. Therefore, such bias-prone and repetitive genomic regions are generally masked before the analyses to overcome biased inferences (Foote et al. 2016). Such masking has important consequences for subsequent coalescent analysis, especially in plant and mammal genomes that tend to have a higher fraction of repetitive content than birds (Kapusta et al. 2017). Similar masking of polymorphisms in repeat regions has been done prior to other population genetic analysis in Populus tremula (Wang et al. 2018a) and Populus trichocarpa (Evans et al. 2014).
In this study, we intend to test the hypothesis that demographic inferences will be strongly and unpredictably affected by the inclusion or exclusion of the repetitive elements. Ne is measured as the within-species nucleotide diversity divided by four times the mutation rate (μ) (Charlesworth 2009). Inclusion of repeats leads to more SNPs being identified and contributes to higher estimates of nucleotide diversity and correspondingly higher estimates of Ne. Hence, we expect to see a decrease in the estimates of Ne after exclusion of repeats, as SNPs will be dropped from those regions and will lower the Ne inferred. The next objective is to investigate how different repeat classes affect the estimates of Ne and their underlying mechanisms. Populus trichocarpa has enough repeat abundance and multiple repeats that have accumulated post divergence in the congenerics (Lin et al. 2018). Furthermore, this plant has much longer contiguous regions occupied by some repeat types (Macas and Neumann 2007) and accumulate in low-recombination regions, which leads to non-uniform accumulation of polymorphisms (Natali et al. 2015). Due to these reasons, we expect to see species-specific trends in Populus trichocarpa. Hence, we use the high-quality genome (Pop_tri_v3) of the black cottonwood (Populus trichocarpa) as an example in this study. The robustness of our results is further verified using human genomic datasets. We use PSMC, multiple SMC (MSMC), SMC++, and the Stairway plot to quantify the effect of repeats on diverse demographic inference approaches.
Materials and methods
Inference of demographic history
Populus trichocarpa
Genome data processing
The published Pop_tri_v3 genome assembly of Populus trichocarpa was used as the reference genome for all of the analyses and was downloaded from NCBI along with repeat annotation. The percentage of Ns in the unmasked genome was found to be 2.5%. We searched the European Nucleotide Archive for genomic sequencing datasets and downloaded the SRA run# SRR6256359 with a mean coverage of ~42.54×. The raw read datasets were mapped to the corresponding unmasked genomes using the short-read aligner BWA-MEM (Li 2013) with default settings.
Variant calling was performed using samtools (Li et al. 2009) mpileup, with additional filtering options to avoid identifying polymorphisms from poorly mapped reads or other potential artifacts. The minimum mapping quality (-q) and base quality (-Q) for the alignment were both set at 20, and the coefficient of downgrading mapping quality (-C) was set at 50. These settings are recommended for BWA-mapped alignments on the PSMC GitHub page. The consensus sequence was called using BCFTOOLS (Li 2011), with the depth parameters for the vcf2fq command of vcfutils.pl decided based on the mean coverage of the dataset. The root-mean-square mapping quality (-q) was set at 25 to exclude sites below this quality score, and sites with a depth greater than twice or less than one-third of the mean depth were excluded. The resultant fastq file of heterozygous sites was converted to psmcfa format using the fq2psmcfa program for a bin size (-s) of 100.
PSMC
To decide the boundaries of the atomic intervals, PSMC (Li and Durbin 2011) needs optimization of the parameters -r, i.e., the ratio of θ (genetic diversity)/ρ (recombination rate), and -t, i.e., the maximum value of TMRCA. The optimization is considered appropriate when every atomic interval has at least ten or more recombination events after the 20th iteration of PSMC. For most of the organisms, a -p of “4 + 25 * 2 + 4 + 6” will give correct results with a sufficient number of recombination events. However, some organisms or genomes will not give enough recombination events with these settings; in such cases, we will have to look at the distribution of atomic intervals across free intervals. For example, if the -p parameter “4 + 25 * 2 + 4 + 6” is set, it has 64 atomic intervals distributed across 28 free intervals, i.e., 1 * 4 + 25 * 2 + 1 * 4 + 1 * 6 (written as free intervals * atomic intervals). Changing the distribution of atomic intervals across free intervals, e.g., “8 + 25 * 2 + 2 + 4” would be the first step to see if a sufficient number of recombination events is obtained. If not, the free intervals can be changed, i.e., “3 * 2 + 1 * 10 + 15 * 2 + 1 * 14 + 1 * 4” (written as free intervals * atomic intervals), to get the sufficient number of recombination events. Only after obtaining a sufficient number of recombination events is the -p parameter finalized. For the first run of PSMC, options were set as -t 5, -r 5, -p “4 + 25 * 2 + 4 + 6.” The output.psmc file was evaluated to see if a sufficient number of recombination events (5th column of the file) occurred in each atomic interval after 20 iterations. In the case of the Populus trichocarpa genome, the default settings were found to be appropriate. After obtaining the PSMC output, the previously published (Tuskan et al. 2006; Bai et al. 2018) mutation rate of 3.75e−08 per nucleotide per generation (2.5e−09 per nucleotide per year) and a generation time of 15 years were used to generate the scaled plot using the psmc_plot.pl script. For bootstrapping analyses, the psmcfa file was first split into equal lengths of 5 MB and was used for 100 runs of PSMC.
MSMC
We used the same Populus trichocarpa dataset for the MSMC (Schiffels and Durbin 2014) analyses. First, the mapped bam file was used to generate a VCF file using samtools mpileup with options -q 20 -Q 20 -C 50, followed by bcftools call, where the consensus sequence was called (i.e., -c), without indels (i.e., -V). Then, the mask files required for msmc were created using the bamCaller.py script of msmc-tools, where sites having less than mean coverage were not considered. These vcf and mask files were then used to produce an input file of msmc using the generate_multihetsep.py script of msmc-tools. The resultant text file was then used as input for the msmc program. A mutation rate of 3.75e−08 per nucleotide per generation was used (Tuskan et al. 2006; Bai et al. 2018).
Homo sapiens
PSMC
To test whether a high-quality dataset such as the 1000 genomes project differs in PSMC results before and after masking compared to the usual samtools-bcftools pipeline, we performed standard PSMC analyses with the same settings as explained above using CEU individual NA12878 (SRA accession # SRR9091899), and also extracted the data for the same individual from the 1000 genome vcf file provided at ftp://ftp.1000genomes.ebi.ac.uk/vol1/ftp/release/20130502/ and performed PSMC with default settings of -N 25 -t 15 -r 5 -p “4 + 25 * 2 + 4 + 6.” Only autosomal chromosomes were used for the analyses.
Processing of population-level re-sequencing dataset
We next used multiple haplotypes and additional demography inference methods for estimating the population histories using genomic data to evaluate the robustness of the different trends seen between masked and unmasked genomes. For this, we downloaded 15 individuals (30 haplotypes) of the CEU population of humans from the 1000 genome project dataset (Table S1). We mapped all these reads to the hg37d5 reference genome, which is used by the 1000 genome project for all of their analyses, using the bwa mem read mapper with default settings. This version of the reference genome includes decoy sequences to alleviate the problem of mismapping of repeat regions. The mapped reads were converted to binary and sorted according to coordinates using samtools. These sorted bam files were then used for further analyses.
Stairway plot
The Stairway plot uses information based on SFS to infer the population size histories. To obtain the SFS for the 15 samples, we used ANGSD for performing multi-sample genotype likelihood estimations, followed by the realSFS module to get unfolded SFS for these samples (Korneliussen et al. 2014). A BED file having coordinates for repeat regions was used to mask the reference fasta to drop these regions before estimating the repeat-masked SFS. We followed the Stairway plot manual to make the blueprint files used to execute the Stairway plot version 2.1.1 (Liu and Fu 2020).
SMC++
SMC++ is efficient for use in multiple haplotypes by combining the SFS information and taking advantage of the linkage disequilibrium in coalescent HMMs (Terhorst et al. 2016). SMC++ requires chromosome-wise multi-haplotype vcf files with optional mask files. We used the recommended MSMC pipeline as stated above for obtaining chromosome-based multi-individual vcf files and mask files. Mask files were generated for masked and unmasked output separately. Later, these files were used to run the SMC++ algorithm. First, the vcf files for each chromosome were converted to SMC input files using the VCF2SMC module with mask files to avoid artifactual and low-coverage sites. The obtained SMC input files for all of the chromosomes were then used to run the SMC++ estimate with options --knots 21 and time points between 1000 AND 5000,000, using a mutation rate of 2.5e−08 per nucleotide per generation. After getting the output, it was used for the SMC++ plot command to obtain the plotting data using a generation time of 25 years.
Repeat annotation
The unmasked genomes were analyzed to identify and annotate repetitive regions. For genome-wide identification of LTRs, the LTR-retriever (Ou and Jiang 2018) program was run using repeat libraries made by concatenating the LTR harvest (Ellinghaus et al. 2008) and LTR_finder v 1.0.6 (Xu and Wang 2007) output. The RepeatModeler program was used for the de novo identification of repeats. Both genome-wide LTR-retriever and RepeatModeler repeat libraries were concatenated and used as input to the RepeatMasker program. The tabulated output file of RepeatMasker was converted to BED format and used for further analyses.
Overlap of repeats with atomic intervals
Separate runs of variant calling (always using a BAM file generated by mapping reads to an unmasked genome) were carried out using the unmasked and masked genomes followed by PSMC analyses. PSMC was run with the -d option for both unmasked and masked datasets, and outputs were produced for a bin size of (-s flag) 100. The bin size was chosen based on the overall heterozygosity of the species. For each run of PSMC, the decode2bed.pl script was used to obtain details of the atomic interval assigned to specific genomic regions. Genomic regions associated with some of the atomic intervals were not output by the program and were not considered in the subsequent analysis. The prevalence of repeat regions in each atomic interval was assessed by intersecting the positions of the repeats with the positions of atomic intervals using BEDTools (Quinlan and Hall 2010). The genomic coordinates of heterozygous sites and the ratio of transitions (Ts) to transversions (Tv) were obtained using the hetlist command of seqtk (Li 2015). Subsequently, the repeat class-specific heterozygosity and Ts/Tv ratio in each atomic interval were calculated using the positions of repeat regions, decoded atomic intervals, and genome-wide list of heterozygote sites as arguments to BEDTools. One repeat class was unmasked at a time, keeping all of the other repeat classes masked before PSMC analyses to evaluate the effect of each repeat class on the PSMC.
Evaluating the impact of repeat classes on the inferences
We used the CallableLoci module of GATK v3.8 (McKenna et al. 2010) to assess the quality of data used, which showed that, in Populus trichocarpa, the variants in most of the repeat types are callable and some belong to the poorly mapped group (Fig. S1). The Kruskal–Wallis test was performed for each atomic interval in each repeat class, and it showed that the fraction of the genome covered by different callability classes (callable, poorly mapped, low coverage, no coverage, and N in the reference) was different. Further, the pairwise Wilcoxon test with Holm multiple testing correction showed that the callable fraction was significantly higher than for the other classes. Hence, poor callability alone cannot explain the impact of repeat classes. For the human 1000 genome dataset, the SFS did not change when different genotype-quality cutoffs were used (Fig. S2).
To know how the estimates of Ne are affected by repeats in some of the atomic intervals, we further investigated the distribution of heterozygous regions in each atomic interval. The heterozygosities for masked and unmasked output were calculated by intersecting each atomic interval region with a list of heterozygous sites using BEDTools. These estimates of heterozygosity of masked and unmasked output were then compared across atomic intervals. Similarly, the lengths of the regions in each atomic interval were determined, and the distribution of lengths of regions contributing to each atomic interval was compared between masked and unmasked genomes. To analyze whether the divergence of repeat types has any role in the distribution of the sequences across atomic intervals, we obtained the values of sequence divergence of each repeat region from RepeatMasker and compared the distribution of sequence divergence levels across atomic intervals.
Results
Repeat regions affect demographic inference
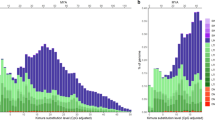
Based on the comparison of Ne trajectories inferred using masked and unmasked genomes, the magnitude of the contribution from repeat regions can be estimated. In the case of the poplar genome, the estimates of Ne for the masked genomes compared to the unmasked genomes were lower during the ancient time period, i.e., after ~1 MYA (mean difference in Ne across atomic intervals 48–64 = 0.63 × 104) and higher during recent times, i.e., 20–100 KYA (mean difference in Ne across atomic intervals 5–17 = 0.45 × 104, see Fig. 1). Interestingly, the magnitude of the difference in Ne estimates between the masked and unmasked genomes seems to be higher for atomic intervals with greater repeat abundance (Fig. S3). In all of our subsequent analyses, we used the PSMC method to demarcate the genomic regions that correspond to different coalescent histories. However, we show that repetitive regions of the genome bias the estimates of Ne similarly in both PSMC and MSMC using data from a single individual (Fig. 1).
PSMC curve for Populus trichocarpa after masking all of the repeat regions in the genome (blue line) and without masking (red line). The unmasked trajectory has dots indicating the fraction of repeats in an atomic interval; the larger the dot size, the more the repeat content in an atomic interval. Ne estimates during recent (20–100 KYA) and ancient (1–5 MYA) times show considerable differences between the two curves, demonstrating the effect of exclusion/inclusion of repeat sequences. The MSMC curve (lines with ♦) for the same single individual of Populus trichocarpa after masking all the repeat regions in the genome (blue line) and without masking (red line) is shown. The masking of repeat regions leads to lower estimates of effective population size (Ne) in the ancient period, in contrast to an increase in Ne estimates in recent times.
To understand whether these differences between masked and unmasked trajectories are consistent in other species with well-established genome and high-quality datasets, we performed the same analyses on humans (Homo sapiens). We observed that the human genome also shows a marked difference between these estimates, but these differences lie in different timescales, i.e., 100–800 KYA and after 1.5 MYA (Fig. 2). In both cases, the masked PSMC inference showed lower estimates of Ne compared to the unmasked inference. We observed a negligible difference between the Ne estimates of the samtools-based pipeline and GATK-based high-quality variant data-based analysis (Fig. 2). The difference between masked and unmasked genomes was much larger than the difference between variant-calling methods.
Masked and unmasked trajectories for all of the programs used are shown by blue and red lines, respectively (see Fig. S4 for separate panels of each method). PSMC curves for one human individual (NA12878) using samtools pipeline (lines with ▲) and using the 1000 genome dataset, i.e., GATK pipeline (lines with ■). Ne estimates during mid (100–800 KYA) and ancient (1.5–3 MYA) times showed a considerable difference, with masked inference showing lower estimates at both time points. However, samtools and 1000 genome project variant calls showed similar trajectories, depicting similar results irrespective of the methods used. SMC++ curves (lines with ●) of humans for 15 individuals (CEU population) from 1000 genomes project dataset are shown. Both masked and unmasked SMC++ curves do not align with each other at any time point, with the masked inference showing lower Ne estimates, similar to the PSMC inference. The Stairway plot of humans for the same 15 individuals also shows lower estimates in the masked (blue line) inference than in the unmasked (red line) inference throughout the timeline.
Multiple individual-based analyses are also affected by repeats
The Ne estimates from SMC++ and the Stairway plot show marked differences between masked and unmasked reference genomes. The same pattern of lower estimates in masked inference seen in PSMC is also found in these methods (Figs. 2 and S4). Hence, we see differences in masked and unmasked trajectories irrespective of the SNP calling pipeline, species, number of haplotypes, and the demography inference method. Despite the precautions taken while identifying variants, atomic intervals with repeats are disproportionately affected while estimating the Ne. To quantify this disproportionate effect, we evaluated the relationship between the repeat content in an atomic interval and the bias observed in the Ne estimate for that atomic interval. We found that the fraction of repeat content in a particular atomic interval was positively correlated (τ = 0.225, p value = 0.019, see Fig. S3) with the absolute difference between masked and unmasked genome-based estimates of Ne. Hence, regions with greater repeat abundance seem to affect the estimates of Ne in a particular atomic interval more strongly.
Repeat class-specific effect in Populus trichocarpa: LTR Gypsy as an example
Repeat class-specific bias in Ne estimates was assessed by including one repeat class at a time along with the non-repeat region (see Fig. 3). Estimates of Ne after inclusion of LTR Gypsy were intermediate between inferences obtained from masked and unmasked genomes during the ancient past, i.e., after 1 MYA (mean difference in Ne compared to the masked genome across atomic intervals 48–64 = 0.29 × 104). In contrast to this, the estimates showed a similar trend as for the unmasked genome during recent times, i.e., 20–100 KYA (mean difference in Ne compared to the masked genome across atomic intervals 5–17 = 0.44 × 104; see Fig. 4). The other repeat classes did not influence the estimates as much as LTRs and were closer to the inference from the masked genome (see Fig. 3). The robustness of the Ne estimates was assessed based on the variability (quantified as CV) between bootstrap replicates using the non-repeat fraction of the genome along with each repeat class. The CV was heterogeneous between time intervals and was relatively higher in recent times (see Fig. 4). The robustness of the estimated values of Ne was comparable between the unmasked (mean of the CV across atomic intervals = 0.04687) and masked (mean of the CV across atomic intervals = 0.047) genomes.
PSMC curves for Populus trichocarpa, with masked (blue) and unmasked (red) genomes. Change in trajectory can be seen with each class of repeat along with the masked genome. Upon including each repeat class and masking other repeat classes show changes specific to each repeat class. The inclusion of LTR Gypsy shows a distinctly different trajectory similar to the unmasked genome during ~20–100 KYA, which shows that the inclusion of LTR Gypsy strongly influences the trajectory in recent times.
PSMC curves for Populus trichocarpa showing the robustness of changes due to masking of repeats. Masked (blue) and unmasked (red) show completely distinctive trajectories, whereas unmasking only LTR Gypsy repeat class (pink) also shows a marked difference. The second y-axis (on the right) shows the coefficient of variation (CV) across the bootstraps for all of the repeat classes. Therefore, changes in Ne due to repeats are robust to bootstrap replications.
Repeat abundance and class vary by atomic interval
In all atomic intervals, the non-repeat fraction was found to be the most abundant (see Fig. 5 (Populus trichocarpa) and Fig. S5 (human)) and suggests that estimates of Ne in all of the atomic intervals are based largely on non-repeat regions. Among the repeat classes in Populus trichocarpa, LTR Gypsy had the highest abundance in most atomic intervals. The extremely high abundance of LTR Gypsy repeats in the first few atomic intervals could have led to the drastic change in the Ne trajectory during recent times (i.e., 20–100 KYA) after the inclusion of LTR Gypsy repeats. LTRs and RC-Helitron have a high abundance at the genome-wide level (see Fig. 6) and have a more substantial influence on Ne estimates (see Fig. 3). In contrast to Populus trichocarpa, in humans, LINEs, SINEs, and LTRs contribute the most (Fig. S6).
The bar plot shows the contribution of various repeat classes to each atomic interval. Non-repeat regions (Sky-blue) are generally most abundant across all intervals, whereas some repeat classes such as LTRs have considerable abundance in some atomic intervals (e.g., atomic intervals 5 and 24). Repeat families such as LTR Gypsy, LTR Copia, and RC Helitron showed higher abundance than other repeat classes.
The bar plot shows the contribution of various repeat classes (percentage of whole-genomic length) to each atomic interval. LTR Gypsy contributed to ~2% in the atomic intervals spanning recent and ancient times, which is one of the major contributing factors to the change in Ne trajectory. Some atomic intervals, such as 5, 10, 12, 24, etc., span a tiny genomic fraction.
Inclusion of repeats results in re-assignment of genomic regions among atomic intervals
Genomic regions assigned to atomic intervals that correspond to older time points have higher heterozygosity levels than recent time points (Fig. S7). The mean heterozygosity is positively correlated (Kendall’s rank correlation test, Fig. S7A: Populus trichocarpa, tau = 0.77, p value = 7.34e−16 , Fig. S7B: Human, tau = 0.93, p value < 2.2e−16 ) with the atomic intervals. Upon masking of repeat regions, a large number of SNPs that contributed to short stretches of high heterozygosity are removed. Consequently, the heterozygosity of most (except for four) of the atomic intervals is reduced after masking (Fig. S7). However, certain atomic intervals show species-specific deviations. For instance, in Populus trichocarpa, atomic interval five consists of mostly RC Helitron and LTR Gypsy repeats with minimal non-repeat contribution (see Fig. 5). The Ne estimate of this atomic interval shows a large increase upon masking (Figs. 3 and 4). Atomic interval 24 has substantial non-repeat content, and its Ne estimates are not as affected as atomic interval five. Hence, the impact of repeats on the inference of demographic history largely affects atomic intervals that lack non-repeat regions.
Genomic regions assigned to atomic intervals that correspond to recent time points have longer lengths than those assigned to older time points (Fig. S8). The mean length of atomic intervals is negatively correlated (Kendall’s rank correlation test, Fig. S7A: Populus trichocarpa, tau = −0.80, p value < 2.2e−16 , Fig. S7A: Human, tau = −0.83, p value < 2.2e−16) with the atomic intervals. Runs of homozygosity along the genome are affected by changes in heterozygosity caused by the masking of repeat regions. Therefore, the lengths of genomic regions that contribute to the atomic intervals are affected. In some cases, the lengths of genomic regions assigned to the atomic interval increase upon masking (Fig. S8; a significant increase is denoted by a red star). This increase in lengths of genomic regions is due to their re-assignment among atomic intervals. Although the lengths of genomic regions assigned to some atomic intervals increase upon masking, the total genomic length used by the PSMC decreases due to the masking of repeats. Hence, some of the atomic intervals will show a contrasting pattern of decrease in lengths after masking (Fig. S8; significant decrease denoted by blue stars *). The redistribution of lengths occurs in both Populus trichocarpa and humans. However, many atomic intervals show an increase (25 atomic intervals) in length distributions than a decrease (15 atomic intervals) in Populus trichocarpa. In contrast to Populus trichocarpa, many atomic intervals show a decrease (18 atomic intervals) in length distribution than an increase (15 atomic intervals) in humans. This re-assignment of genomic regions is a consequence of masking repetitive elements.
Each of the repeat classes independently shows a trend of increase in heterozygosity, similar to the non-repeat regions (see Figs. 7 and S9). The comparable estimates of heterozygosity between repeat and non-repeat regions in each atomic interval suggest that the heterozygous sites identified in repeat regions are not merely variant-calling artifacts. The ratio (Ts/Tv) of the number of transitions (Ts) to the number of transversions (Tv) has been used to evaluate the accuracy of variant call sets (Wang et al. 2015). Regions of the genome with artifactual variant calls would have a Ts/Tv ratio very different from the genomic average. Hence, as an additional validation of the variants identified within repeat regions, we calculated the Ts/Tv ratio for each repeat class by the atomic interval. While the estimates of heterozygosity (depicted by the black line in Figs. 7 and S9) showed an increasing trend toward older atomic intervals, we found that the Ts/Tv ratio (depicted by the red line in Figs. 7 and S9) did not show a consistently discernible trend (see Figs. 7 and S9). Simple repeats, RC Helitron, DNA, DNA hAT tag1, LINE L1, and LTR Caulimovirus repeat classes show a weak trend of increasing Ts/Tv ratio with increasing heterozygosity. However, the largely similar estimates of the Ts/Tv ratio in repeat and non-repeat regions suggest that the heterozygous sites identified in repeat regions are truly polymorphic. The Ts/Tv ratio of some atomic intervals in specific repeat classes do show elevated values and potentially contain numerous erroneous variant calls. However, despite such artifacts, we see that the repeat regions have a consistent coalescent history signal that matches the inference from non-repeat regions.
Change in heterozygosity and corresponding Ts/Tv ratio across atomic intervals in different repeat classes of Populus trichocarpa PSMC (see Fig. S9 for all of the repeat classes). The heterozygosity (black line with left y-axis) increases with atomic intervals (x-axis). In contrast, the Ts/Tv ratio (red line with right y-axis) does not follow this trend for most of the repeat classes. Some of the repeat classes do show elevated Ts/Tv ratios, indicating the possibility of erroneous variants.
Multiple copies of repeats lead to incorrect mapping of reads, which results in erroneous variant calls. Only a few of these repeat copies tend to be present in the genome assembly. The other copies, which have not been assembled in the genome, will end up getting mapped to the copies that have been assembled. Repeat classes with multiple copies of the repeat at varying levels of sequence divergence can artifactually increase the heterozygosity through incorrect mapping. We evaluated the level of sequence divergence for each repeat class with respect to the atomic intervals in which they occurred (Fig. S10). The percent sequence divergence of the repeat did not show any consistent trend across atomic intervals. While most of the atomic intervals showed a wide distribution of percent divergence for the LINE L1 element, atomic intervals 1, 17, and 48 had low levels of variance in percent divergence (Fig. S10G). Satellite repeats had an overall high percent divergence >25 (Fig. S10N), and simple repeats had an average percent divergence <15 (Fig. S10O). The distribution of repeat classes and their percent divergences among atomic intervals cannot explain the changes in Ne observed after masking repeat regions. The distribution of repeat regions along the genome is not random and is known to vary with the recombination rate. Not surprisingly, we found that the repeat content in Populus trichocarpa was negatively correlated (Kendall’s rank correlation test; p value < 0.01) with the Ne (Figs. 8 and S11). Interestingly, the observed negative correlation between repeat content and Ne estimates could be seen for all of the repeat classes (except for LTR Gypsy p value > 0.01).
Repeat content across atomic intervals in Populus trichocarpa PSMC showed a consistently negative correlation (Kendall’s rank correlation test) with the Ne estimated from the masked genome. Each panel of the figure represents a different repeat class (see Fig. S11 for all of the repeat classes). Significance levels are indicated using symbols: *p < 0.1, **p < 0.05, ***p < 0.01.
Discussion
Our results demonstrate that the inclusion of repeat regions does affect the demographic inference. However, this effect is not the same in all species. The heterogeneity in the mutational properties of different repeat classes, their genomic distributions, and abundance are ignored as these are challenging to model and are species-specific. Most of the demographic inference methods have been evaluated and verified using human genomic datasets (Li and Durbin 2011; Terhorst et al. 2016; Liu and Fu 2020). Although the effect of repeats has never been directly evaluated, the contribution of false heterozygotes resulting from segmental duplications has been assessed by simulating long hypermutated regions. Such long hypermutated regions lead to excessively large population size estimates in the ancient time period (Li and Durbin 2011).
In contrast to these simulated scenarios, repeat regions with varying lengths and mutational properties are prevalent in the genome. We see that in the human genome inclusion of repeat regions inflates the estimates of effective population size in all atomic intervals (see Figs. 2 and S4). We compared the demographic histories inferred from masked and unmasked genomes of one individual each of European (CEU) and Yoruban (YRB) descent using PSMC (see Fig. S12). Similar to the pattern seen in the CEU individual, we see that in the YRB individual, the estimates of Ne are inflated upon the inclusion of repeat regions. We also evaluated the effect of the inclusion of SINE repeats with the masked genome in CEU and YRB individuals. In all of the atomic intervals, we see that while the magnitude of Ne estimates is changed, the trajectories are not altered by the inclusion or exclusion of repeats. Overall, human genomic datasets are minimally affected by repeat regions, and comparative inferences are reliable. However, the effect of repeats is not the same in all species.
The example plant dataset (Populus trichocarpa) used by us demonstrates this lineage-specific effect very clearly. Such lineage-specific effects are dependent on the abundance and genomic distribution of repeats. For instance, the LTR content might differ even between closely related species (Zhang et al. 2020) and can heavily influence the results of coalescent inference. Even if all repeat regions are masked before analysis, heterogeneity in the quality of repeat annotation between species might result in the inclusion of specific repeats in the genome of one species while excluding it from the genome of another. The demographic trajectories inferred for Populus trichocarpa in our study are in concordance with previously published reports (Bai et al. 2018; Wang et al. 2020; Chen et al. 2020).
Impact of LTR Gypsy repeats in Populus trichocarpa
The germline mutation rate varies by repeat class and is mostly higher than that of non-repeat regions (Ellegren 2000; Ellegren et al. 2003). However, precise estimates of mutation rate are still scarce and are not available for specific genomic elements (Conrad et al. 2011; Keightley et al. 2014). The abundance of repeats and their mutational properties determine the overall distribution of polymorphisms used for demographic inference. Another aspect of polymorphisms contributed by repeats is determined by the length and genomic location of the repeats. Repeat classes such as LTRs and other transposons tend to be long and can elevate the genetic diversity of continuous stretches of the genome (Neumann et al. 2003). Among LTRs, the LTR Gypsy type of repeats is found preferentially in centromeric regions rather than being randomly distributed across the genome (Natali et al. 2015). Each species has a distinct genomic prevalence of repeats determined by factors such as recombination landscape, the efficacy of selection, and repeat suppression machinery (Wang et al. 2018b). Hence, multiple factors determine the genetic diversity within repeat regions and will affect the inference of Ne.
In Populus trichocarpa, the inclusion of LTR Gypsy showed marked differences in Ne estimates compared to all other types of repeats. Retroelements comprise 176 MBp of the 550 MBp (~32%) genome of Populus trichocarpa. LTRs are the most abundant type of repeat, and the subtype LTR Gypsy is most prevalent in the genome (Tuskan et al. 2006). Gypsy elements are highly redundant due to their high numbers of active and remnant copies being distributed across the genome, with the longest sequence lengths found among all repeats. LTR Gypsy is mostly localized in putative centromeric regions, with suppressed recombination leading to a high abundance of long repeat sequences (Neumann et al. 2011). LTR Gypsy is also more prone to accumulating mutations, leading to an increase in neutral polymorphisms of the genome (Natali et al. 2015). All these unique properties of LTR Gypsy might be responsible for its essential role in the evolution of this plant, as some of these could be species-specific repeats (Ma et al. 2017). For example, Ogre elements are the longest and most recently accumulated LTRs found in Populus trichocarpa (Macas and Neumann 2007). Such recently accumulated repeats are responsible for shaping the genomic landscape, as shown in another Salicaceae species, Populus euphratica (Zhang et al. 2020). Extreme examples include the change in genome size due to repeat accumulation seen in Gossypium (Hawkins et al. 2006) and conifers (Nystedt et al. 2013).
Implications of recombination rate variation
Inference of demographic history from low- vs. high-recombination rate regions of the genome using PSMC in the nematode Caenorhabditis elegans showed distinct patterns of change in population size over time (Thomas et al. 2015). These differing trajectories are thought to be the effect of selection on the highly linked regions of the genome caused by high levels of inbreeding. Specifically, genomic regions with low recombination rates (that also have reduced levels of nucleotide polymorphism) have lower values of Ne estimates compared to high-recombination rate regions. However, closely related species can have distinctive repeat abundance landscapes.
Comparison of demographic trajectories across diverse species of birds (Nadachowska-Brzyska et al. 2015) may be rationalized by the conserved karyotype, low repeat abundance, and a broadly conserved recombination landscape (Singhal et al. 2015; Kapusta et al. 2017). While the recombination rate landscape is conserved across birds, the same is not valid for all taxa. Differences in the recombination rate landscape and its consequences on repeat accumulation also have important implications for comparing demographic histories between species.
Interestingly, the abundance of different types of transposable elements (TEs) exhibits varying levels of correlation with the recombination rate (Kent et al. 2017). This association between TEs and the recombination rate is potentially a result of the co-evolutionary dynamics combined with species-specific idiosyncrasies. Often, TE abundance and recombination rate are negatively correlated. Hence, we reasoned that differences in the abundance of repeat regions in different atomic intervals might correspond to different recombination rates. Consistent with this expectation, the atomic interval-specific repeat abundance for several repeat classes showed a negative correlation with the Ne of that atomic interval (Figs. 8 and S11). However, the correlations were relatively weak and might reflect the imprecise demarcation of the genome into atomic intervals (Gattepaille et al. 2016).
Recommendations for dealing with repeats during coalescent inference
Overall, we see that the trajectories obtained using the masked and unmasked genomes are mainly comparable. However, the absolute estimates of Ne show considerable variability. Previous studies have completely masked repeat regions before estimating the demographic histories. While this strategy is quick and easy to use, the contrasting demographic histories could merely be the result of differing repeat annotations. We suggest that when dealing with a newly sequenced genome, novel repeat classes should be identified and annotated using de novo repeat-finding programs. It needs to be ensured that the repeat annotations of the species/genome assemblies under consideration are of similar quality and are based on the same repeat annotation pipeline.
SNPs in repeat regions can be artifactual and are best avoided through masking. However, in species whose genomes contain a substantial fraction (>30%) of repeats, the non-repeat regions might not have sufficient information about the demographic history. Previous studies have suggested that at least 70% of the genome should have adequate coverage and have good-quality variant calls to obtain reliable demographic inferences (Nadachowska-Brzyska et al. 2015). Our analysis of various repeat classes in black cottonwood and humans suggests that many repeat classes have recorded reliable demographic histories matching those inferred from non-repeat regions. Hence, it is possible to use these repeat regions while performing demographic inference. In species with >30% repeat content, we suggest evaluating the effect of each repeat class by including one repeat class at a time with the non-repeat region (as shown in Fig. 3). We have implemented all these analyses in a ready-to-use pipeline that inputs the BAM alignment and coordinates of repeat regions and provides as output concise plots showing the effects of repeat classes on demographic inference and their abundances across atomic intervals. Based on the deviation of inferences of each repeat class from those of the non-repeat regions, only those repeat classes that match the trajectories of non-repeat regions may be included. This strategy of masking only certain repeat classes based on their deviation from non-repeat classes can be further verified by evaluating the atomic interval-specific changes in heterozygosity caused by specific repeat classes (as done for Populus trichocarpa in Fig. S7A).
Development of new methods and future directions
The recent use of noncoding CpG transitions for inferring prehistoric human demography (Liu 2020) reveals new avenues for methodological advances that focus on specific genomic sites with distinct mutational properties (Kong et al. 2012). Genomic context determined by local sequence content, epigenomic properties, the timing of DNA replication, and recombination rate is all thought to be correlated with the rate of mutation (Schaibley et al. 2013; Carlson et al. 2018). A better understanding of repeat class-specific mutation rates might allow for scaling each repeat type with an appropriate mutation rate. Each repeat class can then serve as a window into the demographic history of different time spans. We envisage that greater accuracy in variant calling within repeat regions will eventually be possible with long-read sequencing methods that will overcome the limitations of mapping artifacts used in short-read sequencing methods. These methodological advances will allow better reconstruction of the genomic sequence in structural variation and SNPs. Accurate identification of such genetic variation may provide greater resolving power while making coalescent inferences.
Conclusion
We have shown that the inclusion of repeat regions of the genome influences the demographic inferences made using state-of-the-art tools such as PSMC, MSMC, SMC++, and the Stairway plot. Most repeat classes can provide inferences consistent with those obtained from non-repeat regions and can be a viable source of demographic history. Species-specific repeat accumulation patterns can result in idiosyncratic effects on the inference of demographic history. The abundance of various repeat classes, their mutational properties, genomic distribution, and other genome dynamics will determine the impact of the repeats on the inference of demographic history. Our analysis of repeat regions is of particular relevance as the quality of genome assemblies continues to improve with use of long-read sequencing technologies that can assemble repeat regions correctly. We speculate that methodological advances may allow the use of repeat class-specific mutation rates for reliable estimation of demographic histories at particular time spans. Finally, we urge the cautious use of variants located within repeat regions while performing demographic analysis and suggest evaluation of the robustness of the results using different repeat classes. The ready-to-use scripts provided with this manuscript will allow investigation of the repeat-induced effects on demographic inference in any species suitable for PSMC analysis.
Data availability
Data are archived at https://github.com/Ajinkya-IISERB/CoalRep/code.
Code availability
Code and the pipeline are archived at https://github.com/Ajinkya-IISERB/CoalRep.
References
Arkhipova IR (2018) Neutral theory, transposable elements, and eukaryotic genome evolution. Mol Biol Evol 35:1332
Bai WN, Yan PC, Zhang BW, Woeste KE, Lin K, Zhang DY (2018) Demographically idiosyncratic responses to climate change and rapid Pleistocene diversification of the walnut genus Juglans (Juglandaceae) revealed by whole-genome sequences. New Phytol 217:1726–1736
Bashir A, Ye C, Price AL, Bafna V (2005) Orthologous repeats and mammalian phylogenetic inference. Genome Res 15:998–1006
Behar DM, Thomas MG, Skorecki K, Hammer MF, Bulygina E, Rosengarten D et al. (2003) Multiple origins of Ashkenazi Levites: Y chromosome evidence for both Near Eastern and European ancestries. Am J Hum Genet 73:768–79
Beichman AC, Phung TN, Lohmueller KE (2017) Comparison of single genome and allele frequency data reveals discordant demographic histories. G3 7:3605–3620
Blumenstiel JP, Chen X, He M, Bergman CM (2014) An age-of-allele test of neutrality for transposable element insertions. Genetics 196:523–538
Bourgeois Y, Ruggiero RP, Hariyani I, Boissinot S (2020) Disentangling the determinants of transposable elements dynamics in vertebrate genomes using empirical evidences and simulations. PLoS Genet 16:e1009082
Cahill JA, Soares AER, Green RE, Shapiro B (2016) Inferring species divergence times using pairwise sequential markovian coalescent modelling and low-coverage genomic data. Philos Trans R Soc B Biol Sci 371:20150138
Carlson J, Locke AE, Flickinger M, Zawistowski M, Levy S, Myers RM et al. (2018) Extremely rare variants reveal patterns of germline mutation rate heterogeneity in humans. Nat Commun 9:3753
Charlesworth B (2009) Fundamental concepts in genetics: effective population size and patterns of molecular evolution and variation. Nat Rev Genet 10:195–205
Chen Z, Ai F, Zhang J, Ma X, Yang W, Wang W et al. (2020) Survival in the tropics despite isolation, inbreeding and asexual reproduction: insights from the genome of the world’s southernmost poplar (Populus ilicifolia). Plant J 103:430–442
Conrad DF, Keebler JEM, Depristo MA, Lindsay SJ, Zhang Y, Casals F et al. (2011) Variation in genome-wide mutation rates within and between human families. Nat Genet 43:712–714
Cornejo OE, Yee M-C, Dominguez V, Andrews M, Sockell A, Strandberg E et al. (2018) Population genomic analyses of the chocolate tree, Theobroma cacao L., provide insights into its domestication process. Commun Biol 1:167
Dodsworth S, Chase MW, Kelly LJ, Leitch IJ, Macas J, Novák P et al. (2015) Genomic repeat abundances contain phylogenetic signal. Syst Biol 64:112–26
Dong F, Kuo H-C, Chen G-L, Wu F, Shan P-F, Wang J et al. (2021) Population genomic, climatic and anthropogenic evidence suggest the role of human forces in endangerment of green peafowl (Pavo muticus). Proc R Soc B Biol Sci 288:20210073. https://doi.org/10.1098/rspb.2021.0073
Ellegren H (2000) Microsatellite mutations in the germline: implications for evolutionary inference. Trends Genet 16:551–558
Ellegren H, Smith NGC, Webster MT (2003) Mutation rate variation in the mammalian genome. Curr Opin Genet Dev 13:562–568
Ellinghaus D, Kurtz S, Willhoeft U (2008) LTRharvest, an efficient and flexible software for de novo detection of LTR retrotransposons. BMC Bioinform 9:18
Evans LM, Slavov GT, Rodgers-Melnick E, Martin J, Ranjan P, Muchero W et al. (2014) Population genomics of Populus trichocarpa identifies signatures of selection and adaptive trait associations. Nat Genet 46:1089–1096
Feigin CY, Newton AH, Doronina L, Schmitz J, Hipsley CA, Mitchell KJ et al. (2018) Genome of the Tasmanian tiger provides insights into the evolution and demography of an extinct marsupial carnivore. Nat Ecol Evol 2:182–192
Fitak RR, Mohandesan E, Corander J, Burger PA (2016) The de novo genome assembly and annotation of a female domestic dromedary of North African origin. Mol Ecol Resour 16:314–24
Foote AD, Vijay N, Ávila-Arcos MC, Baird RW, Durban JW, Fumagalli M et al. (2016) Genome-culture coevolution promotes rapid divergence of killer whale ecotypes. Nat Commun 7:11693
Freedman AH, Gronau I, Schweizer RM, Ortega-Del Vecchyo D, Han E, Silva PM et al. (2014) Genome sequencing highlights the dynamic early history of dogs. PLoS Genet 10:e1004016
Gattepaille L, Günther T, Jakobsson M (2016) Inferring past effective population size from distributions of coalescent times. Genetics 204:1191–1206
Gutenkunst RN, Hernandez RD, Williamson SH, Bustamante CD (2009) Inferring the joint demographic history of multiple populations from multidimensional SNP frequency data. PLoS Genet 5:e1000695
Hawkins JS, Kim HR, Nason JD, Wing RA, Wendel JF (2006) Differential lineage-specific amplification of transposable elements is responsible for genome size variation in Gossypium. Genome Res 16:1252–1261
Hecht LBB, Thompson PC, Rosenthal BM (2018) Comparative demography elucidates the longevity of parasitic and symbiotic relationships. In: Proceedings of the Royal Society B: Biological Sciences, vol 285. Royal Society Publishing, p 20181032
Holliday JA, Zhou L, Bawa R, Zhang M, Oubida RW (2016) Evidence for extensive parallelism but divergent genomic architecture of adaptation along altitudinal and latitudinal gradients in Populus trichocarpa. New Phytol 209:1240–51
Hung C-M, Shaner P-JL, Zink RM, Liu W-C, Chu T-C, Huang W-S et al. (2014) Drastic population fluctuations explain the rapid extinction of the passenger pigeon. Proc Natl Acad Sci U S A 111:10636–41
Ibarra-Laclette E, Lyons E, Hernández-Guzmán G, Pérez-Torres CA, Carretero-Paulet L, Chang T-H et al. (2013) Architecture and evolution of a minute plant genome. Nature 498:94–98
Jaiswal SK, Gupta A, Saxena R, Prasoodanan VPK, Sharma AK, Mittal P et al. (2018) Genome sequence of peacock reveals the peculiar case of a glittering bird. Front Genet 9:392
Jensen-Seaman MI, Furey TS, Payseur BA, Lu Y, Roskin KM, Chen C-F et al. (2004) Comparative recombination rates in the rat, mouse, and human genomes. Genome Res 14:528–38
Kapusta A, Suh A, Feschotte C (2017) Dynamics of genome size evolution in birds and mammals. Proc Natl Acad Sci U S A 114:E1460–E1469
Keightley PD, Ness RW, Halligan DL, Haddrill PR (2014) Estimation of the spontaneous mutation rate per nucleotide site in a Drosophila melanogaster full-sib family. Genetics 196:313–320
Kent TV, Uzunović J, Wright SI (2017) Coevolution between transposable elements and recombination. Philos Trans R Soc B Biol Sci 372:20160458
Kofler R, Nolte V, Schlötterer C (2015) Tempo and mode of transposable element activity in drosophila. PLoS Genet 11:e1005406
Kong A, Frigge ML, Masson G, Besenbacher S, Sulem P, Magnusson G et al. (2012) Rate of de novo mutations and the importance of father’s age to disease risk. Nature 488:471–475
Koonin EV (2009) Evolution of genome architecture. Int J Biochem Cell Biol 41:298–306
Korneliussen TS, Albrechtsen A, Nielsen R (2014) ANGSD: analysis of next generation sequencing data. BMC Bioinform 15:356
Li H (2011) A statistical framework for SNP calling, mutation discovery, association mapping and population genetical parameter estimation from sequencing data. Bioinformatics 27:2987–2993
Li H (2013) Aligning sequence reads, clone sequences and assembly contigs with BWA-MEM. arxiv.
Li H (2015) Seqtk: toolkit for processing sequences in FASTA/Q formats. GitHub.
Li H, Durbin R (2011) Inference of human population history from individual whole-genome sequences. Nature 475:493–496
Li H, Handsaker B, Wysoker A, Fennell T, Ruan J, Homer N et al. (2009) The sequence Alignment/Map format and SAMtools. Bioinformatics 25:2078–2079
Lin YC, Wang J, Delhomme N, Schiffthaler B, Sundström G, Zuccolo A et al. (2018) Functional and evolutionary genomic inferences in Populus through genome and population sequencing of American and European aspen. Proc Natl Acad Sci U S A 115:E10970–E10978
Liu X (2020) Human prehistoric demography revealed by the polymorphic pattern of CpG transitions. Mol Biol Evol 37:2691–2698
Liu X, Fu Y-X (2015) Exploring population size changes using SNP frequency spectra. Nat Genet 47:555–559
Liu X, Fu YX (2020) Stairway Plot 2: demographic history inference with folded SNP frequency spectra. Genome Biol 21:280
Lockton S, Ross-Ibarra J, Gaut BS (2008) Demography and weak selection drive patterns of transposable element diversity in natural populations of Arabidopsis lyrata. Proc Natl Acad Sci U S A 105:13965–13970
Lord E, Dussex N, Kierczak M, Díez-del-Molino D, Ryder OA, Stanton DWG et al. (2020) Pre-extinction demographic stability and genomic signatures of adaptation in the woolly rhinoceros. Curr Biol 30:3871–3879.e7
Ma T, Wang K, Hu Q, Xi Z, Wan D, Wang Q et al. (2017) Ancient polymorphisms and divergence hitchhiking contribute to genomic islands of divergence within a poplar species complex. Proc Natl Acad Sci USA 115:E236–E243
Macas J, Neumann P (2007) Ogre elements—a distinct group of plant Ty3/gypsy-like retrotransposons. Gene 390:108–116
Martin HC, Batty EM, Hussin J, Westall P, Daish T, Kolomyjec S et al. (2018) Insights into platypus population structure and history from whole-genome sequencing. Mol Biol Evol 35:1238–1252
Mays HL, Hung CM, Shaner PJ, Denvir J, Justice M, Yang SF et al. (2018) Genomic analysis of demographic history and ecological niche modeling in the endangered Sumatran rhinoceros Dicerorhinus sumatrensis. Curr Biol 28:70–76.e4
Mazet O, Rodríguez W, Chikhi L (2015) Demographic inference using genetic data from a single individual: Separating population size variation from population structure. Theor Popul Biol 104:46–58
Mazet O, Rodriguez W, Grusea S, Boitard S, Chikhi L (2016) On the importance of being structured: instantaneous coalescence rates and human evolution-lessons for ancestral population size inference?. Heredity 116:362–371
McKenna A, Hanna M, Banks E, Sivachenko A, Cibulskis K, Kernytsky A et al. (2010) The genome analysis toolkit: a MapReduce framework for analyzing next-generation DNA sequencing data. Genome Res 20:1297–1303
McVean GA, Cardin NJ (2005) Approximating the coalescent with recombination. Philos Trans R Soc B Biol Sci 360:1387–1393
Nadachowska-Brzyska K, Burri R, Olason PI, Kawakami T, Smeds L, Ellegren H (2013) Demographic divergence history of pied flycatcher and collared flycatcher inferred from whole-genome re-sequencing data. PLoS Genet 9:e1003942
Nadachowska-Brzyska K, Burri R, Smeds L, Ellegren H (2016) PSMC analysis of effective population sizes in molecular ecology and its application to black-and-white Ficedula flycatchers. Mol Ecol 25:1058–1072
Nadachowska-Brzyska K, Li C, Smeds L, Zhang G, Ellegren H (2015) Temporal dynamics of avian populations during pleistocene revealed by whole-genome sequences. Curr Biol 25:1375–1380
Natali L, Cossu RM, Mascagni F, Giordani T, Cavallini A (2015) A survey of Gypsy and Copia LTR-retrotransposon superfamilies and lineages and their distinct dynamics in the Populus trichocarpa (L.) genome. Tree Genet Genomes 11:1–13.
Natesh M, Vinay KL, Ghosh S, Jayapal R, Mukherjee S, Vijay N et al. (2020) Contrasting trends of population size change for two Eurasian owlet species—Athene brama and Glaucidium radiatum From South Asia over the late quaternary. Front Ecol Evol 8:469
Neumann P, Navrátilová A, Koblížková A, Kejnovsk E, Hřibová E, Hobza R et al. (2011) Plant centromeric retrotransposons: a structural and cytogenetic perspective. Mob DNA 2:4
Neumann P, Požárková D, Macas J (2003) Highly abundant pea LTR retrotransposon Ogre is constitutively transcribed and partially spliced. Plant Mol Biol 53:399–410
Nystedt B, Street NR, Wetterbom A, Zuccolo A, Lin YC, Scofield DG et al. (2013) The Norway spruce genome sequence and conifer genome evolution. Nature 497:579–584
Orlando L, Ginolhac A, Zhang G, Froese D, Albrechtsen A, Stiller M et al. (2013) Recalibrating Equus evolution using the genome sequence of an early Middle Pleistocene horse. Nature 499:74–78
Ou S, Jiang N (2018) LTR_retriever: a highly accurate and sensitive program for identification of long terminal repeat retrotransposons. Plant Physiol 176:1410–1422
Palamara PF, Terhorst J, Song YS, Price AL (2018) High-throughput inference of pairwise coalescence times identifies signals of selection and enriched disease heritability. Nat Genet 50:1311–1317
Palkopoulou E, Mallick S, Skoglund P, Enk J, Rohland N, Li H et al. (2015) Complete genomes reveal signatures of demographic and genetic declines in the woolly mammoth. Curr Biol 25:1395–1400
Pan J, Sasaki M, Kniewel R, Murakami H, Blitzblau HG, Tischfield SE et al. (2011) A hierarchical combination of factors shapes the genome-wide topography of yeast meiotic recombination initiation. Cell 144:719–731
Patil AB, Shinde SS, Raghavendra S, Satish BN, Kushalappa CG, Vijay N (2021) The genome sequence of Mesua ferrea and comparative demographic histories of forest trees. Gene 769:145214
Patton AH, Margres MJ, Stahlke AR, Hendricks S, Lewallen K, Hamede RK et al. (2019) Contemporary demographic reconstruction methods are robust to genome assembly quality: a case study in Tasmanian devils. Mol Biol Evol 36:2906–2921
Prado-Martinez J, Sudmant PH, Kidd JM, Li H, Kelley JL, Lorente-Galdos B et al. (2013) Great ape genetic diversity and population history. Nature 499:471–5
Project AG, Chanderbali AS, Der JP, Lan T, Walts B, Albert VA, et al. (2013) The Amborella genome and the evolution of flowering plants. Science 342:1241089
Quinlan AR, Hall IM (2010) BEDTools: a flexible suite of utilities for comparing genomic features. Bioinformatics 26:841–842
Riba A, Fumagalli MR, Caselle M, Osella M (2020) A model-driven quantitative analysis of retrotransposon distributions in the human genome. Genome Biol Evol 12:2045–2059
Rogers RL, Slatkin M (2017) Excess of genomic defects in a woolly mammoth on Wrangel island. PLoS Genet 13:e1006601
Ruggiero RP, Bourgeois Y, Boissinot S (2017) LINE insertion polymorphisms are abundant but at low frequencies across populations of Anolis carolinensis. Front Genet 8:44
Schaibley VM, Zawistowski M, Wegmann D, Ehm MG, Nelson MR, St Jean PL et al. (2013) The influence of genomic context on mutation patterns in the human genome inferred from rare variants. Genome Res 23:1974–84
Schiffels S, Durbin R (2014) Inferring human population size and separation history from multiple genome sequences. Nat Genet 46:919–925
Schraiber JG, Akey JM (2015) Methods and models for unravelling human evolutionary history. Nat Rev Genet 16:727–740
Sheehan S, Harris K, Song YS (2013) Estimating variable effective population sizes from multiple genomes: a sequentially markov conditional sampling distribution approach. Genetics 194:647–62
Singhal S, Leffler EM, Sannareddy K, Turner I, Venn O, Hooper DM et al. (2015) Stable recombination hotspots in birds. Science 350:928–932
Stritt C, Gordon SP, Wicker T, Vogel JP, Roulin AC (2018) Recent activity in expanding populations and purifying selection have shaped transposable element landscapes across natural accessions of themediterranean grass brachypodium distachyon. Genome Biol Evol 10:304–318
Terhorst J, Kamm JA, Song YS (2016) Robust and scalable inference of population history from hundreds of unphased whole genomes. Nat Genet 49:303–309
Thomas CG, Wang W, Jovelin R, Ghosh R, Lomasko T, Trinh Q et al. (2015) Full-genome evolutionary histories of selfing, splitting, and selection in Caenorhabditis. Genome Res 25:667–78
Tuskan GA, DiFazio S, Jansson S, Bohlmann J, Grigoriev I, Hellsten U et al. (2006) The genome of black cottonwood, Populus trichocarpa (Torr. & Gray). Science 313:1596–1604
Vijay N, Bossu CM, Poelstra JW, Weissensteiner MH, Suh A, Kryukov AP et al. (2016) Evolution of heterogeneous genome differentiation across multiple contact zones in a crow species complex. Nat Commun 7:13195
Vijay N, Park C, Oh J, Jin S, Kern E, Kim HW et al. (2018) Population genomic analysis reveals contrasting demographic changes of two closely related dolphin species in the last glacial. Mol Biol Evol 35:2026–2033
Wang J, Ding J, Tan B, Robinson KM, Michelson IH, Johansson A et al. (2018a) A major locus controls local adaptation and adaptive life history variation in a perennial plant. Genome Biol 19:72
Wang Y, Liang W, Tang T (2018b) Constant conflict between Gypsy LTR retrotransposons and CHH methylation within a stress-adapted mangrove genome. New Phytol 220:922–935
Wang J, Raskin L, Samuels DC, Shyr Y, Guo Y (2015) Genome measures used for quality control are dependent on gene function and ancestry. Bioinformatics 31:318–23
Wang J, Street NR, Park E, Liu J, Ingvarsson PK (2020) Evidence for widespread selection in shaping the genomic landscape during speciation of Populus. Mol Ecol 29:1120–1136
Wright SI, Agrawal N, Bureau TE (2003) Effects of recombination rate and gene density on transposable element distributions in Arabidopsis thaliana. Genome Res 13:1897–1903
Xu Z, Wang H (2007) LTR-FINDER: an efficient tool for the prediction of full-length LTR retrotransposons. Nucleic Acids Res 35:W265–W268
Zhang Z, Chen Y, Zhang J, Ma X, Li Y, Li M et al. (2020) Improved genome assembly provides new insights into genome evolution in a desert poplar (Populus euphratica). Mol Ecol Resour 20:781–794
Zhang G, Li C, Li Q, Li B, Larkin DM, Lee C et al. (2014) Comparative genomics reveals insights into avian genome evolution and adaptation. Science 346:1311–1320
Zhou Y, Massonnet M, Sanjak JS, Cantu D, Gaut BS (2017) Evolutionary genomics of grape (Vitis vinifera ssp. vinifera) domestication. Proc Natl Acad Sci USA 114:11715–11720
Acknowledgements
We thank the Ministry of Human Resource Development for fellowship to ABP. Computational analyses were done on the Har Gobind Khorana Computational Biology cluster established and maintained by combining funds from IISER Bhopal under Grant # INST/BIO/2017/019, IYBA 2018 from DBT, and ECRA from DST.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Associate Editor: Pär K. Ingvarsson
Supplementary information
Rights and permissions
About this article
Cite this article
Patil, A.B., Vijay, N. Repetitive genomic regions and the inference of demographic history. Heredity 127, 151–166 (2021). https://doi.org/10.1038/s41437-021-00443-8
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41437-021-00443-8
This article is cited by
-
High quality genomes produced from single MinION flow cells clarify polyploid and demographic histories of critically endangered Fraxinus (ash) species
Communications Biology (2024)
-
Impact of model assumptions on demographic inferences: the case study of two sympatric mouse lemurs in northwestern Madagascar
BMC Ecology and Evolution (2021)