Abstract
There has been a long history of the use of mathematics in genetics, ranging from the use of statistics to analyse genetic data to genetic models of evolutionary processes. Contemporary research into the genomic basis of disease and complex traits exemplifies the importance of statistical methods in genetics. Some examples of the development and application of population genetic models are described, which are intended to highlight the utility of such models for understanding variation and evolution in natural populations. The effects of selection on variability at sites linked to the targets of selection illustrate how fruitful interactions between theory and data can be.
Similar content being viewed by others
Introduction
Two outstanding geneticists, Alfred Sturtevant and George Beadle, started their splendid 1939 textbook of genetics (Sturtevant and Beadle 1939) with the remark ‘Genetics is a quantitative subject. It deals with ratios, and with the geometrical relationships of chromosomes. Unlike most sciences that are based largely on mathematical techniques, it makes use of its own system of units. Physics, chemistry, astronomy, and physiology all deal with atoms, molecules, electrons, centimeters, seconds, grams—their measuring systems are all reducible to these common units. Genetics has none of these as a recognizable component in its fundamental units, yet it is a mathematically formulated subject that is logically complete and self contained’.
This statement may surprise the large number of contemporary workers in genetics, who use high-tech methods to analyse the functions of genes by means of qualitative experiments, and think in terms of the molecular mechanisms underlying the cellular or developmental processes, in which they are interested. However, for those who work on transmission genetics, analyse the genetics of complex traits, or study genetic aspects of evolution, the core importance of mathematical approaches is obvious. It is probably no accident that Gregor Mendel was trained in mathematics before he undertook his epoch-making experiments. Indeed, R.A. Fisher argued convincingly that Mendel had framed his theory of particulate inheritance before undertaking his breeding work, and knew what ratios to expect in his crosses (Fisher 1936).
As far as I know, only two of the past Presidents of the Genetics Society, Fisher and J.B.S. Haldane, were well trained as mathematicians (Fisher studied mathematics at Cambridge; Haldane studied zoology, mathematics and classics at Oxford). While my own work has involved a good deal of mathematical modelling, I cannot claim the same level of ability as these two great men. I was attracted to genetics through a childhood fascination with biology, having become somewhat disenchanted by the fact that much of biology involved learning innumerable, seemingly disconnected, facts and lengthy Graeco-Latin names. The intellectual elegance of genetics, where hypotheses can be tested by quantitative experiments, was an illumination to me as a teenager—especially as the more you understand, the less you have to learn by the heart. The fact that mathematical models formed a core part of genetics, especially as applied to evolutionary questions, were a further revelation. I had always liked mathematics, except for geometry (my visual imagination is defective), although I am not especially good at it. But the mathematics used in much of genetics is not very difficult, and it has been possible to make useful contributions to theoretical genetics with mediocre mathematical ability. This is, however, becoming increasingly difficult, since many aspects of statistical genetics require the use of advanced mathematical methods.
I would like to present some examples of the ways in which applications of mathematics have contributed to progress in genetics—Haldane, of course, made similar points in his famous refutation of Ernst Mayr’s (Mayr 1959) criticism of classical theoretical population genetics as ‘bean-bag genetics' (Haldane 1964). The obvious starting point, on which I will not dwell, is that transmission genetics involves models of the frequencies of genotypes in experimental crosses or in the progeny of matings between individuals from natural populations. Tests of basic genetic hypotheses, such as Mendelian ratios, necessarily involve asking whether the deviations of the data from the predicted value could reasonably be caused simply by sampling error. Similarly, estimation of the parameters of genetic models, such as the frequencies of recombination between loci, requires the proper use of statistical inference procedures, especially in species like humans where controlled crosses cannot be carried out.
It is no accident that Fisher, Haldane and Sewall Wright all made contributions to statistics, with Fisher being commonly regarded as the pioneer of modern methods of significance testing and inference procedures. He would not have been pleased by the current fashion for Bayesian methods of inferring the posterior probabilities of genetic parameters, of which he had been a fierce critic on the grounds that ‘they require for their truth the postulation of knowledge beyond that obtained by direct observation' (Fisher 1935). Similarly, the genetics of quantitative traits have been based on mathematical models of how multiple Mendelian variants contribute to variation in the traits, and how the resemblances between relatives can be explained in terms of these models, starting with work by Wilhelm Weinberg, Fisher and Wright early in the last century (Provine 1971). Contemporary research in human genetics, complex trait genetics, animal- and plant-selective breeding and population genomics utilises evermore complex and computationally intensive methods (Walsh and Lynch 2017). You simply cannot avoid the use of tools provided by the application of mathematical statistics to genetic problems if you work in these areas.
Mathematics and the basic processes of evolution
My own research interests are in evolutionary aspects of genetics. Here, mathematical modelling of the behaviour of genetic variants in populations has been fundamental, starting soon after the rediscovery of Mendel’s work in 1900. In the first chapter of The Genetical Theory of Natural Selection, unquestionably the most important book on evolution after The Origin of Species, Fisher described how the particulate nature of Mendelian inheritance resolves the difficulties that Darwin encountered in explaining the origin of the variation that is needed for natural selection to work (Fisher 1930, 1999). Fisher argued that Darwin’s belief in blending inheritance led him to conclude that characters acquired during the development of the parents could frequently be transmitted to the offspring (what we now call Lamarckian inheritance—Darwin called it pangenesis), in order to offset the rapid loss of variability that occurs with blending (the genetic variance is halved every generation). If there is no blending of the material contributed to an offspring by the two parents, as with Mendelian inheritance, then this problem disappears, and there is no need to postulate a high rate of origin of new genetic variability in every generation.
The formal statement of this principle, for diploid randomly mating populations, is the Hardy–Weinberg law (Hardy 1908; Weinberg 1908). But the constancy of allele frequencies in an infinitely large population that underlies this law holds for any mating system, although there may be only an asymptotic approach to the equilibrium allele frequencies. In populations with age structure, like humans, the approach to equilibrium may take some time, even for an autosomal locus (Charlesworth 1974). Nonetheless, the basic conclusion, that the mechanics of inheritance conserves rather than destroys variation, is correct, with some qualifications with respect to phenomena such as the effects of biased gene conversion on allele frequencies (Charlesworth and Charlesworth 2010, p.35). We could not know this without analysing mathematical models.
However, we need to know where variation comes from in the first place. There is now a large body of work on the rate at which new variation in quantitative traits arises through mutation, to which my lab has made some modest contributions with respect to components of fitness (Houle et al. 1994; Houle et al. 1997; Charlesworth et al. 2004; Charlesworth 2015). The general picture is that there is only a low rate of increase in variance due to mutation in higher organisms like Drosophila melanogaster, of the order of 1000th the variance found in a natural population (Halligan and Keightley 2009; Walsh and Lynch, 2017). Current levels of variability are the joint product of mutation and other evolutionary forces, such as selection and genetic drift.
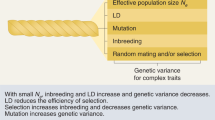
Important modelling work, initiated by Alan Robertson in 1960, has generated predictions about the ultimate change in the population mean of a trait that can be caused by selection on standing variation in a sexually reproducing population. This change is approximately equal to the product of twice the effective population size (Ne) and the response to selection in the first generation (Robertson 1960; Barton 2017; Walsh and Lynch 2017). In large, sexually reproducing populations, a very large and sustained response to selection in a quantitative trait can thus be produced from variation that was present in the initial generation, resulting in phenotypes far outside the range of variability in the original population, as is seen in many experiments on artificial selection (Hill 2010). Long-continued selection that exploits new mutations can have even more dramatic effects (Hill 2010), and the rate of evolution by the fixation of new selectively favourable mutations is also proportional to Ne (Kimura and Ohta 1971, p.11).
The dependence of selection response on Ne leads on to the question—what do we mean by the effective population size? This seminal concept was introduced by Wright (1931) as a way of describing the effect of genetic drift in a population that does not fit the assumptions of the simple model of a discrete generation population introduced by Fisher (1922). This model assumes N randomly mating diploid individuals with no sex differences, such that the 2N copies of a gene at a given locus that are present in the adults of the next generation are a random (binomial) sample from an infinite pool of gametes produced by the members of the preceding generation. The asymptotic rate of genetic drift under more complex scenarios (such as different numbers of breeding males and females) is equated to 1/(2Ne) instead of the 1/(2N) that appears in the simple “Wright-Fisher” model, as it has come to be termed (why is not it called the “Fisher model”?). Ne is often much smaller than the number of breeding adults in the population (Crow and Morton 1955; Frankham 1995).
In the case of humans, for example, DNA sequence diversity and mutation rate estimates suggest a value of Ne of ~25,000. This figure comes from the equation derived by Kimura (1971) for the equilibrium level of diversity per nucleotide site for selectively neutral variants: π = 4Neu, where u is the mutation rate per nucleotide site per generation. For sites that are likely to be close to neutrality, mean π in humans is approximately equal to 0.001, and u is around 10–8 (Kong et al. 2012), yielding Ne = 25,000. This apparent conflict with the current human population size of 7.6 billion probably largely reflects the fact that the harmonic mean (the reciprocal of the mean of the reciprocals) of the effective population sizes in each generation gives the Ne that is relevant to current levels of variability (Slatkin and Hudson 1991). With a large and rapid expansion in population size, the harmonic mean of Ne will be much closer to the ancestral value of Ne than the current value. Another contributory factor may be the effects of selection at linked sites in reducing variability, discussed in the next section.
This raises the questions of what we mean by generation time and effective population size in species like humans, which have overlapping generations and separate sexes. These questions have been answered by theoretical analyses of populations with age structure, to which I devoted a good deal of research time during the first part of my career (Charlesworth 1994). The first question was answered by showing that the generation time is given by the mean of the average ages of mothers and fathers at the time of conception. It can differ between autosomal, X-linked and mitochondrial genes because of differences among these components of the genome in the relative contributions of males and females to the offspring, combined with sex differences in survival rates and age-specific rates of reproduction. The importance of these life-history variables for the interpretation of data on rates of molecular evolution in different evolutionary lineages is now becoming recognised in studies of humans and their primate relatives (Amster and Sella 2016).
The first satisfactory analysis of the second problem was presented by Joe Felsenstein (1971), with later contributions by people such as Bill Hill (1972, 1979) and myself (Charlesworth 2001; Evans and Charlesworth 2013). Similar difficulties arise in defining Ne in spatially structured populations; without going into details, it turns out that different definitions apply to different aspects of variability within and between local populations (Charlesworth and Charlesworth 2010, Chap. 7). However, a remarkable result, originally due to Takeo Maruyama (Maruyama 1971), is that the mean neutral diversity within a local population at equilibrium under drift, mutation and migration between local populations is often independent of migration rates, and satisfies the equation mentioned above that applies to a single population, replacing Ne with the sum of the Ne values for each local population. This is important for comparing levels of DNA sequence variability between different species, since division of a species into partially isolated local populations is the rule rather than the exception. The relative independence of the mean within-population variability from migration rates between populations facilitates such comparisons.
Modelling the effects of linkage on evolution and variation
I will close by discussing a subject that has preoccupied many population geneticists since the advent of data on genome-wide molecular variability, initially provided by gel electrophoresis of proteins, then by restriction mapping and sequencing of small parts of genomes, and now by whole-genome sequencing of multiple individuals (Charlesworth and Charlesworth 2010, Chap. 1). This is the extent to which evolution at a given site in the genome is influenced by selection acting on genetically linked sites, which was first discussed by Fisher (1930). That such influences are not simply a figment of the theoretician’s imagination is shown by the fact that both the level of variability of a gene and its rate of adaptive sequence evolution are often positively correlated with its rate of recombination (Begun and Aquadro 1992; Cutter and Payseur 2013; Charlesworth and Campos 2014; Booker et al. 2017).
A key concept is the idea that the genotypic state at one site in the genome is not necessarily independent of that at another; the extent of this lack of independence among two variable sites is measured by the coefficient of linkage disequilibrium, a term invented by Richard Lewontin (my post-doctoral adviser) and Ken-Ichi Kojima (Lewontin and Kojima 1960). Their theoretical work confirmed earlier work by (Wright 1952; and Kimura 1956), which showed that linkage disequilibrium (LD) can be stably maintained when alleles at two different loci interact epistatically with respect to fitness, using Fisher’s definition of epistasis as a departure from linearity of the effects on a phenotype of combinations of genotypes at different loci (Fisher 1918). This led to a cottage industry of theoretical modelling of the interaction between selection and linkage, with the broad conclusion that interactions in fitness effects have to be strong in relation to the rate of recombination between the loci for significant LD to be maintained at equilibrium (Charlesworth and Charlesworth 2010, Chap. 8). Apart from a valiant attempt to produce a multiple locus model that maintained extreme LD across the genome (Franklin and Lewontin 1970), this work has led to a consensus that LD is unlikely to be found in sexually reproducing populations except between closely linked loci or between loci under unusually strong epistatic selection.
Indeed, when LD is measured using DNA sequence variants, it is usually found to be absent except between sites that are closely linked genetically, other than in highly inbred populations such as C. elegans, where homozygosity greatly reduces the effective rate of recombination (Charlesworth and Charlesworth 2010, Chap 8). It is very likely that most of this LD is generated by random drift acting on neutral variants, following the predictions of models developed 50 years ago (Hill and Robertson 1968; Sved 1968). These theoretical predictions concerning LD forms the underpinning for the method of Genome Wide Association Mapping, which is currently a major research enterprise with many applications to medicine and agriculture (Visscher et al. 2017). This provides an example of how an apparently highly academic problem has unexpected practical utility, and how it may take many years for practical applications to emerge from a scientific advance.
The first process to be studied in which selection on sites in genomes affects neutral variants was associative overdominance (AOD) (Ohta and Kimura 1970; Sved 1968, 1972), the phenomenon of an apparent selective advantage for heterozygotes at loci that are in reality neutral. LD caused by drift in a randomly mating population can arise between a neutral locus and one or more loci under selection. If alleles selected at the loci under selection experience heterozygote advantage or segregate for partially recessive deleterious alleles that are maintained by mutation pressure, homozygotes at the neutral locus can have lower fitnesses on average than heterozygotes, especially if the neutral and selected loci are closely linked.
For nearly 50 years, it was thought that any heterozygote advantage generated by AOD in a randomly mating population would delay loss of variability at the neutral site, compared with the rate predicted by standard neutral theory. However, the selection coefficients generated at the neutral locus by AOD do not change allele frequencies at the neutral loci (Charlesworth 1991; Zhao and Charlesworth 2016), so that the apparent heterozygote advantage cannot affect neutral variability. Nonetheless, a retardation of loss of neutral variability due to linkage to partially recessive deleterious mutations can occur if the product of the selection coefficient s against homozygotes and Ne is of the order of 1 or less (Zhao and Charlesworth 2016). In other regions of parameter space, loss of neutral variability is accelerated by the presence of deleterious mutations, which causes the elimination of linked neutral variants, effectively resulting in a reduction in Ne. This is the process known as background selection, discovered in 1993 by quite different reasoning (Charlesworth et al.,1993), and which is likely to prevail over AOD in most regions of the genome in large natural populations (Zhao and Charlesworth 2016). There is some preliminary evidence that AOD influences patterns of sequence variability in regions of the genome where crossing over is absent and Ne is greatly reduced by the effects of selection at linked sites, so that Nes values are likely to be of order 1 or less for many deleterious mutations (unpublished data of H. Becher and B. Charlesworth).
Another effect of selection on variability at linked neutral sites is the hitchhiking of neutral variants by selectively advantageous mutations (Maynard Smith and Haigh 1974), now often known as selective sweeps. This pioneering paper has led to many studies that infer the past action of selection from the footprints of neutral variability associated with sweeps (Jensen et al. 2016). John Maynard Smith was in the process of revising the paper when I arrived at the University of Sussex as a young lecturer; he remarked that the reviewer must have been Bill Hill or Alan Robertson, “as they are the only people in the country bright enough to understand it”. (John always used to refer to mathematics as ‘doing sums’, hence the title of this paper.)
This paper was stimulated by the fact that levels of variability estimated from allozyme polymorphism studies appeared to show little relationship with population size estimates (Lewontin 1974). Maynard Smith and Haigh proposed that selective sweeps might have a sufficiently large effect on variability that the effect of population size on neutral variability is swamped, an idea taken further by John Gillespie (Gillespie 2000). Understanding how these different effects of selection on linked sites affect genome-wide patterns of variation in evolution is an ongoing research endeavour, with evidence from population genomic data that background selection and sweeps both play important roles (Booker et al. 2017). There is currently a vigorous debate about whether or not selective sweeps have such a pervasive effect on levels of variability within populations that the traditional models of genetic drift and neutral molecular evolution have lost their relevance (Kern and Hahn 2018; Jensen et al. 2019).
Interestingly, the same basic equation for the effect of selection at one locus on allele frequencies at a linked neutral locus is now known to underly all three processes (AOD, selective sweeps and background selection) (Zhao and Charlesworth 2016). It is a special case of the Price equation, which quantifies the effect of selection on a trait in terms of its covariance with fitness (Robertson 1968; Price 1970), and has had many applications in quantitative trait genetics and social evolution (Gardner 2008; Zhang and Hill 2010; Walsh and Lynch 2017). An important role of population genetics theory is to provide a unified view of evolutionary processes, as well as making predictions that can be empirically tested, so that this progress towards unifying apparently disparate findings is pleasing.
Conclusion
I hope to have provided evidence that the mathematical modelling of population genetic processes is crucial for a proper understanding of how evolution works, although there is of course much scope for intuition and verbal arguments when carefully handled (The Genetical Theory of Natural Selection is full of examples of these). There are many situations in which biological complexity means that detailed population genetic models are intractable, and where we have to resort to computer simulations, or approximate representations of the evolutionary process such as game theory to produce useful results, but these are based on the same underlying principles. Over the past 20 years or so, the field has moved steadily away from modelling evolutionary processes to developing statistical tools for estimating relevant parameters from large datasets (see Walsh and Lynch 2017 for a comprehensive review). Nonetheless, there is still plenty of work to be done on improving our understanding of the properties of the basic processes of evolution.
The late, greatly loved, James Crow used to say that he had no objection to graduate students in his department not taking his course on population genetics, but that he would like them to sign a statement that they would not make any pronouncements about evolution. There are still many papers published with confused ideas about evolution, suggesting that we need a ‘Crow’s Law’, requiring authors who discuss evolution to have acquired a knowledge of basic population genetics.
References
Amster G, Sella G (2016) Life history effects on the molecular clocks of autosomes and sex chromosomes. Proc Natl Acad Sci USA 113:1588–1593
Barton NH (2017) How does epistasis influence the response to selection? Heredity 118:96–109
Begun D, Aquadro CF (1992) Levels of naturally occurring DNA polymorphism correlate with recombination rate in Drosophila melanogaster. Nature 356:519–520
Booker TR, Jackson BC, Keightley PD (2017) Detecting positive selection in the genome. BMC Biol 15:98
Charlesworth B (1974) The Hardy-Weinberg law with overlapping generations. Adv Appl Probab 6:4–6
Charlesworth B (1994) Evolution in age-structured populations, 2nd edn. Cambridge University Press, Cambridge, UK
Charlesworth B (2001) The effect of life-history and mode of inheritance on neutral genetic variability. Genet Res 77:153–166
Charlesworth B (2015) Causes of natural variation in fitness: evidence from studies of Drosophila populations. Proc Natl Acad Sci USA 12:1662–1669
Charlesworth B, Borthwick H, Bartolomé C, Pignatelli P (2004) Estimates of the genomic mutation rate for detrimental alleles in Drosophila melanogaster. Genetics 168:1105–1109
Charlesworth B, Campos JL (2014) The relations between recombination rate and patterns of molecular evolution and variation in Drosophila. Ann Rev Genet 48:383–403
Charlesworth B, Charlesworth D (2010) Elements of evolutionary genetics. Roberts and Company, Greenwood Village, CO
Charlesworth B, Morgan MT, Charlesworth D (1993) The effect of deleterious mutations on neutral molecular variation. Genetics 134:1289–1303
Charlesworth D (1991) The apparent selection on neutral marker loci in partially inbreeding populations. Genet Res Camb 57:159–195
Crow JF, Morton NE (1955) Measurement of gene-frequency drift in small populations. Evolution 9:202–214
Cutter AD, Payseur BA (2013) Genomic signatures of selection at linked sites: unifying the disparity among species. Nat Rev Genet 14:262–272
Evans BJ, Charlesworth B (2013) The effect of non-independent mate pairing on the effective population size. Genetics 183:1–12
Felsenstein J (1971) Inbreeding and variance effective numbers in populations with overlapping generations. Genetics 68:581–597
Fisher RA (1918) The correlation between relatives on the supposition of Mendelian inheritance. Trans Roy Soc Edinb 52:499–433
Fisher RA (1922) On the dominance ratio. Proc Roy Soc Edinb 42:321–341
Fisher RA (1930) The genetical theory of natural selection. Oxford University Press, Oxford, U.K.
Fisher RA (1935) The design of experiments. Oliver and Boyd, Edinburgh
Fisher RA (1936) Has Mendel’s work been rediscovered? Ann Sci 1:15–137
Fisher RA (1999) The genetical theory of natural selection. A complete variorum edition. Oxford University Press, Oxford
Frankham R (1995) Effective population-size adult-population size ratios in wildlife—a review. Genet Res 66:95–107
Franklin IR, Lewontin RC (1970) Is the gene the unit of selection? Genetics 65:701–734
Gardner A (2008) The Price equation. Curr Biol 18:R198–202
Gillespie JH (2000) Genetic drift in an infinite population: the pseudohitchhiking model. Genetics 155:909–919
Haldane JBS (1964) A defense of beanbag genetics. Perspect Biol Med 7:343–349
Halligan DL, Keightley PD (2009) Spontaneous mutation accumulation studies in evolutionary genetics. Ann Rev Ecol Evol Syst 40:151–172
Hardy GH (1908) Mendelian proportions in a mixed population. Science 28:49–50
Hill WG (1972) Effective size of populations with overlapping generations. Theor Pop Biol 3:278–289
Hill WG (1979) A note on effective population size with overlapping generations. Genetics 92:317–322
Hill WG (2010) Understanding and using quantitative genetic variation. Philos Trans R Soc B 365:73–85
Hill WG, Robertson A (1968) Linkage disequilibrium in finite populations. Theor Appl Genet 38:226–231
Houle D, Hughes KA, Hoffmaster DK, Ihara JT, Assimacopoulos S, Charlesworth B (1994) The effect of spontaneous mutation on quantitative traits. I. Variances and covariances of life history traits. Genetics 138:773–785
Houle D, Hughes KA, Assimacopoulos S, Charlesworth B (1997) The effects of spontaneous mutation on quantitative traits. II. Dominance of mutations with effects on life-history traits. Genet Res 70:27–34
Jensen JD, Foll M, Bernatchez L (2016) The past, present and future of genomic scans for selection. Mol Ecol 25:1–4
Jensen JD, Payseur BS, Stephan W, Aquadro CF, Lynch M, Charlesworth D, et al. (2019) The importance of the Neutral Theory in 1968 and 50 years on: A response to Kern and Hahn 2018. Evolution 73:111–114
Kern AD, Hahn MW (2018) The neutral theory in the light of natural selection. Mol Biol Evol 35:1366–1371
Kimura M (1956) A model of a system which leads to closer linkage by selection. Evolution 9:419–435
Kimura M (1971) Theoretical foundations of population genetics at the molecular level. Theor Pop Biol 2:174–208
Kimura M, Ohta T (1971) Theoretical aspects of population genetics. Princeton University Press, Princeton, N.J.
Kong A, Frigge ML, Masson G, Besenbacher S, Sulem P, et al. (2012) Rate of de novo mutations and the importance of father’s age to disease risk. Nature 488:471–475
Lewontin RC, Kojima K-I (1960) The evolutionary dynamics of complex polymorphisms. Evolution 14:458–472
Lewontin RC (1974) The genetic basis of evolutionary change. Columbia University Press, New York, NY
Maruyama T (1971) An invariant property of a subdivided population. Genet Res 18:81–84
Maynard Smith J, Haigh J (1974) The hitch-hiking effect of a favourable gene. Genet Res 23:23–35
Mayr E (1959) Where are we? Cold Spring Harb Symp Quant Biol 24:1–14
Ohta T, Kimura M (1970) Development of associative overdominance through linkage disequilibrium in finite populations. Genet Res 18:277–286
Price GR (1970) Selection and covariance. Nature 227:520–521
Provine WB (1971) The origins of theoretical population genetics. University of Chicago Press, Chicago, IL
Robertson A (1960) A theory of limits in artificial selection. P R Soc B 153:234–249
Robertson A (1968) The spectrum of genetic variation. InLewontin RC (Ed.). Population biology. Syracuse University Press, Syracuse, NY
Slatkin M, Hudson RR (1991) Pairwise comparisons of mitochondrial DNA sequences in stable and exponentially growing populations. Genetics 143:579–587
Sturtevant AH, Beadle GW (1939) An introduction to genetics. W.B. Saunders, Philadelphia, PA
Sved JA (1968) The stability of linked systems of loci with a small population size. Genetics 59:543–563
Sved JA (1972) Heterosis at the level of the chromosome and at the level of the gene. Theor Pop Biol 3:491–506
Visscher PM, Wray NR, Zhang Q, McCarthy MI, Brown M, Yang J (2017) 10 Years of GWAS discovery: Biology, function, and translation. Am J Hum Genet 101:5–22
Walsh JB, Lynch M (2017) Evolution and selection of quantitative traits. Oxford University Press, Oxford
Weinberg W (1908) Über den Nachweis der Vererbung beim Menschen. Jhr Ver vat Nat Württemb 64:369–382
Wright S (1931) Evolution in Mendelian populations. Genetics 16:97–159
Wright S, (1952) The genetics of quantitative trait variability. Pp 5-41 in Quantitative Inheritance, eds. Reeve ECR and Waddington CH. HM Stationery Office, London
Zhang X-S, Hill WG (2010) Change and maintenance of variation in quantitative traits in the context of the Price equation. Theor Pop Biol 77:14–22
Zhao L, Charlesworth B (2016) Resolving the conflict between associative overdominance and background selection. Genetics 203:1315–1334
Acknowledgements
I thank the editors, Barbara Mable and Alison Woollard, and two reviewers for suggestions for improvements to the original version of this paper.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Charlesworth, B. In defence of doing sums in genetics. Heredity 123, 44–49 (2019). https://doi.org/10.1038/s41437-019-0195-1
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41437-019-0195-1