Introduction

Integration, a characteristic of the multivariate phenotype, describes patterns of correlation among functional traits (Pigliucci 2003; Perez-Barrales et al. 2014; Margres et al. 2015). While most often studied at the phenotypic level (Klingenberg and Marugan-Lobon 2013), if the goal is to understand multivariate evolution then studies of genetic integration are particularly informative (Klingenberg 2014). This is because the degree to which any trait can evolve under selection ultimately depends not only on the extent to which it varies due to genetic factors (referred to as ‘genetic variance’), but also on the genetic correlations it shares with other traits (Lande 1979, 1980; Lande and Arnold 1983; Arnold 1992; Arnold et al. 2008; Björklund et al. 2013). These patterns of genetic (co)variation within and between traits can be represented as the genetic variance/covariance matrix (G). While phenotypic integration is itself expected to arise from past selection favoring particular trait combinations, the structure of G also has the potential to facilitate or constrain adaptive evolutionary responses to current selection (Porto et al. 2009; Walsh and Blows 2009). This is because genetic correlations among traits will prevent any one trait from evolving independently of others, even if this would in principle be advantageous (Cheverud 1996; Armbruster et al. 2014).

In recent years, it has become increasingly evident that genetic variances and correlations do not remain static as organisms develop and age (Badyaev and Martin 2000; Blumstein et al. 2013; Class and Brommer 2015). Genetic variances associated with life history (Charmantier et al. 2006) and morphological traits (Björklund 1997; Badyaev and Martin 2000) often vary across ontogeny. For specific trait pairs, it is also known that genetic correlations can change with age or life stage (Moran 1994; Watkins 2001; Aguirre et al. 2014). However, few studies have examined changes in a more fully multivariate context, comparing G among larger sets of traits to test for shifting patterns of genetic integration across development (Cheverud et al. 1983; Aguirre et al. 2014). Because selection acts on multivariate phenotypes (Ellis et al. 2014), and potentially in different ways over the full timeline of development (Gignac and Santana 2016), scrutinizing changes in G across ontogeny may help us better understand not only past evolutionary processes but also the potential for future adaptive evolution. The latter point follows because age-specific G matrices can be used to evaluate the potential for genetic constraint in relation to selection acting on phenotypic state at that age. However, it is also true that changes in G across age represent a (multivariate) genotype-by-age interaction (G × A), which can equally be conceptualized as genetic variance for the developmental trajectory (just as G × E is genetic variance for plasticity; e.g., Wilson et al. 2008; Roff and Wilson 2014 for didactic explanations of this equivalence). Thus, to the extent that current selection acts directly on development as a process (rather than on age-specific phenotypic state), the presence of G × A is required for further evolution of the developmental trajectory.

While valuable, wider estimation of age-specific G matrices for traits known (or hypothesized) to contribute to functional integration is logistically challenging. Data requirements are high and further logistic constraints can arise from the characteristics being studied (Damián et al. 2017). For sexual diploid organisms, it is also generally necessary to utilize large breeding designs, or recover pedigree information using molecular data. When G cannot readily be estimated then P, the phenotypic variance–covariance matrix, has been used in its place (Marroig and Cheverud 2001; Steppan et al. 2002). This strategy has become especially commonplace in studies related to morphological integration (Eroukhmanoff and Svensson 2008). The primary criticism of such an approach is that, because P combines both genetic (G) and environmental (E) components of (co)variance, its reliability as a substitute for G cannot be assured (Arnold 1981; Lofsvold 1986; Kruuk et al. 2008). Despite this, P has been shown to be a reliable predictor of G on many occasions (Atchley et al. 1981; Cheverud 1995; Arnold and Phillips 1999) and has given rise to Cheverud’s conjecture (Cheverud 1988), which states that phenotypic correlations can be used as a substitute for genetic correlations. However, both G and E could change independently of one another across development, such that changes in P may not reflect changes in G (Badyaev and Martin 2000; Mitteroecker and Bookstein 2009). Because of this, P may be an appropriate substitute for G only at certain stages of ontogeny. Few studies (Cheverud et al. 1983; Leamy and Cheverud 1984; Badyaev and Martin 2000), however, have looked at whether the relationship between P and G is stable over development.

Mangrove rivulus fish, Kryptolebias marmoratus, are an excellent vertebrate model in which to test for ontogenetic changes in G using a quantitative genetic framework. Individuals exist as self-fertilizing hermaphrodites (Earley et al. 2012), a unique breeding strategy among vertebrates that allows for the production of many replicates of a single genotype without the need for complex breeding designs. We focus here on a set of morphological characters that we have previously shown are associated with a fitness-related functional performance characteristic—terrestrial jumping—using animals that were not involved in the present study (Styga et al. 2018). Terrestrial jumping is an important behavior in mangrove rivulus fish, as it allows individuals to effectively traverse land to locate new pools of water or patches of damp leaf litter during periods of low tide (Magellan 2016). A jump is produced when an individual flexes its axial muscles, places its body weight on its caudal peduncle (i.e. the area directly adjacent to its caudal fin), and launches itself from the ground (Gibb et al. 2011; Ashley-Ross et al. 2014). The fitness advantage associated with high terrestrial jumping may be most apparent in the field, where other less terrestrially adept fish species (e.g., Gambusia) have been found dead in dried pools, while K. marmoratus has been found living on land just outside of these pools (Taylor 2012). Because of the association between skeletal morphology and jumping performance, positive selection on jumping has been postulated to drive corresponding changes in morphology (Gibb et al. 2013).

We have previously found that jumping performance is significantly correlated with bone dimensions within the caudal peduncle, the posterior portion of the body of a fish (Styga et al. 2018). Jumping is positively correlated with lengths of the epural (EPL) and hypural (HYPL), and negatively correlated with the angle of the epural (EPA) relative to the vertebral centrum (Fig. S1). However, these phenotypic relationships were only present in young (<120 days post hatching, DPH) fish (see Fig. 2 in Styga et al. 2018), and not in mature (250–500 DPH) or old (>500 DPH) fish, possibly reflecting a decreased reliance on these bones for jumping at later ages (Styga et al. 2018). Therefore, in the present study, we focus on studying ontogenetic variation in the genetic (co)variance structure among these morphological traits at various points from hatching to sexual maturity (0–120 DPH range) (Cole and Noakes 1997). In what follows, we characterize (co)variation at both phenotypic (P) and genetic (G) levels for six skeletal characteristics (Fig. S1), and standard length (SL), at three developmental stages (1, 15, and 100 DPH). In mangrove rivulus, the skeletal morphology of the caudal peduncle is not perfectly bilaterally symmetrical (Styga et al. 2018); therefore, we assessed phenotypic and genetic (co)variation for traits on opposing sides of the vertebral column (i.e., EPL and parahypural length [PHPL]; EPA and parahypural angle [PHPA]). We determine integration among these traits at both phenotypic and genetic levels, and also test Cheverud’s conjecture (Cheverud 1988) that phenotypic correlations can be used to reliably estimate genetic correlations at each age. We formally test the hypotheses that: (i) phenotypic (co)variance (P) among traits will vary among age classes, (ii) traits are genetically variable, (iii) trait genetic variance will be age-dependent, (iv) the full genetic (co)variance (or correlation) structure G will change between ages, and (v) P provides a valid proxy of G matrix at each stage in development.

Methods

Animal care and specimen collection

Specimens (n = 1066) that were used in this study were obtained from (F2–F12) progenitors acquired from 44 genotypes; however, most specimens were obtained from F2 or F3 progenitor stocks (Table S1). Because the vast majority of animals (91%) came from F2 or F3 progenitor stocks, we did not include ‘generation’ in our statistical models. All experimental fish were produced by selfing of genetically distinct progenitors with each progenitor having a unique genotype. We utilized 44 isogenic or near-isogenic lineages from our progenitor stock. Microsatellites were used to identify distinct multilocus genotypes (i.e. unique combinations of alleles present across 32 loci), with isogenic lineages being derived from wild-caught progenitors that were homozygous at all 32 loci, and near-isogenic lineages being derived from wild-caught progenitors that were homozygous at, on average, 28 loci (range: 16–31, median: 30) (Mackiewicz et al. 2006; Tatarenkov et al. 2011). K. marmoratus is an androdioecous species, meaning that only male or hermaphroditic individuals make up the population (Turner et al. 1992). In our study, we focused on morphological variation in hermaphrodites. As a result, we excluded any males from our study, which are easily recognizable by the presence of orange pigmentation on the body and a faded (or absent) eyespot on the dorsal portion of the caudal peduncle (Scarsella et al. 2017).

Progenitors, their eggs, and hatchlings were housed under common garden conditions (12 h light: 12 h dark photoperiod cycle, at 26 °C, and in 25 ppt saltwater). Progenitors were fed 4 mL brine shrimp nauplii (Artemia spp.) while hatchlings were fed 1 mL brine shrimp nauplii on a daily basis. Both progenitors and hatchlings were housed individually for the duration of the experiment. Each progenitor was housed in 750 mL Rubbermaid® TakeAlong® Deep Square containers with spawning substrate (i.e. Poly-Fil®), which was checked for eggs weekly. Once obtained from the spawning substrate, eggs were transferred to 59 mL, clear polystyrene cups until hatching. Complete water changes were conducted on each egg cup weekly to refresh the water. The date on which eggs were laid was also recorded. At the time of hatching, each individual larval fish was transferred to one 473 mL plastic cup filled 75% with 25 ppt water. Hatchlings were kept in these enclosures until they reached a predetermined age. Hatching date was recorded for all individuals. We included time spent in the egg (interval [days] between date laid and hatching date; hereafter referred to as ‘Time’) as a covariate in our models (see below) to account for phenotypic variance due to differences in developmental time within the egg. All fish husbandry was done in accordance with the University of Alabama’s Institutional Animal Care and Use Committee (Protocol #14-05-0070). A total of 10–15 individuals were collected from most genotype-age combinations (1, 15, and 100 days post hatching [DPH]) (Table S1). Although our sampling for each genotype–age combination was not completely balanced (Table S1), other studies have found that unbalanced designs in quantitative genetic studies do not mandate restrictive assumptions about variance/covariance structures (Fry 1992). We limited our focus to the first 100 DPH because this is the age, on average, at which K. marmoratus typically reaches sexual maturity (Cole and Noakes 1997), and because jumping performance is only significantly correlated with caudal peduncle bone morphology before this age (Styga et al. 2018). Each individual was euthanized in a lethal dose of pharmaceutical grade MS-222 (Finquel®), which was buffered to a neutral pH with sodium bicarbonate. Each hatchling was then stored individually in a 1.5 mL centrifuge tubes filled with 100% ethanol prior to morphometric analysis.

Bone morphometrics

Specimens were cleared and stained individually in 1.5 mL centrifuge tubes, using a modified version of the procedure developed by Webb and Byrd (1994) (Table S2). The clearing and staining process produces transparent specimens with bones stained deep red, which we then photographed alongside a metric ruler in standard ichthyological position under a Zeiss 2000-C stereoscope using a Canon® Powershot G9 (Fig. S1). Images were then scaled to the nearest mm in ImageJ software (Schneider et al. 2012). Within ImageJ, we measured SL of the specimen, length and angle of epural (EPL and EPA) and parahypural bones (PHPL and PHPA), and length and width of hypurals (HYPL and HYPW) (seven measurements; Fig. S1) from each fish. Although ossification is often not complete at the beginning of larval development in fishes (Mabee et al. 2000), in our study, all individuals were fully ossified at 1 DPH (Fig. S2). Therefore, we did not have to consider variance in the presence/absence of bones across ages when estimating G.

Statistical analysis

We analyzed data using both univariate and multivariate linear mixed effect models to test our various hypotheses (described in detail below). Models were fitted with ASreml-R 3.0 (Butler 2009; Gilmour et al. 2002) in R version 3.4.1 (R Core Team 2017). All trait values were converted to standard deviation units (SDU) using the observed SD across all ages. This facilitates multivariate model fitting by removing among-trait scaling differences while retaining any among-age differences in (co)variance structures. Except where explicitly stated otherwise, all results are presented on this scale. In some instances, results are also presented in within-age class standard deviations such that, for example, age-specific genetic variances can be interpreted analogously to age-specific heritabilities. In addition to bone measurements, we treat SL as a morphological trait in its own right that may be genetically correlated with other traits. Any such correlations with SL might shape evolutionary change in other aspects of morphology (Marroig and Cheverud 2005), so we modeled this as an additional response variable rather than a ‘nuisance’ covariate.

To estimate genetic parameters, we included a random effect of genotype. Because experimental fish were produced by selfing of genetically distinct progenitors, this analysis partitions “among genotype” from total variance analogous to a study using recombinant inbred lines (as opposed to a family-based analysis of an outcrossing diploid). Statistical inferences were based on comparing nested models using likelihood ratio tests (LRTs) and on generating approximated 95% confidence intervals (see below). For LRTs we estimated χ2n as twice the difference in model log likelihoods. The number of degrees of freedom (n) was conservatively set to the number of additional parameters in the more complex model except when testing a single variance component in which case we assumed the test statistic to be asymptotically distributed as an equal mix of χ20 and χ21 (written below as χ20,1; Visscher 2006). In each model we controlled statistically for any effect of ‘Time’, defined as the differences in number of days between when an individual egg was laid and when it hatched, by including it as a fixed effect on all response variables. Although not directly relevant to the biological hypotheses being tested and so not discussed further below, statistical inferences on ‘Time' are presented in Table S3 for completeness.

Phenotypic (co)variance within and across ages

We estimated age-specific phenotypic variance–covariance matrices (P1, P15, P100) using a separate multivariate (seven traits) model for each age. These models had no random effects, such that all phenotypic (co)variance (conditional on ‘Time’) is allocated to the residual component. Using the matrix estimates and the sampling covariances of each element with them, we applied a parametric bootstrap approach (as described in Boulton et al. 2015) with 5000 draws to generate approximately 95% confidence intervals for each element (and, for covariance terms, the corresponding correlation) of P1, P15, and P100. Confidence intervals are approximate since the bootstrap approach makes an assumption of multivariate normality that may well be violated (see Boulton et al. 2015; Houle and Meyer 2015). Consequently, we do not calculate p-values but conclude (nominal) statistical significance when 95% confidence intervals do not include zero. We used bootstrap samples to test for significant differences between three aspects of age-specific P matrices: total phenotypic integration, as calculated by the mean squared correlation among all traits; total phenotypic variation, as calculated by the matrix ‘trace’ (i.e. sum of diagonal elements); and pairwise-trait phenotypic correlations (rP) (see Houslay et al. 2018). For each pair of ages we also calculate the elements of the ‘difference matrices’ (e.g. P1–P15) and use the bootstrapped samples to generate 95% confidence intervals for each element (i.e. pairwise difference between age groups in a variance or covariance estimate). We do this because, while non-overlapping 95% confidence intervals on age-specific elements of P denote (nominally) significant differences at α = 0.05, it does not always follow that the difference in effect size is non-significant when 95% intervals do overlap (Austin and Hux 2002).

Genetic variation and G × A for each trait

To determine whether individual traits harbored significant genetic variance across ontogeny, and whether there was a genotype-by-age interaction (G × A), we fitted a series of three nested trivariate models using age-specific observations as the three response variables (e.g., SL age 1, SL age 15, SL age 100). Each model included a fixed effect of ‘Time’ on each response and a heterogeneous residual structure allowing non-genetic (i.e., residual) variance to differ among age-classes. Model A contained no genetic effects, Model B allowed genetic variance but assumed a single genetic parameter and an absence of G × A (such that, for any pair of ages x,y, VAx = VAy and rGx,y = + 1), while Model C estimated a fully unstructured matrix (i.e., genetic variance for each age and covariance between ages). LRT comparison of A and B provides a test for genetic variance, while comparison of B and C tests for G × A.

Genetic integration of morphological traits

We then used multivariate (seven traits) models to estimate the age-specific genetic variance–covariance matrices (G1, G15, G100) among morphological traits and test for changes across ontogeny (in a similar manner to our analyses of P1, P15, P100). For each age-specific model we included a fixed effect of ‘Time’ and a random effect of genotype on each trait. The non-genetic (residual) structure was modeled as an unstructured matrix, as was G. However, for comparison we also fitted a simpler model in which we used diagonal matrix (i.e., genetic variances only, all among-trait covariances assumed to be zero). LRT comparison of full and simplified (i.e., diagonal G only) provided a test of whether significant genetic covariance exists across all traits at the age in question. Although the data were scaled to overall (i.e., across all age classes) standard deviations as described earlier, we also estimated age-specific G matrices with data scaled to within-age SDUs. This scaling does not affect correlation structure but means that the diagonal elements can be interpreted as analogous to heritabilities (i.e. the proportion of variance—at that age—that is attributable to genetic effects). Comparisons among age classes then employed the bootstrapping procedure described earlier to compare the total genetic variation (i.e. trace, on both scales) across ages, pairwise–trait correlations (r) between each age group (see Houslay et al. 2018), and the level of genetic integration (calculated as the mean squared correlation across all traits).

Finally, as a test of Cheverud’s conjecture, we used our bootstrapped samples for P and G at each distinct age group (e.g., P1 vs. G1) to test whether these matrices differ significantly in estimated correlation structure among morphological traits.

Results

Phenotypic (co)variance within and across ages

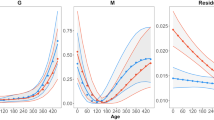
Confidence intervals estimated from our bootstrapping procedure revealed that the sum of phenotypic variance for all traits (i.e. trace) was significantly higher at P100 than at P1 and P15, while multivariate phenotypic variance did not differ significantly between P1 and P15 (Fig. 1; Table S4). Interestingly, different trait types contributed in opposing ways to the changes (and/or lack thereof) in P matrix trace with age. Specifically, while phenotypic variance in all linear distance measurements (EPL, PHPL, HYPL, HYPW, and SL) increased with ontogeny, the opposite pattern was seen for the angular measurements (EPA and PHPA) (Table 1). For each of the seven traits, we found significant differences in phenotypic variance between P1 and P15, P1 and P100, and P15 and P100 (Table 2).

Fig. 1
figure 1

Variation in overall phenotypic variance (Trace of the P matrix), overall genetic variance (Trace of the G-matrix; variance scale), overall heritability (Trace of the G-matrix; heritability scale), phenotypic integration (mean squared correlation, P-matrix), and genetic integration (mean squared correlation, G-matrix) across ages (1, 15, and 100 DPH). Confidence intervals are generated from 5000 bootstrap draws. Estimates are significantly different when 95% confidence intervals do not overlap. Also included are representative pictures of each age class with scale bars

Full size image
Table 1 Phenotypic variance (Vp), genetic variance (VG, variance scale), and genetic variance (H2; heritability scale) for each trait at 1, 15, and 100 DPH
Full size table
Table 2 Differences in phenotypic variance (Vp), genetic variance (VG, variance scale), and genetic variance (H2, heritability scale) for each trait between 1 and 15 DPH, 1 and 100 DPH, and 15 and 100 DPH
Full size table

As estimated by the mean-squared correlation, the extent of phenotypic integration (i.e. the relative strength of correlations among traits) differed among ages (point estimates of mean-squared correlation were 0.22, 0.25, and 0.17 at ages 1,15, and 100, respectively). Based on bootstrapped confidence intervals, both P1 and P15 were significantly more integrated than P100 (Fig. 1; Table S4) but P1 and P15 were not significantly different (Fig. 1; Table S4). Consideration of each off-diagonal element of P also revealed numerous differences between ages in the pairwise relationships among traits (Figs. 2 and 3; Tables S5 and S6). Scaled to correlations (which are perhaps easier to interpret than covariance), we find that 16 of the 21 pairwise-trait associations differed significantly between P1 and P15, 10 between P1 and P100, and 9 between P15 and P100 (Fig. 3; Table S6). Nonetheless, despite significant changes in correlation magnitude, it is also the case that many relationships were at least qualitatively consistent across ontogeny. For instance, in each age group: (i) EPL was significantly positively related to PHPL, HYPL, HYPW, and SL, (ii) PHPL was significantly positively related to HYPL, HYPW, and SL; (iii) HYPL was significantly positively related to HYPW and SL; and (iv) HYPW was significantly positively related to SL (Fig. 2; Table S5). On the contrary, only one (i.e. the correlation between PHPA and EPA) of the significant negative correlations evident within P1 (many of which involved PHPA) was maintained throughout ontogeny.

Fig. 2
figure 2

Pairwise-trait phenotypic correlations (rP, below diagonal) and pairwise-trait genetic correlations (rG, above diagonal) for 1, 15, and 100 DPH. Stronger correlations are indicated by narrower ellipses, while weaker correlations are indicated by ellipses approaching a spherical shape. EPL epural length, EPA epural angle, PHPL parahypural length, PHPA parahypural angle, HYPL hypural length, HYPW hypural width, and SL standard length

Full size image
Fig. 3
figure 3

Difference matrices for pairwise-trait phenotypic correlations (rP, below diagonal) and pairwise-trait genetic correlations (rG, above diagonal) from 1, 15, and 100 DPH. Differences are color coded by strength and direction. Differences shown in gray are positive and differences shown in black are negative. When ages are similar, the colored square is small; when ages are very different, the colored square fills the cell. EPL Epural length, EPA Epural angle, PHPL parahypural length, PHPA parahypural angle, HYPL hypural length, HYPW hypural width, and SL standard length

Full size image

Genetic variation and G × A for each trait

Based on the set of trivariate models formulated for each phenotypic trait, LRT comparisons showed that each trait exhibited significant genetic variance across ontogeny (see ‘Genetic variance’ in Table 3). In addition, the unstructured genetic (co)variance model provided a better fit to our data than the model that included a single genetic parameter. Thus, for each trait we find evidence of a significant genotype-by-age interaction (G × A) (Table 3). Significant G × A for each trait means that each trait has age-specific genetic variance, which will be reflected as between-age genetic correlations of less than +1 and/or changes in genetic variance with age. Here, for most traits, between-age genetic correlations were significantly positive between 1 and 15 DPH and 1 and 100 DPH, and significantly negative between 15 and 100 DPH (Table 3). Genetic variance estimates from these models also differed across ages. They are not presented here but were very similar to the corresponding estimates obtained from multi-trait models fitted to each age class (presented and discussed below).

Table 3 Likelihood ratio tests of genetic variance and genotype × age (G × A) interactions for each morphological trait
Full size table

Genetic integration of morphological traits within each age

Multivariate (seven traits) models fitted to each age group, revealed significant among-trait genetic covariance structure contributing to morphological integration (Fig. 2; Table S7). In all three age classes, a model that included genetic covariances among traits was significantly better than the model that assumed a diagonal G matrix only (χ221 = 188, P = <0.001; χ221 = 207, P = <0.001; χ221 = 176, P = <0.001 at ages 1, 15, and 100, respectively). Confidence intervals estimated from our bootstrapping procedure revealed that total genetic variance for the multivariate phenotype (i.e. trace of G) was significantly lower at G15 and G1 than at G100 (Fig. 1; Table S4). The trace of G1 did not differ significantly from that of G15. For individual traits, nominally significant differences in genetic variance were found in 11 out of 21 possible between-age comparisons (Table 2). One trait (SL) had a significant change in genetic variance between 1 and 15 DPH, and five traits changed significantly between 15 and 100 DPH, and 1 and 100, respectively. These significant effects were driven by a clear pattern of increasing genetic variance with age for the linear distance traits (but not for the angular measurements EPA and PHPA). Note, however, that no such pattern is evident when expressing (total) genetic variance as a proportion of (total) phenotypic variance within each age class (i.e. on a ‘heritability’ scale). On this scale, there were no significant differences between ages in G matrix traces (Fig. 1; Table S4) or in trait-specific ‘heritabilities’ (Table 2).

Using mean squared-genetic correlation to estimate age-specific genetic integration we found a qualitative pattern of decreasing integration with increased age, but we note that comparisons of this metric across age-specific G matrices were not statistically significant (Fig. 1; Table S4). Despite the lack of significant change in overall genetic integration, there were some differences in pairwise genetic correlations between age groups that were significant at the nominal level (Figs. 2 and 3; Table S7 and S8). Specifically, of the 21 pairwise genetic correlations in G, five estimates differed significantly between G1 and G15, five between G1 and G100, but none between G15 and G100 (Fig. 3; Table S8). Although this provides evidence for changes in genetic correlation structure, we acknowledge the possibility of Type I error here and also note that, as in P, most between-trait associations in G were qualitatively maintained across ontogeny. For instance, in each age group: (i) EPL showed a positive genetic correlation with PHPL, HYPL, HYPW, and SL; (ii) PHPL showed a positive genetic correlation with HYPL, HYPW, and SL; (iii) HYPL showed a positive genetic correlation with HYPW and SL; and (iv) HYPW showed a positive genetic correlation with SL.

Similarity of correlations in P and G within each age

At each age, we found support for Cheverud’s conjecture—pairwise correlations in P did an excellent job of predicting correlations in G (Table S9). Of the 21 pairwise trait correlations at each age, only four differed significantly between P1 and G1, two between P15 and G15, and two between P100 and G100. In seven of these eight instances, genetic and phenotypic correlation estimates were consistent in sign. The mean (SE) difference in magnitude between phenotypic and genetic correlations was −0.04 (0.04) at age 1, −0.1 (0.02) at age 15 and −0.09 (0.01) at age 100.

Discussion

Our results provide evidence in support of all five hypotheses advanced. First, for the set of morphological traits examined, we found that the among-trait phenotypic variance–covariance-correlation structure P differed between ages (Fig. 2; Table S5). In particular, the variance of traits measured as linear distances increases with age (Table 1). For a given size-related trait, differences in development (i.e. growth) must cause increased variance in size with age (Chevin 2015). Thus, the pattern detected here means that there is variation in the multivariate developmental trajectory. Notably however, this not only impacts variances, but also leads to an overall decline in phenotypic integration with age. Second, we show that phenotypic variance is underpinned by genetic variation for all traits at all ages (Table 3). Third, for each trait considered individually there is evidence of genotype-by-age interaction (G × A) and fluctuations in genetic correlations between ages (Table 3). Thus, there appears to be genetic variance in developmental trajectory. Fourth, at the multivariate level, G × A is reflected by changes in G across ages (Fig. 2; Table 3). In particular, there is an increase in overall (multivariate) genetic variance with age (Fig. 1; Table S4), which mirrors the phenotypic pattern (Fig. 1; Table S4). Genetic integration among the traits also appears to decline with age (Fig. 1; Table S4), although we acknowledge that this effect is not statistically significant. Finally, we also find support for our fifth hypothesis—that P is a valid proxy for G—in terms of understanding the among-trait correlation structure at each developmental stage (Table S9). In general, phenotypic correlations should more closely approximate genetic correlations as genetic variance underlying traits increases (Lande 1982; Hadfield et al. 2007; Delahaie et al. 2017). Thus, because genetic variance was relatively high for most of our traits at all ages considered, the similarity between age-specific G and P matrices is perhaps not surprising. We also note that all fish were raised under standardized lab conditions such that environmental sources of trait (co)variation were both limited and common to all genotypes.

Genetic effects and constraints on future evolution

Morphological traits, and the relationships between them, are influenced heavily by genetic factors at each stage in ontogeny. We found that genetic variance across all traits was significantly lower at 1 and 15 compared to 100 DPH (Fig. 1). The increase in overall (multivariate) genetic variance with age might initially suggest that selection on caudal peduncle morphology should be more effective at driving evolutionary change in older fish. However, the non-genetic component of variance also increases such that the relative contribution of genetic factors to phenotypic variance is actually relatively stable. Indeed, when traits were scaled to standard deviation units calculated within each age group (i.e. the ‘heritability’ scale), we found that for most traits (not including EPA and PHPA), genetic variance was large, explaining >40% of the phenotypic variance within each age group.

The maintenance of high genetic variance for most traits across ontogeny may be related to high spatial heterogeneity within the mangrove ecosystem. Noting that our lab population was founded from multiple field collection sites, spatial heterogeneity (within and among field sites) may have selected different genotypes (i.e., isogenic lineages)—with different phenotypes—to occupy specific habitats (Pantel et al. 2011). This scenario, which is often referred to as the ‘frozen niche model’, can maintain standing levels of genetic variance in asexual (or, in our case, selfing) species similar to those found in sexual species (Jokela et al. 1997; Negovetic and Jokela 2001; Niklasson et al. 2004).

Genetic relationships between traits were largely stable in sign over ontogeny, although some changes in genetic correlations (notably in magnitude) with age were found. In general, covariance in G influences multivariate evolutionary trajectories by imposing constraints on the response to selection (Badyaev and Martin 2000; Huchard et al. 2014; Nilsson-Örtman et al. 2015). In the simplest case of two traits, a genetic correlation may prevent traits from becoming independently optimized by selection, resulting in a potential trade-off. In this study, the positive correlation between HYPL and EPA at 1 DPH may represent one of these trade-offs. HYPL is positively, and EPA is negatively, related to jumping performance in young fish (i.e. <120 DPH) (Styga et al. 2018). Although the functional link between these bones and jumping may not be relevant to 1 DPH individuals because they do not jump, it may be important for other performance characteristics used by 1 DPH individuals such as the aquatic C-start, which utilizes similar motor patterns as the tail-flip jump (Perlman and Ashley-Ross 2016). Although the same relationship was also found at 100 DPH it may not represent a trade-off here because there appears to be decreased reliance on these bones as key determinants of jumping performance at this age (Styga et al. 2018). Indeed, at adulthood, other characteristics (i.e. strong muscles and well-developed neuromuscular junctions) may be playing a greater role in influencing jumping performance.

Taking a more fully multivariate view, despite the relatively high levels of genetic variance overall (at each age), if there are directions in multivariate trait space characterized by low genetic variance, then adaptive evolution in this direction is—at least relatively—constrained (Schluter 1996; Björklund et al. 2013). In fact, though the pattern was not significant, comparison of G matrices among ages suggests higher genetic integration in the youngest fish. This actually implies greater constraint here, at least in the limited sense that traits comprising the multivariate phenotype are less able to evolve independently at, for example, 1 DPH vs. 100 DPH. It is difficult to say more precisely what this means for expected evolution of the caudal peduncle since we currently lack quantitative estimates for age-specific selection gradients on morphological phenotype. An alternative view of the same phenomenon—namely multivariate G × A—arises if we consider the developmental process (rather than age-specific state) as the ‘target’ of selection. G × A means there is genetic variance in, and so evolutionary potential of, the ontogenetic trajectory of (multivariate) morphology. In this study, (genetically) distinct developmental trajectories increase the observed (genetic) variation in morphology over 100 days of development.

Does the G matrix reflect past selection?

G (and P) might reflect historical selection favoring particular trait combinations at different ages (Herrel and Gibb 2006; Gignac and Santana 2016; Penna et al. 2017). For example, strong correlations among bones and muscles in young jackrabbits and guinea pigs appear to result from strong selection for hopping and running performance, respectively, in this age group (Carrier 1983; Trillmich et al. 2003). However, ontogenetic variation in covariance structure may reflect historical age-dependent correlational selection on interactions among multiple traits so long as those interactions (at one time) improved fitness (Armbruster et al. 2014). Alternatively, directional selection on multiple traits simultaneously may have contributed to age-dependent genetic covariance (Penna et al. 2017). Either way, we expect that if historical selection on performance has been strong, then there should be strong correlations between traits in the direction that would have increased performance. In the case of the skeletal morphology within the caudal peduncle and its relationship to jumping performance, this means that G should depict a strong negative correlation between EPA and EPL/HYPL, and strong positive correlation between HYPL and EPL (Styga et al. 2018).

In this study, we found that the genetic correlations at 15 and 100 DPH are largely consistent with strong historical selection on jumping performance, although there were a few caveats (i.e. some of the correlations between traits in the direction that would increase jumping performance were not significant). We also found that genetic correlations at 1 DPH were not consistent with strong historical selection on jumping performance at this age (i.e. there was a significant positive relationship between HYPL and EPA). This result should, however, be considered in the context that 1 DPH individuals do not jump (Ashely-Ross pers. comm.).

The known functional relationship between caudal peduncle morphology and terrestrial locomotion performance (Styga et al. 2018) does not preclude other relationships that may complicate our interpretation. For instance, burst swimming facilitates predator avoidance in many fish larvae (Hale 1999), and might hypothetically require a totally different morphological architecture (Gibb et al. 2013). Equally, relationships among bone dimensions could change adaptively with age to maintain locomotor performance in the face of other development change not considered here (e.g., change in mass, gonad or digestive morphology) (Badyaev and Martin 2000). It is also possible that phenotypic integration is only critical for jumping performance early on (i.e. 15 DPH) because other mechanisms (e.g. motor learning) are able to compensate later. It seems clear that the complex relationships between natural selection, form and function, and genetic covariance structure across ontogeny require further investigation.

Our study investigated ontogenetic variation in genetic (co)variance, while maximally controlling for any environmental variation, in a vertebrate species that exhibits a unique reproductive system where self-fertilization predominates. Because offspring were derived from isogenic lines, the G estimated from this study should be viewed as a broad-sense genetic variance–covariance matrix instead of an additive genetic variance–covariance matrix common in other quantitative genetic studies (Careau et al. 2015). As such, while G does a good job of predicting P at each stage in ontogeny, we should be wary of generalizing without considerable scrutiny to outbred sexual diploids and to situations where individuals are likely to vary due to exposure to environmental factors, unless those factors can be identified and controlled/modeled.

Summary

We have demonstrated that genetic (co)variance structures among performance-related morphological traits are age dependent. This multivariate G x A can be conceptualized in two alternative ways: as shifting patterns of evolutionary constraint for responses to selection on age-specific morphology; or as the presence of genetic variance in the multivariate developmental trajectory itself. Regardless of whether the primary interest is in predicting future evolution or in understanding historical processes, it is important to bear in mind that adaptive phenotypes are produced by selection acting on heritable variation present throughout the full scope of development (Kingsolver and Pfenning 2014). Consequently, appreciating whether, and to what extent, G matrices change across ontogeny is an important—albeit empirically challenging—task. In this regard, we note that support for our final hypothesis is encouraging in a pragmatic sense. Specifically, in accordance with Cheverud’s conjecture, phenotypic correlations did an excellent job at predicting genetic correlations at each stage in development. While using P as a proxy for G always entails assumptions, our results suggest age-specific phenotypic patterns provide useful information for understanding the evolution of integration and development of multivariate morphology.

Data archiving

The data used in this manuscript has been achieved in Dryad repository: https://doi.org/10.5061/dryad.m56pj5b.