Abstract
Region-based genome-wide scans are usually performed by use of a priori chosen analysis regions. Such an approach will likely miss the region comprising the strongest signal and, thus, may result in increased type II error rates and decreased power. Here, we propose a genomic exhaustive scan approach that analyzes all possible subsequences and does not rely on a prior definition of the analysis regions. As a prime instance, we present a computationally ultraefficient implementation using the rare-variant collapsing test for phenotypic association, the genomic exhaustive collapsing scan (GECS). Our implementation allows for the identification of regions comprising the strongest signals in large, genome-wide rare-variant association studies while controlling the family-wise error rate via permutation. Application of GECS to two genomic data sets revealed several novel significantly associated regions for age-related macular degeneration and for schizophrenia. Our approach also offers a high potential to improve genome-wide scans for selection, methylation, and other analyses.
Similar content being viewed by others
Introduction
Genomic scans assess genomic regions (usually subsequences) with respect to some statistical measure and, ideally, quantify its consistency with the null hypothesis. Prominent applications include the detection of allele frequency differences between cases and controls in genetic association studies [1], the departure of the site-frequency spectrum (SFS) from the expectation under neutral evolution in selection analysis [2] and of differential methylation patterns in epigenomics [3]. Although statistical tests differ, the basic procedure remains similar across these applications by comprising [1] the prior definition of a set of contiguous analysis regions (bins) Bij, characterized by start positions i and end positions j (“binning”), sometimes defined by setting scanning parameter values (“sliding window”) [2]; the calculation of a suitable summary or test statistic, T(Bij), for each bin [3]; the distributional assessment of the statistics in order to identify extreme values, frequently including the calculation of p values, and often, but not always, followed by control of the family-wise error rate (FWER).
With long chromosomal sequences, it is not known in advance which subset of possible subsequences is most suitable for statistical summarization and testing, i.e., which regions will provide the highest power. Use of a priori fixed regions, including sliding-window approaches with fixed bins, will result in a highly likely increase in the type II error rate and, correspondingly, reduced power, because regions comprising the strongest signal(s) will almost certainly not be chosen prior to the analysis. A more probable scenario is that a region of interest will only partially coincide with the chosen analysis region. As a consequence, the signal will be diluted by inclusion of nonrelevant variants, split across multiple analysis regions, or both. Fixed, predetermined binning therefore represents a major limitation of current genomic scans. Moreover, due to unknown correlation structures between regions, the correction for multiple testing is often performed in a conservative way, e.g., by use of Bonferroni correction for the number of tested regions [4].
Here, we focus on the application of the exhaustive scan approach to rare-variant (RV) association studies based on sequenced or genotyped data. RV analysis is motivated by the observation that although genome-wide association studies (GWAS) have usually identified common risk alleles for a wide range of complex diseases [5], most of these alleles cause at most moderate increases in risk and contribute little to the overall heritability of diseases individually, leaving large portions of human diseases’ heritability unexplained [5, 6]. This observation motivated studies to focus on the role of RVs, aiming to deliver functionally interpretable variants of moderate-to-large effect sizes and explaining additional disease risk variability. Region-based RV association analyses are based on the assumption that multiple RVs in physical proximity have similar effects on the phenotype. Under this assumption, multiple RVs in a genomic region can be aggregated and analyzed as a unit. In this context, the most common approach is to define fixed bins by either using the locations of known protein-coding genes as regions of analysis or by using a sliding-window approach with two fixed parameters, namely the window size and the step size. Either choice is fundamentally limited in scope, and will consider only a tiny fraction of possible subsequences.
In RV analysis, “rareness” itself is another parameter that is usually defined by a threshold of the minor allele frequency, MAFT. Alternatively, weighting schemes have been proposed that assign lower weights to variants with higher allele counts. This does not fully solve the problem of rareness thresholds, as the shape of the weighting function is usually chosen somewhat arbitrarily and without a stringent justification of its usefulness.
Noteworthy progress towards non-parametric RV analysis has been made in [7], who proposed the Variable-Threshold (VT) approach, in which test statistics for all possible MAFT are computed and the optimal MAFT is adapted from the data. The method uses permutation testing to adjust for the large number of tested hypotheses within a bin; it is therefore computationally more intense. In [8], the VT method was extended to the collapsing and the CMAT tests [9], whereas the method became computationally impractical for regression models.
However, even if the problem of the unknown “rareness” can be alleviated, the problem of the choice of analysis regions remains, which has been acknowledged before [10,11,12,13]. The present work can be regarded as the extension of the VT method to binning of analysis regions (“variable binning”).
Here, we suggest to perform an exhaustive scan for phenotypic association using a simple RV test (collapsing method, COLL) as the test statistic [14]. COLL dichotomizes samples by their carrier status, i.e., whether the corresponding individual is carrying at least one rare allele in the analysis region. In a case–control study design, a 1-df χ2-test can be applied to the resulting 2 × 2 contingency table. Interestingly, despite its relatively simple disease model, the power of COLL is comparable with more sophisticated methods for a wide range of disease models [9]. However, COLL is inherently limited in that it can only be applied to binary phenotypes only, does not account for covariates, and has limited power if the associated RVs in the region have different effect directions. A large number of more advanced tests have been developed, see [8, 15, 16] for categorizations. A notable example is the sequence kernel association test (SKAT) [17], which is a variance-component test and sensitive to mixed effect directions in a region, allows for inclusion of covariates, and can be used with binary and quantitative phenotypes.
Here, we propose the use of exhaustive scans to all possible contiguous subsequences and to perform multiple-testing correction by obtaining the distribution of extreme p values from replicates of the data simulated under the null hypothesis by repeatedly permuting case–control status. We introduce this approach, in an exemplary way, for a specific application, namely the genomic exhaustive collapsing scan (GECS) approach for COLL, and present a computationally efficient implementation of GECS. We show that although the number of possible contiguous bins for all RVs at a single chromosome is very large, namely n(n + 1)/2 with n variants, the number of distinct bins dramatically reduces by about three to four orders of magnitude, rendering GECS feasible and scalable even for whole-genome sequence data in large sample sets. Furthermore, this acceleration allows control of the FWER via repeated case–control status permutation that provides optimal power to detect association [18]. Based on simulations, we derive empirical thresholds for genome-wide significance in case–control WGS studies for different sample sizes and minor allele frequency thresholds, in an approach analogous to [19]. In applying GECS to two real-world data sets, we show that our approach is feasible and scalable with large, modern association studies and provides a fine-grained, base-pair resolution of associated regions contained in the data (Fig. 1), which will enable a deeper understanding of the effect of RVs on the etiology of complex diseases.
Methods
GECS algorithm
Our method is based on the observation that under the collapsing test COLL (see Supplementary Note a), test statistics for all locally distinct bins can be computed efficiently without explicit computation of each bin. In pseudocode, the algorithm can be formulated as follows:
Here, n is the number of variants on a linear chromosome, Bij is the set of carriers of a minor allele (which can be conveniently parametrized by a binary array) and T(Bij) is the corresponding test statistic. See Supplementary Notes b–d for a more detailed justification and description of the algorithm.
Simulation studies
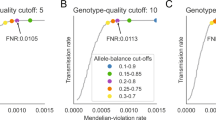
We performed extensive simulation studies (Fig. 1) to (i) determine genome-wide significance thresholds for region-agnostic RV testing (Table 1), (ii) assess the statistical power of our approach (Figs. 2, 3 and S5–S12), and (iii) benchmark the feasibility of GECS for analysis of large genomic data sets (see Supplementary Note f) for the description of the studies and (Supplementary Note g) for the results.
Results are given for studies with proportion of neutral rare variants (PNV) = 0.3, different simulated window sizes (x-axis), and different proportions of detrimental rare variants (PDV) (y-axis). Black lines: GECS; red lines: SMA. In each grid cell, the power is presented on the y-axis and OR intervals on the x-axis. For an overview see Table S20.
Results are given for studies with proportion of neutral rare variants (PNV) = 0.3, different simulated window sizes (x-axis), and different proportions of detrimental rare variants (PDV) (y-axis). Black lines: GECS; red lines: SMA. In each grid cell, the power is presented on the y-axis and OR intervals on the x-axis. For an overview see Table S20.
Real-world data set analysis
Advanced age-related macular degeneration (AAMD) GWAS from the International AMD Genomics Consortium (dbGaP accession: phs001039.v1.p1) and schizophrenia (SCZD) exome sequencing study from a population-based schizophrenia Swedish case-control cohort (dbGaP accession: phs000473.v2.p2). We validated the most interesting bins by performing association testing with SKAT (p′ values, see Supplementary Note h). For the description of the data sets, the quality control, and the analysis setup see Supplementary Note e and h.
Results
Real-data analysis
Advanced age-related macular degeneration (AAMD)
We applied GECS to the whole-genome imputed case–control data of the subset of samples with European ancestry and cases with AAMD (Table S3). The strongest signals were detected in bins overlapping with protein-coding genes, including human leukocyte antigen B (HLA-B), HLA-DRA, and MICB in chromosome 6, FYB in chromosome 5, CFD, and NRTN in chromosome 9, and PLEKHA1 in chromosome 10 (Table S10). These genes, among others, are involved in the regulation of the immune system process and innate immune response. The set of genes overlapping significant bins were enriched in the activation of immune response pathway, in particular, the positive regulation of immune response (7.36-fold enrichment, Bonferroni-corrected p value of 4.4 × 10−4; see Table S11). In addition, GECS reidentified and refine most of the previously reported RV associations with AAMD (e.g., CFI, C3, SKIV2L, SYN3, and C9) (Table S12) [20, 21]. Odds ratios of identified bins ranged between 0.5 and 3.45, indicating that carrier status can be both positively and negatively correlated with AAMD. Significant bins with OR > 1 were overrepresented on chromosome 6, with OR values ranging between 1.1 and 1.4 and bin sizes ranging between 2 and 26 rare variants.
Notably, bin 6.I (chr6: 31,323,455–31,323,745 bp, hg19) of 12 rare variants (MAF ≤ 0.05) was found to be significant with a p value of 3.48 × 10−10, p′ value of 2.76 × 10−11, and OR of 1.18 [1.12, 1.24]. This bin overlaps with the protein-coding HLA-B, which plays a very important role in the immune system (Fig. S17). Interestingly, a previous study found a positive correlation between the HLA-B allele HLA-B27 with AAMD [22]. Also, bin 6.II (chr6: 31,473,707–31,474, 883 bp) overlapped with the MICB gene and comprised six rare variants (MAF ≤ 0.05). This bin was found to be significantly associated with AAMD with p value 1.71 × 10−10, p′ value of 2.08 × 10−13, and OR = 1.27 [1.19, 1.38] (Fig. S18). An example for a bin with OR < 1 is 10.I (chr10: 124,226,492–124,249,185 bp), which comprised 64 rare variants (MAF ≤ 0.05), was found to be associated with AAMD with p value of 2.09 × 10−84, p′ value of 2.96 × 10−30, and OR = 0.62 [0.59, 0.65]. Notably, this bin, with an apparently protective effect of rare alleles overlaps with HTRA1, which has been functionally studied in the context of AMD [23]. The association signal was independent from multiple common variants found to be associated with AAMD in this gene [24, 25]. Another noteworthy finding was bin 6.IV (chr6: 31,878,006–31,878,721 bp) with five rare variants in the C2 gene (MAF ≤ 0.05) was found to be significantly associated with AMD with p value of 3.78 × 10−80, p′ value of 1.23 × 10−70, and OR = 0.53 [0.50, 0.57] (Fig. S19). Our finding is in line with the known role of some protective haplotypes in the C2-AS1 region were found to be significantly reducing the risk of AMD [26]. For more results, see Supplementary Note i.
Schizophrenia
We applied GECS to the WES variant data (Table S5). The analysis was conducted with three MAF thresholds, and the genome-wide significance threshold in the combined study comprised 1.87 × 10−08 (Tables 2, Figs. S21–24). Most of the alleles identified to be significantly associated to schizophrenia had OR < 1, so that the carrier status appeared to be protective (Table 3, S15). For example, bins like 15.I (chr15: 73,044,829–73,044,833 bp), 17.I (chr17: 49,239,143–49,239,143 bp), and 22.I (chr22: 17,687,954–17,688,129 bp) overlapped with genes on chromosome 15 (ADPGK), 17 (NME1, NME2), and 22 (CERC1) (Table S16). These genes are involved in the purine nucleoside triphosphate biosynthetic process, which has previously been demonstrated as to be strongly linked to the development of schizophrenia [27]. On the other hand, bin 19.I (chr9: 8,999,386–9,028,410 bp), comprising 62 rare SNPs (MAF ≤ 0.03), was found to be significant, with p value 2.59 × 10−09, p′ value 3.11 × 10−10, and OR = 1.29 [1.19, 1.40], covering exonic regions of the MUC16 gene (Fig. S25). Although some rare alleles in MUC16 were reported in association to schizophrenia, none of the 62 rare alleles in this bin were reported before. Moreover, genes covered by bins 15.I, 17.I, 19.I, and 22.I were found to have a function in the small molecule metabolic processes. Interestingly, gene PRSS3 was covered by bin 9.I (9: 33,796,672–33,798,630) comprising 20 rare variants (MAF ≤ 0.05), p′ value of 3.89 × 10−11, and OR = 1.37 [1.24, 1.52]. This gene was not previously reported to be related to schizophrenia. The relatively small sizes of the detected significant bins in the WES data of schizophrenia indicate that the availability of large whole-genome sequencing studies will enable a considerable power gain for our method (Table S17).
Discussion
While genome-wide scans with heuristically predetermined analysis regions are an established approach, they are limited in their scope, resolution, and power by requiring a prior choice of the analysis regions. In the context of selection analysis, Akey fittingly compared the scan with a hatchet and called for more refined scalpel-like approaches [28]. We argue that in Akey’s analogy, the exhaustive scan is an electron microscope, as it allows for base-pair-level analysis of genomic regions, with genome-wide, nonconservative, optimally powerful correction for multiple testing using replicates of the data generated under the null hypothesis.
GECS is scalable to large association studies of imputed and sequenced variant data, as demonstrated by our simulation of the null model. The efficiency of our implementation allowed us to estimate significance thresholds for RV analysis in whole-genome sequenced data for association studies comprising up to 20,000 individuals. As a by-product, the analysis offered another opportunity to study significance thresholds (FWER control at 5%) for single-marker analysis (SMA), which, even for small sample sizes of N = 1000, was found to be stricter (α = 2.95 × 10−8) than the commonly used threshold of α = 5.0 × 10−8. This result is consistent with previously published results [19, 29] and highlights the need to abandon the “agreed-upon” significance threshold of 5.0 × 10−8, which is anticonservative for large-scale association studies.
The estimates of α allow us to assess the absolute power of the region-based exhaustive scan in future whole-genome deeply sequenced data sets. In contrast to previous studies [9], the power study is free from the assumption that the simulated region and the analysis region happen to coincide. Since the exhaustive scan is guaranteed to identify the most strongly associated regions, our FWER control accounts for the multiple-testing “cost” of finding these regions, which was ignored in previous studies. Overall, the power of GECS is higher, or at least comparable with SMA for small to moderate odds ratios of associated rare variants (1.01 ≤ OR < 3), being the OR range expected to be most commonly found in complex diseases. For large sample sizes and large effect sizes, GECS, in general, offers no advantage to detect association. This result reflects the expectation that given a large sample size, enough rare alleles will be present to detect associated variants with sufficient power in single-variant tests [30].
We applied GECS to real-world data sets, namely of AAMD (imputed microarray data) and of schizophrenia (WES), and performed very stringent quality control of both sets to avoid possible type I errors. Application of GECS to AAMD confirmed a multitude of previously reported rare associated SNPs, for which SMA was underpowered to pick up many signals due to the low MAFs. We confirmed that exhaustively scanning for association through all possible combinations of contiguous rare variants from different MAF thresholds alleviates the limitations posed by previous fixed-bin strategies. The in-depth follow-up analysis showed high enrichment of genes covered by identified bins in pathways with key roles in the development and function of immune system. Our approach was also successfully applied to the schizophrenia data set, however, judging by the limited spatial extent of the resulting bins, the approach might be underpowered due to limited coverage of the genome in WES studies and will probably improve with availability of WGS data.
GECS is a powerful approach for detecting phenotypic association of genomic regions harboring rare variants and for refining our understanding of their contribution to predisposition for complex diseases. We conclude that our approach is well-suited for whole-genome and whole-exome association analyses. However, GECS utilizes the simple allele counting function of COLL to achieve perfect, essentially base-pair-level spatial resolution. As COLL is only able do dichotomize individuals by the carrier status, the test is not able to distinguish between carriers of one or more minor alleles. We alleviated the limitations of COLL by performing follow-up analysis of candidate regions with locally exhaustive scans using SKAT. Enabling the exhaustive scan with more sophisticated tests that take more sources of information into account, like allele counts and covariates, might reveal further associated candidate regions. The challenge of extending the exhaustive scan approach to more complex association tests is purely computational in nature. Our algorithm does not generalize to other published association tests in a straightforward manner, so that new solutions will be required to generalize the exhaustive association scan beyond the collapsing method.
Application of exhaustive scans is not limited to association testing and could be useful in further applications, in particular for studying methylation and evolutionary selection. In fact, our preliminary results show that the exhaustive scan is feasible for the study of selection when used with SFS-based tests such as Tajima’s D (data not shown). This is due to the fact that the computational complexity of SFS-based tests is independent from the number of individuals in the study, since only allele count data is required. As a consequence, the quadratic space of all contingent regions can be computed by brute force, even for very large data sets. Moreover, modern, efficient coalescent simulators such as msprime [31] and fastsimcoal2 [32] can be used to simulate the null model under neutral evolution under realistic demographic histories [33], which can be used for FWER-controlled p values.
In summary, we developed a method that allows for an exhaustive scan of all possible contiguous genomic regions with the collapsing test and eliminates the choice of candidate bins. Instead, the space of all possible bins is tested. This eliminates binning as a source of type II error and is expected to improve power. Furthermore, the speed-up by several orders of magnitude allows for computation of nonconservative genome-wide significance thresholds by permutation, leading to improved power when compared with conservative correction methods such as Bonferroni’s. We show that GECS indeed improves statistical power in both simulated and empirical data sets.
Data availability
The software is written in C++ and is available at https://github.com/ddrichel/GECS.
References
Christophersen IE, Rienstra M, Roselli C, Yin X, Geelhoed B, Barnard J, et al. Large-scale analyses of common and rare variants identify 12 new loci associated with atrial fibrillation. Nat Genet. 2017;49:946.
Nielsen R, Williamson S, Kim Y, Hubisz MJ, Clark AG, Bustamante C. Genomic scans for selective sweeps using SNP data. Genome Res. 2005;15:1566–75.
Jaffe AE, Murakami P, Lee H, Leek JT, Fallin MD, Feinberg AP, et al. Bump hunting to identify differentially methylated regions in epigenetic epidemiology studies. Int J Epidemiol. 2012;41:200–9.
Chen SY, Feng Z, Yi X. A general introduction to adjustment for multiple comparisons. J Thorac Dis. 2017;9:1725–9.
Manolio TA, Collins FS, Cox NJ, Goldstein DB, Hindorff LA, Hunter DJ, et al. Finding the missing heritability of complex diseases. Nature. 2009;461:747–53.
Feldman MW, Ramachandran S. Missing compared to what? Revisiting heritability, genes and culture. Philos Trans R Soc Lond B Biol Sci. 2018;373:20170064.
Price AL, Kryukov GV, de Bakker PI, Purcell SM, Staples J, Wei LJ, et al. Pooled association tests for rare variants in exon-resequencing studies. Am J Hum Genet. 2010;86:832–8.
Drichel D, Herold C, Lacour A, Ramirez A, Jessen F, Maier W, et al. Rare variant testing of imputed data: an analysis pipeline typified. Hum Heredity. 2014;78:164–78.
Zawistowski M, Gopalakrishnan S, Ding J, Li Y, Grimm S, Zollner S. Extending rare-variant testing strategies: analysis of noncoding sequence and imputed genotypes. Am J Hum Genet. 2010;87:604–17.
Wu MC, Kraft P, Epstein MP, Taylor DM, Chanock SJ, Hunter DJ, et al. Powerful SNP-set analysis for case-control genome-wide association studies. Am J Hum Genet. 2010;86:929–42.
Fier H, Won S, Prokopenko D, AlChawa T, Ludwig KU, Fimmers R, et al. ‘Location, location, location’: a spatial approach for rare variant analysis and an application to a study on non-syndromic cleft lip with or without cleft palate. Bioinformatics. 2012;28:3027–33.
Freedman R. Schizophrenia. N Engl J Med. 2003;349:1738–49.
Timpson NJ, Greenwood CMT, Soranzo N, Lawson DJ, Richards JB. Genetic architecture: the shape of the genetic contribution to human traits and disease. Nat Rev Genet. 2018;19:110–24.
Li B, Leal SM. Methods for detecting associations with rare variants for common diseases: application to analysis of sequence data. Am J Hum Genet. 2008;83:311–21
Basu S, Pan W. Comparison of statistical tests for disease association with rare variants. Genet Epidemiol. 2011;35:606–19.
Lee S, Abecasis GR, Boehnke M, Lin X. Rare-variant association analysis: study designs and statistical tests. Am J Hum Genet. 2014;95:5–23.
Wu MC, Lee S, Cai T, Li Y, Boehnke M, Lin X. Rare-variant association testing for sequencing data with the sequence kernel association test. Am J Hum Genet. 2011;89:82–93.
Meinshausen N, Maathuis MH, Buhlmann P. Asymptotic optimality of the Westfall-Young permutation procedure for multiple testing under dependence. Ann Stat. 2011;39:3369–91.
Pulit SL, de With SA, de Bakker PI. Resetting the bar: statistical significance in whole-genome sequencing-based association studies of global populations. Genet Epidemiol. 2017;41:145–51.
Fritsche LG, Igl W, Bailey JN, Grassmann F, Sengupta S, Bragg-Gresham JL, et al. A large genome-wide association study of age-related macular degeneration highlights contributions of rare and common variants. Nat Genet. 2016;48:134–43.
Geerlings MJ, Kersten E, Groenewoud JMM, Fritsche LG, Hoyng CB, de Jong EK, et al. Geographic distribution of rare variants associated with age-related macular degeneration. Mol Vis. 2018;24:75–82.
Villegas Becerril E, Gonzalez Fernandez R, Perula Torres L, Lacomba MS, Gallardo Galera JM. HLA B27 as predisposition factor to suffer age related macular degeneration. Cell Mol Immunol. 2009;6:303–7.
Ng TK, Liang XY, Pang CP. HTRA1 in age-related macular degeneration. Asia Pac J Ophthalmol. 2012;1:51–63.
Liang XY, Lai TY, Liu DT, Fan AH, Chen LJ, Tam PO, et al. Differentiation of exudative age-related macular degeneration and polypoidal choroidal vasculopathy in the ARMS2/HTRA1 locus. Investig Ophthalmol Vis Sci. 2012;53:3175–82.
McKibbin M, Ali M, Bansal S, Baxter PD, West K, Williams G, et al. CFH, VEGF and HTRA1 promoter genotype may influence the response to intravitreal ranibizumab therapy for neovascular age-related macular degeneration. Br J Ophthalmol. 2012;96:208–12
Gold B, Merriam JE, Zernant J, Hancox LS, Taiber AJ, Gehrs K, et al. Variation in factor B (BF) and complement component 2 (C2) genes is associated with age-related macular degeneration. Nat Genet. 2006;38:458–62.
Fumagalli M, Lecca D, Abbracchio MP, Ceruti S. Pathophysiological role of purines and pyrimidines in neurodevelopment: unveiling new pharmacological approaches to congenital brain diseases. Front Pharmacol. 2017;8:941.
Akey JM. Constructing genomic maps of positive selection in humans: where do we go from here? Genome Res. 2009;19:711–22.
Auton A, Brooks LD, Durbin RM, Garrison EP, Kang HM, Korbel JO, et al. A global reference for human genetic variation. Nature. 2015;526:68–74.
Auer PL, Leal SM. From exomes to genomes: challenges and solutions in population-based genetic association studies. Eur J Hum Genet. 2017;25:395–6.
Kelleher J, Etheridge AM, McVean G. Efficient coalescent simulation and genealogical analysis for large sample sizes. PLoS Comput Biol. 2016;12:e1004842.
Excoffier L, Dupanloup I, Huerta-Sánchez E, Sousa VC, Foll M. Robust demographic inference from genomic and SNP data. PLoS Genet. 2013;9:e1003905.
Gazave E, Ma L, Chang D, Coventry A, Gao F, Muzny D, et al. Neutral genomic regions refine models of recent rapid human population growth. Proc Natl Acad Sci USA. 2014;111:757–62.
Acknowledgements
We would like to thank Dr Gabrielle Thorn for her organizing support.
Funding
The work was supported by the German Research Foundation grant BE 38/28/9–1. The funding organization did not have any influence on the design, conduct, or conclusions of the study. Open Access Funding provided by Projekt DEAL.
Author information
Authors and Affiliations
Contributions
DD conceived the study. GK performed the simulations and the data analysis. DD and GK wrote the analysis software, with contributions by TB. DD supervised the study, with some contributions by TB and MN. GK, DD, MN, and TB wrote the manuscript. All authors read, revised, and approved the final manuscript.
Corresponding author
Ethics declarations
Conflict of interest
For the sake of completeness, we declare that TB and DD provide compensated consulting services outside of academia, TB as an employee of xValue GmbH, and DD as an independent consultant. Although past and current clients might include biotech, life science, and pharma companies, the services are not related to the presented work and both authors are unaware of any possible conflict of interest.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Kanoungi, G., Nothnagel, M., Becker, T. et al. The exhaustive genomic scan approach, with an application to rare-variant association analysis. Eur J Hum Genet 28, 1283–1291 (2020). https://doi.org/10.1038/s41431-020-0639-3
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41431-020-0639-3