Introduction

Disorder in materials is undesirable because it prevents investigations of the intrinsic properties of the material. In correlated superconductors, however, disorder can be useful in manipulating superconducting properties. Even though the superconducting (SC) transition temperature (Tc) is decreased with a moderate level of disorder, the current-carrying capacity in high magnetic fields can be improved because disordered regions prevent vortex creep1,2. Strong disorder, however, breaks the coherence of SC electron pairs and gives rise to a change from the SC ground state to an insulating or non-SC metallic state at the quantum breakdown of superconductivity (QBS)3,4,5,6,7,8,9,10,11,12,13,14. As disorder increases, superconducting islands may appear in the destroyed background of non-SC regions owing to inhomogeneous suppression of superconductivity3,4,5,6,11. Because the presence of SC islands and the phase coherence among them are important to the emergence of superconductivity, numerous experimental and theoretical efforts have been expended to understand the role of disorder in the SC state3,4,5,6,7,8,9,10,11,12,13,14. However, systematic control of disorder in correlated superconductors has been technically difficult.

Ion beam irradiation is one approach that provides engineered disorder in SC materials. For example, low-energy ion irradiation produces atomic lattice displacements in crystalline materials because elastic scattering between incident ions and atoms in the target material is dominant15,16,17. In addition, the tunability and simplicity of this technique make the localization of Cooper pairs in disordered SC systems easier to control. The quasi-two-dimensional superconductor MgB2 is an ideal example for this study because of its high Tc of 40 K and the possibility of localizing Cooper pairs near the QBS in disordered MgB218,19.

In this work, we report magnetic-field-induced quantum breakdown of superconductivity in MgB2 thin films via irradiation with 140-keV Fe-ion beams. The metallic characteristics of MgB2 were significantly suppressed after low-energy ion irradiation. When subjected to a magnetic field, the irradiated MgB2 films revealed QBS at a critical field Hc of 3.2 Tesla. The superconductor-to-insulator transition (SIT) within the SC state indicates that SC islands are formed in the MgB2 film due to irradiation and that phase coherence between them is destroyed by the applied magnetic field. When the irradiated MgB2 layer (SD) is in contact with a pristine, undamaged MgB2 layer (SS), the SIT-like behavior disappears. Here, the two layers comprise a SD/SS bilayer. Suppressed superconductivity in the damaged SD layer was gradually restored to that of its pristine state as the thickness of the SS was increased, revealing a giant superconducting proximity effect (GSPE). These discoveries suggest that SC islands embedded in the normal matrix are the origin of GSPE and QBS in magnesium diboride bilayers and should provide valuable insights into the development of SC junctions and their applications.

Materials and methods

MgB2 thin films were fabricated using a hybrid physical-chemical vapor deposition (HPCVD) method, which is an effective technique for fabricating high-quality MgB2 thin films20,21. For Fe-ion irradiation, c-axis-oriented MgB2 thin films with various total thicknesses (t) of 215 (MB215nm), 440 (MB440nm), and 600 nm (MB600nm) were fabricated on c-cut Al2O3 substrates at a growth temperature of 680 °C, a pressure of 100 Torr and flow rates for H2 and B2H6 of 100 and 50 sccm, respectively. The fabrication and quality of the films were described in detail in previous studies20,22.

Fe ions with an energy of 140 keV were used to irradiate MgB2 thin films at the Korea Multi-purpose Accelerator Complex (KOMAC) at room temperature. Samples MB215nm, MB440nm, and MB600nm were placed together in a sample holder for irradiation. The mean projected ion range (Rp) and the thickness tD of the irradiated MgB2 thin films were simulated with Monte Carlo simulations. The Stopping and Range of Ions in Matter (SRIM) (The projected range of Fe ions and the damage events in the MgB2 thin film were calculated using the SRIM software (http://www.srim.org/).), a MgB2 target density of 2.57 g/cm3 and averaged displacement threshold energy values of 20 eV (Mg) and 46 eV (B) were used23. As the total damage and the damage profile depend on dose level for the same incident energy, different dose levels were used to obtain various tD values ranging from 126 to 203 nm (see Figs. S1 and S2 in SI).

Changes in the c-axis lattice constants of MgB2 layers damaged by Fe-ion irradiation were investigated by X-ray diffraction (θ–2θ scan) before and after irradiation. Values of Tc for the MgB2 bilayers before and after irradiation were determined by using the temperature dependence of electrical resistivity (ρ), as obtained using a Physical Property Measurement System (PPMS 9 T, Quantum Design). Bulk superconductivity was evaluated by using the zero-field-cooled (ZFC) dc magnetization (M) obtained with a Magnetic Property Measurement System (MPMS 5 T, Quantum Design). A standard four-probe method was used for electrical-resistivity measurements. Measurements of the magnetic field dependence of resistivities of the MB215nm bilayers with γt = 0.12 and 0.06 were performed using the PPMS. The temperature dependences of the zero-bias conductances (ZBCs) of pristine MB600nm and the bilayer with γt = 1.96 were measured in various magnetic fields by soft point-contact spectroscopy (SPCS) in the PPMS (14 T, Quantum Design). Soft-point contacts on the surface of MB600nm were made with a gold wire (diameter: 30 μm) imbedded in a drop of Ag paint at the end nm. The total contact diameter of the Ag paint on the film surface was ~50–100 μm, where thousands of parallel nanoscale junctions were assumed to exist between individual Ag particles and the film surface for SPCS24.

Results and discussion

Figure 1a schematically illustrates the effects on a pristine crystal caused by low-energy iron-ion irradiation. Because elastic scattering of the incident ions by nuclei in the materials is dominant for low-energy ion irradiation, lattice displacements, together with the formation of vacancies and interstitials, take place in the irradiated crystal, leading to changes in SC critical properties15,16,17. To probe tunable SC properties by introducing lattice disorder, we used low-energy iron-ion irradiation to fabricate MgB2 bilayers composed of SD (damaged MgB2 layer) and SS (undamaged MgB2 layer), as depicted in Fig. 1b. The superconductivity of SD was destroyed by the disorder produced from ion irradiation, whereas the superconductivity of SS was maintained as that of the pristine state because it was unaffected by irradiation.

Fig. 1: Formation of MgB2 bilayers by 140-keV Fe-ion irradiation.
figure 1

Schematics of a displacement damage caused by elastic scattering between the incident Fe ions and Mg/B atoms and b MgB2 bilayer (SD/SS) formed by ion irradiation. The SD layer, with a thickness of tD, is the MgB2 layer damaged by ion irradiation, whereas the SS layer, with a thickness of tS, is the undamaged MgB2 layer. c Enlarged views near the (002) peaks of XRD patterns for Fe-ion-irradiated MB600nm. The (002) peak of MB600nm is split into two, with the first (1st) and the second (2nd) peaks reflecting the formation of MgB2 bilayers. The 1st and 2nd peaks correspond to the undamaged and damaged MgB2 layers, respectively, as indicated by the arrows. d The c-axis lattice parameters of the pristine film and the bilayer, where cpri. from the 1st peak and c2nd from the 2nd peak are similar for all samples irrespective of the thicknesses of the films and the irradiation dose levels.

Full size image

Figure 1c shows a representative enlarged view near the (002) peaks of X-ray diffraction (XRD) patterns for MgB2 with a thickness of 600 nm (see Fig. S3 in SI). The (002) peak splitting indicates the separation of films into two layers after ion irradiation, and the peak position for the irradiated part of the film shifted to a smaller angle as the dose of irradiating Fe ions was increased; this corresponded to an increase in the c-axis lattice constant, as presented in Fig. 1d. The appearance of a secondary peak at a lower angle reflects the formation of MgB2 bilayers owing to the separation of damaged and undamaged MgB2 layers. All MgB2 films with thicknesses of 215, 440, and 600 nm, which are identified as MB215nm, MB440nm, and MB600nm, respectively, show the same dose dependences of the c-axis lattice constant and changes in the c-axis lattice constant Δc, which are plotted as the left and right ordinates of Fig. 1d, respectively. The Δc values calculated from the position of the second (2nd) peak as a function of the dose are similar for all samples regardless of the thicknesses of the films, showing that the damaged MgB2 layers in all the films have similar degrees of disorder produced by irradiation.

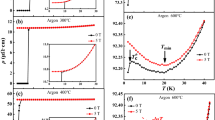
Figure 2a–d contains plots of the electrical resistivities (ρ) of MgB2 films with a total thickness of 215 nm as a function of temperature for the pristine layer and the bilayers (SD/SS) with γt = 0.54, 0.30, and 0.06, respectively (see Fig. S4 in SI). Here, γt is the ratio (γt = tS/tD) between the thickness tS of SS and thickness tD of SD layers, and the value of ρ(T) is normalized by the resistivity value (ρn) at the onset temperature of the SC transition for each sample. The ρ(T) for pristine MB215nm decreased with decreasing temperature, exhibiting metallic behavior. As the thickness ratio γt decreased, the metallic characteristic was suppressed owing to an increase in the relative thickness of disordered layer SD. For the bilayer with γt = 0.06, ρ(T) reached a minimum near 112 K and increased with further decreases in temperature, exhibiting insulating behavior. Below 40 K, ρ(T) began to decrease because of the SC islands formed in the irradiated films.

Fig. 2: Temperature dependences of the electrical resistivity and the magnetizations of bilayers of MB215nm.
figure 2

a–d Representative temperature dependences of electrical resistivity (ρ) are shown for pristine MB215nm and MgB2 bilayers with γt = 0.54, 0.30, and 0.06. Here, ρ(T) is normalized to its value at Tc onset (=ρn) for each sample for comparison. e–h Temperature dependences of zero-field-cooled (ZFC) and field-cooled (FC) dc magnetizations (M) for the same sample set as in Fig. 2a–d; the ZFC and FC M data were measured at 5 Oe for all samples. The SC volume fraction inferred from the ZFC M of the pristine film was assumed to be 100% at 2 K, while those of the bilayers with different values of γt were estimated in comparison with the ZFC M value of the pristine film.

Full size image

The dependence on the thickness ratio γt of the SC volume fraction of the MgB2 bilayers is presented in Fig. 2e–h, which shows the zero-field-cooled (ZFC) and field-cooled (FC) dc magnetizations measured at 5 Oe for all samples (see Fig. S5 in SI). The SC volume fraction of pristine MB215nm at 2 K was assumed to be 100%, while that of bilayers with different values of γt was estimated relative to pristine MB215nm. As γt decreased, the SC volume fraction decreased, and the SC transition width of the ZFC M(T) curve broadened because the magnetic field easily penetrated into disordered MgB2 SC regions. When the value of the thickness ratio γt was 0.06, interestingly, the ZFC and the FC M(T) for the bilayer showed clear separation at quite high temperatures even though the SC volume fraction was < 0.1%. Taken together with ρ(T), the small volume fraction of M(T) resulting in the film with γt = 0.06 is suggestive of the formation of local SC regions in the damaged MgB2 layer.

Superconductivity in disordered SC systems is not suppressed homogeneously, but disorder-induced inhomogeneity does occur, and local SC regions can be formed. The magnetic field, one of the nonthermal control parameters that can introduce a quantum phase transition at zero Kelvin, is expected to be effective in suppressing phase coherence between local SC regions, i.e., SC islands, thus driving quantum breakdown of superconductivity in disordered SC thin films3,4,5,6,11,12,13,14,25,26,27,28. Figure 3a, b presents ρ(T) of MgB2 bilayers with a total thickness (t = tD + tS) of 215 nm for γt = 0.12 and 0.06, respectively, with several magnetic fields applied perpendicular to the film plane. Evidence for a magnetic-field-induced QBS was observed for both bilayers, wherein ρ(T) increased with decreasing temperature below the SC transition temperature, Tc. At 0 Tesla, the resistivity gradually decreased with decreasing temperature owing to the superconducting transition in SC islands and the weak correlation between SC islands for T < Tc. As the applied magnetic field was increased, the rate of decrease in ρ(T) became weaker because of the suppression of phase coherence between SC islands. At 3 T, ρ(T) was almost constant, showing a plateau behavior. With a further increase in the field, ρ(T) increased with decreasing temperature, reflecting insulating behavior due to the destruction of interisland coupling (see Fig. S6 in SI). The magnetic field dependences of the resistivities are plotted for various temperatures in the insets of Fig. 3c, d. A crossover from an SC state to an insulating-like state is observed at the critical field (Hc) near 3.2 T for both bilayers, indicating that the SC islands were weakly coupled for 0 ≤ H ≤ Hc but electrically isolated for Hc < H ≤ Hc2.

Fig. 3: Quantum breakdown of superconductivity in magnesium diboride.
figure 3

Temperature dependences of the electrical resistivity (ρ) of the MB215nm bilayers with γt = (a) 0.12 and (b) 0.06 in magnetic fields applied perpendicular to the ab plane. The ρ(T)s of both MB215nm bilayers are lower at temperatures below Tc but show an upturn in the SC state when the magnetic field is larger than 3 T. Magnetoresistivities ρ(H, T) are plotted as functions of |H – Hc|/T1/zν for the bilayers with γt = (c) 0.12 and (d) 0.06. The insets of (c) and (d) show ρ(H) for several temperatures ranging from 2 to 6 K, in which the field dependences of the resistivities for the bilayers with γt = 0.12 and 0.06 exhibit single crossing points at 3.3 and 3.2 T, respectively. The magnetoresistivities ρ(H, T) of both bilayers are well scaled with the exponent zν = 7/3, indicating that quantum percolation between SC islands leads to a quantum breakdown of superconductivity (QBS) in the disordered MgB2 layers.

Full size image

The main panels of Fig. 3c, d reveal scaling of the resistivity as a function of |H−Hc|/T1/zν on a semilogarithmic scale. The dynamic exponent z is determined by a characteristic energy Ω ∝ ξ−z, where the SC correlation length ξ(H) ∝ |H−Hc|−ν. The best scaling was observed when the exponent product zν was 7/3, which is consistent with quantum percolation, indicating that quantum breakdown of superconductivity at Hc occurred owing to the destruction of phase coherence between SC islands in disordered MgB2 films3,12,13,29 (see Fig. S7 for classical percolation results in SI). We note that the critical resistance at the crossing point of magnetoresistance Hc was considerably smaller than the predicted quantum resistance (RQ = h/4e2 = 6.45 kΩ) at the quantum critical point3,5,29,30, indicating the possibility of an anomalous metallic phase in disordered MgB2 thin films3,10,30,31,32,33,34,35. A large charge carrier density and fermionic (unpaired electrons) excitations have been proposed for the origin of unusual metallic behavior and small critical sheet resistance33,34,35. The fact that MgB2 has a relatively large charge carrier density36 indicates that the anomalous metallic phase in disordered MgB2 thin films could be associated with contributions from a large number of unpaired electrons to the background conduction bath. However, further studies are required to understand the QBS in quasi-2D MgB2.

Figure 4a shows the γt dependence of the SC transition temperature (Tc,BL) of MgB2 bilayers, where Tc,BL was normalized by the Tc of the corresponding pristine MgB2 thin film (Tc,pri.) (see Figs. S8 and S9 in SI). The Tc,pri. values of MB215nm, MB440nm, and MB600nm were 39.3, 39.7, and 40 K, respectively. As tS increased, Tc,BL initially increased rapidly and saturated to Tc,pri. even though the thickness of the damaged layer, tD, was considerably larger than the coherence length of MgB2 (ξMgB2 ~ 7 nm). The presence of proximity effects up to the surface of SD was evidenced by SPCS (see Figs. S10 and S11 in SI). Although the behavior of Tc,BL with respect to the thickness ratio γt was similar to results for the proximity effect in N/S bilayers, the length scale of the proximity effect in SD/SS was considerably larger than the value predicted using conventional theory37,38. Here, the red solid line in Fig. 4a was obtained from the Werthamer theory in which the spatial variation in the BCS electron–electron interaction is considered37.

Fig. 4: Giant superconducting proximity effect in the MgB2 bilayer.
figure 4

a The SC transition temperature (Tc,BL) of MgB2 bilayers as a function of γt, where Tc,BL is normalized to the Tc of the corresponding pristine MgB2 thin film (Tc,pri.). Square, circular, and triangular symbols represent the three films with different thicknesses of 215 nm (MB215nm), 440 nm (MB440nm), and 600 nm (MB600nm), respectively. The thickness tD of layer SD (126–203 nm) was controlled by varying the dose of irradiated Fe ions. The red solid line is a fitting curve obtained by using the Werthamer theory that considers the spatial variation in the attractive electron–electron interaction. b Schematic view of the GSPE in the bilayer SD/SS. SC islands (SCI) in the SD layer sequentially form Josephson-junction chains between the SC islands. Phase coherence between the SC islands is enhanced by Cooper pairs that leak from the SS layer, which can lead to a power-law decay of the order parameter as a function of the distance from the SD/SS boundary, Δ(x) ∝ 1/x, rather than an exponential decay of Δ(x) ∝ exp(−x/ξD). Here, ξD is the leaking distance of the order parameter to the SD layer from the boundary of the SD and SS layers. The regular array of SC islands is exaggerated for simplicity, and the spacing between them could be larger than the coherence length of MgB2.

Full size image

The long-range proximity effect, the so-called giant superconducting proximity effect (GSPE), with an anomalously large leakage distance for Cooper pairs was often observed between two superconductors composed of the same materials but with different Tc values39,40,41,42,43,44. For example, when an optimally doped La1.85Sr0.15CuO4 (LSCO) layer with Tc ≈ 45 K was in contact with an underdoped La2CuO4-d (LCO) layer with Tc ≈ 25 K, GSPE was observed at temperatures higher than the Tc of LCO41. Several scenarios, such as phase fluctuations, amplitude fluctuations, and proximity-induced interface superconductivity, were proposed to explain the origin of the GSPE43,45,46,47,48. Figure 4b is a simple cartoon used to describe the GSPE in MgB2 bilayers (SD/SS), and the unusual proximity length scale may be understood by the presence of spatially distributed SC islands in SD. Phase coherence between the SC islands in SD can be enhanced by leaking of Cooper pairs from SS, sequentially forming strong Josephson-junction chains between the SC islands. The enhanced length scale from the proximity effect, in turn, gives rise to the suppression of the QBS in SD25,26,46. These findings underscore that SC islands formed in the normal matrix are the origin of the GSPE in the MgB2 bilayers composed of a damaged layer (SD) and an undamaged layer (SS).

Conclusion

In conclusion, we observe field-induced quantum breakdown of superconductivity in disordered MgB2 and a local pairing-induced GSPE in SD/SS MgB2 bilayers fabricated with low-energy ion irradiation. When an applied magnetic field is sufficiently high to break phase coherence among SC islands in SD, QBS is observed at a critical field Hc, the scaling of which is consistent with that of the quantum percolation model. As the thickness of SS is increased, the suppressed superconductivity of SD is recovered to that of the pristine state, and the QBS does not occur, not even at fields larger than Hc. Taken together, these findings underpin the conclusion that local superconducting pairing is the origin of QBS and the GSPE in the MgB2 bilayer.