Abstract
Inorganic perovskites have recently attracted much attention as promising new nanocrystalline materials that have interesting fundamental phenomena and great potential in several applications. Herein, we reveal unusual structural and electronic changes in nanocrystalline cesium lead bromide (CsPbBr3) as a function of temperature using high-resolution spectroscopic ellipsometry, high-resolution transmission electron microscopy and terahertz spectroscopy measurements supported by first-principles calculations. New dual phases of crystalline and electronic structures are observed due to the nanocrystalline nature of the material. Interestingly, a change in the electronic structure occurs below 150 K, and the rate at which the nanocrystal transitions from the tetragonal to orthorhombic phase is found to be nonlinear with temperature. Our results show the importance of the charge and lattice interplay in determining the dual phases and fundamental properties of nanocrystalline materials.
Similar content being viewed by others
Introduction
The development of advanced and novel materials for use in solar cell technology has led to a recent surge of interest in inorganic/organic perovskites1,2,3,4,5,6. A number of perovskites have been developed, namely, cesium lead halides (CsPbX3) and methylammonium lead halides (CH3NH3PbX3 or MAPbX3), where X = I, Br or Cl. While a great deal of effort has been devoted to improving their efficiency1,5,6, our fundamental understanding of the crystalline and electronic structure phases, which are important for all electronic applications, is still lacking. Time-resolved terahertz (THz) spectroscopy experiments, for instance, have shown that at low temperatures, the large free-carrier density and mobility of CsPbBr3 and MAPbI3 make them ideal materials for charge-separation layers in photovoltaic cells7. However, the degradation of MAPbI3 perovskites in air at high temperatures and with light illumination ultimately makes them unsuitable to be used in devices that would be exposed to constant light and heat8. It is not understood what causes such fundamental changes; however, it has been argued that the changes might be due to some structural phase changes upon heating and cooling.
On the other hand, using the purely inorganic, nanocrystalline perovskite, CsPbBr3, relatively efficient solar cells have been produced9,10, and the efficiency of other inorganic Cs-based halide perovskites has been theoretically investigated via first-principle calculations11. Cesium lead halides can be completely color tuned based purely on the choice and mixture of halides used, which is a very useful trait in optoelectronic devices12,13. Furthermore, CsPbBr3 has been shown to have very high but comparable hole and electron mobilities and is also a potential material for gamma and X-ray detection14. Interestingly, by replacing some of the MA cations with smaller cesium atoms, MAPbI3 can be stabilized at high temperatures15. This technique also increases the stability of formamidinium lead halide (HC(NH2)2PbX3 or FAPbX3) solar cells and reduces the charge trapping density with the substitution of just 10% FA with Cs16. While most efforts have been devoted to exploring their potential applications, few studies have been performed to understand their fundamental structural properties.
One of the main issues with nanocrystalline perovskites is probing their crystalline and electronic structural properties as a function of temperature across different transition temperatures and phases17. We choose nanocrystalline CsPbBr3 as a model system. CsPbBr3 has been shown to undergo two structural phase changes in the single-crystal form: the orthorhombic (Pbnm) to tetragonal (P4/mbm) phase transition at 361 K and the tetragonal (P4/mbm) to (Pm\(\overline 3\)m) cubic transition at 403 K, both of which occur far above room temperature18,19. However, these transition temperatures are lower for CsPbBr3 quantum dots and powders20,21. Our understanding of both the electronic and crystalline structures of nanocrystalline CsPbBr3, particularly below these transition temperatures, is still lacking17. Recently, there have been reports that nanocrystalline CsPbBr3 can exist in multiple structural phases at once, including several reports of orthorhombic and cubic phases coexisting at room temperature22,23. However, colloidally prepared CsPbBr3 quantum dots appear to only show a single phase at room temperature24,25, although the PbBr6 octahedra undergo significant rotation21. The existence of dual structural phases also has significant effects on both the optoelectronic output and the efficiency of devices made with CsPbBr3 and is crucial in determining how they perform at different temperatures17,24,25.
In this article, we find unusual dual phases of the crystalline and electronic structures of nanocrystalline CsPbBr3 using a new methodology that simultaneously probes structural and electronic properties. An experiment based on temperature- and angle-dependent spectroscopic ellipsometry combined with high-resolution transmission electron microscopy (HR-TEM) and THz measurements as a function of temperature and supported by first-principle calculations is a powerful way to reveal the fundamental properties of nanocrystalline materials. Using this method, we are also able to determine the proportionality of the nanocrystals in each phase in a nondestructive manner, which HR-TEM and diffraction studies are unable to do alone20,21,22,23,24,25. This finding has significant repercussions regarding the electronic structure and therefore the band gap and efficiency of future solar cell devices that will be produced.
Materials and methods
Sample preparation
The synthesis procedure for the CsPbBr3 samples follows that in refs. 13,26. Cs2CO3 (0.8 g), oleic acid (OA) (2.5 mL), and octadecene (ODE) (30 mL) were loaded into a 100 mL four-neck flask with degasing at 100 °C for 30 min. The mixture was heated to 150 °C and reacted for another 0.5 h until all the Cs2CO3 was consumed. ODE (10 mL), OA (1 mL), oleylamine (OAm) (1 mL), and 0.36 mmol of PbBr2 were loaded into another four-neck flask that was heated to 160 °C. Then, 1 mL of the Cs precursor was injected into the first hot mixture for the reaction. After 5 s, the reaction mixture was cooled by an ice-water bath. The nanocrystals were washed with 20 mL of acetone. Finally, the products were dispersed in toluene. The thin films of the CsPbBr3 nanocrystals were made by spin-coating the solution onto a z-cut quartz substrate at a speed of 1000 r/min for 3 min.
Spectroscopic ellipsometry
Spectroscopic ellipsometry measurements were carried out using a variable-angle spectroscopic ellipsometer (V-VASE, J.A. Woollam Co.) with a rotating analyzer and compensator. Two sets of measurements on the CsPbBr3 samples were taken in the energy range of 0.6–6.0 eV, and the samples were inside an ultrahigh vacuum cryostat with a base pressure of 10−8 mbar. The samples were cooled to 77 K using liquid nitrogen, and measurements were taken at angles of 68, 70, and 72 degrees, which were limited by the UHV windows. The first sample was then cooled to 7 K using liquid helium before being heated slowly to temperatures of 77, 100, 150, 160, 170, 180, 200, 250, 300, and 350 K. No change was observed between the first and second measurements at 77 K to show reproducibility and sample stabilization. The second sample was heated slowly to temperatures of 400 K and then slowly cooled to 390, 380, 370, 360, 350, 300, 250, 200, 160, 150, 140, 130, 120, 110, 100, 90, 80, and 77 K. The cooling/heating of the samples were uniform and slow, and they were kept at each temperature for 2 h as the measurements were taken. The analysis of the ellipsometry data was performed using the W-VASE analysis program, and the complex dielectric function was obtained using a fitting procedure that models the data27. The first sample was determined to have an average thickness of ~30.4 nm from the fitting of the data, while the second sample has an average thickness of ~30.1 nm. These results were further supported by the atomic force microscopy (AFM) measurements.
First-principles calculations
We use first-principles calculations based on density functional theory to obtain the electronic band structure and optical transitions of the inorganic CsPbBr3 perovskite. We employed a first-principles approach based on Kohn–Sham density functional theory (KS-DFT)28,29,30,31, as implemented in the QUANTUM ESPRESSO code32. The exchange-correlation energy was described by the generalized gradient approximation (GGA) using the Perdew–Burke–Ernzerhof (PBE) functional28,33. Interactions between valence and core electrons were described by Troullier–Martins pseudopotentials34. The Kohn–Sham orbitals were expanded in a plane-wave basis with a cutoff energy of 60 Ry, and for the charge density, a cutoff of 240 Ry was used. The Brillouin zone (BZ) was sampled using a G-centered 6 × 6 × 6 grid following the scheme proposed by Monkhorst-Pack35. For the dielectric constant calculations, a fine 20 × 20 × 20 grid and a total of 400 bands were employed.
Terahertz spectroscopy
Our THz spectra of the CsPbBr3 perovskite thin film samples were measured using a THz time domain spectrometer (TeraView TPS 3000) combined with a Janis ST-100-FTIR continuous flow cryostat, a homemade three-axis alignment stage and a Cryo Industries cryo-cooler (20–30 K). During the entire experimental measurement, the sample was kept under vacuum (10−7 mbar). The THz waveforms transmitted from the sample on a z-cut quartz substrate [Esam(t)] and a bare z-cut quartz substrate [Eref(t)] were measured as raw data. The amplitude and phase of the THz electric field were obtained by performing a Fourier transform on Esam(t) and Eref(t), respectively. Since THz-TDS detects both the amplitude and phase of the THz electric field, there was no need to employ the Kramers-Kronig transformation during the data analysis. By extracting the complex refractive index with the analytical expression of the transmission \(\widetilde T\left( \omega \right) = \widetilde E_{sam}\left( \omega \right)/\widetilde E_{ref}\left( \omega \right)\), we could extract the exact solution of the material refractive index and then the complex optical conductivity in the THz range.
HR-TEM measurements
High-resolution transmission electron microscopy measurements are made on the third thin-film nanocrystalline CsPbBr3 sample. TEM sample preparation was performed in a Helios NanoLab 600 DualBeam focused ion beam (ThermoFisher) and thinned at low energy (2 keV) down to 30–40 nm in the area of interest. The cross-section of the 30-nm thick CsPbBr3 layer was viewed with a Titan TEM (ThermoFisher) operated at 200 kV. For this, the sample was placed in a double tilt liquid nitrogen cooling holder, Model 636 (Gatan), with a SmartSet Model 900 cold stage controller (Gatan). This setup allowed us to control the temperature at fixed values between 100 and 300 K. At each set temperature, TEM images and diffraction patterns were acquired from the same sample position. A 10 µm condenser aperture was used to form a relatively parallel beam of ~30 nm in diameter, illuminating the center of the CsPbBr3 film. Four diffraction patterns were taken at each temperature, each of which was saved and summed after careful alignment. The center of the summed diffraction patterns was precisely determined, and from here, a rotational intensity profile was measured using the DM script ‘Interactive Rotational Profile’ by B. Schaffer (Gatan). The rotational profile was plotted for each temperature. The background intensity in this rotational profile was relatively strong at low spatial frequencies, resulting from the bright direct beam, which was not blocked during the acquisition with the OneView camera (Gatan).
Results and discussion
The complex dielectric function of nanocrystalline samples of CsPbBr3 is determined with spectroscopic ellipsometry as a function of temperature. The real (∈1) and imaginary (∈2) parts of the complex dielectric function, shown in Fig. 1a, b, respectively, are modeled based on the fitting of the output data, ψ and Δ (the ratio of the amplitude and difference in phase between the incident and reflected light, respectively). Using these results, an average film thickness of ~30.4 nm is determined for CsPbBr3. Note that, as the thin films are spin-coated, the samples may not be uniform and can have up to as much as 5 nm variance in thickness across the whole surface. Excitonic features are found at approximately 2.40−2.50 eV. There are also a number of features between the band gap edge and approximately 5.0 eV, which become more prominent as the sample is cooled to 7 K. We notice that at 350 K, there are virtually no features other than the band gap edge and the main peak at 4.80 eV. This lack of features is due to the broadening of the peaks through phonon interactions, which are also responsible for the amplitude reduction and discussed later. By looking at the difference in the complex dielectric function of CsPbBr3 at 350 K and lower temperatures, we can see these features more clearly upon cooling (Fig. 1c, d). For reproducibility, a second sample of thin-film nanocrystalline CsPbBr3 is also measured as a function of temperature with smaller 10 K intervals between 77–160 K and 350–400 K. The real and imaginary parts of the complex dielectric function are shown in Supplementary Figs. S1a, b, respectively. The film thickness of this sample was determined to be ~30.1 nm on average.
Intriguingly, there are some spectral regions where there is a drastic increase in spectral weights upon cooling, e.g., at ~3.4–4.1 eV and above ~4.6 eV, whereas in other regions, there is very little change when the temperature is lowered from 300 to 77 K, for example at ~2.5−3.4 eV and ~4.1−4.6 eV. This difference shows a significant structural change occurs within CsPbBr3 below room temperature, as further supported by temperature-dependent THz and HR-TEM measurements and supported with theoretical calculations discussed later. Structural phase changes have been reported in CsPbBr3 at 361 K, where there is an orthorhombic-to-tetragonal phase transition, and at 403 K, where the phase transition is from tetragonal to cubic18,19,36,37, both of which occur above room temperature. A significant change can also be seen in the complex dielectric function of the second sample between 360 and 370 K in Supplementary Fig. S1.
Our observation of significant spectral weight transfer as a function of temperature is a fingerprint of the electronic correlation in this system. The overall magnitude of ∈2 shown in Fig. 1b decreases with increasing temperature, with a constant loss of 26.5% in intensity over the measured spectrum with increasing temperature up to 350 K (see details in the Supplementary section). This difference means that the electron–electron correlations affect (or are affected by) these phase transitions 38.
To determine how the electronic structure of nanocrystalline CsPbBr3 changes below room temperature, we calculate the temperature coefficients of the critical points at E0 ≈ 2.45, E1 ≈ 3.9 and E2 ≈ 4.4−4.5 eV using both sets of spectroscopic ellipsometry data. This calculation is crucial in determining how both the optoelectronic output and efficiency of devices made with CsPbBr3 will perform as a function of temperature. The results are shown in Fig. 2 (the detailed calculations of these points are given in the Supplementary information). In all three cases, there is not only a clear change in the temperature coefficient between 100 and 150 K but also a distinct shift in the energy of the critical points. This shift confirms that there is strong coupling between the electronic and structural changes below 150 K. There is also an interesting feature of a blueshift in the E0 and E1 critical points with temperature, while E2 redshifts significantly. These shifts will be explained later.
The binding energy of the exciton can also be calculated from the ellipsometry data by using the temperature dependence of the absorption line width of the excitonic peak, which also takes into account the thermal broadening39,40. From the calculations (see the supplementary for details), a binding energy of 13.4 ± 4.0 meV and an attempt frequency of 22 ± 4 fs−1 are found. These changes along with the ~0.1 eV change in E0 also confirm the significant impact that the temperature change has on the optoelectronic nature of nanocrystalline CsPbBr3, and it is important to determine exactly how and why these changes occur. The first step in this process is to identify the changes in the structural phase of PbBr3 with temperature.
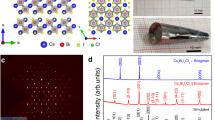
One way to determine the structural phase of a material is through X-ray diffraction (XRD), either powder diffraction or single-crystal diffraction. However, it is challenging to study thin-film nanocrystals on a substrate. Therefore, we performed HR-TEM as a function of temperature to study changes in the crystal structure and nanocrystal size of the CsPbBr3 samples. A thin film with a 30-nm nanocrystal size (third sample) can be seen in Fig. 3a at a temperature of 100 K, and it is clear that many nanocrystals of different orientations are present with sizes on the order of 10 nm. We can estimate that the nanocrystal sizes are on the order of 10 nm, with sizes ranging from ~5 to ~50 nm. Note that the precise average and root-mean-squared nanocrystal size of the thin film cannot be accurately determined through HR-TEM. As the temperature slowly increases to 300 K, the size of the nanocrystals appears to change very little.
Figure 3b shows the selected area electron diffraction (SAED) pattern from Fig. 3a at 100 K, and Fig. 3c shows the azimuthal integration of the thin-film SAED patterns from the same area as the temperature is increased slowly from 100 to 300 K and back to 100 K again. It is clear that there is a shift in some of the peaks as the temperature changes, especially in the peaks at 1.4 and 2.5 nm−1, indicating a gradual structural transition rather than lattice stretching. There is also a significant loss in intensity as the sample is slowly heated and again when the temperature is reduced back to 100 K. This loss is likely due to damage from the electron beam over time and the formation of Pb nanoparticles within the lattice41. XRD has been previously performed on CsPbBr3 using powder diffraction14 and HR-TEM20,21,22,23,24,25,42,43,44. However, from this result alone, it has been difficult to determine the difference between the orthorhombic, tetragonal and cubic structural lattices of CsPbBr3. The azimuthal integration of the SAED patterns is very similar to that from refs. 42,43, and the exception is the large peak just above 2 nm−1, which has been deduced to be from the substrate. The other peaks appear to consist of multiple peaks that shift in spectral weight as the temperature is increased, while the peak at 2 nm−1 does not change shape with temperature. This point is where spectroscopic ellipsometry becomes an important tool to resolve this issue because even though the structural phases of nanocrystals may be similar, their electronic structures can be different, particularly at high energy regimes, as further elaborated below.
Although HR-TEM is a useful tool to image nanocrystalline materials such as CsPbBr3, the electron beam has been known to damage the crystal structure of very thin films, and the degradation results in the formation of Pb nanocrystals22,41. In most of these cases, the thin films are on the order of several atoms22 to several nm thick41 as opposed to an average of approximately 30 nm, an order of magnitude thicker. However, the loss in intensity in Fig. 3c as the sample is heated and then cooled again is likely the result of electron beam damage. This result further emphasizes the importance of spectroscopic ellipsometry as a nondestructive technique for simultaneously probing the structure and electronic structure of nanocrystalline perovskite systems, which, in most cases, are sensitive to damage such as that from an electron beam.
While the lattice properties of the structural phases of CsPbBr3 are very similar, the energy band structures of the different lattices are likely more distinguishable. To determine the difference between the different lattice structures, first-principle calculations of the band structures of CsPbBr3 are carried out and then compared with the higher-order transitions seen in the SE spectra in Fig. 1b.
Calculations of the CsPbBr3 band structure are performed using density functional theory (DFT) simulations with spin-orbit coupling (SOC) to identify the optical transitions represented by the critical points shown in Figs. 1b, d and 2. We consider the previously reported orthorhombic and tetragonal structures, as well as an alternative tetragonal model with the space group I4/mcm, similar to an existing phase of MAPbI3 (Fig. 4b). We find that each crystal structure results in different optical transitions. Based on our calculations, the previously reported P4/mbm phase is inconsistent with the electronic transition at 3.45–3.50 eV described below. Instead, we find that a phase transition between the tetragonal I4/mcm phase and the low-temperature orthorhombic phase (Fig. 4a) is consistent with the experimental data. The band structures for the two phases are shown in Fig. 4c, d, and the relevant optical transitions are identified in Fig. 4e, taking into account that the calculated band gaps for the tetragonal and orthorhombic phases are underestimated by 0.6 and 0.4 eV, respectively. The denotations in Fig. 4c–e are based on the point in the Brillouin zone where the optically allowed transition takes place (S, Z or Γ), whether it is the orthorhombic or tetragonal lattice under consideration (O or T), and the lowest allowed transition under consideration (1, 2, 3, etc.).
Structural diagrams of CsPbBr3 in the a orthorhombic and b tetragonal phases. Inset orthorhombic Brillouin Zone. Calculated energy dispersion bands of CsPbBr3 in the c orthorhombic and d I4/mcm tetragonal structural phases from the DFT simulations. e High energy critical points in ∈2 matched to the allowed energy transitions from the calculations of both structural phases.
At higher temperatures, the prominent optical features are smeared, revealing the complexity of the optical transitions. Interestingly, we identify optical transitions within the spectra that are unique to both the tetragonal and orthorhombic phases even as low as 7 K. More specifically, the emergence of the peak at 3.90 eV marked Γ/ST2 does match optically allowed transitions within the tetragonal lattice, along with the peak at 3.50 eV and the excitonic peak, which also match orthorhombic optically allowed transitions and do not match any optically allowed transition in the orthorhombic lattice. This result reveals the existence of both orthorhombic and tetragonal lattices, even at very low temperatures. As CsPbBr3 is a nanocrystalline material, the two structural phases can coexist because some of the nanocrystals can transition from the tetragonal phase to the orthorhombic phase, while the rest remain in the tetragonal phase. Several materials have exhibited structural phase duality, such as nanocrystalline Ni45, Cu3SnS4 nanocrystals46, and most notably, Na0.5Bi0.5TiO3 perovskite, where structural phase duality exists over two temperature ranges: the tetragonal/cubic phase between 773 and 813 K and the rhombohedral/tetragonal phase over 528–673 K47. In this case, the optical transitions associated with the orthorhombic phase begin to appear at 361 K, which is the temperature at which the single-crystal phase change was recorded12,19,36,37. The peaks associated with the transitions become stronger as CsPbBr3 cools to 7 K, which would make it the largest recorded temperature range over which a structural phase duality exists. This result is further corroborated by the change in the spectral weight within the peaks seen in Fig. 3c and the change in the weak phonon modes with temperature recorded by THz spectroscopy shown later in Fig. 6.
Because the rate of change of the sample temperature between measurements is very low and evenly applied across the sample and the sample is kept at the same temperature for 2 h, we can rule out sudden changes in temperature as the cause for both orthorhombic and tetragonal lattices appearing in the sample. The existence of different structural phases in CsPbBr3 at single temperatures comes from the expansion/contraction of the crystal lattices and electronic correlation with temperature and the resulting tilts in the PbBr6 octahedra to relieve the stress and strain that builds up within the lattice22,24,47. In single crystals, this would happen across the entire lattice at once, whereas in nanocrystalline materials, the nanocrystals would undergo phase changes until the stress/strain is relieved, which means that not all of the nanocrystals need to change at once.
Our result also explains and reconciles previous studies on nuclear-quadrupole resonance (NQR)36 and neutron scattering18 measurements. Previously, NQR measurements of bromine in CsPbBr3 suggested a second-order phase transition below 170 K36. Neutron scattering experiments of CsPbBr3 showed a splitting of Bragg peaks at low temperatures18. Note that a low-temperature phase change has also been observed in a similar perovskite, CsPbF3, where the transition between a rhombohedral to cubic lattice occurs at 187 K48. The splitting of the Bragg peaks occurs because both orthogonal and tetragonal peaks appear at the lowest temperature. Interestingly, the peak shifts are shown in Fig. 2 and the NQR scans of bromine in ref. 36 show a more pronounced change between 100 and 150 K, which does not indicate a linear rate of transition between the orthorhombic and tetragonal lattices. This new information means that as the tetragonal-to-orthorhombic ratio of the nanocrystals shifts in favor of the latter as the samples are cooled, a change in the electronic structure occurs and is dependent on the number of nanocrystals that have undergone the phase transition.
The different temperature coefficients for critical points among E2 and E1 and E0 (as shown in Fig. 2 are because these transitions have different origins. E2 mostly involves optical transitions from the valence band in the orthorhombic phase (ZO2), while E1 and E0 mostly originate from optical transitions from the valence band in the tetragonal phase (Γ/ST2) and the exciton. We note that in most cases, a blueshift in peak energy is observed with increasing temperature; however, this may not always be the case. The peaks observed in the spectra optically match the allowed transitions between energy bands at different points in the Brillouin zone, such as those seen in Fig. 4. Changes in the material, such as externally applied changes in temperature and internal changes in pressure with the transition between orthorhombic and tetragonal lattices, can alter the energy bands. In some cases, the conduction or valence bands may shift lower or higher depending on their position within the Brillouin zone, which would result in a small decrease/increase in the peak energy. This effect is also dependent on whether the lattice itself is orthorhombic or tetragonal. The opposing shifts in temperature observed in the E1 and E2 peaks from Fig. 2 (corresponding to the tetragonal Γ/ST2 and orthorhombic Z2 transitions, respectively) are most likely a combination of all these factors.
To quantify the ratio of the structural phases and determine exactly how the nanocrystalline structure changes with temperature, the imaginary part of the dielectric function (∈2) from both the tetragonal and orthorhombic band structure simulations is calculated and compared with the experimental data. Figure 5a shows the x, y, and z components of the calculated ∈2 from both the orthorhombic and tetragonal phases. The ∈2 of the tetragonal phase, shown in red, is almost isotropic with very little change between the x, y, and z directions, while the x, y, and z components of ∈2 in the orthorhombic phase, shown in blue, are very different.
a The x, y, and z components of ε2 calculated from the tetragonal and orthorhombic band structures. b Comparison of the combined tetragonal and orthorhombic ∈2 in different ratios with the data at 7, 100, 150, and 300 K. The results are offset by 0.1 unit for clarity. c The percentage of orthorhombic nanocrystals as a function of temperature.
The calculated ∈2 of both phases are then combined in different ratios and compared to the data in an effort to find the best fit for each temperature. This is achieved by combining the ∈2 of the tetragonal and orthorhombic lattices shown in Fig. 5a in increments of 1% (e.g., 1% orthorhombic plus 99% tetragonal) and performing a simple least-squares regression fit for the data between 3.0 and 5.5 eV, which is calculated assuming isotropic contributions due to the many different lattice orientations of the nanocrystalline material, as shown in Fig. 3a. The results of the best fits for 7, 100, 150, and 300 K are shown in Fig. 5b along with the data. Each set has been shifted by 0.1 units in the y-axis for clarity.
The simulations of ∈2 fit very well with the data between 3.20 and 5.20 eV. Below 3.20 eV, electron-hole interactions become very important, whereas stronger electron–electron correlations become important above 5.20 eV. The best fit for the 300 K data involves a combination of 75% tetragonal and 25% orthorhombic nanocrystals, while at 7 K, this ratio shifts to 50% for each phase. This difference is consistent with a decrease in tetragonal nanocrystals from the initial phase change at 361 K. Figure 5c shows the calculated percentage of orthorhombic nanocrystals for a range of temperatures between 7 and 360 K. However, between 100 and 150 K, the percentage of orthorhombic nanocrystals is approximately 33%, whereas at 100 K, it increases to 45%, as shown in Fig. 5c. This increase means that the rate of change of the nanocrystals in the material from orthorhombic to tetragonal is not linear with temperature as predicted earlier, and this nonlinearity is reflected in the rapid change in the electronic structure below 150 K seen in Fig. 2a. Many factors, such as nanocrystal size, orientation, surface ligands, and termination49, can affect the rate of change of the phase transition, and this is a subject for further investigation.
Optical conductivity measurements were taken for CsPbBr3 in the THz range to probe the possible phonon modes within the nanocrystalline samples. AFM measurements show the film thickness of a fourth CsPbBr3 sample is 212 ± 23 nm. The extracted optical conductivity σ1(ω) is shown as dots in Fig. 6a. There are two main peaks at ~1.6 and ~2.4 THz, and a two-Lorentz-oscillator model is used, which gives a very good fit for the data (solid lines in Fig. 6a):
a Data (dots) and best fits (solid lines) in the temperature range of 20–300 K. The results are offset by 150 Ω−1 m−1 for clarity. Notice the gradual appearance of the 2.0 THz shoulder below 150 K. b Fitting parameters of the two-Lorentz-oscillator model as a function of temperature for the peak near 1.6 THz and the peak near 2.4 THz.
The fitting parameters are shown in Fig. 6b, and the error bars take into account the film roughness. According to the DFT calculations shown in Fig. 3d of ref. 50, there are only two modes at ~1.3 and ~2.8 THz in the cubic phase. Our 300 K data, whose peaks appear at ~1.6 and ~2.4 THz, agree reasonably well with these DFT calculations.
However, as we can see in Fig. 6a, we observe two additional small peaks. The 1.1-THz peak exists at all temperatures, while the 2.0-THz shoulder only exists below 150 K. This shoulder feature is also observed for CH3NH3PbI351 and CH3NH3PbBr352 perovskite thin films, which can be attributed to the tetragonal-to-orthorhombic phase transition near 150 K. Our similar observations, albeit for this inorganic nanocrystalline CsPbBr3 sample, are therefore consistent with the results from spectroscopic ellipsometry in this paper.
Conclusion
We observed a dual phase of crystalline and electronic structures due to the nanocrystalline nature of the material as a function of temperature. These changes are the result of individual nanocrystals transitioning from a tetragonal to orthorhombic structure to relieve the stress/strain build up during shifts in temperature. Significant changes in the electronic structure below 150 K are found due to the increased rate of the structural phase transition in the nanocrystals between 150 and 100 K, and this transition rate is not linear with temperature.
Furthermore, a new method of detecting phase transitions in thin-film nanocrystalline materials in a nondestructive manner is introduced through the identification of optical transitions within the electronic structure and the comparison of experimental data and theoretical models of the complex dielectric function. This method allows us to determine the proportionality of nanocrystals in both the orthorhombic or tetragonal phases and thus determine the exact nature of change in the material, both structurally and electronically, with temperature. This insight and new methodology for structural phase and electronic changes within CsPbBr3 can be applied to many other nanocrystalline materials and can directly impact the performance of these materials in nanostructures.
References
Kojima, A., Teshima, K., Shirai, Y. & Miyasaka, T. Organometal halide perovskites as visible-light sensitizers for photovoltaic cells. J. Am. Chem. Soc. 131, 6050–6051 (2009).
Kim, H. S. et al. Lead iodide perovskite sensitized all-solid-state submicron thin film mesoscopic solar cell with efficiency exceeding 9%. Sci. Rep. 2, 591 (2012).
Lee, M. M. et al. Efficient hybrid solar cells based on meso-superstructured organometal halide perovskites. Science 338, 643–647 (2012).
Heo, J. H. et al. Efficient inorganic-organic hybrid heterojunction solar cells containing perovskite compound and polymeric hole conductors. Nat. Photon 7, 486–491 (2013).
Burschka, J. et al. Sequential deposition as a route to high-performance perovskite-sensitized solar cells. Nature 499, 316–319 (2013).
Liu, M., Johnston, M. B. & Snaith, H. J. Efficient planar heterojunction perovskite solar cells by vapour deposition. Nature 501, 395–398 (2013).
La-o-vorakiat, C. et al. Elucidating the role of disorder and free-carrier recombination kinetics in CH3NH3PbI3 perovskite films. Nat. Commun. 6, 11054 (2015).
De Wolf, S. et al. Organometallic halide perovskites: sharp optical absorption edge and its relation to photovoltaic performance. J. Phys. Chem. Lett. 5, 1035–1039 (2014).
Beal, R. E. et al. Cesium lead halide perovskites with improved stability for tandem solar cells. J. Phys. Chem. Lett. 7, 746–751 (2016).
Kulbak, M., Cahen, D. & Hodes, G. How important is the organic part of lead halide perovskite photovoltaic cells? Efficient CsPbBr3 cells. J. Phys. Chem. Lett. 6, 2452–2456 (2015).
Huang, L. Y. & Lambrecht, W. R. Electronic band structure trends of perovskite halides: Beyond Pb and Sn to Ge and Si. Phys. Rev. B 93, 195211 (2016).
Akkerman, Q. A. et al. Tuning the optical properties of cesium lead halide perovskite nano-crystals by anion exchange reactions. J. Am. Chem. Soc. 137, 10276 (2015).
Protesescu, L. et al. Nanocrystals of cesium lead halide perovskites (CsPbX3, X=Cl, Br, and I): novel optoelectronic materials showing bright emission with wide color gamut. Nano Lett. 15, 3692 (2015).
Stoumpos, C. C. et al. Crystal growth of the perovskite semiconductor CsPbBr3: A new material for high-energy radiation detection. Cryst. Growth Des. 13, 2722–2727 (2013).
Kulbak, M. et al. Cesium enhances long-term stability of lead bromide perovskite-based solar cells. J. Phys. Chem. Lett. 7, 167–172 (2015).
Lee, J. W. et al. Formamidinium and cesium hybridization for photo-and moisture-stable perovskite solar cell. Adv. Energy Mater 5, 1501310 (2015).
Ramade, J. et al. Fine structure of excitons and electron–hole exchange energy in polymorphic CsPbBr3 single nanocrystals. Nanoscale 10, 6393 (2018).
Sakuma, T. et al. Low-energy excitation in CsPbX3 (X=Cl, Br). Solid State Ion. 154, 237–242 (2002).
Hirotsu, S., Harada, J., Iizumi, M. & Gesi, K. Structural phase transitions in CsPbBr3. J. Phys. Soc. Jpn. 37, 1393–1398 (1974).
Cottingham, P. & Brutchey, R. L. Depressed phase transitions and thermally persistent local distortions in CsPbBr3 quantum dots. Chem. Mater. 30, 6711 (2018).
Bertolotti, F. et al. Coherent nanotwins and dynamic disorder in cesium lead halide perovskite nanocrystals. ACS nano 11, 3819 (2017).
Yu, Y. et al. Atomic resolution imaging of halide perovskites. Nano Lett. 16, 7530 (2016).
Brennan, M. C., Kuno, M. & Rouvimov, S. Crystal structure of individual CsPbBr3 perovskite nanocubes. Inorg. Chem. 58, 1555 (2018).
Cottingham, P. & Brutchey, R. L. On the crystal structure of colloidally prepared CsPbBr3 quantum dots. Chem. Comms 52, 5246 (2016).
Swarnkar, A. et al. Colloidal CsPbBr3 perovskite nanocrystals: luminescence beyond traditional quantum dots. Angew. Chem. Int. Ed. 54, 15424 (2015).
Wang, Y. et al. All‐inorganic colloidal perovskite quantum dots: a new class of lasing materials with favorable characteristics. Adv. Mater. 27, 7101 (2015).
Asmara, T. C., Santoso, I. & Rusydi, A. Self-consistent iteration procedure in analyzing reflectivity and spectroscopic ellipsometry data of multilayered materials and their interfaces. Rev. Sci. Instrum. 85, 3663 (2014).
Kohn, W. & Sham, L. J. Self-consistent equations including exchange and correlation effects. Phys. Rev. 140, A1133 (1965).
Yettapu, G. R. et al. Terahertz conductivity within colloidal CsPbBr3 perovskite nanocrystals: remarkably high carrier mobilities and large diffusion lengths. Nano Lett. 16, 4838 (2016).
MacDonald, A. H. & Vosko, S. H. A relativistic density functional formalism. J. Phys. C: Sol. Stat. Phys. 12, 2977 (1979).
Dal Corso, A. & Conte, A. M. Spin-orbit coupling with ultrasoft pseudopotentials: application to Au and Pt. Phys. Rev. B 71, 115106 (2005).
Giannozzi, P. et al. QUANTUM ESPRESSO: a modular and open-source software project for quantum simulations of materials. J. Phys. Cond. Matt. 21, 395502 (2009).
Perdew, J. P., Burke, K. & Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865 (1996).
Troullier, N. & Martins, J. L. Efficient pseudopotentials for plane-wave calculations. Phys. Rev. B 43, 1993 (1991).
Monkhorst, H. J. & Pack, J. D. Special points for Brillouin-zone integrations. Phys. Rev. B 13, 5188 (1976).
Volkov, A. F., Venevtsev, Y. N. & Semin, G. K. Nuclear quadrupole resonance (NQR) of 79Br and 81Br in perovskite and orthorhombic forms of CsPbBr3 and CsPbJ3. Phys. Status Solidi (b) 35, K167–K169 (1969).
Sharma, S., Weiden, N. & Weiss, A. Phase transitions in CsSnCl3 and CsPbBr3: An NMR and NQR Study. Z. f.ür. Naturforsch. A 46, 329–336 (1991).
Asmara, T. C. et al. Large spectral weight transfer in optical conductivity of SrTiO3 induced by intrinsic vacancies. J. Appl. Phys. 115, 213706 (2014).
D’Innocenzo, V. et al. Excitons versus free charges in organo-lead tri-halide pervoskites. Nat. Commun. 5, 3586 (2014).
Jiang, Y. et al. Temperature dependent optical properties of CH3NH3PbI3 perovskite by spectroscopic ellipsometry. Appl. Phys. Lett. 108, 061905 (2016).
Dang, Z. et al. In situ transmission electron microscopy study of electron beam-induced transformations in colloidal cesium lead halide perovskite nanocrystals. ACS Nano 11, 2124 (2017).
Zhang, M. et al. Growth and characterization of all-inorganic lead halide perovskite semiconductor CsPbBr3 single crystals. CrystEngComm 19, 6797 (2017).
Dang, Z. et al. High-resolution TEM study of colloidal cesium lead bromide nanocrystals. In European Microscopy Congress 2016: Proceedings. (Wiley-VCH Verlag GmbH & Co. KGaA).
Li, G. et al. Shape and phase evolution from CsPbBr3 perovskite nanocubes to tetragonal CsPb2Br5 nanosheets with an indirect bandgap. Chem. Comms 52, 11296 (2016).
Han, M. et al. Controllable synthesis and magnetic properties of cubic and hexagonal phase nickel nano-crystals. Adv. Mater. 19, 1096 (2007).
Yi, L., Wang, D. & Gao, M. Synthesis of Cu3SnS4 nano-crystals and nanosheets by using Cu31S16 as seeds. Cryst. Eng. Comm. 14, 401 (2012).
Jones, G. O. & Thomas, P. A. Investigation of the structure and phase transitions in the novel A-site substituted distorted perovskite compound Na0.5Bi0.5TiO3. Acta Cryst. Sec. B: Struct. Sci. 58, 168 (2002).
Berastegui, P., Hull, S. & Eriksson, S. G. A low-temperature structural phase transition in CsPbF3. J. Phys. Condens. Matt 13, 5077 (2001). 2001.
De Roo, J. et al. Highly dynamic ligand binding and light absorption coefficient of cesium lead bromide perovskite nanocrystals. ACS nano 10, 2071 (2016).
Yang, J. et al. Acoustic-optical phonon up-conversion and hot-phonon bottleneck in lead-halide perovskites. Nat. Comms 8, 14120 (2017).
La-o-vorakiat, C. et al. Phonon mode transformation across the orthohombic–tetragonal phase transition in a lead iodide perovskite CH3NH3PbI3: a terahertz time-domain spectroscopy approach. J. Phys. Chem. Lett. 7, 1 (2016).
Zhao, D. et al. Low-frequency optical phonon modes and carrier mobility in the halide perovskite CH3NH3PbBr3 using terahertz time-domain spectroscopy. Appl. Phys. Lett. 111, 201903 (2017).
Acknowledgements
This work was supported by the Ministry of Education AcRF Tier-2 (Grants No. MOE2015-T2-2-065, MOE2015-T2-1-099, MOE2015-T2-2-147, MOE2016-T2-1-054, and MOE2017-T2-1-135), the Singapore National Research Foundation under its Competitive Research Funding (NRF-CRP 8-2011-06, R-398-000-087-281, and NRF-CRP15-2015-01) and under its Medium Sized Centre Program (Centre for Advanced 2D Materials and Graphene Research Centre), NUS YIA, MOE-AcRF Tier-1 (Grants No. R-144-000-398-114, No. R-144-000-368-112, No. R-144-000-346-112, No. R-144-000-364-112, and No. R-144-000-423-114), HU-NUS (R-144-000-400-133), and NUS Core Support C-380-003-003-001. The authors would like to acknowledge the Singapore Synchrotron Light Source (SSLS) for providing the facility necessary for conducting the research. The SSLS is a National Research Infrastructure under the National Research Foundation Singapore.
Author information
Authors and Affiliations
Contributions
T.J.W., X.C. and A.R. performed the spectroscopic ellipsometry measurements and detailed analysis. M.B., H.K.H. and T.J.W. performed the HR-TEM measurements and analysis. D.Z., Q.C. and E.E.M.C. performed the THz measurements and analysis. Y.W., E.E.M.C. and H.D.S. prepared the samples. L.C.-G., A.C., T.J.W. and A.R. performed the theoretical calculations and analysis of the optical spectra. T.J. W, L.C.-G. and A.R. comprehensively analyzed all data and wrote the paper with help from M.B.H.B., A.H.C.-N., A.T.S.W. and input from all coauthors. A.R. provided the idea for using spectroscopic ellipsometry on nanocrystalline perovskites, and A.R., H.D.S. and E.E.M.C. initiated and led the project.
Corresponding authors
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Whitcher, T.J., Gomes, L.C., Zhao, D. et al. Dual phases of crystalline and electronic structures in the nanocrystalline perovskite CsPbBr3. NPG Asia Mater 11, 70 (2019). https://doi.org/10.1038/s41427-019-0170-6
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41427-019-0170-6
This article is cited by
-
Electronic and optical properties of bulk and surface of CsPbBr3 inorganic halide perovskite a first principles DFT 1/2 approach
Scientific Reports (2021)
-
Spin–orbit coupling effect on energy level splitting and band structure inversion in CsPbBr3
Journal of Materials Science (2021)