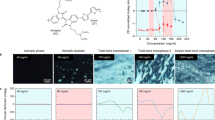
Abstract
The fabrication of molecular structures with a desired morphology, e.g., nanotubes, nanoribbons, nanosprings, and sponges, is essential for the advancement of nanotechnology. Unfortunately, realization of this objective is expensive and complicated. Here, we report that irradiating a film comprising azobenzene derivatives with UV light produces oriented arrays of helical nanofilaments via the photoisomerization-induced Weigert effect. As a result, structural colors are observed due to the extrinsic chiral reflection in the visible wavelength range, and the reflected color can be tuned by adjusting the molecular length of the azobenzene derivative. This simple fabrication method can be used for fabricating large, reversible, and patternable color reflectors, providing a new platform for interference-based structural coloration as it exists in nature, such as morpho butterflies, green-winged teal, and various beetles.
Similar content being viewed by others
Introduction
It is known that certain bent-core liquid-crystalline (LC) molecules spontaneously form helical nanofilaments (HNFs; B4 phase) or, more precisely, bundles of twisted crystal layers, usually with a diameter (w) of ~40 nm and a helical pitch (p) 200–300 nm depending on the molecular length (Fig. 1a, b)1,2,3,4,5. The aromatic cores and aliphatic tails in bent-shaped molecules show a typical bookshelf-like arrangement in the smectic layers, but in-layer mismatch happens upon cooling from the smectic phase to the HNF phase. During this transition, the twisted structures of the HNFs are driven by local saddle-splay deformation of layers, and both right- and left-handed helices are formed because of the absence of molecular chirality. Only recently has it been shown that filaments of the B4 phase can be perfectly aligned in a confined environment, e.g., in the cylindrical nanopores of an aluminum oxide matrix6,7. Although this method is efficient and simple, unfortunately, its application in optical devices is rather limited owing to the presence of an inorganic scaffold. Here, we describe an efficient method for aligning HNFs by engineering the molecular structure, i.e., by incorporating photochromic azobenzene units. Azobenzene molecules in their trans-isomer state reveal different UV light absorption efficiencies and thus have different effective orientation potentials (U(θ)) depending on the angle (θ) between the transition dipole of the azo group and the illuminating linearly polarized light, which can be expressed as
where V0 is the strength of the potential and is larger than 08.
a Randomly oriented HNFs grown from randomly oriented molecules in an isotropic, nematic, or smectic phase (c). b Oriented HNFs are observed upon illuminating the sample with unpolarized UV light, causing repetition of the trans–cis photoisomerization process. d, e Alignment of the mesogenic cores along the light propagation direction by the Weigert effect, which causes the growth of the helical filaments vertically with respect to the sample substrate (b). Molecular structures of D-n dimers and their phase sequence (f)
When azo-mesogens are exposed to linearly polarized UV light, only molecules oriented with their transition dipoles parallel to the direction of polarization (θ = 0°) respond and undergo trans–cis photoisomerization, whereas the molecules perpendicular to this direction (θ = 90°) remain in the trans-state. In a dynamic system, after a number of consecutive trans–cis and cis–trans isomerization cycles, the equilibrium is strongly biased toward molecules oriented perpendicular to the direction of light polarization, which is known as the “angular hole burning” or the “Weigert effect”8. Under irradiation with unpolarized light, the azobenzene units tend to orient along the direction of light propagation, the only direction perpendicular to the electric field of the incident light (Supplementary Fig. S1). We show that using the Weigert effect, aligned arrays of helical nanostructures can be obtained, which is the basis for patternable and reversible structural color reflectors. There have been attempts to control the orientation of chiral LC materials showing a cholesteric or blue phase; however, it was necessary to add a photochromic dopant or an azo-moiety-containing alignment layer9,10. Indeed, the robustness or temperature range in previous studies was frequently poor for practical applications, so our robust HNF-based platform is promising for realizing realistic chiral color reflectors.
Materials and methods
Fabrication of color reflectors with UV irradiation
The sandwich-type cells were made of a silicon (Si) wafer and glass; both substrates were washed with acetone, ethanol, and DI water. The spacing between the substrates was maintained at 3 μm using silica particle spacers. The D-n LC materials were injected into the cells in the isotropic liquid phase (~170 °C) via capillary forces. The temperature and cooling rates of the samples were precisely controlled by a heating stage (LTS350, Linkam, UK). The cells were irradiated with UV light from a diode lamp at an effective power density of 280 mW/cm2 for D-5 and 160 mW/cm2 for D-7, D-9, and D-11. During irradiation, the sample was cooled to the temperature range of the B4 phase (~140 °C) at a rate of 1 °C/min. Polarized optical microscopy (POM) (LV100POL, Nikon, Tokyo, Japan) was used to observe the optical textures of the LC film. Field-emission scanning electron microscopy (SEM) (S4800, Hitachi) was used to examine the morphology of the HNFs. Grazing incidence X-ray diffraction (GIXRD) analysis was performed at the 9A U-SAXS and 6D C&S UNIST-PAL beamlines of the Pohang Accelerator Laboratory. The energy of the focused beam was 11.06 keV, and the 320-mm sample-to-detector distance allowed simultaneous observation of the molecules and layer orientation. The diffraction patterns were recorded with a 2D CCD camera (Rayonix SX165). The reflectance spectra of the aligned HNFs were recorded on a spectrometer (USB-2000+, Ocean Optics).
Simulation
To investigate the origin of the reflected colors of the helical nanostructure, simulations were performed using the finite element method (FEM). The numerical calculation in the frequency domain, based on the finite integration technique (FIT) first proposed by T. Weiland in 1976, uses the integral form of Maxwell’s equation as follows11:
To solve these equations numerically, a finite calculation method was used under the consideration that the structure comprised small repetitively arranged unit cells. In the case of the complex curved structures of HNFs, the FIT algorithm combined with the perfect boundary approximation technique was applied12. Finally, any electromagnetic field problem on the discrete grid space can be solved using the matrix equation
where Mε, Mμ, and Mσ represent the matrices for permittivity, permeability, and conductivity, respectively. Such numerical analysis for complex structures is well established. For a reasonable numerical calculation, we set the refractive index (n) for D-n molecules as 1.6. Other parameters, such as the helical pitch (p), were estimated from SEM analyses. The HNF pitches for the series D-5, D-7, D-9, and D-11 were found to be 206, 231.8, 271.3, and 282.7 nm, respectively. The diameter of the HNF was set to 40 nm1.
Results and discussion
LC materials and controlling the HNF alignment
Flexible dimers (D-n) with odd numbers (n = 5, 7, 9, 11) of carbon atoms in their internal spacers, which link two rigid linear cores with an azobenzene group each (Fig. 1f), were studied11,13. For the dimers studied here, the HNF phase is observed in the temperature range below that of the smectic (n = 5, 7) or nematic phase (n = 9, 11). Irradiation with UV light has no direct effect on the B4 phase; however, effective photoisomerization occurs in the fluid LC phases, viz. the smectic and nematic phases. Moreover, photoisomerization with unpolarized UV light induces the reorientation of the dimeric molecules by the Weigert effect; the polar director of molecules on average is aligned along the light propagation direction and thus is parallel to the surface (Fig. 1d, e). The orientation of the molecules by light governs the growth of the HNFs in the direction of light propagation, vertical to the surface (Fig. 1b), which is quite different from the original states of the HNF and fluid LC phases (Fig. 1a, c).
For this study, dimeric molecules in a sandwich cell composed of a Si wafer and glass were used (Fig. 2a, b). The intrinsic broadband absorption property of the Si wafer (black substrate) effectively eliminates incoherent scattering, rendering the reflected color relatively vivid and clearly visible to the unaided eye (Fig. 3). The HNF orientation process is fully reversible: it can be subsequently heated to the fluidic LC phase or isotropic liquid. The orientation of the filaments by light was confirmed by SEM studies (Fig. 2). Well-oriented HNFs are observed only in the cell area irradiated by UV light (Fig. 2d), whereas randomly oriented and coiled HNFs are observed in the unirradiated parts of the cell (Fig. 2c). The SEM images of well-aligned HNFs also reveal that the helical pitch, p, increases from ~200 to ~280 nm as the alkyl linker length of the dimer is increased from n = 5 to 11 (Fig. 2d). The crystal structure and morphology of the HNF phase was also investigated by GIXRD with a synchrotron source (Supplementary Figs. S2–S4). Small-angle diffraction signals reflecting the layer structure in the sample exposed to UV light have a well-defined azimuthal direction, which is slightly tilted with respect to the sample surface, confirming the vertical orientation of the filaments. In contrast, the degeneration of the azimuthal angle of signal positions is clearly observed for the unirradiated sample. The observation of wide-angle peaks with characteristic diagonal positions also supports the vertical alignment of the filaments, as previously reported6,11. This finding is the typical GIXRD result of the HNF phase, which is quite different from the results of other chiral structures, for example, the twist bend nematic phase that shows broad wide-angle GIXRD peaks even though it is well aligned14. In situ GIXRD patterns of the sample in the smectic C phase also show that the smectic layers that are deformed by UV irradiation are restored upon illumination with visible light (Supplementary Fig. S5).
a Experimental setup for the irradiation of the LC sample confined between a Si wafer and glass with unpolarized UV light. The yellow region represents the area masked with black paper, while the blue region represents the area exposed to UV light. The heating stage is placed beneath the sample to control the phase transition. b Schematic representation of HNFs in the shadowed (yellow) and UV-irradiated areas (blue). c SEM images of randomly oriented HNFs grown in the photomasked area. d Aligned HNFs grown in the UV light-illuminated areas. The helical pitch p varies with the variation in the internal spacer length of the dimer
a Photomasked and UV-irradiated areas, as viewed between cross-polarizers; the reflection in the UV-irradiated area shifts from blue to green with increasing dimer spacer length. b Schematic illustration of the reflected color upon illumination with white light. c The reflected colors of the sample when viewed against a black background and d the “dye” color when a white background is used. e Reflection spectra of dimers D-5 to D-11. f Angle-independent reflecting behavior of the D-5 sample is observed by varying the viewing angle
The influence of UV irradiation during the phase transition was directly investigated with POM (Supplementary Fig. S6). The nematic textures show reversible behavior with and without UV irradiation, transforming to dark and schlieren textures, respectively (Supplementary Fig. S6a, b). Without UV irradiation, the typical schlieren texture is observed in the nematic phase at 148 °C, changing to the dark texture in the B4 phase (Supplementary Fig. S6c). In contrast, under UV irradiation, the nematic texture is dark, showing the homeotropic molecular arrangement, which transforms to the green domain to reveal oriented HNFs (Supplementary Fig. S6d).
Optical properties of the fabricated structural color reflectors and simulations
Clear differences in the reflection of white light by the UV-irradiated and photomasked area are observed by reflection-mode optical microscopy when the sample is placed between crossed polarizers (Fig. 3). Optical analyses were also performed on the glass surface covered with the LC material after removing the Si wafer to see the transmission color. The color of the sample is dependent on the background against which the sample is observed. When a black background that strongly absorbs the light transmitted through the sample is used, the reflection color is enhanced (Fig. 3c), and when a white background that scatters light is used, the sample shows only a weak-yellow color related to the absorption of the azo units (Fig. 3d). For quantitative optical analysis, spectroscopic investigations were carried out to show the reflectance spectrum of the D-n series (Fig. 3e). By collecting the scattered signal with an integrating sphere, the total reflection from the helical structures was measured, showing 35–40% efficiency. As demonstrated by the optical observations, the wavelength of the reflected light shifts from blue to green as the linker chain length of the dimer increases from 5 to 11; the reflected light wavelengths are 456 nm for D-5, 492 nm for D-7, 530 nm for D-9, and 549 nm for D-11. These results are consistent with the increase in the helical pitch observed by SEM imaging (Fig. 2d). To interpret the mechanism of light reflection by the helical nanostructures observed in SEM images, we performed numerical simulations using the FEM (Supplementary Fig. S7), which is based on the integration form of the Maxwell equation15. For this purpose, the simplified in-plane hexagonal model of the HNF arrays was used. The two parameters of pitch and diameter used in the calculation were directly extracted from the SEM images (Fig. 2d). The results of the numerical simulation on the nanostructure provide four polarized reflection coefficients: rXX, rXy, ryX, and ryy where the first and second subscripts represent the polarization axes of the incident and reflected light, respectively. The direction of the polarization plane of the incident light has no effect on the resultant reflectance because of the same polarized reflection coefficients, rXX = ryy and rXy = ryX, thus revealing the in-plane symmetry of the modeled HNF structure. Therefore, the unpolarized reflectance can be defined as the sum of the parallel and cross-polarized reflectance, \({R} = {\mathrm{r}}_{{\mathrm{xx}}}^2 + {\mathrm{r}}_{{\mathrm{xy}}}^2 + 2{\mathrm{r}}_{{\mathrm{xx}}}{\mathrm{r}}_{{\mathrm{xy}}}\). In the numerical calculation results (Supplementary Fig. S7), the trend in each resonance is consistent with the spectroscopic results. The two evident resonance peaks observed in each curve are exactly matched with one and half helical pitches, corresponding to longer and shorter wavelength resonances, respectively. Interestingly, each resonance frequency does not exactly reveal the Bragg reflection explained by the equation λ = np16. In addition to the theoretical evidence observed in Fig. S7, the refractive index (n) and extinction coefficient (k) measured experimentally by an ellipsometer show the presence of an electromagnetic effect (Supplementary Fig. S8). It is shown that the refractive index near the resonance frequency (Fig. 3e) does not reach n = 2, which is estimated by the Bragg equation. This evidence shows that the origin of the resonances is metamaterial characteristics along with electromagnetic coupling in dielectric metamaterials17. HNF structures that have dense nanostructures may have the field enhancement by the electromagnetic coupling effect in the vicinity of their structures and eventually increase the refractive index, according to the relation17,18, where εr and μr are the permittivity and permeability of the HNFs, respectively. Additional proof of this phenomenon can be obtained from the simulated electric field distribution in Fig. S9. The total electric field distribution at the resonant frequency is dramatically enhanced as the gap distance between HNFs is decreased.
To compare this reflector with a conventional 1D color reflector, we performed angle-dependent reflection measurements. The HNF-based color reflectors exhibit reduced angle-dependent characteristics. As the viewing angle changes, the reflection color does not change significantly compared with the conventional 1D color reflectors (Fig. 3f and Supplementary Fig. S10). This result can be explained by the uneven pseudolayers made of bundles of HNFs, as observed in the SEM images (e.g., the red-dashed horizontal line in Fig. 2d), in which the black and white lines are not on the horizontal line but rather are effectively deviated from the red-dashed line. These disordered elements in the ordered HNFs result in removal of the directionality, which is essential for a noniridescent color reflector, as found in a morpho butterfly19. This phenomenon is comparable to the case of the close-packed structure-based color reflectors such as photonic crystals comprising colloidal particles20,21.
Our method establishes a simple way to control the orientation of helical nanostructures in well-defined areas of the sample and therefore to produce “patternable color reflectors”9 (Fig. 4). The complex helical nanostructures can be easily written on with UV light and erased by heating (Fig. 4a, b). The detailed reversible procedure is based on the mechanism in Fig. 1, in which UV irradiation of the fluid LC phases is carried out. The pattern size obtained using a simple light-emitting diode UV lamp is ~10 μm (Fig. 4c, d), which could be easily improved by employing better optics.
a, b show patterns formed by irradiating the sample with UV light through a mask marked “KAIST”. The color pattern in the B4 phase was written by UV light irradiation of the fluid LC phases and erased by heating the fluid phases. c, d show the line color patterns with a 40-μm line width at different magnifications
Conclusions
A combination of the patterned irradiation technique and a material capable of self-assembling into helical nanostructures enabled the realization of patternable color reflectors. The fabrication process is low cost (requires a simple UV light source) and minimally time consuming (a sample with a few centimeter diameter can be processed in a few hours), which is advantageous considering that the fabrication of structural color reflectors by conventional nanofabrication methods using photolithography tools and dielectric material deposition is costly and complex. The proposed technology is only the starting point for the application of helical nanostructures, with the final goal being the exploitation of HNFs’ chirality in applications such as chiral catalysis, medicine, chiral separation, and chiro-optics. For example, using arrays of oriented HNFs with defined chirality, a three-dimensional Weyl point in a photonic system can be obtained with a loss-free surface state for a broad spectrum of light22,23. Other interesting topics might be topological photonics and metamaterials for the unidirectional transfer of photons, plasmons, and even acoustic waves24,25,26.
References
Hough, L. E. et al. Helical nanofilament phases. Science 325, 456–460 (2009).
Zhang, C., Diorio, N., Lavrentovich, O. D. & Jákli, A. Helical nanofilaments of bent-core liquid crystals with a second twist. Nat. Commun. 5, 3302 (2014).
Yoon, D. K. et al. Orientation of a helical nanofilament (B4) liquid-crystal phase: topographic control of confinement, shear flow, and temperature gradients. Adv. Mater. 23, 1962–1967 (2011).
Le, K. V., Takezoe, H. & Araoka, F. Chiral superstructure mesophases of achiral bent-shaped molecules—hierarchical chirality amplification and physical properties. Adv. Mater. 29, 1602737 (2017).
Li, L., Salamonczyk, M., Jákli, A. & Hegmann, T. A dual modulated homochiral helical nanofilament phase with local columnar ordering formed by bent core liquid crystals: effects of molecular chirality. Small 12, 3944–3955 (2016).
Kim, H. et al. Multistep hierarchical self-assembly of chiral nanopore arrays. Proc. Natl Acad. Sci. USA. 111, 14342–14347 (2014).
Lee, S. et al. Physico-chemical confinement of helical nanofilaments. Soft Matter 11, 3653–3659 (2015).
Toshchevikov, V., Petrova, T. & Saphiannikova, M. Kinetics of light-induced ordering and deformation in LC azobenzene-containing materials. Soft Matter 13, 2823–2835 (2017).
Zheng, Z.-G et al. Three-dimensional control of the helical axis of a chiral nematic liquid crystal by light. Nature 531, 352–356 (2016).
Zheng, Z.-G. et al. Light-patterned crystallographic direction of a self-organizied 3D soft photonic crystal. Adv. Mater. 29, 1703165 (2017).
Kim, H. et al. Linakage-length dependent structuring behaviour of bent-core molecules in helical nanostructures. Soft Matter 12, 3326–3330 (2016).
Krietenstein, B. The perfect boundary approximation technique facing the challenge of high precision field computation. In Proceedings of the XIX International Linear Accelerator Conference (LINAC98). 860–862 (1998).
Zep, A., Sitkowska, K., Pociecha, D. & Gorecka, E. Photoresponsive helical nanofilament of B4 phase. J. Mater. Chem. C 2, 2323–2327 (2014).
You, R. et al. Nanoconfined heliconical structure of twist-bend nematic liquid crystal phase. Liq. Cryst. 46, 316–325 (2019).
Weiland, T. A discretization method for the solution of Maxwell’s equations for six-componen fields. Electron. Commun. 31, 116–120 (1977).
Xiang, J. et al. Electrically tunable selective reflection of light from ultraviolet to visible and infrared by heliconical choleterics. Adv. Mater. 27, 3014–3018 (2015).
Jahani, S. & Jacob, Z. All-dielectric metamaterials. Nat. Nanotechnol. 11, 23–26 (2016).
Shin, J., Shen, J.-T. & Fan, S. Three-dimensional metamaterials with an ultrahigh effective refractive index over a broad bandwidth. Phys. Rev. Lett. 102, 093903 (2009).
Chung, K. et al. Flexible, angle-independent, structural color reflectors inspired by morpho butterfly wings. Adv. Mater. 24, 2375–2379 (2012).
Lee, H. S., Shim, T. S., Hwang, H., Yang, S.-M. & Kim, S.-H. Colloidal photonic crystals toward structural color palettes for security materials. Chem. Mater. 25, 2684–2690 (2013).
Cho, S., Shim, T. S., Kim, J. H., Kim, D.-H. & Kim, S.-H. Selective coloration of melanin nanospheres through resonant mie scattering. Adv. Mater. 29, 1700256 (2017).
Noh, J. et al. Experimental observation of optical Weyl points and Fermi arc-like surface states. Nat. Phys. 13, 611–617 (2017).
Yang, B. et al. Ideal Weyl points and helicoid surface states in artificial photonic crystal structure. Science 359, 1013–1016 (2018).
Slobozhanyuk, A. et al. Three-dimensional all-dielectric photonic topological insulator. Nat. Photonics 11, 130–136 (2017).
Jin, D. et al. Infrared topological plasmons in graphene. Phys. Rev. Lett. 118, 245301 (2017).
Peng, Y.-G. et al. Experimental demonstration of anomalous Floquet topological insulator for sound. Nat. Commun. 7, 13368 (2016).
Acknowledgements
This study was supported by a grant from the National Research Foundation (NRF) and funded by the Korean Government (MSIT) (2017R1E1A1A01072798, 2017M3C1A3013923, 2017R1A5A1014862, and 2018R1A5A1025208). The experiments at PLS-II were supported in part by MSIT and Pohang University of Science and Technology. This work was also partially supported by IBS-R011-D1 and UMO-2016/22/A/ST5/00319.
Author information
Authors and Affiliations
Contributions
W.P. and D.K.Y. designed the research project; A.Z., D.P. and E.G. synthesized the dimers and performed the initial characterization of the dimers; W.P. carried out the optical and electron microscopy studies; W. P., H.A. and T.J.S. performed the GIXRD experiments; W.P., K.I.S., T.S.J. and J.H.K. carried out the spectroscopic investigations; T.H. and T.-T.K. performed the simulations; and W.P., T.H., D.P., E.G. and D.K.Y. analyzed the results and wrote the manuscript.
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Park, W., Ha, T., Kim, TT. et al. Directed self-assembly of a helical nanofilament liquid crystal phase for use as structural color reflectors. NPG Asia Mater 11, 45 (2019). https://doi.org/10.1038/s41427-019-0146-6
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41427-019-0146-6
This article is cited by
-
Precise orientation control of a liquid crystal organic semiconductor via anisotropic surface treatment
NPG Asia Materials (2022)