Introduction

For the last several years, the search for materials with large magnetoresistances (MRs) and studies on related phenomena have been in the forefront of worldwide research activity1,2,3,4,5,6,7 owing to their widespread application in the field of magnetic sensors, magnetic memory devices, magnetic switches, etc8,9,10,11,12. The highest value of MR in principle can be achieved if the resistivity of the material can be transformed from an extreme insulating material (such as mica) to a very good metallic material (such as copper) by applying a magnetic field.

In perovskite manganite, an insulating state is observed in the charge-ordered antiferromagnetic (CO-AFM) sample, which generally appears near half doping. The critical magnetic field, which is required to destabilize the CO-AFM state, increases with decreasing bandwidth. The CO-AFM state can be weakened by introducing ferromagnetic proximity as follows: (i) by effectively increasing the bandwidth of the eg electrons via substitution of larger cations at the A-sites13,14,15,16, (ii) via B-site doping (e.g., Cr or Ru doping on Mn sites)17,18,19, and (iii) by making FM-AFM core-shell nanostructures (or nanoparticles)20,21,22. Thus, inducing a ferromagnetic phase fraction in an antiferromagnetic manganite or, in other words, engineering electronic phase separation is an effective tool to enhance the MR. Recently, a great amount of effort has been devoted to control the electronic phase separation in bulk and low dimensional manganites23,24,25,26,27,28,29.

It is known that the CO-AFM state in a low bandwidth Sm0.5Ca0.5MnO3 (SCMO) is very stable30, and an ~ 500 kOe (at temperature (T) = 4.2 K) critical magnetic field (HCR) is required to destabilize the CO state. On the other hand, CO-AFM and FM metallic phases coexist in Sm0.5Sr0.5MnO3 and are metallic at low temperatures31,32. In our case, we prepared Sm0.5Ca0.25Sr0.25MnO3 (SCSMO) by replacing half of the Ca2+ ions with Sr2+ ions. This substitution reduces the charge-ordering temperature (TCO) and Neel temperature (TN) of SCSMO by ~ 50 K compared with its parent compound SCMO14. Although SCSMO remains a strong insulator (~ 1012 Ohm-cm) at low temperature, the critical field decreases to 48 kOe (for SCSMO) from 500 kOe (for SCMO).

For the prepared polycrystalline SCSMO, surprisingly, we obtain an unprecedented MR of ~ 1015% at 10 K upon application of a 90 kOe magnetic field. This MR value in the bulk SCSMO sample is undoubtedly a record value compared with the previously observed MR in any charge-ordered compounds. For example, the MR value for the La0.5Ca0.5MnO3 compound is 108% at 57 K for an 80 kOe applied field. Via a substrate-induced strain, a huge MR of 1011% has also been observed in Nd0.5Ca0.5MnO3 thin film at 50 K upon application of a 70 kOe magnetic field33. The charge-ordered Pr0.5Ca0.5MnO3 compound shows an MR of 108% at 60 K upon application of a 150 kOe magnetic field owing to the strain induced by the substrate34. Moreover, a thin film made of our parent compound SCMO shows an MR of 106% upon application of a 200 kOe external field at 57 K35. In contrast, the MR value of our SCSMO sample reaches 106% at 50 K in an only 30 kOe magnetic field.

We also find an ultrasharp metamagnetic transition36,37,38,39 below 10 K. We explain the metamagnetic as well as ultrasharp metamagnetic transition using a martensitic scenario. Our Monte Carlo simulations using a two-band double-exchange model show that A-site disorder suppresses the CE-type phase, but the system remains insulating without any external magnetic field. In an external magnetic field, the inhomogeneous disorder seeds the ferromagnetic metallic clusters into the system, and as a result, resistivity decreases at low temperatures, which gives rise to a large MR.

Materials and methods

Sample preparation

The polycrystalline SCSMO compound was prepared via the well-known sol–gel chemistry route. For the sample preparation, high purity (99.99%) Sm2O3, CaCO3, Sr(NO3)2, MnO2, oxalic acid, and citric acid were used as the constituents. The appropriate amounts of Sm2O3 and CaCO3 were converted to their nitrate forms using concentrated nitric acid (HNO3) and dissolved into Millipore water. Because MnO2 does not dissolve directly in HNO3, the appropriate amount of oxalic acid was used to convert it into the oxalate form, which easily dissolves in Millipore water in the presence of nitric acid. After preparation of the individual clear solutions of the constituent elements (Sm2O3, CaCO3, Sr(NO3)2, and MnO2), all solutions were homogenously mixed by using a magnetic stirrer for 30 minutes. To make the precursor solution, a suitable amount of citric acid was added to this homogenous solution. Extra water was slowly evaporated by continuously heating this solution using a water bath while maintaining the temperature of the water bath at ~ 80 °C. This slow evaporation continued until gel formation. After the gel formed, it decomposed at a slightly higher temperature (~ 150 °C), and a black porous powder was formed. To evaporate the extra citric acid, porous powder was directly heated at 500 °C for 4 h. To obtain crystalline single-phase bulk compounds, the powder sample was first pelletized and heated at 1300 °C for the time period of ~ 36 h.

TEM measurements

High-resolution transmission electron microscopy (HRTEM) was performed using a FEI Tecnai, F30 microscope with a point-to-point resolution of 1.8 Å. The composition of the prepared sample was determined via energy dispersive X-ray spectroscopy (EDS) analysis using an analyzer mounted on the same microscope.

Electrical transport measurement

Resistance measurements in the absence of an external magnetic field were carried out using a Keithley source and measure unit 2651 A via the four probe method in the temperature range of 20 K to 300 K. The low temperature, measurement of the zero field resistivity was extended below 20 K using a Keithley Electrometer 6517 A in the capacitor arrangement method, and below 10 K, the resistance value exceeded our measurement limit-I (1013 ohm). In-field resistivity measurements were carried out using the 2651 A with the measurement limit-II of 1011 ohm.

Magnetic property measurements

Magnetic properties were measured using a superconducting quantum interference device magnetometer (SQUID-VSM) from Quantum Design in the temperature range of 2–300 K with a maximum magnetic field value of 70 kOe.

XRD measurements

Room temperature powder X-ray diffraction (XRD) and temperature-dependent XRD measurements in the temperature range of 15–300 K were performed using a RIGAKU-TTRAX-III diffractometer with a rotating anode Cu source of wavelength λ = 1.54 Å (CuKα). Measurements were performed at a 9 kW power. To observe the effect of the magnetic field on the XRD linewidth broadening, zero field and 70 kOe in-field followed by zero field measurements were performed using the low temperature and high magnetic field XRD setup at UGC-DAE CSR (Indore).

Heat capacity measurements

The magnetic field dependence as well as temperature dependence of the heat capacity of the sample was determined using the physical property measurements system from Quantum Design.

Results and discussion

Synthesis and structural characterization

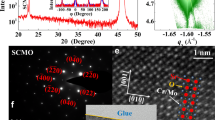
High-quality polycrystalline SCSMO was prepared via the well-known sol–gel technique (see the methods for details). The crystalline structure and single-phase nature of the sample were studied using room temperature XRD and transmission electron microscopy (TEM). The XRD pattern (see Fig. 1a) (analysis is discussed in supplementary section I(A)) and the TEM diffraction pattern (see Fig. 1e) show the orthorhombic crystallographic symmetry (Pnma) of the sample. Room temperature chemical analysis using EDS measurement (see supplementary section I(C)) shows that the elements are distributed homogeneously and stoichiometrically.

Fig. 1: XRD and TEM analysis
figure 1

a, b show the profile fitting of the room temperature (RT) and low temperature (15 K) XRD data using Pnma and (Pnma + P21/m) space groups. The insets of a and b show the fitting of the peaks at 2θ = 47.5°, where a new monoclinic phase (P21/m) appears at low temperature. c displays the evolution of the new peak of the P21/m space group with temperature. d shows the XRD linewidth modification in the presence of a zero magnetic field and a 70 kOe magnetic field and after removing the field. e displays typical (100) zone axis ED patterns at room temperature. The pattern was indexed using an orthorhombic structure (Pnma). f demonstrates a (001) bright-field image recorded at 100 K during TEM measurements. For HRTEM analysis, please see Supplementary section I(B)

Full size image

We also present XRD analysis at several low temperatures in Fig. 1b–d. With lowering of the temperature, another crystallographic phase with monoclinic symmetry P21/m along with the room temperature symmetry Pnma, i.e., combinations of Pnma and P21/m, appears below T ≤ 120 K. The evolution of the new peak corresponding to the P21/m monoclinic space group is shown in Fig. 1c. This figure indicates that below 120 K, the new peak appears at 2θ = 47.5°, and its intensity remains almost constant below 100 K. This implies that below 100 K, the P21/m phase becomes trapped within the host Pnma phase, creating a lattice strain in the host Pnma phase. Strain is also evident from the TEM analysis (see Fig. 1f) at 100 K. It was previously shown that the antiferromagnetic transition is associated with structural transition from the orthorhombic to orthorhombic + monoclinic phase at 135 K in Sm0.5Sr0.5MnO340,41. Therefore, the monoclinic structure favors the antiferromagnetic phase in Sm0.5Sr0.5MnO3. In our case, the SCSMO compound also undergoes the same kind of structural transition at 120 K. We will show in the next section that the system also undergoes an antiferromagnetic transition at 120 K. Thus, the monoclinic P21/m phase (shown in Fig. 1b, c) is associated with the CE-AFM phase.

The effect of the external magnetic field (70 kOe) on the XRD linewidth broadening at 2 K (see Fig. 1d) indicates a decrease in the linewidth (full width at half maxima) at 2θ = 47.5° from 0.58° to 0.46°, which then remains at the same value even after removing the field. This shows that strain decreases in an external magnetic field and then remains as it is even after removing the field.

Magnetic and magnetotransport measurements

The temperature-dependent magnetization and resistivity for different applied magnetic fields are shown in Fig. 2a, b. Interestingly, below 60 K, magnetization increases, but the ferromagnetic fraction is very small for the 100 Oe magnetic field, as confirmed by the thermoremanent magnetization measurements (discussed in supplementary section I(D)). As a result, the system without any magnetic field remains insulating at low temperature, as shown in Fig. 2b, but the stability of the CO-AFM state decreases (discussed in the next paragraph). This is unlike our previously studied core-shell (ferromagnetic core and antiferromagnetic shell) nanostructures22, for which a comparatively small resistivity (~ 102 Ohm-cm) was obtained at low temperatures. Below a certain temperature (T < 10 K), the value of the resistance is R ~ 1013 ohm for SCSMO, which is the limiting value of our measuring instruments (see the methods section for details). The ordering temperatures (TCO and TN) are indicated in the inset of Fig. 2a, b, and a similar TCO is also obtained from the heat capacity measurement (please see supplementary section I(E)).

Fig. 2: Magnetotransport properties
figure 2

a Variation of magnetization with temperature in 100 Oe and 30 kOe external magnetic fields. The inset shows the signature of CO and AFM ordering, indicated by arrows, from the temperature derivative of M(T) data taken in the field cooled warming (FCW) protocol in the presence of a 100 Oe magnetic field. b Temperature-dependent resistivity without (red) and with (30 kOe (blue), 50 kOe (olive) and 90 kOe (violet)) external magnetic fields. The dotted lines represent the resistivity data taken during the field cooling cycle, and the solid lines represent the FCW cycle. The inset shows the variation of the activation energy (EA ∞ d[ln(ρ)]/dT−1) with temperature, calculated from the temperature dependence of the zero field resistivity data, and the ordering temperatures are indicated by arrows. c Magnetic field dependence of MR on temperature for different magnetic fields. d Magnetization vs. magnetic field and e resistivity vs. magnetic field at different temperatures. The inset in d shows the temperature dependence of HCR and zero field cooled (ZFC) magnetization in a 100 Oe magnetic field. f Magnetic field-dependent magnetoresistance at three different temperatures. See the materials and methods section for an explanation of limit-I and limit-II, mentioned in b and e, respectively

Full size image

A 30 kOe magnetic field induces a larger ferromagnetic fraction, and as a result, the resistivity decreases considerably (from 1013 Ohm-cm to ρ ~ 17.5 Ohm-cm at T = 2.5 K) at low temperatures (see Fig. 2a, b). This shows not only that TCO decreases but also that the robustness of the CO-AFM state is reduced in SCSMO. A huge hysteresis is observed between the field cooling and heating cycles for 30 kOe in the temperature range of 50 K < T < 100 K in both the magnetization and resistivity curves, which is the signature of field-induced electronic phase separation42. With a further increase in the applied magnetic field, this coexistence is suppressed, and the low temperature resistivity goes to 10−2 Ohm-cm (for 90 kOe).

To quantify the field-induced change in resistivity, we plot the MR ( = (ρ(H) − ρ(0))/ρ(H) × 100) vs. temperature at different magnetic fields in Fig. 2c. MR is ~ 10% for 20 kOe but astonishingly increases to 1013% for a 30 kOe external magnetic field and to as large as ~ 1015% at 10 K for a 90 kOe magnetic field. The MR value as high as 1015% in the polycrystalline stable SCSMO compound is a unique observation.

The isothermal magnetization measured in the zero field cooled (ZFC) protocol at different temperatures (presented in Fig. 2d) shows the field-induced metamagnetic transitions. The experimentally obtained saturation magnetic moment (3.82 μB) at 30 K is close to the estimated magnetic moment for the full saturation of the Mn3+/Mn4+ and Sm3+ ions (3.85 μB). This clearly indicates that the CO-AFM state transforms completely upon application of the magnetic field via the metamagnetic transition near the critical magnetic field HCR. The temperature variation of HCR measured from M(H) isotherms is opposite to that of ZFC magnetization, as shown in the inset of Fig. 2d. The FM components present in the ZFC sample act as nucleation centers and grow at the expense of AFM components in an external magnetic field, resulting in a metamagnetic transition at HCR. As the ZFC magnetization increases from 2 K to 50 K, the enhanced thermal energy reduces HCR from 47.8 kOe at 2 K to 34.5 kOe at 50 K. For T > 50 K, HCR increases owing to reduction of the ZFC magnetization. In the absence of AFM components, above TN, the field-induced metamagnetic transition vanishes.

Figure 2e shows the resistivity vs. magnetic field isotherms measured at different temperatures. Interestingly, the isotherms measured at lower temperature (10 K) show an exceptionally sharp metamagnetic jump. With increasing temperature, the loop area between increasing and decreasing field sweeps decreases, and at 100 K, it almost disappears. Thus, we believe that field-induced phase coexistence is sustained up to ~ 120 K, which is the antiferromagnetic ordering temperature. Another point to note here is that the system remains in the low resistivity state even after removing the field for T < 50 K. Owing to the resistivity measurement limitation, the resistivity is limited to 1010 ohm-cm in an external magnetic field, and as a result, we can only measure the MR for temperatures above 25 K. The MR is equal to 1012% (104%) at 25 K (80 K) for a 45 kOe magnetic field, as shown in Fig. 2f, and will be even larger for lower temperatures.

Ultrasharp metamagnetic transition

Interestingly, the resistivity (and magnetization) vs. magnetic field isotherms (see Fig. 3a) at 2 K show exceptionally ultrasharp steps with a width of ~ 10 Oe (the smallest step used during the measurement is 3 Oe). To explore the origin of this ultrasharp metamagnetic transition, we now measure the heat capacity (C) with a magnetic field. During the field increasing cycle, the heat capacity data show a step-like behavior at ~ 48 kOe, as shown in Fig. 3b, which has a one-to-one correspondence with the step-like behavior observed in the magnetization and resistivity isotherms. This is opposite to the case observed in earlier studies where C decreased sharply with H at the transition point, which was associated with the rise in temperature of the system owing to the release of energy that assisted the abrupt field-induced transition36,43. The sharp increase in the heat capacity at the 48 kOe magnetic field rules out the possibility of an exothermic temperature-driven avalanche metamagnetic transition being observed in our system, and we believe that the system changes martensitically.

Fig. 3: Ultrasharp metamagnetic transition
figure 3

a Magnetization (and resistivity) vs. magnetic field at 2 K. See the Materials and methods section for an explanation of limit-II. b Variation of heat capacity with an external magnetic field at 2 K. Here, the red and blue symbols represent the C(H) data taken during increasing and decreasing fields, respectively. c Effect on isothermal magnetization of different cooling fields at 2 K

Full size image

To ascertain the martensitic nature, we also studied the isothermal magnetization (at 2 K) for different cooling fields 9see Fig. 3c). With increasing cooling field, the FM fraction increases, and as a result, the interfacial elastic energy increases. Owing to this, the critical field increases with increasing cooling field. At the same time, the critical field decreases slightly when we increase the sweep rate from 10 Oe/sec to 200 Oe/sec for the ZFC sample (see supplementary section I(F) for details). This is because the lattice has adequate time to accommodate the induced interfacial strain between the AF and FM domains at a lower sweep rate, and a larger magnetic field is required to break the energy barrier. Both of these scenarios indicate the martensitic nature of the transition43,44,45,46,47. Our resistivity relaxation study (see supplementary section I(G)) also confirms the martensitic nature of the metamagnetic transitions (Fig. 2d, e) at higher temperatures.

Theoretical simulation

In this section, we discuss the physical origin of the huge MR using a two-band double-exchange model including superexchange (J) and electron–phonon coupling (λ). Our model Hamiltonian19,48,49,50,51 (see Supplementary Section II for details), effectively a lattice of Mn ions, qualitatively reproduces the phase diagram of manganites. For SCMO (and SSMO)-like materials, involving two A-type elements30, one generally adds \(\mathop {\sum}\nolimits_i {\varepsilon _in_i}\) such that \(\overline {\varepsilon _i} = 0\) to model the A-site cationic disorder48,51. Considering the fact that the Sr2+ ions randomly occupy the A-sites in the polycrystalline SCSMO compound and are larger in size compared with both Sm3+ and Ca2+, chemical disorder is created. This is also evident from the HRTEM images at room temperature, shown in Supplementary Section I(B) (Fig. 1b, c). Therefore, to model SCSMO, we neglect the disorder between Sm and Ca elements and incorporate the Sr disorder by adding \(\mathop {\sum}\nolimits_i {\varepsilon _in_i}\) at each Mn site selected from the distribution \(P\left( {\varepsilon _i} \right) = \frac{1}{4}\delta \left( {\varepsilon _i - \Delta } \right) + \frac{3}{4}\delta \left( {\varepsilon _i + \Delta } \right)\), where Δ is the quenched disorder potential. We add a Zeeman coupling term −\(\mathop {\sum }\limits_i h \cdot {\boldsymbol{S}}_i\) to the Hamiltonian in an external magnetic field, where Si are Mn t2g spins, to analyze the MR. We measure J, λ, Δ, h, and temperature (T) in units of kinetic hopping parameter t. The estimated value of t in manganites is 0.2 eV48.

A spin-fermion Monte Carlo technique based on the traveling cluster approximation52 is used on a two-dimensional 24 × 24 lattice (see supplementary section II for details). We use J/t = 0.1 and λ/t = 1.65, which reproduces the CE-CO-OO-I phase19 at an electron density n = 1 − x = 0.5. The electron density is the number of itinerant eg electrons per Mn site in our calculations. The system, as shown in Fig. 4a, b, remains insulating at low temperatures for Δ/t = 0.3 and h = 0, and the ferromagnetic structure factor S(0,0) is ~ 0.001 (for an outline of the resistivity and the magnetic structure factor calculations, please see Supplementary Section II).

Fig. 4: Monte Carlo results
figure 4

Temperature dependence of a the resistivity ρ in units of ha/2Π2e2 and b the FM structure factor S (0,0) at different external magnetic field h/t values for λ/t = 1.65, J/t = 0.1, and Δ/t = 0.3 (SCSMO-like materials). The legends in a, b are the same. The electron density is fixed at n = 0.5 in all figures. c Temperature dependence of ρ for λ/t = 1.73, J/t = 0.105, and Δ/t = 0 (SCMO-like materials). d Temperature dependence of the FM structure factor S(0,0) (inset: resistivity) for three sets of parameters (mimicking SCMO, SCSMO, and SSMO) in a very small magnetic field h = 0.002. See the text for details

Full size image

The resistivity at low temperatures decreases with magnetic field h (Fig. 4a), similar to our experimental results. This is owing to the increase of the FM correlations at low temperatures (Fig. 4b). On the other hand, SCMO-like materials (Fig. 4c) remain insulating at all temperatures, even for h = 0.03. Recall that SCMO (SSMO) has a smaller (larger) bandwidth than SCSMO. In our model calculations, a larger λ/t (and J/t) corresponds to a smaller bandwidth, or vice versa. For clarity, we use Δ/t = 0 (owing to the small mismatch between the Sm and Ca ionic radii) and set λ/t = 1.73 and J/t = 0.105 for SCMO-like materials. For SSMO-like materials, we set binary disorder48,51 with Δ/t = 0.3, and use λ/t = 1.57 and J/t = 0.095. The FM correlations at low temperatures increase, and the resistivity decreases from SCMO-like to SCSMO-like to SSMO-like materials (Fig. 4d), which is qualitatively similar to the experimental results30,31,32.

We turn now to understand the MR in SCSMO by plotting Monte Carlo snapshots obtained at T = 0.01. For h = 0.002, the system remains insulating (see Fig. 4d) owing to the CE-type correlations without any significant ferromagnetic charge-disordered regions (see Fig. 5a, c) in the system. For h = 0.02, ferromagnetic clusters coexist with zig–zag ferromagnetic chains, and the electron density is roughly homogeneous (~ 0.65) within the ferromagnetic clusters (see Fig. 5b, d). Moreover, the ferromagnetic clusters in SCSMO become connected with each other at reasonably large magnetic fields, unlike SCMO-like materials, for which the resistivity decreases at lower temperatures. Therefore, overall, the disorder due to Sr ions present in SCSMO weakens the CE-type state of SCMO and seeds the ferromagnetic charge-disordered clusters, but the system remains insulating at low temperatures. In an external magnetic field, ferromagnetic clusters grow and become connected, giving rise to a large MR in SCSMO samples.

Fig. 5
figure 5

Monte Carlo snapshots  a, b The z components of simulated Mn (t2g) spins. c, d The electron density for each site on a 24 × 24 lattice at T = 0.01 using λ/t = 1.65, J/t = 0.1, and Δ/t = 0.3. In a, c h/t = 0.002, and in b, d h/t = 0.02.

Full size image

Conclusion

In summary, by controlling electronic phase separation in narrow bandwidth CO-AFM material, a record MR value (~ 1013% in a 30 kOe external magnetic field and ~ 1015% in a 90 kOe external magnetic field at 10 K) till date is obtained in an SCSMO polycrystalline compound. The observed huge MR value has been explained by model Hamiltonian calculations. We also observed a magnetic field-induced ultrasharp metamagnetic transition at low temperatures. The many orders of magnitude higher MR than any other magnetoresistive materials reported thus far will motivate experimenters to design efficient magnetic materials for future applications.