Abstract
An important transition in the economic history of countries occurs when they move from a regime of low prosperity, high child mortality and high fertility to a state of high prosperity, low child mortality and low fertility. Researchers have proposed various theories to explain this demographic transition and its relation to economic growth. In this article, we test the validity of some of these theories by fitting a non-linear dynamic model for the available cross-country data. Our approach fills the gap between the micro-level models that discuss causative mechanisms but do not consider if alternative models may fit the data well, and models from growth econometrics that show the impact of different factors on economic growth but do not include non-linearities and complex interactions. In our model, mortality and fertility decline and economic growth are endogenized by considering a simultaneous system of equations in the change variables. The model shows that the transition is best described in terms of a development cycle involving child mortality, fertility and GDP per capita. Fertility rate decreases when child mortality is low, and is weakly dependent on GDP. As fertility rates fall, GDP increases, and as GDP increases, child mortality falls. We further test the hypothesis that female education drives down fertility rates rather than child mortality, but find only weak evidence for it. The Bayesian methodology we use ensures robust models and we identify non-linear interactions between indicators to capture real-world non-linearities. Hence, our models can be used in policymaking to predict short-term evolutions in the indicator variables. We also discuss how our approach can be used to evaluate policy initiatives such as the Millennium Development Goals or the Sustainable Development Goals and set more accurate, country-specific development targets.
Similar content being viewed by others
Introduction
The Industrial Revolution that brought unprecedented economic growth to Western Europe and North America also coincided with a new epoch in population dynamics (Galor, 2005). Countries moved from a regime of high mortality and high fertility to a regime of low mortality and low fertility, a process that researchers call the demographic transition (Kalemli-Ozcan, 2002). A key question for economists is whether economic growth causes the demographic transition or vice versa. In this article, we address this question by looking at the relationship between child mortality, fertility and economic growth.
One part of the relationship between economic growth and demography is clear. There is evidence of the impact of economic growth on child mortality: looking across all countries, there is a strong negative correlation between a country’s income per capita and child mortality (Cutler et al., 2006). So while inequalities and corruption may cause distortions due to inefficiencies and wastage of resources (Filmer and Pritchett, 1999; Rajkumar and Swaroop, 2008), the general pattern is that more money tends to produce better health-care systems. It is plausible that child mortality also impacts economic growth. For example, Heckman and Walker (1990) showed that the return to human capital is highest before the age of 5 years.
The relationship between the other socio-economic indicators is more complicated. Exogenous child mortality decline should lead to a fertility decline as women have fewer children if they know the chance of their survival is high (Kalemli-Ozcan, 2002). But there are many caveats due to specific factors (Ben-Porath, 1976; Barro, 1991; Haines, 1998). For instance, if the loss of a child affects the mother’s health, there may be a subsequent fertility decline following from a child mortality increase (Rutstein and Medica, 1978). Moreover, families make sequential fertility choice decisions, accounting for the gender and health of surviving children, before choosing to have more children (Sah, 1991; Wolpin, 1997).
Economic growth might also directly influence fertility decisions. In the classic Barro–Becker model (Becker, 1981; Barro and Becker, 1989), fertility choice is due to opportunity costs as increased wages for women result in less time spent on child bearing and child rearing. The Barro–Becker model has been highly influential and extended by others (Tamura, 1996; Strulik, 2004). Empirically its predictions are confirmed for Swedish fertility data (Eckstein et al., 1999), which show that two-thirds of fertility decline can be explained by child mortality decline and the remaining one-third can be explained by increase in wages. More broadly, using a quality–quantity trade-off model, Kögel and Prskawetz (2001) and Tamura (2002) show that an endogenous switch from an agricultural to a manufacturing economy has implications for fertility, which explains the coincidence of industrialization with fertility and mortality declines in countries.
The impact of fertility choice decisions at the individual level on country-level economic growth have proved difficult to quantify. Cigno (1998) proposed that at low development “death-reducing public expenditures are most effective”, but at high development these “crowd out parental expenditures and result in fertility decline”. However, Kalemli-Ozcan (2002, 2003) shows that the importance of fertility choice under uncertainty of child survival could explain empirical observations of the demographic transition of a wide range of countries. Moreover, Strulik (2004) suggests that child quality expenditures can initiate economic take-offs and result in perpetual growth, while its absence may cause economic stagnation with high fertility. Similarly, Galor (2005) and co-workers (Galor and Weil, 1996, 1999; Galor and Moav, 2002) suggest that the quality–quantity trade-off is endogenously triggered by technological progress, which leads to an increase in returns to education.
In spite of the insights that theoretical models bring, discussions about the underlying mechanisms tend to be “open-ended” (Brock et al., 2007). It is not clear if alternative models may fit observations better. On the other hand, the econometrics approach advocated by Durlauf et al. (2005) and Brock et al. (2007) focuses primarily on economic growth and includes the demographic transition only insofar as it impacts this growth. For instance, in the Barro regressions literature (Barro, 1991), life expectancy (which increases with exogenous child mortality decline) is an important covariate of economic growth. Similarly, using a Bayesian approach and a large number of covariates, Sala-i Martin (1997), Fernandez et al. (2001) and Ley and Steel (2009), among others, study the causes of economic growth with some thoroughness and show the importance of life expectancy (and, by implication, child mortality) in explaining economic growth in countries. However, these analyses ignore non-linearities and the complex interactions that are essential features of the process.
Our approach fills the gap between the detailed mechanistic models (for example, Kalemli-Ozcan, 2002; Galor, 2005; Kögel and Prskawetz, 2001; Barro and Becker, 1989) and the growth econometric models (for example, Barro, 1991; Durlauf et al., 2005; Sala-i Martin, 1997) in explaining the demographic transition. We fit polynomial models of changes in the key state variables (economic growth, child mortality decline and fertility decline), where each polynomial term represents a specific mechanism through which the change takes place. The non-linear and interaction terms model complex mechanisms beyond just linear correlations. We show that the three key variables of child mortality, fertility rate and GDP are linked to each other in the form of a development cycle.
On the theoretical side, our approach provides a broader appreciation of the non-linearities and interaction effects that are an integral part of complex socio-economic processes such as the demographic transition. On the policymaking side, our approach ensures that the models are robust and useful in short-run scenarios because we model yearly changes as a function of the interactions between the variables of interest. This provides policymakers effective decision-making tools on a yearly basis while remaining flexible enough to incorporate new data that become available over time.
The key results we obtain in this article are as follows. Our model shows that economic growth does not directly impact the fertility rate, but influences it through the intermediate variable child mortality. Similarly, the fertility rate affects child mortality only indirectly by increasing or decreasing the economic growth. These conclusions are important for the theoretical understanding of the economic growth and the demographic transition processes, and our results confirm the theory in Kalemli-Ozcan (2002) on the impact of endogenous child mortality change on fertility decline.
We also use our model to test the effect of female education on fertility rates. This is important for policymakers because a number of initiatives have been undertaken to reduce poverty in Sub-Saharan Africa, India and so on by reducing fertility rates through investments in female education based on prior research (Cochrane, 1979). However, Cleland (2000) suggests reductions in child mortality are more critical in reducing fertility rates. Our model shows that, up to first-order effects, female education is an important variable in reducing fertility rates. But when we account for the non-linearities in the system and higher-order effects, reducing child mortality is more important than improving female education for reducing fertility rate.
Such analyses show how our approach can be used to evaluate policy initiatives such as the Millennium Development Goals (MDGs) with quantitative specificity. For instance, our analysis supports the conclusion of Easterly (2009), Vandemoortele (2009) and others that the MDGs were unfair to Sub-Saharan Africa. We show that this is due to the differences in development trajectories in these countries caused by the inherent non-linearity in child mortality decline with respect to GDP. We suggest that, instead of setting arbitrary development targets, our non-linear dynamic model can be used to set country-specific development targets in the future, providing more feasible and fairer goals, especially for the upcoming Sustainable Development Goals initiative.
Methods
Data
The data are from the World Bank “World Development Indicators” dataset (WDI, 2015). This contains data for over 200 countries for a period of more than 50 years. For the economic indicator, we use the GDP per capita (in constant 2005 dollars). We use the log GDP value and call the variable G in the analysis.
We use child mortality as the mortality indicator (denoted by C). Child mortality refers to the number of children not surviving to age 5 per 1,000 live births and is a strong indicator of child health. The total fertility rate is the fertility measure (denoted by A) and is defined as the average number of children a woman has in the course of her reproductive lifetime.
We define the educational indicator E to be the average years of schooling for the female population as collected in the Barro–Lee dataset (Barro and Lee, 2010). Since the data are available only on a 5-yearly basis in that dataset, we use linear interpolation to obtain yearly data points.
The entire dataset is also available in the Palgrave Communications’ Dataverse repository (Ranganathan et al., 2015a).
Model
The changes in the variables are modelled endogenously so that the model specifies how changes in each of the state variables takes place as a function of the current state of the system. For the demographic transition, the state of the system is defined by the values of C, G and A and we model the time evolution of these variables. We estimate the model from cross-country data and write the estimating equations in terms of the variable values for a given country at a given time instant as:
where we assume ϵC(i, t), ϵG(i, t) and ϵA(i, t) are i.i.d normally distributed and independent for different countries i and at different time instants t. The functions fC(.), fG(.), fA(.) are modelled using polynomial basis functions in the state variables C, G, A. We include first-order and quadratic terms in the variables and their inverses along with all possible two-variable and three-variable interaction terms in the variables and their inverses. For example, the full specification of fC is
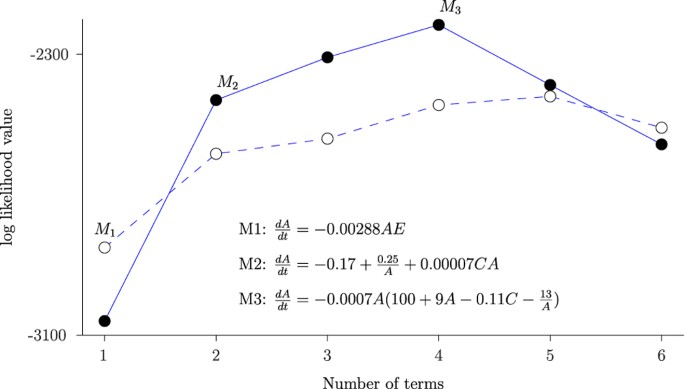
Thus, there are 33 terms in the full model specification, and the objective of the model selection algorithm we now present is to find the most efficient submodel that fits the data well. We do this in two stages. First, we rank all models with a given number of terms based on their log-likelihood score so that M1, M2, M3, … are the best possible models that include only 1, 2, 3, … polynomial terms, respectively. The log-likelihood scores for these models are an increasing function of the number of terms in the model.
In the second stage, we select the best model among these preselected models using the Bayesian marginal likelihood score, similar to the Bayes factor. For this, we assume a uniform, non-informative prior on the parameter space, so that every possible model coefficient is weighted equally (conditioned on the corresponding term being included in the submodel). This penalizes more complex models with larger number of terms as the dimension of the parameter space increases with increasing number of terms (see Ranganathan et al., 2014 for a fuller description of the approach).
We perform an additional test to find the best explanatory variable for each model. For instance, for the ΔC model, we test among all submodels that contain only C and one of the other two variables to test if two variables are sufficient to explain the ΔC data instead of all three. If we find that the ΔC data is explained well with only C and G variables and their interaction terms, we say that G explains changes in C adequately and is the variable with the most explanatory power for the ΔC model.
Robustness tests
We assumed the errors are independent for different countries and different time instants. However, performing independent estimations for the three variables is suboptimal if the error terms across the variables are correlated for the same countries at the same time instants (as may happen if there are systematic reasons for changes in the variable due to omitted variables, for example). We use a generalized least squares approach called the seemingly unrelated regressions (Amemiya, 1985) to handle this case. This involves an iterative procedure where Ordinary Least Squares (OLS) estimates of the model coefficicients are first computed and the error covariance matrix is estimated based on this first model estimate. This error covariace matrix is then used to recompute the model coefficients and this two-step procedure is iterated until convergence.
Another issue related to model robustness is to test how the model performs on different subsamples of the data. We have fitted the data for all countries to obtain our models. Researchers have shown that development patterns may differ vastly in countries with different socio-economic conditions (for example, Masanjala and Papageorgiou, 2008; Crespo Cuaresma, 2011). So we expect that applying our method to specific groups of countries, such as only low-income countries or those in Sub-Saharan Africa, should give significantly different models from the overall model we look at here. But using non-random subsamples to test for robustness restricts our modelling to only a particular region of the phase space, which is not consistent with our goal of identifying the overall trend in the data.
We instead test for robustness using random subsamples with different fractions of the data used for training the model (50%, 60%, 70%, 80% and 95% of the full sample) and with 100 different iterations for each case. Estimates of model fit for each of these models are obtained on the remaining out-of-sample test data. If our models are robust, they will be chosen as the best in most of the iterations for different subsamples. As more of the data are used for training, the probability of the training subsample being representative of the full data increases but the probability of the out-of-sample data being representative of the full data simultaneously decreases. As we use the out-of-sample data for evaluating model fitting error, other models are selected more often than for smaller training fractions due to unrepresentative test sets. However robust models should still be chosen more frequently than these other models. Hence, we report two numbers for each given size of training dataset—the absolute frequency with which our model is chosen as the best model for the different subsamples, and the relative position of our model in the list of models selected for different subsamples.
Multicollinearity is an issue when using a large number of regressors that are related to each other. It is possible that some terms are correlated with each other and this results in less efficient models being accepted. In evaluating models based on the Bayes factor, there is an implicit penalty to increasing the number of terms indefinitely but it is useful to perform direct tests to detect multicollinearity. Durlauf et al. (2008) suggest methods from within the Bayesian framework but we look at a standard diagnostic test—the condition numbers or condition indices defined as the ratios of the individual singular values to the largest singular value in the singular value decomposition of XTX, where X is the design matrix (Belsley et al., 1980). Condition numbers of over 50 (or 30 for conservative estimates) are considered to indicate presence of significant multicollinearity that may affect the OLS estimates.
Adding other explanatory variables
Our methodology expresses changes in the three variables only as a function of these three variables. However, it is well known that other variables, while not being part of the system in terms of the demographic transition, are important predictors of changes in these variables. For instance, education affects GDP growth, and has been postulated to cause fertility decline (Barro, 1991) and child mortality decline (Galor, 2005). Omitting these variables limits the explanatory power of our models.
However, these additional variables can be added in a straightforward manner to the model specification. If we wish to include the education variable into the full model for fertility decline, we can modify equation (3) so that we have
Similarly, if we wish to add more explanatory variables V1, V2, … that are known to be good predictors of ΔA, but we are interested only in the linear effect of Vj on ΔA, we modify the equation as
where αj are the regression coefficients. This straightforward extension allows us to refine our models easily to get better fits by the addition of more explanatory variables.
Lagged effects
In socio-economic systems, indicator variables may have lagged effects on one another. To model these effects from within our framework, we find the Bayes factor of the best models with a lagged variable instead of the actual variable. For example, to investigate the possible lag effect for G in the ΔC model, we consider the modified estimating equation
for different values of the lag parameter τ and find the model that best fits the data using the methodology described above, while also evaluating the best lag parameter value.
For practical purposes, in this article, we modify this proposed approach slightly so that we first evaluate the best model using the methodology described above for the unlagged variables. For this best model, we investigate lag effects by evaluating the models for different values of the lag parameters. The first approach is more consistent with the Bayesian framework we have described earlier, but datasets with lagged variables are more sparse and the models that we obtain using the first approach may not be robust enough for lag analysis. Hence, we use the second approach to analyse lagged effects.
Results
We apply the methods to the dataset with child mortality, log GDP per capita and fertility rate and find that the best dynamic model for the three key indicator variables (C, G and A) is given by
On the basis of Bayes factor values, we find that fertility rate is less important than GDP as a predictor of changes in child mortality. Similarly, to explain changes in fertility rate, the Bayes factor for models with only two variables C and A is relatively close to that of the models where all three variables are used. In the case of GDP, the two variable A and G model has a higher Bayes factor than the three variable model, which includes C. But alternative models for GDP also have similar Bayes factor values and hence it is not clear that this is the best possible ΔG model based on the data.
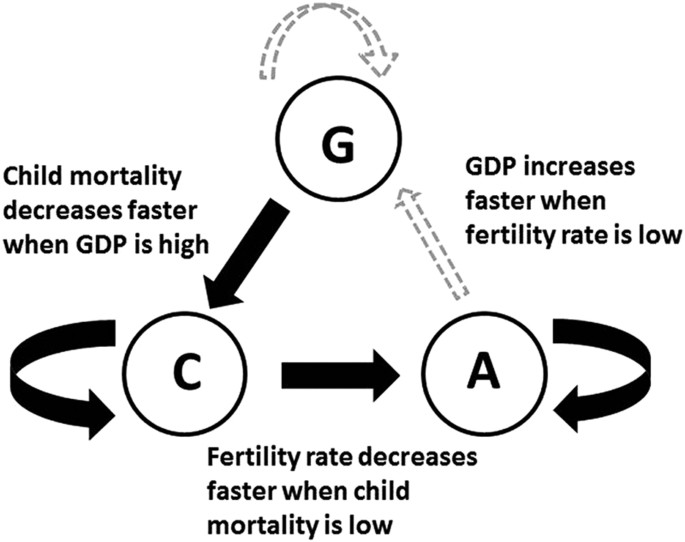
The interaction effects between the variables can be represented as shown in Fig. 1. The overall cycle illustrated here is that child mortality decreases faster with higher GDP, fertility rate decreases faster when child mortality is low and decreases in fertility rate are faster at higher levels of GDP. In going through the cycle, we can see that there is a tendency of countries to go from the regime of high mortality, high fertility and low prosperity to a regime of low mortality, low fertility and high prosperity as described in the demographic transition literature.
The Development Cycle as seen in the data for the three indicator variables. GDP drives changes in child mortality, which drives changes in fertility rate, which in turn drives changes in GDP. The arrow widths indicate the confidence in the model. The ΔC and ΔA models have much higher R2 values than the ΔG model.
In addition to pointing to the basic structure of interactions, the models above also show the non-linearities involved. For example, the ΔC model summarizes a number of important facts about how child mortality has changed across different countries over the last 50 years. Child mortality declines non-linearly with C and G, and the mean proportional decrease per year is given by −ΔC/C=0.0028(1.6G−0.02C). Percentage decrease in child mortality is therefore larger when GDP is high and when child mortality is low. Interestingly, without the second-order effect (the C2 term in the equation (4)), this mechanism is similar to the equation for endogenous change in mortality assumed in Kalemli-Ozcan (2002). Equation (4) shows a clear tendency to move towards low levels of child mortality, with a stable equilibrium point (that is, point where ΔC=0) at C*=0. There is a secondary effect that indicates that child mortality decreases more slowly with insufficient investment in child health. For instance, for two countries with the same G value but different C values, the country with the higher child mortality will experience a slower proportional decrease.
Similarly, we see that the fertility rate decreases faster when A is high, but this decrease is slowed if C is also high. There is also a secondary effect, which slows the percentage decrease in the fertility rate when A is low. The model shown above has two non-trivial equilibrium points (at roughly A*=10 and A*=1.5) obtained by solving the equation ΔA=0. The steady-state value A*=10 would correspond to a country with relatively low G and high C, and corresponds to the high mortality, high fertility and low economic growth regime in the demographic transition. The steady-state value A*=1.5 corresponds to a low mortality, low fertility and high economic growth regime. Thus, the two steady states correspond to the two opposite ends of the spectrum described in the demographic transition literature.
In the ΔG model, a high fertility rate slows economic growth. Solving ΔG=0 gives two equilibrium points, G*=4.4 and G*=11.6, suggesting that there is a slowdown in growth at both low and high GDP. We interpret the steady-state value of G*=4.4 as evidence of a transitory “poverty trap” (Ranganathan et al., 2015b), where countries are forced by certain self-reinforcing mechanisms to be trapped in a state of poverty without escape except through external means (Bowles et al., 2006). The other steady state G*=11.6 indicates a slowing of economic growth in rich countries.
Robustness tests
To evaluate the validity of the OLS estimates, we first test if the different error terms for different variables in the model are uncorrelated. We find there is only limited correlation (the maximum off-diagonal term in the scaled covariance matrix is 12% of the diagonal term). Hence, we are justified in assuming that the errors across variables are almost uncorrelated and we use the models obtained using this assumption. Performing generalized least squares using the seemingly unrelated regressions approach does not significantly alter the coefficients of the different terms and the iterative procedure converges quickly.
When we perform random subsample robustness tests on the models with 100 different subsamples, we find that the models specified by equations (4)–(6), are chosen a significant proportion of the time (69%, 45%, 96%, respectively, for the ΔC, ΔG, ΔA models) when 50% of the data are used for training. These numbers are necessarily lower (28%, 12% and 17%, respectively) when 95% of the data are used for training, as each test set is now very specific. However, our overall models remain the best models in terms of relative frequency. The ΔG and ΔA models in equations (5) and (6) are chosen more often than any other model for any fraction of training data used, while the ΔC model in equation (4) is chosen as the best model most often for all fractions of training data except for 95%, when it is chosen second most often. These results cumulatively support the conclusion that the models selected using our methodology are robust.
Next, we test if multicollinearity is a significant issue affecting the OLS estimates. Using the condition number test, we find that the ΔC model predictors CG and C2 are not significantly correlated (condition numbers={1, 4.76}). For the ΔA model, we find slight evidence of multicollinearity (condition numbers={1, 3.3, 7.5, 35.67}) slightly above the conservative threshold of 30 but still below 50. For the ΔG model there is significant multicollinearity (condition numbers={1, 10.45, 246.8}). But as we noted earlier, a number of alternative models fit the ΔG data closely. In fact, while the other two models have R2 values of 0.29 and 0.26, the ΔG model has a very low R2 value of less than 0.01 suggesting a very weak relationship.
Additional variables: the effect of education on fertility
There are a number of important covariates to be considered when looking at changes in fertility rates (Barro, 1991). Many policymakers work with female education as an important tool to reduce fertility rate and increase economic growth (Cochrane, 1979; UN, 2002). International organizations such as the United Nations Population Fund and the World Bank advocate better schooling for girls as a means of achieving lower child mortality and fertility rate. However,the evidence is not conclusive as significant fertility declines have occurred without noticeable changes in female education (Cleland, 2000; Basu, 2002). To test the hypothesis on whether female education is significant for fertility decline, we construct a model relating it to total fertility and test it against a model that relates child mortality to fertility.
We test the ΔA models containing only the two variables A and C in equation (6) against ΔA models containing only A and E. If C is a more significant predictor than E of ΔA, then those models will have higher Bayes factors. Figure 2 shows that education is the best single explanatory variable when only first-order effects are considered. For models that contain 2, 3 and 4 polynomial terms, models with C are better than models with E as the explanatory variable. If we go on to compute Bayes factor values for ΔA models with all these three variables (A, E and C) we find that the best 2, 3 and 4 term models involve only A and C. We conclude based on this that while higher female educational attainment does predict first-order decreases in fertility rate well, child mortality is the more effective predictor overall.
This explains empirical findings (Cleland, 2000; Basu, 2002)—while investments in female education are valuable, improvement in child health and investments in health-care systems in general might be more important.
Lagged effects
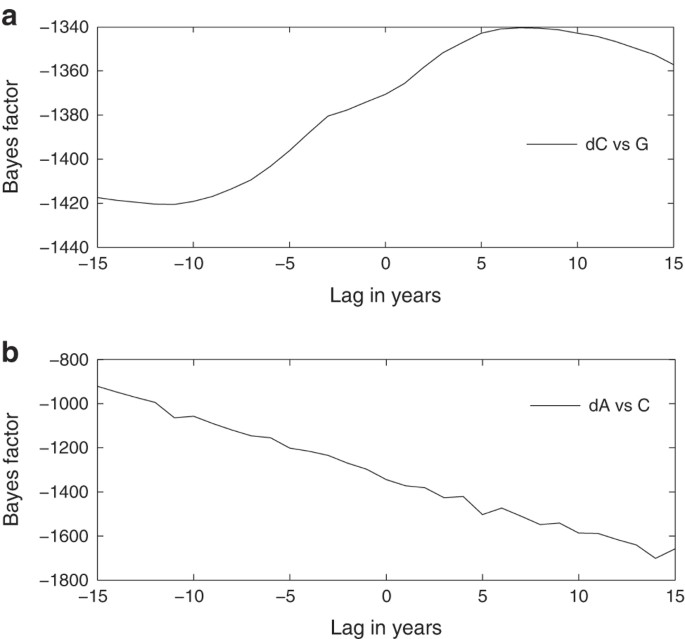
We find the lagged effect of G on ΔC by evaluating the set of models
for values of τ ranging between −15 and 15 years and find that the rate of decrease in child mortality depends on the level of GDP in the preceding 5 years. There is no lagged effect of C on changes in C.
We repeat the same procedure for the ΔA model
now with C(t−τ) as the lagged variable. The results suggest that the longer lead we use on child mortality the better prediction we get on fertility rate decrease. This suggests that women use their future prediction of the probability of their child surviving when making fertility choice decisions. The greater the probability of future survival, the lower the fertility rate (this is again in agreement with the mechanism in the Kalemli-Ozcan, 2002 model). Finally, the ΔG model does not show significant improvement when using a lagged variable.
Some caution is required in the interpretation of these results. The dataset for lagged variables is necessarily shorter than that used in the original non-lagged fitting. Given the significant amount of missing data for poorer countries, the long lags might be a selection effect for richer countries where this data are available. As larger datasets become available for developing countries, these results should become clearer (Fig. 3).
The log-Bayes factor plots for the ΔC and ΔA models as a function of the lag in G and C, respectively. (The Bayes factor values are reported in the log scale). The ΔC model suggests that a lag time of around 5 years in G is the best parameter for the ΔC models. A long lead time is suggested for C in the ΔA model.
Discussion
We have constructed a model of the demographic transition and its relationship to economic growth using the key indicator variables log GDP per capita, child mortality and total fertility rate. Our important substantive findings relate to the sequence of events in the demographic transition and may be seen as a test of the theory proposed by Kalemli-Ozcan (2002, 2003). Child mortality is reduced as a result of economic growth with a possible lagged effect. The reduction in child mortality, or possibly anticipation of this change, then drives fertility rates down. Although a predictor of fertility, female education plays a less important role than child mortality. Finally, economic growth is mostly independent of the other indicators, but is weakly driven by lowered fertility. The link back to child mortality completes the development cycle.
The innovation of the approach we have presented here lies in identifying the dynamic interactions that best explain the demographic transition and its effects on economic growth. Our approach provides (1) an emphasis on yearly changes instead of long-run equilibria that may not be attained; (2) the modelling of non-linearities and interaction effects, which is the norm in most realistic complex systems; and (3) a robust model that best explains empirical evidence on the demographic transition. An important question is how we interpret our results in terms of causal mechanisms. Can we use the equations we have derived to understand the actions of people living in the countries from which data were collected? To address this question we now give an interpretation of the models we have obtained in the context of earlier theoretical literature.
Various causative mechanisms are proposed for the onset of the demographic transition. For instance, Becker (1981) and a large body of literature following his work explains the demographic transition as a consequence of increased investments in human capital due to economic growth or technological progress. Increased returns on education are also thought to initiate the demographic transition and therefore a decline in fertility (Galor and Weil, 1999).
Our analysis and the cycle presented in Fig. 1 supports the models developed by Kalemli-Ozcan (2002, 2003) and emphasizes endogenously lowered child mortality over increased economic opportunities as the more immediate cause of drops in fertility rates. From an individual mother’s point of view, if the probability of children surviving is lower, then having more children increases biological fitness. While GDP has some effect on changes in fertility rate, the best single predictor of decreases in fertility rate is child mortality. Economic growth, however, comes into the picture indirectly as high GDP increases the survival probability, probably as a result of improvements in economic and social conditions.
Similarly, we find that while female education does predict decreases in fertility, child mortality remains a better predictor of these decreases. The decision whether or not to have a child may well involve a trade-off against other economic and education opportunities (Becker et al., 1990), but it is changes in the overall costs (and not just economic cost) of child bearing and child rearing that have the greatest role in decreasing fertility.
Although the emphasis on child mortality in the development cycle in Fig. 1 is different from that emphasized in some of the earlier work, the change in focus is relatively small. Importantly, none of our findings shift us a long way from those hypotheses previously proposed about human development. Instead, our analysis sharpens the picture by finding those models that are closest to all the available aggregate data. By fitting rate of change of indicators to their current state we have looked explicitly at how the state of the world in one year leads to the state of the world the following year.
This allows us to make robust short-term predictions on the evolution of the state of the system as defined by the three variables. There has been strong criticism of the MDGs (Easterly, 2009; Vandemoortele, 2009) for setting arbitrary development targets. As our methodology models changes in the child mortality, we can integrate it forward simultaneously with the other variables to make quantitative predictions on future values of child mortality for each specific country (as we have done in Ranganathan et al., 2015b). With this expected future value as a baseline value and a desired policy improvement based quantitatively on deviations from the business-as-usual scenario (say one standard deviation better than business-as-usual value), a feasible but fair development target can be set for each country.
From an econometric standpoint, in modelling the demographic transition, we have omitted many covariates specific to each indicator variable and hence do not explain the processes fully. For instance, adult mortality is an important variable and Kalemli-Ozcan (2002) and Soares (2005) include it in their models of fertility choice. The long lead time in our lagged effects analysis of the fertility rate model (equation (7)) suggests the importance of considering adult mortality. Child mortality levels are correlated with adult mortality levels and the inclusion of future child mortality levels in our model could be a proxy for women using future adult mortality levels in making decisions based on whether their children will survive into adulthood. Similarly, the growth econometrics literature has discussed in detail the important covariates of economic growth and these need to be included in our models to explain changes in log GDP (Barro, 1991; Durlauf et al., 2008; Ley and Steel, 2009).
However, our approach captures the interactions between the key variables and can be extended in a straightforward manner (as discussed in the Methods section) to include other variables of interest. We can add these additional variables either as control variables with only linear effects on the change variable or into the full framework of our methodology with non-linear and interaction effects. This will directly contribute to improving model fit and our understanding of the particular processes. Endogeneity is an important consideration when adding more explanatory variables. We show that our models are reasonably robust to the data but the addition of new variables may make the statistical estimates inefficient and this needs to be considered carefully.
From the statistical methods standpoint, we use non-informative priors on the parameter and the model space because we use an exploratory approach to obtain the model that best explains the data. To define “best fit”, we assumed that any submodel (equivalent to specifying the set of non-zero coefficients in the full model) is equally likely and that any model coefficient has an equal prior probability of being present. This is equivalent to assuming a discrete uniform prior on the model space (George, 2010). Chipman (1996) suggests the use of heredity priors to ensure that interaction terms are likely to be present only in models where the main effects are present. When we test our models with the strong heredity priors suggested by Chipman (1996), we find models with different terms. However, we prefer the uniform prior on the model space because some mechanisms can be better represented by using higher-order interaction terms without main effects. For instance, the ΔC model in equation (4) includes interaction and non-linear effects and no main effects, and hence would not be selected if a strong heredity prior were used. But the model we find suggests a mechanism whereby proportional changes (ΔC/C) as opposed to absolute changes (ΔC) are linearly related to the main effects C and G.
Finally, from the mechanistic standpoint, the approach we have taken in this article can be contrasted with one that starts from the point of view of underlying micro-level interactions of economic agents. There are a number of limitations to the micro-level modelling approach, with respect to providing succinct and empirically accurate models of data. First, although based on observations, such models do not necessarily provide the best fit to the existing data as they do not test alternative models. Instead, correlational evidence is provided for particular assumptions or predictions. The advantage of the Bayes factor-based analyses we have performed here is that they provide a likelihood measure over a number of plausible models. A second limitation of micro-level economic models is that they usually involve specific mathematical forms that limit the range of models, which can be studied formally using the available tools. While these restrictions help mathematical analysis, they are not necessarily feasible in terms of mechanisms and restrict the degree to which non-linearities in the data can be captured by the model. A third limitation is that, despite their mathematical tractability, the statement of such models is often not amenable to direct policy applications in comparison with a set of equations such as equations (4)–(6), which can be used to predict short-term evolutions in the state variables robustly.
At the same time, while the approach we have outlined in this article avoids these limitations, we use no underlying assumptions and thus provide no a priori causal basis for our models. This criticism must be taken seriously because, without identifying underlying mechanisms, there are always a multitude of possible models. But letting the data reveal the patterns helps us discuss, in a post-analysis stage as we have done above, how the derived models relate to the micro-level motives of economic actors.
Data Availability
The datasets analysed are available in Palgrave Communications’ Dataverse repository (Ranganathan et al., 2015a): http://dx.doi.org/10.7910/DVN/1ZUDJI. These datasets are from the World Bank World Development Indicators dataset and the Barro–Lee dataset.
Additional Information
How to cite this article: Ranganathan S, Swain RB, Sumpter DJT (2015) The demographic transition and economic growth: implications for development policy. Palgrave Communications. 1:15033 doi: 10.1057/palcomms.2015.33.
References
Amemiya T (1985) Advanced Econometrics. Blackwell: Oxford.
Barro RJ (1991) Economic growth in a cross-section of countries. The Quarterly Journal of Economics; 106 (2): 407–443.
Barro RJ and Becker GS (1989) Fertility choice in a model of economic growth. Econometrica; 57 (2): 481–501.
Barro RJ and Lee J-W (2010) A new data set of educational attainment in the world, 1950–2010. Working Paper 15902, National Bureau of Economic Research, http://www.nber.org/papers/w15902.
Basu AM (2002) Why does education lead to lower fertility? A critical review of some of the possibilities. World Development 30 (10): 1779–1790.
Becker GS (1981) A Treatise on the Family. Harvard University Press: Cambridge, MA.
Becker GS, Murphy KM and Tamura R (1990) Human capital, fertility, and economic growth. Journal of Political Economy 98 (5), S12–S37.
Belsley DA, Kuh E and Welsch RE (1980) Regression Diagnostics: Identifying Influential Data and Sources of Collinearity. John Wiley & Sons: New York, USA.
Ben-Porath Y (1976) Fertility Response to Child Mortality: Micro Data from Israel. M. Falk Institute for Economic Research: Israel.
Bowles S, Durlauf SN and Hoff K (2006) Poverty Traps. Princeton University Press: Princeton, New Jersey.
Brock W, Durlauf SN and West KD (2007) Model uncertainty and policy evaluation: Some theory and empirics. Journal of Econometrics; 136 (2): 629–664.
Chipman H (1996) Bayesian variable selection with related predictors. The Canadian Journal of Statistics/La Revue Canadienne de Statistique; 4 (1): 17–36.
Cigno A (1998) Fertility decisions when infant survival is endogenous. Journal of Population Economics; 11 (1): 21–28.
Cleland JG (2000) The Effects of Improved Survival on Fertility: A Reassessment. Population Council: New York, pp 60–92.
Cochrane SH (1979) Fertility and Education: What Do We Really Know? Johns Hopkins University Press: Baltimore, MD.
Crespo Cuaresma J (2011) How different is Africa? A comment on Masanjala and Papageorgiou. Journal of Applied Econometrics; 26 (6): 1041–1047.
Cutler DM, Deaton AS and Lleras-Muney A (2006) The determinants of mortality. NBER Working Paper 11963, Cambridge, MA.
Durlauf SN, Johnson PA, Temple JR (2005) Growth econometrics In: Aghion P and Durlauf SN (eds) Handbook of Economic Growth; Vol. 1. Elsevier: Amsterdam, pp 555–677.
Durlauf SN, Kourtellos A and Tan CM (2008) Are any growth theories robust? The Economic Journal; 118 (527): 329–346.
Easterly W (2009) How the Millennium Development Goals are unfair to Africa. World Development; 37 (1): 26–35.
Eckstein Z, Mira P and Wolpin KI (1999) A quantitative analysis of Swedish fertility dynamics: 1751–1990. Review of Economic Dynamics 2 (1): 137–165.
Fernandez C, Ley E and Steel MF (2001) Model uncertainty in cross-country growth regressions. Journal of Applied Econometrics; 16 (5): 563–576.
Filmer D and Pritchett L (1999) The impact of public spending on health: Does money matter? Social Science & Medicine; 49 (10): 1309–1323.
Galor O (2005) The transition from stagnation to growth: Unified growth theory In: Aghion P and Durlauf SN (eds) Handbook of Economic Growth. Elsevier: Amsterdam.
Galor O and Moav O (2002) Natural selection and the origin of economic growth. The Quarterly Journal of Economics 117 (4): 1133–1191.
Galor O and Weil DN (1996) The gender gap, fertility, and growth. The American Economic Review; 86 (3): 374–387.
Galor O and Weil DN (1999) From Malthusian stagnation to modern growth. The American Economic Review; 89 (2): 150–154.
George EI (2010) Dilution priors: Compensating for model space redundancy. In: Berger JO, Cai TT and Johnstone IM (eds). Borrowing Strength: Theory Powering Applications-A Festschrift for Lawrence D. Brown. Institute of Mathematical Statistics: Beachwood, Ohio, USA, pp 158–165.
Haines MR (1998) The relationship between infant and child mortality and fertility: Some historical and contemporary evidence for the United States. In: Montgomery MR and Cohen B (eds). From Death to Birth: Mortality Decline and Reproductive Change. National Academy Press: Washington DC, pp 227–253.
Heckman JJ and Walker JR (1990) The relationship between wages and income and the timing and spacing of births: Evidence from Swedish longitudinal data. Econometrica; 58 (6): 1411–1441.
Kalemli-Ozcan S (2002) Does the mortality decline promote economic growth. Journal of Economic Growth; 7 (4): 411–439.
Kalemli-Ozcan S (2003) A stochastic model of mortality, fertility, and human capital investment. Journal of Development Economics; 70 (1): 103–118.
Kögel T and Prskawetz A (2001) Agricultural productivity growth and escape from the Malthusian trap. Journal of Economic Growth; 6 (4): 337–357.
Ley E and Steel MF (2009) On the effect of prior assumptions in Bayesian model averaging with applications to growth regression. Journal of Applied Econometrics; 24 (4): 651–674.
Masanjala WH and Papageorgiou C (2008) Rough and lonely road to prosperity: A reexamination of the sources of growth in Africa using Bayesian model averaging. Journal of Applied Econometrics; 23 (5): 671–682.
Rajkumar AS and Swaroop V (2008) Public spending and outcomes: Does governance matter? Journal of Development Economics; 86 (1): 96–111.
Ranganathan S, Swain RB and Sumpter DJT (2015a) The demographic transition and economic growth: Implications for development policy. Dataverse. http://dx.doi.org/10.7910/DVN/1ZUDJI, accessed 16 September 2015.
Ranganathan S, Nicolis SC, Spaiser V and Sumpter DJ (2015b) Understanding democracy and development traps using a data-driven approach. Big Data; 3 (1): 22–33.
Ranganathan S, Spaiser V, Mann RP and Sumpter DJ (2014) Bayesian dynamical systems modelling in the social sciences. PloS One; 9 (1): e86468.
Rutstein S and Medica V (1978) The Latin American experience. In: Preston SH (ed). The Effects of Child and Infant Mortality on Fertility; Academic Press, New York, USA, pp. 93–112.
Sah RK (1991) The effects of child mortality changes on fertility choice and parental welfare. Journal of Political Economy; 99 (3): 582–606.
Sala-i Martin X (1997) I just ran four million regressions. NBER Working Paper 6252, Cambridge, MA.
Soares RR (2005) Mortality reductions, educational attainment, and fertility choice. American Economic Review; 95 (3): 580–601.
Strulik H (2004) Economic growth and stagnation with endogenous health and fertility. Journal of Population Economics; 17 (3): 433–453.
Tamura R (1996) From decay to growth: A demographic transition to economic growth. Journal of Economic Dynamics and Control 20 (6–7): 1237–1261.
Tamura R (2002) Human capital and the switch from agriculture to industry. Journal of Economic Dynamics and Control; 27 (2): 207–242.
UN. (2002) Completing the fertility transition. Population Bulletin of the UN Special Issues (48/49).
Vandemoortele J (2009) The MDG conundrum: Meeting the targets without missing the point. Development Policy Review; 27 (4): 355–371.
WDI. (2015) World Development Indicators 2015. The World Bank, http://elibrary.worldbank.org/doi/abs/10.1596/978-1-4648-0440-3, accessed 16 September 2015.
Wolpin KI (1997) Determinants and consequences of the mortality and health of infants and children. In: Rosenzweig MR and Stark O (eds). Handbook of Population and Family Economics; Elsevier: Amsterdam, pp 483–557.
Acknowledgements
This work was funded by ERC grant 1DC-AB and Swedish Research Council grant D049040.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
This work is licensed under a Creative Commons Attribution 3.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/3.0/
About this article
Cite this article
Ranganathan, S., Swain, R. & Sumpter, D. The demographic transition and economic growth: implications for development policy. Palgrave Commun 1, 15033 (2015). https://doi.org/10.1057/palcomms.2015.33
Received:
Accepted:
Published:
DOI: https://doi.org/10.1057/palcomms.2015.33
This article is cited by
-
Climate and land-use changes drive biodiversity turnover in arthropod assemblages over 150 years
Nature Ecology & Evolution (2021)
-
Economic growth and population transition in China and India 1990–2018
China Population and Development Studies (2021)