Achieving quantum precision limit in adaptive qubit state tomography

Abstract

The precision limit in quantum state tomography is of great interest not only to practical applications but also to foundational studies. However, little is known about this subject in the multiparameter setting even theoretically due to the subtle information trade-off among incompatible observables. In the case of a qubit, the theoretic precision limit was determined by Hayashi as well as Gill and Massar, but attaining the precision limit in experiments has remained a challenging task. Here we report the first experiment that achieves this precision limit in adaptive quantum state tomography on optical polarisation qubits. The two-step adaptive strategy used in our experiment is very easy to implement in practice. Yet it is surprisingly powerful in optimising most figures of merit of practical interest. Our study may have significant implications for multiparameter quantum estimation problems, such as quantum metrology. Meanwhile, it may promote our understanding about the complementarity principle and uncertainty relations from the information theoretic perspective.

Introduction

Quantum state tomography is a procedure for inferring the state of a quantum system from quantum measurements and data processing.^1–3 It is a primitive of various quantum information processing tasks such as quantum computation, communication, cryptography and metrology.^4–8 In sharp contrast with the classical world, any measurement on a generic quantum system necessarily induces a disturbance, limiting further attempts to extract information from the system. Therefore, many identically prepared systems are usually required for reliable state determination. Conversely, the precision limit in quantum state tomography offers a perfect window for understanding the distinction between quantum physics and classical physics.^9–12

Recently, great efforts have been directed to improving the tomographic efficiency given limited quantum resources.^13,14 For example, adaptive measurements have been realised in experiments, which may improve the scaling of the infidelity in certain scenarios.^14,15 However, most studies have been tailored to deal with specific figures of merit under special settings such as pure state or single-parameter models, which admit no easy generalisation to the more challenging and exciting multiparameter estimation problems with general figures of merit. In particular, the tomographic precision limit in the multiparameter setting is still poorly understood; experimental studies are especially rare. To fill this gap, in this work we report the first experiment that achieves the quantum precision limit in adaptive quantum state tomography on optical polarisation qubits.

Results

Quantum precision limit

In practice, the tomographic precision limit is determined by experimental settings. As technology advances, it is ultimately limited by basic principles of quantum mechanics. One fundamental limit is known as the quantum Cramér–Rao bound^16–19 (Supplementary Methods). In the one-parameter setting, this bound can be saturated locally by measuring a suitable observable, which may depend on the parameter point. To saturate the bound globally, it is usually necessary to use adaptive measurements. A simple and effective choice is known as the two-step adaptive strategy,^20,21 whose basic idea can be sketched as follows. Suppose N copies of the true state are available for tomography. First, we perform a generic informationally complete measurement on N₁ copies (usually $N_{1}N$ especially when N is large) of the true state and compute the maximum likelihood estimator (MLE)¹ according to the measurement statistics. Then we perform the optimal measurement with respect to the estimator on the remaining N₂=N−N₁ copies and compute the MLE again.

In the multiparameter setting, however, the quantum Cramér–Rao bound generally cannot be saturated except when the optimal observables corresponding to different parameters can be chosen to be compatible. The existence of incompatible observables underlies the main distinction between quantum state estimation and classical state estimation and is the main reason why multiparameter estimation problems are difficult and poorly understood. Up to now, the optimal solutions have been found only for a few special cases,^2,18 of which the qubit model is the most prominent.^9,21,22

To devise a good measurement scheme in the multiparameter setting, it is indispensable to take into account the subtle information trade-off among incompatible observables. A vivid manifestation of such trade-off is the wave–particle duality relation between fringe visibility $\mathcal{V}$ and path distinguishability $\mathcal{D}$^23,24

$$\begin{array}{}\text{(1)}& {\mathcal{D}}^2+{\mathcal{V}}^{2}1\end{array}$$

This phenomenon is not limited to the double-slit experiment but presents itself whenever we are trying to extract information about incompatible observables. It is especially important in understanding multiparameter estimation problems. Suppose the state of the quantum system is parametrised by a set of parameters denoted collectively by θ, then such trade-off can be succinctly summarised by the following inequality derived by Gill and Massar,²¹

$$\begin{array}{}\text{(2)}& \mathrm{tr}\left\{J^{-1}\left(\theta \right)I\left(\theta \right)\right\}⩽d-1\end{array}$$

which is applicable to any measurement on a d-level system. Here I(θ) and J(θ) are the Fisher and quantum Fisher information matrices, respectively (Supplementary Methods). The Gill–Massar (GM) inequality may be seen as a generalisation of the wave–particle duality relation in the language of quantum estimation theory. To appreciate its significance, it is instructive to point out that the upper bound would be d²−1 if all observables in quantum theory were compatible or, equivalently, if the quantum Cramér–Rao bound could always be saturated.

The GM inequality imposes a fundamental precision limit on quantum state tomography based on individual (non-collective) measurements. For example, it sets a lower bound for the scaled weighted mean square error (WMSE) of any unbiased estimator,^9,21

$$\begin{array}{}\text{(3)}& {ℰ}_W^{\mathrm{GM}}=\frac{{\left(\mathrm{tr}\sqrt{J^{-\mathrm{1/2}}W{J}^{-\mathrm{1/2}}}\right)}^2}{d-1}\end{array}$$

where W is the weighting matrix. Note that the GM bound for the WMSE is ${ℰ}_W^{\mathrm{GM}}/N$ if the sample size is N. In the case of a qubit, the GM bound agrees with the bound derived by Hayashi,²² and can always be saturated locally by mutually unbiased measurements^9,21 (Supplementary Methods). Recently, the GM inequality and GM bound have been turned into a powerful tool for studying a number of foundational issues entangled with incompatible observables,¹¹ such as the complementarity principle²⁵ and uncertainty relations.²⁶ The cross fertilisation of quantum estimation theory and foundational studies is due to lead to deeper understanding of both subjects.^9–12 Determination of the quantum precision limit in the multiparameter setting is thus of primary interest from both practical and foundational perspectives.

Attaining quantum precision limit with two-step adaptive strategy

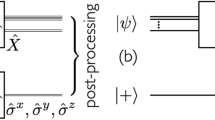
Here we report the first experimental verification of the GM bound in adaptive quantum state tomography on optical polarisation qubits. Our tomographic protocol consists of two-step adaptive measurements and MLE, as illustrated in Figure 1. In each step, we need to implement only three projective measurements that are mutually unbiased. Despite the simplicity of this approach, it is capable of attaining the quantum precision limit with respect to most figures of merit of interest. To facilitate applications of our approach, we have determined the precision limits and local optimal measurements with respect to a large family of figures of merit in the Supplementary Methods. For example, the GM bound for the scaled MSE is given by^9,27

$$\begin{array}{}\text{(4)}& {ℰ}^{\mathrm{GM}}={(2+\sqrt{1-s^2})}^2\end{array}$$

where s is the length of the Bloch vector of the true state. By contrast, the scaled MSE achievable by standard tomography using mutually unbiased measurements is given by 3(3−s²).^9,28 For concreteness, the two-step adaptive strategy for minimising the MSE is sketched as follows:

• 1 Measure σ_x, σ_y and σ_z on N₁/3 copies of the qubit, respectively, and compute the MLE ${\hat{\rho }}_1$ based on the measurement statistics. Denote the Bloch vector of ${\hat{\rho }}_1$ by ${\stackrel{\mathit{ˆ}}{\mathit{s}}}_1$.

• 2 Choose a unitary transformation $U\left({\stackrel{\mathit{ˆ}}{\mathit{s}}}_1\right)$ that rotates ${\stackrel{\mathit{ˆ}}{\mathit{s}}}_1$ to the z direction and apply this unitary transformation to the remaining N₂=N−N₁ copies of the qubit state. Measure σ_x, σ_y and σ_z with the following probabilities (see Supplementary Methods for more details),

Figure 1

Quantum state tomography with two-step adaptive strategy. The observables ${\mathit{\sigma }}_x^{\prime }$, ${\mathit{\sigma }}_y^{\text{'}}$ and ${\sigma }_z^{\text{'}}$ depend on the estimator ${\hat{\rho }}_1$ obtained in the first step and are related to σ_x, σ_y and σ_z via the unitary transformation $U\left({\stackrel{\mathit{ˆ}}{\mathit{s}}}_1\right)$ described in the main text. The probabilities p₁, p₂ and p₃ depend on both the estimator ${\hat{\rho }}_1$ and the figure of merit. In the large N limit, it suffices to use the measurement statistics of step 2 to construct the second MLE. In practice, it is preferable to use the measurement statistics of both steps.

$$\begin{array}{}\text{(5)}& \begin{array}{cc}{p}_1=p_2=\frac{1}{2+\sqrt{1-{\hat{s}}_1^2}}& p_3=\frac{\sqrt{1-{\hat{s}}_1^2}}{2+\sqrt{1-{\hat{s}}_1^2}}\end{array}\end{array}$$

where ${\hat{s}}_1$ is the length of ${\stackrel{\mathbf{ˆ}}{\mathbf{s}}}_1$. Construct the MLE ${\hat{\rho }}_2$ again based on the measurement statistics.

Experimental set-up

The experimental set-up is shown in Figure 2. A 2-mm-long β-barium borate crystal cut for type 1 phase-matched spontaneous parametric downconversion process is pumped at 404 nm by a 40-mW V-polarised beam. A pair of H-polarised photons with wave length λ=808 nm is created via spontaneous parametric downconversion process. One photon passes through an interference filter whose full width at half maximum (FWHM) is 3 nm, resulting in a coherence length of 270λ, and is detected by a single-photon detector acting as a trigger. The polarisation state of the other photon is prepared by half-wave plate (HWP)1, a 770λ quartz crystal, and quarter-wave plate (QWP)1. The quartz crystal, whose optic axis is aligned in the horizontal direction, completely decoheres horizontal and vertical polarisation components. The rotation angle of half-wave plate 1 determines the ratio of H- and V polarisation components, thereby together with the quartz crystal changing the purity of the state or the length of the Bloch vector. QWP1 is used to change the direction of the Bloch vector. QWP2 and half-wave plate 2 followed by a PBS are used to perform arbitrary projective measurements on the qubit. The rotation angles of half-wave plate 2 and QWP2 are controlled by a labview programme. The coincidence counts are measured by the coincidence circuit and are analysed by the computer. Without loss of generality, all polarisation states in our experiments are prepared such that the Bloch vectors are aligned along the direction (0.490, −0.631, 0.602). This is realised by setting QWP1 at the fixed deviation angle of 19.57°. The true state is calibrated with about 10⁷ photons.

Figure 2

Experimental set-up. A pair of horizontally polarised photons are generated via pumping a β-barium borate crystal. One is detected as a trigger and the other is sent through a half-wave plate (HWP), a QWP and a 770λ quartz crystal in between, marked as the state preparation module (green), to change the length and direction of the Bloch vector. After preparation, the photon polarisation is measured by a configuration of QWP2, HWP2 and a polarising beam splitter (PBS), marked as the adaptive measurement module (pink).

To achieve high tomographic precision in experiments, it is crucial to reduce the systematic error to a very low level besides adopting the correct adaptive strategy. To this end, we have implemented error-compensation measurements proposed in ref. 29, wherein multiple nominally equivalent measurement settings are applied to sub-ensembles such that main systematic errors cancel out in the first order. This method is capable of reducing the systematic error from 5×10⁻⁵ to 8×10⁻⁶, which is about 100 times smaller than the statistical error when N=9,000 (Supplementary Methods).

Quantum precision limit with respect to various figures of merit

To illustrate the power of the two-step adaptive strategy described above, here we investigate quantum precision limits with respect to a variety of figures of merit. In the first experiment, we verify this limit concerning the MSE with N₁=3,000 and N₂=6,000. Here the values of N₁ and N₂ are determined by numerical simulation to optimise the tomographic precision. The MSE is determined by averaging over 4,000 repetitions. As comparison, we also implement two other tomographic strategies. In the first one, σ_x, σ_y and σ_z are measured on N/3 copies of the qubit, respectively, and the MLE is computed as before. This standard tomography is widely used in practice because of its simplicity. In the second one, σ_x, σ_y and σ_z are measured with probabilities p₁, p₂ and p₃ as specified in Equation (5) with ${\hat{s}}_1$ replaced by s after rotating the Bloch vector of each of the N copies of the qubit state to the z axis. This ‘known-state tomography’ assumes knowledge of the true state in designing the optimal measurement though not in reconstructing the state. It is not feasible in most practical situations, where the state is in fact unknown, but it is useful as a benchmark.

Figure 3 shows the MSEs associated with the three measurement strategies mentioned above along with the theoretical MSE of the standard tomography and the GM bound. The experimental data agree very well with the theoretical prediction. In contrast with the adaptive strategy proposed in ref. 14, which offers no advantage over standard tomography with respect to the MSE, our two-step adaptive strategy is significantly more efficient than standard tomography. What is remarkable, the MSE achievable by the two-step adaptive scheme is quite close to that of known-state tomography and saturates the GM bound approximately.

Figure 3

Precision limit with respect to the MSE. Experimental results of standard, adaptive and known-state tomography are shown together with the theoretical MSE of the standard tomography and the GM bound. Here s is the length of the Bloch vector. In the experiment, N=9,000 and N₁=3,000; each data point averages over 4,000 repetitions and the error bar denotes the s.d. of the mean. The MSE of the standard tomography is lower than the theoretical value when the purity of the state is sufficiently high (depending on N) because the estimator is biased due to the influence of the boundary of the state space.

Next, we investigate the quantum precision limit with respect to the mean square Bures distance (MSB). Incidentally, the GM bound for the MSB is equal to 9/(4N) (Supplementary Methods), which is independent of the unknown qubit state. The two-step adaptive strategy for minimising the MSB is quite similar to that for minimising the MSE except that in the second step σ_x, σ_y and σ_z are measured with probability 1/3 each. Similar modification applies to the ‘known-state tomography’. Unlike the previous case, it is not necessary to implement error-compensation measurements²⁹ because a simple measurement strategy can already achieve a sufficiently high precision. Here our two-step adaptive strategy is similar to the one proposed in ref. 14, which is tailored to minimise the infidelity. This is not surprising as the infinitesimal square Bures distance is equal to the infidelity. Our study provides further justification of the approach in ref. 14 from a wider context.

The upper plot of Figure 4 shows the MSBs associated with three measurement strategies along with the theoretical precision limit set by the GM bound. In standard tomography, the MSB increases rapidly as the purity of the true state increases. In sharp contrast, the MSB achievable by the two-step adaptive scheme is almost independent of the purity and is much smaller than that of standard tomography, the more so the higher purity of the true state. Moreover, it saturates the GM bound approximately, except when the true state is nearly pure. The small gap from the bound is mainly due to the fact that the experiment under investigation is not close enough to the asymptotic regime as the ratio N₁/N is non-negligible. Meanwhile, the efficiency gap of the standard measurement from the local optimal measurement is significant for states with high purities.

Figure 4

Precision limit with respect to the MSB and WMSEs. In the experiment, N=1,200 and N₁=300; each data point is an average over 1,000 repetitions and the error bar denotes the s.d. of the mean. (Upper plot) MSBs of standard, adaptive and known-state tomography together with the GM bound. The MSB of the known-state tomography is slightly smaller than the GM bound when the purity of the true state is sufficiently high (depending on N) because the estimator is biased due to the influence of the boundary of the state space. (Lower plot) WMSEs with respect to the family of monotone Riemannian metrics determined by Equation (6) for a state with s=0.9.

A prominent merit of our approach is its versatility in dealing with various figures of merit as emphasised before. To further demonstrate this point, we now turn to verifying the precision limit with respect to WMSEs based on monotone Riemannian metrics^30–32 (Supplementary Methods). For concreteness, we shall focus on the family of metrics characterised by the following equation

$$\begin{array}{}\text{(6)}& \mathrm{d}{l}^2=\frac{1}{4}(\frac{\mathrm{d}{s}^2}{1-s^2}+\frac{s^2{\mathrm{d\Omega }}^2}{f_n\left(\frac{1-s}{1+s}\right)(1+s)})\end{array}$$

where dΩ² is the metric on the unit sphere and f_n(t)=[(1+t^1/n)/2]ⁿ. The GM bound for the scaled WMSE turns out to be

$$\begin{array}{}\text{(7)}& \begin{array}{cc}{ℰ}_{f_n}^{\mathrm{GM}}=\frac{1}{4}{(\frac{2}{h}+1)}^2,& h={\left[\frac{{(1+s)}^{\mathrm{1/}n}+{(1-s)}^{\mathrm{1/}n}}{2}\right]}^{n\mathrm{/2}}\end{array}\end{array}$$

The metric reduces to the Bures metric when n=1 and the quantum Chernoff metric³³ when n=2. Other metrics can also be treated on the same footing. The two-step adaptive strategy is quite similar to the one in the previous case, except that in the second step σ_x, σ_y and σ_z should be measured with the probabilities $p_1=p_2\mathrm{=1/}\left(2+\hat{h}\right)$ and $p_3=\hat{h}/\left(2+\hat{h}\right)$, where $\hat{h}$ is defined in the same way as h in Equation (7) but with s replaced by ${\hat{s}}_1$. The lower plot of Figure 4 shows the experimental results for a true state whose Bloch vector has length 0.9. The WMSEs achieved by the two-step adaptive strategy are much smaller than that of standard tomography as in the previous case. Moreover, they agree very well with GM bounds.

Discussion

We have implemented optimal adaptive qubit state tomography of mixed states in the multiparameter setting. The two-step adaptive strategy used in our experiment is very easy to realise in practice. Yet it is surprisingly powerful: it is applicable to optimising most figures of merit of practical interest, such as the WMSE based on the Bures metric, quantum Chernoff metric or any other metric commonly used. Moreover, it is capable of attaining the precision limit set by the GM bound approximately. Our experiment represents a significant step towards optimal quantum state tomography in the multiparameter setting, which may have profound implications for multiparameter quantum metrology. Furthermore, our study exemplifies the subtle connection between the complementarity principle and quantum precision limit, thereby promoting the cross fertilisation of quantum estimation theory and foundational studies.

Materials and methods

Data collection

To stabilise the collecting efficiency, multimode fibres are used to direct photons from free space to single-photon detectors. The whole experimental set-up is covered by a black hood to keep away stray light from outside; the multimode fibres are wrapped up by black plastic films to suppress laser scattering. To balance the data-collection time and random coincidences, the power of the continuous pumping laser is adjusted to 40 mW, and the coincidence window is set at 2 ns. The resulting coincidence rate is 8,000/s, and the coincidence efficiency is about 8%.