Abstract
Fragile materials1 ranging from sand to fire retardant to toothpaste are able to exhibit both solid and fluid-like properties across the jamming transition. Unlike ordinary fusion, systems of grains, foams and colloids jam and cease to flow under conditions that still remain unknown. Here, we quantify jamming using a thermodynamic approach by accounting for the structural ageing and the shear-induced compressibility2 of dry sand. Specifically, the jamming threshold is defined using a non-thermal temperature3 that measures the ‘fluffiness’ of a granular mixture. The thermodynamic model, cast in terms of pressure, temperature and free volume, also successfully predicts the entropic data of five molecular glasses. Notably, the predicted configurational entropy averts the Kauzmann paradox4—an unresolved crisis where the configurational entropy becomes negative—entirely. Without any free parameters, the proposed equation-of-state also governs the mechanism of shear banding and the associated features of shear softening5,6 and thickness invariance2,7.
Similar content being viewed by others
Main
Despite their mundane appearance, granular materials exhibit a wide range of intriguing phenomena8,9. Dry sand, for instance, can deform readily9 but can also jam abruptly, for example, as observed in the sudden stoppage of flow in an hourglass or a salt shaker. The abruptness of jamming refers to the narrow range of packing fractions10 (0.62–0.64) under which the material no longer deforms. Molecular systems also exhibit similar jamming phenomena. For example, liquids such as wood glue become extremely viscous and resistant to flow when cooled within a narrow range of temperatures11 (2–3 ∘C) below the freezing point. This jamming behaviour shared by both granular fluids and viscous liquids is astonishing8,12,13 and suggestive of a common underlying mechanism, but thus far, a definitive theoretical connection remains unknown.
Jamming was defined14,15 as a means to unify all fragile systems1 and has been qualitatively described using three independent variables: pressure, packing fraction and an effective temperature13. It is known, however, that granular packings are metastable: any perturbation in the magnitude or the direction of the applied stress will cause structural ageing1,10, during which particles rearrange through irreversible compaction. It is thus problematic to neglect ageing and assume, for example, that the temperature at which jamming occurs can be defined by pressure and packing fraction alone. Still, many studies of fragile systems neglect the implications of ageing, possibly because of the narrow range in the temperature and packing density of glassy and granular systems near structural arrest. Here, we present a new perspective on jamming that includes a connection to the glass transition of viscous liquids. The proposed equation-of-state (EOS) will introduce jamming as path-dependent states definable by the stationary observables pressure, packing density and shear rate.
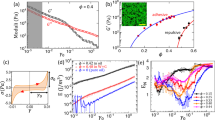
Recent shear flow experiments2 deduced the EOS of dense granular flows. We observed that the external pressure, P, in terms of shear rate, ɣ̇, and the free volume16, ɛ, has the form

For dry sand, the constants κ1≈7×10−4 Pa−1 and κ2≈2×10−5 s. These constants also match values found independently from experimental data using the cyclic rule2. The free volume ɛ≡(V −VRCP) is the flowing shear-band volume V referenced to its dynamic random-close-packing volume, VRCP. It is normalized by a fit value of the minimum free volume ɛ0. As shown in Fig. 1, equation (1) indicates that the isochoric flows are shear weakening at intermediate shear velocities. The experimental data, spanning five decades from 0.001 to 10 rad s−1, reveal that the pressure dips and reaches a minimum between the quasi-static and grain-inertial regimes17. As may be expected, the weakening mechanism also applies to isobaric flows. Indeed, isobaric shear compacting is the counterpart to isochoric shear weakening; the solid volume fraction peaks within intermediate shear velocities. These isochoric and isobaric flow regimes, however, are interdependent; together, they constitute the transitional regime of granular flow. (A flow sweet spot is observed near ɣ̇≈200 s−1.)
Measurements are made using a torsional rheometer (AR-2000, TA Instruments). Compacted beach sand (grain size≈438±188 μm, from Santa Monica) is confined concentrically while the top surface shears through logarithmically distributed velocities. The theoretical fit uses equation (1) with an extra grain-inertial term17, M ρ D2ɣ̇2, in terms of grain density, ρ, averaged grain diameter, D, and fitting constant, M. The sweet spot signifies the optimum efficiency in achieving steady-state flow. Shear rate ɣ̇ is calculated on the basis of a two-grain-diameter thickness2. The values for the isochoric fit are C=0.990±0.004, κ1=7.3±0.4×10−4 Pa−1, κ2=2.1±0.8×10−5 s and M=0.9±0.7×10−3. For the isobaric fit, the values are C=0.990±0.008, κ1=7.0±0.3×10−4 Pa−1, κ2=2.5±0.6×10−5 s and M=2.1±0.5×10−3; ɛ0≈4.1×10−9 m3 from all fits.
The shear-softening scenario presented above has been observed in driven metallic5 and colloidal6 glasses, substances that are disordered solids that lack the periodicity of crystals. Why do granular fluids flow like glassy liquids? To explain, we measured the volume compaction of a sand column (radius ≈10 cm) sheared at constant velocity. Figure 2 shows that granular compaction occurs at a rate that decreases nonlinearly in time with a decaying relaxation constant, τ. The result is fitted using the Kohlrausch–Williams–Watts4,18 equation,

The equation models the normalized change in the sand column height, h(t), as a function of time, t, and the Kolrausch exponent, β. As noted previously18, the relaxation constant τ is Arrhenius at high temperatures, that is, τ∼exp(H/kBT) where kB is the Boltzmann constant, T is the thermal temperature and H is the single ‘void-hopping’ activation energy11.
Reduced column height of sand, (h(t)−h(tmax))/(h(0)−h(tmax)), versus compaction time, t; the fit uses the Kohlrausch–Williams–Watts relation of equation (2). The τ-dependent relaxation, ageing, is non-Arrhenius; different activation energies correspond to different stages of structural ageing. The relaxation is also non-exponential; the inset shows that the Kohlrausch exponent, β, reaches a steady-state value of ≈0.5 after ≈1 h to reflect the onset of cooperative particle motion representative of jammed systems. The non-Arrhenius and the non-exponential relaxations are reminiscent of the key features of glassy liquids. The sample uses 2.6 g of beach sand sheared at a constant velocity of 0.15 rad s−1. The system maintains a constant compression at ≈1.5 kPa while recording height data at 0.1 Hz. Note that the entire figure consists of a single experiment where all runs are renormalized by their individual values of Δhmax.
From Fig. 2, inset, we observed that the relaxation is defined by a stretched exponential with a Kolrauch exponent that approaches β≈0.6 as  . The value of β<1 corresponds physically to the multiple relaxation mechanisms4,11,16 of granular compaction. Furthermore, its inverse dependence on τ signifies an increase of the apparent activation energy as packing density increases18, progressively hindering the process of particle rearrangement. This age-dependent activation energy of granular fluids is a type of non-Arrhenius behaviour11,16 reminiscent of heterogeneous glassy liquids.
. The value of β<1 corresponds physically to the multiple relaxation mechanisms4,11,16 of granular compaction. Furthermore, its inverse dependence on τ signifies an increase of the apparent activation energy as packing density increases18, progressively hindering the process of particle rearrangement. This age-dependent activation energy of granular fluids is a type of non-Arrhenius behaviour11,16 reminiscent of heterogeneous glassy liquids.
The steady-state rheology of Fig. 1 is ageing and path independent, on the basis of the reversible branch of packing fraction (0.62–0.64) observed experimentally10. The irreversible branch has an expected broader density range (0.555–0.645) (ref. 19). Figure 2, however, suggests that any constitutive model such as equation (1) must account for the continued compaction of granular flow even on much longer timescales (≫105 s). This implies that the phenomenological equation (1) is a special case of a more fundamental theory. To find it, we incorporate an ageing temperature,  , into equation (1). The temperature
, into equation (1). The temperature  ∼10−7 J (or equivalently, ∼1015 K as kB∼10−23 J K−1) was measured by Song et al. 20 for millimetre-sized acrylic beads sheared in gravity, which is significant considering the fact that these particles (size ≫1 μm) are not subjected to thermal fluctuations. This fictive notion of hot and cold will explain a thermodynamic theory that governs the dynamics of both reversible shear flow and irreversible compaction.
∼10−7 J (or equivalently, ∼1015 K as kB∼10−23 J K−1) was measured by Song et al. 20 for millimetre-sized acrylic beads sheared in gravity, which is significant considering the fact that these particles (size ≫1 μm) are not subjected to thermal fluctuations. This fictive notion of hot and cold will explain a thermodynamic theory that governs the dynamics of both reversible shear flow and irreversible compaction.
To build a meaningful generalization of equation (1), we will incorporate  into the Helmholtz free energy of flowing sand, Fsand. Using the thermodynamic relation21 of P=−(dF/dɛ), Fsand is derived from equation (1) as
into the Helmholtz free energy of flowing sand, Fsand. Using the thermodynamic relation21 of P=−(dF/dɛ), Fsand is derived from equation (1) as

The variables have been recombined into new quantities that are defined as follows: N≡ɛ/ν,ζ≡κ2 ɣ̇ and
ɣ̇ and  ≡v/κ1 where ν is grain volume (∼10−11 m3 for 300 μm particles). Thus far, the manipulation of equation (1) has been strictly algebraic and the original definition of the constants was entirely empiric. The recasting, however, suggests thermodynamic interpretations of the parameters. The variable N is the number of grains and ζ is the average dissipation per grain. Later we will verify these assumptions, in particular the use of
≡v/κ1 where ν is grain volume (∼10−11 m3 for 300 μm particles). Thus far, the manipulation of equation (1) has been strictly algebraic and the original definition of the constants was entirely empiric. The recasting, however, suggests thermodynamic interpretations of the parameters. The variable N is the number of grains and ζ is the average dissipation per grain. Later we will verify these assumptions, in particular the use of  , by predicting the configurational entropy of various molecular glass-formers.
, by predicting the configurational entropy of various molecular glass-formers.
The free energy of sand makes two critical predictions as confirmed by experiment. First, microscopically, the constant κ1=v/ is an elastic property of the material normalized by the only energy scale8 of the system,
is an elastic property of the material normalized by the only energy scale8 of the system,  . Macroscopically, κ1 is deduced from the experiment2 as κ1=−1/ɛ(dɛ/dP)ɣ̇, in a quantity defined as the mechanical compressibility of granular flows. Second, the energy of the flow supplied from the shearing surface is fully dissipated at steady state. The normalized energy, κ2ɣ̇, would therefore scale as the viscous loss of the flow, ζ=υ η ɣ̇ where η is the effective viscosity of the granular mixture. Comparing the flow of sand and other fluids drained through a funnel (0.25′′ opening), we measured a granular viscosity of ∼10−1 Pa s that matches mineral oil viscosity at room temperature. Using the value8 of
. Macroscopically, κ1 is deduced from the experiment2 as κ1=−1/ɛ(dɛ/dP)ɣ̇, in a quantity defined as the mechanical compressibility of granular flows. Second, the energy of the flow supplied from the shearing surface is fully dissipated at steady state. The normalized energy, κ2ɣ̇, would therefore scale as the viscous loss of the flow, ζ=υ η ɣ̇ where η is the effective viscosity of the granular mixture. Comparing the flow of sand and other fluids drained through a funnel (0.25′′ opening), we measured a granular viscosity of ∼10−1 Pa s that matches mineral oil viscosity at room temperature. Using the value8 of  ∼10−7 J, we compute κ1∼10−4 Pa−1 and κ2∼10−5 s. These values not only fit to the data of Fig. 1, they also have consistent thermodynamic interpretations.
∼10−7 J, we compute κ1∼10−4 Pa−1 and κ2∼10−5 s. These values not only fit to the data of Fig. 1, they also have consistent thermodynamic interpretations.
A unifying theory of jamming must also account for the slow dynamics of glassy liquids. From the volume relaxation of Fig. 2, we observed that sand compacts with a Kolrauch exponent of β≈0.6. Interestingly, typical values of 0.2<β<1 are also observed in molecular glasses near jamming. To unify their dynamics, we recall that a glass is a liquid in which crystallization is bypassed during cooling16. This is the exact scenario exhibited by sand; the angular particles jam because the bulk crystallization never nucleates on densification. In light of these similarities, we propose that the EOS of equation (1), as a function of the ageing temperature, encompasses the path-dependent states of both jamming and glass transition. In Fig. 3, two examples of jammed states are shown by two metastable1 isothermal surfaces, each defined by a particular ageing temperature,  .
.
The shaded surface corresponds to equation (1) by substituting in κ1≡v/ and κ2≡η ν/
and κ2≡η ν/ . The jamming parameter, J(P,ɛ,ɣ̇,
. The jamming parameter, J(P,ɛ,ɣ̇, ), is defined by dividing equation (1) by P(ɛ,ɣ̇). The axes are pressure, P v/
), is defined by dividing equation (1) by P(ɛ,ɣ̇). The axes are pressure, P v/ , shear rate, ζ/
, shear rate, ζ/ , and the free volume, ɛ/ɛ0, in normalized forms. The jamming transitions given at J(
, and the free volume, ɛ/ɛ0, in normalized forms. The jamming transitions given at J( )=1 (solid) and J(
)=1 (solid) and J( ′)=1 (mesh) represent two examples of equilibrium metastable packing arrangements, where the packing at
′)=1 (mesh) represent two examples of equilibrium metastable packing arrangements, where the packing at  is denser than the one at
is denser than the one at  ′ such that
′ such that  ′>
′> . The unjammed path initiates above the jamming transition where J>1, but terminates at J=1 when compaction or structural ageing stops within experimental time. This ensures that the ageing temperature
. The unjammed path initiates above the jamming transition where J>1, but terminates at J=1 when compaction or structural ageing stops within experimental time. This ensures that the ageing temperature  remains constant so that the values of ɛ0, κ1 and κ2 are stationary in equation (1). The surface is convex if a logarithmic scale is used (see the concavity of the quasi-static fit in Fig. 1).
remains constant so that the values of ɛ0, κ1 and κ2 are stationary in equation (1). The surface is convex if a logarithmic scale is used (see the concavity of the quasi-static fit in Fig. 1).
To substantiate the above claims, we use Edwards’s proposition3 that the granular temperature reflects the ‘fluffiness’ of densely packed grains. To see how ‘fluffiness’ relates to particle configuration, we derive the entropy difference, ΔSsand, between the jammed and crystalline states of granular packing. We compute the total entropy S=−kB(dF/d ) from equation (3) and cancel the contributions of the dissipation term in the entropy difference21. Conceptually, dissipation is irrelevant to the architectural arrangement of particles. The result is
) from equation (3) and cancel the contributions of the dissipation term in the entropy difference21. Conceptually, dissipation is irrelevant to the architectural arrangement of particles. The result is

Parameters P, ɛ and  are all measured above an ideal jamming condition very near the hypothetical crystalline phase. Therefore, ideally, at the minimum free volume ɛ=ɛ0, ΔSsand=N kB is the communal entropy22. (The communal entropy, kBN≈k[ln(VN/N!)−ln(V/N)N] using the Stirling approximation21, accounts for the entropy difference between a liquid and a solid.) In the case for a non-ideal packing (ɛ>ɛ0), however, work must be done to constrain the otherwise purely random particles/molecules to sample only the jammed/glassy states4,18—the possible configurational states for all particles. This work reduces the communal entropy by an amount of the configurational entropy, Sc=N kBln(ɛ/ɛ0), scaling in proportion to the volume above ideal packing, ɛ. In other words, as interpreted from equation (4), equally jammed (or fluffy) configurations can be realized for high packing densities as for low ones at the expense of structural order23.
are all measured above an ideal jamming condition very near the hypothetical crystalline phase. Therefore, ideally, at the minimum free volume ɛ=ɛ0, ΔSsand=N kB is the communal entropy22. (The communal entropy, kBN≈k[ln(VN/N!)−ln(V/N)N] using the Stirling approximation21, accounts for the entropy difference between a liquid and a solid.) In the case for a non-ideal packing (ɛ>ɛ0), however, work must be done to constrain the otherwise purely random particles/molecules to sample only the jammed/glassy states4,18—the possible configurational states for all particles. This work reduces the communal entropy by an amount of the configurational entropy, Sc=N kBln(ɛ/ɛ0), scaling in proportion to the volume above ideal packing, ɛ. In other words, as interpreted from equation (4), equally jammed (or fluffy) configurations can be realized for high packing densities as for low ones at the expense of structural order23.
To verify the configurational entropy Sc, we solve equation (1) for ln(ɛ/ɛ0) so that

for C≈1 and P≪ /ν—which is true for most glasses under atmospheric pressure and thus pressure effects are typically negligible. Figure 4 shows the fit of equation (5) to the configurational entropy data of five different glass-formers. At thermal equilibrium, the ageing temperature of equation (5) is rescaled as
/ν—which is true for most glasses under atmospheric pressure and thus pressure effects are typically negligible. Figure 4 shows the fit of equation (5) to the configurational entropy data of five different glass-formers. At thermal equilibrium, the ageing temperature of equation (5) is rescaled as  =kB(T−T0), in terms of the Kauzmann temperature T0, to preserve the third law of thermodynamics. The results show a good agreement between theory and experiment in both Kauzmann and fragility plots4. Notably, the Kauzmann paradox4,11 is entirely averted.
=kB(T−T0), in terms of the Kauzmann temperature T0, to preserve the third law of thermodynamics. The results show a good agreement between theory and experiment in both Kauzmann and fragility plots4. Notably, the Kauzmann paradox4,11 is entirely averted.
The fit agrees well with the entropic data, providing strong evidence for the unification of granular jamming and glass transition. Notably, the entropy averts the Kauzmann paradox (green dashed line), in a prediction unlike the one made by the most elegant glass model4 so far (red dotted–dashed line). Inset: Fragility plot of sc glass/s c versus Tglass/T for the same five glass-formers, and the dashed line here is not physical being above the fusion point. The fitting function uses equation (5) where the molar entropy, s c, is given as  for T≥T0 and R is the universal gas constant. The values of fragility4,11 x, ζ/kB and the Kauzmann temperature T0, are respectively listed from strong to fragile: 3.24, 8.97 and 45 K (59.5) for 1-butene26; 3.55, 17.7 and 80.6 K (84.0) for 3-bromopentane27; 3.24, 30.7 and 114 K (153) for ethylene glycol28; 4.22, 38.9 and 87.8 K (100) for toluene29; and 6.01, 65.5 and 182 K (204) for ortho-terphenyl30. The values in parentheses are the glass-transition temperatures. The matching x between 1-butane and ethylene glycol indicates that the fragility index alone cannot quantify the glass transition completely. The molar configurational entropy is derived using the equation,
for T≥T0 and R is the universal gas constant. The values of fragility4,11 x, ζ/kB and the Kauzmann temperature T0, are respectively listed from strong to fragile: 3.24, 8.97 and 45 K (59.5) for 1-butene26; 3.55, 17.7 and 80.6 K (84.0) for 3-bromopentane27; 3.24, 30.7 and 114 K (153) for ethylene glycol28; 4.22, 38.9 and 87.8 K (100) for toluene29; and 6.01, 65.5 and 182 K (204) for ortho-terphenyl30. The values in parentheses are the glass-transition temperatures. The matching x between 1-butane and ethylene glycol indicates that the fragility index alone cannot quantify the glass transition completely. The molar configurational entropy is derived using the equation,  for T≤Tfusion, and C pliq and C pcr are the experimentally measured isobaric (molar) heat capacities of the liquid and crystalline states. The interpolation/extrapolation of the heat-capacity data were in terms of second-order polynomials.
for T≤Tfusion, and C pliq and C pcr are the experimentally measured isobaric (molar) heat capacities of the liquid and crystalline states. The interpolation/extrapolation of the heat-capacity data were in terms of second-order polynomials.
The shear flow experiment of sand has guided a new classification of jamming as a solid–liquid transition uniquely defined at different structural temperatures. The path-dependent transition is purely kinetic, and yet the transition itself is in structural equilibrium with the ageing temperature for  ≥kB(T−T0) (ref. 8). In contrast, other variations14,15 of the theory rely on an effective granular temperature that is unrelated to the architectural arrangement of particles. Ultimately, the state variables that govern the isothermal states of jamming are pressure, shear rate5 and the free volume16.
≥kB(T−T0) (ref. 8). In contrast, other variations14,15 of the theory rely on an effective granular temperature that is unrelated to the architectural arrangement of particles. Ultimately, the state variables that govern the isothermal states of jamming are pressure, shear rate5 and the free volume16.
Moreover, the EOS for dense granular flows has provided strong evidence for the unification of jamming in fragile materials. Broadly speaking, it considers the elastic, the entropic, the free volume and the hydrodynamic bases of other glass theories presented so far. This view of jamming applies to phenomena such as stick–slip nucleation in seismic fault ruptures24, shear banding in metallic alloys5, strain softening in colloidal glasses6 and even stop-and-go driving in traffic jams25. These types of flow, defiant of conservative fluid models, are closely governed by dynamics that straddle the tipping point of jamming.
References
Cates, M. E., Wittmer, J. P., Bouchaud, J. P. & Claudin, P. Jamming, force chains, and fragile matter. Phys. Rev. Lett. 81, 1841–1844 (1998).
Lu, K., Brodsky, E. E. & Kavehpour, H. P. Shear-weakening of the transitional regime for granular flow. J. Fluid Mech. 587, 347–372 (2007).
Edwards, S. F. & Oakeshott, R. B. S. Theory of powders. Physica A 157, 1080–1090 (1989).
Debenedetti, P. G. & Stillinger, F. H. Supercooled liquids and the glass transition. Nature 410, 259–267 (2001).
Demetriou, M. D. et al. Cooperative shear model for the rheology of glass-forming metallic liquids. Phys. Rev. Lett. 97, 065502 (2006).
Kobelev, V. & Schweizer, K. S. Strain softening, yielding, and shear thinning in glassy colloidal suspensions. Phys. Rev. E 71, 021401 (2005).
Lewandowski, J. J. & Greer, A. L. Temperature rise at shear bands in metallic glasses. Nature Mater. 5, 15–18 (2006).
Wang, P., Song, C. M. & Makse, H. A. Dynamic particle tracking reveals the ageing temperature of a colloidal glass. Nature Phys. 2, 526–531 (2006).
Lohse, D. et al. Impact on soft sand: Void collapse and jet formation. Phys. Rev. Lett. 93, 198003 (2004).
Nowak, E. R., Knight, J. B., Povinelli, M. L., Jaeger, H. M. & Nagel, S. R. Reversibility and irreversibility in the packing of vibrated granular material. Powder Technol. 94, 79–83 (1997).
Angell, C. A. Formation of glasses from liquids and biopolymers. Science 267, 1924–1935 (1995).
D’Anna, G. & Gremaud, G. The jamming route to the glass state in weakly perturbed granular media. Nature 413, 407–409 (2001).
Ono, I. K. et al. Effective temperatures of a driven system near jamming. Phys. Rev. Lett. 89, 095703 (2002).
Trappe, V., Prasad, V., Cipelletti, L., Segre, P. N. & Weitz, D. A. Jamming phase diagram for attractive particles. Nature 411, 772–775 (2001).
Langer, S. A. & Liu, A. J. Sheared foam as a supercooled liquid? Europhys. Lett. 49, 68–74 (2000).
Turnbull, D. & Cohen, M. H. Free-volume model of amorphous phase - glass transition. J. Chem. Phys. 34, 120 (1961).
Savage, S. B. Analyses of slow high-concentration flows of granular materials. J. Fluid Mech. 377, 1–26 (1998).
Sastry, S., Debenedetti, P. G. & Stillinger, F. H. Signatures of distinct dynamical regimes in the energy landscape of a glass-forming liquid. Nature 393, 554–557 (1998).
Onoda, G. Y. & Liniger, E. G. Random loose packings of uniform spheres and the dilatancy onset. Phys. Rev. Lett. 64, 2727–2730 (1990).
Song, C. M., Wang, P. & Makse, H. A. Experimental measurement of an effective temperature for jammed granular materials. Proc. Natl Acad. Sci. USA 102, 2299–2304 (2005).
Reif, F. Fundamentals of Statistical and Thermal Physics (McGraw-Hill, New York, 1965).
Hirschfelder, J., Stevenson, D. & Eyring, H. A theory of liquid structure. J. Chem. Phys. 5, 896–912 (1937).
Wei, J. et al. Molecular Modeling and Theory in Chemical Engineering Vol. 28 (Academic, New York, 2001).
Scholz, C. H. Earthquakes and friction laws. Nature 391, 37–42 (1998).
Nagatani, T. Gas kinetics of traffic jam. J. Phys. Soc. Japan 66, 1219–1224 (1997).
Takeda, K., Yamamuro, O. & Suga, H. Thermodynamic study of 1-butene—exothermic and endothermic enthalpy relaxations near the glass-transition. J. Phys. Chem. Solids 52, 607–615 (1991).
Takahara, S., Yamamuro, O. & Matsuo, T. Calorimetric study of 3-bromopentane—correlation between structural relaxation-time and configurational entropy. J. Phys. Chem. 99, 9589–9592 (1995).
Takeda, K., Yamamuro, O., Tsukushi, I., Matsuo, T. & Suga, H. Calorimetric study of ethylene glycol and 1,3-propanediol: Configurational entropy in supercooled polyalcohols. J. Mol. Struct. 479, 227–235 (1999).
Yamamuro, O. et al. Calorimetric study of glassy and liquid toluene and ethylbenzene: Thermodynamic approach to spatial heterogeneity in glass-forming molecular liquids. J. Phys. Chem. B 102, 1605–1609 (1998).
Chang, S. S. & Bestul, A. B. Heat-capacity and thermodynamic properties of ortho-terphenyl crystal, glass, and liquid. J. Chem. Phys. 56, 503 (1972).
Acknowledgements
This work is partially supported by the Airforce Office of Scientific Research (Surface & Interfacial Science program, Grant number FA9550-07-1-0324).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Lu, K., Brodsky, E. & Kavehpour, H. A thermodynamic unification of jamming. Nature Phys 4, 404–407 (2008). https://doi.org/10.1038/nphys934
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nphys934
This article is cited by
-
Probability analysis of contact forces in quasi-solid-liquid phase transition of granular shear flow
Science China Physics, Mechanics and Astronomy (2013)
-
Similarities between protein folding and granular jamming
Nature Communications (2012)