Abstract
If liquids, polymers, bio-materials, metals and molten salts can avoid crystallization during cooling or compression, they freeze into a microscopically disordered solid-like state, a glass1,2. On approaching the glass transition, particles become trapped in transient cages—in which they rattle on picosecond timescales—formed by their nearest neighbours; the particles spend increasing amounts of time in their cages as the average escape time, or structural relaxation time τα, increases from a few picoseconds to thousands of seconds through the transition. Owing to the huge difference between relaxation and vibrational timescales, theoretical3,4,5,6,7,8,9 studies addressing the underlying rattling process have challenged our understanding of the structural relaxation. Numerical10,11,12,13 and experimental studies on liquids14 and glasses8,15,16,17,18,19 support the theories, but not without controversies20 (for a review see ref. 21). Here we show computer simulations that, when compared with experiments, reveal the universal correlation of the structural relaxation time (as well as the viscosity η) and the rattling amplitude from glassy to low-viscosity states. According to the emerging picture the glass softens when the rattling amplitude exceeds a critical value, in agreement with the Lindemann criterion for the melting of crystalline solids22 and the free-volume model23.
Similar content being viewed by others
Main
In the solid state atoms oscillate with mean square amplitude 〈u2〉 around their equilibrium positions (henceforth to be referred to as the Debye–Waller (DW) factor). With increasing temperature, solids meet different fates depending on the structural degree of order. In the crystalline state the ordered structure melts at Tm, whereas in the amorphous state the disordered structure softens at the glass transition temperature Tg, above which flow occurs with viscosity η. The empirical law Tg≃2/3Tm (refs 1, 2, 7) suggests that the two phenomena have a common basis. In fact, this viewpoint motivated extensions to glasses24 of the Lindemann melting criterion for crystalline solids22 and pictures the glass transition as a freezing in an aperiodic crystal structure (ACS)5.
According to the ACS model, the viscous flow is due to activated jumps over energy barriers ΔE∝kBT a2/〈u2〉, where a is the displacement to overcome the barrier, kB is the Boltzmann constant and T the temperature. The usual rate theory leads to the Hall–Wolynes (HW) equation5,21 τα,η∝exp(a2/2〈u2〉). 〈u2〉 is the DW factor of the liquid, that is, it is the amplitude of the rattling motion within the cage of the surrounding atoms. This vibrational regime is assumed to occur on short timescales largely separated by those of the brownian diffusion. The ACS model is expected to fail when τα becomes comparable to the typical rattling times corresponding to picosecond timescales, a condition that is met at high temperatures (for example, in selenium it occurs at Tm+104 K (ref. 14)).
Several tests of the HW equation have been carried out21. However, either the crystal or the glass contributions after extrapolation in the liquid regime are usually subtracted from 〈u2〉. In selenium, the curve log η versus 1/〈u2〉 is concave, whereas if the glass or the crystal contribution is removed a convex curve or a straight line—the latter agreeing with the HW equation—is seen, respectively14. The fact that many glass-formers have no underlying crystalline phases, as well as the fact that in many studies removing the glass contribution, unlike selenium, leads to the HW equation, raises some ambiguities about the above subtractions.
It seems natural to generalize the HW equation by adopting a suitable distribution p(a2) of the square displacement to overcome the energy barriers, independent of state parameters, for example the temperature or the density. This is motivated by the observation that, irrespective of the relaxation time, the distance a particle moves during the structural relaxation is about the same, comparable to the molecular diameter1. Differently, the amplitude of the vibrational dynamics 〈u2〉 is expected to be affected by state parameters7,9. We choose a gaussian form for p(a2) with  average and σa22 variance. Averaging the HW equation over this distribution leads to
average and σa22 variance. Averaging the HW equation over this distribution leads to

Equation (1) yields the leading dependence on 〈u2〉 even if the gaussian is truncated to account for a minimum displacement. In addition to the central limit theorem, other motivations support the gaussian form of p(a2). For example, if the kinetic unit is undergoing a harmonic motion due to an effective spring with constant k, 〈u2〉∝kBT/k, equation (1) reduces to a form reported for both supercooled liquids25 and polymers26. Furthermore, along the same line of reasoning, we may reinterpret the gaussian form of p(a2) as a gaussian distribution of the energy barriers ΔE∝k a2 (ref. 27).
We show that the dependence of the structural relaxation time on the DW factor collapses to a universal master curve provided by equation (1). We devised a two-step strategy. First, a master curve is constructed using extensive molecular-dynamics (MD) numerical simulations for a bead–spring model28 of a polymer melt. Then a suitable scaling of both the numerical and experimental data is introduced to convert the MD master curve into the universal one including both strong and fragile glasses1 and polymers; the latter, apart from a few studies17,19, have been little considered.
We now discuss the MD simulations. They involved changes in the temperature T, the density ρ, the chain length M and the interaction potential Up,q(r). To characterize the short-time dynamics and the structural relaxation we use the monomer mean square displacement (MSD) 〈r2(t)〉 and the incoherent intermediate scattering function (ISF) Fs(qmax,t), qmax being the q-vector of the maximum of the static structure factor (see the Methods section).
Figure 1 shows typical MSD and ISF curves. At very short times (ballistic regime), MSD increases according to  with μ the monomer mass and t the time and ISF starts to decay. The repeated collisions with the other monomers slow the displacement of the tagged one, evinced by a knee of MSD at
with μ the monomer mass and t the time and ISF starts to decay. The repeated collisions with the other monomers slow the displacement of the tagged one, evinced by a knee of MSD at  , where Ω0 is an effective collision frequency: Ω0 is the mean small-oscillation frequency of the monomer in the potential well produced by the surrounding ones kept at their equilibrium positions29. At later times a quasi-plateau region, also found in the ISF, occurs when the temperature is lowered and/or the density increased. This signals the increased caging of the particle. The latter is released after an average time τα, defined by the relation Fs(qmax,τα)=e−1 (other definitions differ by an overall constant due to the superposition of the ISF curves at long times by a suitable logarithmic shift; see the inset of Fig. 1b). For t≳τα MSD increases more steeply. The monomers of short chains (M≲3) undergo diffusive motion, 〈r2(t)〉∝tδ, with δ=1. For longer chains, owing to the increased connectivity, the onset of the diffusion is preceded by a subdiffusive region (δ<1, Rouse regime)23.
, where Ω0 is an effective collision frequency: Ω0 is the mean small-oscillation frequency of the monomer in the potential well produced by the surrounding ones kept at their equilibrium positions29. At later times a quasi-plateau region, also found in the ISF, occurs when the temperature is lowered and/or the density increased. This signals the increased caging of the particle. The latter is released after an average time τα, defined by the relation Fs(qmax,τα)=e−1 (other definitions differ by an overall constant due to the superposition of the ISF curves at long times by a suitable logarithmic shift; see the inset of Fig. 1b). For t≳τα MSD increases more steeply. The monomers of short chains (M≲3) undergo diffusive motion, 〈r2(t)〉∝tδ, with δ=1. For longer chains, owing to the increased connectivity, the onset of the diffusion is preceded by a subdiffusive region (δ<1, Rouse regime)23.
a, MSD time dependence in selected cases (see the Supplementary Information). The MSDs are multiplied by the indicated factors. Inset: Corresponding MSD slope Δ(t); the uncertainty range on the position of the minimum at  (black line) is bounded by the vertical coloured lines. b, Corresponding ISF curves. Inset: Superposition of the ISF curves. Four sets of clustered curves (A–D) show that, if states have equal τα values (marked with dots on each curve), the MSD and ISF curves coincide from times rather longer than τα down to the crossover to the ballistic regime at least.
(black line) is bounded by the vertical coloured lines. b, Corresponding ISF curves. Inset: Superposition of the ISF curves. Four sets of clustered curves (A–D) show that, if states have equal τα values (marked with dots on each curve), the MSD and ISF curves coincide from times rather longer than τα down to the crossover to the ballistic regime at least.
The dynamics of the model polymer depends in a complex way on the state parameters. Nonetheless, we systematically found that, if two states (labelled by multiplets {T,ρ,M,p,q}) have equal relaxation times τα, the corresponding MSD and ISF curves coincide from times rather longer than τα down to the crossover to the ballistic regime and even at shorter times if the states have equal temperatures. Examples are shown in Fig. 1. Notice that the coincidence of MSD and ISF curves of states with equal τα at intermediate times (t≲τα) must not be confused with the customary superposition of ISF curves at long times (t≳τα) following a suitable logarithmic time shift (see the inset of Fig. 1b).
The above findings clearly show that a correlation between the structural relaxation and the fast dynamics sets in. We assess it by correlating τα and the DW factor 〈u2〉.
Prior to the discussion of the DW factor, we have to clarify whether the fast dynamics of the monomers takes place in cages. In this respect, we point out that the product Ω0τα∼20 for states with the fastest relaxation and much larger for states with slower relaxation; that is, the structure lifetime is at least one order of magnitude longer than the collision time. Furthermore, in the present study we always observe (not shown) that the time velocity correlation function (VCF), after a first large drop due to pair collisions, reverses the sign because the monomer rebounds from the cage wall29.
We now show that the DW factor is a characteristic length scale of the rattling motion into the cage. The measure of the DW factor must take place in a time window where both the inertial and the relaxation effects are not present. To clearly identify this time window we consider the quantity Δ(t)≡∂log〈r2(t)〉/∂logt; representative plots of Δ(t) are given in the inset of Fig. 1a. Δ(t) shows a clear minimum at  (corresponding to an inflection point in the log–log plot of 〈r2(t)〉), which separates two regimes. At short times,
(corresponding to an inflection point in the log–log plot of 〈r2(t)〉), which separates two regimes. At short times,  , the VCF always exceeds the noise floor (not shown) and the inertial effects become apparent. At long times,
, the VCF always exceeds the noise floor (not shown) and the inertial effects become apparent. At long times,  , relaxation sets in. The short- and the long-time limits of Δ(t) correspond to the ballistic (Δ(0)=2) and the diffusive regimes (
, relaxation sets in. The short- and the long-time limits of Δ(t) correspond to the ballistic (Δ(0)=2) and the diffusive regimes ( ), respectively. To observe a minimum of Δ(t) requires that the VCF shows a negative tail at long times. A monotonically decreasing VCF, that is, no cage effect, leads to a monotonically decreasing Δ(t). Therefore, the MSD at
), respectively. To observe a minimum of Δ(t) requires that the VCF shows a negative tail at long times. A monotonically decreasing VCF, that is, no cage effect, leads to a monotonically decreasing Δ(t). Therefore, the MSD at  is a mean localization length and the DW factor is
is a mean localization length and the DW factor is  (the same definition has been adopted, with no justification, in ref. 11). Notice that
(the same definition has been adopted, with no justification, in ref. 11). Notice that  , corresponding to about 1–10 ps (ref. 28), is consistent with the timescales of the experimental measurement of the DW factor; see, for example, ref. 14.
, corresponding to about 1–10 ps (ref. 28), is consistent with the timescales of the experimental measurement of the DW factor; see, for example, ref. 14.
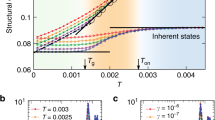
Figure 2 shows the dependence of the structural relaxation time τα on the DW factor. The data collapse on a well-defined master curve well fitted by equation (1). States with different densities, chain lengths and interaction potentials are included in Fig. 2, corresponding to different degrees of anharmonicity of the rattling motion in the cage (that is, nonlinear temperature dependence of the DW factor) and then to different fragilities4,7,10,12,15,18,19,21. The scaling shows that for our model system both the average value  and the spread σa 2 of the square displacement needed to overcome the energy barriers are not affected by the anharmonicity. The best-fit value of the average is
and the spread σa 2 of the square displacement needed to overcome the energy barriers are not affected by the anharmonicity. The best-fit value of the average is  , consistent with both the observation that 〈r2(t=τα)〉1/2≲0.5 (see Fig. 1) and the well-known result that the atomic MSD during the structural relaxation is less than one atomic radius (∼0.5 in MD units)1.
, consistent with both the observation that 〈r2(t=τα)〉1/2≲0.5 (see Fig. 1) and the well-known result that the atomic MSD during the structural relaxation is less than one atomic radius (∼0.5 in MD units)1.
Circles identify the cases plotted in Fig. 1. The dashed curve is equation (1), logτα=α+β〈u2〉−1+γ〈u2〉−2 with α=−0.424(1),  , γ=σa22/8ln10=3.41(3)×10−3. Additional data on the collective relaxation time τ are also plotted11 (
, γ=σa22/8ln10=3.41(3)×10−3. Additional data on the collective relaxation time τ are also plotted11 ( ). The dotted curve is obtained by vertically shifting the dashed curve (α′=α+0.205(5)). Inset: The maximum of the non-gaussian parameter α2max of clusters A–E of states versus the ratio of the quadratic and the linear terms of equation (1) with respect to 〈u2〉−1.
). The dotted curve is obtained by vertically shifting the dashed curve (α′=α+0.205(5)). Inset: The maximum of the non-gaussian parameter α2max of clusters A–E of states versus the ratio of the quadratic and the linear terms of equation (1) with respect to 〈u2〉−1.
The concavity of the master curve in Fig. 2 is a signature of the heterogeneity of the structural relaxation. The best fit of our MD data with equation (1) gives σa2∼0.25, indicating a distribution of the displacement required to overcome the energy barriers. The magnitude of the ratio of the quadratic and the linear terms of equation (1) with respect to 〈u2〉−1,  , discriminates two different regimes. If the DW factor 〈u2〉 is small enough that R is larger than unity, the distribution of the displacement required to overcome the energy barriers shows up. In this case, because different a values produce different monomer mobility, a heterogeneous mobility distribution is expected. On the other hand, if R is smaller than unity, the dynamics is homogeneous. To support this scenario we recall that, on approaching the glass transition, a spatial distribution of mobilities develops with increasing non-gaussian features of the molecular displacement2,7,30. The features are characterized by the maximum α2max of the time-dependent non-gaussian parameter α2(t) (see the Methods section)30. States with coinciding ISF and MSD shown in Fig. 1 have coinciding α2(t) curves too (not shown). For these states we sketch the relation between α2max and R in the inset of Fig. 2. It is seen that, when R exceeds the unit value, α2max increases exponentially. Notably, the inset of Fig. 2 reduces to an activated law for strong glass-formers, where 〈u2〉 is nearly proportional to T; this law has been observed for silica30.
, discriminates two different regimes. If the DW factor 〈u2〉 is small enough that R is larger than unity, the distribution of the displacement required to overcome the energy barriers shows up. In this case, because different a values produce different monomer mobility, a heterogeneous mobility distribution is expected. On the other hand, if R is smaller than unity, the dynamics is homogeneous. To support this scenario we recall that, on approaching the glass transition, a spatial distribution of mobilities develops with increasing non-gaussian features of the molecular displacement2,7,30. The features are characterized by the maximum α2max of the time-dependent non-gaussian parameter α2(t) (see the Methods section)30. States with coinciding ISF and MSD shown in Fig. 1 have coinciding α2(t) curves too (not shown). For these states we sketch the relation between α2max and R in the inset of Fig. 2. It is seen that, when R exceeds the unit value, α2max increases exponentially. Notably, the inset of Fig. 2 reduces to an activated law for strong glass-formers, where 〈u2〉 is nearly proportional to T; this law has been observed for silica30.
Equation (1) with the best-fit parameters from Fig. 2 offers the opportunity to find the DW factor 〈ug2〉 at the glass transition of the model polymer system. At the glass transition τα=τα g≡102 s in laboratory units1, which corresponds to τα g=1013–1014 in dimensionless MD units (the time unit corresponds to 1–10 ps (ref. 28)). Equation (1) yields 〈ug2〉1/2=0.129(1). This amplitude corresponds to the ratio v0∼(2〈ug2〉1/2)3=0.017 between the volume that is accessible to the monomer centre of mass and the monomer volume. It has been proposed that the glass transition takes place under iso-free-volume conditions with the universal value  (ref. 23). Furthermore, an extension of the ACS model (leading to the HW equation) predicts that, just as for a crystalline solid22, there is a Lindemann criterion for the stability of glasses: the ratio f=〈ug2〉1/2/d, d being the average next-neighbour distance of the atoms in the lattice, is a quasi-universal number24 (
(ref. 23). Furthermore, an extension of the ACS model (leading to the HW equation) predicts that, just as for a crystalline solid22, there is a Lindemann criterion for the stability of glasses: the ratio f=〈ug2〉1/2/d, d being the average next-neighbour distance of the atoms in the lattice, is a quasi-universal number24 ( ). Our data yield f∼0.12–0.13 (d is taken from the monomer radial distribution function), which is close to f=0.129 for the melting of a hard-sphere face-centred cubic solid22.
). Our data yield f∼0.12–0.13 (d is taken from the monomer radial distribution function), which is close to f=0.129 for the melting of a hard-sphere face-centred cubic solid22.
We are now in a position to show that equation (1) with the best-fit parameters from Fig. 2 may be recast as a universal curve by considering the reduced variable  . For MD data we set 〈ug2〉1/2=0.129. Figure 3 shows scaling for several glass-formers and polymers in a wide range of the fragility m, which measures the rapidity with which viscosity and structural relaxation change as the glassy state is approached1. The scaling in Fig. 3 must not be ascribed to 〈ug2〉, which does not correlate with m (compare m from Fig. 3 and 〈ug2〉 from the Supplementary Information, Table S1). Instead, it shows that both the reduced mean square displacement
. For MD data we set 〈ug2〉1/2=0.129. Figure 3 shows scaling for several glass-formers and polymers in a wide range of the fragility m, which measures the rapidity with which viscosity and structural relaxation change as the glassy state is approached1. The scaling in Fig. 3 must not be ascribed to 〈ug2〉, which does not correlate with m (compare m from Fig. 3 and 〈ug2〉 from the Supplementary Information, Table S1). Instead, it shows that both the reduced mean square displacement  to overcome the energy barriers and the spread σa2/〈ug2〉 are fragility independent, and then also the curvature of the master curve, which indicates the heterogeneity of the structural relaxation.
to overcome the energy barriers and the spread σa2/〈ug2〉 are fragility independent, and then also the curvature of the master curve, which indicates the heterogeneity of the structural relaxation.
 .
.The grey area marks the glass transition. The continuous black line is equation (1) rewritten as  with
with  and
and  ; α,β,γ from Fig. 2. The numbers in parentheses denote the fragility m. The uncertainty on the time
; α,β,γ from Fig. 2. The numbers in parentheses denote the fragility m. The uncertainty on the time  involved in the definition of the DW factor (
involved in the definition of the DW factor ( ) leads to an error on the black curve, which is bounded between the two coloured continuous curves corresponding to the two definitions 〈u2〉≡〈r2(t=0.6)〉 (magenta, 〈ug2〉1/2=0.134(1)) and 〈u2〉≡〈r2(t=1.4)〉 (orange, 〈ug2〉1/2=0.122(1)).
) leads to an error on the black curve, which is bounded between the two coloured continuous curves corresponding to the two definitions 〈u2〉≡〈r2(t=0.6)〉 (magenta, 〈ug2〉1/2=0.134(1)) and 〈u2〉≡〈r2(t=1.4)〉 (orange, 〈ug2〉1/2=0.122(1)).
The experimental data in Fig. 3 were collected by changing the temperature. In this respect, the universal scaling of Fig. 3 proves that the well-known increasing deviation of 〈u2(T)〉 from the linear temperature dependence of the harmonic behaviour by increasing the fragility index m (refs 4, 7, 9, 18, 19) just mirrors the corresponding increasing bending of τα(T) versus Tg/T in the Angell plot1 from the glass transition region to the liquid state. However, the glass transition may be reached under isothermal conditions by increasing the density or the connectivity (here expressed by the chain length) as well. Our MD results highlight the correlation of structural relaxation and vibrational dynamics also for these alternative routes. This prediction awaits experimental confirmation.
Methods
In our numerical simulations each chain is pictured as a freely jointed linear sequence of M soft spheres, the monomers, with M=2, 3, 5, 10. For details see Supplementary Information and ref. 28. The non-bonded monomers belonging to the same or different chains interact via the potential  with
with  (refs 12, 29). All quantities are in reduced units: length in units of σ, temperature in units of ε/kB and time in units of
(refs 12, 29). All quantities are in reduced units: length in units of σ, temperature in units of ε/kB and time in units of  , where μ is the monomer mass. The potential is cut and shifted to zero by Ucut at r=2.5. The bond length is b=0.97. Changing the p and q parameters does not affect the position
, where μ is the monomer mass. The potential is cut and shifted to zero by Ucut at r=2.5. The bond length is b=0.97. Changing the p and q parameters does not affect the position  or the depth ε of the potential minimum but only the steepness of the repulsive and the attractive wings. The monomer MSD 〈r2(t)〉 is defined as
or the depth ε of the potential minimum but only the steepness of the repulsive and the attractive wings. The monomer MSD 〈r2(t)〉 is defined as  , where the sum runs over the total number of N monomers and the brackets denote a suitable ensemble average. The incoherent ISF Fs(qmax,t) is defined as
, where the sum runs over the total number of N monomers and the brackets denote a suitable ensemble average. The incoherent ISF Fs(qmax,t) is defined as  , qmax being the q-vector of the maximum of the static structure factor. The time-dependent non-gaussian parameter is defined as α2(t)=(3〈r4(t)〉/5〈r2(t)〉2)−1 and vanishes if the displacement r is gaussian.
, qmax being the q-vector of the maximum of the static structure factor. The time-dependent non-gaussian parameter is defined as α2(t)=(3〈r4(t)〉/5〈r2(t)〉2)−1 and vanishes if the displacement r is gaussian.
To prepare Fig. 3, data about the structural relaxation (in seconds) and the viscosity (in Pa s) were scaled to the MD master curve by logarithmic vertical shifts +11.5(5) and +1.5(5), respectively, apart from B2O3 (+8.4(5) and −2.2(5)). Data of polymers refer to τα. Data related to B2O3,OTP and ferrocene/dibutylphthalate include two independent sets, one for τα, the other for η, which for simplicity’s sake are presented with the same symbol. See Supplementary Information for the data sources and further details.
References
Angell, C. A. Relaxation in liquids, polymers and plastic crystals—strong/fragile patterns and problems. J. Non-Cryst. Solids 131–133, 13–31 (1991).
Debenedetti, P. G. & Stillinger, F. H. Supercooled liquids and the glass transition. Nature 410, 259–267 (2001).
Tobolsky, A., Powell, R. E. & Eyring, H. in Frontiers in Chemistry Vol. 1 (eds Burk, R. E. & Grummit, O.) 125–190 (Interscience, New York, 1943).
Angell, C. A. Formation of glasses from liquids and biopolymers. Science 267, 1924–1935 (1995).
Hall, R. W. & Wolynes, P. G. The aperiodic crystal picture and free energy barriers in glasses. J. Chem. Phys. 86, 2943–2948 (1987).
Dyre, J. C., Olsen, N. B. & Christensen, T. Local elastic expansion model for viscous-flow activation energies of glass-forming molecular liquids. Phys. Rev. B 53, 2171–2174 (1996).
Ngai, K. L. Dynamic and thermodynamic properties of glass-forming substances. J. Non-Cryst. Solids 275, 7–51 (2000).
Martinez, L.-M. & Angell, C. A. A thermodynamic connection to the fragility of glass-forming liquids. Nature 410, 663–667 (2001).
Ngai, K. L. Why the fast relaxation in the picosecond to nanosecond time range can sense the glass transition. Phil. Mag. 84, 1341–1353 (2004).
Shao, J. & Angell, C. A. Proc. XVIIth International Congress on Glass, Beijing Vol. 1, 311–320 (Chinese Ceramic Society, Beijing, 1995).
Starr, F. W., Sastry, S., Douglas, J. F. & Glotzer, S. What do we learn from the local geometry of glass-forming liquids? Phys. Rev. Lett. 89, 125501 (2002).
Bordat, P., Affouard, F., Descamps, M. & Ngai, K. L. Does the interaction potential determine both the fragility of a liquid and the vibrational properties of its glassy state? Phys. Rev. Lett. 93, 105502 (2004).
Widmer-Cooper, A. & Harrowell, P. Predicting the long-time dynamic heterogeneity in a supercooled liquid on the basis of short-time heterogeneities. Phys. Rev. Lett. 96, 185701 (2006).
Buchenau, U. & Zorn, R. A relation between fast and slow motions in glassy and liquid selenium. Europhys. Lett. 18, 523–528 (1992).
Sokolov, A. P., Rössler, E., Kisliuk, A. & Quitmann, D. Dynamics of strong and fragile glass formers: Differences and correlation with low-temperature properties. Phys. Rev. Lett. 71, 2062–2065 (1993).
Scopigno, T., Ruocco, G., Sette, F. & Monaco, G. Is the fragility of a liquid embedded in the properties of its glass? Science 302, 849–852 (2003).
Buchenau, U. & Wischnewski, A. Fragility and compressibility at the glass transition. Phys. Rev. B 70, 092201 (2004).
Novikov, V. N. & Sokolov, A. P. Poisson’s ratio and the fragility of glass-forming liquids. Nature 431, 961–963 (2004).
Novikov, V. N., Ding, Y. & Sokolov, A. P. Correlation of fragility of supercooled liquids with elastic properties of glasses. Phys. Rev. E 71, 061501 (2005).
Yannopoulos, S. N. & Johari, G. P. Poisson’s ratio and liquid’s fragility. Nature 442, E7–E8 (2006).
Dyre, J. C. The glass transition and elastic models of glass-forming liquids. Rev. Mod. Phys. 78, 953–972 (2006).
Löwen, H. Melting, freezing and colloidal suspensions. Phys. Rep. 237, 249–324 (1994).
Gedde, U. W. Polymer Physics (Chapman and Hall, London, 1995).
Xia, X. & Wolynes, P. G. Fragilities of liquids predicted from the random first order transition theory of glasses. Proc. Natl Acad. Sci. 97, 2990–2994 (2000).
Bässler, H. Viscous flow in supercooled liquids analyzed in terms of transport theory for random media with energetic disorder. Phys. Rev. Lett. 58, 767–770 (1987).
Ferry, J. D., Grandine, L. D. Jr & Fitzgerald, E. R. The relaxation distribution function of polyisobutylene in the transition from rubber-like to glass-like behavior. J. Appl. Phys. 24, 911–916 (1953).
Monthus, C. & Bouchaud, J.-P. Models of traps and glass phenomenology. J. Phys. A 29, 3847–3869 (1996).
Kröger, M. Simple models for complex nonequilibrium fluids. Phys. Rep. 390, 453–551 (2004).
Boon, J. P. & Yip, S. Molecular Hydrodynamics (Dover, New York, 1980).
Glotzer, S. C. & Vogel, M. Temperature dependence of spatially heterogeneous dynamics in a model of viscous silica. Phys. Rev. E 70, 061504 (2004).
Acknowledgements
The authors acknowledge discussions with C. A. Angell, S. Capaccioli, G. Carini, P. G. Debenedetti, J. Dyre, A. Fontana, K. L. Ngai, G. Ruocco, F. Sciortino and S. N. Shore. A. Wischnewski is thanked for providing the DW data of silica. Computational resources by ‘Laboratorio per il Calcolo Scientifico’ (Physics Department, University of Pisa) and financial support from MIUR within the PRIN project ‘Aging, fluctuation and response in out-of-equilibrium glassy systems’ are acknowledged.
Author information
Authors and Affiliations
Corresponding author
Supplementary information
Supplementary Information
Simulations and Experimental data and scaling (PDF 139 kb)
Rights and permissions
About this article
Cite this article
Larini, L., Ottochian, A., De Michele, C. et al. Universal scaling between structural relaxation and vibrational dynamics in glass-forming liquids and polymers. Nature Phys 4, 42–45 (2008). https://doi.org/10.1038/nphys788
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nphys788
This article is cited by
-
Direction-dependent dynamics of colloidal particle pairs and the Stokes-Einstein relation in quasi-two-dimensional fluids
Nature Communications (2023)
-
Thermal expansion and the glass transition
Nature Physics (2023)
-
A Thermodynamic Perspective on Polymer Glass Formation
Chinese Journal of Polymer Science (2023)
-
Origin of the boson peak in amorphous solids
Nature Physics (2022)
-
Systematic coarse-graining of epoxy resins with machine learning-informed energy renormalization
npj Computational Materials (2021)