Abstract
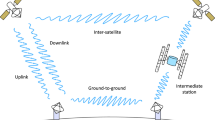
Quantum entanglement is the main resource to endow the field of quantum information processing with powers that exceed those of classical communication and computation. In view of applications such as quantum cryptography or quantum teleportation, extension of quantum-entanglement-based protocols to global distances is of considerable practical interest. Here we experimentally demonstrate entanglement-based quantum key distribution over 144 km. One photon is measured locally at the Canary Island of La Palma, whereas the other is sent over an optical free-space link to Tenerife, where the Optical Ground Station of the European Space Agency acts as the receiver. This exceeds previous free-space experiments by more than an order of magnitude in distance, and is an essential step towards future satellite-based quantum communication and experimental tests on quantum physics in space.
This is a preview of subscription content, access via your institution
Access options
Subscribe to this journal
Receive 12 print issues and online access
$209.00 per year
only $17.42 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout





Similar content being viewed by others
References
Schroedinger, E. Die gegenwaertige Situation in der Quantenmechanik. Die Naturwissenschaften 49, 823–828 (1935).
Einstein, A., Podolsky, B. & Rosen, N. Can quantum-mechanical description of physical reality be considered complete? Phys. Rev. 47, 777–780 (1935).
Ekert, A. K. Quantum cryptography based on Bell’s theorem. Phys. Rev. Lett. 67, 661–663 (1991).
Bennett, C. H. & Brassard, G. Proc. IEEE Int. Conf. on Computers, Systems and Signal Processing, Bangalore, India 175–179 (IEEE, New York, 1984).
Jennewein, T. et al. Quantum cryptography with entangled photons. Phys. Rev. Lett. 84, 4729–4732 (2000).
Bennett, C. H. et al. Teleporting an unknown quantum state via dual classical and EPR channels. Phys. Rev. Lett. 70, 1895–1899 (1993).
Bouwmeester, D. et al. Experimental quantum teleportation. Nature 390, 575–579 (1997).
Riebe, M. et al. Experimental quantum teleportation with atoms. Nature 429, 734–737 (2004).
Barrett, M. D. et al. Deterministic quantum teleportation of atomic qubits. Nature 429, 737–739 (2004).
Ursin, R. et al. Quantum teleportation link across the Danube. Nature 430, 849 (2004).
Deutsch, D. & Ekert, A. Quantum computation. Phys. World 11, 47–52 (1998).
Walther, P. et al. Experimental one-way quantum computing. Nature 434, 169–176 (2005).
Prevedel, R. et al. High-speed linear optics quantum computing using active feed-forward. Nature 445, 65–69 (2007).
Aspect, A., Dalibard, J. & Roger, G. Experimental test of Bell’s inequalities using time-varying analyzers. Phys. Rev. Lett. 49, 1804–1807 (1982).
Weihs, G., Jennewein, T., Simon, C., Weinfurter, H. & Zeilinger, A. Violation of Bell’s inequality under strict Einstein locality conditions. Phys. Rev. Lett. 81, 5039–5043 (1998).
Aspelmeyer, M. et al. Long-distance free-space distribution of entangled photons. Science 301, 621–623 (2003).
Resch, K. J. et al. Distributing entanglement and single photons through an intra-city, free-space quantum channel. Opt. Express 13, 202–209 (2005).
Peng, C.-Z. et al. Experimental free-space distribution of entangled photon pairs over a noisy ground atmosphere of 13 km. Phys. Rev. Lett. 94, 150501 (2005).
Tittel, W. et al. Experimental demonstration of quantum correlations over more than 10 km. Phys. Rev. A 57, 3229–3232 (1998).
Marcikic, I. et al. Distribution of time-bin entangled qubits over 50 km of optical fiber. Phys. Rev. Lett. 93, 180502 (2004).
Takesue, H. et al. Differential phase shift quantum key distribution experiment over 105 km fibre. New J. Phys. 7, 232 (2005).
Waks, E., Zeevi, A. & Yamamoto, Y. Security of quantum key distribution with entangled photons against individual attacks. Phys. Rev. A 65, 52310 (2002).
Briegel, H.-J., Dür, W., Cirac, J. I. & Zoller, P. Quantum repeaters: The role of imperfect local operations in quantum communication. Phys. Rev. Lett. 81, 5932–5935 (1998).
Nordholt, J. E., Hughes, R. J., Morgan, G. L., Peterson, C. G. & Wipf, C. C. Present and future quantum key distribution. Proc. SPIE 4635, 116–126 (2002).
Kaltenbaek, R. et al. Proof-of-concept experiments for quantum physics in space. Proc. SPIE Proc. Quantum Commun. Quantum Imaging 5161, 252–268 (2003).
Kwiat, P. G. et al. New high-intensity source of polarization-entangled photon pairs. Phys. Rev. Lett. 75, 4337–4341 (1995).
Gisin, N., Ribordy, G., Tittel, W. & Zbinden, H. Quantum cryptography. Rev. Mod. Phys. 74, 145–195 (2002).
Pfennigbauer, M. et al. Satellite-based quantum communication terminal employing state-of-the-art technology. J. Opt. Netw. 4, 549–560 (2005).
Czichy, R. et al. Design of an optical ground station for in-orbit checkout of free space laser communication payloads. SPIE 2381, 26–37 (1995).
Comeron, A. et al. Propagation experiments in the near infrared along a 150-km path and from stars in the Canarian archipelago. Proc. SPIE 4687, 78–90 (2002).
Lange, R., Smutny, B., Wandernoth, B., Czichy, R. & Giggenbach, D. 142 km, 5.625 Gbps free-space optical link based on homodyne BPSK modulation. Proc. SPIE 6105, 61050A1–61050A9 (2006).
Eltermann, L. UV, visible, and IR attenuation for altitudes to 50 km. Environ. Res. Pap. 285, AFCRL–68–0153 (1968).
Kurtsiefer, C. et al. Quantum cryptography: A step towards global key distribution. Nature 419, 450 (2002).
Hughes, R. J., Nordholt, J. E., Derkacs, D. & Peterson, C. G. Practical free-space quantum key distribution over 10 km in daylight and at night. New J. Phys. 4, 43 (2002).
Fried, D. L. Statistics of a geometric representation of a wavefront distortion. J. Opt. Soc. Am. 55, 1427–1435 (1965).
Clauser, J. F., Horne, M. A., Shimony, A. & Holt, R. A. Proposed experiment to test local hidden-variable theories. Phys. Rev. Lett. 23, 880–884 (1969).
Bennett, C. H., Brassard, G. & Mermin, N. D. Quantum cryptography without Bell’s theorem. Phys. Rev. Lett. 68, 557–559 (1992).
Brassard, G. & Salvail, L. EUROCRYPT ’93: Workshop on the Theory and Application of Cryptographic Techniques on Advances in Cryptology 410–423 (Lecture Notes in Computer Science, Vol. 765, Springer, New York, 1994).
Bennett, C. H., Brassard, G. & Robert, J. M. Privacy amplification by public discussion. SIAM J. Comput. 17, 210–229 (1988).
Carter, J. L. & Wegman, M. N. Universal classes of hash functions. J. Comput. Syst. Sci. 19, 143–154 (1979).
Wegman, M. N. & Carter, J. L. Proc. 20th Ann. Symp. Found. Comput. Sci. 175–182 (IEEE Computer Society, 1979).
Luetkenhaus, N. Security against individual attacks for realistic quantum key distribution. Phys. Rev. A 61, 052304 (2000).
Weinfurter, H. & Zukowski, M. Four-photon entanglement from down-conversion. Phys. Rev. A 64, 010102(R) (2001).
Bell, J. S. Free variables and local causality. Dialectica 39, 103–106 (1985).
Acknowledgements
The authors wish to thank F. Sanchez (Director IAC) and A. Alonso (IAC), T. Augusteijn and the staff of the Nordic Optical Telescope (NOT) and the staff of the Telescopio Nazionale Galileo (TNG) in La Palma for their support at the trial sites. Furthermore, we thank C. Brukner and J. Kofler for helpful discussions. This work was supported by ESA under the General Studies Programme (QIPS study, ESA contract number 18805/04/NL/HE), the Austrian Science Foundation (FWF) under project number SFB1520, the A8-Quantum information Highway project of the Bavarian High-Tech Initiative, the European projects SECOQC and QAP and the ASAP programme of the Austrian Space Agency (FFG). Additional support was provided by the ESA, the Swiss National Science Foundation (SNF) and the DOC program of the Austrian Academy of Sciences.
Author information
Authors and Affiliations
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
About this article
Cite this article
Ursin, R., Tiefenbacher, F., Schmitt-Manderbach, T. et al. Entanglement-based quantum communication over 144 km. Nature Phys 3, 481–486 (2007). https://doi.org/10.1038/nphys629
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nphys629
This article is cited by
-
Optimal entanglement distribution policies in homogeneous repeater chains with cutoffs
npj Quantum Information (2023)
-
Applications of single photons to quantum communication and computing
Nature Reviews Physics (2023)
-
Atomically-thin single-photon sources for quantum communication
npj 2D Materials and Applications (2023)
-
Training a quantum measurement device to discriminate unknown non-orthogonal quantum states
Scientific Reports (2023)
-
Optical manipulation of quantum optic entanglement using graphene clad surface plasmonic polariton device
Quantum Information Processing (2023)