Main

Experiments on ultracold Fermi gases at microkelvin temperatures are revolutionizing many areas of physics. Their exceptional simplicity allows tests of many-body theory in areas long thought to be inaccessible. The ability to widely tune the effective interaction between fermions via a broad Feshbach resonance in gases of 6Li and 40K has allowed resonance models proposed in high-Tc superconductivity theory11 to be implemented with fermionic ultracold atoms12. Fortunately, the Pauli exclusion principle stabilizes the resulting excited molecular states against collisional damping13. This has permitted the experimental observation of the smooth evolution of the Fermi gas from the attractive regime of Bardeen–Cooper–Schrieffer (BCS) superfluidity through to a regime where molecules form a Bose–Einstein condensate (BEC)14,15,16,17,18,19. On the cusp of this BCS–BEC cross-over, there is a strongly interacting regime—the so-called unitarity limit3, which leaves the interatomic distance as the only relevant length scale.

At this point, the gas is expected to show a universal thermodynamic behaviour, independent of any microscopic details of the underlying interactions. The ground-state energy E0 of a homogeneous gas at zero temperature should be proportional to the free Fermi energy, EF. Thus, E0=EF(1+β), where β is a universal many-body parameter. Substantial experimental efforts have been carried out to verify the existence of universality4,5, though so far there has been no conclusive confirmation. This is mainly due to the lack of reliable thermometry in the strongly interacting regime10, leading to an uncertainty in the finite-temperature corrections.

The universal parameters estimated from energies at the lowest accessible (but unknown) temperature range from β=−0.68±0.10 to β=−0.54±0.05 (refs 6,8,16,17). Because these are not at zero temperature, there is an unknown correction factor required to obtain the ground-state energy, and hence the true value of β. There is a similar range of estimated theoretical values, though a more precise value of β=−0.58±0.01 was recently obtained from zero-temperature quantum Monte Carlo simulations20.

This situation has dramatically improved in the most recent thermodynamic measurements on strongly interacting Fermi gases of 40K and 6Li atoms7,8, which allow accurate estimates of the energy in the universal regime from the fermionic cloud size5. In experiments on 40K carried out at JILA7, an adiabatic magnetic-field sweep is used to compare measurements of the cloud size in the strongly interacting and weakly interacting regimes, so that the non-interacting temperature is also known from the cloud size after the sweep. An important conceptual advance of the Duke group5, who use 6Li, was the realization that such sweeps give a model-independent measurement of the entropy versus energy in the strongly interacting regime, thus allowing a precision test8 of theoretical predictions of universal thermodynamics. A different approach at Rice6, also with 6Li, makes use of the detailed density distribution to estimate temperature and entropy.

These ground-breaking investigations provide measurements accurate to the level of a few per cent, which is an exceptional accuracy in this challenging field of ultralow-temperature physics.

In this letter, we re-analyse all the available experimental data from these three laboratories, thus obtaining the measured entropy–energy relation of two completely different strongly interacting trapped Fermi gases. We compare this directly with a single universal theoretical prediction. We use a diagrammatic approach based on functional path integrals9,21 together with the local density approximation to treat the inhomogeneous trap. Below the superfluid transition, our calculations include pairing fluctuations, which are important in the strongly interacting regime, owing to the onset of molecule formation. This approach is described in detail elsewhere9. Above threshold we use the well known Nozières–Schmidt–Rink (NSR) theory22,23,24. We demonstrate a quantitative test of these thermodynamic predictions by comparing experimental results on both types of atom with a single theoretical curve, as shown in Fig. 1. There are no adjustable parameters, so this provides strong evidence for universality.

Figure 1: Illustration of the universal thermodynamics of a strongly interacting Fermi gas.
figure 1

Comparison between theoretical predictions and experimental measurements on the entropy–energy (S–E) relation of strongly interacting Fermi gases in a harmonic trap. The inset highlights the low-entropy region. The energy is in units of the Fermi energy, which is the highest single-particle energy level of a non-interacting gas in the same trap with the same number of fermions, N. The brown solid curve is our theoretical prediction, and the black dash–dotted curve is the ideal-gas energy. The experimental data are on 6Li and 40K fermionic atoms, with error bars taken from the experimental papers using appropriate conversions. All results agree with a single, universal theoretical curve.

Full size image

Further, by using power-law extrapolation to estimate finite-temperature corrections, we are able to show that all the experimental data give rise to a universal many-body coefficient of β≃−0.59±0.07. This is in excellent agreement both with the Monte Carlo results20, β=−0.58±0.01, and our earlier theoretical prediction9 of β≈−0.599.

We summarize the experimental procedures, as typified by the JILA work using 40K atomic gas7. Here, the strongly interacting gas is prepared in a harmonic trap at the Feshbach resonance, and the potential energy is measured from the observed radius. Next, the magnetic field is swept adiabatically to a zero-scattering-length field, and the potential energy at this field is again measured, which gives the non-interacting temperature. From these data, we obtain the entropy of the interacting gas7, as the energy–entropy relation of a non-interacting Fermi gas is known. The total energy is also obtained, as it is twice the potential energy at the resonance, owing to the virial theorem5. Figure 2a gives the predicted potential energy ratio as a function of the non-interacting temperature in the presence of a harmonic trap, together with the experimental measurements. The observed reduction of the potential energy in the strongly interacting regime is theoretically reproduced. Converting the non-interacting temperature and the potential energy into the total entropy and energy, respectively, we obtain the entropy–energy relation for 40K gas in Fig. 2b. We find an excellent agreement between the experimental data and theoretical predictions below threshold. There is a small discrepancy just above the critical temperature of (T/TF)0≈0.25 or the critical entropy of Sc≃2.2N kB, where we expect that the above threshold NSR theory may be less reliable. This effect is clearly visible in Fig. 2a, which gives the original experimental measurements. The nonlinear transformation used to obtain the entropy–energy relation in Fig. 2b means that conventional rectangular error bars give only a qualitative indication of the uncertainties in this figure.

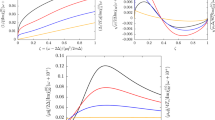
Figure 2: Analysis of the 40K experiment in JILA.
figure 2

a, Experimental data on the potential energy Epot normalized to that in the non-interacting regime Epot0 for a 40K gas at unitarity, as a function of the non-interacting gas temperature (T/TF)0. It converges to unity as expected (dashed green horizontal line). The experimental data are compared with our theoretical prediction for a harmonically trapped, strongly interacting Fermi gas. b, Comparison between theory and experiment on the entropy dependence of the energy for a unitarity gas. The experimental entropy is calculated from the non-interacting temperature, with error bars converted from the experimental data. The energy is double Epot owing to the virial theorem5.

Full size image

Next, we discuss in greater detail the 6Li experiment at Duke8, which has greater accuracy but involves some extra corrections owing to the anharmonic trap used, and residual interactions in the weakly interacting cloud. The strongly interacting Fermi gas of N=1.3(2)×105 atoms is prepared in a shallow gaussian (anharmonic) trap at a magnetic field B=840 G, slightly above the resonance position B0=834 G. Here V0 gives the trap energy scale, m is the atomic mass, and ωz are the transverse and axial trap frequencies and ρ and z are the transverse and axial coordinates of the spheroidal trap geometry. The coupling constant kFa=−30.0, where kF is the Fermi wavevector and a is the s-wave interatomic scattering length, is sufficiently large to ensure the onset of the universal thermodynamic behaviour. Experimentally, the entropy of the gas is measured by an adiabatic passage to a weak interacting field B=1,200 G, where kFa=−0.75 and the entropy and temperature are known from the cloud size after the sweep. The energy E is determined model independently from the mean square radius of the strongly interacting fermion cloud 〈z2〉840 measured at 840 G, according to the virial theorem5,8,

where is the Fermi energy for an ideal harmonically trapped gas at the trap centre, and zF2 is defined by 3m ωz2zF2≡EF. The correction factor 1−κ accounts for the anharmonicity in the shallow trapping potential V0≃10EF.

Figure 3a shows the bare experimental data on the ratio of the mean square axial cloud size at 1,200 G to that at 840 G, as a function of the energy at 840 G, as compared with the theoretical simulations with the same realistic parameters, except that we use a resonance field B0 for the strongly interacting gas. Good agreement is found, with no free parameters. As before, there is a small discrepancy between the raw data and theoretical predictions, just above the critical energy. We have recalculated the entropy corrections due to residual interactions in the 1,200 G cloud to improve the accuracy at the 1% level, by using an above-threshold NSR theory. Calibration of the entropy from the measured mean square axial cloud size at 1,200 G using the theoretically predicted dependence of the entropy on the size (inset in Fig. 3b) leads to the comparison for the entropy–energy relation, as shown in Fig. 3b. The agreement is even more impressive.

Figure 3: Analysis of the 6Li experiment at Duke.
figure 3

a, Experimental data on the ratio of the mean square cloud size at 1,200 G, 〈z2〉1,200, to that at 840 G, 〈z2〉840, for a 6Li gas, as a function of total energy, are compared to the theoretical simulations. The data are obtained by an adiabatic passage from a strongly interacting field B=840 G to a weakly interacting field B=1,200 G. The total energy is measured at 840 G by using the virial theorem, and is normalized with respect to the Fermi energy of a non-interacting gas. The theoretical curve is calculated under the same procedure and parameters, except that the starting field is at the Feshbach resonance B=834 G. As shown by the dashed green horizontal line, the ratio converges to unity at high energy as the gas becomes more ideal. The arrow points to the theoretically predicted energy at the transition point. b, Experimental data on the entropy dependence of the energy for a strongly interacting gas at 840 G, compared with the predictions from our strong-interaction theory. The result for an ideal gas is also plotted. The entropy and error bars of the gas are calibrated from the experimental mean square axial cloud size 〈z2〉1,200, using our theoretical dependence of the entropy on the cloud size (as shown in the inset), which should be extremely accurate in the weakly interacting regime.

Full size image

We can now describe the procedures used to obtain Fig. 1, which illustrates the universal thermodynamic behaviour of a strongly interacting Fermi gas. Here we have plotted all the measured data in a single figure, and compared them with our prediction for the entropy dependence of the energy of a harmonically trapped, strongly interacting Fermi gas, as well as that of an ideal Fermi gas. The slight shift of the experimental data in the Duke experiment due to the anharmonicity of the trap has been corrected, by subtracting the (small) theoretical difference between a shallow gaussian trap and a harmonic trap for the energy at the same entropy. We also plot a single data point from the 6Li experiment at Rice6 for the energy at their lowest entropy. The agreement between theory and experiment is excellent for almost all the measured data. Exactly the same theory is used in all cases, with results from three different laboratories6,7,8. The universal thermodynamics of a strongly interacting Fermi gas is strikingly demonstrated, independently of which atomic species we compare with.

Just above the critical entropy Sc≃2.2N kB, for the superfluid–normal-fluid phase transition, there is a suggestion of a discrepancy between theoretical predictions and these precise measurements. At this point the above-threshold NSR theory is least accurate10. The data here may even indicate a first-order superfluid phase transition. We note that the exact order of phase transition for a strongly interacting Fermi gas is still an open question25, and merits further investigation.

A key feature of current ultracold Fermi-gas experiments is that the lowest attainable entropy is around S=0.7N kB, which corresponds to a temperature of 0.10–0.15TF at unitarity. This non-zero entropy or temperature affects the precise determination of the universal many-body parameter β. To remove the temperature dependence, we assume that in the low-entropy regime (below the phase transition) there is a power-law dependence of the energy on the entropy: E−E0∝Sα, as anticipated theoretically. For non-interacting Fermi and Bose gases, the power-law exponents are 2 and 4/3, respectively. The thermodynamics of a unitary gas should lie between an ideal Fermi gas and an ideal Bose–Einstein condensate. The fitting procedure leads to E0/(N EF)=0.48±0.03 and E0/(N EF)=0.48±0.04, for the Duke and JILA experiments, respectively, with a similar power-law exponent α=1.7±0.4. Here the error bar accounts only for the fitting error. Using the relation E0/N=(3/4)(1+β)1/2EF for a harmonic trap4, this gives rise to β≃−0.59±0.07: which agrees fairly well with the most accurate quantum Monte Carlo simulations20, β=−0.58±0.01, and our theoretical prediction9, β≈−0.599. Our theoretical power-law prediction is α=1.5 in the LDA regime, which also agrees with experiment.

Methods

We briefly explain our analytic theory. This is an approximate method using perturbation theory summed to all orders, because no exact results are known. In the homogeneous gas case, it relies on the many-body T-matrix approximation to account for the effects of collective Bogoliubov–Anderson modes, and extends the standard NSR approach to the broken-symmetry state9. This amounts to considering the contributions of gaussian fluctuations around the mean-field saddle point to the thermodynamic potential (with Nambu notation),

where

are respectively the diagonal and off-diagonal parts of the pair propagator. Here, Q=(q,i νn), K=(k,i ωm), and (q and k are wavevectors, νn and ωm bosonic and fermionic Matsubara frequencies, respectively), m is the fermion mass, T the temperature, and εk=ℏ2k2/2m, G11 and G12 are BCS Green functions with a variational order parameter Δ. Together with the mean-field contribution

with excitation energy Ek=[(εk−μ)2+Δ2]1/2 and Fermi distribution function f(x)=1/(1+ex/kBT), we obtain the full thermodynamic potential Ω=Ωmf+Ωpf. All the observables are calculated straightforwardly following the thermodynamic relations, once the chemical potential μ and the order parameter Δ are determined. Number conservation in the form n=−∂ Ω/∂ μ is strictly satisfied, yielding an exact identity for the pressure P and energy density U of a unitarity gas: P=2U/3 (refs 3,5). For simplicity, in our calculations we determine the order parameter at the level of the mean field, using the gap equation ∂ Ωmf/∂ Δ=0. Part of our approach was also previously derived using a functional integral method21. In the case of the normal Fermi liquid with vanishing order parameter, the usual NSR formalism is recovered22.

This type of perturbation theory with bare BCS Green functions in the pair propagators constitutes the simplest description of the BCS–BEC cross-over, including the essential pair fluctuations. More sophisticated approximations with dressed Green functions in the pair propagators, that is, the G G0 (ref. 26) and the fully self-consistent G G schemes27,28, have also been proposed. In ref. 10, we carried out a comparative study of these different approximation schemes for a unitarity gas in the normal state. A related calculation in the superfluid phase has also been carried out recently25. Compared with the latest path-integral Monte Carlo simulations29,30, our analytic perturbation scheme seems to be the optimal choice for the calculations of the type required for the entropy–energy relation. However, there is a small region around the critical temperature where none of the current calculations are reliable, and we see indications of this in the data.

To include the effects of the trap, we use the local-density approximation by assuming that the system can be treated as locally uniform, with a position-dependent local chemical potential μ(r)=μ−V (r), where V (r) is the trapping potential. The local entropy and energy, calculated directly from the local thermodynamic potential using thermodynamic relations, are then summed to give the total entropy and energy. We note that in the presence of a harmonic trap the exact identity P=2U/3 yields the virial theorem5, which states that the potential energy of the gas is a half of its total energy.