Nearly ferromagnetic Fermi-liquid behaviour in YFe₂Zn₂₀ and high-temperature ferromagnetism of GdFe₂Zn₂₀

Abstract

One of the historic goals of alchemy was to turn base elements into precious ones. Although the practice of alchemy has been superseded by chemistry and solid-state physics, the desire to dramatically change or tune the properties of a compound, preferably through small changes in stoichiometry or composition, remains. This desire becomes even more compelling for compounds that can be tuned to extremes in behaviour. Here, we report that the RT₂Zn₂₀ (R=rare earth and T=transition metal) family of compounds manifests exactly this type of versatility, even though they are more than 85% Zn. By tuning T, we find that YFe₂Zn₂₀ is closer to ferromagnetism than elemental Pd, the classic example of a nearly ferromagnetic Fermi liquid. By submerging Gd in this highly polarizable Fermi liquid, we tune the system to a remarkably high-temperature ferromagnetic (T_C=86 K) state for a compound with less than 5% Gd. Although this is not quite turning lead into gold, it is essentially tuning Zn to become a variety of model compounds.

Main

The field of condensed-matter physics has been interested in the effects of electron correlations from its inception^1,2. To this day, the properties of elemental Fe as well as Pd continue to present problems that interest both experimentalists as well as theorists³. Materials such as Pd or Pt, that are just under the Stoner limit (often referred to as nearly ferromagnetic Fermi liquids), or materials just over the Stoner limit, such as ZrZn₂ or Sc₃In on the ferromagnetic side, are of particular interest^1,2,3. Of even greater interest are new examples of nearly ferromagnetic Fermi liquids that can be tuned with a greater degree of ease than the pure elements: that is, those that can accommodate controlled substitutions on a number of unique crystallographic sites in a manner that allows for (1) a tuning of the band filling/Fermi surface and (2) the introduction of local-moment-bearing ions onto a unique crystallographic site. Such a versatile system would open the field to a greater range of experimental studies of strongly correlated electronic states as well as potentially allowing for more detailed studies of quantum criticality and possibly even novel superconducting states.

Here, we present our first results of an extensive study of the dilute, rare-earth-bearing, intermetallic series RT₂Zn₂₀ (R=rare earth and T=transition metal) that supports a wide range of R ions for T in and near the Fe, Co and Ni columns of the periodic table. In particular, we will show how YFe₂Zn₂₀ is an archetypical example of a nearly ferromagnetic Fermi liquid and how, by embedding Gd ions into this highly polarizable medium, GdFe₂Zn₂₀ can have a remarkably high ferromagnetic ordering temperature of 86 K, even though it contains less than 5% atomic Gd and the Fe is not moment-bearing in the paramagnetic state.

The RT₂Zn₂₀ series of compounds was discovered in 1997 by Nasch et al. ⁴ and is isostructural to the cubic CeCr₂Al₂₀ structure ( space group)^5,6. The rare-earth and transition-metal ions each occupy their own single, unique crystallographic sites (8a and 16d respectively), whereas the Zn ions have three unique crystallographic sites (96g, 48f and 16c). In addition, the rare-earth site is one of cubic point symmetry (). The coordination polyhedra for R and T consist fully of Zn, meaning that there are no R–R, T–T or R–T nearest neighbours and the shortest R–R spacing is ∼6 Å. The lattice parameters for the series are ∼14 Å. Although the crystallography of this series was well detailed, so far, there have been no measurements of these compounds’ physical properties. This, to some extent, is not unexpected because the limited data sets available on the RT₂Al₂₀ compounds^6,7 indicated very low ordering temperatures, consistent with the very low R concentrations.

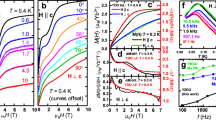
Figures 1 and 2 show the temperature-dependent electrical resistivity, specific heat and low-field magnetization data, as well as anisotropic M(H) data, for GdFe₂Zn₂₀ and GdCo₂Zn₂₀. There are two conspicuous differences between the physical properties of these compounds: (1) GdFe₂Zn₂₀ orders ferromagnetically, whereas GdCo₂Zn₂₀ orders antiferromagnetically and (2) GeFe₂Zn₂₀ orders at a remarkably high temperature of T_C=86 K, whereas GdCo₂Zn₂₀ orders at the more representative T_N=5.7 K. From Fig. 2a, the high-temperature Curie constant can be determined, giving effective moments (8.05μ_B and 8.15μ_B for T=Fe and T=Co respectively) consistent with the effective moment of Gd³⁺, indicating that, in the paramagnetic state, there is little or no contribution from the transition metal. The saturated moment deduced from the data in Fig. 2b is close to that associated with Gd³⁺; slightly lower for GdFe₂Zn₂₀ and slightly higher for GdCo₂Zn₂₀. The magnetic entropy associated with each phase transition is approximately Rln 8 (where R is the gas constant), with more uncertainty associated with the subtraction of the YT₂Zn₂₀ data for T=Fe than for T=Co owing to the much higher ordering temperature. The remarkably high ordering temperature found for GdFe₂Zn₂₀ is not unique to the R=Gd member of the RFe₂Zn₂₀ series. For R=Gd–Tm, transitions to ferromagnetically ordered states occur at temperatures that roughly scale with the de Gennes parameter (T_C≈86,57,46,29,11,5 K for R=Gd, Tb, Dy, Ho, Er, Tm respectively).

Figure 1: Temperature-dependent specific heat, resistivity and low-field (H=1,000 Oe) magnetization divided by applied field for two GdT₂Zn₂₀ compounds.

a, GdFe₂Zn₂₀; the full scale represents 30 e.m.u. mol⁻¹, 500 J mol⁻¹ K⁻¹ and 1.0 for M/H, specific heat (C_p) and normalized electrical resistivitiy (ρ(T)/ρ(300 K)), respectively. b, GdCo₂Zn₂₀; the full scale represents 1.4 e.m.u. mol⁻¹, 50 J mol⁻¹ K⁻¹ and 0.20 for M/H, C_p and ρ(T)/ρ(300 K), respectively. For GdFe₂Zn₂₀, ρ(300 K)=73 μΩ cm and for GdCo₂Zn₂₀,ρ(300 K)=60 μΩ cm.

Figure 2: Magnetic properties of GdFe₂Zn₂₀ and GdCo₂Zn₂₀ compounds.

a, H/M as a function of T (the lines show the region used for the high-temperature Curie–Weiss fit). Inset: A single crystal of YFe₂Zn₂₀ next to a millimetre scale. b, Anisotropic M(H) (T=1.85 K). For each sample, measurements for , and are shown.

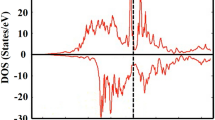
To better understand this conspicuous difference in ordering temperatures, band-structure calculations were carried out. Figure 3 shows the density of states as a function of energy for both LuFe₂Zn₂₀ and LuCo₂Zn₂₀. The upper curve in each panel shows the total density of states, whereas the lower curve shows the density of states associated with the transition-metal ion. It should be noted that the difference between LuFe₂Zn₂₀ and LuCo₂Zn₂₀ density of states can be rationalized in terms of the rigid band approximation, with the Fermi level for LuCo₂Zn₂₀ being ∼0.3 eV higher than that for LuFe₂Zn₂₀, associated with the two extra electrons per formula unit. Calculations done on YFe₂Zn₂₀ and GdFe₂Zn₂₀ as well as on YCo₂Zn₂₀ and GdCo₂Zn₂₀ lead to similar density of states curves and further analysis of the GdFe₂Zn₂₀ and GdCo₂Zn₂₀band-structural results leads to the prediction that for GdFe₂Zn₂₀ the ground state will be ferromagnetic with a total saturated moment of approximately 6.8μ_B (with a small induced moment on the Fe opposing the Gd moment) and for GdCo₂Zn₂₀ the saturated moment will be 7.15μ_B (with practically no induced moment on Co). These results are consistent with the saturated values of the magnetization seen in Fig. 2b.

Figure 3: Density of states as a function of energy for LuFe₂Zn₂₀ and LuCo₂Zn₂₀.

The upper curve shows total density, whereas the lower curve shows the partial density of states associated with Fe or Co.

These calculations indicate that the RFe₂Zn₂₀ compounds should manifest a higher electronic density of states at the Fermi level, N(E_F), than the RCo₂Zn₂₀ analogues and raise the question of whether or not this is the primary reason for the remarkably high T_C found for GdFe₂Zn₂₀. In addition, they raise the question of how correlated the electronic state is in the nominally non-magnetic Lu- or Y-based analogues. To address these questions, two substitutional series were grown: Y(Fe_xCo_1−x)₂Zn₂₀ and Gd(Fe_xCo_1−x)₂Zn₂₀. Figure 4 shows thermodynamic data taken on the Y(Fe_xCo_1−x)₂Zn₂₀ series. For x=0, the low-temperature, linear component of the specific heat (γ) is relatively small (19 mJ mol⁻¹ K⁻²) and the susceptibility is weakly paramagnetic and essentially temperature independent. As x is increased, there is a monotonic (but clearly super-linear) increase in the samples’ paramagnetism as well as, for larger x values, an increase in the low-temperature γ values. For YFe₂Zn₂₀ (x=1), the value of γ has increased to over 250% of that for YCo₂Zn₂₀ and the susceptibility has become both large and temperature dependent. Figure 5 shows data on the analogous Gd(Fe_xCo_1−x)₂Zn₂₀ series. As x is increased, the ground state rapidly becomes ferromagnetic (only x=0 was antiferromagnetic) and the transition temperature increases monotonically (but again in a super-linear fashion) and the high-field, saturated magnetization decreases weakly, in a monotonic fashion.

Figure 4: Thermodynamic properties of the Y(Fe_xCo_1−x)₂Zn₂₀ series.

a, Temperature-dependent magnetic susceptibility. Inset: Temperature dependence of paramagnetic Θ for GdFe₂Zn₂₀ (see text). b, Low-temperature C/T as a function of T². c, Linear coefficient of the specific heat, γ, magnetic susceptibility for T→0 corrected for core diamagnetism (−2.3×10⁻⁴ e.m.u. mol⁻¹ for Y(Fe_xCo_1−x)₂Zn₂₀ using table 5.7 (p. 306) of ref. 9), χ₀, and Stoner enhancement factor, Z, as a function of Fe concentration, x. The full scale represents 60 mJ mol⁻¹ K⁻², 6.5×10⁻³ e.m.u. mol⁻¹ and 1.0 for γ, χ₀ and Z respectively. Inset: Ratio χ₀/γ versus x.

Figure 5: Magnetic ordering temperature in the Gd(Fe_xCo_1−x)₂Zn₂₀ series as a function of Fe concentration x.

Note that data from two samples of x=0.88 are shown. Inset: M_sat as a function of x Fe.

Taken together, Figs 4 and 5 demonstrate a clear correlation between x, the linear component of the electronic specific heat, the enhanced magnetic susceptibility of the Y-based series and the Curie temperature and the saturated magnetization of the Gd-based series. This correlation can be more clearly seen if the relation between the linear component of the specific heat and the low-temperature susceptibility of the Y-based series is placed in the context of a nearly ferromagnetic Fermi liquid: that is, if the Stoner enhancement parameter, Z, for each member of the series can be determined⁸. For such systems, the static susceptibility (corrected for the core diamagnetism⁹) is χ=χ₀/(1−Z), where χ₀=μ_BN(E_F). Given that the linear component of the specific heat is given by γ₀=(πk_B)²N(E_F)/3, if both the low-temperature specific heat and magnetic susceptibility can be measured, then the parameter Z can be deduced (Z=1−(3μ_B²/π²k_B²)(γ₀/χ₀)), where k_B and μ_B are the Boltzmann constant and the Bohr magneton respectively. The canonical example of such a system is elemental Pd for which, using data from ref. 10, Z=0.83. For YFe₂Zn₂₀, Z=0.89, a value that places it even closer to the Stoner limit than Pd. It should be noted that the temperature-dependent susceptibility of YFe₂Zn₂₀ is also remarkably similar to that of Pd (see ref. 3 and references therein). The x dependence of the experimentally determined values of γ and χ(T=0), as well as the inferred value of Z, for the Y(Fe_xCo_1−x)₂Zn₂₀ series is plotted in Fig. 4c. By choosing x, Y(Fe_xCo_1−x)₂Zn₂₀ can be tuned from being exceptionally close to the Stoner limit to being well removed from it. Corrections to these inferred Z values coming from the difference between the measured electronic specific heat coefficient, γ, and the Sommerfeld coefficient, γ₀, where γ=γ₀(1+λ) only serves to slightly increase Z because λ, the electron mass enhancement parameter, is positive definite. By comparing the γ₀ inferred from the band structure to our measured values of γ, we can estimate λ=0.85 and 0.22 for x=1 and x=0 respectively, and this shifts Z to 0.94 for YFe₂Zn₂₀ and to 0.50 for YCo₂Zn₂₀. The Wilson ratio, R, which is proportional to χ₀/γ apparently increases drastically approaching the Fe end in the Y(Fe_xCo_1−x)₂Zn₂₀ series (Fig. 4c, inset).

When the non-magnetic Y ion is replaced by the large Heisenberg moment associated with the S=7/2Gd³⁺ ion, as x is varied from zero to one in the Gd(Fe_xCo_1−x)₂Zn₂₀ series, the Gd local moments will be in an increasingly polarizable matrix, one that is becoming a nearly ferromagnetic Fermi liquid. This results in an increasingly strong coupling between the Gd local moments as x is increased. Figure 5 shows the x dependence of T_C and μ_sat for the Gd(Fe_xCo_1−x)₂Zn₂₀. The value of T_C increases in a monotonic but highly nonlinear fashion in a manner reminiscent of the behaviour associated with the increasingly polarizability of Y(Fe_xCo_1−x)₂Zn₂₀ seen in Fig. 4c. The μ_sat value for the field applied along the [111] direction varies systematically from the slightly enhanced value of 7.3 μ_B found for GdCo₂Zn₂₀ to the slightly deficient value of 6.5 μ_B found for GdFe₂Zn₂₀.

In addition to x dependence, this conceptually simple and compelling framework can also be used to understand the rather curious temperature dependence of the 1/χ versus T data for GdFe₂Zn₂₀ seen in Fig. 2a. As T is decreased, the electronic background that the Gd³⁺ ion is immersed in becomes increasingly polarizable (as shown in Fig. 4a for x=1), leading to a temperature-dependent coupling that in turn leads to the nonlinearity of the 1/χ versus T data. If a constant effective moment for the Gd³⁺ is assumed, then a temperature-dependent, paramagnetic Θ can be extracted from the data in Fig. 2a: χ(T)=χ₀+C/(T−Θ). This temperature-dependent Θ, shown in Fig. 4a, tracks the electronic susceptibility of the YFe₂Zn₂₀ remarkably well, both increasing by ∼1.7 on cooling from 300 to 100 K.

One consequence of placing Gd ions into a matrix so close to the Stoner limit is an enhanced sensitivity to small sample-to-sample variations. This is most clearly illustrated by the data for the Gd(Fe_0.88Co_0.12)₂Zn₂₀ samples shown in Fig. 5. Although the samples have the same nominal composition, there is a clear difference in their transition temperatures. However, this difference is not too significant given the large dT_C/dx slope seen in Fig. 5. On the other hand, measurements on four separate samples of Gd(Fe_0.25Co_0.75)₂Zn₂₀ did not show any significant variations in T_C. Such sensitivity of correlated electron states to small disorder is not uncommon, giving rise to significant variation in measured T_C for samples of Sc₃In and ZrZn₂ (ref. 1) as well as dramatic changes in the transport properties of heavy fermions such as YbNi₂B₂C (refs 11, 12, 13).

The broader RT₂Zn₂₀ family of compounds offers an even larger phase space for the study of correlated electron physics (for T=Fe, Ru and Os as well as for R=Yb and Ce)¹⁴ and for the study of local-moment physics, all in the limit of a dilute, rare-earth-bearing, intermetallic series. The study of these compounds is a topic of ongoing research and promises to be a fruitful new phase space for several years to come.

Methods

Single crystals of RFe₂Zn₂₀, RCo₂Zn₂₀ and R(Fe_xCo_1−x)₂Zn₂₀ (R=Gd, Y) were grown from high-temperature solutions¹⁵ rich in Zn using initial compositions of R₂T₄Zn₉₄. The constituent elements were placed in an alumina crucible, sealed in a quartz ampule under ∼1/3 atmosphere Ar and heated in a box furnace to 1,000 ^∘C and then slowly cooled to 600 ^∘C over up to 100 h. The resulting single crystals were large and often manifested clear [111] facets (see Fig. 2a, inset). For R(Fe_xCo_1−x)₂Zn₂₀, x values are nominal values, but these are confirmed by elemental analysis as well as compliance with Vegard’s law, with the lattice parameter varying linearly between the x=0 and 1 end points. Field- and temperature-dependent magnetization measurements were made using Quantum Design magnetic property measurement system units, whereas transport and specific-heat measurements were made using Quantum Design physical property measurement system units with ³He options. The electronic band structure was calculated using the atomic sphere approximation tight-binding linear muffin-tin orbital method^16,17 within the local density approximation with Barth–Hedin¹⁸ exchange correlation using the experimental values of the lattice parameters. The number of atoms in the reduced unit cell is 46. A mesh of 16 k points in the irreducible part of the Brillouin zone was used. The 4f electrons of Gd and Lu atoms were treated as core states (polarized in the case of Gd atoms).