Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

  • Article
  • Published:

Finite-temperature phase diagram of a polarized Fermi condensate

Nature Physics volume 3, pages 124–128 (2007)Cite this article

Abstract

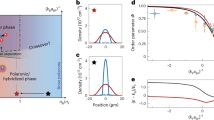
The two-component Fermi gas is the simplest fermion system exhibiting superfluidity, and as such is relevant to topics ranging from superconductivity to quantum chromodynamics. Ultracold atomic gases provide an exceptionally clean realization of this system, where interatomic interactions and atom spin populations are both independently tuneable. Here we show that the finite-temperature phase diagram contains a region of phase separation between the superfluid and normal states that touches the boundary of second-order superfluid transitions at a tricritical point, reminiscent of the phase diagram of 3He–4He mixtures. A variation of interaction strength then results in a line of tricritical points that terminates at zero temperature on the molecular Bose–Einstein condensate side. On this basis, we argue that tricritical points are fundamental to understanding experiments on polarized atomic Fermi gases.

This is a preview of subscription content, access via your institution

Access options

Buy this article

  • Purchase on Springer Link
  • Instant access to full article PDF
Buy now

Prices may be subject to local taxes which are calculated during checkout

Figure 1: The zero-temperature phase diagram within mean-field theory for both Zeeman field h/ɛF and magnetization m/n (inset) versus interaction 1/kFa.
Figure 2: Finite-temperature phase diagram as a function of magnetization m/n and interaction 1/kFa.
Figure 3: Finite-temperature phase diagram for the two-channel model of a narrow Feshbach resonance, where the coupling between open and closed channels is weak: γ=0.1.
Figure 4: Phase diagram at 1/kFa=0 in the μ/h–T/h plane.

Similar content being viewed by others

References

  1. Regal, C. A., Greiner, M. & Jin, D. S. Observation of resonance condensation of fermionic atom pairs. Phys. Rev. Lett. 92, 040403 (2004).

    Article  ADS  Google Scholar 

  2. Zwierlein, M. W. et al. Condensation of pairs of fermionic atoms near a Feshbach resonance. Phys. Rev. Lett. 92, 120403 (2004).

    Article  ADS  Google Scholar 

  3. Chin, C. et al. Observation of the pairing gap in a strongly interacting Fermi gas. Science 305, 1128–1130 (2004).

    Article  ADS  Google Scholar 

  4. Bourdel, T. et al. Experimental study of the BEC-BCS crossover region in lithium 6. Phys. Rev. Lett. 93, 050401 (2004).

    Article  ADS  Google Scholar 

  5. Kinast, J., Hemmer, S. L., Gehm, M. E., Turlapov, A. & Thomas, J. E. Evidence for superfluidity in a resonantly interacting Fermi gas. Phys. Rev. Lett. 92, 150402 (2004).

    Article  ADS  Google Scholar 

  6. Zwierlein, M. W., Abo-Shaeer, J. R., Schirotzek, A., Schunck, C. H. & Ketterle, W. Vortices and superfluidity in a strongly interacting Fermi gas. Nature 435, 1047–1051 (2005).

    Article  ADS  Google Scholar 

  7. Fulde, P. & Ferrell, R. A. Superconductivity in a strong spin-exchange field. Phys. Rev. 135, A550–A563 (1964).

    Article  ADS  Google Scholar 

  8. Larkin, A. I. & Ovchinnikov, Yu. N. Inhomogeneous state of superconductors. Sov. Phys. JETP 20, 762–769 (1965).

    MathSciNet  Google Scholar 

  9. Sedrakian, A., Mur-Petit, J., Polls, A. & Müther, H. Pairing in a two-component ultracold Fermi gas: Phases with broken-space symmetries. Phys. Rev. A 72, 013613 (2005).

    Article  ADS  Google Scholar 

  10. Zwierlein, M. W., Schirotzek, A., Schunck, C. H. & Ketterle, W. Fermionic superfluidity with imbalanced spin populations. Science 311, 492–496 (2006).

    Article  ADS  Google Scholar 

  11. Partridge, G. B., Li, W., Kamar, R. I., Liao, Y. & Hulet, R. G. Pairing and phase separation in a polarized Fermi gas. Science 311, 503–505 (2006).

    Article  ADS  Google Scholar 

  12. Zwierlein, M. W., Schunck, C. H., Schirotzek, A. & Ketterle, W. Direct observation of the superfluid phase transition in ultracold Fermi gases. Nature 442, 54–58 (2006).

    Article  ADS  Google Scholar 

  13. Shin, Y., Zwierlein, M. W., Schunck, C. H., Schirotzek, A. & Ketterle, W. Observation of phase separation in a strongly-interacting imbalanced Fermi gas. Phys. Rev. Lett. 97, 030401 (2006).

    Article  ADS  Google Scholar 

  14. Bedaque, P. F., Caldas, H. & Rupak, G. Phase separation in asymmetrical Fermion superfluids. Phys. Rev. Lett. 91, 247002 (2003).

    Article  ADS  Google Scholar 

  15. Carlson, J. & Reddy, S. Asymmetric two-component Fermion systems in strong coupling. Phys. Rev. Lett. 95, 060401 (2005).

    Article  ADS  Google Scholar 

  16. Pao, C.-H., Wu, S.-T. & Yip, S.-K. Superfluid stability in BEC-BCS crossover. Phys. Rev. B 73, 132506 (2005).

    Article  ADS  Google Scholar 

  17. Son, D. T. & Stephanov, M. A. Phase diagram of cold polarized Fermi gas. Phys. Rev. A 74, 013614 (2005).

    Article  ADS  Google Scholar 

  18. Mizushima, T., Machida, K. & Ichioka, M. Direct imaging of spatially modulated superfluid phases in atomic Fermion systems. Phys. Rev. Lett. 94, 060404 (2005).

    Article  ADS  Google Scholar 

  19. Sheehy, D. E. & Radzihovsky, L. BEC-BCS crossover in “magnetized” Feshbach-resonantly paired superfluids. Phys. Rev. Lett. 96, 060401 (2006).

    Article  ADS  Google Scholar 

  20. Mannarelli, M., Nardulli, G. & Ruggieri, M. Evaluating the phase diagram of superconductors with asymmetric spin populations. Phys. Rev. A 74, 033606 (2006).

    Article  ADS  Google Scholar 

  21. Pieri, P. & Strinati, G. C. Trapped fermions with density imbalance in the Bose–Einstein condensate limit. Phys. Rev. Lett. 96, 150404 (2005).

    Article  Google Scholar 

  22. Liu, X.-J. & Hu, H. BCS-BEC crossover in an asymmetric two-component Fermi gas. Europhys. Lett. 75, 364–370 (2006).

    Article  ADS  Google Scholar 

  23. Hu, H. & Liu, X.-J. Mean-field phase diagrams of imbalanced Fermi gases near a Feshbach resonance. Phys. Rev. A 73, 051603 (2006).

    Article  ADS  Google Scholar 

  24. Chien, C.-C., Chen, Q., He, Y. & Levin, K. Intermediate-temperature superfluidity in an atomic Fermi gas with population imbalance. Phys. Rev. Lett. 97, 090402 (2006).

    Article  ADS  Google Scholar 

  25. Gu, Z.-C., Warner, G. & Zhou, F. Fermion pairing with population imbalance: Energy landscape and phase separation in a constrained Hilbert subspace. Preprint at <http:/www.arxiv.org/cond-mat/0603091> (2006).

  26. Martikainen, J.-P. Ultracold polarized Fermi gas at intermediate temperatures. Phys. Rev. A 74, 013602 (2006).

    Article  ADS  Google Scholar 

  27. Iskin, M. & Sá de Melo, C. A. R. Two-species fermion mixtures with population imbalance. Phys. Rev. Lett. 97, 100404 (2006).

    Article  ADS  Google Scholar 

  28. De Silva, T. N. & Mueller, E. J. Profiles of near-resonant population-imbalanced trapped Fermi gases. Phys. Rev. A 73, 051602 (2006).

    Article  ADS  Google Scholar 

  29. Haque, M. & Stoof, H. T. C. Pairing of a trapped resonantly interacting fermion mixture with unequal spin populations. Phys. Rev. A 74, 011602 (2006).

    Article  ADS  Google Scholar 

  30. Yi, W. & Duan, L.-M. Trapped fermions across a Feshbach resonance with population imbalance. Phys. Rev. A 73, 031604 (2006).

    Article  ADS  Google Scholar 

  31. Kinnunen, J., Jensen, L. M. & Törmä, P. Strongly interacting Fermi gases with density imbalance. Phys. Rev. Lett. 96, 110403 (2006).

    Article  ADS  Google Scholar 

  32. Noziéres, P. & Schmitt-Rink, S. Bose condensation in an attractive fermion gas: From weak to strong coupling superconductivity. J. Low Temp. Phys. 59, 195–211 (1985).

    Article  ADS  Google Scholar 

  33. Sarma, G. On the influence of a uniform exchange field acting on the spins of the conduction electrons in a superconductor. J. Phys. Chem. Solids 24, 1029–1032 (1963).

    Article  ADS  Google Scholar 

  34. Casalbuoni, R. & Nardulli, G. Inhomogeneous superconductivity in condensed matter and QCD. Rev. Mod. Phys. 76, 263–320 (2004).

    Article  ADS  Google Scholar 

  35. Combescot, R. & Mora, C. The low-temperature Fulde-Ferrell-Larkin-Ovchinnikov phases in 3 dimensions. Europhys. Lett. 68, 79–85 (2004).

    Article  ADS  Google Scholar 

  36. Andreev, A. V., Gurarie, V. & Radzihovsky, L. Nonequilibrium dynamics and thermodynamics of a degenerate Fermi gas across a Feshbach resonance. Phys. Rev. Lett. 93, 130402 (2004).

    Article  ADS  Google Scholar 

  37. Timmermans, E., Furuya, K., Milonni, P. W. & Kerman, A. K. Prospect of creating a composite Fermi-Bose superfluid. Phys. Lett. A 285, 228–233 (2001).

    Article  ADS  Google Scholar 

  38. Holland, M., Kokkelmans, S. J. J. M. F., Chiofalo, M. L. & Walser, R. Resonance superfluidity in a quantum degenerate Fermi gas. Phys. Rev. Lett. 87, 120406 (2001).

    Article  ADS  Google Scholar 

  39. Chevy, F. Density profile of a trapped strongly interacting Fermi gas with unbalanced spin populations. Phys. Rev. Lett. 96, 130401 (2006).

    Article  ADS  Google Scholar 

  40. De Silva, T. N. & Mueller, E. J. Surface tension in unitary Fermi gases with population imbalance. Phys. Rev. Lett. 97, 070402 (2006).

    Article  ADS  Google Scholar 

  41. Yi, W. & Duan, L.-M. Detecting the breached-pair phase in a polarized ultracold Fermi gas. Phys. Rev. Lett. 97, 120401 (2006).

    Article  ADS  Google Scholar 

  42. Altman, E., Demler, E. & Lukin, M. D. Probing many-body states of ultracold atoms via noise correlations. Phys. Rev. A 70, 013603 (2004).

    Article  ADS  Google Scholar 

  43. Gubbels, K. B., Romans, M. W. J. & Stoof, H. T. C. Sarma phase in trapped unbalanced Fermi gases. Phys. Rev. Lett. 97, 210402 (2006).

    Article  ADS  Google Scholar 

  44. Partridge, G. B. et al. Deformation of a trapped Fermi gas with unequal spin populations. Phys. Rev. Lett. 97, 190407 (2006).

    Article  ADS  Google Scholar 

Download references

Acknowledgements

We are grateful to P. B. Littlewood for stimulating discussions and J. Keeling for help with the numerics. This work has been supported by the EPSRC.

Author information

Authors and Affiliations

  1. Cavendish Laboratory, J J Thomson Avenue, Cambridge CB3 0HE, UK

    M. M. Parish, F. M. Marchetti & B. D. Simons

  2. Rudolf Peierls Centre for Theoretical Physics, 1 Keble Road, Oxford OX1 3NP, UK

    A. Lamacraft

  3. All Souls College, Oxford OX1 4AL, UK

    A. Lamacraft

Authors
  1. M. M. Parish
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. F. M. Marchetti
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. A. Lamacraft
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. B. D. Simons
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to M. M. Parish.

Ethics declarations

Competing interests

The authors declare no competing financial interests.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Parish, M., Marchetti, F., Lamacraft, A. et al. Finite-temperature phase diagram of a polarized Fermi condensate. Nature Phys 3, 124–128 (2007). https://doi.org/10.1038/nphys520

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1038/nphys520

This article is cited by

Search

Advanced search

Quick links

Nature Briefing

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing